샤논-파노 부호화

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 명칭
3. 섀넌 부호화 (Predefined Word Lengths)
4. 패노 부호화 (Binary Splitting)
5. 다른 부호화 방법과의 비교
- 5.1. 허프만 부호화 (Huffman Coding)
- 5.2. 허프만 부호화의 예시
참조

1. 개요

섀넌-파노 부호화는 클로드 섀넌과 로버트 패노의 이름을 따서 명명되었으며, 정보를 압축하는 데 사용되는 접두 부호 방식이다. 섀넌 부호화와 패노 부호화는 서로 다른 알고리즘을 사용하지만, 두 방식 모두 섀넌-파노 부호화로 불린다. 섀넌 부호화는 미리 정의된 단어 길이를 사용하고, 패노 부호화는 확률의 이진 분할을 사용한다. 섀넌 부호화는 기호의 확률에 따라 부호어 길이를 결정하고, 누적 확률을 사용하여 부호어를 할당한다. 패노 부호화는 기호를 확률 순으로 정렬하고, 각 집합의 확률 합이 비슷하도록 이진 분할을 반복하여 부호어를 생성한다. 샤논-파노 부호화는 허프만 부호화와 산술 부호화에 비해 압축 효율이 낮아, 현재는 덜 사용된다. 한국에서는 정보 이론 교육 및 연구 자료로 활용되며, 성능 개선 및 응용에 대한 연구가 진행되고 있다.

더 읽어볼만한 페이지

무손실 압축 알고리즘 - VP9
VP9는 구글이 개발한 오픈 소스 비디오 코덱으로, VP8보다 압축 효율을 높이고 HEVC보다 나은 성능을 목표로 개발되었으며, WebM 형식으로 사용되고 주요 웹 브라우저와 넷플릭스, 유튜브 등에서 지원했으나 AV1의 등장으로 개발이 중단되었다.
무손실 압축 알고리즘 - FLAC
FLAC은 조시 콜슨이 개발한 무손실 오디오 코덱으로, 원본 음질을 유지하면서 파일 크기를 줄이기 위해 오디오 데이터를 압축하며, 4~32비트 샘플 크기, 최대 8 채널을 지원하고, 미국 국립 문서 기록 관리청에서 디지털 오디오에 선호되는 형식으로 지정되었다.

샤논-파노 부호화

2. 명칭

섀넌-파노 부호화라는 이름은 클로드 섀넌과 로버트 패노의 이름을 따서 지어졌지만, 두 사람이 제안한 알고리즘은 서로 다르다.^[2] 섀넌이 자신의 부호화 방식에 대한 논의에서 패노의 방식을 언급하며 "실질적으로 동일하다"라고 칭했고,^[3] 두 방식 모두 효율적이지만 유사한 성능을 가진 최적화되지 않은 접두 부호 방식이라는 점에서 유사하기 때문에 이러한 혼란이 발생했다.

혼란을 피하기 위해 섀넌이 제안한 방식은 '섀넌 부호화', 패노가 제안한 방식은 '패노 부호화'로 구분하기도 한다.^[2]

3. 섀넌 부호화 (Predefined Word Lengths)

섀넌 부호화는 각 기호에 대해 미리 정해진 코드 길이를 사용한다. 확률 ${\displaystyle p_{1},p_{2},\dots ,p_{n}}$을 가진 소스에서 원하는 부호어 길이는 ${\displaystyle l_{i}=\lceil -\log _{2}p_{i}\rceil }$이다. 여기서 ${\displaystyle \lceil x\rceil }$는 천장 함수로, ${\displaystyle x}$보다 크거나 같은 가장 작은 정수를 의미한다. 부호어 길이를 결정한 다음, 부호어 자체를 선택하는 방법에는 두 가지가 있다.

첫 번째 방법은 확률이 높은 기호에서 낮은 기호 순서로 부호어를 선택하여, 각 부호어가 접두사 없는 속성을 유지하는 올바른 길이의 사전식 첫 번째 단어로 선택하는 것이다.

두 번째 방법은 누적 확률을 사용하는 방식이다. 먼저 확률을 감소하는 순서로 작성한다. ${\displaystyle p_{1}\geq p_{2}\geq \cdots \geq p_{n}}$. 누적 확률은 ${\displaystyle c_{1}=0,\qquad c_{i}=\sum _{j=1}^{i-1}p_{j}{\text{ for }}i\geq 2}$ 와 같이 정의된다. 기호 ${\displaystyle i}$에 대한 부호어는 ${\displaystyle c_{i}}$의 이진수 전개에서 처음 ${\displaystyle l_{i}}$개의 이진 숫자로 선택된다.

기대 코드 길이는 엔트로피 H(X) 보다 1비트 이상 크지 않다.

3. 1. 섀넌의 알고리즘

섀넌의 방법은 모든 부호어의 길이를 결정한 다음, 해당 단어 길이를 가진 접두사 코드를 선택하는 것으로 시작한다.

확률 ${\displaystyle p_{1},p_{2},\dots ,p_{n}}$을 가진 소스에서 원하는 부호어 길이는 ${\displaystyle l_{i}=\lceil -\log _{2}p_{i}\rceil }$이다. 여기서 ${\displaystyle \lceil x\rceil }$는 천장 함수로, ${\displaystyle x}$보다 크거나 같은 가장 작은 정수를 의미한다.

부호어 길이가 결정되면, 부호어 자체를 선택해야 한다. 한 가지 방법은 가장 확률이 높은 기호에서 가장 확률이 낮은 기호 순서로 부호어를 선택하여 각 부호어를 접두사 없는 속성을 유지하는 올바른 길이의 사전식 첫 번째 단어로 선택하는 것이다.

두 번째 방법은 누적 확률을 사용한다. 먼저, 확률을 감소하는 순서로 작성한다. ${\displaystyle p_{1}\geq p_{2}\geq \cdots \geq p_{n}}$. 그런 다음, 누적 확률은 다음과 같이 정의된다.

:${\displaystyle c_{1}=0,\qquad c_{i}=\sum _{j=1}^{i-1}p_{j}{\text{ for }}i\geq 2}$

따라서 ${\displaystyle c_{1}=0,c_{2}=p_{1},c_{3}=p_{1}+p_{2}}$ 등이다.

기호 ${\displaystyle i}$에 대한 부호어는 ${\displaystyle c_{i}}$의 이진수 전개에서 처음 ${\displaystyle l_{i}}$개의 이진 숫자로 선택된다.

3. 2. 섀넌 부호화의 예시

섀넌의 방법은 모든 부호어의 길이를 먼저 결정하고, 그 길이에 맞는 접두사 코드를 선택하는 방식으로 동작한다.

어떤 소스에서 기호가 나타날 확률

p_1, p_2, \dots, p_n

이 주어졌을 때, 각 기호에 대한 부호어의 이상적인 길이는

l_i = \lceil -\log_2 p_i \rceil

로 계산된다. 여기서

\lceil x \rceil

는 천장 함수로,

x

보다 크거나 같은 가장 작은 정수를 의미한다.

부호어의 길이가 결정되면, 실제 부호어를 선택해야 한다. 한 가지 방법은 확률이 높은 기호부터 낮은 기호 순서로, 각 부호어를 접두사 없는 속성을 유지하는 범위 내에서 사전식으로 가장 빠른 단어를 선택하는 것이다.

다른 방법은 누적 확률을 이용하는 것이다. 먼저 확률을 내림차순으로 정렬한다. (

p_1 \geq p_2 \geq \cdots \geq p_n

). 누적 확률은

c_1 = 0, \qquad c_i = \sum_{j=1}^{i-1} p_j \text{ for }i \geq 2 ,

와 같이 정의된다. 즉,

c_1 = 0, c_2 = p_1, c_3 = p_1 + p_2

와 같이 계산된다. 기호

i

의 부호어는

c_i

를 이진수로 표현했을 때, 소수점 아래 처음

l_i

개의 숫자로 결정한다.

다음은 알파벳이 작은 경우에 대한 샤논-파노 부호화의 예시이다. 5개의 소스 기호가 있고, 총 39개의 기호가 관찰되었다고 가정하면, 각 기호의 확률을 추정할 수 있다.

기호	A	B	C	D	E
개수	15	7	6	6	5
확률	0.385	0.179	0.154	0.154	0.128

이 소스의 엔트로피는 $H(X) = 2.186$ 비트이다.

샤논-파노 부호화를 위해, 각 기호에 대한 이상적인 단어 길이 $l_i = \lceil -\log_2 p_i \rceil$ 를 계산한다.

기호	A	B	C	D	E
확률	0.385	0.179	0.154	0.154	0.128
$-\log_2 p_i$	1.379	2.480	2.700	2.700	2.963
단어 길이 $\lceil -\log_2 p_i \rceil$	2	3	3	3	3

사전순으로 부호어를 선택하는 방법에서는, 접두사 없는 속성을 만족하면서 길이가 맞는 첫 번째 단어를 순서대로 선택한다. A는 00을 할당받는다. B는 00으로 시작할 수 없으므로, 길이 3에서 가능한 첫 번째 단어인 010을 할당받는다. 이와 같이 진행하면 다음 부호어를 얻는다.

기호	A	B	C	D	E
확률	0.385	0.179	0.154	0.154	0.128
단어 길이 $\lceil -\log_2 p_i \rceil$	2	3	3	3	3
부호어	00	010	011	100	101

누적 확률을 사용하는 방법에서는, 다음과 같이 계산한다.

기호	A	B	C	D	E
확률	0.385	0.179	0.154	0.154	0.128
누적 확률	0.000	0.385	0.564	0.718	0.872
이진수 표현	0.00000	0.01100	0.10010	0.10110	0.11011
단어 길이 $\lceil -\log_2 p_i \rceil$	2	3	3	3	3
부호어	00	011	100	101	110

두 가지 방법 모두 부호어는 다르지만, 단어 길이는 A는 2비트, B, C, D, E는 3비트로 동일하다. 따라서 평균 길이는 다음과 같다.

: $\frac{2\,\text{비트}\cdot(15) + 3\,\text{비트} \cdot (7+6+6+5)}{39\, \text{기호}} \approx 2.62\,\text{기호당 비트}$

이는 엔트로피 값보다 1비트 이내이다.

3. 3. 기대 코드 길이 (Expected Word Length)

샤논 부호화에서 단어 길이는 다음 식을 만족한다.

:

l_i = \lceil -\log_2 p_i \rceil \leq -\log_2 p_i + 1 .

따라서 기대 단어 길이는 다음 식을 만족한다.

:

\mathbb E L = \sum_{i=1}^n p_il_i \leq \sum_{i=1}^n p_i (-\log_2 p_i + 1) = -\sum_{i=1}^n p_i \log_2 p_i + \sum_{i=1}^n p_i = H(X) + 1.

여기서

H(X) = - \textstyle\sum_{i=1}^n p_i \log_2 p_i

는 엔트로피이며, 샤넌의 소스 부호화 정리에 따르면 모든 부호는 평균 길이

H(X)

이상을 가져야 한다. 따라서 샤논-파노 부호는 항상 최적의 기대 단어 길이에서 1비트 이내에 있음을 알 수 있다.

4. 패노 부호화 (Binary Splitting)

패노 부호화는 주어진 심볼들을 확률에 따라 정렬한 후, 총 확률이 최대한 비슷하게 두 그룹으로 나누는 과정을 반복하여 코드를 생성한다. 먼저 심볼들을 확률이 높은 것부터 낮은 순서로 정렬한다. 그 후, 전체 확률을 가능한 한 균등하게 두 그룹으로 나눈다. 첫 번째 그룹에는 '0', 두 번째 그룹에는 '1'을 할당하여 코드의 첫 번째 비트를 결정한다. 이 과정을 각 그룹의 심볼이 하나만 남을 때까지 반복한다.^[14]

예를 들어, 5개의 기호 (A, B, C, D, E)가 있고, 각각의 출현 횟수와 확률이 다음과 같다고 가정하자.

기호	A	B	C	D	E
개수	15	7	6	6	5
출현 확률	0.38461538	0.17948718	0.15384615	0.15384615	0.12820513

먼저, B와 C 사이를 나누어 두 그룹으로 분할한다. 그러면 왼쪽 그룹(A, B)은 총 22개, 오른쪽 그룹(C, D, E)은 총 17개가 된다. 이 분할은 두 그룹 간의 개수 차이를 가장 작게 만든다. 왼쪽 그룹에는 '0', 오른쪽 그룹에는 '1'을 할당한다. 그 다음, 왼쪽 그룹을 다시 A와 B로 나누어 A에는 '0', B에는 '1'을 부여한다. 오른쪽 그룹도 같은 방식으로 나누어 C에는 '0', D와 E에는 '1'을 할당하고, 다시 D와 E를 분할한다.

이러한 분할 과정을 통해 생성된 각 기호의 부호는 다음과 같다.

기호	A	B	C	D	E
부호	00	01	10	110	111

이 경우, 가장 많이 나타나는 세 기호(A, B, C)는 2비트 코드를, 나머지 두 기호(D, E)는 3비트 코드를 가진다.

이 알고리즘은 비교적 효율적인 가변 길이 코드를 생성하지만, 항상 최적의 코드를 생성하지는 않는다. 예를 들어, 확률 집합 {0.35, 0.17, 0.17, 0.16, 0.15}에 대해서는 샤논-파노 부호화가 최적이 아닌 코드를 할당한다.

4. 1. 패노 부호화의 개요

파노 부호화는 1948년 클로드 섀넌의 정보 이론 논문인 "통신의 수학적 이론"에서 제안된 접두 부호 방식이다.^[14] 기호의 출현 확률에 기초하여 부호를 할당한다. 허프만 부호와 달리 모든 기호의 코드 길이가 이론상의 이상값인

{-\log} P(x)

의 1비트 이내에 있다는 것이 보장된다.

파노 부호화는 다음과 같은 순서로 진행된다.

# 기호를 출현 확률이 높은 것부터 낮은 순서로 정렬한다.

# 각 집합의 확률의 합이 가능한 한 같아지도록 이등분한다.

# 분할된 한쪽 집합에는 "0", 다른 쪽 집합에는 "1"을 할당하여 부호의 첫 번째 자릿수로 한다.

# 분할하여 만들어진 두 집합을 각각 다시 이등분하고, 마찬가지로 0과 1을 할당한다.

# 각 집합에 포함된 기호가 하나가 될 때까지 위의 과정을 반복하면 각 기호의 부호를 얻을 수 있다.

이 알고리즘은 상당히 효율적인 가변 길이 부호를 생성한다. 분할된 두 집합의 출현 확률이 거의 동일하면, 이를 구별하는 데 사용되는 1비트의 정보가 가장 효율적으로 사용된다. 하지만 샤논-파노 부호화는 항상 최적의 부호를 생성하지는 않는다. 예를 들어, {0.35, 0.17, 0.17, 0.16, 0.15}와 같은 확률 분포에서는 최적이 아닌 부호가 생성될 수 있다.

이러한 이유로 샤논-파노 부호화는 실제로 자주 사용되지는 않으며, 대부분의 경우 허프만 부호화나 산술 부호화, 레인지 코더가 사용된다. 그러나 샤논-파노 부호화의 파노 버전은 `ZIP` 파일 형식의 일부인 `IMPLODE` 압축 방식에 사용된다.

예시를 통해 샤논-파노 부호화 과정을 살펴보자. 5 종류의 기호가 다음과 같은 개수로 나타나는 데이터를 생각해보자.

기호	A	B	C	D	E
개수	15	7	6	6	5
출현 확률	0.38461538	0.17948718	0.15384615	0.15384615	0.12820513

먼저 기호를 출현 개수 순서대로 나열한다. B와 C 사이에서 분할하면 왼쪽 집합(A, B)은 총 22개, 오른쪽 집합(C, D, E)은 총 17개가 된다. 이 분할이 두 집합의 총 개수 차이를 가장 작게 만든다. 왼쪽 집합에는 "0", 오른쪽 집합에는 "1"을 부여하여 각 부호의 첫 번째 자릿수로 한다.

왼쪽 집합은 A와 B로 다시 분할하고, A에 "0", B에 "1"을 부여한다. 오른쪽 집합은 C와 D 사이에서 분할하고, 마찬가지로 "0"과 "1"을 부여한다. 마지막으로 D, E 집합을 D와 E로 분할한다.

이 과정을 통해 다음과 같은 부호 트리가 생성된다.

결과적으로 가장 빈도가 높은 3개의 기호(A, B, C)는 2비트 부호, 빈도가 낮은 2개의 기호(D, E)는 3비트 부호가 할당된다.

기호	A	B	C	D	E
부호	00	01	10	110	111

문자당 평균 부호 길이는 다음과 같다.

: $\frac{2\,\text{bits}\cdot(15+7+6) + 3\,\text{bits} \cdot (6+5)}{39\, \text{symbols}} \approx 2.28\,\text{bits per symbol.}$

4. 2. 섀넌-패노 트리

섀넌-패노 트리는 효과적인 코드 테이블을 정의하도록 설계된 사양에 따라 구축된다. 실제 알고리즘은 다음과 같다.

# 주어진 기호 목록에 대해 각 기호의 상대적 발생 빈도를 알 수 있도록 해당하는 확률 또는 빈도 수를 개발한다.

# 가장 자주 발생하는 기호가 왼쪽에, 가장 드물게 발생하는 기호가 오른쪽에 오도록 빈도에 따라 기호 목록을 정렬한다.

# 목록을 두 부분으로 나눈다. 왼쪽 부분의 총 빈도 수는 오른쪽 부분의 총 빈도 수와 가능한 한 가깝게 만든다.

# 목록의 왼쪽 부분에는 이진 숫자 0이 할당되고 오른쪽 부분에는 숫자 1이 할당된다. 이는 첫 번째 부분의 기호에 대한 코드가 모두 0으로 시작하고 두 번째 부분의 코드가 모두 1로 시작함을 의미한다.

# 각 두 부분에 대해 단계 3과 4를 재귀적으로 적용하여 그룹을 세분화하고 각 기호가 트리의 해당 코드 리프가 될 때까지 코드에 비트를 추가한다.

5 종류의 기호가 다음과 같은 개수로 나타나는 데이터를 생각해보자.

기호	A	B	C	D	E
개수	15	7	6	6	5
출현 확률	0.38461538	0.17948718	0.15384615	0.15384615	0.12820513

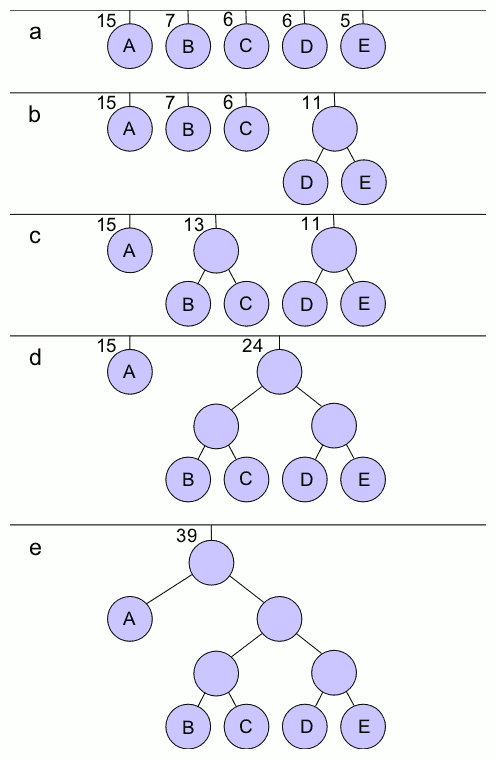
기호는 왼쪽에서 오른쪽으로 출현 개수 순서대로 나열되어 있다(위 그림의 a 상태). 여기서 B와 C 사이에서 분할하면 왼쪽 집합은 총 22개, 오른쪽 집합은 총 17개가 된다. 이 분할이 두 집합의 총 개수의 차이가 가장 작아지는 분할이다. 여기서 왼쪽 집합에 포함된 기호 A, B에 "0", 오른쪽 집합에 포함된 기호 C, D, E에 "1"을 부여하여 각 부호의 첫 번째 자릿수로 한다(위 그림의 b 상태).

왼쪽 집합은 포함된 기호가 2개뿐이므로, A와 B 사이에서 분할하여 알고리즘이 종료된다. A에 "0", B에 "1"을 부여하여 부호의 두 번째 자릿수로 하고, A의 부호는 "00", B의 부호는 "01"이 된다. 왼쪽 집합은 C와 D 사이에서 분할하여 마찬가지로 "0", "1"을 부여한다(위 그림의 c 상태). 또한 D, E 집합은 D와 E로 분할된다(위 그림의 d 상태).

위의 4번의 분할 절차에 의해 부호 트리가 생성된다. 가장 빈도가 높은 3개의 기호는 모두 2비트의 부호가 할당되고, 빈도가 낮은 2개의 기호에는 3비트의 부호가 할당되었다.

기호	A	B	C	D	E
부호	00	01	10	110	111

문자당 평균 부호 길이는 다음과 같다.

: $\frac{2\,\text{bits}\cdot(15+7+6) + 3\,\text{bits} \cdot (6+5)}{39\, \text{symbols}} \approx 2.28\,\text{bits per symbol.}$

4. 3. 패노 부호화의 예시

파노 부호화의 예시는 다음과 같다.

5 종류의 기호가 다음과 같은 개수로 나타나는 데이터를 생각한다.

기호	A	B	C	D	E
빈도	15	7	6	6	5
확률	0.385	0.179	0.154	0.154	0.128

모든 기호는 빈도에 따라 왼쪽에서 오른쪽으로 정렬된다. B와 C 사이에 분할선을 배치하면 왼쪽 그룹의 총합은 22가 되고 오른쪽 그룹의 총합은 17이 된다. 이는 두 그룹 간의 총합 차이를 최소화한다.

이 분할을 통해 A와 B는 각각 0 비트로 시작하는 코드를, C, D, E는 모두 1로 시작하는 코드를 갖게 된다. 이후, 트리의 왼쪽 절반은 A와 B 사이에서 다시 분할되어, A는 코드 00, B는 코드 01을 갖는다.

네 번의 분할 절차를 거쳐 코드 트리가 생성된다. 최종 트리에서 가장 빈도가 높은 세 기호는 모두 2비트 코드를, 빈도가 낮은 두 기호는 3비트 코드를 갖는다.

기호	A	B	C	D	E
확률	0.385	0.179	0.154	0.154	0.128
첫 번째 분할	0		1
두 번째 분할	0	1	0	1
세 번째 분할	0	1	0	0	1
코드워드	00	01	10	110	111

A, B, C는 2비트, D와 E는 3비트 길이의 코드를 가지므로, 평균 길이는 다음과 같다.

: $\frac{2\,\text{비트}\cdot(15+7+6) + 3\,\text{비트} \cdot (6+5)}{39\, \text{기호}} \approx 2.28\,\text{비트/기호.}$

허프만 부호화를 사용하면 평균 2.23비트/기호가 되므로, 이 예시에서는 파노 부호화가 허프만 부호화보다 비효율적임을 알 수 있다.^[1]

4. 4. 기대 코드 길이

Krajči 외^[2]에 의해 파노 부호화의 기대 길이는

\mathbb{E}L \leq H(X) + 1 - p_\text{min}

으로 상한이 정해진다는 것이 밝혀졌다. 여기서

p_\text{min} = \textstyle\min_i p_i

는 가장 적게 나타나는 기호의 확률이다.

5 종류의 기호가 다음과 같은 개수로 나타나는 데이터를 생각한다.

기호	A	B	C	D	E
개수	15	7	6	6	5
출현 확률	0.38461538	0.17948718	0.15384615	0.15384615	0.12820513

위 데이터를 기반으로 샤논-파노 부호화를 적용하면 다음과 같은 부호가 생성된다.

기호	A	B	C	D	E
부호	00	01	10	110	111

가장 빈도가 높은 3개의 기호(A, B, C)는 모두 2비트의 부호가 할당되고, 빈도가 낮은 2개의 기호(D, E)에는 3비트의 부호가 할당되었다. 따라서 문자당 평균 부호 길이는 다음과 같이 계산된다.

: $\frac{2\,\text{bits}\cdot(15+7+6) + 3\,\text{bits} \cdot (6+5)}{39\, \text{symbols}} \approx 2.28\,\text{bits per symbol.}$

5. 다른 부호화 방법과의 비교

허프만 부호화는 각 기호가 정수 비트 수로 구성된 코드로 표현된다는 제약 하에, 계산이 비교적 간단하면서도 항상 가능한 가장 짧은 기대 코드 워드 길이를 달성하는 접두사 코드를 생성한다. 기호별 허프만 부호화는 기호의 확률이 독립적이고 1/2의 거듭제곱일 때만 최적이다.^[12]

산술 부호화는 기호의 실제 정보 내용을 더 가깝게 근사하는 분수 비트 수로 인코딩할 수 있어, 허프만 부호화나 샤논-파노 부호화보다 더 높은 압축률을 제공한다. 그러나 산술 부호화는 계산 비용이 더 많이 들고 여러 특허의 적용을 받기 때문에 널리 사용되지는 않는다.^[12]

샤논-파노 부호화는 샤논의 정보원 부호화 정리의 증명을 위해 사용된 샤논 부호화나, 산술 부호의 선구자인 Shannon–Fano–Elias coding^영어(엘리아스 부호화)와는 다르다.

5. 1. 허프만 부호화 (Huffman Coding)

몇 년 후, 데이비드 A. 허프만은 주어진 기호 확률에 대해 항상 최적의 트리를 생성하는 다른 알고리즘을 제시했다.^[13] 파노의 샤논-파노 트리가 루트에서 잎으로 분할하여 생성되는 반면, 허프만 알고리즘은 반대 방향으로 작동하여 잎에서 루트로 병합한다. 허프만 부호화의 과정은 다음과 같다.

# 각 기호에 대한 리프 노드를 생성하고 발생 빈도를 우선순위로 사용하여 이를 우선순위 큐에 추가한다.

# 큐에 노드가 두 개 이상 있는 동안:

## 큐에서 확률 또는 빈도가 가장 낮은 두 노드를 제거한다.

## 이 노드에 이미 할당된 모든 코드에 각각 0과 1을 앞에 붙인다.

## 이 두 노드를 자식으로 하고 확률을 두 노드의 확률 합과 동일하게 하는 새로운 내부 노드를 생성한다.

## 새 노드를 큐에 추가한다.

# 나머지 노드는 루트 노드이고 트리가 완성된다.

5. 2. 허프만 부호화의 예시

몇 년 후, 데이비드 A. 허프만 (1952)^[13]은 주어진 기호 확률에 대해 항상 최적의 트리를 생성하는 다른 알고리즘을 제시했다. 파노의 샤논-파노 트리가 루트에서 잎으로 분할하여 생성되는 반면, 허프만 알고리즘은 반대 방향으로 작동하여 잎에서 루트로 병합한다.

# 각 기호에 대한 리프 노드를 생성하고 발생 빈도를 우선순위로 사용하여 이를 우선순위 큐에 추가한다.

# 큐에 노드가 두 개 이상 있는 동안:

## 큐에서 확률 또는 빈도가 가장 낮은 두 노드를 제거한다.

## 이 노드에 이미 할당된 모든 코드에 각각 0과 1을 앞에 붙인다.

## 이 두 노드를 자식으로 하고 확률을 두 노드의 확률 합과 동일하게 하는 새로운 내부 노드를 생성한다.

## 새 노드를 큐에 추가한다.

# 나머지 노드는 루트 노드이고 트리가 완성된다.

위의 샤논-파노 부호화 예제와 동일한 빈도를 사용한다.

기호	A	B	C	D	E
횟수	15	7	6	6	5
확률	0.385	0.179	0.154	0.154	0.128

이 경우, D와 E는 가장 낮은 빈도를 가지므로 각각 0과 1이 할당되고, 결합된 확률은 0.282가 된다. 이제 가장 낮은 쌍은 B와 C이므로 0과 1이 할당되고 결합된 확률은 0.333이 된다. 이로 인해 BC와 DE가 가장 낮은 확률을 갖게 되므로 0과 1이 해당 코드 앞에 추가되고 결합된다. 그러면 A와 BCDE만 남게 되는데, 각각 0과 1이 앞에 추가된 다음 결합된다. 이로써 단일 노드가 남게 되고 알고리즘이 완료된다.

이번에 다른 문자에 대한 코드 길이는 A의 경우 1비트이고 다른 모든 문자의 경우 3비트이다.

기호	A	B	C	D	E
코드워드	0	100	101	110	111

결과적으로 A는 1비트, B, C, D, E는 각 3비트의 길이가 되며, 평균 길이는 다음과 같다.

: $\frac{1\,\text{bit}\cdot 15 + 3\,\text{bits} \cdot (7+6+6+5)}{39\, \text{symbols}} \approx 2.23\,\text{bits per symbol.}$

허프만 코드는 샤논-파노 코드의 두 유형보다 성능이 뛰어나며, 예상 길이는 각각 2.62와 2.28이었다.

참조

_[1] 논문 Entropy Coding and Different Coding Techniques https://pdfs.semanti[...] 2016-05
_[2] 간행물 Performance analysis of Fano coding 2015
_[3] 서적 The Bell System Technical Journal 1948-07: Vol 27 Iss 3 https://archive.org/[...] AT & T Bell Laboratories 1948-07-01
_[4] 서적 Elements of Information Theory Wiley–Interscience 2006
_[5] 서적 Communication Theory Cambridge University Press 1991
_[6] 서적 Information and Coding Theory Springer 2012
_[7] 서적 Mathematics of Information and Coding American Mathematical Society 2007
_[8] 서적 A First Course in Information Theory Springer 2002
_[9] 서적 Data Compression: The Complete Reference Springer 2013
_[10] 서적 Data Communications and Computer Networks Phi Publishing 2006
_[11] 웹사이트 'APPNOTE.TXT - .ZIP File Format Specification' http://www.pkware.co[...] PKWARE Inc 2007-09-28
_[12] 서적 Fundamentals of Multimedia https://books.google[...] Springer Science & Business Media 2014-04-09
_[13] 논문 A Method for the Construction of Minimum-Redundancy Codes http://compression.r[...]
_[14] 문서 Fano 1949

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com