각기둥
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
각기둥은 두 개의 평행한 밑면과 옆면으로 이루어진 다면체이다. 밑면의 모양에 따라 삼각기둥, 사각기둥, 오각기둥 등으로 나뉘며, 밑면이 원인 경우 원기둥으로 불린다. 각기둥의 겉넓이는 밑넓이의 2배에 옆넓이를 더한 값으로 계산되며, 밑면이 정다각형인 각기둥은 정각기둥, 모든 면이 정다각형인 정각기둥은 아르키메데스 정각기둥이라고 한다. 또한 직각기둥, 사각기둥, 꼬인 각기둥, 잘린 각기둥 등 다양한 종류가 있으며, 각기둥의 부피와 겉넓이를 구하는 공식이 존재한다. 각기둥은 각뿔대, 별 각기둥, 교차 각기둥, 토로이달 각기둥 등과 관련이 있으며, 고차원적으로 일반화된 각기둥 다포체도 존재한다.
더 읽어볼만한 페이지
- 고른 다면체 - 사면반육면체
사면반육면체는 7개의 면, 12개의 모서리, 6개의 꼭짓점을 가지며 오일러 지표가 1인 무방향성 다면체이다. - 고른 다면체 - 깎은 큰 십이면체
깎은 큰 십이면체는 정십각형 12개와 별 모양 오각형 12개로 이루어진 다면체로, 큰 십이면체를 깎아서 만들 수 있으며 작은 별 오각 십이면체와 쌍대 관계를 가진다. - 기둥형 다면체 - 직육면체
직육면체는 6개의 직사각형 면으로 이루어진 볼록 다면체로, 모든 이면각이 직각이고 마주보는 면이 합동인 특징을 가지며, 정사각형 직육면체와 정육면체 같은 특수한 경우가 있고 부피, 표면적, 공간 대각선은 가로, 세로, 높이로 계산하며, 공간 감각과 기하학적 개념 이해에 중요한 역할을 한다. - 기둥형 다면체 - 오각지붕
오각지붕은 5개의 정삼각형, 5개의 정사각형, 1개의 정오각형, 1개의 정십각형으로 이루어진 존슨의 다면체이며, 회전 대칭을 갖고, 다양한 다면체를 구성하는 데 사용된다.
| 각기둥 | |
|---|---|
| 개요 | |
 | |
| 설명 | 두 개의 평행한 n각형 밑면과 n개의 평행사변형 옆면으로 이루어진 입체 |
| 종류 | 균일의 의미에서 준정다면체 |
| 오일러 지표 | 2 |
| 면 | 2개의 n각형 정다각형 n개의 정사각형 |
| 변 | 3n |
| 꼭짓점 | 2n |
| 꼭짓점 배열 | 4.4.n |
| 슐레플리 기호 | {n}×{ } t{2,n} |
| 비트호프 기호 | 해당 없음 |
| 콕서터 다이어그램 | 해당 없음 |
| 콘웨이 다면체 표기법 | Pn |
| 대칭군 | Dnh, [n,2], (*n22), 크기 4n |
| 회전군 | Dn, [n,2]⁺, (n22), 크기 2n |
| 겉넓이 | 해당 없음 |
| 부피 | 해당 없음 |
| 쌍대 | 볼록 쌍대-균일 n각 쌍뿔 |
| 성질 | 볼록, 정다각형 면, 아이소고날, 평행 이동된 밑면, 옆면 ⊥ 밑면 |
| 꼭짓점 도형 | 해당 없음 |
 | |
| 명칭 | |
| 영어 | prism |
| 한국어 | 각기둥 |
| 문화어 | 모기둥 (n = 9일 때) |
2. 종류
각기둥은 여러 기준에 따라 다양하게 분류할 수 있다.
가장 일반적인 분류는 밑면의 모양에 따른 것이다. 밑면이 삼각형이면 삼각기둥, 사각형이면 사각기둥, 오각형이면 오각기둥 등으로 부르며, 일반적으로 밑면이 n각형인 경우 '''n각기둥'''이라고 한다.
또한, 옆면과 밑면이 이루는 각도에 따라 분류할 수도 있다. 옆면이 밑면과 수직인 '''직각기둥'''(right prism|라이트 프리즘eng)과 옆면이 밑면에 대해 기울어진 '''사각기둥'''(oblique prism|오블리크 프리즘eng)으로 나뉜다. 일반적으로 교육 과정에서는 직각기둥을 주로 다룬다.
밑면의 모양이 정다각형인지 여부에 따라서도 구분할 수 있다. 밑면이 정다각형인 각기둥을 '''정각기둥'''(regular prism|레귤러 프리즘eng)이라고 부른다. 더 나아가 밑면과 옆면이 모두 정다각형으로 이루어진 특별한 경우도 존재한다.
2. 1. 밑면에 따른 종류
각기둥은 밑면의 모양에 따라 이름이 붙여진다. 밑면이 삼각형이면 '''삼각기둥''', 사각형이면 '''사각기둥''', 오각형이면 '''오각기둥''' 등으로 불린다. 일반적으로 밑면이 n각형인 각기둥을 '''n각기둥'''이라고 한다.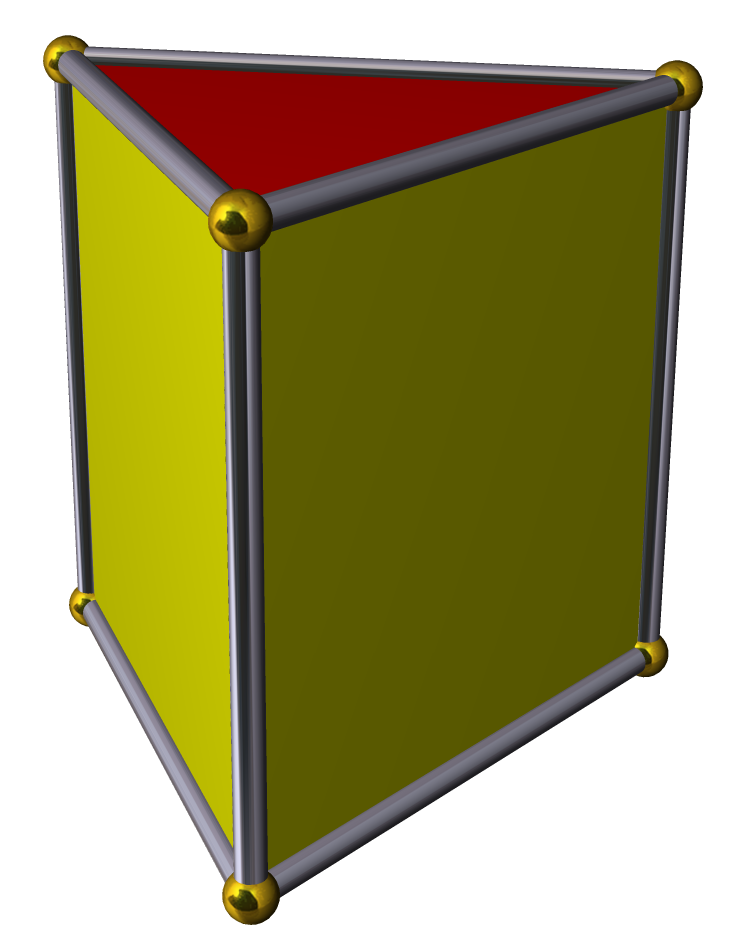

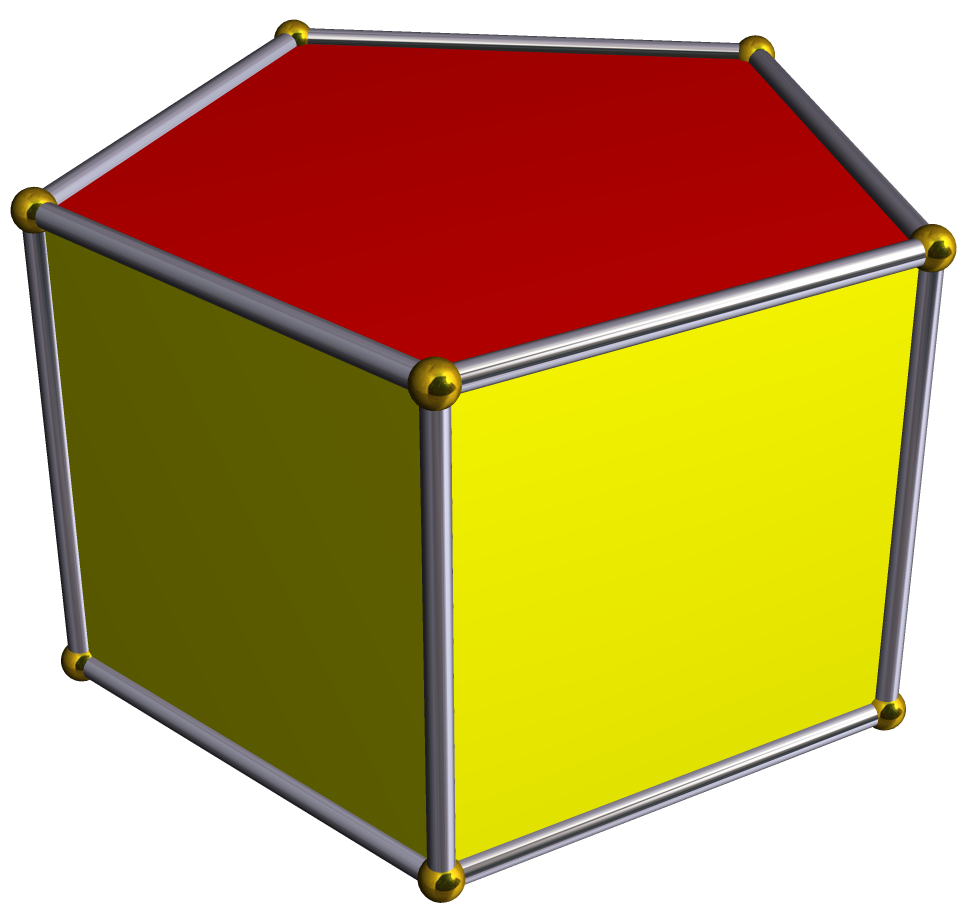
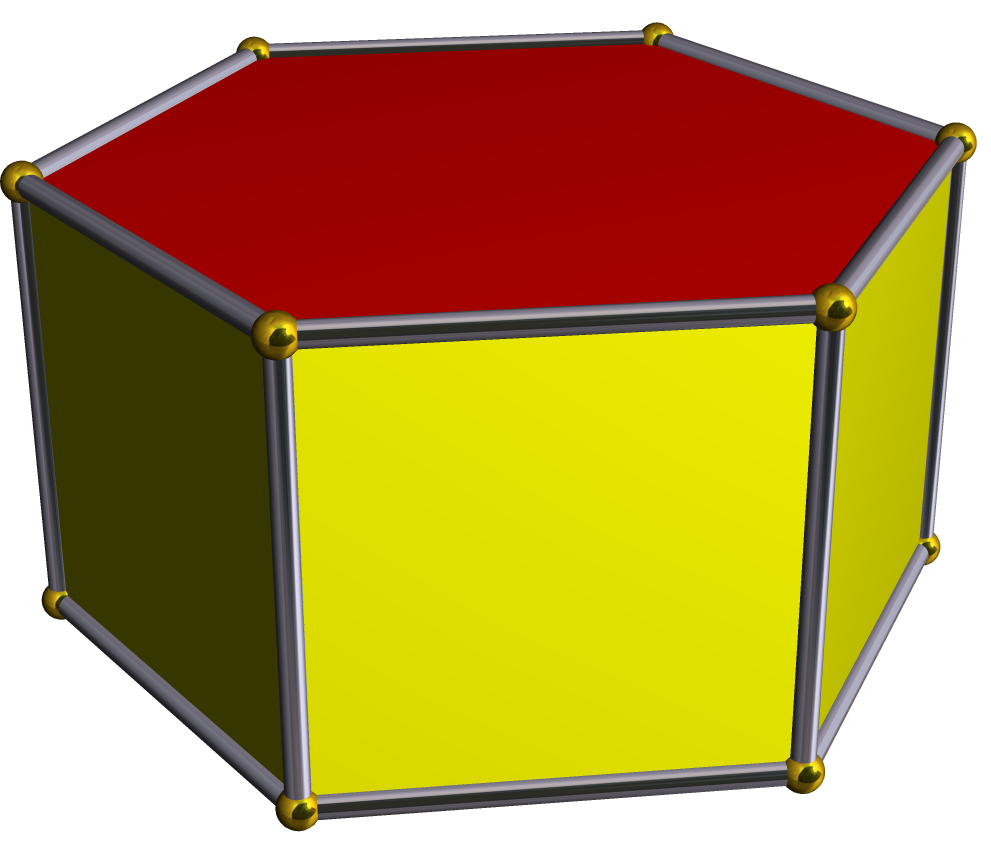
몇 가지 구체적인 예시는 다음과 같다.
- 삼각기둥
- 사각기둥: 밑면이 직사각형인 직각기둥은 '''육면체''' 또는 '''직육면체'''라고도 불린다. 밑면이 정사각형인 직각기둥은 '''정사각기둥'''이라고 하며, 특히 모든 모서리 길이가 같은 경우 '''정육면체'''라고 한다.
- 오각기둥
- 육각기둥
밑면이 정다각형인 각기둥을 '''정각기둥'''(regular prism영어)이라고 한다. 예를 들어, 밑면이 정사각형인 정사각기둥은 정각기둥의 일종이다.
또한 밑면이 원인 원기둥도 넓은 의미에서 각기둥의 극한 형태로 생각할 수 있다.
2. 2. 직각기둥과 사각기둥
옆면이 밑면과 수직으로 만나는 각기둥을 직각기둥(right prism|라이트 프리즘eng)이라고 한다.[5] 직각기둥의 옆면은 모두 직사각형이다. 이는 '오른 각기둥'이라고도 부른다.반면, 옆면이 밑면과 수직이 아닌 각기둥, 즉 옆면이 밑면에 대해 기울어져 있는 각기둥을 사각기둥(oblique prism|오블리크 프리즘eng)이라고 한다. 사각기둥의 옆면은 모두 평행사변형이다. 이는 '기울어진 각기둥'이라고도 부른다.
평행육면체는 밑면이 평행사변형인 사각기둥의 한 예시이다.
2. 3. 정각기둥과 균등 각기둥
정각기둥(regular prism영어)은 밑면이 정다각형인 각기둥이다.균등 각기둥(uniform prism영어) 또는 준정 각기둥(semiregular prism영어)은 밑면이 정다각형이고 모든 모서리의 길이가 같은 직각기둥이다. 따라서 균등 각기둥의 모든 옆면은 정사각형이며, 모든 면이 정다각형이다. 이러한 각기둥은 등각이기 때문에 균등 다면체에 속한다. 균등 각기둥은 준정 다면체의 두 무한 집합 중 하나를 형성하며, 다른 하나는 엇각기둥(antiprism)이다. 균등 n-각기둥은 슐레플리 기호 }를 갖는다.
균등 각기둥은 아르키메데스 각기둥(Archimedean prism영어)이라고도 불린다. 아르키메데스 각기둥은 준정다면체의 조건을 만족하지만, 무한히 많이 존재하고 2차원 대칭성만 가지므로 일반적으로 준정다면체 분류에는 포함하지 않는다. 균등 정사각기둥은 정육면체이다.
3. 공식
4. 성질
(내용 없음 - 하위 섹션에서 부피, 겉넓이 등 구체적인 성질을 다루고 있으며, 주어진 원본 소스의 내용은 '부피' 하위 섹션과 중복됩니다.)
4. 1. 부피
각기둥의 부피는 밑면의 넓이와 높이의 곱으로 구할 수 있다.밑면의 넓이를 , 높이를 라고 할 때, 각기둥의 부피 는 다음과 같다.
:
4. 2. 겉넓이
밑면의 넓이를 , 밑면의 둘레를 , 높이를 라고 할 때, 직각 기둥의 겉넓이 는 두 밑면의 넓이와 옆면의 넓이를 합한 것과 같다. 옆면의 넓이는 밑면의 둘레와 높이를 곱한 값이므로, 겉넓이는 다음과 같이 계산할 수 있다.:
특히, 밑면이 한 변의 길이가 인 정각형이고 높이가 인 직각 기둥의 겉넓이는 다음과 같이 나타낼 수 있다. 여기서 는 코탄젠트 함수를 의미한다.
:
4. 3. 대칭
(내용 없음 - 원본 소스에 해당 섹션 관련 정보가 없습니다.)5. 관련 다면체
(내용 없음 - 원본 소스가 비어 있고, 하위 섹션에서 관련 내용을 다루고 있어 중복을 피하기 위해 본문 내용을 생성하지 않음)
5. 1. 잘린 각기둥
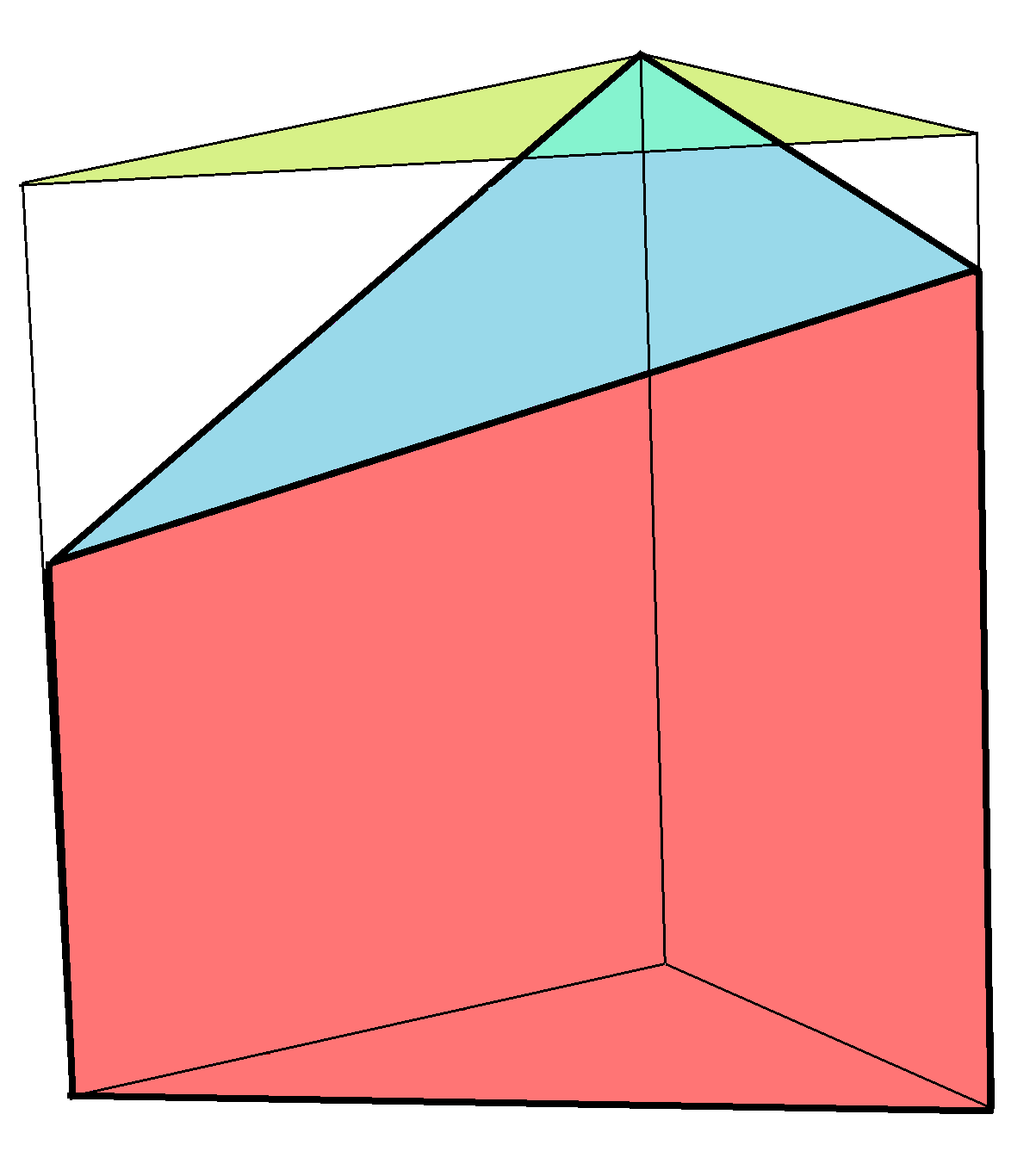
'''잘린 각기둥'''은 각기둥을 밑면에 평행하지 않은 평면으로 잘라서 만들어지는 다면체이다. 잘린 각기둥의 두 밑면은 서로 합동이 아니며, 옆면은 평행사변형이 아니다.
5. 2. 꼬인 각기둥
'''꼬인 각기둥'''은 정''n''-각기둥의 각 정사각형 면을 대각선으로 이등분하여 만들어진 비볼록 다면체이다. 일반적으로 상단을 동일한 방향으로 π/''n'' 라디안 (180/''n'' 도)만큼 꼬아서 면이 오목하게 된다.[7][8]꼬인 각기둥은 새로운 꼭짓점을 추가하지 않고 사면체로 분할될 수 없다. 가장 간단한 꼬인 각기둥은 삼각형 밑면을 가지고 있으며 쇤하르트 다면체라고 불린다.
''n''-각 '''꼬인 각기둥'''은 ''n''-각 균일 엇각기둥과 위상학적으로 동일하지만, 대칭군은 절반인 D''n'', [''n'',2]+ (차수 2''n'')이다. 꼬인 각기둥은 삼각형 쌍 사이에 사면체가 제거된 비볼록 엇각기둥으로 볼 수도 있다.
| 3-각 | 4-각 | 12-각 | |
|---|---|---|---|
 쇤하르트 다면체 | 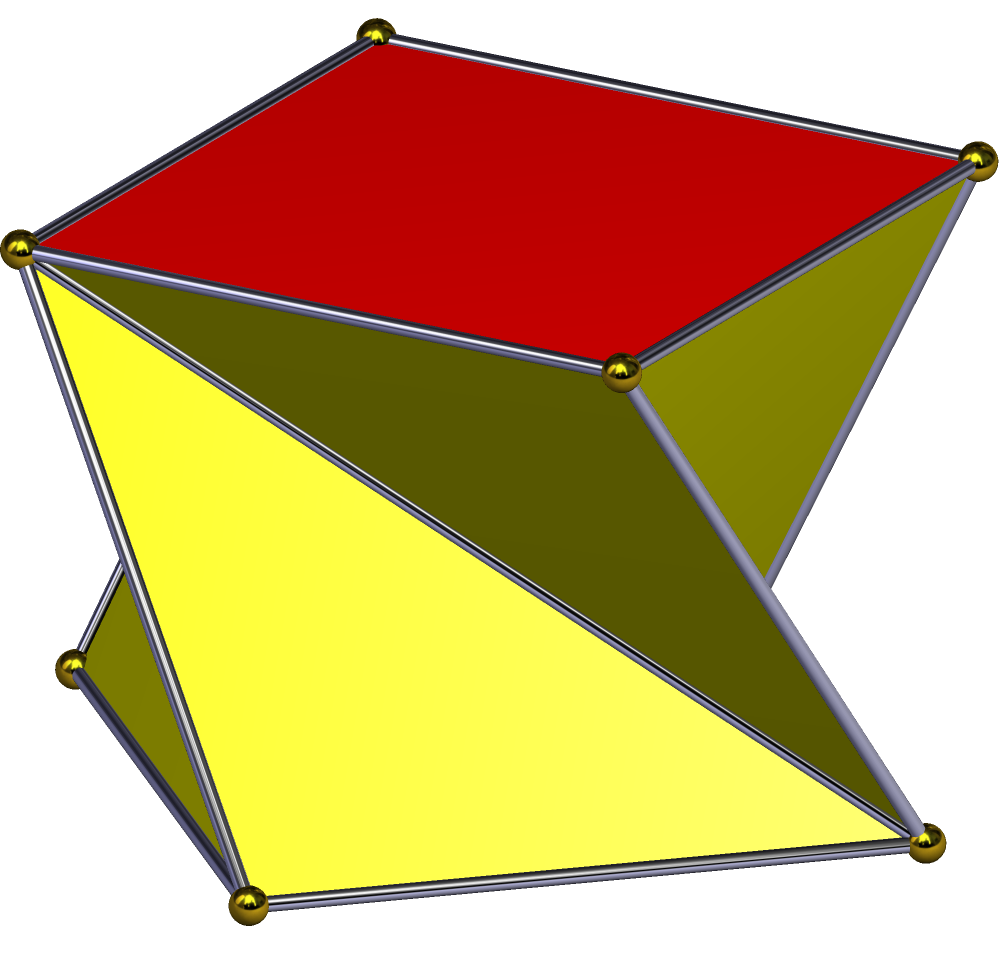 꼬인 사각 기둥 | 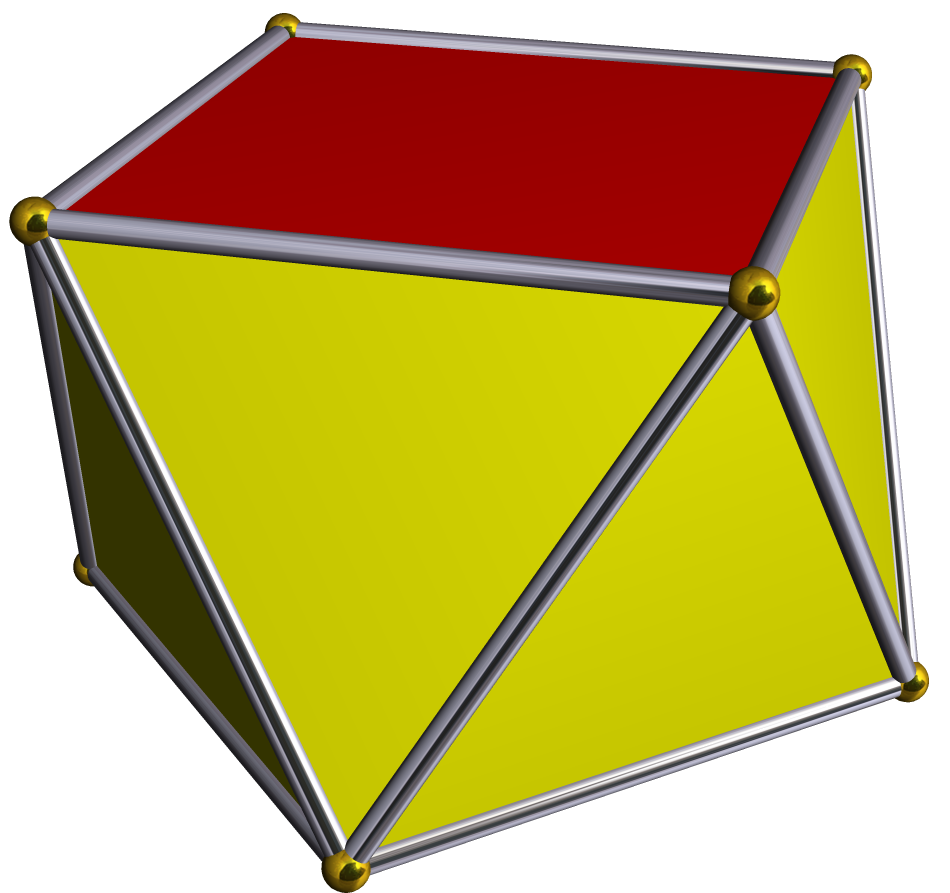 사각 엇각기둥 | 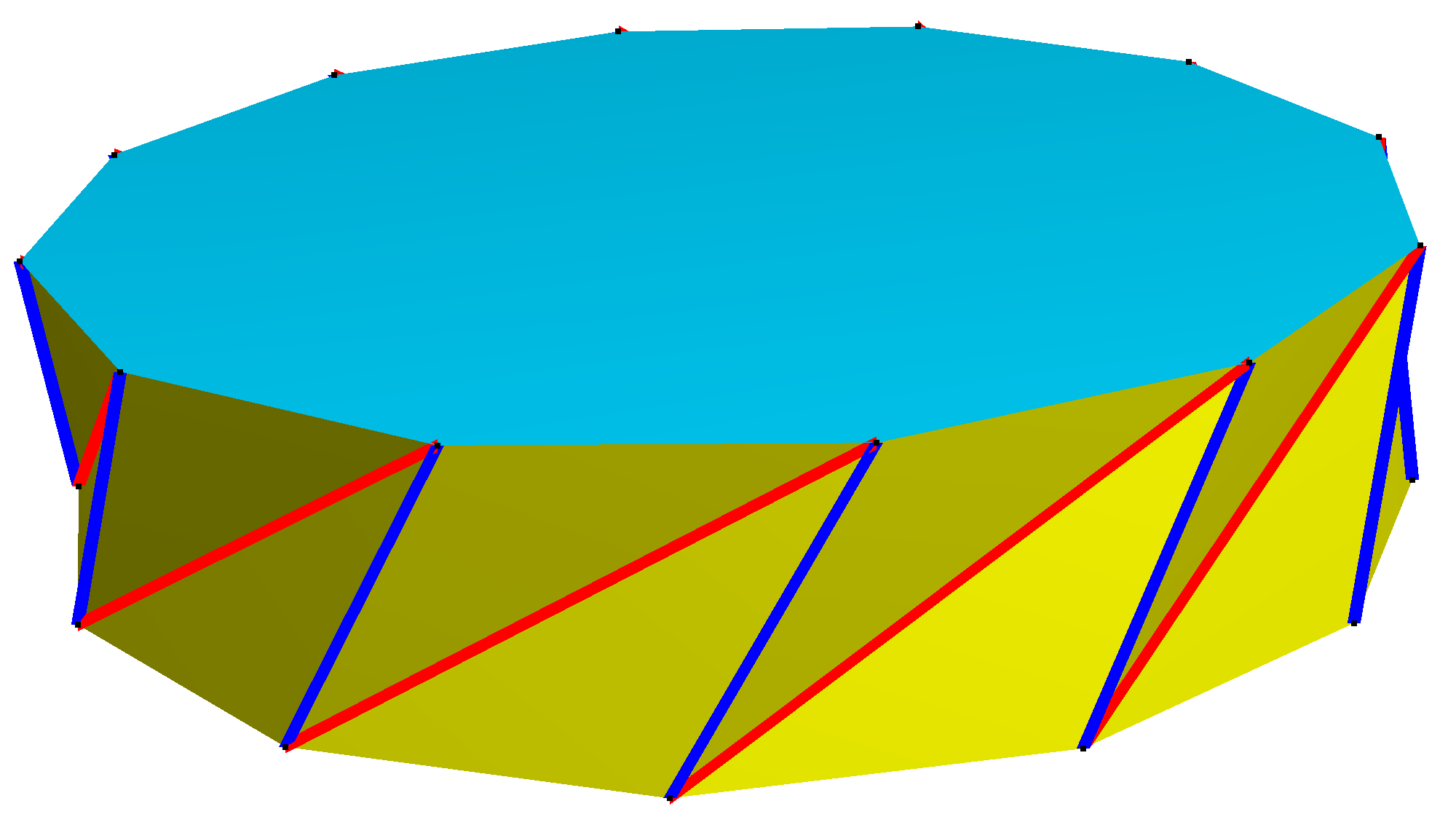 꼬인 십이각 엇각기둥 |
5. 3. 각뿔대
각뿔대는 각기둥과 유사한 구조로, 옆면은 사다리꼴이며 상단과 하단의 다각형 크기가 서로 다르다.
5. 4. 별 각기둥
'''별 각기둥'''은 위아래에 동일한 별 다각형 면을 가지고, 서로 평행하며 거리를 두고, 직사각형 면으로 연결된 비볼록 다면체이다. ''균일 별 각기둥''은 슐레플리 기호 `{''p''/''q''} × {}`를 가지며, ''p''개의 직사각형과 2개의 `{''p''/''q''}` 면을 갖는다. 위상적으로 ''p''각기둥과 동일하다.| { } × { }180 × { } | ta{3} × { } | {5/2} × { } | {7/2} × { } | {7/3} × { } | {8/3} × { } | |
|---|---|---|---|---|---|---|
| D2h, 차수 8 | D3h, 차수 12 | D5h, 차수 20 | D7h, 차수 28 | D8h, 차수 32 | ||
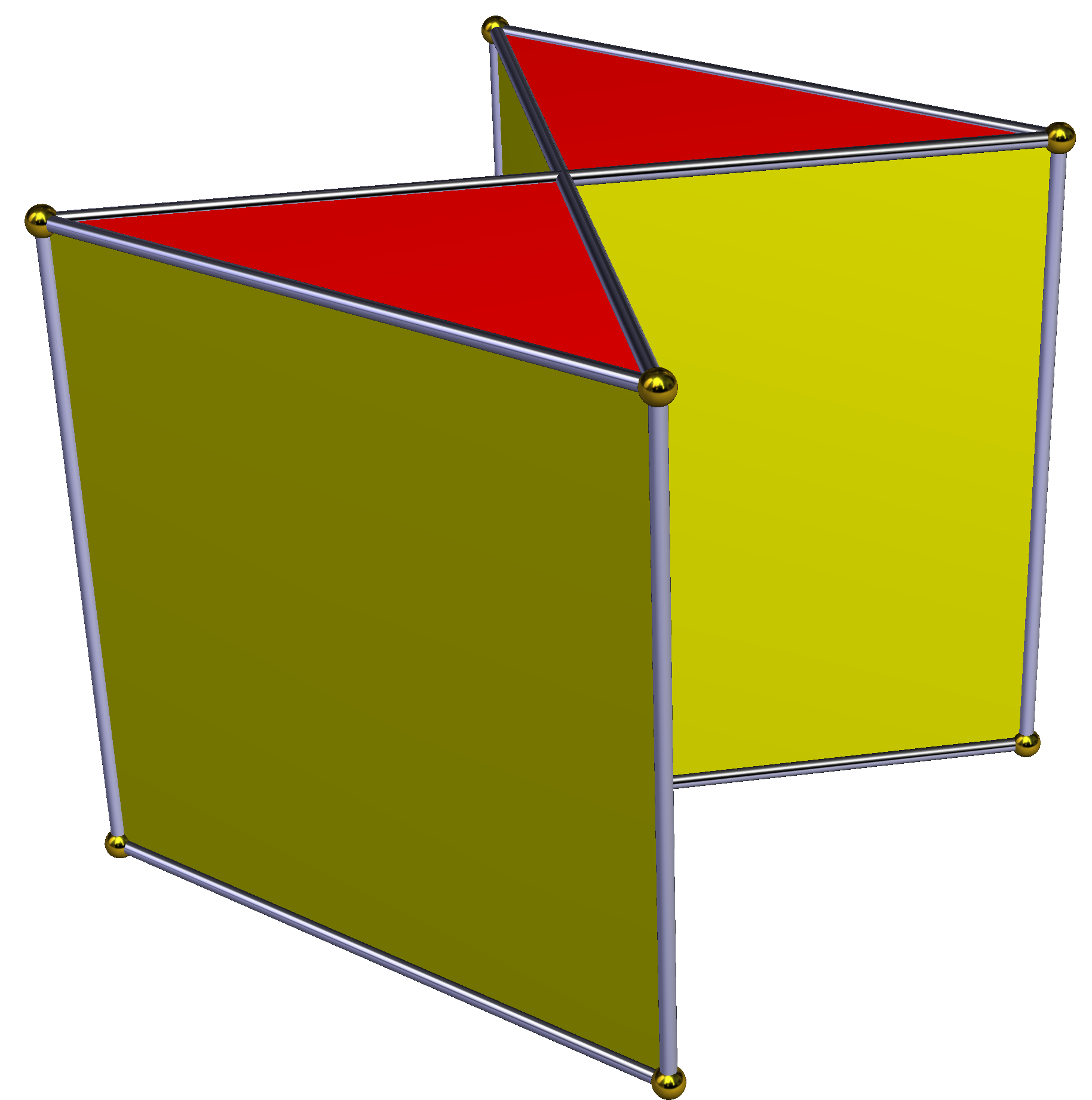 | 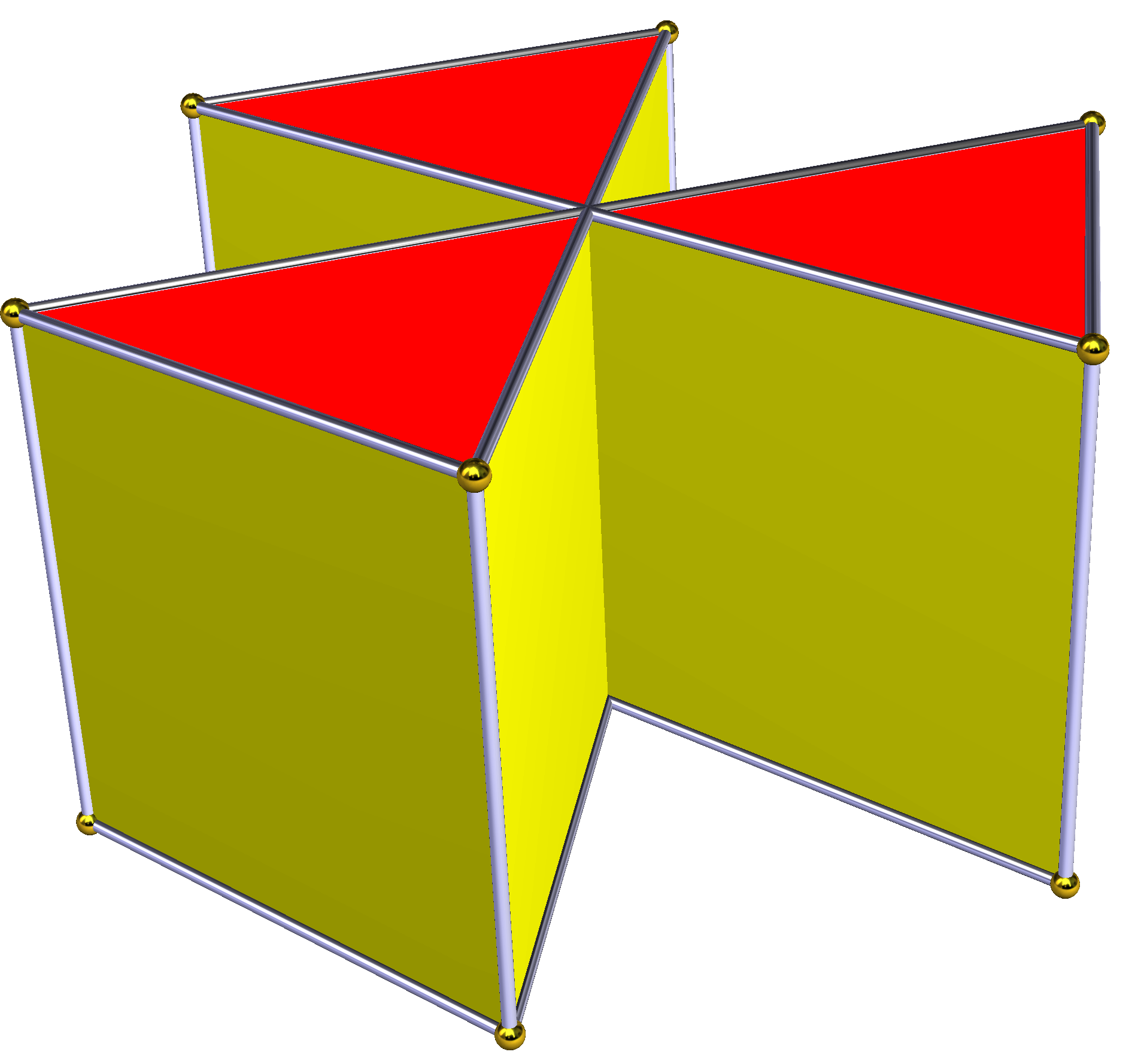 | 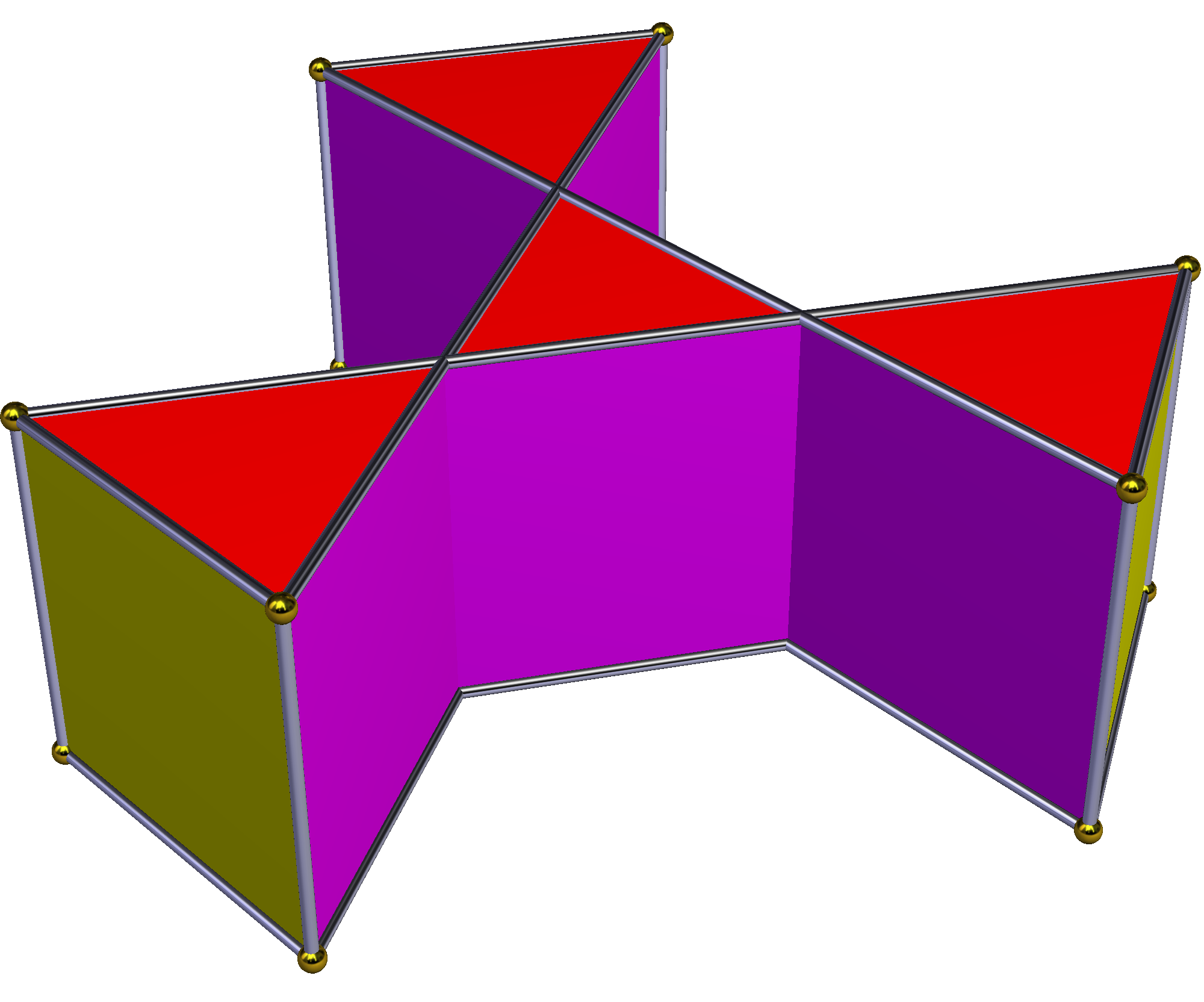 | 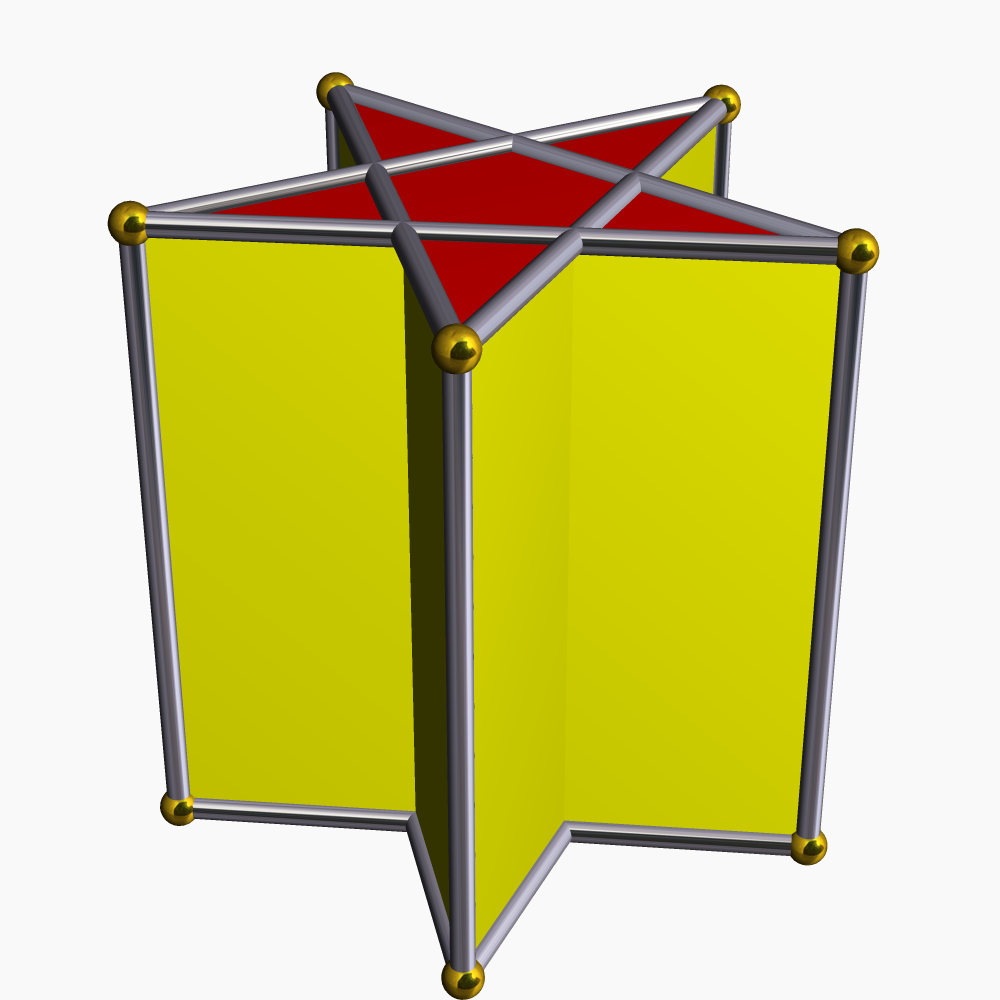 | 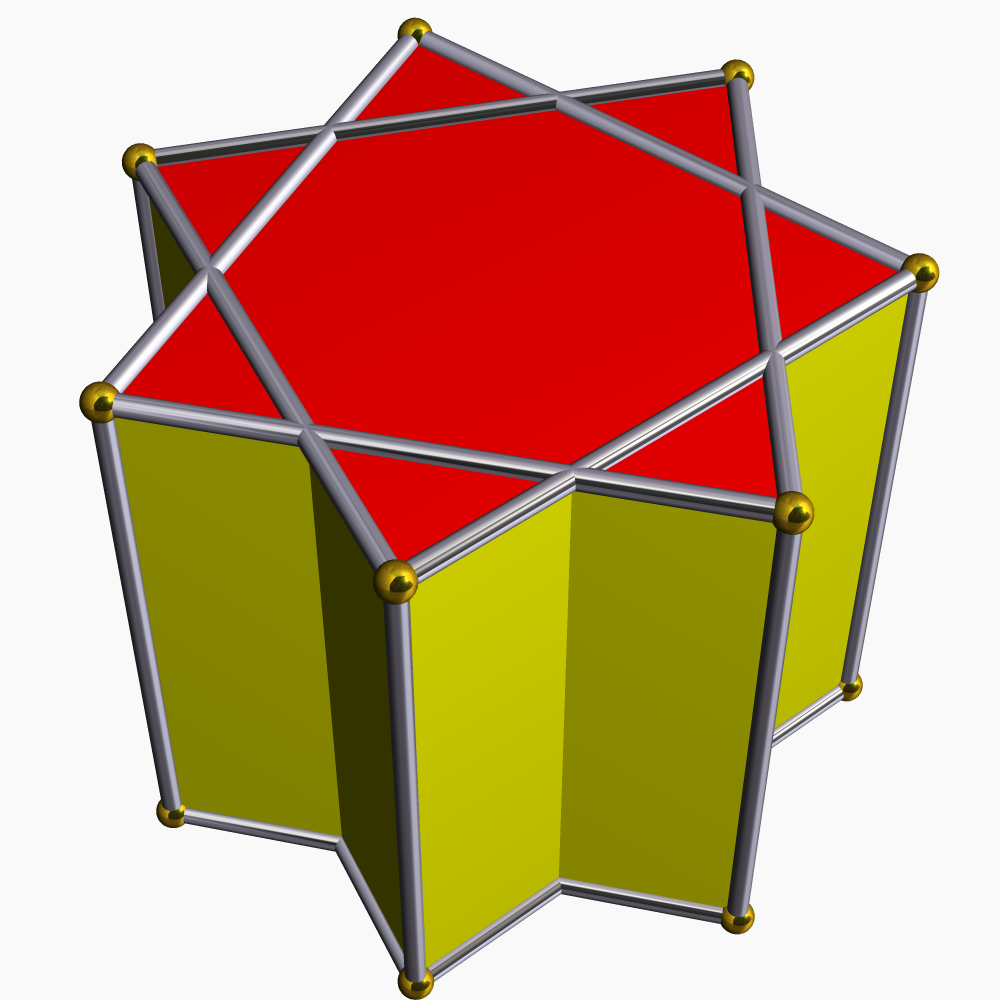 | 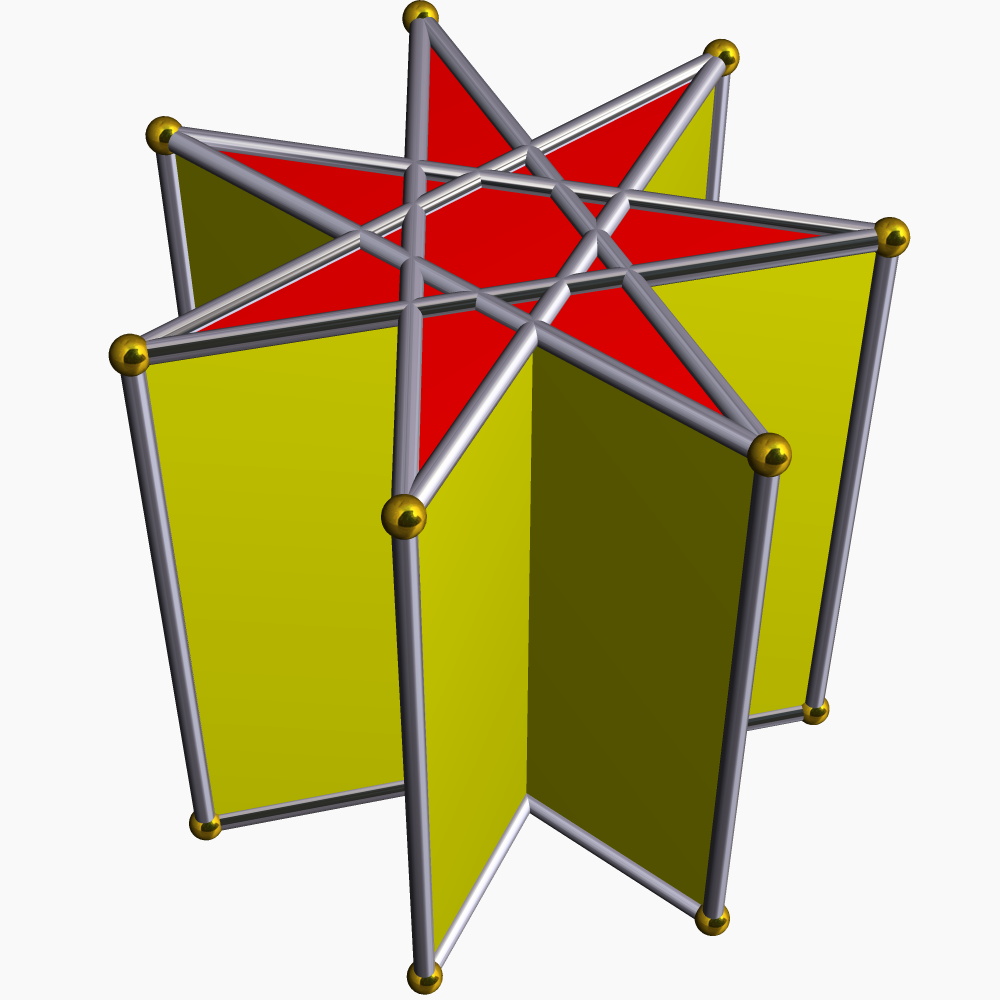 | 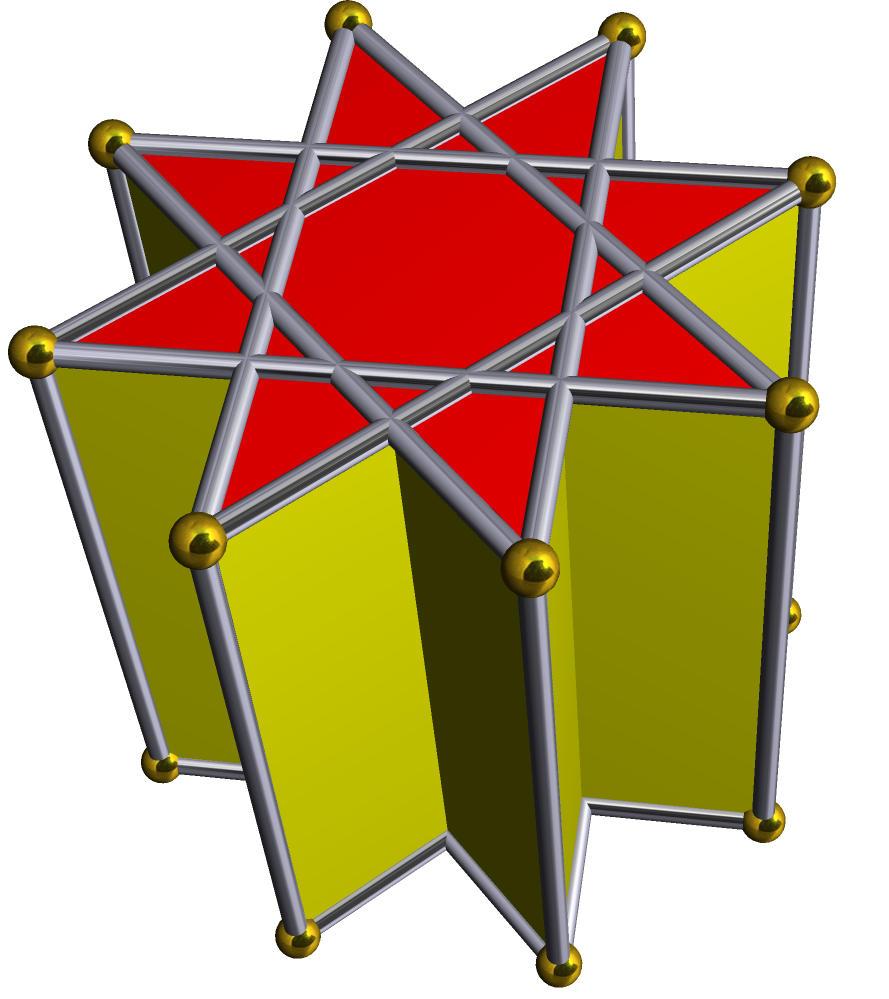 |
5. 5. 교차 각기둥
'''교차 각기둥'''은 각기둥에서 한 밑면의 꼭짓점을 이 밑면의 점대칭 중심을 기준으로 180° 회전시켜 구성한 비볼록 다면체이다. 이 과정에서 옆면의 직사각형 면은 교차 직사각형 형태로 변형된다. 밑면이 정다각형일 경우, 교차 각기둥의 외형은 n각형 모래시계와 같다. 모든 빗변은 도형의 중심을 통과하지만, 꼭짓점 자체가 중심에 위치하는 것은 아니다. 위상학적으로 교차 각기둥은 일반적인 n각기둥과 동일한 구조를 가진다.| 대칭군 | 대칭군 | 대칭군 | 대칭군 | 대칭군 | |||
|---|---|---|---|---|---|---|---|
| D2h, 차수 8 | D3d, 차수 12 | D4h, 차수 16 | D5d, 차수 20 | D6d, 차수 24 | |||
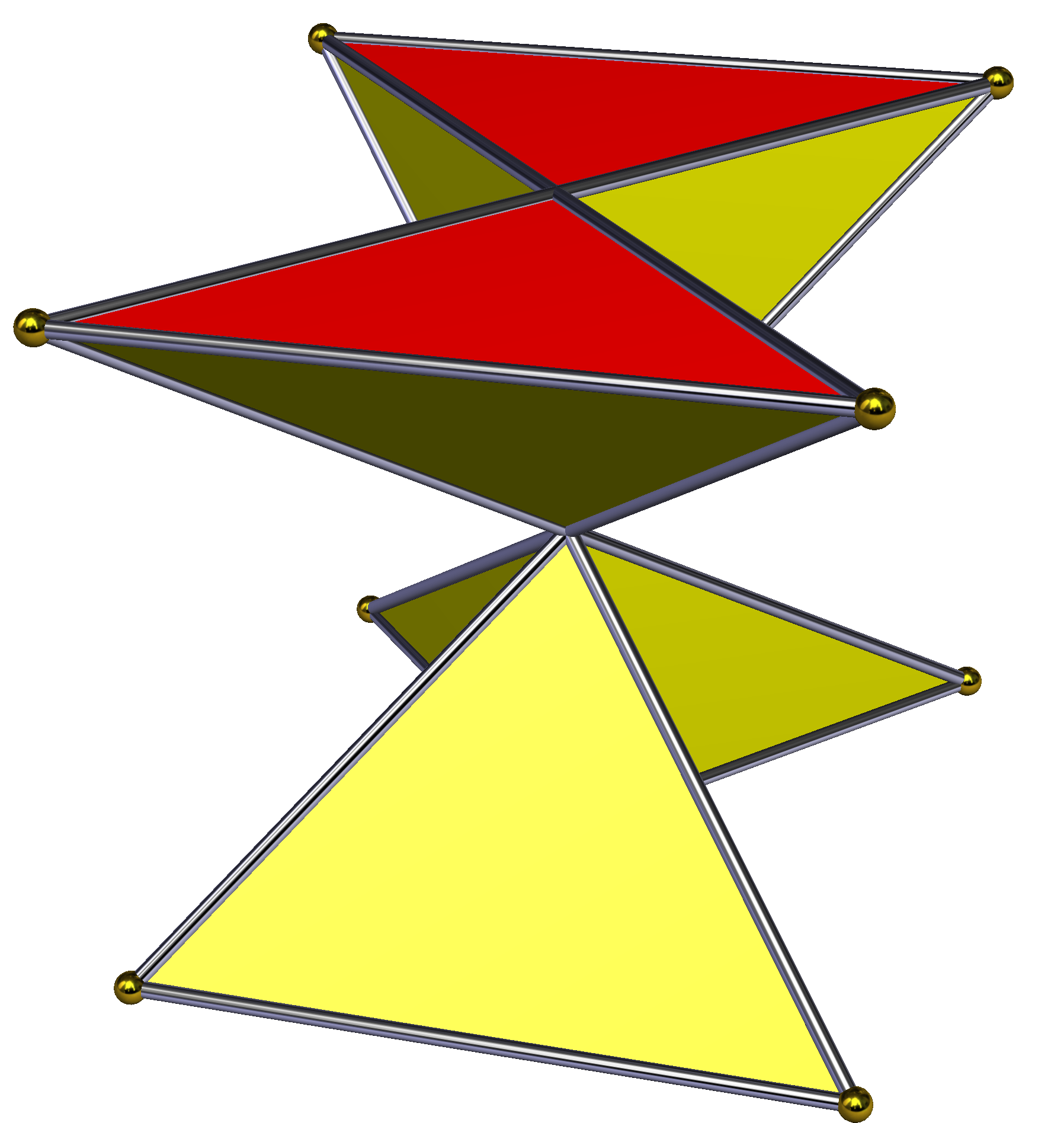 | 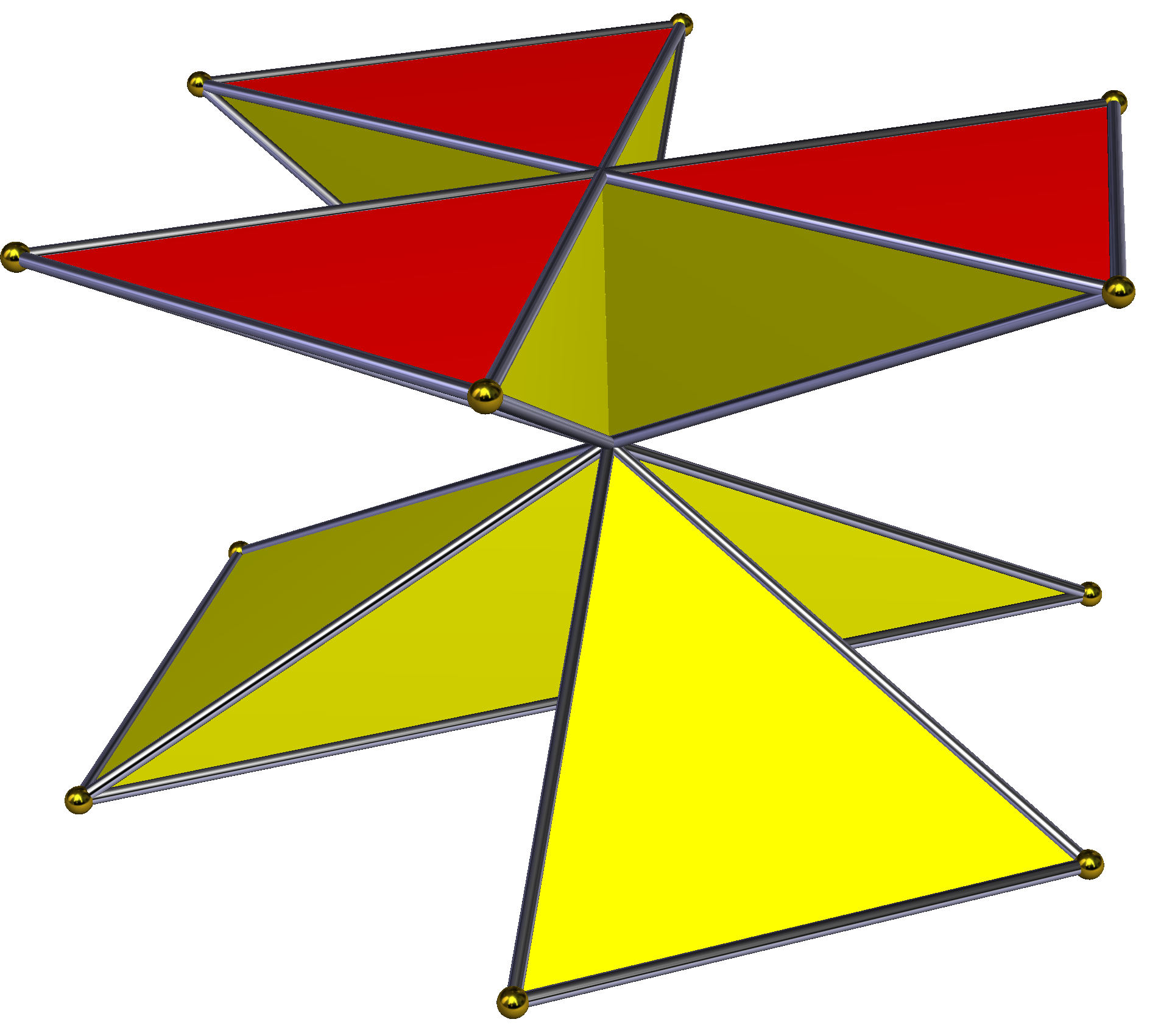 | 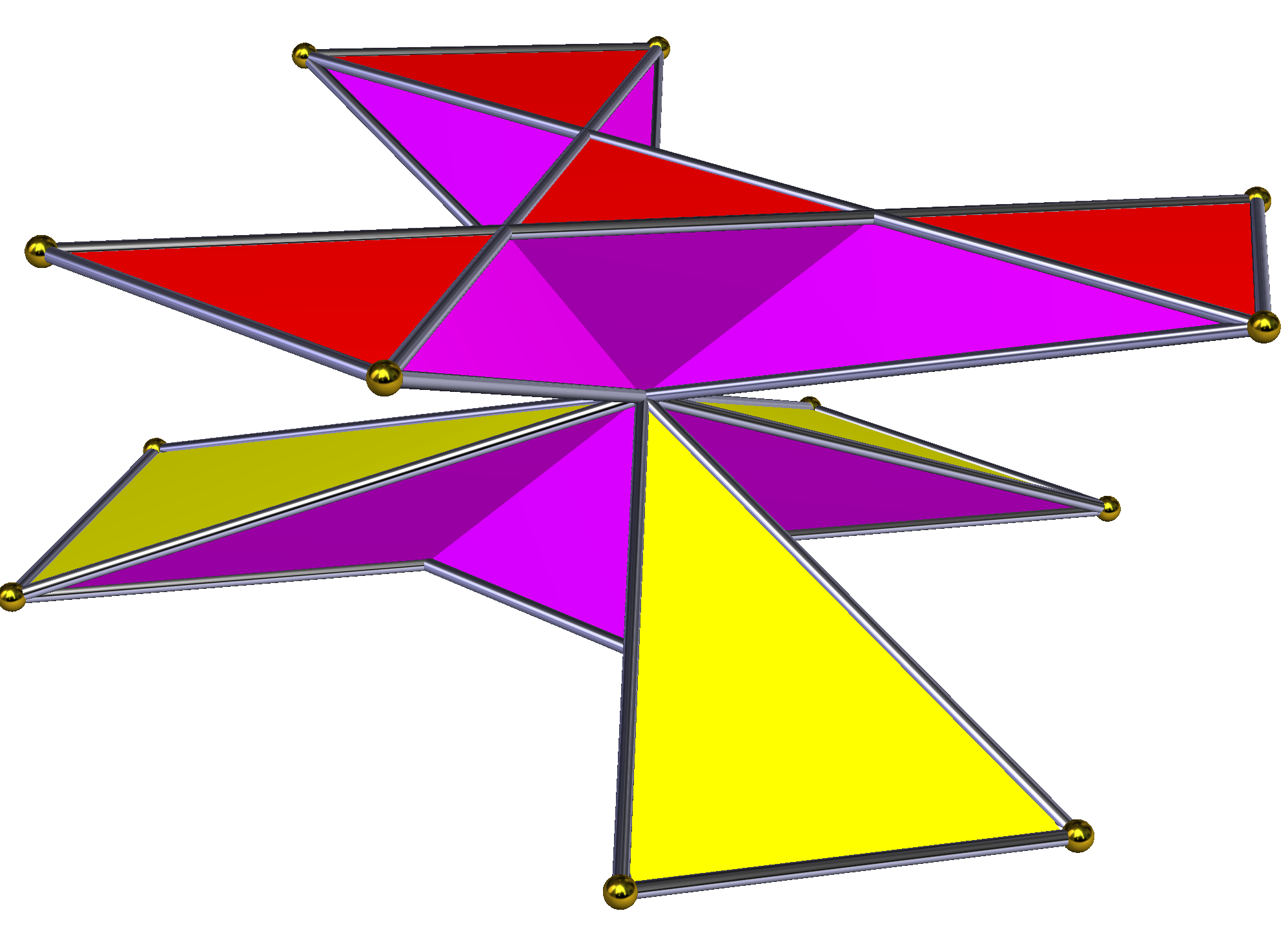 | 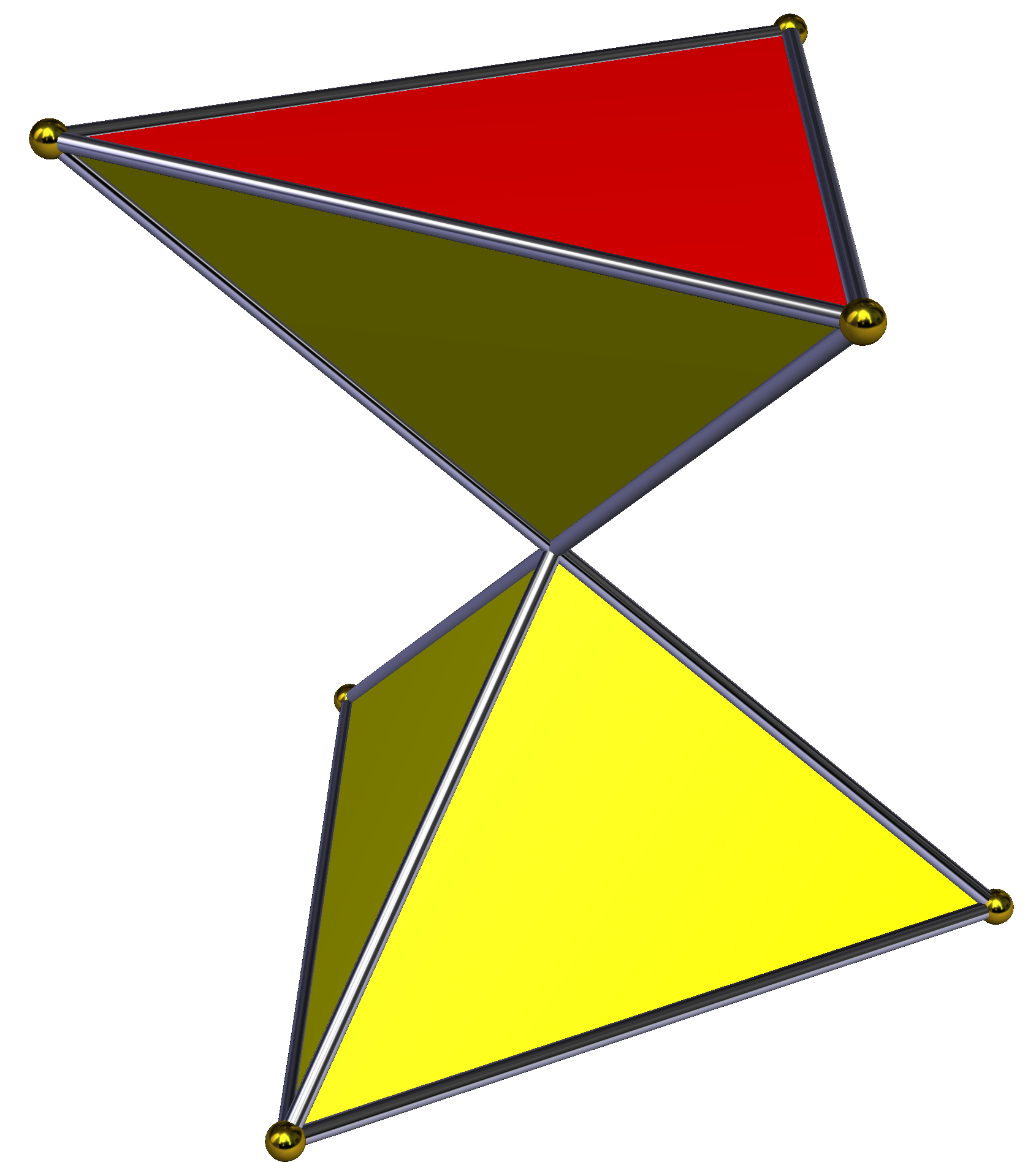 | 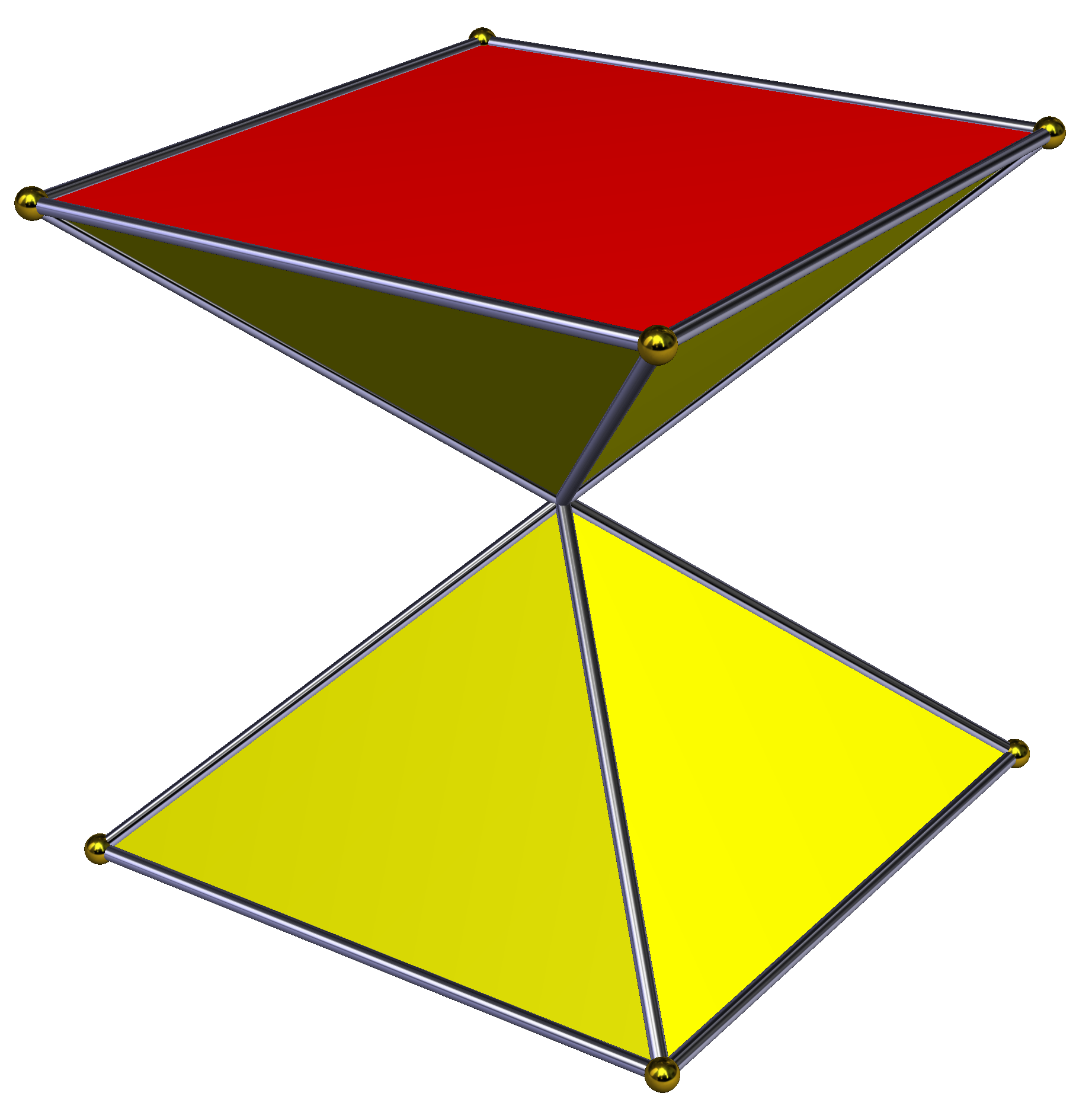 | 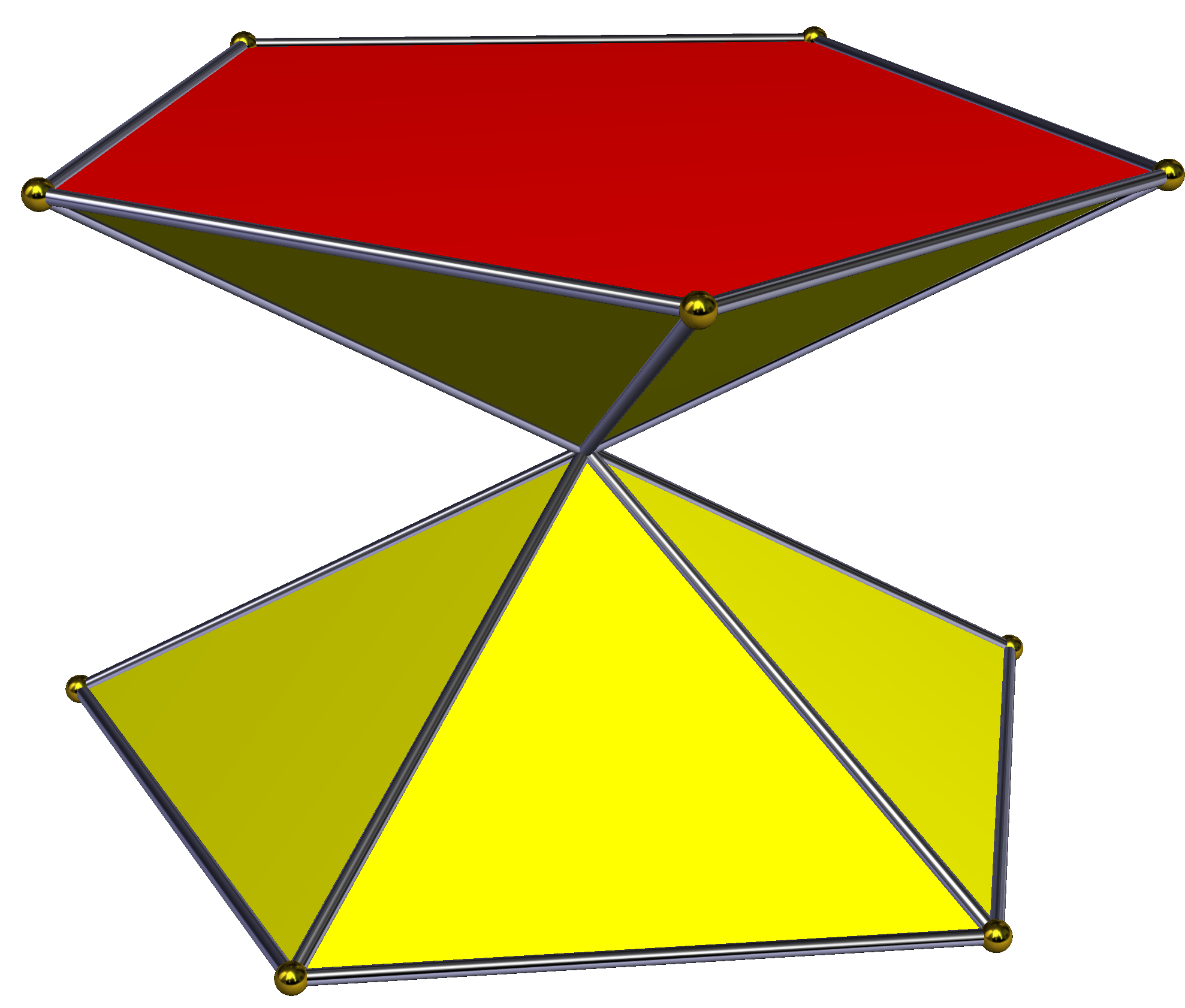 | 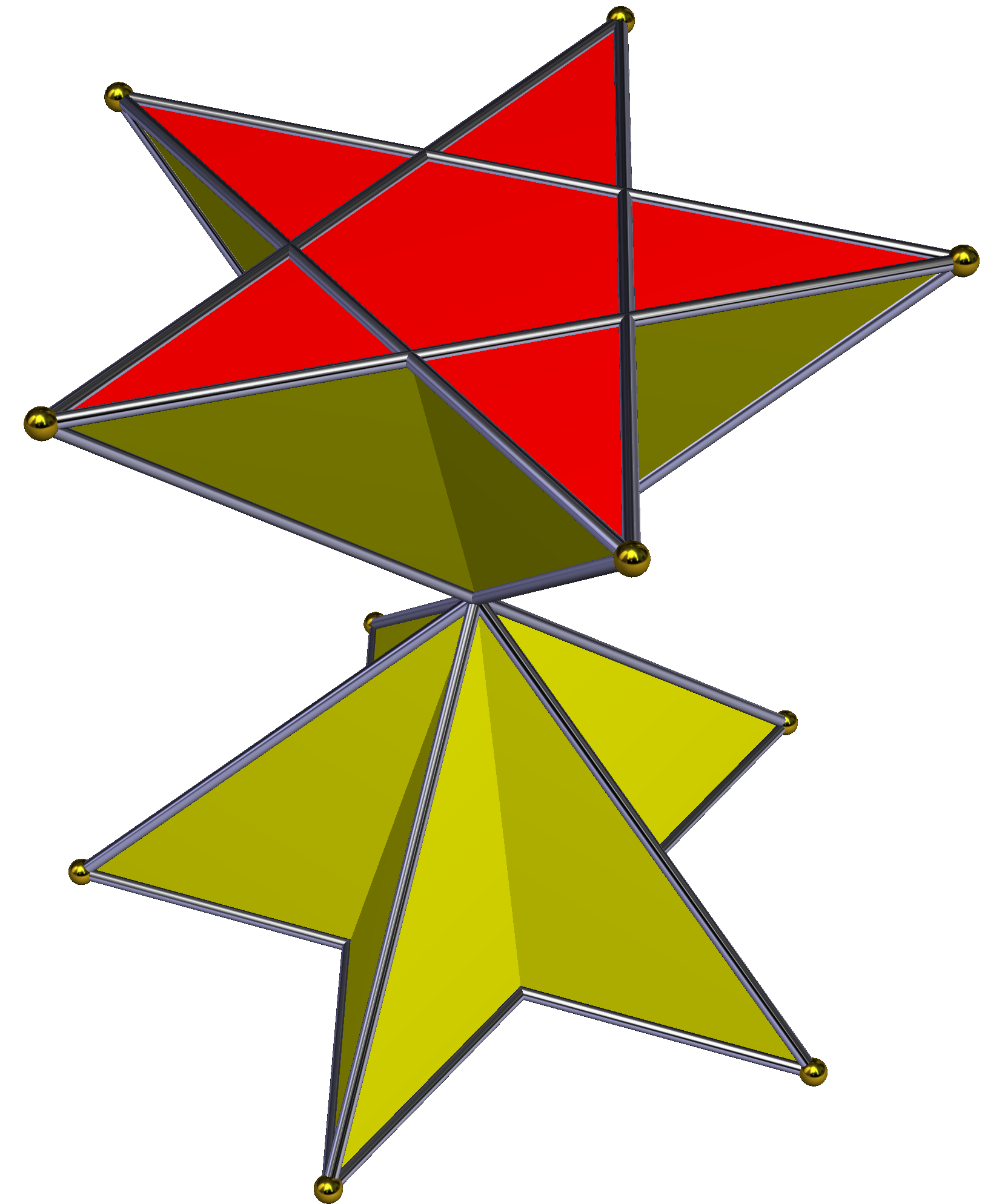 | 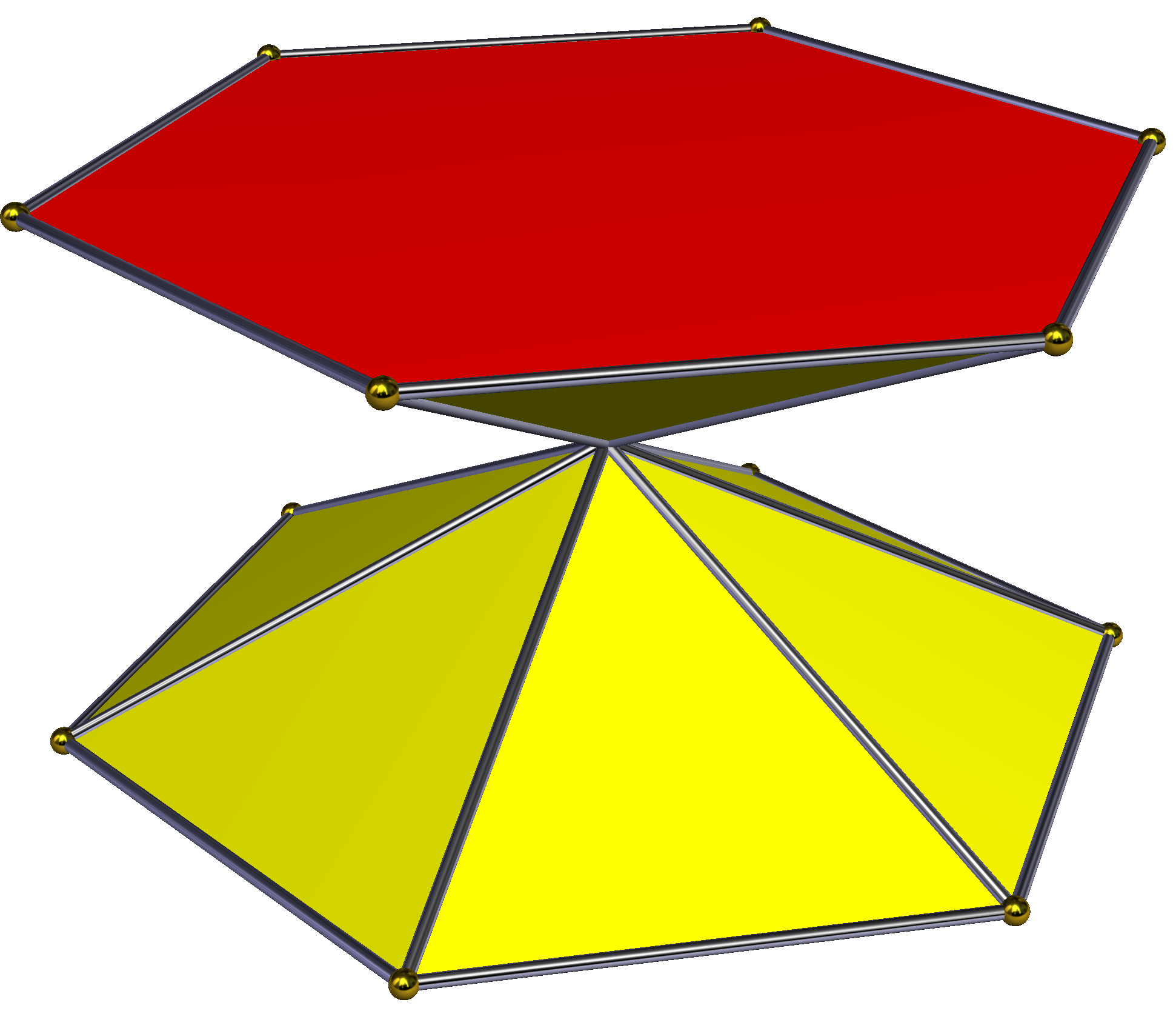 |
5. 6. 토로이달 각기둥
'''토로이달 각기둥'''은 밑면과 윗면이 없는, '교차 각기둥'과 같은 비볼록 다면체이며, 단순한 직사각형 옆면이 다면체를 닫고 있다. 이것은 짝수 변을 가진 밑면 다각형에 대해서만 가능하다. 이들은 위상적 토러스로, 오일러 지표는 0이다. 위상적 다면체 전개도는 정사각형 타일링의 두 행( 정점 배치 4.4.4.4)에서 잘라낼 수 있다. 각 직사각형에 연결된 n개의 정사각형 띠이다. n각형 토로이달 각기둥은 2n개의 꼭짓점, 2n개의 면(n개의 정사각형과 n개의 교차 직사각형), 그리고 4n개의 모서리를 갖는다. 이는 위상적으로 자기 쌍대 다면체이다.| D4h, 차수 16 | D6h, 차수 24 |
|---|---|
| V = 8, E = 16, F = 8 | V = 12, E = 24, F = 12 |
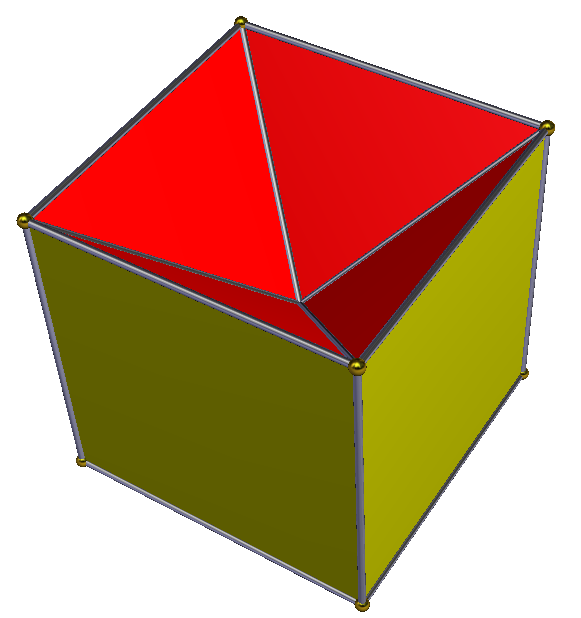 | 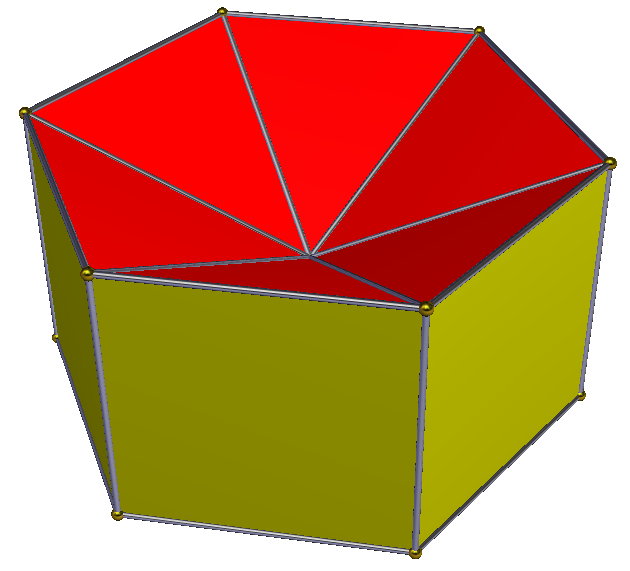 |
6. 각기둥 다포체
각기둥 다포체는 각기둥의 고차원적인 일반화이다. ''n''차원 각기둥 다포체는 다음 차원으로 이동된 두 개의 (''n'' − 1)차원 다포체로 구성된다.
각기둥 다포체를 만들 때, 원래 다포체의 각 차원 요소 수는 특정 규칙에 따라 변한다. ''Fi''개의 ''i''차원 면 요소(''i'' = 0, ..., ''n'')를 가진 ''n''차원 다포체를 기반으로 (''n'' + 1)차원 각기둥 다포체를 만들면, 이 각기둥 다포체는 2''Fi'' + ''F''''i''−1개의 ''i''차원 면 요소를 가진다. (단, ''F''−1 = 0, ''Fn'' = 1)
| 원본 다포체 (n차원) | 각기둥 다포체 (n+1차원) | ||
|---|---|---|---|
| 요소 | 개수 | 요소 | 개수 |
| 다각형 (n=2) | 3차원 각기둥 | ||
| 꼭짓점 | n | 꼭짓점 | 2n |
| 모서리 | n | 모서리 | 3n |
| 면 | 1 | 면 | 2 + n |
| 다면체 (n=3) | 4차원 각기둥 | ||
| 꼭짓점 | V | 꼭짓점 | 2V |
| 모서리 | E | 모서리 | 2E + V |
| 면 | F | 면 | 2F + E |
| 세포 | 1 | 세포 | 2 + F |
| 4차원 다포체 (n=4) | 5차원 각기둥 | ||
| 꼭짓점 | V | 꼭짓점 | 2V |
| 모서리 | E | 모서리 | 2E + V |
| 면 | F | 면 | 2F + E |
| 세포 | C | 세포 | 2C + F |
| 초세포 | 1 | 초세포 | 2 + C |
더 자세한 내용은 Uniform 4-다포체 및 Uniform 5-다포체 문서를 참조할 수 있다.
슐래플리 기호 {''p'',''q'',...,''t''}로 표현되는 정규 ''n''-다포체는 두 슐래플리 기호의 데카르트 곱으로 표현되는 균일 각기둥 (''n'' + 1)-다포체를 형성할 수 있다: {''p'',''q'',...,''t''}×{ }.
| 차원 | 원본 다포체 | 슐래플리 기호 | 각기둥 다포체 | 슐래플리 기호 | 비고 | 이미지 |
|---|---|---|---|---|---|---|
| 0 | 점 | 없음 | 선분 | { } | -- | |
| 1 | 선분 | { } | 직사각형 | { }×{ } | 두 개의 평행 이동된 선분으로 만들어짐. 정사각형인 경우 대칭을 줄여 {4}로 표현 가능. | -- |
| 2 | 다각형 ({p}) | {p} | 3차원 각기둥 | {p}×{ } | 두 개의 평행 이동된 다각형이 직사각형으로 연결됨. p=4이고 밑면이 정사각형이면 정육면체 ({4}×{ } = {4,3}). | -- |
| 3 | 다면체 ({p,q}) | {p,q} | 4차원 각기둥 | {p,q}×{ } | 두 개의 평행 이동된 다면체가 3차원 각기둥 세포로 연결됨. 밑면이 정육면체이면 초정육면체 ({4,3}×{ } = {4,3,3}). | -- |
고차 각기둥 다포체는 두 개 이상의 다포체의 데카르트 곱으로도 존재할 수 있다. 곱 다포체의 차원은 구성 요소의 차원의 합이다. 이러한 예시는 4차원 공간에 처음 존재하며, 두 다각형의 곱으로 만들어지는 4차원 다포체를 이중각기둥(duoprism)이라고 부른다.
정규 이중각기둥은 {''p''}×{''q''}로 표현되며, ''pq''개의 꼭짓점, 2''pq''개의 모서리, ''pq''개의 정사각형 면, ''p''개의 ''q''-각형 면, ''q''개의 ''p''-각형 면을 가진다. 이는 ''p''개의 ''q''-각형 각기둥과 ''q''개의 ''p''-각형 각기둥으로 경계가 정해진다.
예를 들어, {4}×{4}인 ''4-4 이중각기둥''은 초정육면체의 낮은 대칭 형태이며, {4,3}×{ }인 ''정육면체 각기둥''도 마찬가지이다. {4}×{4}×{ } (4-4 이중각기둥 각기둥), {4,3}×{4} (정육면체-4 이중각기둥), {4,3,3}×{ } (초정육면체 각기둥)은 5-정육면체의 낮은 대칭 형태이다.
참조
[1]
서적
Geometries and Transformations
Cambridge University Press
[2]
논문
Isogonal Prismatoids
[3]
서적
A Royal Road to Geometry: Or, an Easy and Familiar Introduction to the Mathematics
https://books.google[...]
author, and sold
[4]
서적
Key to the Complete Treatise on Practical Geometry and Mensuration: Containing Full Demonstrations of the Rules
https://books.google[...]
Longman, Brown, Green, and Longmans
[5]
서적
Solid Mensuration with proofs
[6]
서적
Engaging Young Students In Mathematics Through Competitions: World Perspectives And Practices
https://books.google[...]
World Scientific
[7]
서적
The facts on file: Geometry handbook
https://archive.org/[...]
[8]
웹사이트
Pictures of Twisted Prisms
http://www.korthalsa[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com