정육면체
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
정육면체는 모든 모서리의 길이가 같고, 각 면이 정사각형인 직육면체의 특수한 경우이다. 여섯 개의 면, 열두 개의 모서리, 여덟 개의 꼭짓점을 가지며, 다섯 개의 플라톤 입체 중 하나이다. 정육면체는 직육면체, 평행육면체, 대칭다면체, 육면체의 특수한 경우이며, 마주보는 면은 평행하고 인접한 면은 수직으로 교차한다. 부피는 한 변의 길이의 세제곱으로 계산되며, 겉넓이는 여섯 배의 면적과 같다. 정육면체는 공간을 채울 수 있는 유일한 정다면체이며, 건축, 디자인 등 다양한 분야에서 활용된다.
더 읽어볼만한 페이지
- 정다면체 - 사면체
사면체는 기하학에서 네 개의 꼭짓점, 여섯 개의 모서리, 네 개의 면으로 이루어진 다면체이며, 정사면체를 포함하여 다양한 종류가 존재하고 부피, 겉넓이 등을 계산하는 공식이 있으며, 다양한 분야에서 응용된다. - 정다면체 - 정팔면체
정팔면체는 8개의 면이 정삼각형으로 이루어진 정다면체로서 높은 대칭성을 가지며 정육면체와 쌍대 관계를 가지고 건축 및 디자인 분야에서 활용되고 공간을 채울 수 있는 특징을 지닌다. - 정육면체 - 카바
카바는 사우디아라비아 메카에 있는 이슬람교의 가장 신성한 장소로, 이슬람 이전부터 아랍인들의 성역이었으며 무함마드에 의해 이슬람의 중심 성지가 되었고, 아브라함과 이스마엘이 건설했다는 기록이 있는 '검은 돌'을 포함한 여러 유물이 있는 곳이며, 하즈와 움라 순례의 중심지이다. - 정육면체 - 입방정계
입방정계는 단순 입방, 체심 입방, 면심 입방의 세 가지 브라베 격자를 가지며, 다양한 결정 구조를 포함하여 물질의 특성을 결정하는 중요한 요소이다. - 수학 - 회귀 분석
회귀 분석은 종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하고 분석하는 통계적 기법으로, 최소 제곱법 개발 이후 골턴의 연구로 '회귀' 용어가 도입되어 다양한 분야에서 예측 및 인과 관계 분석에 활용된다. - 수학 - 수학적 최적화
수학적 최적화는 주어진 집합에서 실수 또는 정수 변수를 갖는 함수의 최댓값이나 최솟값을 찾는 문제로, 변수 종류, 제약 조건, 목적 함수 개수에 따라 다양한 분야로 나뉘며 여러 학문 분야에서 활용된다.
| 정육면체 | |
|---|---|
| 개요 | |
 | |
| 종류 | 플라톤의 입체 |
| 다른 이름 | 정육면체 입방체 헥사헤드론(hexahedron) |
| 면의 수 | 6 |
| 모서리의 수 | 12 |
| 꼭짓점의 수 | 8 |
| 면 | 정사각형 |
| 꼭짓점 도형 | 4.4.4 (43) |
| 대칭군 | 정팔면체 대칭 (Oh) |
| 쌍대다면체 | 정팔면체 |
| 성질 | 볼록 다면체, 면-추이, 모서리-추이, 꼭짓점-추이 |
| 기하학적 특징 | |
| 각도 | 90° |
| 슐레플리 기호 | {4, 3} |
| 위토프 기호 | 3 | 2 4 |
| 활용 | |
| 관련 항목 | 평행다면체 띠면체 플레시오헤드론 해너 폴리토프 |
| 영어 | |
| 영어 이름 | cube |
| 접두사 | regular hexahedron (정육면체) |
| 기타 언어 | |
| 독일어 | Würfel (뷔아펠) |
| 프랑스어 | cube |
| 스페인어 | cubo |
2. 성질
- 직육면체, 비틀린 이면각뿔의 특수한 형태이며, 평행다면체, 대칭다면체, 육면체의 일종이다.
- 1m3는 한 변이 1m인 정육면체의 부피로 정의된다. 1dm3(=1L), 1cm3 등도 마찬가지이다.
- 전개도는 11가지이다.
- 각 변의 길이가 1인 작은 정육면체를 ''k''3개 사용하여 각 변의 길이 ''k''인 정육면체를 만들었을 때, 동시에 볼 수 있는 작은 정육면체는 최대 3''k''2−3''k''+1개이다.
- 정다면체 중 유일하게 단독으로 공간 채우기가 가능하며, 이때의 배치는 단순 입방 격자 구조가 된다.
- 면의 수는 6, 변의 수는 12, 꼭짓점의 수는 8이다. 이들은 en의 제4단계(Layer 3)의 삼각형 각 단계의 숫자의 총합과 같다.
- 꼭짓점 모양은 정삼각형이며, 3개의 변과 3개의 정사각형이 모인다. 이들은 파스칼의 삼각형의 제4단계의 2, 3번째 값과 같다.
- 정팔면체와 쌍대이다.
2. 1. 기하학적 성질
정육면체는 모서리의 길이가 모두 같은 직육면체의 특수한 경우이다. 다른 직육면체와 마찬가지로, 정육면체의 각 면은 네 개의 꼭짓점을 가지며, 각 꼭짓점은 세 개의 합동인 선분(모서리)에 연결된다. 이러한 모서리들은 정사각형 면을 형성하며, 따라서 두 인접한 정사각형 사이의 이면각은 정사각형의 내각인 90°가 된다. 따라서 정육면체는 여섯 개의 면, 열두 개의 모서리, 여덟 개의 꼭짓점을 갖는다. 모든 정다각형이 합동이며 각 꼭짓점에서 같은 수의 면이 만나는 다면체인 다섯 개의 플라톤 입체 중 하나로 분류된다.정육면체는 팔면체 대칭군 을 갖는다. 이는 평면으로 절반으로 자르는 반사 대칭과 축을 중심으로 회전시켜 모양이 바뀌지 않는 회전 대칭으로 구성된다. 반사 대칭은 9개가 있는데, 5개는 모서리의 중간점을 지나 정육면체를 자르고, 4개는 대각선으로 자른다. 정육면체는 팔면체 회전 대칭군 를 갖는다. 세 개의 축은 정육면체의 마주보는 면의 중심을 지나고, 여섯 개의 축은 마주보는 모서리의 중간점을 지나며, 네 개의 축은 마주보는 꼭짓점을 지난다. 이러한 축들은 각각 4회 회전 대칭(0°, 90°, 180°, 270°), 2회 회전 대칭(0° 및 180°), 3회 회전 대칭(0°, 120°, 240°)이다.[1]
쌍대 다면체는 극대칭이라고 알려진 과정을 통해 각 다면체의 꼭짓점에 접하는 평면으로부터 얻을 수 있다. 일반적으로 쌍대 다면체의 한 가지 특징은 다면체와 그 쌍대 다면체가 3차원 대칭 점군을 공유한다는 것이다. 정육면체의 쌍대 다면체는 정팔면체이며, 두 다면체 모두 팔면체 대칭이라는 동일한 대칭을 갖는다.[2]
정육면체는 면 전이적인데, 이는 두 정사각형이 서로 같고 회전과 반사를 통해 사상될 수 있음을 의미한다. 또한 모든 꼭짓점이 동등하며 그 대칭성 하에서 등거리적으로 사상될 수 있는 꼭짓점 전이적이며, 각 꼭짓점을 둘러싼 면의 종류가 같고 순서가 같거나 반대이며, 모든 두 인접한 면은 같은 이면각을 갖는다는 것을 의미하는 모서리 전이적이다. 따라서 정육면체는 이러한 성질을 필요로 하기 때문에 정다면체이다.[3]
정육면체는 모든 직육면체 중 특별한 경우이다. 정육면체는 모서리의 길이가 모두 같은 직사각형 직육면체로 나타낼 수 있으며, 모든 면이 정사각형이다.[4] 또한 모든 모서리의 길이가 같은 평행육면체로 간주할 수 있다.[5]
정육면체는 플레시오헤드론(plesiohedron)이며, 공간 채우기 다면체의 특별한 종류로, 대칭적 델로네 집합(Delone set)의 보로노이 셀(Voronoi cell)로 정의할 수 있다.[6] 플레시오헤드론에는 평행다면체(parallelohedron)가 포함되는데, 이는 회전 없이 병진하여 공간을 채울 수 있다. 이를 벌집(Honeycomb (geometry))이라고 하며, 각 복제본의 각 면은 다른 복제본의 같은 면에 붙어 있다. 평행다면체에는 다섯 가지 종류가 있으며, 그중 하나가 직육면체이다.[7] 모든 3차원 평행다면체는 조노헤드론(zonohedron)이며, 중심 대칭(centrally symmetric) 다면체로, 면은 중심 대칭 다각형(Zonogon)이다.[8]
- 마주보는 면들은 평행하며, 인접하는 면들은 서로 수직으로 교차한다. 한 꼭짓점을 공유하는 변들은 수직으로 교차하지만, 접점을 갖지 않는 변들은 평행하거나 꼬인 위치에 있다. (직육면체의 성질)[9]
- 정다면체 중 유일하게 단독으로 공간 채우기가 가능하며, 이때의 이 입체의 배치는 단순 입방 격자 구조가 된다.[10]
- 면의 수는 6, 변의 수는 12, 꼭짓점의 수는 8이다. 이들은 en의 제4단계(Layer 3)의 삼각형 각 단계의 숫자의 총합과 같다. 반대쪽 꼭짓점끼리 잇는 대각선을 따라 볼 경우, 면 (기하학), 변, 꼭짓점은 각 단계의 값대로 분할된다.[11]
- 꼭짓점 모양은 정삼각형이며, 3개의 변과 3개의 정사각형이 모인다. 이들은 파스칼의 삼각형의 제4단계의 2, 3번째 값과 같다.[12]
- 정팔면체와 쌍대이다.[13]
2. 2. 공식
한 모서리의 길이가 인 정육면체의 부피와 겉넓이는 다음과 같다.:
:
정육면체의 면대각선은 한 변의 길이가 인 정사각형의 대각선으로, 이다. 그리고 정육면체의 공간대각선은 같은 면에 놓이지 않은 두 꼭짓점을 잇는 선분으로, 으로 나타낼 수 있다. 두 공식 모두 피타고라스 정리를 이용하여 구할 수 있다.
또한 외접한 구의 반지름은 , 모서리와 접하는 구의 반지름은 , 내접한 구의 반지름은 이다.
2. 3. 단위 정육면체
좌표평면상에서 모든 변의 길이와 면의 넓이가 1인 정육면체이다. 원점을 한 꼭짓점으로 하며, 각 꼭짓점의 좌표는 이진법으로 0~7까지의 수들에 대응시킬 수 있다.
각 변의 길이를 단위 길이로 측정하는 단위 정육면체의 경우, 각 면은 단위 정사각형이며 전체 부피는 1세제곱 단위이다.[3] 라인강의 루퍼트 공작의 이름을 딴 루퍼트의 정육면체는 약 6% 더 긴 변을 가지고 있음에도 불구하고, 단위 정육면체에 뚫린 구멍을 통과할 수 있는 가장 큰 정육면체이다.[5]
3. 그래프 표현
정육면체의 뼈대는 8개의 꼭짓점과 12개의 모서리를 갖는 그래프를 이룬다. 초입방체 그래프의 특수한 경우이다.[51] 슈타이니츠의 정리에 따르면, 그래프는 다면체의 골격으로 나타낼 수 있다. 정육면체의 골격은 플라톤 그래프인 '''정육면체 그래프'''라고 불리며, 정육면체와 같은 수인 8개의 꼭짓점과 12개의 모서리를 가지고 있다.
정육면체 그래프는 초입방체 그래프의 특수한 경우이며, 두 개의 정사각형 그래프()를 곱하여 만들 수 있다. 즉, 두 개의 정사각형의 각 꼭짓점을 모서리로 연결하여 구성된다. 정육면체 그래프는 으로 표시할 수 있다.
정육면체 그래프는 평면 그래프이면서 3-연결 그래프이다. 즉, 그래프의 모서리는 다른 모서리를 교차하지 않고 모든 꼭짓점에 연결되며, 세 개 이상의 꼭짓점을 가진 그래프에서 두 개의 꼭짓점을 제거해도 모서리는 연결된 상태를 유지한다. 또한, 정육면체 그래프는 단위 거리 그래프와 프리즘 그래프의 예시이다.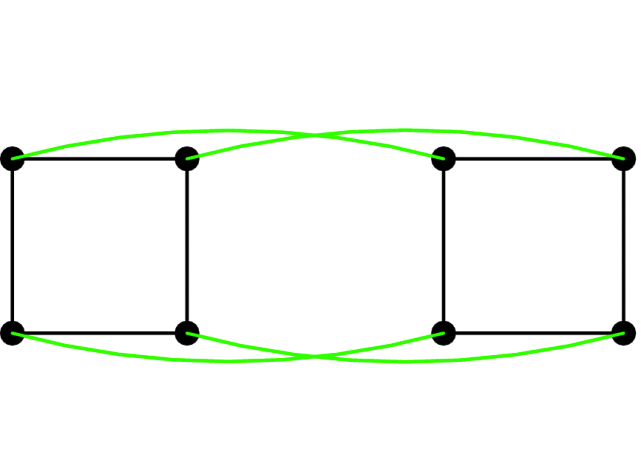
4. 전개도
정육면체를 만드는 기본적인 방법은 전개도를 사용하는 것이다. 전개도는 모서리로 연결된 다각형들을 배열하여 다면체를 구성하는 것이다. 정육면체의 전개도는 11가지가 존재한다.[1]
5. 역사 및 문화
플라톤 다면체는 고대부터 알려진 다면체의 집합이다. 플라톤은 『티마이오스』에서 정육면체를 지구의 원소와 연관시켰고,[1] 유클리드는 『원론』에서 정육면체를 포함한 플라톤 다면체를 정의하고 그 성질을 연구했다.[2]
요하네스 케플러는 우주의 조화에서 정육면체를 포함한 플라톤 다면체들을 스케치했고, 우주 신비에서는 플라톤 다면체를 이용한 태양계 모형을 제시했다. 케플러의 태양계 모형에서 다면체들은 안쪽에서 바깥쪽으로 정팔면체, 정이십면체, 정십이면체, 정사면체, 정육면체 순으로 배열되었다.[1]
5. 1. 고대
플라톤 다면체는 고대부터 알려진 다면체의 집합이다. 플라톤은 그의 저서 『티마이오스』에서 정육면체를 흙(지구)의 원소와 연관시켰다.[1] 유클리드는 『원론』에서 정육면체를 정의하고 그 성질을 연구했다.[2] 중국의 고대 문헌 『구장산술』에서는 정육면체의 부분을 나누어 연구했다.5. 2. 근대
요하네스 케플러는 그의 저서 『우주의 조화』에서 정육면체를 포함한 플라톤 다면체들을 스케치했고, 『우주 신비』에서는 플라톤 다면체를 이용한 태양계 모형을 제시했다.[1] 케플러가 제시한 태양계 모형에서 정렬된 다면체는 안쪽에서 바깥쪽으로 정팔면체, 정이십면체, 정십이면체, 정사면체, 그리고 정육면체 순이었다.[1]6. 관련 다면체
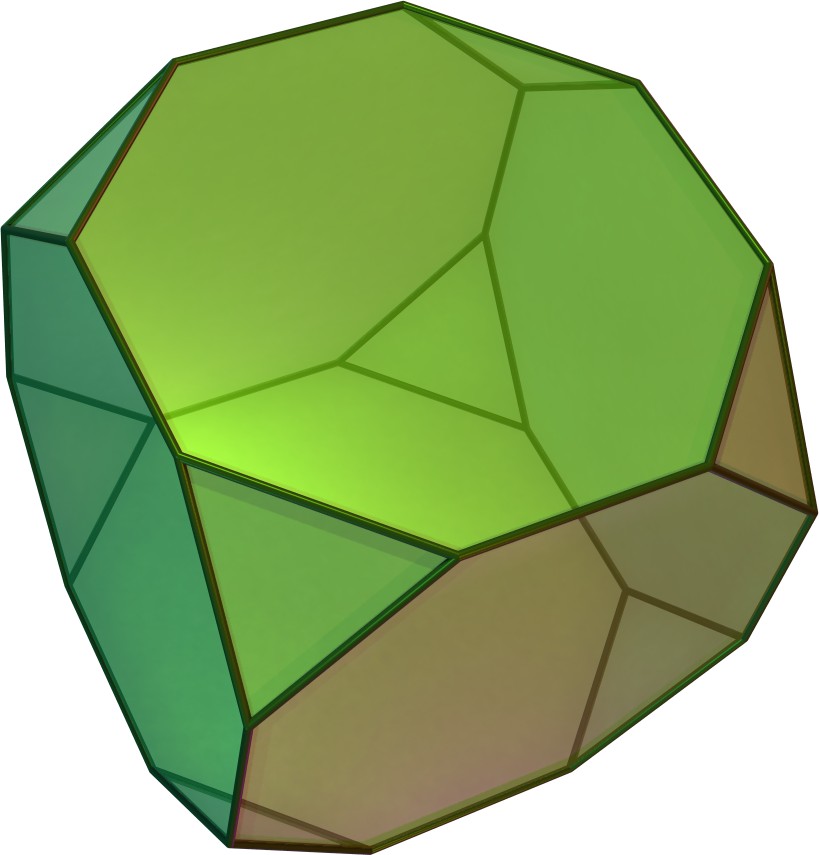
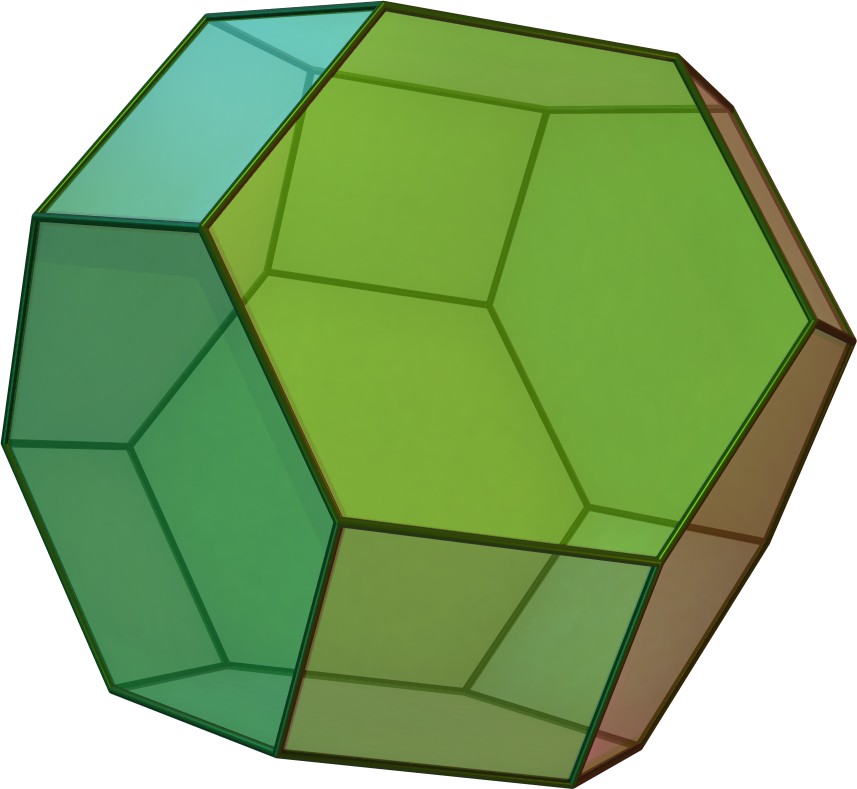
깎은 정육면체는 정육면체의 각 꼭짓점을 절단하여 만들 수 있는 아르키메데스 다면체이다. 모서리가 잘리면 마름모십이면체가 된다. 육팔면체와 깎은 정팔면체 또한 정육면체와 관련이 있는 다면체이다.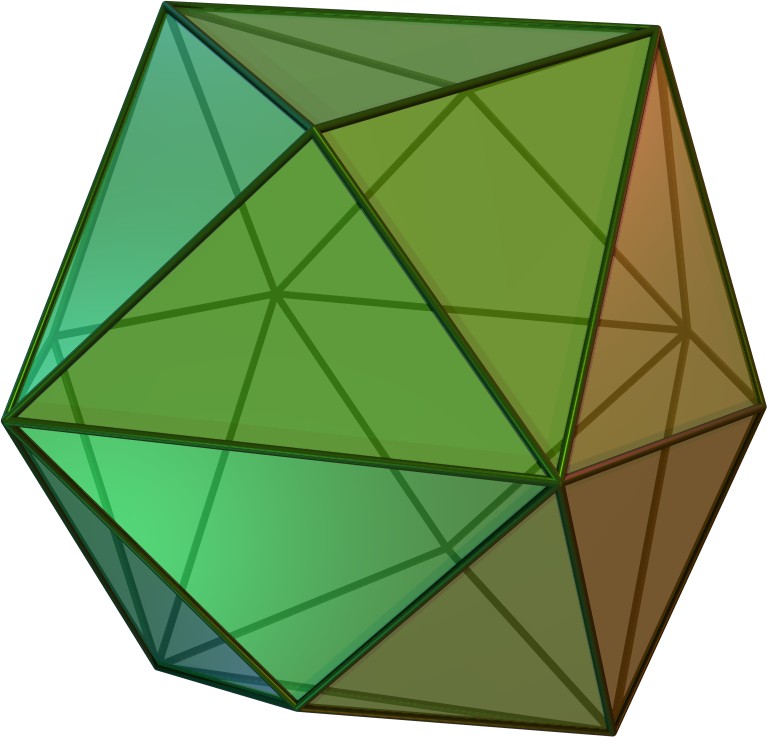
정육면체를 변형하여 만들 수 있는 다면체로는 별팔면체와 사방십이면체 등이 있다. 별팔면체는 정육면체의 깎기(faceting), 즉 새로운 꼭짓점을 만들지 않고 다각형 면의 일부를 제거하면 만들 수 있다. 사방십이면체는 정육면체의 각 정사각형 면에 정사각뿔을 붙여 만들 수 있다.
그 외에도 정사면체, 정십이면체 등 다른 정다면체와도 관련이 있다.
7. 응용
정육면체는 유일하게 단독으로 공간 채우기가 가능하며, 이때의 배치는 단순 입방 격자 구조가 된다.[1] 1m3와 같이 부피 단위의 정의에도 사용된다. 1m3는 한 변이 1m인 정육면체의 부피로 정의되며, 1dm3(=1L), cm3 등도 마찬가지이다.[1] 정육면체는 건축, 디자인, 결정학 등 다양한 분야에서 활용된다.
8. 추가 정보
정육면체는 구조 행렬로 나타낼 수 있다. 구조 행렬은 행과 열이 다면체의 요소(꼭짓점, 모서리, 면)에 대응하는 행렬이다. 행렬의 대각선은 다면체에 나타나는 각 요소의 개수를 나타내고, 대각선이 아닌 부분은 열 요소가 행 요소에 포함되거나 위치하는 개수를 나타낸다. 정육면체는 8개의 꼭짓점, 12개의 모서리, 6개의 면을 가지고 있으며, 행렬 대각선의 각 요소는 8, 12, 6으로 표시된다. 가운데 행의 첫 번째 열은 각 모서리에 (즉, 양 끝에) 2개의 꼭짓점이 있음을 나타내며, 2로 표시된다. 첫 번째 행의 가운데 열은 각 꼭짓점에서 3개의 모서리가 만남을 나타내며, 3으로 표시된다. 구조 행렬은 다음과 같다.[11]
참조
[1]
서적
Convex Polyhedra
Springer
[2]
서적
The Princeton Companion to Mathematics
https://books.google[...]
Princeton University Press
[3]
서적
Gems of Geometry
https://books.google[...]
Springer
[4]
서적
Technical Mathematics
https://books.google[...]
John Wiley & Sons
[5]
학술지
Finite 3-orbit polyhedra in ordinary space, II
[6]
서적
Polyhedra
https://archive.org/[...]
Cambridge University Press
[7]
서적
Regular Polytopes
https://archive.org/[...]
Dover Publications
[8]
서적
Mathematical models
Clarendon Press
[9]
서적
A First Course in Graph Theory
https://books.google[...]
Dover Publications
[10]
학술지
Zonotopes, dicings, and Voronoi's conjecture on parallelohedra
[10]
학술지
Tilings with congruent tiles
[11]
서적
Beautiful Mathematics
https://books.google[...]
Mathematical Association of America
[12]
학술지
Reflections on a Cube
[13]
학술지
Isogonal Prismatoids
[14]
서적
Convex Polytopes
Springer-Verlag
[15]
학술지
The projection of fourfold figures on a three-flat
[16]
서적
The Thirteen Books of Euclid's Elements
https://archive.org/[...]
Cambridge University Press
[17]
학술지
A survey of the theory of hypercube graphs
[18]
arXiv
Some New Equiprojective Polyhedra
2010-00-00
[19]
서적
Geometry: Our Cultural Heritage
https://books.google[...]
Springer
[20]
학술지
Products of unit distance graphs
[21]
서적
Geometry: Reteaching Masters
Holt Rinehart & Winston
[22]
서적
Number, Shape, & Symmetry: An Introduction to Number Theory, Geometry, and Group Theory
https://books.google[...]
Taylor & Francis
[23]
arXiv
Hypercube unfoldings that tile and
[24]
학술지
Facetting Diagrams
[25]
학술지
Mathematics Hiding in the Nets for a CUBE
[26]
학술지
Convex polyhedra with regular faces
[27]
학술지
Platonic passages
Mathematical Association of America
2017-04-00
[28]
서적
Guide to Objective Arithmetic
https://books.google[...]
Pearson Education
[29]
컨퍼런스
Yaroslavl International Conference "Discrete Geometry" dedicated to the centenary of A.D.Alexandrov (Yaroslavl, August 13-18, 2012)
https://www.dcglab.u[...]
P.G. Demidov Yaroslavl State University, International B.N. Delaunay Laboratory
[30]
서적
Comprehensive Inorganic Chemistry II: From Elements to Applications
https://books.google[...]
Newnes
[31]
서적
The Golden Ratio: The Story of Phi, the World's Most Astonishing Number
https://books.google[...]
Broadway Books
[32]
서적
Graph Theory and Computing
https://books.google[...]
Academic Press
[33]
학술지
The Algebra of Geometric Impossibility: Descartes and Montucla on the Impossibility of the Duplication of the Cube and the Trisection of the Angle
https://onlinelibrar[...]
[34]
학술지
Dungeons, dragons, and dice
[35]
서적
Maths Dictionary
https://books.google[...]
Heinemann
[36]
논문
Regular polytope distances
http://forumgeom.fau[...]
[37]
서적
Configuration from a Graphical Viewpoint
https://books.google[...]
Springer
[38]
학회발표
19th Japan Conference on Discrete and Computational Geometry, Graphs, and Games (JCDCG^3 2016)
[39]
문서
Table I(i), pp. 292–293. See the columns labeled , , and , Coxeter's notation for the circumradius, midradius, and inradius, respectively, also noting that Coxeter uses as the edge length (see p. 2).
[40]
서적
Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem
https://books.google[...]
Hindustan Book Agency
[41]
서적
The Mathematics of Finite Networks: An Introduction to Operator Graph Theory
https://books.google[...]
Cambridge University Press
[42]
서적
Introduction to the Mathematics of Quasicrystals
Academic Press
[43]
논문
Space-filling zonotopes
[44]
서적
Methods of Geometry
https://books.google[...]
John Wiley & Sons
[45]
논문
Composite Concave Cupolae as Geometric and Architectural Forms
https://www.helderma[...]
[46]
서적
Interdisciplinarity, Creativity, and Learning: Mathematics With Literature, Paradoxes, History, Technology, and Modeling
Information Age Publishing, Inc.
[47]
논문
Junction of Non-composite Polyhedra
https://www.ams.org/[...]
[48]
서적
The Beauty of Geometry: Twelve Essays
https://books.google[...]
Dover Publications
[49]
서적
ICGG 2018 - Proceedings of the 18th International Conference on Geometry and Graphics 40th Anniversary - Milan, Italy, August 3-7, 2018
Springer
[50]
서적
Lectures on Polytopes
Springer-Verlag
[51]
웹인용
Cubical graph
https://mathworld.wo[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com




