다중공선성

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

다중공선성은 회귀 분석에서 둘 이상의 설명 변수가 높은 선형 관계를 갖는 상황을 의미한다. 이는 변수 간의 완전한 선형 관계인 공선성의 확장된 개념으로, 최소제곱법을 사용한 회귀 계수 추정의 어려움을 야기하고, 표준 오차를 증가시켜 통계적 유의성을 떨어뜨릴 수 있다. 다중공선성은 불필요한 변수 포함, 더미 변수 함정, 자료 부족, 변수 간 내재적 상관관계 등의 원인으로 발생하며, 변수 제거, 변수 변형, 릿지 회귀, 자료 추가 등의 방법으로 해결할 수 있다. 그러나 변수 제거는 정보 손실을 초래할 수 있으며, 사후 분석은 결과의 신뢰성을 저해할 수 있으므로 주의해야 한다.

더 읽어볼만한 페이지

회귀분석 - 회귀 분석
회귀 분석은 종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하고 분석하는 통계적 기법으로, 최소 제곱법 개발 이후 골턴의 연구로 '회귀' 용어가 도입되어 다양한 분야에서 예측 및 인과 관계 분석에 활용된다.
회귀분석 - 로지스틱 회귀
로지스틱 회귀는 범주형 종속 변수를 다루는 회귀 분석 기법으로, 특히 이항 종속 변수에 널리 사용되며, 오즈에 로짓 변환을 적용하여 결과값이 0과 1 사이의 값을 가지도록 하는 일반화 선형 모형의 특수한 경우이다.
실험 설계 - 무작위 대조 시험
실험 설계 - 실험군과 대조군
실험군과 대조군은 임상 연구에서 새로운 방법이나 약물의 효과를 평가하기 위해 사용되는 두 그룹으로, 대조군은 비교 기준이 되며, 실험군은 새로운 치료법을 받는 그룹이다.
통계학 - 확률
확률은 사건의 가능성을 수치화한 개념으로, 도박에서 시작되어 수학적으로 발전했으며, 다양한 해석과 요소, 응용 분야를 가지며 양자역학, 사회 현상 등에도 적용된다.
통계학 - 사분위수
사분위수는 정렬된 데이터를 4등분하는 세 개의 값으로 데이터 분포 요약 및 이상치 탐지에 활용되며, 제1사분위수(Q₁)는 하위 25%, 제2사분위수(Q₂ 또는 중앙값)는 하위 50%, 제3사분위수(Q₃)는 하위 75%를 나타낸다.

다중공선성
개요
정의	회귀 분석에서 예측 변수 간의 높은 상관 관계
다른 이름	공선성 공선형성 다중 공선성
문제점
모형의 불안정성	계수 추정치의 높은 표준 오차
변수 중요도 해석의 어려움	특정 예측 변수의 효과를 정확히 분리하기 어려움
진단 방법
상관 행렬	예측 변수 간의 상관 계수 확인
분산 팽창 지수 (VIF)	각 예측 변수에 대한 VIF 값 계산 (일반적으로 5 또는 10 이상이면 다중공선성 문제 의심)
고유값 및 조건 지수	모멘트 행렬의 고유값이 0에 가까우면 다중공선성 가능성 높음
해결 방법
변수 제거	상관 관계가 높은 변수 중 하나를 제거
주성분 분석 (PCA)	변수들을 서로 상관 없는 주성분으로 변환
릿지 회귀	계수 추정치에 제약 조건을 추가하여 모형의 안정성을 높임
데이터 추가	데이터가 충분하지 않아 발생하는 문제일 경우, 데이터를 추가하여 해결 가능
추가 정보
주의 사항	다중공선성이 항상 나쁜 것은 아님. 예측에는 영향이 없을 수 있지만, 변수 해석에는 영향을 미침

2. 정의

다중공선성은 둘 이상의 독립 변수들이 서로 높은 선형 관계를 가질 때 발생한다.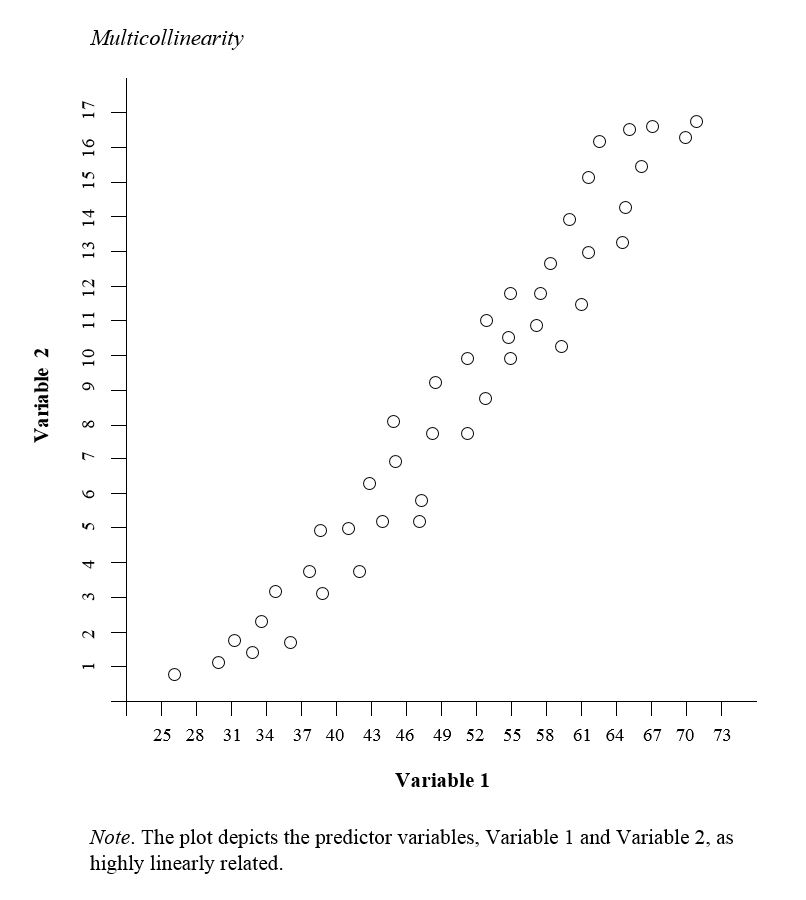

실제로는 데이터 세트에서 완전한 다중공선성에 직면하는 경우는 거의 없다. 보다 일반적으로는, 둘 이상의 독립 변수 사이에 근사적인 선형 관계가 있을 경우에 다중공선성의 문제가 발생한다.

수학적으로, 변수들 사이에 하나 이상의 엄밀한 선형 관계가 존재하지 않더라도, 다음과 같이 오차항

v_i

를 더한 형태로 식이 성립하는 경우가 있다.

:

\lambda_0 + \lambda_1 X_{1i} + \lambda_2 X_{2i} + \cdots + \lambda_k X_{ki} + v_i = 0

이 경우, 변수 사이에 정확한 선형 관계는 없지만,

v_i

의 분산이

\lambda

값의 몇몇 세트에 대해 작은 경우, 변수

X_j

는 거의 완전한 다중공선성을 가진다. 이 경우, 행렬 X^TX는 역행렬을 가지지만, 불량 조건이다. 따라서, 컴퓨터 알고리즘이 근사적인 역행렬을 계산할 수 있는지는 불분명하다. 또한, 계산할 수 있었다고 해도, 계산된 역행렬은 데이터의 약간의 변화(반올림 오차나 샘플된 데이터 포인트의 약간의 변화의 영향이 커지기 때문에)에 매우 민감하며, 매우 부정확하거나, 샘플에 의존할 가능성이 있다.

중회귀 방정식

:

Y_{i} = \beta _0 + \beta _1 X_{1i} + \cdots + \beta _k X_{ki} + \varepsilon _{i}

의 파라미터 추정치를 구하기 위해 최소제곱법(OLS)을 이용할 경우, 행렬

X^{T} X

의 역행렬을 구해야 한다.

2. 1. 완전 다중공선성

완전 다중공선성은 예측 변수가 선형 종속 관계에 있는 상황을 의미한다. 즉, 하나의 변수를 다른 변수의 정확한 선형 함수로 나타낼 수 있다.^[8] 최소 자승법은 행렬

X^{\mathsf{T}}X

의 역행렬을 구해야 하는데, 독립 변수 간에 정확한 선형 관계가 있는 경우 이 행렬의 역행렬은 존재하지 않게 된다.

:

X = \begin{bmatrix}1 & X_{11} & \cdots & X_{k1}  \\\vdots & \vdots & & \vdots \\1 & X_{1N} & \cdots & X_{kN}\end{bmatrix}

여기서 ''

N \times (k+1)

'' 행렬이며, ''

N

''은 관측치 수, ''

k

''는 설명 변수 수, ''

N \ge k+1

''이다. 독립 변수 간에 정확한 선형 관계가 있는 경우,

X

의 열 중 적어도 하나는 다른 열들의 선형 결합이 되므로

X

(그리고

X^{\mathsf{T}}X

)의 계수는 ''

k+1

''보다 작고, 행렬

X^{\mathsf{T}}X

는 역행렬이 존재하지 않게 된다.

완전 공선성은 일반적으로 회귀 분석에 중복 변수를 포함시켜 발생한다. 예를 들어, 소득, 지출, 저축 변수가 있을 때 소득은 정의상 지출과 저축의 합과 같으므로, 회귀 분석에 이 3개의 변수를 모두 동시에 포함하는 것은 옳지 않다. 마찬가지로, 모든 범주(예: 여름, 가을, 겨울, 봄)에 대한 더미 변수와 절편 항을 포함하면 완전 공선성이 발생하는데, 이를 더미 변수 함정이라고 한다.^[9]

최소 제곱법을 사용하려고 시도할 때 관측치보다 변수가 더 많은 매우 광범위한 데이터 세트의 경우에도 완전 공선성이 발생할 수 있다.

'''공선성'''은 두 설명 변수 사이에 직선적인 관련성이 있는 것이다. 두 변수 사이에 정확한 선형 관계가 있는 경우, 두 변수는 완전한 공선성을 가진다. 예를 들어,

X_{1}

과

X_{2}

는 모든 관측치 i 에 대해 다음과 같은 파라미터

\lambda_0

과

\lambda_1

이 존재할 경우, 완전한 공선성을 가진다고 할 수 있다.

:

X_{2i} = \lambda_0 + \lambda_1 X_{1i}

'''다중공선성'''은 중회귀 모델에서 2개 이상의 설명 변수가 높은 선형 관계에 있는 상황을 가리킨다. 예를 들어, 위의 식과 같이, 두 독립 변수의 상관 관계가 1 또는 -1과 같을 경우, 완전한 다중공선성이 있다고 할 수 있다.

수학적으로, 어떤 변수 사이에 하나 이상의 엄밀한 선형 관계가 존재하는 경우, 그 변수들의 집합은 완전한 다중공선성을 가진다. 예를 들어, 다음과 같은 경우이다.

:

\lambda_0 + \lambda_1 X_{1i} + \lambda_2 X_{2i} + \cdots + \lambda_k X_{ki} = 0

여기서,

\lambda_k

는 상수이며,

X_{ki}

는 k번째 설명 변수에 관한 i번째 관측치이다.

2. 2. 불완전 다중공선성

불완전 다중공선성은 독립 변수들 간에 높은 상관관계가 존재하지만, 완벽한 선형 관계는 아닌 경우를 말한다. 이 경우 회귀 계수의 추정은 가능하지만, 추정치의 표준 오차가 커져 통계적 유의성이 떨어질 수 있다.^[8]

변수

X_j

가 거의 공선성을 띨 때, 행렬

X^{\mathsf{T}}X

는 역행렬을 가지지만, 조건이 나쁜 행렬이 된다. 컴퓨터 알고리즘은 근사 역행렬을 계산할 수도 있고, 그렇지 못할 수도 있다. 설령 계산할 수 있다 하더라도, 결과로 얻은 역행렬은 큰 반올림 오차를 가질 수 있다. 행렬의 조건 불량을 측정하는 표준 척도는 조건 지수이다. 이는 행렬의 역행렬이 유한 정밀 숫자로 수치적으로 불안정하여, 계산된 역행렬이 원래 행렬의 작은 변화에 민감할 가능성이 있음을 나타낸다. 조건수는 설계 행렬의 최대 특이값을 최소 특이값으로 나누어 계산한다.^[10] 공선 변수의 맥락에서 분산 팽창 요인은 특정 계수의 조건수이다.

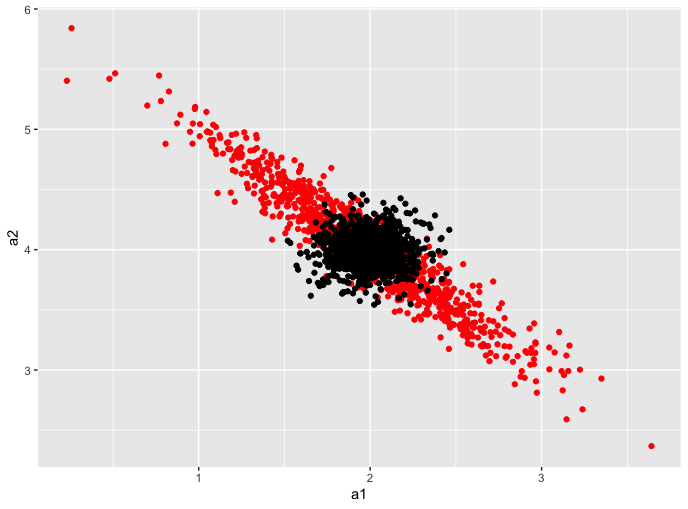
수치적 문제 외에도 불완전한 공선성은 변수의 정확한 추정을 어렵게 만든다. 즉, 상관관계가 높은 변수는 추정치가 부실하고 표준 오차가 커진다.

예를 들어, 앨리스가 비가 올 때마다 부츠를 신고, 비가 올 때만 물웅덩이가 있다고 가정해 보자. 그렇다면 앨리스가 비가 발에 닿지 않도록 부츠를 신는 것인지, 아니면 물웅덩이에 발을 담갔을 때 발을 건조하게 유지하기 위해 부츠를 신는 것인지 알 수 없다.

두 변수 각각이 얼마나 중요한지 식별하려고 할 때의 문제는 이 변수들이 서로 교란된다는 것이다. 즉, 관찰 결과가 두 변수 모두에 의해 동일하게 잘 설명되므로 관찰된 상관관계를 유발하는 변수가 무엇인지 알 수 없다.

이 정보를 발견하는 데에는 두 가지 방법이 있다.

1. 사전 정보 또는 이론을 사용한다. 예를 들어 앨리스가 물웅덩이에 절대 발을 담그지 않는다는 것을 알게 된다면, 물웅덩이에 들어가는 것을 피하기 위해 부츠가 필요한 것이 아니므로 앨리스가 부츠를 신는 이유가 물웅덩이가 아니라고 합리적으로 주장할 수 있다.

2. 더 많은 데이터를 수집한다. 앨리스를 충분히 관찰하면 결국 비는 오지 않지만 물웅덩이가 있는 날(예: 앨리스가 집을 나서기 전에 비가 그치는 경우)을 보게 될 것이다.

3. 진단법

다중공선성은 다음과 같은 방법으로 진단할 수 있다.

결정계수(R²) 값이 높아 회귀식의 설명력은 높지만, 식 안의 독립변수의 P값(P-value)이 커서 개별 인자들이 유의하지 않는 경우가 있다. 이런 경우 독립변수들 간에 높은 상관관계가 있다고 의심할 수 있다.
예측 변수를 추가하거나 제거했을 때 추정 회귀 계수의 큰 변화가 생기는 경우
다중 회귀에서 영향을 받는 변수의 회귀 계수가 유의하지 않지만, 그 계수가 모두 0이라는 복합 가설(결합 가설)이 기각되는 경우 (F 검정 사용)
다변량 회귀에서 특정 설명 변수의 계수가 유의하지 않더라도, 해당 설명 변수에 대한 피설명 변수의 단순 회귀에서 해당 계수가 0에서 유의하게 다른 경우. 이러한 상황은 다변량 회귀에서 다중공선성을 나타낸다.
데이터 섭동 처리: 데이터에 임의의 노이즈를 더하여 여러 번 회귀를 반복하고, 계수가 얼마나 변하는지를 관찰하여 다중공선성을 탐지할 수 있다.^[22]

이 외에도 상관관계 분석, 분산팽창요인(VIF), 조건수, Farrar–Glauber 검정 등의 방법이 존재한다.

3. 1. 상관관계 분석

독립 변수들 간의 상관 계수를 확인하여 높은 상관관계가 있는지 확인한다. 상관 값(비대각 요소)이 0.4 이상이면 다중공선성 문제가 있다고 해석될 수 있다. 그러나 이 방법은 매우 문제가 많아 권장되지 않는다. 직관적으로 표현하면 상관은 두 변수의 관계를 나타내는 반면, 공선성은 다변수 현상이기 때문이다.^[22]

3. 2. 분산팽창요인 (VIF)

분산 팽창 요인(VIF, Variance Inflation Factor)은 특정 계수의 조건수이다. VIF는 설명 변수 ''j''를 다른 모든 설명 변수에 회귀했을 때의 결정 계수

R_{j}^2

를 통해 다음과 같이 계산할 수 있다.^[16]

:

\mathrm{tolerance} = 1-R_{j}^2,\quad \mathrm{VIF} = \frac{1}{\mathrm{tolerance}}

공차가 0.20 미만 또는 0.10 미만이거나, VIF가 5 이상 또는 10 이상이면 다중공선성 문제가 있음을 나타낸다.^[16] VIF 값을 통해 각 독립 변수가 다른 독립 변수들에 의해 얼마나 잘 설명되는지 측정할 수 있으며, 일반적으로 VIF가 10 이상이면 다중공선성이 심각하다고 판단한다.

3. 3. 결정계수와 P값

결정계수(R²) 값이 높아 회귀식의 설명력은 높지만, 식 안의 독립변수의 P값(P-value)이 커서 개별 인자들이 유의하지 않은 경우가 있다. 이런 경우 독립변수들 간에 높은 상관관계가 있다고 의심된다.^[16]

3. 4. 조건수

행렬의 조건 불량을 측정하는 표준 척도는 조건 지수이다. 이는 행렬의 역행렬이 유한 정밀도의 숫자로 수치적으로 불안정하여, 계산된 역행렬이 원래 행렬의 작은 변화에 민감할 가능성이 있음을 나타낸다. 조건수는 설계 행렬의 최대 특이값을 최소 특이값으로 나누어 계산한다.^[10]

조건수가 30 이상인 경우, 해당 회귀는 심각한 다중공선성을 가질 수 있다. 높은 조건수와 관련된 2개 이상의 변수가 설명되는 분산의 비율이 높은 경우에도 다중공선성이 존재한다. 이 방법의 장점은 어떤 변수가 문제의 원인이 되는지 나타낼 수 있다는 것이다.^[21]

3. 5. Farrar–Glauber 검정

Farrar–Glauber 검정은 변수 간 직교성을 검정하여 다중공선성 여부를 판단하는 방법이다.^[17] 변수가 직교하면 다중공선성은 없다. 변수가 직교하지 않으면 적어도 어느 정도의 다중공선성이 존재한다. 그러나 C. Robert Wichers는 Farrar-Glauber 편상관 검정이 주어진 편상관이 다른 다중공선성 패턴에 대응할 수 있다는 점에서 효과가 없다고 주장한다.^[18] Farrar-Glauber 검정은 다른 연구자들로부터도 비판받았다.^[19]^[20]

4. 원인

다중공선성은 다음과 같은 원인으로 발생할 수 있다.

공선성: 두 설명 변수 사이에 직선적인 관련성이 있는 경우이다. 두 변수 사이에 정확한 선형 관계가 있으면 완전한 공선성을 가진다. 예를 들어, 모든 관측치 $i$ 에 대해 $X_{2i} = \lambda_0 + \lambda_1 X_{1i}$ 와 같은 파라미터 $\lambda_0$ 과 $\lambda_1$ 이 존재하면, $X_{1}$ 과 $X_{2}$ 는 완전한 공선성을 가진다.

다중공선성: 중회귀 모델에서 2개 이상의 설명 변수가 높은 선형 관계를 가지는 상황이다. 두 독립 변수의 상관 관계가 1 또는 -1과 같으면 완전한 다중공선성이 있다고 할 수 있다. 실제로는 데이터 세트에서 완전한 다중공선성을 가지는 경우는 거의 없고, 2개 이상의 독립 변수 사이에 근사적인 선형 관계가 있을 때 다중공선성 문제가 발생한다.

수학적으로, 변수들 사이에 하나 이상의 엄밀한 선형 관계가 존재하면, 그 변수들은 완전한 다중공선성을 가진다. 예를 들면 다음과 같다.

:

\lambda_0 + \lambda_1 X_{1i} + \lambda_2 X_{2i} + \cdots + \lambda_k X_{ki} = 0

여기서

\lambda_k

는 상수이고,

X_{ki}

는 k번째 설명 변수에 관한 i번째 관측치이다.

최소제곱법(OLS) 추정에서는 행렬

X^{T} X

의 역행렬을 구해야 한다.

:

X = \begin{bmatrix}1 & X_{11} & \cdots & X_{k1} \\\vdots & \vdots & & \vdots \\1 & X_{1N} & \cdots & X_{kN}\end{bmatrix}

위 행렬은 N×(k+1) 행렬이며, N은 관측치 수, k는 설명 변수 수이다(N은 k+1 이상). 독립 변수 사이에 엄밀한 선형 관계(완전 다중공선성)가 있으면, X 열 중 적어도 하나는 다른 열의 선형 결합이 되므로, X (또는 X^TX)의 랭크는 k+1보다 작아지고, 행렬 X^TX는 역행렬을 가질 수 없다.

완전 다중공선성은 불필요한 정보를 포함하는 원시 데이터 세트를 다룰 때 자주 발생한다. 그러나 중복을 제거하더라도 연구 대상 시스템 고유의 상관 관계로 인해 근사적인 다중공선성을 가진 변수가 남는 경우가 많다. 이 경우, 위의 식 대신 오차항

v_i

를 더한 형태의 식이 성립한다.

:

\lambda_0 + \lambda_1 X_{1i} + \lambda_2 X_{2i} + \cdots + \lambda_k X_{ki} + v_i = 0

이 경우, 변수 사이에 정확한 선형 관계는 없지만,

v_i

의 분산이

\lambda

값의 특정 조합에 대해 작으면, 변수

X_j

는 거의 완전한 다중공선성을 가진다. 이때, 행렬 X^TX는 역행렬을 가지지만, 불량 조건이 된다. 따라서 컴퓨터 알고리즘이 근사적인 역행렬을 계산할 수 있는지 불분명하며, 계산하더라도 데이터의 작은 변화(반올림 오차나 표본 데이터의 작은 변화)에 민감하여 부정확하거나 표본에 의존적일 수 있다.

4. 1. 불필요한 변수 포함

정의상 서로 연관된 변수들을 동시에 회귀 모형에 포함시키는 경우 완전 다중공선성이 발생할 수 있다. 예를 들어, 소득, 지출, 저축은 소득이 지출과 저축의 합과 같기 때문에, 이 세 변수를 모두 회귀 분석에 동시에 포함하는 것은 옳지 않다.^[9]

4. 2. 더미 변수 함정

모든 범주(예: 여름, 가을, 겨울, 봄)에 대한 더미 변수와 절편 항을 함께 포함하면 완전 공선성이 발생한다. 이것을 더미 변수 함정이라고 한다.^[9]

4. 3. 자료 부족

완전 다중공선성은 예측 변수가 선형 종속 관계에 있는 상황을 의미한다(하나의 변수를 다른 변수의 정확한 선형 함수로 나타낼 수 있다).^[8] 최소 자승법은 다음 행렬

X^{\mathsf{T}}X

의 역행렬을 구해야 한다.

:

X = \begin{bmatrix}1 & X_{11} & \cdots & X_{k1}  \\\vdots & \vdots & & \vdots \\1 & X_{1N} & \cdots & X_{kN}\end{bmatrix}

여기서 ''

N \times (k+1)

'' 행렬이며, ''

N

''은 관측치 수, ''

k

''는 설명 변수 수, ''

N \ge k+1

''이다. 독립 변수 간에 정확한 선형 관계가 있는 경우,

X

의 열 중 적어도 하나는 다른 열들의 선형 결합이 되므로

X

(그리고

X^{\mathsf{T}}X

)의 계수는 ''

k+1

''보다 작고, 행렬

X^{\mathsf{T}}X

는 역행렬이 존재하지 않게 된다.

4. 4. 변수 간 내재적 상관관계

완전 다중공선성은 예측 변수가 선형 종속 관계에 있는 상황을 의미한다. 즉, 하나의 변수를 다른 변수의 정확한 선형 함수로 나타낼 수 있다.^[8] 최소 자승법은 행렬

X^{\mathsf{T}}X

의 역행렬을 구해야 하는데, 이는 다음과 같다.

:

X = \begin{bmatrix}1 & X_{11} & \cdots & X_{k1}  \\\vdots & \vdots & & \vdots \\1 & X_{1N} & \cdots & X_{kN}\end{bmatrix}

여기서 ''

N \times (k+1)

'' 행렬이며, ''

N

''은 관측치 수, ''

k

''는 설명 변수 수이고, ''

N \ge k+1

''이다. 독립 변수 간에 정확한 선형 관계가 있는 경우,

X

의 열 중 적어도 하나는 다른 열들의 선형 결합이 되므로

X

(그리고

X^{\mathsf{T}}X

)의 계수는 ''

k+1

''보다 작고, 행렬

X^{\mathsf{T}}X

는 역행렬이 존재하지 않게 된다.

5. 문제점

다중공선성은 예측 변수 간에 선형 종속 관계가 있을 때 발생하며, 다음과 같은 문제점을 야기한다.

완전 다중공선성: 예측 변수들이 선형 종속 관계에 있는 상황이다. 예를 들어 소득, 지출, 저축 변수에서 소득이 지출과 저축의 합과 같다면, 회귀 분석에 세 변수를 모두 포함하는 것은 옳지 않다. 모든 범주에 대한 더미 변수와 절편 항을 포함해도 완전 공선성이 발생하는데, 이를 더미 변수 함정이라고 한다.^[9]
불완전 다중공선성: 수치적 문제 외에도 변수의 정확한 추정을 어렵게 만든다. 상관관계가 높은 변수는 추정치가 부실하고 표준 오차가 커진다.
정확도 저하: 다른 변수를 통제하면서 특정 변수의 종속 변수 $Y$ 에 대한 영향을 추정할 때, 예측 변수가 서로 무상관인 경우보다 정확도가 낮아진다. 공선적인 변수들은 종속 변수에 대한 동일한 정보를 포함하여 중복되기 때문이다.
표준 오차 증가: 영향을 받는 계수의 표준 오차가 커지는 경향이 있다. 계수가 0이라는 가설 검정에서 설명 변수의 효과가 없다는 잘못된 귀무 가설을 기각하지 못하는 제2종 오류가 발생할 수 있다.
모델 불안정성: 입력 데이터의 작은 변화가 모델의 큰 변화로 이어지고, 파라미터 추정값의 부호가 바뀔 수도 있다.^[21]
과적합: 회귀 분석 모델에서 과적합을 유발할 수 있다.

5. 1. 회귀 계수 추정의 어려움

다중공선성이 있으면 회귀 계수 추정치가 불안정해지고 표준 오차가 커져서 통계적으로 유의미한 결과를 얻기 어려워진다.

최소 자승법을 사용한 회귀 분석에서, 독립 변수 간에 완전한 선형 관계가 있으면

X^{\mathsf{T}}X

행렬의 역행렬이 존재하지 않아 회귀 계수를 추정할 수 없다. 변수

X_j

가 거의 공선성을 띨 때는

X^{\mathsf{T}}X

가 역행렬을 가지지만 조건이 나쁜 행렬이 되어 큰 반올림 오차를 유발할 수 있다.

불완전한 다중공선성은 변수의 정확한 추정을 어렵게 만들고, 추정치의 표준 오차를 증가시킨다. 예를 들어, 앨리스가 비가 올 때마다 부츠를 신고, 비가 올 때만 물웅덩이가 생긴다면, 앨리스가 부츠를 신는 이유가 비 때문인지 물웅덩이 때문인지 구별하기 어렵다. 이는 두 변수가 서로 교란되기 때문이다. 이러한 교란 문제를 해결하기 위해서는 사전 정보나 이론을 활용하거나, 더 많은 데이터를 수집해야 한다.

다중공선성이 있는 경우, 특정 변수의 영향을 추정하는 것은 예측 변수가 서로 무상관인 경우보다 정확도가 낮아진다. 이는 공선적인 변수들이 종속 변수에 대한 동일한 정보를 포함하고 있어 중복되기 때문이다. 다중공선성은 또한 영향을 받는 계수의 표준 오차를 증가시켜, 귀무 가설을 기각하지 못하는 제2종 오류를 발생시킬 수 있다. 입력 데이터의 작은 변화가 모델의 큰 변화를 초래하고, 심지어 파라미터 추정값의 부호가 바뀔 수도 있다.^[21]

다중공선성은 회귀 분석 모델에서 과적합을 일으킬 수 있다. 최적의 회귀 모델은 예측 변수들이 종속 변수와는 높은 상관 관계를 가지지만, 예측 변수들끼리는 낮은 상관 관계를 갖는 모델이다. 다중공선성은 계수값 추정치를 부정확하게 만들어 표본 외 예측값을 부정확하게 만들고, 새로운 데이터의 다중공선성 패턴이 적합된 데이터와 다르면 예측에 큰 오차를 유발할 수 있다.^[23]

5. 2. 잘못된 변수 선택

다중공선성이 있으면, 다른 변수를 통제하면서 특정 변수가 종속 변수 Y에 미치는 영향을 정확하게 추정하기 어렵다. 이는 예측 변수들이 서로 무관한 경우보다 정확도가 낮아지는 경향을 보인다. 회귀 계수는 보통 다른 변수를 일정하게 유지하면서 독립 변수 X₁을 1단위 변화시켰을 때의 효과를 추정하는 것으로 해석된다. 그러나 주어진 데이터에서 X₁이 다른 독립 변수 X₂와 높은 상관관계를 가지면, X₁의 모든 변화가 X₂의 변화와 독립적인 관측값을 얻기 어렵기 때문에, X₁의 독립적인 변화 효과에 대한 부정확한 추정치를 얻게 된다.^[21]

어떤 의미에서 공선적인 변수들은 종속 변수에 대해 동일한 정보를 포함한다. 명목상으로는 "다른" 측정값이지만 실제로는 동일한 현상을 나타내는 경우 중복이라고 할 수 있다. 변수들이 다른 이름을 가지고 다른 수치 측정 척도를 사용하더라도 서로 높은 상관관계를 가지면 중복성을 가진다.

다중공선성의 특징 중 하나는 영향을 받는 계수의 표준 오차가 커지는 경향이 있다는 것이다. 이 경우, 계수가 0이라는 가설 검정에서 설명 변수의 효과가 없다는 잘못된 귀무 가설을 기각하지 못하는 제2종 오류가 발생할 수 있다.

또한 다중공선성은 입력 데이터의 작은 변화가 모델의 큰 변화로 이어질 수 있으며, 심지어 파라미터 추정값의 부호가 바뀔 수도 있다는 문제를 야기한다.^[21]

이러한 데이터 중복성의 주요 위험은 회귀 분석 모델에서 과적합이 발생할 수 있다는 것이다. 최적의 회귀 모델은 예측 변수 각각이 종속 변수와는 높은 상관관계를 갖지만, 예측 변수 간에는 최소한의 상관관계를 갖는 모델이다. 이러한 모델은 "저노이즈"라고 불리며 통계적으로 강건하다.^[23]

5. 3. 과적합 위험

다중공선성은 회귀 분석 모델에서 과적합을 일으킬 위험이 있다. 최상의 회귀 모델은 예측 변수들이 각각 종속 변수와는 높은 상관관계를 가지지만, 예측 변수들끼리는 최소한의 상관관계만 가지는 모델이다. 이러한 모델은 "저노이즈"라고 불리며, 통계적으로 강건하다. 즉, 동일한 모집단에서 추출된 여러 샘플에서 안정적인 예측을 제공한다.^[23]

그러나 다중공선성이 존재하면, 입력 데이터의 작은 변화에도 모델이 크게 변동하여 파라미터 추정값의 부호가 바뀌는 등의 문제가 발생할 수 있다.^[21] 또한, 다중공선성은 계수 추정치의 표준 오차를 증가시켜, 귀무 가설을 기각하지 못하는 제2종 오류를 발생시킬 가능성을 높인다.

기본적인 사양이 올바르다면, 다중공선성이 실제로 결과를 왜곡하지는 않지만, 관련 독립 변수들의 표준 오차를 크게 만든다. 더 큰 문제는 회귀 모델을 다른 데이터에 적용할 때 발생한다. 다중공선성 때문에 계수 추정치가 부정확해지면, 표본 외 예측값도 부정확해진다. 새로운 데이터의 다중공선성 패턴이 기존 데이터와 다르면, 예측 오차가 커질 수 있다.^[23]

5. 4. 해석의 어려움

다중공선성이 있으면, 다른 변수를 통제하면서 특정 변수가 종속 변수 Y에 미치는 영향을 추정하기 어려워진다. 이는 예측 변수들이 서로 무관한 경우보다 정확도가 낮아지는 경향을 보인다.^[21] 회귀 계수의 일반적인 해석은 다른 변수를 일정하게 유지하면서 독립 변수 X₁을 1단위 변화시켰을 때의 효과를 추정하는 것이다. 그러나 주어진 데이터에서 X₁이 다른 독립 변수 X₂와 높은 상관 관계를 가지면, X₁과 X₂는 특정 선형 확률적 관계를 갖는 관측값 집합을 가지게 된다. 따라서 X₁의 모든 변화가 X₂의 변화와 독립적인 관측값 집합은 존재하지 않으므로, X₁의 독립적인 변화 효과에 대한 부정확한 추정치를 얻게 된다.^[21]

어떤 의미에서 공선적인 변수들은 종속 변수에 대해 동일한 정보를 포함한다. 명목상 "다른" 측정값이 실제로 동일한 현상을 정량화하는 경우 중복이라고 할 수 있다. 변수들의 이름이 다르고 다른 수치 측정 척도를 사용하더라도 서로 높은 상관 관계를 가지면 중복성을 갖는다.

다중공선성의 특징 중 하나는 영향을 받는 계수의 표준 오차가 커지는 경향이 있다는 것이다. 이 경우 계수가 0이라는 가설 검정에서 설명 변수의 효과가 없다는 잘못된 귀무 가설을 기각하지 못하는 제2종 오류가 발생할 수 있다.

또한 다중공선성은 입력 데이터의 작은 변화가 모델의 큰 변화로 이어지게 하고, 심지어 파라미터 추정값의 부호가 바뀔 수도 있게 만든다.^[21]

이러한 데이터 중복성의 주요 위험은 회귀 분석 모델에서 과적합이 발생하는 것이다. 최상의 회귀 모델은 예측 변수 각각이 종속 변수와 높은 상관 관계를 갖지만, 서로 간에는 최소한의 상관 관계만 갖는 모델이다. 이러한 모델은 "저노이즈"라고 불리며, 통계적으로 강건하다.^[23]

기본적인 사양이 올바른 한, 다중공선성은 실제 결과를 왜곡하지 않으며, 관련된 독립 변수에 큰 표준 오차를 발생시킬 뿐이다. 그러나 회귀의 일반적인 사용은 모델에서 계수를 가져와 다른 데이터에 적용하는 것이다. 다중공선성으로 인해 계수값 추정치가 부정확해지면, 표본 외 예측값도 부정확해진다. 새로운 데이터의 다중공선성 패턴이 적합된 데이터와 다르면, 이러한 외삽은 예측에 큰 오차를 발생시킬 수 있다.^[23]

6. 해결법

다중공선성 문제를 해결하기 위한 다양한 방법들이 존재한다.

변수 제거: 상관관계가 높은 독립 변수 중 하나, 혹은 일부를 제거한다. 하지만 변수를 제거하면 정보가 손실되므로 신중하게 선택해야 한다.^[24]
변수 변형: 변수들을 결합하거나 변환하여 새로운 변수를 생성할 수 있다. 예를 들어, 주성분 분석(PCA)을 통해 변수들을 변형할 수 있다.^[8]
능형 회귀 (Ridge Regression): 정규화 회귀 기법 중 하나인 능형 회귀는 회귀 계수에 벌점을 부과하여 다중공선성의 영향을 완화한다.^[3]
자료 추가: 더 많은 자료를 확보하면 독립 변수 간의 상관관계를 줄일 수 있다. 가능하다면 더 많은 데이터를 통해 더 정확한 파라미터 추정치(더 낮은 표준 오차)를 얻을 수 있다.^[24]
표준화: 예측 변수를 표준화하면 다중공선성을 완화할 수 있다.^[11]
샤플리 값: 게임 이론의 샤플리 값을 사용하면, 모델이 다중공선성의 영향을 설명할 수 있다. 샤플리 값은 각 예측 변수에 값을 할당하고, 중요성의 모든 가능한 조합을 평가한다.^[26]

완전 다중공선성은 예측 변수가 선형 종속 관계에 있는 상황을 의미한다.^[8] 변수

X_j

가 거의 공선성을 띨 때, 행렬

X^{\mathsf{T}}X

는 역행렬을 가지지만, 조건이 나쁜 행렬이 된다.

이러한 문제를 해결하기 위해 다음과 같은 방법을 사용할 수 있다.

표준화된 예측 변수 사용^[11]
데이터의 직교 표현 사용^[12]
직교 다항식을 사용하여 상관관계가 없는 변수의 함수로 회귀식을 다시 작성^[12]

이외에도, 연구자는 데이터를 수집하기 ''전에'' 최적 실험 설계를 통해 공선성을 피할 수 있다. 예를 들어, 봄, 여름, 가을, 겨울과 같은 더미 변수를 모든 범주에 넣고 회귀에 상수항을 추가하면 완벽한 다중공선성이 보장된다. 또한, 데이터의 독립적인 하위 집합을 사용하여 추정하고, 해당 추정값을 데이터 세트 전체에 적용해볼 수 있다.

6. 1. 변수 제거

상관관계가 높은 독립 변수 중 하나, 혹은 일부를 제거하는 방법이 있다. 그러나 변수를 제거하면 정보가 손실되므로 신중하게 선택해야 한다.^[24] 변수 제거는 탈락한 변수와 상관관계가 있는 나머지 설명 변수의 계수 추정치에 편향을 발생시켜, 특정 집단에 불리하게 작용할 수 있다는 점을 인지해야 한다.^[24]

6. 2. 변수 변형

변수들을 결합하거나 변환하여 새로운 변수를 생성할 수 있다. 예를 들어, 주성분 분석(PCA)을 통해 변수들을 변형할 수 있다.^[8]

표준화된 예측 변수를 사용하면 다중공선성을 해결할 수 있다. 다항식 항(예:

x_1

,

x_1^2

)이나 상호작용 항(예:

x_1 \times x_2

)을 포함하는 경우, 특히 해당 변수의 범위가 제한적일 때 다중공선성이 발생할 수 있는데, 예측 변수를 표준화하면 최대 3차 다항식에 대해 이러한 종류의 다중공선성을 제거할 수 있다.^[11] 더 높은 차수의 다항식의 경우, 직교 다항식 표현은 일반적으로 모든 공선성 문제를 해결한다.^[12]

데이터의 직교 표현을 사용하는 것도 방법이다.^[12] 특히 다항식 항의 경우, 직교 다항식을 사용하여 상관관계가 없는 변수의 함수로 회귀식을 다시 작성할 수 있다.

예측 변수를 평균화하는 방법도 있다. 다항식 항(

x_1

,

x_1^2

,

x_1^3

등)이나 상호 작용 항(

x_1 \times x_2

등)을 생성하면, 문제의 변수가 제한된 범위(예: [2,4])에 있는 경우 다중공선성을 일으킬 수 있는데, 평균화는 이 특수한 다중공선성을 해소한다.^[25]

릿지 회귀나 부분 최소 자승 회귀 등을 사용할 수도 있다.

6. 3. 능형 회귀 (Ridge Regression)

정규화 회귀 기법 중 하나인 능형 회귀(Ridge Regression)는 회귀 계수에 벌점을 부과하여 다중공선성의 영향을 완화한다. Ridge Regression^영어는 최소제곱법 회귀보다 더 나은 성능을 보이며, "쓸모없는" 예측 변수를 자동으로 감지하고 제거하여 문제를 해결한다.^[3] 이외에도 부분 최소 자승 회귀 등의 방법을 사용할 수 있다.

6. 4. 자료 추가

더 많은 자료를 확보하면 독립 변수 간의 상관관계를 줄일 수 있다. 가능하다면 더 많은 데이터를 통해 더 정확한 파라미터 추정치(더 낮은 표준 오차)를 얻을 수 있다. 이는 회귀 계수 추정치의 분산을 표본 크기와 다중공선성의 정도에 따라 나타내는 분산 팽창 계수 식에서도 확인할 수 있다.^[24]

6. 5. 표준화

예측 변수를 표준화하면 다중공선성을 완화할 수 있다.^[11] 특히, 다항식 항(예:

x_1

,

x_1^2

)이나 교호작용 항(예:

x_1 \times x_2

)을 사용하는 경우, 해당 변수의 범위가 제한적이라면 다중공선성이 발생할 수 있는데, 예측 변수를 표준화하면 최대 3차 다항식에 대해 이러한 특수한 종류의 다중공선성을 제거할 수 있다.^[11] 독립 변수를 표준화하는 것은 조건 지수가 30을 초과하는 경우의 오판정을 줄일 수 있다.

6. 6. 샤플리 값

게임 이론의 샤플리 값을 사용하면, 모델이 다중공선성의 영향을 설명할 수 있다. 샤플리 값은 각 예측 변수에 값을 할당하고, 중요성의 모든 가능한 조합을 평가한다.^[26]

7. 오용 및 주의사항

다중공선성 해결을 위해 제시된 방법들이 오용될 수 있음에 주의해야 한다. 다중공선성을 해결하기 위한 다양한 방법이 존재하지만, 이러한 방법들은 연구자가 데이터를 수집하기 *전에* 절차와 분석을 결정해야 한다.^[3]

정규화 회귀 기법(예: 릿지 회귀, LASSO, 엘라스틱 넷 회귀, 스파이크 앤 슬래브 회귀)은 다중공선성에 강건하며, 베이즈 계층 모형은 데이터로부터 유익한 사전 정보를 학습하여 정규화를 자동 수행한다.

빈도주의 통계적 추론에서 발생하는 문제들이 다중공선성과 관련된 것으로 오해되기도 한다.^[3] 계수가 "잘못된 부호"를 갖거나 신뢰 구간이 "현실적이지 않은 값"을 포함한다는 불만은 모델에 통합되지 않은 중요한 사전 정보가 있음을 나타낼 수 있다. 베이즈 선형 회귀 기법을 사용하면 이러한 사전 정보를 통합할 수 있다.^[3]

에드워드 레이머는 "약한 증거 문제의 해결책은 더 많고 더 나은 데이터"라고 언급하며, 주어진 데이터 집합 내에서 약한 증거에 대해 할 수 있는 일은 없다고 말했다.^[3] 다모다르 구자라티는 "우리는 [우리의 데이터]가 때로는 관심 매개변수에 대해 그다지 유익하지 않다는 것을 올바르게 받아들여야 한다"고 썼다.^[1] 올리비에 블랑샤르는 "다중공선성은 최소제곱법의 문제가 아니라 신의 뜻이다."라고 말했다.^[7] 즉, 관측 데이터로 작업할 때 연구자는 다중공선성을 "수정"할 수 없고, 단지 받아들일 수 있을 뿐이다.

몇몇 상황에서 효과가 있는 전략들이 존재하지만, 고급 기법을 사용하더라도 여전히 큰 표준 오차가 발생할 수 있다. 이런 경우, 다중공선성에 대한 올바른 대응은 "아무것도 하지 않는 것"이다.^[1] 과학적 방법은 종종 귀무 결과 또는 결론을 내릴 수 없는 결과를 포함한다.

7. 1. 단계적 회귀의 문제점

분산 팽창 인자는 변수 포함/제외를 위해 단계적 회귀 분석의 기준으로 오용되는 경우가 많으며, 이는 "논리적 근거가 없을 뿐만 아니라 경험 법칙으로도 근본적으로 오해의 소지가 있다".^[2]

공선성이 있는 변수를 제외하면 표준 오차가 인위적으로 작아지지만, 회귀 계수의 실제(추정되지 않은) 표준 오차는 감소하지 않는다.^[1] 분산 팽창 인자가 높은 변수를 제외하면 회귀 분석 결과를 사후 분석으로 전환하여 계산된 표준 오차와 p-값이 무효화된다.^[14]

공선성은 큰 표준 오차와 p-값을 유발하여 논문 게재를 더 어렵게 만들 수 있으므로, 일부 연구자는 강력한 상관 관계가 있는 변수를 회귀 분석에서 제거하여 연구 부정행위로 불편한 데이터를 데이터 조작하려 한다. 이 절차는 p-해킹, 데이터 마이닝, 사후 분석의 더 광범위한 범주에 속한다. 유용한 공선성 예측 변수를 제거하면 일반적으로 모델의 정확도와 계수 추정이 악화된다.

마찬가지로, 공선성을 "처리"할 수 있는 모델을 찾을 때까지 다양한 모델 또는 추정 절차(예: 최소 자승법, 릿지 회귀 등)를 시도하면 분기 경로 문제가 발생한다. 사후 분석에서 파생된 p-값과 신뢰 구간은 모델 선택 절차의 불확실성을 무시함으로써 무효화된다.

결과에 거의 또는 전혀 영향을 미치지 않는 것으로 사전에 알려진 중요하지 않은 예측 변수를 제외하는 것은 합리적이다. 예를 들어, 지역 치즈 생산량은 마천루의 높이를 예측하는 데 사용해서는 안 된다. 그러나 이것은 어떤 데이터도 관찰하기 전에 모델을 처음 지정할 때 수행해야 하며, 잠재적으로 유익한 변수는 항상 포함해야 한다.

7. 2. 사후 분석의 위험성

분산 팽창 인자가 높은 변수를 회귀 분석에서 제외하면 표준 오차가 인위적으로 작아지지만, 회귀 계수의 실제 표준 오차는 감소하지 않는다.^[1] 이러한 행위는 회귀 분석 결과를 사후 분석으로 전환하여 계산된 표준 오차와 p-값을 무효화한다.^[14]

공선성은 큰 표준 오차와 p-값을 유발하여 논문 게재를 더 어렵게 만들 수 있다. 따라서 일부 연구자는 강력한 상관 관계가 있는 변수를 회귀 분석에서 제거하여 연구 부정행위로 불편한 데이터를 데이터 조작하려 한다. 이 절차는 p-해킹, 데이터 마이닝, 사후 분석의 더 광범위한 범주에 속한다. 그러나 공선성 예측 변수를 제거하면 일반적으로 모델의 정확도와 계수 추정이 악화된다.

마찬가지로, 공선성을 "처리"할 수 있는 모델을 찾을 때까지 다양한 모델 또는 추정 절차(예: 최소 자승법, 릿지 회귀 등)를 시도하면 분기 경로 문제가 발생한다. 사후 분석에서 파생된 p-값과 신뢰 구간은 모델 선택 절차의 불확실성을 무시하므로 무효화된다.

7. 3. 데이터 조작의 유혹

다중공선성이 있는 변수를 제거하여 연구 결과를 유리하게 조작하려는 시도는 연구 부정행위에 해당하며, 데이터 조작, p-해킹, 데이터 마이닝, 사후 분석과 같은 문제를 야기한다.^[14] 이러한 행위는 연구 윤리에 어긋난다.^[1]

공선성이 있는 변수를 제거하면 표준 오차가 인위적으로 작아 보일 수 있지만, 실제 회귀 계수의 표준 오차는 줄어들지 않는다.^[1] 또한, 분산 팽창 인자가 높은 변수를 제외하면 회귀 분석 결과를 사후 분석으로 만들어 계산된 표준 오차와 p-값을 무효화한다.^[14]

다양한 모델을 시도하여 공선성을 "처리"하는 것은 분기 경로 문제를 야기하며, 사후 분석에서 파생된 p-값과 신뢰 구간은 모델 선택 절차의 불확실성을 무시하여 무효화된다.

8. 한국 사회에의 적용 및 고려사항

한국 사회는 급격한 경제 성장과 사회 변화를 겪으면서 다양한 요인들이 복잡하게 얽혀 있는 경우가 많다. 이러한 사회적 특성은 통계 분석에서 다중공선성 문제를 야기할 수 있으며, 특히 사회 현상을 설명하는 회귀 분석 모델에서 예측의 신뢰도를 떨어뜨릴 수 있다.

예를 들어, 교육 수준, 소득, 직업, 거주 지역 등은 서로 강한 상관관계를 가질 수 있다. 이러한 변수들을 독립 변수로 사용하여 특정 사회 현상(예: 정치적 성향, 소비 패턴, 건강 상태)을 분석할 때, 다중공선성 문제로 인해 각 변수의 독립적인 영향력을 정확하게 파악하기 어려워진다.

따라서 한국 사회를 대상으로 하는 통계 분석에서는 다중공선성 문제를 더욱 신중하게 고려해야 한다. 변수 간의 상관관계를 면밀히 검토하고, 분산팽창인자(VIF) 등을 활용하여 다중공선성 발생 여부를 진단해야 한다. 필요한 경우, 변수 제거, 변수 변환, 주성분 분석(PCA) 등 적절한 방법을 통해 다중공선성 문제를 완화하고 분석 결과의 신뢰도를 높여야 한다.

참조

_[1] 서적 Basic Econometrics https://archive.org/[...] McGraw−Hill
_[2] 간행물 The VIF Score. What is it Good For? Absolutely Nothing http://journals.sage[...] 2023-12-13
_[3] 간행물 Multicollinearity: A Bayesian Interpretation https://www.jstor.or[...] 1973
_[4] 웹사이트 Econometrics Beat: Dave Giles' Blog: Micronumerosity https://davegiles.bl[...] 2023-09-03
_[5] 서적 Econometric Theory Wiley
_[6] 서적 A Course in Econometrics Harvard University Press
_[7] 간행물 Comment http://www.tandfonli[...] 1987-10
_[8] 서적 An introduction to statistical learning: with applications in R https://link.springe[...] Springer 2024-11-01
_[9] 웹사이트 Dummy Variable Trap - What is the Dummy Variable Trap? https://www.learndat[...] 2024-01-18
_[10] 서적 Conditioning Diagnostics: Collinearity and Weak Data in Regression https://archive.org/[...] Wiley
_[11] 웹사이트 12.6 - Reducing Structural Multicollinearity https://newonlinecou[...] 2019-03-16
_[12] 웹사이트 Computational Tricks with Turing (Non-Centered Parametrization and QR Decomposition) https://storopoli.io[...] 2023-09-03
_[13] 간행물 Why High-Order Polynomials Should Not Be Used in Regression Discontinuity Designs https://www.tandfonl[...] 2019-07-03
_[14] 간행물 The garden of forking paths http://www.stat.colu[...] 2013-11-14
_[15] 서적 わかりやすい薬学系の統計学入門講談社
_[16] 간행물 A Caution Regarding Rules of Thumb for Variance Inflation Factors
_[17] 간행물 Multicollinearity in Regression Analysis: The Problem Revisited https://doi.org/10.2[...]
_[18] 간행물 The Detection of Multicollinearity: A Comment
_[19] 간행물 Multicollinearity in Regression Analysis
_[20] 간행물 Tests for the Severity of Multicolinearity in Regression Analysis: A Comment
_[21] 서적 Conditioning Diagnostics: Collinearity and Weak Data in Regression https://archive.org/[...] Wiley
_[22] 웹사이트 perturb: Tools for evaluating collinearity https://cran.r-proje[...] 2015-07-18
_[23] 서적 Regression Analysis by Example https://archive.org/[...] John Wiley and Sons
_[24] 서적 Basic Econometrics https://archive.org/[...] McGraw−Hill
_[25] 웹사이트 12.6 - Reducing Structural Multicollinearity https://newonlinecou[...] 2019-03-16
_[26] 간행물 Analysis of Regression in Game Theory Approach
_[27] 간행물 Customer attrition analysis for financial services using proportional hazard models
_[28] 간행물 Lateral collinearity and misleading results in variance-based SEM: An illustration and recommendations http://www.scriptwar[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com