표준 점수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 공식
- 2.1. Z 점수
- 2.2. T 점수
3. 특징
4. 적용
5. 비판 및 논란
참조

1. 개요

표준 점수는 원점수가 평균에서 얼마나 떨어져 있는지를 나타내는 값으로, 원점수를 표준화하여 다른 집단이나 척도 간의 비교를 가능하게 한다. Z 점수, T 점수 등이 있으며, Z 점수는 원점수를 모집단의 평균과 표준편차를 사용하여 변환한 값이고, T 점수는 Z 점수를 평균 50, 표준 편차 10으로 변환한 값이다. 표준 점수는 예측 구간 계산, 공정 관리, 서로 다른 척도의 점수 비교, 다변량 분석 등 다양한 분야에 적용된다. 대한민국 수능, 일본의 학력 편차치 등 교육 평가에도 활용되며, 특히 일본에서는 학교 서열화에 기여한다는 비판이 있다.

2. 공식

표준 점수는 원점수 x가 평균 μ에서 표준편차 σ의 몇 배만큼 떨어져 있는지를 나타내는 값이다. z 점수는 다음과 같이 계산한다.^[3]

: $z = \frac{x - \mu}{\sigma}$

x: 정상화되는 원점수
σ: 모집단의 표준편차
μ: 모집단의 평균

z 점수는 원점수 x를 표준화된 값으로 변환하는 선형변환(linear transformation)이다.

t값(t score)은 z 점수를 사용하여 자연수 및 백분위수로 변환한 값으로, 다음과 같이 계산한다.

:

t=10z+50

t값은 z값이 소수점, 음수, 양수로 분포하는 것을 자연수와 백분위수로 표현하여 데이터의 가독성을 높여준다.

모집단의 평균과 표준 편차를 알 수 없는 경우, 표본 평균과 표본 표준 편차를 사용하여 표준 점수를 추정할 수 있다.^[4]^[5]^[6]^[7]

:

z = {x- \bar{x} \over S}

$\bar{x}$ : 표본의 평균
''S'': 표본의 표준 편차

수리 통계학에서 확률 변수 ''X''의 표준화는 기댓값

\operatorname{E}[X]

를 빼고 그 차이를 표준 편차

\sigma(X) = \sqrt{\operatorname{Var}(X)}

로 나누어 계산한다.

:

Z = {X - \operatorname{E}[X] \over \sigma(X)}

확률 변수가 X의 임의 표본

\ X_1,\dots, X_n

의 표본 평균인 경우, 표준화된 버전은 다음과 같다.

:

\bar{X}={1 \over n} \sum_{i=1}^n X_i

:

Z = \frac{\bar{X}-\operatorname{E}[\bar{X}]}{\sigma(X)/\sqrt{n}}

2. 1. Z 점수

표준값 z는 원수치인 x가 평균에서 얼마나 떨어져 있는지를 나타낸다. 음수이면 평균 이하, 양수이면 평균 이상이다.^[3]

:

z = \frac{x - \mu}{\sigma}

여기서 x는 정상화되는 원수치이다.
σ는 모집단에서의 표준편차이다.
μ는 모집단에서의 평균이다.

따라서 원점수 x로부터 표준점수 z로의 선형변환(linear transformation)이다.

'''z'''의 절댓값은 원점수 ''x''와 모집단 평균 사이의 거리를 표준 편차 단위로 나타낸다. 원점수가 평균보다 낮으면 '''z'''는 음수이고, 평균보다 높으면 양수이다.

이 공식을 사용하여 '''z'''를 계산하려면 표본 평균 또는 표본 편차가 아닌 모집단 평균과 모집단 표준 편차를 사용해야 한다. 그러나 전체 모집단이 측정되는 표준화 시험과 같은 경우를 제외하고는 모집단의 실제 평균과 표준 편차를 아는 것은 비현실적인 경우가 많다.

모집단 평균과 모집단 표준 편차를 알 수 없는 경우, 표본 평균과 표본 표준 편차를 모집단 값의 추정치로 사용하여 표준 점수를 추정할 수 있다.^[4]^[5]^[6]^[7]

이 경우, '''z'''-점수는 다음과 같다.

:

z = {x- \bar{x} \over S}

여기서:

:

\bar{x}

는 표본의 평균이고,

: ''S''는 표본의 표준 편차이다.

모집단과 표본 통계의 사용 간의 구분은 종종 이루어지지 않지만, 어느 경우든 방정식의 분자와 분모는 동일한 측정 단위를 가지므로, 단위가 나눗셈을 통해 상쇄되어 '''z'''는 무차원량으로 남게 된다.

수리 통계학에서 확률 변수 ''X''는 기댓값

\operatorname{E}[X]

를 빼고 그 차이를 표준 편차

\sigma(X) = \sqrt{\operatorname{Var}(X)}

로 나누어 '''표준화'''한다.

:

Z = {X - \operatorname{E}[X] \over \sigma(X)}

고려 중인 확률 변수가 X의 임의 표본

\ X_1,\dots, X_n

의 표본 평균인 경우:

:

\bar{X}={1 \over n} \sum_{i=1}^n X_i

표준화된 버전은 다음과 같다.

:

Z = \frac{\bar{X}-\operatorname{E}[\bar{X}]}{\sigma(X)/\sqrt{n}}

2. 2. T 점수

표준값 z는 원점수 x가 평균에서 얼마나 떨어져 있는지를 나타낸다. 음수이면 평균 이하, 양수이면 평균 이상이다.

:

z = \frac{x - \mu}{\sigma}

여기서 x는 정상화되는 원점수이다.
σ는 모집단에서의 표준편차이다.
μ는 모집단에서의 평균이다.

따라서 원점수 x로부터 표준점수 z로의 선형변환(linear transformation)이다.

한편 소수점과 음수와 양수의 정수값을 갖는 표준점수(z)로부터 자연수 및 백분위수로 변환하는 과정을 통해서 t값(t score)을 구할 수 있다.

:

t=10z+50

t값(t score)은 z값이 소수로서 음수와 양수에 걸쳐 분포하는 것을 재설정해줌으로써 자연수와 백분위수로 표현해 보여줄 수 있다는 점에서 데이터의 가독성이 보다 높아진다.

교육 평가에서, '''T-점수'''는 평균 50, 표준 편차 10을 갖도록 변환 및 조정된 표준 점수 Z이다.^[14]^[15]^[16]

'''편차값'''은 평균이 50, 표준 편차(SD)가 10이 되도록 변환한 점수이다. T 점수(T값, T-score)도 같은 뜻이다. 교육 분야에서 자주 사용된다.

3. 특징

표준값들의 평균은 0, 표준편차는 1이다.(편차치(t)값들의 평균은 50, 표준편차는 10이다.)^[1] 표준점수(z) 0.0(= (편차치 t) 50) 이상은 전체의 50%이다.^[1] 표준점수 1.0(=편차치 60) 이상은 전체의 15.866%이다.^[1] 표준점수 2.0(=편차치 70) 이상은 전체의 2.275%이다.^[1] 표준점수 3.0(=편차치 80) 이상은 전체의 0.13499%이다.^[1] 표준점수 4.0(=편차치 90) 이상은 전체의 0.00315%이다.^[1] 표준점수 5.0(=편차치 100) 이상은 전체의 0.00002%이다.^[1]

-|]]

평균, 표준 편차를 변환해도 그 비율은 변하지 않으므로, 정규 분포상에서 특정 점수 사이에 포함되는 비율은 정해져 있다.^[1]

예를 들어 편차 IQ는 전체의 약 68.26%의 사람이 85~115의 점수를 얻고, 약 95.44%의 사람이 70~130의 점수를 얻는다.^[1]

-|]]

이 비율을 바탕으로 점수가 낮은 곳부터 순위를 매긴 것을 '''백분위 순위'''라고 한다(아래 그림은 편차 IQ의 경우).^[1]

예를 들어, IQ 85는 모집단의 아래에서 16 백분위의 순위에 있음을 의미한다.^[1]

-|]]

4. 적용

표준 점수는 서로 다른 척도로 측정된 점수를 비교하기 위해 Z-점수로 변환할 수 있다. Dietz 외^[9]는 (구) SAT와 ACT 고등학교 시험에서 학생들의 점수를 비교하는 예시를 제시했다. 다음 표는 SAT와 ACT 총점의 평균 및 표준 편차를 보여준다.

	SAT	ACT
평균	1500	21
표준 편차	300	5

SAT에서 1800점을 받은 학생 A와 ACT에서 24점을 받은 학생 B를 비교했을 때, 학생 A의 Z-점수는 $z = {x- \mu \over \sigma} = {1800- 1500 \over 300} = 1$ 이고, 학생 B의 Z-점수는 $z = {x- \mu \over \sigma} = {24- 21 \over 5} = 0.6$ 이다. 학생 A의 Z-점수가 더 높으므로, 다른 시험 응시자에 비해 학생 A가 학생 B보다 더 좋은 성적을 냈다고 볼 수 있다.^[9]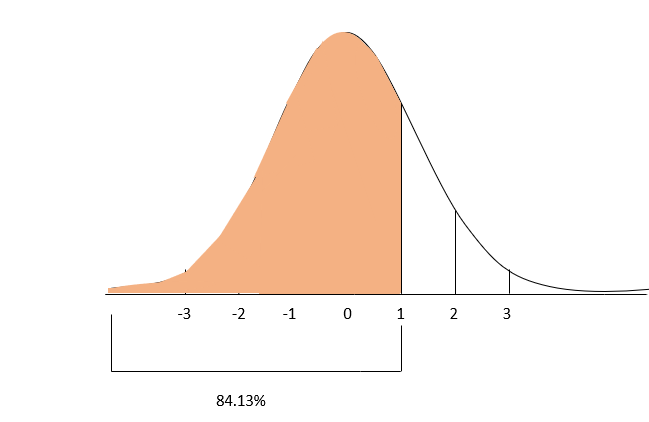

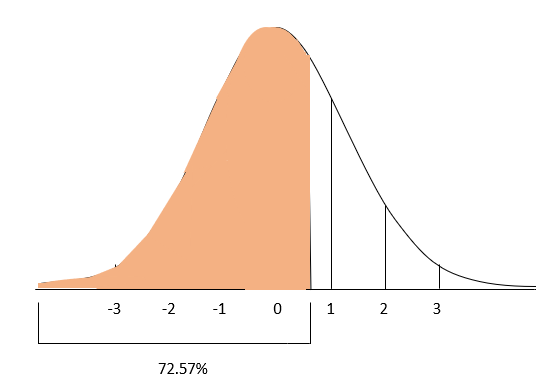
학생 A의 ''z'' 점수는 1로, 학생 A가 평균보다 1 표준 편차 위에 있음을 의미한다. 따라서 학생 A는 SAT에서 84.13 백분위에 해당하는 성적을 받았다.

학생 B의 ''z'' 점수는 0.6으로, 학생 B가 평균보다 0.6 표준 편차 위에 있음을 의미한다. 따라서 학생 B는 SAT에서 72.57 백분위에 해당하는 성적을 받았다.

ACT와 SAT 점수가 정규 분포를 따른다고 가정하면, Z-점수를 사용하여 A와 B 학생보다 낮은 점수를 받은 응시자의 비율을 계산할 수 있다.

표준 점수는 예측 구간 계산에도 사용될 수 있다. 예측 구간 [L, U]는 미래 관측치 X가 높은 확률

\gamma

로 구간 내에 위치하도록 하는 구간이다. X의 표준 점수 Z에 대해

P\left( \frac{L-\mu}{\sigma} < Z < \frac{U-\mu}{\sigma} \right) = \gamma

가 주어지고, 분위수 z를

P\left( -z < Z < z \right) = \gamma

와 같이 결정하면,

L=\mu-z\sigma,\ U=\mu+z\sigma

가 된다.^[8]

공정 제어 응용 분야에서 Z 값은 공정이 목표에서 얼마나 벗어났는지를 평가하는 데 사용된다.

다변량 기법 중 다차원 척도법이나 군집 분석과 같은 경우, 데이터 내 단위 간 거리는 중요한 의미를 갖는다. 다변량 데이터 집합의 변수들이 서로 다른 척도를 가질 때, 표준화를 거친 후 거리를 계산하는 것이 더 타당하다.^[10] 주성분 분석에서도 서로 다른 척도 또는 매우 다른 범위를 가진 공통 척도로 측정된 변수는 종종 표준화된다.^[11]

다중 회귀 분석 전에 변수를 표준화하는 것은 해석을 돕기 위해 사용되기도 한다.^[12] 그러나 예측 변수가 서로 상관 관계가 있을 때 회귀 계수는 모델의 다른 예측 변수의 영향을 받으므로, 표준화 여부에 관계없이 회귀 계수를 해석하는 데 주의해야 한다.^[13]

교육 평가에서 T-점수는 평균 50, 표준 편차 10을 갖도록 변환 및 조정된 표준 점수 Z이다.^[14]^[15]^[16]

4. 1. 지능검사

지능 검사 시험의 결과를 내기 위해 표준점수가 사용된다. '''편차값'''은 평균이 50, 표준 편차(SD)가 10이 되도록 변환한 점수이다. T 점수(T값, T-score)도 같은 뜻이다. 교육 분야에서 자주 사용된다.

'''편차 IQ'''는 정규 분포 상에서 평균이 100, 표준 편차(SD)가 15(웨슬러식의 경우) 또는 16(비네식의 경우)이 되도록 변환한 점수이다.^[1]

평균, 표준 편차를 변환해도 그 비율은 변하지 않으므로, 정규 분포상에서 특정 점수 사이에 포함되는 비율은 정해져 있다.^[1] 예를 들어 편차 IQ는 전체의 약 68.26%의 사람이 85~115의 점수를 얻고, 약 95.44%의 사람이 70~130의 점수를 얻는다.^[1]

이 비율을 바탕으로 점수가 낮은 곳부터 순위를 매긴 것을 '''백분위 순위'''라고 한다(위 그림은 편차 IQ의 경우).^[1] 예를 들어, IQ 85는 모집단의 아래에서 16 백분위의 순위에 있음을 의미한다.^[1]

4. 2. 대한민국 수능 제도

2005학년도부터 대한민국에서도 대학수학능력시험 성적표에 등급 이외에 표준점수와 백분위가 같이 나오게 된다. 이는 모든 응시자가 채점된 후 각 개인 응시자가 전체 순위 중 어디쯤에 위치하는지를 알려줄 수 있는 상대평가점수이다.^[20]

:

S = z \sigma + m

여기서,

S

는 표준점수,

z

는 Z점수,

\sigma

는 표준점수의 표준편차(국어·수학 영역은 20점, 기타 10점),

m

은 표준점수의 평균(국어·수학 영역은 100점, 기타 50점)이다.^[20]

:

z = \frac{x - m_0}{\sigma_0}

여기서,

x

는 수험생의 원점수,

m_0

는 해당 과목의 수험생 평균,

\sigma_0

는 해당 과목의 수험생 표준편차이다.

이러한 Z점수는 수능시험을 주관하는 한국교육과정평가원에서 표준점수, 9등급 점수와 함께 성적표에 공개한다.

4. 3. 일본의 교육제도

일본의 교육 제도에서 학력 편차치(T score)는 각 학교 및 학생 간의 서열을 객관적으로 평가하기 위한 자료로 활용되고 있다. 예를 들어 어느 고등학교의 편차치가 70이라면 일류대학인 도쿄 대학에 많은 학생들을 입학시킨다는 것이며, 30인 경우는 거의 그렇지 못하다는 것이다. 이로 인해 모든 학교와 학생들의 서열화를 부추겨 차별과 계급화를 심화시킨다는 비판이 있다. '편차치'는 일본인들에게는 대중화된 수학 용어이며 일반적으로 '편차치'라고 하면 '학력 편차치'를 의미한다.

대규모 모의시험을 치르는 수험생에게 이러한 편차치는 각 시험에서 시험의 난이도에 상관없이 객관적으로 자신의 점수를 평가하는 자료이며, 자신이 목표로 하는 학교에 입학할 수 있는 합격 가능성을 나타내는 것이다. 1980년대에 일본의 교사 쿠와타 쇼우조우(桑田昭三)에 의해 연구되었으며, 현재는 학원이나 학교에서 중학교, 고등학교 및 대학교 진학 지도를 위해 널리 이용되고 있다.

5. 비판 및 논란

표준 점수는 그 자체로 유용한 정보를 제공하지만, 사용과 해석에 있어서 주의가 필요하며 여러 비판과 논란의 대상이 되기도 한다.

원점수 정보 손실: 표준 점수는 원점수의 분포를 변환한 것이기 때문에, 원점수 자체의 정보(예: 평균, 특정 점수 획득 학생 수)를 알 수 없다.
집단 의존성: 표준 점수는 응시 집단의 평균과 표준편차에 따라 달라지므로, 서로 다른 집단의 표준 점수를 직접 비교하는 것은 무의미하다. 예를 들어, A 시험의 표준 점수 120점과 B 시험의 표준 점수 120점은 동일한 수준의 성취도를 의미하지 않는다.
왜곡 가능성: 표준 점수는 원점수 분포를 정규분포에 가깝게 변환하는 과정에서 왜곡이 발생할 수 있다. 특히, 극단적인 점수 분포를 보이는 경우 표준 점수의 의미가 달라질 수 있다.
서열 조장: 표준 점수는 학생들을 상대적인 서열로 나타내기 때문에, 과도한 경쟁과 서열화를 조장할 수 있다는 비판이 있다.
교육적 활용 제한: 표준 점수는 학생의 상대적 위치를 파악하는 데는 유용하지만, 개별 학생의 학업 성취도 변화나 강점·약점을 파악하는 데는 한계가 있다.

참조

_[1] 서적 2015 European School of High-Energy Physics: Bansko, Bulgaria 02 - 15 Sep 2015 https://cds.cern.ch/[...] CERN 2017
_[2] 간행물 Practical Statistics for High Energy Physics https://e-publishing[...] 2017-11-06
_[3] 서적 Advanced Engineering Mathematics Wiley
_[4] 서적 Schaum's Outlines Statistics McGraw Hill
_[5] 서적 Statistics for Engineering and the Sciences Pearson / Prentice Hall
_[6] 서적 Primer of Applied Regression & Analysis of Variance McGraw Hill
_[7] 서적 Foundational and Applied Statistics for Biologists Chapman & Hall / CRC Press
_[8] 서적 Advanced Engineering Mathematics Wiley
_[9] 서적 OpenIntro Statistics https://www.openintr[...] openintro.org
_[10] 서적 An Introduction to Applied Multivariate Analysis with R Springer
_[11] 서적 Applied Multivariate Statistical Analysis Pearson / Prentice Hall
_[12] 서적 Practical Multivariate Analysis Chapman & Hall/CRC
_[13] 서적 Applied Linear Regression Models McGraw Hill
_[14] 서적 Assessment: In Special and Inclusive Education https://books.google[...] Cengage Learning 2009-01-29
_[15] 서적 Essentials of Testing and Assessment: A Practical Guide for Counselors, Social Workers, and Psychologists https://books.google[...] Cengage Learning 2014-01-01
_[16] 서적 Clinical Assessment of Child and Adolescent Intelligence https://books.google[...] Springer 2005-08-16
_[17] 웹사이트 Bone Mass Measurement: What the Numbers Mean https://www.niams.ni[...] National Institute of Health 2017-08-05
_[18] 웹사이트 使われている統計技法 https://www.noma.co.[...] 2022-02-02
_[19] 웹사이트 使われている統計技法 https://www.noma.co.[...] 2022-02-02
_[20] 문서 2017학년도 이전에는 영어 영역도 포함된다.

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com