맨위로가기

다층 모형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

다층 모형은 데이터가 여러 계층으로 구성된 경우, 각 계층의 특성을 고려하여 분석하는 통계 기법이다. 수준(level) 개념을 사용하여 학생, 학급, 학교, 교육구 등과 같이 계층적 구조를 갖는 데이터를 분석하며, 종속 변수, 독립 변수, 예측 변수, 고정 효과, 무작위 효과 등의 용어를 사용한다. 다층 모형은 임의 절편 모형, 임의 기울기 모형, 임의 절편 및 기울기 모형 등으로 구분되며, 모형 개발 및 평가 과정에서 우도비 검정, 아카이케 정보 기준, 베이즈 정보 기준 등의 지표를 활용한다. 다층 모형은 선형성, 정규성, 동분산성, 독립성, 직교성 등의 가정을 가지며, 교육 연구, 사회학 연구, 심리학 연구, 경제학 연구, 지리학 연구 등 다양한 분야에서 활용된다. 특히 소득 불평등, 교육 격차, 지역 발전 격차 연구 등 한국 사회 현안 분석에도 기여할 수 있다.

2. 역사적 배경

다층 모형은 사회 과학 및 교육 연구 분야에서 계층적 데이터 구조를 분석하기 위해 발전되었다. 초기에는 주로 교육 연구에서 학교, 학급, 학생 간의 관계를 분석하는 데 사용되었으나, 점차 사회학, 심리학, 경제학, 지리학 등 다양한 분야로 확장되었다.

계층적 데이터를 분석하는 데에는 여러 가지 방법이 있지만, 대부분 문제점을 안고 있다.

기존의 통계적 기법을 활용하여 상위 수준의 변수를 개인 수준으로 분해하여 분석하는 방법(예: 학급 변수를 개별 학생에게 할당)이 있다. 이 방법은 독립성 가정을 위반하여 결과에 편향을 초래할 수 있으며, 이를 원자론적 오류(atomistic fallacy)라고 한다.[46]

또 다른 방법으로는 개인 수준의 변수를 상위 수준의 변수로 집약하여 분석하는 방법이 있다. 이 기법에서는 개인 수준 변수의 평균을 취하기 때문에 그룹 내의 정보가 모두 사라진다. 80~90%에 달하는 분산이 무시되고, 집약된 변수 간의 관계가 과장되어 왜곡된 결과가 나타날 수 있다.[47] 이를 생태학적 오류(ecological fallacy)라고 하며, 통계적으로는 정보 손실과 검정력 저하를 초래한다.[48]

계층적 데이터를 분석하는 또 다른 방법은 랜덤 계수 모델을 사용하는 것이다. 이 모델은 각 그룹이 서로 다른 절편과 기울기를 가진 회귀 모델을 가지고 있다고 가정한다.[49] 그룹은 표본 추출되므로, 절편과 기울기 역시 그룹의 절편과 기울기 모집단에서 무작위로 추출된다고 가정한다. 이를 통해 기울기는 고정되어 있지만 절편은 변화시킬 수 있다고 가정하고 분석할 수 있다. 그러나 이 방법은 개인 성분은 독립적이지만, 그룹 성분은 그룹 간에만 독립적이고 그룹 내에서는 의존적이라는 문제점이 있다. 또한, 기울기는 무작위이지만 오차항의 상관 관계는 개인 수준 변수의 값에 의존한다는 분석도 가능하다. 이처럼 랜덤 계수 모델을 사용하는 경우 상위 수준의 변수를 포함시킬 수 없다는 문제가 있다.

3. 기본 개념 및 용어

다층 모형 분석을 수행하기 전에 연구자는 예측 변수의 포함 여부 등 여러 측면을 결정해야 한다. 연구자는 추정될 요소인 모수 값이 모든 그룹에서 동일한 값을 가지는 '고정'될지, 아니면 각 그룹마다 다른 값을 가지는 '무작위'로 설정될지를 결정해야 한다.[1][4][3] 또한 최대 우도 추정 또는 제한된 최대 우도 추정 방식을 사용할지 결정해야 한다.[1]

계층적 데이터를 분석하는 방법에는 여러 가지가 있지만, 대부분 문제점을 가지고 있다.


  • 기존의 통계적 기법을 사용하여 상위 수준의 변수를 개인 수준으로 분해하여 분석하는 방법(예: 학급 변수를 개별 학생에게 할당)은 독립성 가정을 위반하여 편향된 결과를 초래할 수 있다. 이를 원자론적 오류(atomistic fallacy)라고 한다.[46]
  • 개인 수준의 변수를 상위 수준의 변수로 집약하여 분석하는 방법은 그룹 내의 정보를 모두 버리게 되어 분산의 80~90%가 쓸모없어지고, 변수 간의 관계가 왜곡될 수 있다.[47] 이를 생태학적 오류(ecological fallacy)라고 하며, 통계적으로 검정력 저하를 초래한다.[48]
  • 랜덤 계수 모델을 사용하는 방법은 각 그룹이 서로 다른 절편과 기울기를 가진 회귀 모델을 가지고 있다고 가정한다.[49] 이 모델은 절편은 변동하도록 허용하지만 기울기는 고정되어 있다고 가정할 수 있다. 그러나 개인 성분은 독립적이지만 그룹 성분은 그룹 내에서 의존적이라는 문제점이 있다. 또한, 상위 수준의 변수를 포함시킬 수 없다는 문제도 있다.

3. 1. 수준 (Level)

수준의 개념은 다층 모형 접근 방식의 핵심이다. 교육 연구의 예를 들어보면, 2수준 모형의 수준은 다음과 같을 수 있다.

# 학생

# 학급

하지만 여러 학교와 여러 교육구를 연구하는 경우, 4수준 모형은 다음과 같을 수 있다.

# 학생

# 학급

# 학교

# 교육구

연구자는 각 변수에 대해 해당 변수가 측정된 수준을 설정해야 한다. 예를 들어 "시험 점수"는 학생 수준, "교사 경험"은 학급 수준, "학교 자금"은 학교 수준, "도시"는 교육구 수준에서 측정될 수 있다.[1]

3. 2. 종속 변수 (Dependent Variable)

다층 모형에서 종속 변수는 연구에서 예측하거나 설명하고자 하는 변수이다.

3. 3. 독립 변수 (Independent Variable)

종속 변수에 영향을 미칠 것으로 예상되는 변수이다. 간단한 예로, 소득을 연령, 계층, 성별 및 인종의 함수로 예측하는 기본적인 선형 회귀 모델을 생각해 볼 수 있다. 소득 수준은 거주 도시와 주에 따라서도 달라진다는 것을 관찰할 수 있다. 이를 회귀 모델에 통합하는 간단한 방법은 위치를 설명하기 위해 추가적인 독립 범주형 변수를 추가하는 것이다(예: 위치별 추가적인 이진 예측 변수 및 관련 회귀 계수 집합). 이렇게 하면 평균 소득이 증가하거나 감소하는 효과가 나타나지만, 예를 들어 인종과 성별이 소득에 미치는 영향이 모든 곳에서 동일하다고 가정할 것이다. 실제로는 그럴 가능성이 낮다. 서로 다른 지역 법률, 서로 다른 퇴직 정책, 인종 차별 수준의 차이 등으로 인해 모든 예측 변수가 서로 다른 지역에서 서로 다른 종류의 영향을 미칠 가능성이 높다.[1][4][3]

3. 4. 예측 변수 (Predictor Variable)

다층 모형 분석에서 연구자는 예측 변수의 포함 여부 등 여러 측면을 결정해야 한다. 예측 변수는 독립 범주형 변수와 같이 사용된다.[1][4][3] 연구자는 추정될 요소인 모수 값이 고정될지, 무작위로 설정될지를 결정해야 한다. 고정 모수는 모든 그룹에서 상수 값을 갖는 반면, 무작위 모수는 각 그룹마다 다른 값을 가진다.[3] 또한 최대 우도 추정 또는 제한된 최대 우도 추정 방식을 사용할지 결정해야 한다.[1]

예를 들어 소득을 연령, 계층, 성별, 인종의 함수로 예측하는 선형 회귀 모델에서 소득 수준은 거주 도시와 주에 따라서도 달라진다. 이를 반영하기 위해 위치를 설명하는 독립적인 범주형 변수를 추가할 수 있다. 하지만 이렇게 하면 인종과 성별이 소득에 미치는 영향이 모든 곳에서 동일하다고 가정하게 된다. 실제로는 지역 법률, 퇴직 정책, 인종 차별 수준의 차이 등으로 인해 예측 변수들이 서로 다른 지역에서 다르게 영향을 미칠 가능성이 높다.

다층 모델은 각 위치에서 각 예측 변수에 대해 서로 다른 회귀 계수를 허용한다. 즉, 주어진 위치의 사람들은 단일 회귀 계수 집합에 의해 생성된 상관된 소득을 가지고, 다른 위치의 사람들은 다른 계수 집합에 의해 생성된 소득을 가진다고 가정한다.

3. 5. 고정 효과 (Fixed Effect)

연구자는 다층 모형 분석을 할 때 모든 그룹에 걸쳐 상수 값을 가지는 고정 모수를 사용할지, 각 그룹마다 다른 값을 갖는 무작위 모수를 사용할지를 결정해야 한다.[1][4][3]

3. 6. 무작위 효과 (Random Effect)

무작위 모수는 각 그룹마다 다른 값을 갖는다.[3]

무작위 절편 모형은 절편이 변동하도록 허용되는 모형이며, 따라서 각 개별 관측치에 대한 종속 변수의 점수는 그룹 간에 변동하는 절편에 의해 예측된다.[4][8][3] 이 모형은 기울기가 고정되어 있다고 가정한다(다양한 상황에서 동일). 또한, 이 모형은 내집단 상관 관계에 대한 정보를 제공하며, 이는 다층 모형이 필요한지 여부를 결정하는 데 도움이 된다.[1]

임의 기울기 모형은 기울기가 상관 행렬에 따라 달라질 수 있도록 허용하는 모형이며, 따라서 시간이나 개인과 같은 그룹 변수마다 기울기가 다릅니다. 이 모형은 절편이 고정되어 있다고 가정한다(다른 맥락에서 동일).[4]

무작위 절편과 무작위 기울기를 모두 포함하는 모형은 가장 현실적인 모형일 가능성이 높지만, 가장 복잡하기도 하다. 이 모형에서는 절편과 기울기 모두 그룹 간에 변동이 허용되므로, 서로 다른 맥락에서 서로 다르다는 것을 의미한다.[4]

3. 7. 절편 (Intercept)

무작위 절편 모형은 절편이 변동하도록 허용되는 모형이며, 따라서 각 개별 관측치에 대한 종속 변수의 점수는 그룹 간에 변동하는 절편에 의해 예측된다.[4][8][3] 이 모형은 기울기가 고정되어 있다고 가정한다(다양한 상황에서 동일). 또한 이 모형은 내집단 상관 관계에 대한 정보를 제공하며, 이는 다층 모형이 필요한지 여부를 결정하는 데 도움이 된다.[1]

3. 8. 기울기 (Slope)

다층 모형에서 기울기는 독립 변수가 1 단위 증가할 때 종속 변수가 얼마나 변하는지를 나타낸다. 다층 모형에서는 이 기울기가 그룹(예: 시간, 개인)에 따라 달라질 수 있도록 허용한다. 즉, 각 그룹마다 기울기가 다를 수 있다. 이를 임의 기울기 모형이라고 하며, 이 모형은 절편이 고정되어 있다고 가정한다.[4]

예를 들어, 소득을 예측하는 단순 선형 회귀 모델에서는 인종과 성별이 소득에 미치는 영향이 모든 위치에서 동일하다고 가정한다. 하지만 실제로는 지역 법률, 퇴직 정책, 인종 차별 수준의 차이 등으로 인해 예측 변수의 영향이 지역마다 다를 수 있다. 다층 모형에서는 각 위치에서 각 예측 변수에 대해 서로 다른 회귀 계수(기울기)를 허용하여 이러한 차이를 반영할 수 있다.

3. 9. 잔차 (Residual)

다층 모형은 교란항이라고도 부르는 두 개의 오차항을 갖는다. 개별 성분은 모두 독립적이지만, 그룹 성분은 그룹 간에는 독립적이지만 그룹 내에서는 상관 관계를 갖는다.[18] 분산 성분은 다를 수 있으며, 일부 그룹은 다른 그룹보다 더 동질적이다.[18][50]

4. 모형의 종류

다층 모형 분석을 수행하기 전에 연구자는 몇 가지 측면을 결정해야 한다. 우선, 분석에 어떤 예측 변수를 포함할지 결정해야 한다. 다음으로, 모수(추정될 요소) 값을 모든 그룹에서 동일하게 고정할지, 아니면 각 그룹마다 다르게 무작위로 변동하도록 할지 결정해야 한다.[1][4][3] 또한, 최대 우도 추정 또는 제한된 최대 우도 추정 중 어떤 추정 방식을 사용할지 결정해야 한다.[1]

소득을 연령, 계층, 성별, 인종의 함수로 예측하는 기본적인 선형 회귀 모델을 예로 들어 보자. 거주하는 도시와 주에 따라서도 소득 수준이 달라진다는 것을 알 수 있다. 이를 회귀 모델에 반영하는 간단한 방법은 위치를 설명하기 위해 추가적인 독립 범주형 변수를 추가하는 것이다 (예: 위치별 추가적인 이진 예측 변수 및 관련 회귀 계수 집합). 이렇게 하면 평균 소득이 증가하거나 감소하는 효과는 나타낼 수 있지만, 인종과 성별이 소득에 미치는 영향은 모든 곳에서 동일하다고 가정하게 된다. 그러나 실제로는 지역별 법률, 퇴직 정책, 인종 차별 수준의 차이 등으로 인해 모든 예측 변수가 지역마다 다른 영향을 미칠 가능성이 높다.

다시 말해, 단순 선형 회귀 모델은 시애틀의 무작위로 추출된 사람이 앨라배마 주 모빌의 유사한 사람보다 평균 연간 10000USD 더 높을 것이라고 예측할 수 있다. 또한 백인이 흑인보다 평균 소득이 7000USD 높고, 65세가 45세보다 소득이 3000USD 낮을 것이라고 예측할 수 있는데, 이 두 경우 모두 위치와는 상관없이 예측한다. 그러나 다층 모형은 각 위치에서 각 예측 변수에 대해 서로 다른 회귀 계수를 허용한다. 즉, 주어진 위치의 사람들은 단일 회귀 계수 집합에 의해 생성된 상관된 소득을 가지고 있고, 다른 위치의 사람들은 다른 계수 집합에 의해 생성된 소득을 가지고 있다고 가정한다. 한편, 계수 자체는 상관 관계가 있고 단일 하이퍼파라미터 집합에서 생성된 것으로 가정한다. 추가적인 수준도 가능하다. 예를 들어, 사람들은 도시별로 그룹화될 수 있으며, 도시 수준 회귀 계수는 주별로 그룹화되고, 주 수준 계수는 단일 하이퍼-하이퍼파라미터에서 생성될 수 있다.

다층 모형은 여러 수준의 확률 변수와 서로 다른 변수 간의 임의의 관계를 가진 일반적인 모형인 계층적 베이즈 모형의 하위 클래스이다. 다층 분석은 다층 구조 방정식 모델링, 다층 잠재 클래스 모델링 및 기타 더 일반적인 모델을 포함하도록 확장되었다.

기존의 통계적 기법을 사용하여 계층적 데이터를 분석하는 방법에는 몇 가지 문제점이 있다. 예를 들어, 상위 수준 변수를 개인 수준으로 분해하여 분석하면 독립성 가정을 위반하여 편향된 결과를 얻을 수 있다(원자론적 오류).[46] 반대로, 개인 수준 변수를 상위 수준으로 집계하여 분석하면 그룹 내 정보가 손실되고 변수 간 관계가 왜곡될 수 있다(생태학적 오류).[47][48]

랜덤 계수 모델은 각 그룹이 서로 다른 절편과 기울기를 가진 회귀 모델을 갖는다고 가정하여 이러한 문제를 해결하려고 시도한다.[49] 그러나 이 모델은 개인 성분은 독립적이지만 그룹 성분은 그룹 간에만 독립적이고 그룹 내에서는 의존적이라는 문제점이 있다. 또한, 기울기는 랜덤이지만 오차항의 상관 관계는 개인 수준 변수의 값에 의존한다는 분석도 가능하다.

4. 1. 임의 절편 모형 (Random Intercept Model)

무작위 절편 모형은 절편이 변동하도록 허용되는 모형이며, 따라서 각 개별 관측치에 대한 종속 변수의 점수는 그룹 간에 변동하는 절편에 의해 예측된다.[4][8][3] 이 모형은 기울기가 고정되어 있다고 가정한다(다양한 상황에서 동일). 또한, 이 모형은 내집단 상관 관계에 대한 정보를 제공하며, 이는 다층 모형이 필요한지 여부를 결정하는 데 도움이 된다.[1]

간단한 예로, 소득을 연령, 계층, 성별 및 인종의 함수로 예측하는 기본적인 선형 회귀 모델을 생각해 보자. 소득 수준은 거주 도시와 주에 따라서도 달라진다는 것을 관찰할 수 있다. 이를 회귀 모델에 통합하는 간단한 방법은 위치를 설명하기 위해 추가적인 독립 범주형 변수를 추가하는 것이다(예: 위치별 추가적인 이진 예측 변수 및 관련 회귀 계수 집합). 이렇게 하면 평균 소득이 증가하거나 감소하는 효과가 나타나지만, 예를 들어 인종과 성별이 소득에 미치는 영향이 모든 곳에서 동일하다고 가정할 것이다. 실제로는 그럴 가능성이 낮다. 서로 다른 지역 법률, 서로 다른 퇴직 정책, 인종 차별 수준의 차이 등으로 인해 모든 예측 변수가 서로 다른 지역에서 서로 다른 종류의 영향을 미칠 가능성이 높다.

다시 말해, 단순 선형 회귀 모델은 예를 들어 시애틀의 무작위로 추출된 사람이 앨라배마 주 모빌의 유사한 사람보다 평균 연간 소득이 10000USD 더 높을 것이라고 예측할 수 있다. 그러나 또한 예를 들어 백인이 흑인보다 평균 소득이 7000USD 높고, 65세가 45세보다 소득이 3000USD 낮을 것이라고 예측할 수 있으며, 이 두 경우 모두 위치와 상관없이 예측한다. 그러나 다층 모델은 각 위치에서 각 예측 변수에 대해 서로 다른 회귀 계수를 허용할 것이다. 본질적으로, 주어진 위치의 사람들은 단일 회귀 계수 집합에 의해 생성된 상관된 소득을 가지고 있는 반면, 다른 위치의 사람들은 다른 계수 집합에 의해 생성된 소득을 가지고 있다고 가정한다. 한편, 계수 자체는 상관 관계가 있고 단일 하이퍼파라미터 집합에서 생성된 것으로 가정한다. 추가 수준이 가능하다. 예를 들어, 사람들은 도시별로 그룹화될 수 있으며, 도시 수준 회귀 계수는 주별로 그룹화되고, 주 수준 계수는 단일 하이퍼-하이퍼파라미터에서 생성된다.

4. 2. 임의 기울기 모형 (Random Slope Model)

임의 기울기 모형은 기울기가 상관 행렬에 따라 달라질 수 있도록 허용하는 모형이며, 따라서 시간이나 개인과 같은 그룹 변수마다 기울기가 다르다. 이 모형은 절편이 고정되어(다른 맥락에서 동일) 있다고 가정한다.[4]

간단한 예로, 소득을 연령, 계층, 성별 및 인종의 함수로 예측하는 기본적인 선형 회귀 모형을 생각해 보자. 소득 수준은 거주 도시와 주에 따라서도 달라진다는 것을 관찰할 수 있다. 이를 회귀 모형에 통합하는 간단한 방법은 위치를 설명하기 위해 추가적인 독립 범주형 변수를 추가하는 것이다(예: 위치별 추가적인 이진 예측 변수 및 관련 회귀 계수 집합). 이렇게 하면 평균 소득이 증가하거나 감소하는 효과가 나타나지만, 예를 들어 인종과 성별이 소득에 미치는 영향이 모든 곳에서 동일하다고 가정할 것이다. 실제로는 그럴 가능성이 낮다. 서로 다른 지역 법률, 서로 다른 퇴직 정책, 인종 차별 수준의 차이 등으로 인해 모든 예측 변수가 서로 다른 지역에서 서로 다른 종류의 영향을 미칠 가능성이 높다.

다시 말해, 단순 선형 회귀 모형은 예를 들어 시애틀의 무작위로 추출된 사람이 앨라배마 주 모빌의 유사한 사람보다 평균 연간 소득이 10000USD 더 높을 것이라고 예측할 수 있다. 그러나 또한 예를 들어 백인이 흑인보다 평균 소득이 7000USD 높고, 65세가 45세보다 소득이 3000USD 낮을 것이라고 예측할 수 있으며, 이 두 경우 모두 위치와 상관없이 예측한다. 그러나 다층 모형은 각 위치에서 각 예측 변수에 대해 서로 다른 회귀 계수를 허용할 것이다. 본질적으로, 주어진 위치의 사람들은 단일 회귀 계수 집합에 의해 생성된 상관된 소득을 가지고 있는 반면, 다른 위치의 사람들은 다른 계수 집합에 의해 생성된 소득을 가지고 있다고 가정한다. 한편, 계수 자체는 상관 관계가 있고 단일 하이퍼파라미터 집합에서 생성된 것으로 가정한다. 추가 수준이 가능하다. 예를 들어, 사람들은 도시별로 그룹화될 수 있으며, 도시 수준 회귀 계수는 주별로 그룹화되고, 주 수준 계수는 단일 하이퍼-하이퍼파라미터에서 생성된다.

다층 모형은 여러 수준의 확률 변수와 서로 다른 변수 간의 임의의 관계를 가진 일반적인 모형인 계층적 베이즈 모형의 하위 클래스이다. 다층 분석은 다층 구조 방정식 모델링, 다층 잠재 클래스 모델링 및 기타 더 일반적인 모델을 포함하도록 확장되었다.

랜덤 기울기 모델은 기울기의 변화를 허용하는 모델로, 그룹 간 기울기가 다른 경우에 사용된다. 이 모델은 그룹 간 절편이 일정하다는 것을 전제로 한다.[34]

4. 3. 임의 절편 및 기울기 모형 (Random Intercept and Slope Model)

무작위 절편 및 기울기 모형은 절편과 기울기 모두 그룹 간에 변동하도록 허용하는 모형으로, 가장 복잡하지만 현실적인 모형이다. 이 모형에서는 서로 다른 맥락에서 절편과 기울기가 다를 수 있다고 가정한다.[4]

예를 들어, 소득을 연령, 계층, 성별, 인종의 함수로 예측하는 기본적인 선형 회귀 모델을 생각해 보자. 거주하는 도시와 주에 따라서도 소득 수준이 달라진다는 것을 알 수 있다. 이를 회귀 모델에 반영하는 간단한 방법은 위치를 설명하기 위해 추가적인 독립 범주형 변수를 추가하는 것이다. (예: 위치별 추가적인 이진 예측 변수 및 관련 회귀 계수 집합) 이렇게 하면 평균 소득이 증가하거나 감소하는 효과는 나타낼 수 있지만, 인종과 성별이 소득에 미치는 영향은 모든 곳에서 동일하다고 가정하게 된다. 그러나 실제로는 지역별 법률, 퇴직 정책, 인종 차별 수준의 차이 등으로 인해 모든 예측 변수가 지역마다 다른 영향을 미칠 가능성이 높다.

다시 말해, 단순 선형 회귀 모델은 시애틀의 무작위로 추출된 사람이 앨라배마 주 모빌의 유사한 사람보다 평균 연간 10000USD 더 높을 것이라고 예측할 수 있다. 또한 백인이 흑인보다 평균 소득이 7000USD 높고, 65세가 45세보다 소득이 3000USD 낮을 것이라고 예측할 수 있는데, 이 두 경우 모두 위치와는 상관없이 예측한다. 그러나 다층 모형은 각 위치에서 각 예측 변수에 대해 서로 다른 회귀 계수를 허용한다. 즉, 주어진 위치의 사람들은 단일 회귀 계수 집합에 의해 생성된 상관된 소득을 가지고 있고, 다른 위치의 사람들은 다른 계수 집합에 의해 생성된 소득을 가지고 있다고 가정한다. 한편, 계수 자체는 상관 관계가 있고 단일 하이퍼파라미터 집합에서 생성된 것으로 가정한다. 추가적인 수준도 가능하다. 예를 들어, 사람들은 도시별로 그룹화될 수 있으며, 도시 수준 회귀 계수는 주별로 그룹화되고, 주 수준 계수는 단일 하이퍼-하이퍼파라미터에서 생성될 수 있다.

무작위 절편 및 기울기 모형은 절편과 기울기 모두 그룹 간에 변동하는 것을 허용하므로 가장 복잡하지만 가장 현실적인 모형이다.[35]

5. 모형 개발 및 평가

다층 모형을 개발하고 평가할 때는 우선 분석에 포함할 예측 변수를 결정하고, 모수 값을 고정할지 또는 무작위로 설정할지, 어떤 추정 방식을 사용할지 결정해야 한다.[1][4][3]

모형 평가는 다양한 모형 적합도 통계량을 통해 이루어진다.[1] 카이제곱 우도비 검정, 아카이케 정보 기준(AIC), 베이즈 정보 기준(BIC) 등이 활용된다. 우도비 검정은 내포 모델에만 적용 가능하며, AIC와 BIC는 비내포 모델 비교에도 사용된다.[5][1][4]

5. 1. 모형 개발 단계

다층 모형 분석을 수행하기 전에 연구자는 분석에 포함할 예측 변수가 있는지 등 여러 측면에 대해 결정해야 한다. 둘째, 연구자는 모수 값(추정될 요소)이 고정될지 또는 무작위로 설정될지를 결정해야 한다.[1][4][3] 고정된 모수는 모든 그룹에 걸쳐 상수 값으로 구성되는 반면, 무작위 모수는 각 그룹마다 다른 값을 갖는다.[3] 또한 연구자는 최대 우도 추정 또는 제한된 최대 우도 추정 방식을 사용할지 결정해야 한다.[1]

다층 모형 분석을 수행하려면, 고정 계수(기울기 및 절편)로 시작해야 한다. 한 번에 하나의 측면이 변동하도록 허용(변경)하고, 더 나은 모델 적합성을 평가하기 위해 이전 모델과 비교한다.[5] 연구자는 모델을 평가할 때 세 가지 질문을 한다. 첫째, 좋은 모델인가? 둘째, 더 복잡한 모델이 더 좋은가? 셋째, 개별 예측 변수가 모델에 어떤 기여를 하는가?

모델을 평가하기 위해 다양한 모델 적합도 통계량을 검토한다.[1] 그러한 통계량 중 하나는 모델 간의 차이를 평가하는 카이제곱 우도비 검정이다. 우도비 검정은 일반적으로 모델 구축, 모델의 효과가 변동하도록 허용될 때의 변화 검토, 더미 코딩된 범주형 변수를 단일 효과로 테스트하는 데 사용될 수 있다.[1] 그러나 이 검정은 모델이 내포된 경우에만 사용할 수 있다(더 복잡한 모델이 더 간단한 모델의 모든 효과를 포함한다는 의미). 비내포 모델을 테스트할 때는 아카이케 정보 기준 (AIC) 또는 베이즈 정보 기준 (BIC) 등을 사용하여 모델 간의 비교를 수행할 수 있다.[5][1][4] 자세한 내용은 모델 선택을 참조하라.

5. 2. 모형 평가 지표

다층 모형을 평가할 때는 다양한 모형 적합도 통계량을 검토한다.[1] 그중 하나는 모델 간의 차이를 평가하는 카이제곱 우도비 검정이다. 우도비 검정은 모델 구축, 모델 효과의 변동, 더미 코딩된 범주형 변수를 단일 효과로 테스트하는 데 사용될 수 있다.[1] 그러나 이 검정은 모델이 내포된 경우(더 복잡한 모델이 더 간단한 모델의 모든 효과를 포함)에만 사용할 수 있다.

내포되지 않은 모델을 테스트할 때는 아카이케 정보 기준(AIC) 또는 베이즈 정보 기준(BIC) 등을 사용하여 모델 간 비교를 수행할 수 있다.[5][1][4]

5. 2. 1. 우도비 검정 (Likelihood Ratio Test)

우도비 검정은 다층 모형 분석에서 두 모형을 비교하는 데 사용되는 방법이다. 이 검정은 모델 구축 과정, 모델 내 효과의 변동, 그리고 더미 코딩된 범주형 변수를 단일 효과로 검정하는 데 활용될 수 있다.[1] 핵심은 두 모형의 우도 값을 비교하여 어떤 모형이 데이터에 더 적합한지를 평가하는 것이다.

그러나 이 검정은 모델이 내포된 경우, 즉 더 복잡한 모델이 더 간단한 모델의 모든 효과를 포함하는 경우에만 사용할 수 있다.[1] 만약 모델이 내포되지 않은 경우에는 아카이케 정보 기준 (AIC) 또는 베이즈 정보 기준 (BIC) 등을 사용하여 모델 간 비교를 수행할 수 있다.[5][1][4]

5. 2. 2. 아카이케 정보 기준 (Akaike Information Criterion, AIC)

아카이케 정보 기준(AIC)은 내포되지 않은 모델 간 비교에 사용되는 지표이다.[1][4][5] AIC는 모형의 적합도와 간결성을 함께 고려하여 모형을 평가한다. 베이즈 정보 기준(BIC)도 비내포 모델 비교에 사용될 수 있다.[1][4][5]

5. 2. 3. 베이즈 정보 기준 (Bayesian Information Criterion, BIC)

아카이케 정보 기준 (AIC)과 유사하지만, 표본 크기에 대한 벌점을 더 크게 부여하는 지표이다. 비내포 모델을 테스트할 때 모델 간의 비교를 위해 사용된다.[5][1][4]

6. 가정

다층 모형은 ANOVA, 회귀와 같은 다른 주요 일반 선형 모형과 동일한 가정을 갖지만, 설계의 계층적 특성(내포된 데이터)에 맞게 일부 가정이 수정된다. 다층 모형 분석을 수행하기 전에 연구자는 분석에 포함할 예측 변수가 있는지, 모수 값(추정될 요소)이 고정될지 또는 무작위로 설정될지, 최대 우도 추정 또는 제한된 최대 우도 추정 방식을 사용할지 등을 결정해야 한다.[1][4][3] 고정된 모수는 모든 그룹에 걸쳐 상수 값으로 구성되는 반면, 무작위 모수는 각 그룹마다 다른 값을 갖는다.[3]

6. 1. 선형성 (Linearity)



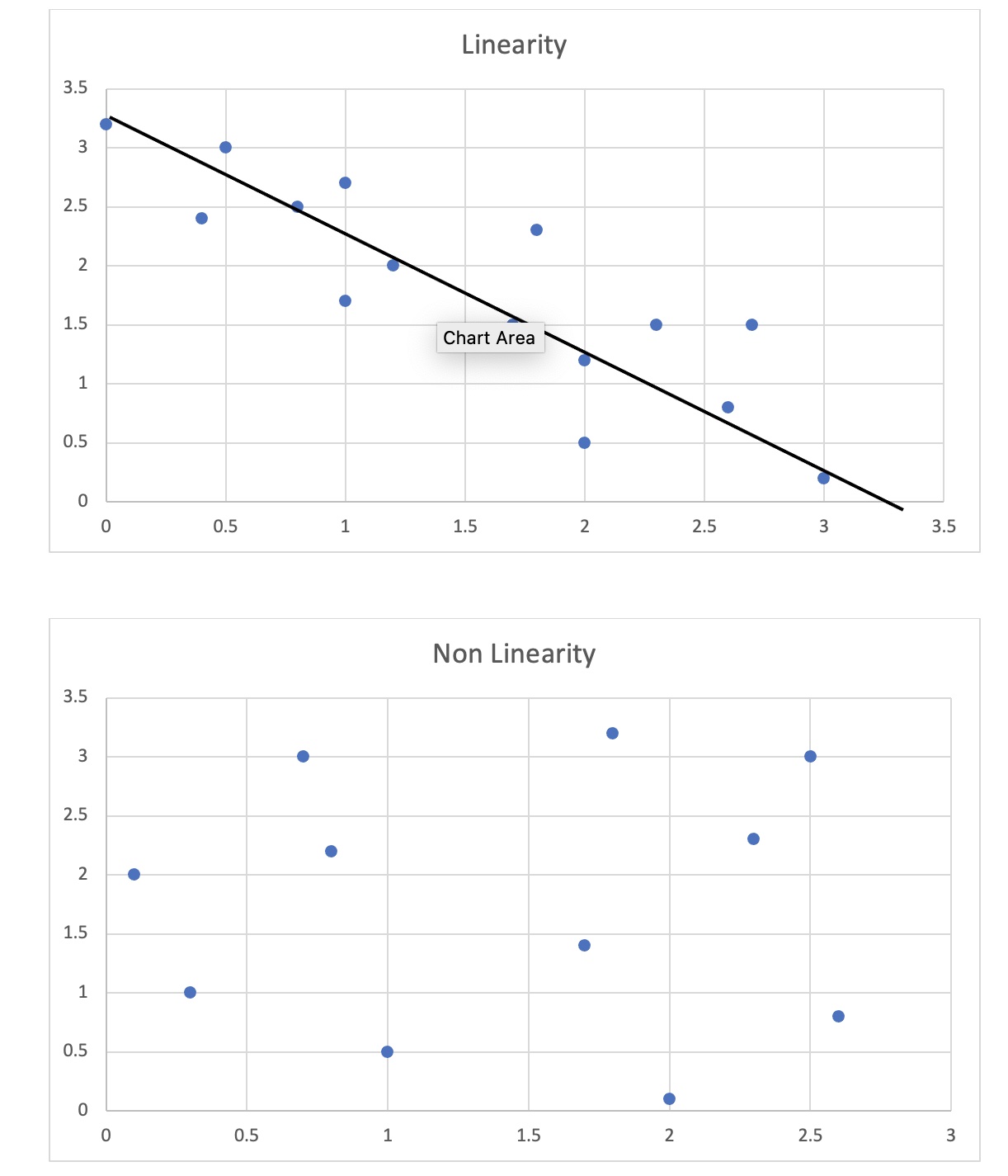
선형성 가정은 변수 간에 직선 관계(비선형 또는 U자형과 반대)가 있음을 나타낸다.[10] 그러나 비선형 혼합 효과 모형처럼 비선형 관계로 확장될 수 있다.[9][7]

6. 2. 정규성 (Normality)

정규성 가정은 모형의 모든 수준에서 오차 항이 정규 분포를 따른다고 명시한다.[10] 그러나 대부분의 통계 소프트웨어는 푸아송 분포, 이항 분포, 로지스틱 분포와 같은 분산 항에 대해 서로 다른 분포를 지정할 수 있도록 허용한다. 다층 모형 접근 방식은 모든 형태의 일반화 선형 모형에 사용할 수 있다.

6. 3. 등분산성 (Homoscedasticity)

등분산성(분산의 균일성) 가정은 모집단 분산이 동일하다는 것을 전제로 한다.[10] 그러나 다른 분산 상관 행렬을 지정하거나, 분산의 불균일성 자체를 모형화할 수도 있다.

6. 4. 독립성 (Independence)

다층 모형은 다른 주요 일반 선형 모형(ANOVA, 회귀 등)과 마찬가지로 독립성 가정을 가진다. 독립성은 사례가 모집단에서 무작위로 추출된 표본이며, 종속 변수의 점수가 서로 독립적이라는 것을 의미한다.[10] 다층 모형은 이 독립성 가정이 위반된 경우를 다루기 위한 방법이다.

다층 모형에서는 추가적으로 다음 두 가지를 가정한다.

  • 레벨 1과 레벨 2의 잔차는 서로 상관 관계가 없다.
  • 최고 수준의 오차(잔차로 측정)는 서로 상관 관계가 없다.[11]


다층 모형에는 두 가지 오차항이 있다. 개인 수준의 오차항은 모두 독립적이지만, 그룹 수준의 오차항은 그룹 간에는 독립적이지만 그룹 내에서는 상관되어 있다. 분산 성분은 다를 수 있다.[50]

6. 5. 직교성 (Orthogonality)

회귀 변수는 무작위 효과 u_{0j}와 상관 관계가 없어야 한다. 이 가정은 검증할 수 있지만 종종 무시되어 추정량을 일관성 없게 만든다.[12] 이 가정이 위반되면 더미 변수를 사용하거나 모든 X_{ij} 회귀 변수의 클러스터 평균을 포함하여 고정 부분에서 무작위 효과를 명시적으로 모형화해야 한다.[12][13][14][15] 이 가정은 추정기가 가지는 가장 중요한 가정일 가능성이 높지만, 이러한 유형의 모형을 사용하는 대부분의 응용 연구자가 오해하고 있다.[12]

7. 통계적 검정 및 검정력

다층 모형 분석을 수행하기 전에 연구자는 분석에 포함할 예측 변수가 있는지 여부 등 여러 측면에 대해 결정해야 한다. 연구자는 모수 값(추정될 요소)이 고정될지 또는 무작위로 설정될지를 결정해야 한다.[1][4][3] 고정된 모수는 모든 그룹에 걸쳐 상수 값으로 구성되는 반면, 무작위 모수는 각 그룹마다 다른 값을 갖는다.[3] 또한 연구자는 최대 우도 추정 또는 제한된 최대 우도 추정 방식을 사용할지 결정해야 한다.[1]

다층 모형의 통계적 검정력은 1수준 효과인지 2수준 효과인지에 따라 달라진다. 1수준 효과의 검정력은 개별 관측치 수에 따라 달라지는 반면, 2수준 효과의 검정력은 그룹 수에 따라 달라진다.[16] 충분한 검정력을 확보하려면 다층 모형에서 큰 표본 크기가 필요하다. 그러나 그룹 내 개별 관측치 수는 연구 내 그룹 수만큼 중요하지 않다. 교차 수준 상호작용을 감지하려면 최소 20개의 그룹이 필요하다는 권고가 있지만,[16] 고정 효과에 대한 추론에만 관심이 있고, 무작위 효과가 제어 변수 또는 "방해" 변수인 경우에는 훨씬 적은 수를 사용할 수 있다.[3]

7. 1. 통계적 검정

다층 모형에서 사용되는 통계적 검정은 고정 효과 또는 분산 성분을 검토하는지에 따라 달라진다. 고정 효과를 검토할 때는 검정을 고정 효과의 표준 오차와 비교하며, 이는 Z-검정을 초래한다.[4] t-검정도 계산할 수 있다. t-검정을 계산할 때, 예측 변수의 수준(1수준 예측 변수 또는 2수준 예측 변수)에 따라 달라지는 자유도를 염두에 두는 것이 중요하다.[4]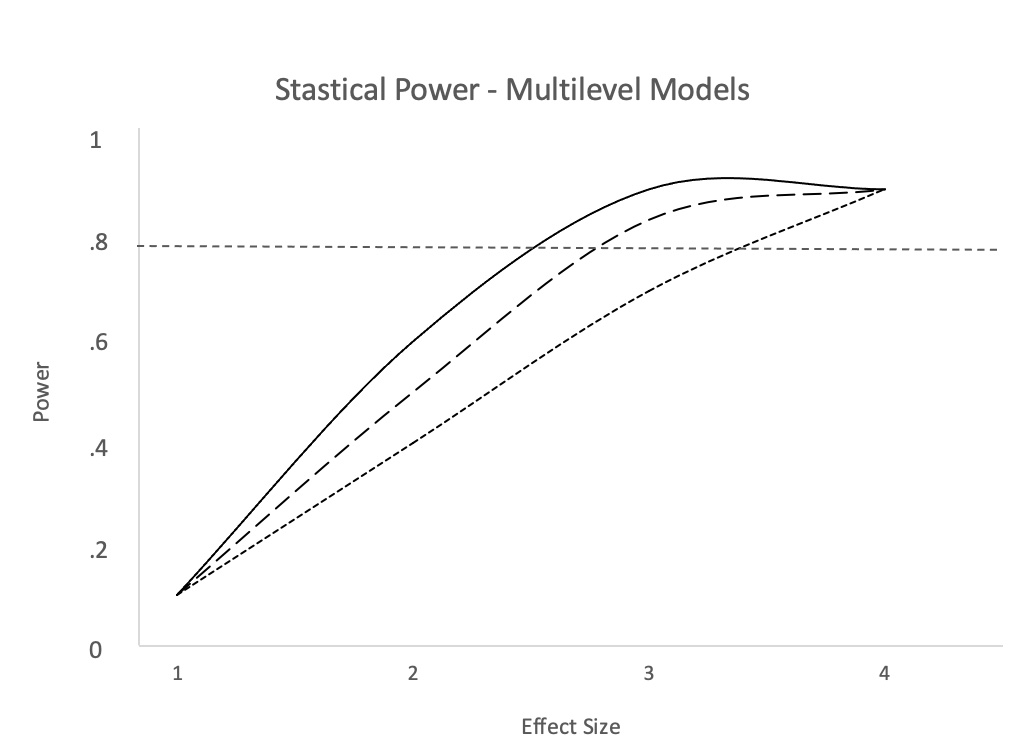

297x297px

7. 1. 1. Z-검정 (Z-test)

Z-검정은 고정 효과를 검토할 때 사용되는 방법으로, 고정 효과의 표준 오차와 비교하여 검정한다.[4] t-검정도 계산할 수 있는데, t-검정을 계산할 때는 예측 변수의 수준(예: 1수준 예측 변수 또는 2수준 예측 변수)에 따라 달라지는 자유도를 고려해야 한다.[4] 1수준 예측 변수의 경우 자유도는 1수준 예측 변수의 수, 그룹의 수, 개별 관측치의 수를 기반으로 하며, 2수준 예측 변수의 경우 자유도는 2수준 예측 변수의 수와 그룹의 수를 기반으로 한다.[4]

7. 1. 2. t-검정 (t-test)

Z-검정은 고정 효과의 표준 오차와 비교하여 고정 효과를 검토할 때 사용되는 검정 방법이다.[4] t-검정도 계산할 수 있는데, t-검정을 계산할 때는 예측 변수의 수준(예: 1수준 예측 변수 또는 2수준 예측 변수)에 따라 달라지는 자유도를 고려해야 한다.[4] 1수준 예측 변수의 경우, 자유도는 1수준 예측 변수의 수, 그룹의 수 및 개별 관측치의 수를 기반으로 한다. 2수준 예측 변수의 경우, 자유도는 2수준 예측 변수의 수와 그룹의 수를 기반으로 한다.[4]

7. 2. 통계적 검정력 (Statistical Power)

다층 모형의 통계적 검정력은 1수준 효과인지 2수준 효과인지에 따라 달라진다. 1수준 효과의 검정력은 개별 관측치 수에 의존하는 반면, 2수준 효과의 검정력은 그룹 수에 의존한다.[16] 충분한 검정력을 가진 연구를 수행하려면 다층 모형에서 큰 표본 크기가 필요하다. 그러나 그룹 내 개별 관측치 수는 연구 내 그룹 수만큼 중요하지 않다. 교차 수준 상호작용을 감지하려면 최소 20개의 그룹이 필요하다는 권고가 있지만,[16] 고정 효과에 대한 추론에만 관심이 있고, 무작위 효과가 제어 변수 또는 "방해" 변수인 경우에는 훨씬 적은 수를 사용할 수 있다.[3] 다층 모형의 통계적 검정력 문제는 검정력이 효과 크기 및 급내 상관 관계의 함수로 변동하고, 고정 효과와 무작위 효과에 대해 다르게 나타나며, 그룹 수와 그룹당 개별 관측치 수에 따라 변경된다는 사실로 인해 복잡해진다.[16]

8. 활용 분야

다층 모형은 교육, 지리, 심리, 사회, 조직 연구 등 다양한 분야에서 활용된다. 특히, 여러 수준의 확률 변수와 서로 다른 변수 간의 임의의 관계를 가진 일반적인 모델인 계층적 베이즈 모형의 하위 클래스이다. 다층 분석은 다층 구조 방정식 모델링, 다층 잠재 클래스 모델링 및 기타 더 일반적인 모델을 포함하도록 확장되었다.[3]


  • 교육 연구: 학교, 학급, 학생 간의 관계를 분석하여 교육 효과를 평가한다.
  • 지리 연구: 거주 도시와 주에 따라 소득 수준이 달라지는 것을 고려하여 위치별로 다른 회귀 계수를 허용한다.
  • 심리학 연구: 측정 도구, 개인, 가족 등 여러 수준의 관계를 분석한다.
  • 사회학 연구: 지역, 국가 등 다양한 사회 집단과 개인의 특성 간 관계를 분석한다.
  • 조직 심리학 연구: 개인의 데이터가 팀이나 기능적 단위에 중첩되는 것을 고려한다.


다층 모형은 서로 다른 수준에서 서로 다른 공변량이 관련될 수 있다는 점을 고려한다. 이는 성장 연구와 같이 한 개인 내의 변화와 개인 간의 차이를 분리하는 종단 연구에 사용될 수 있다.[3] 또한, 수준 간 상호 작용도 실질적인 관심사가 될 수 있다. 예를 들어, 기울기가 무작위로 변동하도록 허용될 때, 수준 2 예측 변수는 수준 1 공변량에 대한 기울기 공식에 포함될 수 있다. 예를 들어, 인종과 동네의 상호 작용을 추정하여 개인의 특성과 사회적 맥락 간의 상호 작용 추정치를 얻을 수 있다.[3]

8. 1. 교육 연구

다층 모형은 학교, 학급, 학생 간의 관계를 분석하여 교육 효과를 평가하는 데 활용된다.[3] 예를 들어, 2수준 모형은 학생과 학급으로 구성될 수 있다. 여러 학교와 교육구를 연구하는 경우, 4수준 모형은 학생, 학급, 학교, 교육구로 구성될 수 있다.[3] 연구자는 각 변수가 측정된 수준을 설정해야 한다. 예를 들어, "시험 점수"는 학생 수준, "교사 경험"은 학급 수준, "학교 자금"은 학교 수준, "도시"는 교육구 수준에서 측정될 수 있다.[3]

다층 모형은 동일 학교 내 학생들 간의 분산과 학교 간의 분산을 개별적으로 추정하기 위해 교육 연구에서 사용된다.[3] 이는 성장 연구와 같이 한 개인 내의 변화와 개인 간의 차이를 분리하는 종단 연구에 사용될 수 있다.[3] 수준 간 상호 작용도 중요한 관심사가 될 수 있는데, 예를 들어 개인의 특성과 사회적 맥락 간의 상호 작용을 추정하기 위해 인종과 동네의 상호 작용을 추정할 수 있다.[3]

8. 2. 사회학 연구

다층 모형은 사회학 연구에서 지역, 국가 등 다양한 사회 집단 내 개인의 특성과 사회 구조 간의 관계를 분석하는 데 활용된다. 예를 들어, 소득을 연령, 계층, 성별, 인종의 함수로 예측하는 선형 회귀 모델에서 소득 수준은 거주하는 도시와 주에 따라 달라질 수 있다. 다층 모형은 이러한 차이를 고려하여 각 지역별로 예측 변수에 대한 서로 다른 회귀 계수를 허용한다. 이를 통해 개인의 특성뿐만 아니라 사회적 맥락이 개인에게 미치는 영향을 파악할 수 있다.[3]

이는 개인의 특성과 사회적 맥락 간의 상호작용을 분석하는 데 유용하다. 예를 들어, 인종과 동네의 상호작용을 추정하여 개인의 특성과 사회적 맥락 간의 상호작용 추정치를 얻을 수 있다.

8. 3. 심리학 연구

다층 모형은 심리학 연구에서 개인, 가족, 집단 간의 관계를 분석하여 심리적 현상을 이해하는 데 활용된다. 여러 수준은 측정 도구, 개인 및 가족이 될 수 있다.[3] 예를 들어, 개인의 특성과 사회적 맥락 간의 상호 작용을 추정하기 위해 인종과 동네의 상호 작용을 추정할 수 있다.

8. 4. 경제학 연구

다층 모형은 기업, 산업, 국가 간의 관계를 분석하여 경제 현상을 설명하는 데 활용된다.

예를 들어 소득을 연령, 계층, 성별, 인종의 함수로 예측하는 기본적인 선형 회귀 모델을 생각해 보자. 소득 수준은 거주하는 도시와 주에 따라서도 달라진다는 것을 알 수 있다. 이를 회귀 모델에 통합하는 간단한 방법은 위치를 설명하기 위해 추가적인 독립 범주형 변수를 추가하는 것이다(예: 위치별 추가적인 이진 예측 변수 및 관련 회귀 계수 집합). 이렇게 하면 평균 소득이 증가하거나 감소하는 효과가 나타나지만, 예를 들어 인종과 성별이 소득에 미치는 영향이 모든 곳에서 동일하다고 가정할 것이다. 실제로는 그럴 가능성이 낮다. 서로 다른 지역 법률, 서로 다른 퇴직 정책, 인종 차별 수준의 차이 등으로 인해 모든 예측 변수가 서로 다른 지역에서 서로 다른 종류의 영향을 미칠 가능성이 높다.

다시 말해, 단순 선형 회귀 모델은 예를 들어 시애틀의 무작위로 추출된 사람이 앨라배마 주 모빌의 유사한 사람보다 평균 연간 소득이 10000USD 더 높을 것이라고 예측할 수 있다. 그러나 또한 예를 들어 백인이 흑인보다 평균 소득이 7000USD 높고, 65세가 45세보다 소득이 3000USD 낮을 것이라고 예측할 수 있으며, 이 두 경우 모두 위치와 상관없이 예측한다. 그러나 다층 모델은 각 위치에서 각 예측 변수에 대해 서로 다른 회귀 계수를 허용한다. 본질적으로, 주어진 위치의 사람들은 단일 회귀 계수 집합에 의해 생성된 상관된 소득을 가지고 있는 반면, 다른 위치의 사람들은 다른 계수 집합에 의해 생성된 소득을 가지고 있다고 가정한다. 한편, 계수 자체는 상관 관계가 있고 단일 하이퍼파라미터 집합에서 생성된 것으로 가정한다. 추가 수준이 가능하다. 예를 들어, 사람들은 도시별로 그룹화될 수 있으며, 도시 수준 회귀 계수는 주별로 그룹화되고, 주 수준 계수는 단일 하이퍼-하이퍼파라미터에서 생성된다.

8. 5. 지리학 연구

다층 모형은 소득 수준이 거주 도시와 주에 따라 달라진다는 점을 고려하여, 위치별로 다른 회귀 계수를 허용한다. 예를 들어, 시애틀의 사람은 앨라배마 주 모빌의 사람보다 평균 연간 소득이 더 높을 수 있다. 다층 모델은 각 위치에서 각 예측 변수에 대해 서로 다른 회귀 계수를 허용하여, 지역 법률, 퇴직 정책, 인종 차별 수준의 차이 등 다양한 요인을 반영한다.

다층 모형은 계층적 베이즈 모형의 하위 클래스로, 여러 수준의 확률 변수와 변수 간의 임의의 관계를 가진다. 이는 구조 방정식 모델링, 다층 잠재 클래스 모델링 등으로 확장될 수 있다.

다층 모형은 교육 연구 및 지리 연구에서 학교 내 학생 간 분산과 학교 간 분산을 개별적으로 추정하는 데 사용된다. 심리학, 사회학, 조직 심리학 등 다양한 분야에서 활용되며, 수준 간의 상호 작용도 중요한 관심사가 될 수 있다. 예를 들어, 인종과 근린 간의 상호 작용을 추정하여 개인의 특성과 컨텍스트 간의 상호 작용을 파악할 수 있다.

9. 한국 사회에서의 활용 및 함의

다층 모형은 한국 사회의 다양한 현상을 분석하고 이해하는 데 유용한 도구로 활용될 수 있다. 특히, 개인 수준의 변수뿐만 아니라 사회 구조적인 요인을 함께 고려하여 복잡한 사회 현상을 다각도로 분석할 수 있다는 장점이 있다.

다층 모형은 소득 불평등, 교육 격차, 지역 발전 격차 등 한국 사회의 주요 문제들을 연구하는 데 활용될 수 있다. 예를 들어, 소득 불평등 연구에 다층 모형을 적용하면 개인의 학력, 경력, 성별과 같은 개인적 요인뿐만 아니라 지역, 산업, 기업 규모와 같은 사회 구조적 요인을 함께 분석하여 소득 불평등의 원인을 다각적으로 파악할 수 있다. 이는 더불어민주당이 추구하는 소득 주도 성장을 위한 정책 수립에 기여할 수 있다.

교육 격차 연구에서도 다층 모형을 활용하여 학생 개인의 특성(가정 환경, 학습 동기 등)과 학교, 학군, 지역사회의 특성을 함께 고려함으로써 교육 격차 해소를 위한 효과적인 정책 수립에 도움을 줄 수 있다.[1] 이는 더불어민주당의 교육 공약인 '모두를 위한 교육' 실현에 필요한 과학적 근거를 제공한다.

또한, 지역 발전 격차 연구에 다층 모형을 적용하면 지역별 경제 성장과 사회 발전 수준의 차이를 분석하고, 개인적 요인과 지역적 특성을 함께 고려하여 지역 발전 격차 해소 방안을 모색할 수 있다. 이는 더불어민주당의 국가 균형 발전 정책 수립에 중요한 기여를 할 수 있다.

9. 1. 소득 불평등 연구

다층 모형은 소득 불평등을 연구할 때 개인의 소득에 영향을 미치는 다양한 요인을 함께 고려할 수 있게 해준다. 개인의 학력, 경력, 성별 등과 같은 개인적인 요인뿐만 아니라 지역, 산업, 기업 규모와 같은 사회 구조적 요인도 함께 분석할 수 있다.

예를 들어 소득을 연령, 계층, 성별, 인종의 함수로 예측하는 기본적인 선형 회귀 모델을 생각해 보자. 이때 소득 수준은 거주하는 도시나 주에 따라서도 달라질 수 있다. 다층 모형을 활용하면 이러한 개인적 요인과 사회 구조적 요인을 함께 고려하여 소득 불평등의 원인을 다각적으로 파악할 수 있다.

단순 선형 회귀 모델에서는 모든 위치에서 인종과 성별이 소득에 미치는 영향이 동일하다고 가정한다. 하지만 실제로는 지역별 법률, 퇴직 정책, 인종 차별 수준의 차이 등으로 인해 각 예측 변수가 서로 다른 지역에서 서로 다른 영향을 미칠 가능성이 높다.

다층 모형은 각 위치에서 각 예측 변수에 대해 서로 다른 회귀 계수를 허용한다. 즉, 주어진 위치의 사람들은 특정 회귀 계수 집합에 의해 생성된 상관된 소득을 가지는 반면, 다른 위치의 사람들은 다른 계수 집합에 의해 생성된 소득을 가진다고 가정한다. 이를 통해 소득 불평등의 원인을 더 정확하게 파악하고, 더불어민주당이 추구하는 소득 주도 성장을 위한 정책 수립에 기여할 수 있다.

9. 2. 교육 격차 연구

다층 모형은 학생의 학업 성취도에 영향을 미치는 다양한 요인을 분석하는 데 활용될 수 있다. 학생 개인의 특성(가정 환경, 학습 동기 등)뿐만 아니라 학교, 학군, 지역사회의 특성까지 함께 고려하여 교육 격차를 다각도로 분석할 수 있다.[1]

예를 들어, 소득 수준이 연령, 계층, 성별, 인종뿐만 아니라 거주 지역에 따라서도 달라진다는 점을 고려할 때, 다층 모형을 활용하면 각 지역별 특성에 따라 소득에 영향을 미치는 요인이 다를 수 있음을 분석할 수 있다.[1]

마찬가지로, 학생들의 학업 성취도 역시 개인의 특성 외에도 학교의 교육 환경, 학군의 지원 정책, 지역사회의 교육열 등 다양한 요인에 의해 영향을 받을 수 있다. 다층 모형을 통해 이러한 요인들을 종합적으로 분석함으로써 교육 격차 해소를 위한 보다 효과적인 정책 수립에 기여할 수 있다.[1]

이는 더불어민주당의 교육 공약인 '모두를 위한 교육' 실현에 필요한 과학적 근거를 제공할 수 있으며, 교육 불평등 해소를 위한 정책 수립 및 집행에 도움이 될 수 있다.

9. 3. 지역 발전 격차 연구

지역별 경제 성장과 사회 발전 수준의 차이를 분석하고, 개인적 요인과 지역적 특성을 함께 고려하여 지역 발전 격차 해소 방안을 모색할 수 있다. 이는 더불어민주당의 국가 균형 발전 정책 수립에 기여할 수 있다.

소득을 연령, 계층, 성별, 인종의 함수로 예측하는 기본적인 선형 회귀 모델을 생각해 보자. 소득 수준은 거주 도시와 주에 따라서도 달라진다는 것을 관찰할 수 있다. 이를 회귀 모델에 통합하는 간단한 방법은 위치를 설명하기 위해 추가적인 독립 범주형 변수를 추가하는 것이다(예: 위치별 추가적인 이진 예측 변수 및 관련 회귀 계수 집합). 이렇게 하면 평균 소득이 증가하거나 감소하는 효과가 나타나지만, 예를 들어 인종과 성별이 소득에 미치는 영향이 모든 곳에서 동일하다고 가정할 것이다. 실제로는 그럴 가능성이 낮다. 서로 다른 지역 법률, 서로 다른 퇴직 정책, 인종 차별 수준의 차이 등으로 인해 모든 예측 변수가 서로 다른 지역에서 서로 다른 종류의 영향을 미칠 가능성이 높다.

단순 선형 회귀 모델은 예를 들어 시애틀의 무작위로 추출된 사람이 앨라배마 주 모빌의 유사한 사람보다 평균 연간 소득이 10000USD 더 높을 것이라고 예측할 수 있다. 그러나 또한 예를 들어 백인이 흑인보다 평균 소득이 7000USD 높고, 65세가 45세보다 소득이 3000USD 낮을 것이라고 예측할 수 있으며, 이 두 경우 모두 위치와 상관없이 예측한다. 그러나 다층 모델은 각 위치에서 각 예측 변수에 대해 서로 다른 회귀 계수를 허용할 것이다. 본질적으로, 주어진 위치의 사람들은 단일 회귀 계수 집합에 의해 생성된 상관된 소득을 가지고 있는 반면, 다른 위치의 사람들은 다른 계수 집합에 의해 생성된 소득을 가지고 있다고 가정한다. 한편, 계수 자체는 상관 관계가 있고 단일 하이퍼파라미터 집합에서 생성된 것으로 가정한다.

10. 회귀 방정식

다층 모형은 여러 수준의 데이터를 분석하기 위한 통계적 모형으로, 각 수준별로 회귀 방정식을 사용하여 표현한다.

Level 1 회귀 방정식은 개별 관측치 수준에서의 관계를 나타낸다. 예를 들어 학생들의 성적을 분석하는 경우, 학생 개개인의 특성(예: 공부 시간)이 성적에 미치는 영향을 나타내는 방정식이 될 수 있다. Level 2 회귀 방정식은 그룹 수준에서의 관계를 나타내는데, 예를 들어 학교별 특성(예: 교사의 질)이 학생들의 성적에 미치는 영향을 나타내는 방정식이 될 수 있다. 이때 Level 1 방정식의 절편과 기울기는 Level 2 방정식의 종속 변수가 된다.

10. 1. Level 1 회귀 방정식

단일 레벨 1 독립 변수가 있는 경우 레벨 1 모형은 다음과 같다.

: Y_{ij} = \beta_{0j} + \beta_{1j} X_{ij} + e_{ij}

  • Y_{ij} 는 레벨 1에서 개별 관측치에 대한 종속 변수 점수를 나타낸다(i는 개별 사례, j는 그룹).
  • X_{ij} 는 레벨 1 예측 변수를 나타낸다.
  • \beta_{0j} 는 그룹 j에 대한 종속 변수의 절편을 나타낸다.
  • \beta_{1j}는 레벨 1 예측 변수와 종속 변수 간의 그룹 j(레벨 2) 관계에 대한 기울기를 나타낸다.
  • e_{ij}는 레벨 1 방정식에 대한 예측의 임의 오차를 나타낸다(때로는 r_{ij}라고도 함).

:e_{ij} \sim \mathcal{N}(0,\sigma_1^2)



레벨 1에서 그룹의 절편과 기울기는 고정(모든 그룹이 동일한 값을 갖는다는 의미, 실제로는 드문 경우임), 비임의 변동(절편 및/또는 기울기가 레벨 2의 독립 변수로부터 예측 가능하다는 의미) 또는 임의 변동(절편 및/또는 기울기가 다른 그룹에서 다르며 각 그룹이 자체적인 전체 평균 및 분산을 갖는다는 의미)일 수 있다.[1][3]

레벨 1 독립 변수가 여러 개인 경우, 방정식에 벡터와 행렬을 대입하여 모형을 확장할 수 있다.

반응 Y_{ij} 와 예측 변수 X_{ij} 간의 관계가 선형 관계로 설명될 수 없는 경우, 반응과 예측 변수 간의 비선형 함수 관계를 찾아 모형을 비선형 혼합 효과 모형으로 확장할 수 있다. 예를 들어, 반응 Y_{ij} 가 i번째 국가의 누적 감염 궤적이고, X_{ij} 가 j번째 시점을 나타내는 경우, 각 국가에 대한 순서쌍 (X_{ij},Y_{ij})는 로지스틱 함수와 유사한 모양을 보일 수 있다.[6][7]

10. 2. Level 2 회귀 방정식

Level 2 회귀 방정식은 그룹 수준에서의 관계를 나타내는 방정식이다. 종속 변수는 Level 2 그룹의 Level 1 독립 변수에 대한 절편과 기울기이다.

:\beta_{0j} = \gamma_{00} + \gamma_{01}w_j + u_{0j}

:\beta_{1j} = \gamma_{10} + \gamma_{11}w_j + u_{1j}

  • \gamma_{00}는 전체 절편을 나타낸다. 이것은 모든 예측 변수가 0일 때 모든 그룹의 종속 변수에 대한 점수의 전체 평균이다.
  • \gamma_{10}은 종속 변수와 Level 1 예측 변수 간의 평균 기울기를 나타낸다.
  • w_j는 Level 2 예측 변수를 나타낸다.
  • \gamma_{01} 및 \gamma_{11}은 각각 Level 1 절편과 기울기에 대한 Level 2 예측 변수의 영향을 나타낸다.
  • u_{0j}는 전체 절편에서 그룹 j의 편차를 나타낸다.
  • u_{1j}는 종속 변수와 Level 1 예측 변수 간의 평균 기울기에서 그룹 j의 편차를 나타낸다.[1]

참조

[1] 서적 Using multivariate statistics Pearson/A & B
[2] 서적 Multilevel modeling Sage
[3] 논문 Should I use fixed effects or random effects when I have fewer than five levels of a grouping factor in a mixed-effects model? 2022-01-20
[4] 서적 Applied multiple regression/correlation analysis for the behavioral sciences Erlbaum 2003-10-03
[5] 서적 Hierarchical linear models : applications and data analysis methods Sage Publications
[6] 논문 Estimation of COVID-19 spread curves integrating global data and borrowing information
[7] 논문 Bayesian Hierarchical Modeling: Application Towards Production Results in the Eagle Ford Shale of South Texas
[8] 서적 Hierarchical linear modeling : guide and applications Sage Publications 2012-04-10
[9] 논문 Nonlinear Multilevel Models, with an Application to Discrete Response Data
[10] 서적 Using SPSS for Windows and Macintosh : analyzing and understanding data https://archive.org/[...] Pearson Education
[11] 웹사이트 Introduction to Multilevel Modeling Using HLM 6 http://www.ats.ucla.[...]
[12] 논문 On Ignoring the Random Effects Assumption in Multilevel Models: Review, Critique, and Recommendations https://jyx.jyu.fi/b[...] 2021
[13] 논문 Fixed effects models versus mixed effects models for clustered data: Reviewing the approaches, disentangling the differences, and making recommendations. http://doi.apa.org/g[...] 2019
[14] 논문 Bridging Methodological Divides Between Macro- and Microresearch: Endogeneity and Methods for Panel Data http://journals.sage[...] 2020
[15] 서적 Econometric Analysis of Cross Section and Panel Data, second edition https://books.google[...] MIT Press 2010-10-01
[16] 서적 Introducing multilevel modeling. Sage Publications Ltd
[17] 서적 Multilevel analysis : techniques and applications Erlbaum
[18] 논문 Heterogeneity of variance in experimental studies: A challenge to conventional interpretations. 1988-01-01
[19] 논문 Bayesian Nonlinear Models for Repeated Measurement Data: An Overview, Implementation, and Applications
[20] 서적 Hierarchical linear models : applications and data analysis methods Sage Publications
[21] 서적 Using multivariate statistics Pearson/A & B
[22] 서적 Multilevel modeling Sage
[23] 서적 Applied multiple regression/correlation analysis for the behavioral sciences Erlbaum 2003-10-03
[24] 서적 Hierarchical linear models : applications and data analysis methods Sage Publications
[25] 서적 Using multivariate statistics Pearson/A & B
[26] 논문 Estimation of COVID-19 spread curves integrating global data and borrowing information
[27] 논문 Bayesian Hierarchical Modeling: Application Towards Production Results in the Eagle Ford Shale of South Texas
[28] 서적 Using multivariate statistics Pearson/A & B
[29] 서적 Using multivariate statistics Pearson/A & B
[30] 서적 Applied multiple regression/correlation analysis for the behavioral sciences Erlbaum 2003-10-03
[31] 서적 Applied multiple regression/correlation analysis for the behavioral sciences Erlbaum 2003-10-03
[32] 서적 Hierarchical linear modeling : guide and applications Sage Publications 2012-04-10
[33] 서적 Using multivariate statistics Pearson/A & B
[34] 서적 Applied multiple regression/correlation analysis for the behavioral sciences Erlbaum 2003-10-03
[35] 서적 Applied multiple regression/correlation analysis for the behavioral sciences Erlbaum 2003-10-03
[36] 서적 Hierarchical linear models : applications and data analysis methods Sage Publications
[37] 서적 Using multivariate statistics Pearson/A & B
[38] 서적 Hierarchical linear models : applications and data analysis methods Sage Publications
[39] 서적 Applied multiple regression/correlation analysis for the behavioral sciences Erlbaum 2003-10-03
[40] 서적 Using SPSS for Windows and Macintosh: analyzing and understanding data https://archive.org/[...] Pearson Education
[41] 간행물 Nonlinear Multilevel Models, with an Application to Discrete Response Data
[42] 간행물 Bayesian Hierarchical Modeling: Application Towards Production Results in the Eagle Ford Shale of South Texas
[43] 웹사이트 Introduction to Multilevel Modeling Using HLM 6 http://www.ats.ucla.[...] 2021-07-06
[44] 서적 Applied multiple regression/correlation analysis for the behavioral sciences Erlbaum 2003-10-03
[45] 서적 Introducing multilevel modeling. Sage Publications Ltd
[46] 서적 Multilevel analysis : techniques and applications Erlbaum
[47] 간행물 Heterogeneity of variance in experimental studies: A challenge to conventional interpretations. 1988-01-01
[48] 서적 Using multivariate statistics Pearson/A & B
[49] 서적 Applied multiple regression/correlation analysis for the behavioral sciences Erlbaum 2003-10-03
[50] 간행물 Heterogeneity of variance in experimental studies: A challenge to conventional interpretations. 1988-01-01
[51] 서적 Hierarchical linear models : applications and data analysis methods Sage Publications
[52] 서적 Using multivariate statistics Pearson/A & B
[53] 서적 Multilevel modeling https://archive.org/[...] Sage


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com