무게 (표현론)

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 리 대수의 무게
- 2.2. 무게 가군
3. 성질
- 3.1. 반단순 리 대수의 카르탕 부분 대수의 무게
- 3.2. 단순 리 대수의 무게
4. 표현론에서의 무게
5. 예
참조

1. 개요

무게(weight)는 리 대수와 그 표현론에서 사용되는 개념으로, 리 대수의 선형 범함수, 리 군의 곱셈적 지표, 또는 표현의 무게 공간과 관련된 정보를 제공한다. 리 대수 $\mathfrak{g}$ 의 무게는 리 괄호에 대해 0이 되는 선형 범함수로, 가환 리 대수의 경우 일반 고유값의 개념으로 귀결된다. 무게 공간은 특정 무게에 대응하는 벡터 공간의 부분 공간이며, 무게 벡터는 무게 공간의 원소이다. 표현의 무게는 해당 무게 공간이 0이 아닌 선형 범함수이며, 무게 벡터는 해당 고유값을 갖는 원소의 작용에 대한 동시 고유 벡터이다. 유한 차원 표현은 항상 일반화 무게 가군이며, 최고 무게 정리를 통해 유한 차원 기약 표현을 분류할 수 있다. 무게는 정수 무게, 우세 무게, 기본 무게 등 다양한 형태로 나타나며, 근계, 카르탕 부분 대수 등과 밀접한 관련이 있다.

더 읽어볼만한 페이지

표현론 - 매케이 화살집
매케이 화살집은 유한군 G의 기약 표현을 꼭짓점으로, 텐서곱 분해를 통해 변을 정의하여 군의 표현론적 구조를 시각적으로 나타내는 도구이다.
표현론 - 보렐-베유-보트 정리
보렐-베유-보트 정리는 복소수 반단순 리 군의 표현론에서 층 코호몰로지를 사용하여 리 군의 기약 표현을 설명하며, 보렐-베유 정리와 보트의 일반화를 포함한다.
리 대수 - 베유 대수
베유 대수는 체 K 위의 리 대수 g에 대하여 정의되는 미분 등급 대수이며, g의 쌍대 공간과 그 등급 이동으로 생성되는 외대수와 대칭 대수의 텐서곱으로 표현되고, 리 군의 분류 공간의 주다발의 무한소 형태를 나타내는 완전열과 관련이 있다.
리 대수 - 아핀 리 대수
아핀 리 대수는 카츠-무디 대수의 특수한 경우로, 유한 차원 단순 리 대수에 대응하는 루프 대수의 중심 확장으로 구성되며, 딘킨 도표를 통해 분류되고, 끈 이론과 2차원 등각장론 등 다양한 분야에 응용된다.

무게 (표현론)
정의
설명	리 대수의 표현론에서, 무게는 표현 공간의 기저 벡터에 작용하는 특정한 패턴을 나타내는 값이다. 더 정확히 말하면, 주어진 표현 공간에서 가환 부분 대수의 고유 벡터에 대응하는 고유값이다.
상세 정보
기호	무게 공간은 λ에 의해 표시되며, 여기서 λ는 대수 준동형 A → F이다.
관련 개념	루트 (수학) 최고 무게 표현
추가 설명
추가 설명	무게는 리 대수의 표현을 연구하는 데 중요한 도구이며, 표현의 구조와 성질을 이해하는 데 도움을 준다.
참고 사항
참고	무게는 곱셈적 지표와도 관련이 있다.

2. 정의

리 대수의 표현과 관련된 핵심 개념으로 무게(weight)가 있다.

동일한 체에 대한 n × n 행렬의 집합 ''S''가 있고, 각 행렬은 대각화 가능하며, 임의의 두 행렬은 가환한다고 가정하자. 이 경우 ''S''의 모든 원소를 동시 대각화하는 것이 항상 가능하다.^[1] 유한 차원 벡터 공간 ''V''의 서로 가환하는 반단순 선형 변환 집합 ''S''에 대해, ''V''의 모든 원소의 ''동시 고유 벡터''로 구성된 기저가 존재한다. 이러한 공통 고유 벡터 ''v'' ∈ ''V''는 End(''V'' )의 집합 ''S''로 생성된 부분 대수 ''U'' 위에 선형 범함수를 정의한다. 이 범함수는 ''U''의 각 원소에 벡터 ''v''에 대한 고유값을 연관시키며, 곱셈적이고 항등원을 1로 보낸다. 따라서 ''U''에서 밑체로의 대수 준동형 사상이며, 이 "일반화된 고유값"은 가중치의 개념에 대한 프로토타입이다.

이 개념은 군론에서 곱셈적 문자의 아이디어와 밀접하게 관련되어 있다. 곱셈적 문자는 그룹 ''G''에서 체 '''F'''의 곱셈군으로의 준동형 사상 ''χ''이며, 다음 식을 만족한다.

: $\chi(gh) = \chi(g)\chi(h)$ (모든 ''G''의 ''g'', ''h''에 대해)

만약 ''G''가 '''F''' 위 벡터 공간 ''V''에 대해 작용하고, ''G''의 모든 원소에 대한 각 동시 고유 공간이 존재한다면, 이는 ''G''에 대한 곱셈적 문자를 결정한다. 즉, 그룹 각 원소의 이 공통 고유 공간에 대한 고유값이 된다.

곱셈적 문자 개념은 '''F''' 위 임의의 대수 ''A''로 확장될 수 있다. ''χ'': ''G'' → '''F'''^×를 다음을 만족하는 선형 맵 ''χ'': ''A'' → '''F'''로 대체할 수 있다.

: $\chi(ab) = \chi(a)\chi(b)$

만약 대수 ''A''가 '''F''' 위 벡터 공간 ''V''에 대해 작용하면, 이것은 ''A''에서 '''F'''로의 대수 준동형 사상에 해당하며, ''A''의 각 원소에 그 고유값을 할당한다.

''A''가 리 대수이면 (일반적으로 결합 대수가 아님), 문자 곱셈성을 요구하는 대신, 임의의 리 괄호를 해당 교환자에 매핑하도록 요구한다. 그러나 '''F'''가 가환이므로, 이 맵은 리 괄호에서 0이 되어야 한다.

리 군 또는 대수적 군 ''G''가 주어지면, 곱셈적 문자 θ: ''G'' → '''F'''^×는 미분을 통해 그 리 대수 위에 가중치 ''χ'' = dθ: '''g''' → '''F'''를 유도한다.

2. 1. 리 대수의 무게

체

K

에 대한 리 대수

\mathfrak g

의 '''무게'''

\lambda\in\mathfrak g^\vee

는 다음 성질을 만족시키는

K

-선형 범함수이다. (여기서

(-)^\vee

는 쌍대 공간이다.)

:

\lambda([a,b])=0\qquad\forall a,b\in\mathfrak g

무게는 리 괄호에 대하여 0이므로, 리 대수

\mathfrak g

의 무게는 그 가환화

\mathfrak g/[\mathfrak g,\mathfrak g]

의 무게로 제한될 수 있다. 즉,

\mathfrak g

의 무게는

(\mathfrak g/[\mathfrak g,\mathfrak g])^*

의 원소를 정의한다.

체 '''F''' 위의 리 대수 '''g'''에 대한 '''가중치'''는 모든 ''x'', ''y'' in '''g''에 대해

\lambda([x, y]) = 0

을 만족하는 선형 맵

\lambda:

'''g''' → '''F'''이다. 리 대수 '''g'''에 대한 모든 가중치는 도출 대수

[\mathfrak g, \mathfrak g]

에서 0이 되므로, 아벨 리 대수

\mathfrak g/[\mathfrak g, \mathfrak g]

에 대한 가중치로 내려간다. 따라서 가중치는 주로 아벨 리 대수에 관심이 있으며, 여기서 가환하는 선형 변환 공간에 대한 일반화된 고유값의 간단한 개념으로 축소된다.

2. 2. 무게 가군

체 K, K-리 대수 $\mathfrak{g}$, $\mathfrak{g}$의 표현 $\mathfrak{g} \to \operatorname{\mathfrak{gl}}(V;K)$, $\mathfrak{g}$의 무게 $\lambda \in \mathfrak{g}^*$가 주어졌을 때, 무게 $\lambda$의 '''무게 공간'''(weight space^영어) $V_\lambda$는 다음과 같이 정의되는 $V$의 부분 공간이다.

:$V_\lambda = \{v \in V \colon \forall a \in \mathfrak{g} \colon av = \lambda(a)v\}$

$V_\lambda \neq \{0\}$이면 $\lambda$를 $V$의 '''무게'''라고 하고, 무게 공간의 원소를 '''무게 벡터'''(weight vector^영어)라고 한다. $V$가 그 무게 공간들의 직합이면, $V$를 $\mathfrak{g}$의 '''무게 가군'''(-加群, weight module^영어)이라고 한다.

마찬가지로, 무게 $\lambda$의 '''일반화 무게 공간'''(generalized weight space^영어) $V_\lambda$는 다음과 같이 정의되는 $V$의 부분 공간이다.^[14]

:$V_\lambda=\{v\in V\colon \forall a\in\mathfrak g\colon\exists n\in\mathbb Z^+\colon(a-\lambda(a))^nv=v\}$

$V_\lambda\ne\{0\}$이라면 $\lambda$를 $V$의 '''일반화 무게'''(generalized weight^영어)라고 하고, 무게 공간의 원소를 '''일반화 무게 벡터'''(generalized weight vector^영어)라고 한다. 일반화 무게 공간들의 직합으로 표현되는 표현을 '''일반화 무게 가군'''(generalized weight module^영어)이라고 한다.

3. 성질

복소수체 위의 유한 차원 멱영 리 대수의 모든 유한 차원 표현은 항상 일반화 무게 가군이며,^[14] 복소수체 위의 유한 차원 아벨 리 대수의 모든 유한 차원 표현은 항상 무게 가군이다.

무게, 정수 무게, 근, 양근, 단순근, 우세 무게, 우세 정수 무게, 기본 무게 사이에는 다음과 같은 포함 관계가 성립한다.

무게	⊃	정수 무게	⊃	근
∪		∪
우세 무게	⊃	우세 정수 무게	⊃	기본 무게
		⟒
		영벡터 (0)

밑줄 표시된 개념은 양근 선택에 의존하지만, 나머지는 그렇지 않다.
''기울임꼴''로 표시된 집합은 유한 집합이고, 나머지는 무한 집합이다.^[1]

3. 1. 반단순 리 대수의 카르탕 부분 대수의 무게

반단순 리 대수

\mathfrak g

가 복소수체 위에서 유한 차원이고, 카르탕 부분 대수

\mathfrak h\subseteq\mathfrak g

가 주어졌을 때,

[\mathfrak g,\mathfrak g]=\mathfrak g

이므로

\mathfrak g

위의 모든 무게는 자명하다. 그러나 아벨 리 대수

\mathfrak h

는 자명하지 않을 수 있다.

\mathfrak g

의 모든 유한 차원 표현은

\mathfrak h

에 제한되었을 때

\mathfrak h

의 무게 가군을 이룬다.

딸림표현

V=\mathfrak g

의

\mathfrak h

-무게들을

\mathfrak g

의 '''근'''(根, root^영어)이라고 하며, 이들은

\mathfrak h^*

의 벡터들의 집합으로서 근계를 이룬다. 근

\lambda

에 대응하는 '''쌍대근'''(雙對根, coroot^영어)

\lambda^\vee\in\mathfrak h

은 다음과 같이 정의된다.

:

\lambda^\vee=\frac{2\lambda}{\langle\lambda,\lambda\rangle}

3. 2. 단순 리 대수의 무게

카르탕 부분 대수

\mathfrak h\subseteq\mathfrak g

를 갖는 복소수체 위의 유한 차원 단순 리 대수

\mathfrak g

가 주어졌을 때,

\mathfrak g

의 '''정수 무게'''(整數-, integral weight^영어)

\lambda\in\mathfrak h^*

는 모든 쌍대근

\gamma^\vee=2\gamma/\langle\gamma,\gamma\rangle

에 대하여

\lambda(\gamma^\vee)\in\mathbb Z

인 무게이다. (다시 말해, 모든 근

\gamma

에 대하여,

2\langle \lambda,\gamma\rangle/\langle\gamma,\gamma\rangle \in \mathbb Z

.)^[1]

정수 무게들의 집합

P(\mathfrak g,\mathfrak h)\subseteq\mathbb h

는 덧셈군으로서

\mathbb Z^{\oplus\dim\mathfrak h}

와 동형이며, 이를 '''정수 무게 격자'''(integral weight lattice^영어)라고 한다.^[1]

\mathfrak g

의 근계의 양근

\Delta^+(\mathfrak g,\mathfrak h)\subseteq\Delta(\mathfrak g,\mathfrak h)

및 이를 생성하는 단순근

\operatorname S(\mathfrak g,\mathfrak h)\subseteq \Delta^+(\mathfrak g,\mathfrak h)

를 고르면,

\mathfrak g

의 '''기본 무게'''(基本-, fundamental weight^영어)

\lambda_i

는 선택한 양근 집합에 대한 단순근에 대응되는 쌍대근들의 집합의 쌍대 기저의 원소이다.^[1] 즉, 단순근 집합

\operatorname S(\mathfrak g,\mathfrak h)=(\alpha_i)_{i\in\{1,\dotsc,\dim_{\mathbb h}\}}

에 대하여 다음 조건을 만족시키는 무게

(\omega_i)_{i\in\{1,\dotsc,\dim_{\mathbb h}\}}\subseteq\mathfrak h

이다.

:

2\frac{\langle\omega_i,\alpha_j\rangle}{\langle\alpha_j,\alpha_j\rangle} = \delta_{ij}

이에 따라, 정수 무게는 기본 무게의 정수 계수 선형 결합이 된다.^[1]

\mathfrak g

의 '''우세 무게'''(優勢-, dominant weight^영어)는 기본 무게의 음이 아닌 실수 계수 선형 결합이다. 즉, 무게

\gamma\in\mathfrak h

가 우세 무게가 될 필요충분조건은 모든 양근 (또는 단순근)

\alpha

에 대하여

\langle \gamma,\alpha\rangle\ge0

인 것이다.

\mathfrak g

의 '''우세 정수 무게'''(優勢-, dominant integral weight^영어)는 기본 무게들의 음이 아닌 정수 계수의 선형 결합이다. 우세 무게들의 닫힌집합(즉, 우세 정수 무게들의 볼록포)를 '''기본 바일 방'''(fundamental Weyl chamber^영어)이라고 한다.^[1]

다음과 같은 포함 관계가 성립한다.

무게	⊃	정수 무게	⊃	근
∪		∪
우세 무게	⊃	우세 정수 무게	⊃	기본 무게
		⟒
		영벡터 (0)

여기서

밑줄로 강조된 것들은 양근의 선택에 의존하지만, 나머지는 그렇지 않다.
''기울어지게'' 쓰인 것들은 유한 집합이며, 나머지는 무한 집합이다.^[1]

4. 표현론에서의 무게

리 대수에서 '''가중치'''는 어떤 표현에서 나타나는 특정한 종류의 선형 범함수이다.

집합 ''S''가 같은 체에 대한 $n \times n$ 행렬의 집합으로 주어지고, 각 행렬이 대각화 가능 행렬이며, 임의의 두 행렬이 가환 행렬이면, ''S''의 모든 원소를 동시 대각화하는 것이 항상 가능하다.^[1] 이는 유한 차원 벡터 공간 ''V''의 서로 가환하는 반단순 연산자 선형 변환 집합 ''S''에 대해, ''V''의 모든 원소의 동시 고유 벡터로 구성된 기저가 존재한다는 것과 같다.

이러한 공통 고유 벡터 ''v'' ∈ ''V''는 End(''V'' )의 집합 ''S''에 의해 생성된 부분 대수 ''U'' 위에 선형 범함수를 정의한다. 이 범함수는 ''U''의 각 원소에 벡터 ''v''에 대한 고유값을 연관시키며, 곱셈적이고 항등원을 1로 보낸다. 즉, ''U''에서 밑체로의 대수 준동형 사상이며, 이 "일반화된 고유값"은 가중치 개념의 원형이다.

이 개념은 군론에서 곱셈적 문자와 밀접하게 관련되어 있다. 곱셈적 문자는 그룹 ''G''에서 체 '''F'''의 곱셈군으로의 군 준동형 사상 ''χ''이며, ''χ''(''e'') = 1 (여기서 ''e''는 ''G''의 항등원)이고, 모든 ''G''의 ''g'', ''h''에 대해 $\chi(gh) = \chi(g)\chi(h)$ 가 성립한다.

''G''가 '''F''' 위 벡터 공간 ''V''에 대해 작용하고, ''G''의 모든 원소에 대한 각 동시 고유 공간이 존재한다면, 이는 ''G''에 대한 곱셈적 문자를 결정한다. 즉, 그룹 각 원소의 이 공통 고유 공간에 대한 고유값이다.

곱셈적 문자 개념은 '''F''' 위 임의의 대수 ''A''로 확장될 수 있다. ''χ'': ''G'' → '''F'''^×를 모든 ''a'', ''b'' in ''A''에 대해 $\chi(ab) = \chi(a)\chi(b)$ 를 만족하는 선형 맵 ''χ'': ''A'' → '''F'''로 대체하면 된다. 대수 ''A''가 '''F''' 위 벡터 공간 ''V''에 대해 작용하면, 이것은 ''A''에서 '''F'''로의 대수 준동형 사상에 해당하며, ''A''의 각 원소에 그 고유값을 할당한다.

''A''가 리 대수(일반적으로 결합 대수가 아님)이면, 문자 곱셈성을 요구하는 대신, 임의의 리 괄호를 해당 교환자에 매핑하도록 요구한다. 그러나 '''F'''가 가환이므로, 이 맵은 리 괄호에서 0이 되어야 한다. 즉, ''χ''([''a'',''b'']) = 0이다. 체 '''F''' 위 리 대수 '''g'''에 대한 '''가중치'''는 모든 ''x'', ''y'' in '''g''에 대해 λ([''x'', ''y'']) = 0을 만족하는 선형 맵 λ: '''g''' → '''F'''이다.

리 대수 '''g'''에 대한 모든 가중치는 도출 대수 ['''g''','''g''']에서 0이 되므로, 아벨 리 대수 '''g'''/['''g''','''g''']에 대한 가중치로 내려간다. 따라서 가중치는 주로 아벨 리 대수에 관심이 있으며, 여기서 가환하는 선형 변환 공간에 대한 일반화된 고유값의 간단한 개념으로 축소된다.

리 군 또는 대수적 군 ''G''가 주어지면, 곱셈적 문자 θ: ''G'' → '''F'''^×는 미분을 통해 그 리 대수 위에 가중치 ''χ'' = dθ: '''g''' → '''F'''를 유도한다. (리 군의 경우, 이것은 ''G''의 항등원에서 미분이며, 대수적 군의 경우는 도출 개념을 사용하는 추상화이다.)

4. 1. 표현의 무게

리 대수

\mathfrak{g}

의 벡터 공간 ''V''에 대한 표현

\sigma : \mathfrak{g} \to \operatorname{End}(V)

와

\mathfrak{g}

의 카르탕 부분 대수

\mathfrak{h}

가 주어졌을 때,

\mathfrak{h}

상의 선형 범함수

\lambda : \mathfrak{h} \to \mathbb{C}

에 대해, 가중치 ''λ''를 갖는 ''V''의 '''가중치 공간'''은 부분 공간

V_\lambda

로 다음과 같이 정의된다.

:

V_\lambda:=\{v\in V: \forall H\in \mathfrak{h},\, (\sigma(H))(v)=\lambda(H)v\}

.

표현 ''V''의 '''가중치'''는 해당 가중치 공간이 0이 아닌 선형 범함수 λ이다. 가중치 공간의 0이 아닌 원소를 '''가중치 벡터'''라고 한다. 즉, 가중치 벡터는 λ에 의해 주어진 해당 고유값을 갖는

\mathfrak{h}

의 원소의 작용에 대한 동시 고유 벡터이다.

만약 ''V''가 가중치 공간의 직합, 즉

:

V=\bigoplus_{\lambda\in\mathfrak{h}^*} V_\lambda

이면 ''V''는 ''가중치 모듈''이라고 불리며, 이는 대수의 표현된 모든 원소에 대한 공통 고유 기저가 존재한다는 것, 즉, 동시에 대각화 가능한 행렬이 존재한다는 것에 해당한다.^[1]

''G''가 리 대수

\mathfrak{g}

를 갖는 군이라면, ''G''의 모든 유한 차원 표현은

\mathfrak{g}

의 표현을 유도한다. 그러면 ''G''의 표현의 가중치는

\mathfrak{g}

의 관련 표현의 가중치와 같다.

4. 2. 근 벡터의 작용

리 대수

\mathfrak{g}

의 수반 표현

\mathrm{ad} : \mathfrak{g}\to \operatorname{End}(\mathfrak{g})

에서, 0이 아닌 가중치를 '''근'''(root)이라 하고, 가중치 공간을 '''근 공간'''(root space), 가중치 벡터를 '''근 벡터'''(root vector)라고 한다.

\sigma : \mathfrak{g} \to \operatorname{End}(V)

가

\mathfrak{g}

의 표현이고,

v

가 가중치

\lambda

를 갖는 가중치 벡터이며,

X

가 근

\alpha

를 갖는 근 벡터라면, 다음이 성립한다.

:

\sigma(H)(\sigma(X)(v))=[(\lambda+\alpha)(H)](\sigma(X)(v))

(

\mathfrak{h}

의 모든

H

에 대해)

즉,

\sigma(X)(v)

는 영벡터이거나 가중치

\lambda+\alpha

를 갖는 가중치 벡터이다. 따라서

X

의 작용은 가중치

\lambda

를 갖는 가중치 공간을 가중치

\lambda+\alpha

를 갖는 가중치 공간으로 매핑한다.

4. 3. 정수 원소

\mathfrak h^*_0

를

\mathfrak g

의 근에 의해 생성된

\mathfrak h^*

의 실수 부분 공간이라고 하자. 원소

\lambda\in\mathfrak h_0

가 '''대수적으로 정수적'''이라는 것은 모든 근

\alpha

에 대해 다음을 만족하는 것을 의미한다.

:

(\lambda,H_\alpha)=2\frac{(\lambda,\alpha)}{(\alpha,\alpha)}\in\mathbb{Z}

여기서

(\alpha,\beta)

는 벡터

\alpha,\beta

의 내적을 나타낸다.

'''기본 무게'''

\omega_1,\ldots,\omega_n

는 단순근에 관련된 코근 집합에 이중적인

\mathfrak h_0

의 기저를 형성하는 속성으로 정의된다. 즉, 기본 무게는 다음 조건에 의해 정의된다.

:

2\frac{(\omega_i,\alpha_j)}{(\alpha_j,\alpha_j)}=\delta_{i,j}

여기서

\alpha_1,\ldots\alpha_n

은 단순근이다.

그러면 원소

\lambda

는 기본 무게의 정수 결합인 경우에만 대수적으로 정수적이다.^[4] 모든

\mathfrak g

-정수 무게 집합은

\mathfrak g

에 대한 ''가중치 격자''라고 하는

\mathfrak h_0

의 격자이며,

P(\mathfrak g)

로 표시된다.

대수적으로 정수적인 원소(삼각 격자), 우세 정수적 원소(검은 점), sl(3,C)의 기본 가중치

이 그림은 근계가

A_2

근계인 리 대수

sl(3,\mathbb C)

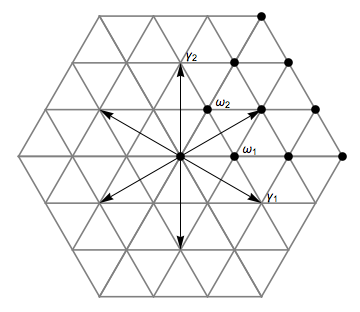
의 예를 보여준다. 두 개의 단순근,

\gamma_1

과

\gamma_2

가 있다. 첫 번째 기본 가중치

\omega_1

은

\gamma_2

에 직교해야 하고,

\gamma_1

의 절반에 직교적으로 투영해야 하며,

\omega_2

도 마찬가지이다. 그러면 가중치 격자는 삼각 격자가 된다.

이제 리 대수

\mathfrak g

가 리 군 ''G''의 리 대수라고 가정하자. 그러면

\mathfrak h

에서

\exp(t)=1\in G

인 각 ''t''에 대해

\lambda\in\mathfrak h_0

는 '''해석적으로 정수적'''('G-정수적')이라고 하며,

(\lambda,t)\in 2\pi i \mathbb{Z}

를 갖는다. ''G''가 단일 연결되어 있으면, ''P''(''G'') = ''P''(

\mathfrak g

)이다. ''G''가 단일 연결되어 있지 않으면, 격자 ''P''(''G'')는 ''P''(

\mathfrak g

)보다 작고, 이들의 몫은 ''G''의 기본군과 동형이다.^[6]

4. 4. 무게 공간의 부분 순서

$\mathfrak h_0$의 두 원소 $\mu$와 $\lambda$에 대해, $\mu$가 $\lambda$보다 '''높다'''($\mu \succeq \lambda$)는 것은 $\mu - \lambda$가 음이 아닌 실수 계수를 갖는 양의 근의 선형 결합으로 표현될 수 있다는 것을 의미한다.^[7] 이는 대략 "높다"는 것이 양의 근의 방향을 의미함을 나타낸다. $\lambda$가 $\mu$보다 "낮다"고 말하며, 이를 $\lambda \preceq \mu$로 쓰기도 한다.

이 관계는 부분 순서이다. 즉, $\mu$가 $\lambda$보다 높지도 낮지도 않은 경우가 있을 수 있다.

$\mathfrak h_0^*$를 $\mathfrak h^*$의 $\mathfrak g$의 루트로 생성되는 실수 부분 공간(그것이 복소수일 때)으로 정의한다.

$\mathfrak h_0^*$의 순서를 정의하는 두 가지 방법이 있다.

첫 번째 방법은 $\mu \le \lambda$를 $\lambda - \mu$가 단순 루트의 비음수 선형 결합인 것으로 정의하는 것이다.

두 번째 방법은 원소 $f \in \mathfrak h_0$에 의해 $\mu \le \lambda$를 $\mu(f) \le \lambda(f)$로 정의하는 것이다. 일반적으로, $f$는 모든 양의 루트 $\beta$에 대해 $\beta(f) > 0$이 되도록 선택된다.

4. 5. 우세 무게

'''우세 무게'''(dominant weight^영어)는 기본 무게의 음이 아닌 실수 계수 선형 결합이다. 즉, 무게

\gamma\in\mathfrak h

가 우세 무게가 될 필요 충분 조건은 모든 양근 (또는 단순근)

\alpha

에 대하여

:

\langle \gamma,\alpha\rangle\ge0

인 것이다.

\mathfrak g

의 '''우세 정수 무게'''(優勢整數-, dominant integral weight^영어)는 기본 무게들의 음이 아닌 정수 계수의 선형 결합이다. 우세 무게들의 닫힌집합(즉, 우세 정수 무게들의 볼록포)를 '''기본 바일 방'''(fundamental Weyl chamber^영어)이라고 한다.

다음은 무게, 정수 무게, 근, 양근, 단순근, 우세 무게, 우세 정수 무게, 기본 무게 사이의 포함 관계를 나타낸 표이다.

무게	⊃	정수 무게	⊃	근	⊃	양근	⊃	단순근
∪		∪
우세 무게	⊃	우세 정수 무게	⊃	기본 무게
		⟒
		영벡터 (0)

밑줄로 강조된 것들은 양근의 선택에 의존하지만, 나머지는 그렇지 않다.
''기울임꼴''로 쓰인 것들은 유한 집합이며, 나머지는 무한 집합이다.

적분 원소 λ는 각 양근 γ에 대해

(\lambda,\gamma)\geq 0

일 경우 ''우세''하다고 한다.^[1] 즉, λ가 기본 가중치의 ''음이 아닌'' 정수 결합일 경우 우세하다.

(\lambda,\gamma)\geq 0

인 모든 λ (반드시 적분일 필요는 없음)의 집합은 주어진 양근 집합과 관련된 ''기본 바일 영역''으로 알려져 있다.

웨이트가 '''우세'''하다는 것은, 각 정 루트에 해당하는 코루트에 대해

\lambda(H_\gamma)\geq 0

임을 의미한다. 이는 기본 웨이트의 비음수 선형 결합임을 의미하는 것과 같다. 우수 웨이트의 볼록 껍질은 ''fundamental 바일 방''이라고 불린다. "우수 웨이트"라는 용어는 우수하고 정수인 웨이트를 나타내기 위해 사용되기도 한다.

4. 6. 최고 무게 정리

\mathfrak g

의 표현

V

의 무게

\lambda

가

V

의 다른 모든 무게보다 더 낮으면 '''최고 무게'''라고 한다.

\mathfrak g

의 유한 차원 기약 표현을 분류하는 이론은 "최고 무게 정리"를 통해 이루어진다.^[8] 이 정리는 다음과 같다.

:(1) 모든 기약 (유한 차원) 표현은 최고 무게를 갖는다.

:(2) 최고 무게는 항상 지배적이고 대수적으로 정수적인 원소이다.

:(3) 동일한 최고 무게를 갖는 두 개의 기약 표현은 동형이다.

:(4) 모든 지배적이고 대수적으로 정수적인 원소는 기약 표현의 최고 무게이다.

마지막 항목이 가장 어렵다. 표현은 베르마 가군을 사용하여 구성할 수 있다.

표현의 가중치가 '''최고 가중치'''라는 것은 위에 주어진 반순서에서 보다 큰 의 다른 가중치가 존재하지 않는다는 것을 의미한다. 때때로, 의 다른 모든 가중치가 보다 진정으로 작다는 더 강한 조건을 부과한다. "최고 가중치"라는 용어는 종종 "최고 가중치 가군"의 최고 가중치를 의미한다.

'''최저 가중치'''도 마찬가지로 정의된다.

모든 가능한 가중치로 구성된 공간은 벡터 공간이다. 이 벡터 공간의 전순서로, 적어도 하나의 비영 계수를 갖는 양의 벡터의 음이 아닌 선형 결합은 다른 양의 벡터인 것을 고정하자.

그러면, 표현이 "최고 가중치 "를 갖는다는 것은 가 가중치이며, 다른 모든 가중치는 보다 작다는 것을 의미한다.

마찬가지로, "최저 가중치 "를 갖는다는 것은 가 가중치이며, 다른 모든 가중치는 보다 크다는 것을 의미한다.

가중치의 가중치 벡터는 의 다른 모든 가중치가 보다 작을 때 '''최고 가중치 벡터'''라고 불린다.

4. 7. 최고 무게 가군

\mathfrak g

의 표현 ''V''가

\mathfrak g

의 모든 양근 공간의 작용에 의해 소멸되는 가중치 벡터 ''v'' ∈ ''V''에 의해 생성되는 경우 ''최고 가중치 모듈''이라고 한다.^[13] 최고 가중치를 갖는 모든 기약

\mathfrak g

-모듈은 반드시 최고 가중치 모듈이지만, 무한 차원인 경우 최고 가중치 모듈이 기약적일 필요는 없다.

각

\lambda\in\mathfrak h^*

에 대해(지배적이거나 정수일 필요는 없음) 최고 가중치 λ를 갖는 유일한(동형까지) 단순 최고 가중치

\mathfrak g

-모듈이 존재하며, 이는 ''L''(λ)로 표기되지만, 이 모듈은 λ가 지배적 정수인 경우를 제외하고는 무한 차원이다. 최고 가중치 λ를 갖는 각 최고 가중치 모듈은 몫 베르마 모듈 ''M''(λ)의 몫임을 보일 수 있다. 이는 베르마 모듈의 정의에서 ''보편성'' 속성을 재진술한 것이다.^[9]

모든 ''유한 차원'' 최고 가중치 모듈은 기약적이다.

5. 예

다음과 같은 A₂ 근계를 생각하자.

평면의 모든 점은 무게이다. (즉, 그 수는 비가산 무한 개이다.)
삼각형 격자의 모든 꼭짓점은 정수 무게이다. (즉, 그 수는 가산 무한 개이다.)
굵게 칠해진 꼭짓점들은 우세 정수 무게이다. (즉, 그 수는 가산 무한 개이다.)
굵게 칠해진 꼭짓점들의 볼록포인 60° 부채꼴 속의 점은 우세 무게이다. (즉, 그 수는 비가산 무한 개이다.)
화살표의 머리들( $\pm\gamma_1$ , $\pm\gamma_2$ , $\pm(\gamma_1+\gamma_2)$ )은 근이다. (즉, 총 6개의 근이 있다.)
양근은 $\gamma_1$ , $\gamma_2$ , $\gamma_1+\gamma_2$ 이다. (즉, 총 3개의 양근이 있다.)
단순근은 $\gamma_1$ , $\gamma_2$ 이다. (즉, 총 2개의 단순근이 있다.)
기본 무게는 $\omega_1$ , $\omega_2$ 이다. (즉, 총 2개의 기본 무게가 있다.)

다음과 같은 B₂ 근계를 생각하자.

평면의 모든 점은 무게이다. (즉, 그 수는 비가산 무한 개이다.)
격자 $\mathbb Z\alpha + \mathbb Z\beta/2$ 의 원소는 정수 무게이다. (즉, 그 수는 가산 무한 개이다.)
$\mathbb N(\alpha+\beta)+\mathbb N(\alpha+\beta/2)$ 의 원소는 우세 정수 무게이다. (즉, 그 수는 가산 무한 개이다.)
제1사분면의 점 가운데, y좌표가 x좌표보다 더 큰 점들로 구성된 45° 부채꼴 속의 점은 우세 무게이다. (즉, 그 수는 비가산 무한 개이다.)
화살표의 머리들( $\pm\alpha$ , $\pm\beta$ , $\pm(\alpha+\beta)$ $\pm(2\alpha+\beta)$ )은 근이다. (즉, 총 8개의 근이 있다.)
양근은 $\alpha$ , $\beta$ , $\alpha+\beta$ , $2\alpha+\beta$ 이다. (즉, 총 4개의 양근이 있다.)
단순근은 $\alpha$ , $\beta$ 이다. (즉, 총 2개의 단순근이 있다.)
기본 무게는 $\alpha+\beta$ , $\alpha+\beta/2$ 이다. (즉, 총 2개의 기본 무게가 있다.)

참조

_[1] 문서 In fact, given a set of commuting matrices over an [[algebraically closed field]], they are [[simultaneously triangularizable]], without needing to assume that they are diagonalizable.
_[2] 문헌
_[3] 문헌
_[4] 문헌
_[5] 문헌
_[6] 문헌
_[7] 문헌
_[8] 문헌
_[9] 문헌
_[10] 문헌
_[11] 문서 実は，[[代数閉体]]上の可換な行列のある集合が与えられると，対角化可能と仮定せずとも，[[同時三角化可能]]である．
_[12] 문헌
_[13] 문헌
_[14] 서적 Lie groups beyond an introduction https://www.springer[...] Birkhäuser 2002

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com