선형 판별 분석
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
선형 판별 분석(LDA)은 두 개 이상의 데이터 집합을 구분하거나, 새로운 데이터의 소속 집합을 예측하기 위한 통계적 방법이다. 1936년 로널드 피셔에 의해 개발되었으며, 피셔의 선형 판별 분석은 정규 분포와 동일한 클래스 공분산을 가정하지 않는 판별자를 설명한다. LDA는 두 개 이상의 클래스를 가진 데이터에 적용 가능하며, 다변량 정규성, 분산/공분산의 동질성, 독립성을 가정한다. 판별 함수를 사용하여 잠재 변수를 생성하고, 최대 우도 추정을 통해 그룹 밀도를 최대화하는 그룹에 데이터를 할당한다. LDA는 파산 예측, 얼굴 인식, 마케팅, 의학, 생물학 등 다양한 분야에 활용되며, 로지스틱 회귀와 유사하지만, 가정이 충족될 경우 더 강력한 결과를 제공할 수 있다. 또한, 고차원 데이터에서도 적용 가능하며, 점진적 LDA를 통해 새로운 데이터를 지속적으로 반영하여 특징을 업데이트할 수 있다.
더 읽어볼만한 페이지
- 통계적 분류 - 서포트 벡터 머신
서포트 벡터 머신(SVM)은 지도 학습 모델로서 분류와 회귀 분석에 사용되며, 데이터 집합을 기반으로 새로운 데이터의 범주를 판단하는 비확률적 이진 선형 분류 모델을 생성하고, 커널 트릭을 통해 비선형 분류에도 활용될 수 있다. - 통계적 분류 - 민감도와 특이도
민감도와 특이도는 의학적 진단에서 검사의 정확성을 평가하는 지표로, 민감도는 실제 양성인 대상 중 양성으로 나타나는 비율, 특이도는 실제 음성인 대상 중 음성으로 나타나는 비율을 의미하며, 선별 검사에서 두 지표를 모두 높여 질병을 정확하게 진단하는 것을 목표로 한다. - 시장 조사 - 세계에서 가장 살기 좋은 도시
세계에서 가장 살기 좋은 도시는 평가 기관별 기준에 따라 순위가 다르지만, 안정성, 의료, 문화, 환경, 교육, 인프라 등 다양한 요소를 고려하며, 유럽과 오세아니아의 도시들이 상위권을 차지하고, 한국 도시들의 삶의 질 향상을 위해서는 녹지 공간 확보, 대중교통 시스템 개선, 시민 참여 확대 등이 필요하다. - 시장 조사 - 쿨헌팅
쿨헌팅은 기업이 젊은 세대의 트렌드를 파악하도록 돕는 마케팅 활동으로, 청소년 문화 예측 보고서 판매, 컨설팅, 표적 집단 면접, 쿨 나르크 활용, 온라인 시장 조사 등의 방법으로 정보를 수집한다. - 분류 알고리즘 - 인공 신경망
- 분류 알고리즘 - 퍼셉트론
퍼셉트론은 프랭크 로젠블랫이 고안한 인공신경망 모델로, 입력 벡터에 가중치를 곱하고 편향을 더한 값을 활성화 함수에 통과시켜 이진 분류를 수행하는 선형 분류기 학습 알고리즘이며, 초기 신경망 연구의 중요한 모델로서 역사적 의미를 가진다.
| 선형 판별 분석 | |
|---|---|
| 개요 | |
| 분야 | 통계학, 패턴 인식, 기계 학습 |
| 종류 | 지도 학습 |
| 세부 사항 | |
| 개발자 | 로날드 피셔 |
| 발표 시기 | 1936년 |
| 관련 항목 | 차원 축소 주성분 분석 인공신경망 데이터 마이닝 패턴 인식 |
| 특징 | |
| 설명 | 선형 판별 분석(Linear Discriminant Analysis, LDA)은 통계학, 패턴 인식, 기계 학습에서 사용되는 지도 학습 방법의 하나이다. |
| 목표 | 클래스 분리를 최대화하는 최적의 선형 변환을 찾는 것이다. |
| 활용 | 차원 축소 분류 패턴 인식 |
2. 역사
이분형 판별 분석은 1936년 로널드 피셔 경에 의해 개발되었다.[9] 이는 하나 또는 여러 개의 연속적인 종속 변수를 하나 이상의 독립적인 범주형 변수로 예측하는 분산 분석 또는 MANOVA와는 다르다. 판별 함수 분석은 일련의 변수가 범주 멤버십을 예측하는 데 효과적인지 여부를 결정하는 데 유용하다.[10]
2. 1. 피셔의 선형 판별 (Fisher's Linear Discriminant)
피셔의 원래 논문[2]은 정규 분포 클래스나 동일한 클래스 공분산과 같은 LDA의 일부 가정을 따르지 않는 약간 다른 판별자를 설명한다.두 개의 관측치 클래스가 평균 과 공분산 을 갖는다고 가정한다. 그러면 특징의 선형 조합 는 의 평균과 의 분산을 갖게 된다(여기서 ). 피셔는 이 두 확률 분포 간의 분리를 클래스 간 분산과 클래스 내 분산의 비율로 정의했다.
:
이 측정은 어떤 의미에서 클래스 라벨링에 대한 신호 대 잡음비의 척도이다. 최대 분리는 다음과 같은 경우에 발생함을 알 수 있다.
:
LDA의 가정이 충족되면 위 방정식은 LDA와 동일하다.
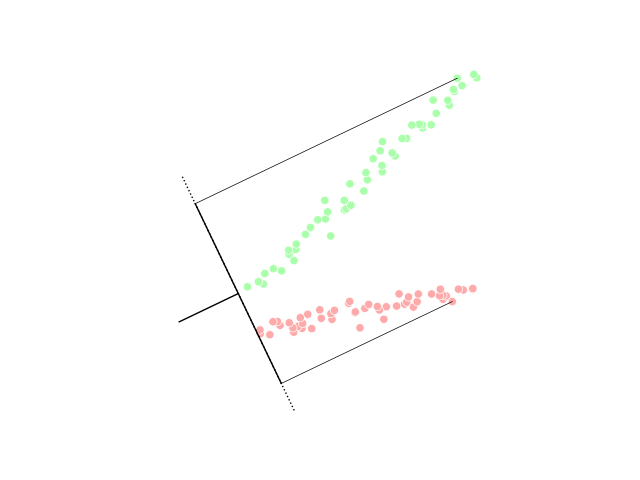
벡터 는 판별 초평면에 대한 법선 벡터이다. 예를 들어, 2차원 문제에서 두 그룹을 가장 잘 나누는 선은 에 수직이다.
일반적으로 구별할 데이터 포인트는 로 투영되며, 데이터 간을 가장 잘 구분하는 임계값은 1차원 분포의 분석에서 선택된다. 임계값에 대한 일반적인 규칙은 없다. 그러나 두 클래스의 점의 투영이 대략 동일한 분포를 나타내는 경우, 좋은 선택은 두 평균의 투영 사이의 초평면, 과 이 될 것이다. 이 경우, 임계 조건 의 매개변수 c는 명시적으로 찾을 수 있다.
:.
오츠의 방법은 피셔의 선형 판별과 관련이 있으며, 흑백 임계값을 최적으로 선택하여 클래스 내 분산을 최소화하고 흑백 픽셀 클래스에 할당된 그레이스케일 간의 클래스 간 분산을 최대화하여 회색조 이미지의 픽셀 히스토그램을 이진화하기 위해 생성되었다.
3. 기본 원리
선형 판별 분석(LDA)의 기본 원리는 데이터를 특정 클래스로 분류하기 위한 최적의 기준을 찾는 것이다. 이 방법은 각 클래스의 데이터 분포와 관련된 통계적 속성을 활용한다.
LDA는 각 클래스의 데이터가 정규 분포를 따른다고 가정한다. 이 가정 하에, 각 클래스의 평균과 공분산을 추정한다. 베이즈 최적 솔루션은 로그 우도 비율을 사용하여 새로운 데이터가 어떤 클래스에 속할 확률을 계산하고, 더 높은 확률을 갖는 클래스로 데이터를 분류한다.
클래스 간 공분산이 동일하다는 등분산성 가정을 추가하고, 공분산이 전체 순위(full rank)를 갖는다고 가정하면, 결정 경계는 선형 방정식으로 단순화된다. 이는 입력 데이터가 특정 클래스에 속하는지 여부가 관찰 값들의 선형 조합에 의해 결정된다는 것을 의미한다. 기하학적으로는, 입력 데이터를 특정 벡터에 투영했을 때, 그 값이 임계값보다 크면 해당 클래스로 분류된다.
피셔는 정규 분포나 동일한 클래스 공분산과 같은 LDA의 일부 가정을 사용하지 않고 약간 다른 판별식을 제시했다. 피셔는 클래스 간 분산과 클래스 내 분산의 비율을 최대화하는 방법을 찾았다. 오츠의 방법은 피셔의 선형 판별 분석과 관련이 있다.
C. R. 라오는 셋 이상의 클래스가 있는 경우, 피셔 판별 분석을 확장하여 모든 클래스 변동성을 포함하는 부분 공간을 찾을 수 있다고 하였다.[19] 클래스 간 산포는 클래스 평균의 표본 공분산으로 정의할 수 있다. 이 경우, 특정 방향의 클래스 분리는 고유 벡터와 고유값을 통해 계산할 수 있다. 가 대각화 가능하다면, 특징 간의 변동성은 ''C'' − 1개의 가장 큰 고유값에 해당하는 고유 벡터로 생성된 부분 공간에 포함된다. 이 고유 벡터는 PCA처럼 특징 감소에 주로 사용된다. 더 작은 고유값에 해당하는 고유 벡터는 훈련 데이터 선택에 민감하므로, 정규화가 필요할 수 있다.
차원 축소 대신 분류가 필요한 경우, "나머지 하나 대 나머지" 방법이나 쌍별 분류 방법등 여러 대안이 있다.
3. 1. 두 클래스에 대한 LDA (LDA for Two Classes)
LDA는 각 클래스의 데이터가 정규 분포를 따른다고 가정한다. 이 가정 하에, 각 클래스의 평균()과 공분산()을 추정한다.[11] 베이즈 최적 솔루션은 로그 우도 비율을 사용하여 새로운 데이터 가 어떤 클래스에 속할 확률을 계산하고, 더 높은 확률을 갖는 클래스로 데이터를 분류한다. 이때, 로그 우도 비율은 다음과 같이 표현된다.:
여기서 T는 임계값이다.
추가적인 가정 없이 위 식을 사용하면, 결과 분류기는 2차 판별 분석(QDA)가 된다.
하지만 LDA는 클래스 간 공분산이 동일하다는 등분산성 가정()을 추가하고, 공분산이 전체 순위(full rank)를 갖는다고 가정한다. 이 경우, 위 식에서 여러 항들이 상쇄되어 결정 경계는 다음과 같은 선형 방정식으로 단순화된다.
:
여기서 이고, 이다.
이는 입력 가 특정 클래스에 속하는지 여부가 관찰 값들의 선형 조합에 의해 결정된다는 것을 의미한다. 기하학적으로는, 입력 를 벡터 에 투영했을 때, 그 값이 임계값 보다 크면 해당 클래스로 분류된다.
피셔의 원래 논문[2]에서는 정규 분포나 동일한 클래스 공분산과 같은 LDA의 일부 가정을 사용하지 않고 약간 다른 판별식을 제시했다. 피셔는 두 클래스의 평균()과 공분산()이 주어졌을 때, 특징의 선형 조합 의 평균과 분산을 이용하여 클래스 간 분산과 클래스 내 분산의 비율(S)을 최대화하는 를 찾았다.
:
이 비율을 최대화하는 는 다음과 같다.
:
LDA의 가정이 만족되면, 위 방정식은 LDA와 동일하다.
벡터 는 판별 초평면(hyperplane)의 법선 벡터이다. 2차원 문제에서 두 그룹을 가장 잘 나누는 선은 에 수직이다.
일반적으로, 데이터를 에 투영한 후, 1차원 분포 분석을 통해 데이터를 가장 잘 구분하는 임계값을 선택한다. 두 클래스의 투영 분포가 유사한 경우, 두 평균의 투영 사이의 초평면을 선택하는 것이 좋다. 이때, 임계값 조건 의 매개변수 c는 다음과 같이 명시적으로 구할 수 있다.
:.
오츠의 방법은 피셔의 선형 판별 분석과 관련이 있다.
3. 2. 다중 클래스 LDA (Multiclass LDA)
C. R. 라오는 셋 이상의 클래스가 있는 경우, 피셔 판별 분석을 확장하여 모든 클래스 변동성을 포함하는 부분 공간을 찾을 수 있다고 하였다.[19] 각 C개의 클래스가 평균 와 동일한 공분산 을 갖는다고 가정하면, 클래스 간 산포는 클래스 평균의 표본 공분산으로 정의할 수 있다.:
여기서 는 클래스 평균의 평균이다. 이 경우 방향의 클래스 분리는 다음과 같이 주어진다.
:
이는 가 의 고유 벡터일 때 분리가 해당 고유값과 같음을 의미한다.
가 대각화 가능하다면, 특징 간의 변동성은 ''C'' − 1개의 가장 큰 고유값에 해당하는 고유 벡터로 생성된 부분 공간에 포함된다. (가 최대 ''C'' − 1의 랭크를 가지기 때문) 이 고유 벡터는 PCA처럼 특징 감소에 주로 사용된다. 더 작은 고유값에 해당하는 고유 벡터는 훈련 데이터 선택에 민감하므로, 정규화가 필요할 수 있다.
차원 축소 대신 분류가 필요한 경우, 여러 대안이 있다. 예를 들어, 클래스를 분할하고 표준 피셔 판별 분석이나 LDA를 사용하여 각 분할을 분류할 수 있다. "나머지 하나 대 나머지" 방법은 한 클래스를 한 그룹에, 나머지를 다른 그룹에 넣고 LDA를 적용하는 방식이다. 이 경우 C개의 분류기가 생성되고, 그 결과가 결합된다. 또 다른 방법은 쌍별 분류로, 각 클래스 쌍에 대해 새로운 분류기를 생성하여 (총 ''C''(''C'' − 1)/2개의 분류기 생성) 개별 분류기를 결합하여 최종 분류를 생성한다.
4. 가정
LDA는 조건부 확률 밀도 함수 및 이 모두 평균 및 공분산 매개변수 및 을 갖는 정규 분포라고 가정한다.[11] 이 가정을 바탕으로, 베이즈 최적 솔루션은 로그 우도 비율이 특정 임계값 T보다 큰 경우 포인트를 두 번째 클래스에서 가져온 것으로 예측한다. 추가적인 가정이 없으면 결과 분류기는 2차 판별 분석(QDA)이 된다.
LDA는 여기서 더 나아가, 클래스 공분산이 동일하며() 공분산이 전체 순위를 갖는다는 등분산성 가정을 추가로 한다. 이 경우, 위의 결정 기준은 점 곱에 대한 임계값이 되며, 이는 입력 가 특정 클래스 에 속한다는 기준이 알려진 관찰의 선형 조합에 대한 함수임을 의미한다.[11]
판별 분석의 가정은 MANOVA의 가정과 동일하며, 주요 내용은 다음과 같다.
- 다변량 정규성: 독립 변수는 그룹 변수의 각 수준에 대해 정규 분포를 따른다.[10][8]
- 분산/공분산의 동질성(등분산성): 그룹 변수 간의 분산은 예측 변수의 수준에 따라 동일하다. Box의 M 통계량으로 검정할 수 있다.[10] 공분산이 같을 때는 선형 판별 분석을 사용하고, 공분산이 같지 않을 때는 이차 판별 분석을 사용한다.[8]
- 독립: 참가자는 무작위로 추출되며, 한 변수에 대한 참가자의 점수는 다른 모든 참가자에 대한 해당 변수의 점수와 독립적이다.[10][8]
판별 분석은 이러한 가정의 약간의 위반에 비교적 강건하며,[12] 이분형 변수를 사용할 때에도 판별 분석이 여전히 신뢰할 수 있다는 것이 입증되었다.[13]
5. 판별 함수 (Discriminant Functions)
LDA는 예측 변수들의 선형 결합을 통해 판별 함수를 생성한다. 가능한 함수의 수는 그룹 수에서 1을 뺀 값()과 예측 변수의 수() 중 더 작은 값이다. 첫 번째 함수는 그룹 간 차이를 최대화하며, 두 번째 함수는 해당 함수에서 차이를 최대화하는 동시에 이전 함수와 상관관계가 없도록 구성된다. 이러한 제약 조건은 후속 함수에도 계속 적용된다.[14]
판별 규칙은 분류 오류를 최소화하기 위해 샘플 공간()에서 "좋은" 영역을 찾는 것이다. 이를 통해 분류 표에서 높은 정확도를 얻을 수 있다.[14]
각 함수의 성능을 평가하기 위해 다음 지표들이 사용된다.
6. 판별 규칙 (Discrimination Rules)
LDA는 데이터를 분류할 때 다음의 여러 판별 규칙을 사용한다.
- 최대 우도 추정: 모집단(그룹) 밀도를 최대화하는 그룹에 를 할당한다.[16]
- 베이즈 판별 규칙: 를 를 최대화하는 그룹에 할당한다. 여기서 ''πi''는 해당 분류의 사전 확률을 나타내고, 는 모집단 밀도를 나타낸다.[16]
- 피셔의 선형 판별 규칙: ''SS''between과 ''SS''within 간의 비율을 최대화하여 그룹을 예측하기 위한 예측 변수의 선형 조합을 찾는다.[16]
7. 고유값과 효과 크기 (Eigenvalues and Effect Size)
선형 판별 분석(LDA)에서 고유값은 각 판별 함수가 그룹을 얼마나 잘 구별하는지를 나타내는 지표로 사용된다.[8] 고유값이 클수록 해당 함수가 그룹을 더 잘 구별한다는 것을 의미한다.[8] 그러나 고유값에는 상한이 없으므로 해석에 주의해야 한다.[10][8]
고유값은 종속 변수가 판별 함수이고 그룹이 IV 수준일 때 분산 분석(ANOVA)에서 ''SS''between(집단 간 변동)과 ''SS''within(집단 내 변동)의 비율로 생각할 수 있다. 가장 큰 고유값은 첫 번째 함수와 관련되고, 두 번째로 큰 고유값은 두 번째 함수와 관련되는 방식이다.
일반적으로 효과 크기 측정값으로 고유값을 사용하는 것은 지지되지 않는다.[10] 대신, 캐노니컬 상관관계가 선호되는 효과 크기 측정값이다. 이는 고유값과 유사하지만, ''SS''between과 ''SS''total(전체 변동)의 비율의 제곱근으로 계산된다. 캐노니컬 상관관계는 그룹과 함수의 상관관계를 나타낸다.[10]
또 다른 효과 크기 측정값은 각 함수에 대한 분산의 백분율이다. 이는 (''λx/Σλi'') X 100으로 계산되며, 여기서 ''λx''는 해당 함수의 고유값이고 Σ''λi''는 모든 고유값의 합이다. 이를 통해 특정 함수가 다른 함수에 비해 얼마나 강력하게 예측하는지 알 수 있다.[10]
정확하게 분류된 백분율도 효과 크기로 분석할 수 있다. 카파 값은 우연의 일치를 보정하여 정확하게 분류된 백분율을 설명할 수 있다.[10]
8. 점진적 LDA (Incremental LDA)
일반적인 선형 판별 분석(LDA) 구현은 모든 샘플을 미리 사용할 수 있어야 한다. 하지만 전체 데이터 세트를 사용할 수 없고 입력 데이터가 스트림으로 관찰되는 상황이 있다. 이 경우, 전체 데이터 세트에 알고리즘을 실행하지 않고 새 샘플을 관찰하여 계산된 LDA 특징을 업데이트하는 기능을 LDA 특징 추출에 적용하는 것이 바람직하다. 예를 들어, 모바일 로봇 공학 또는 온라인 얼굴 인식과 같은 많은 실시간 애플리케이션에서 새로운 관찰이 가능해지는 즉시 추출된 LDA 특징을 업데이트하는 것이 중요하다. 새 샘플을 관찰하여 LDA 특징을 업데이트할 수 있는 LDA 특징 추출 기법은 ''점진적 LDA 알고리즘''이며, 이 아이디어는 지난 20년 동안 광범위하게 연구되었다.[20] Chatterjee와 Roychowdhury는 LDA 특징을 업데이트하기 위한 점진적 자기 조직 LDA 알고리즘을 제안했다.[21] 다른 연구에서 Demir와 Ozmehmet는 오류 수정 및 Hebbian 학습 규칙을 사용하여 LDA 특징을 점진적으로 업데이트하기 위한 온라인 로컬 학습 알고리즘을 제안했다.[22] 이후, Aliyari 등은 새 샘플을 관찰하여 LDA 특징을 업데이트하는 빠른 점진적 알고리즘을 도출했다.[20]
9. 응용 분야
LDA는 다양한 분야에서 활용된다.
- 파산 예측: 재무 비율 및 기타 재무 변수를 기반으로 기업의 파산 여부를 예측하는 데 사용된다. 에드워드 알트만의 1968년 모델[26]은 이 분야의 선도적인 모델이다.[27][28][29]
- 얼굴 인식: 컴퓨터화된 얼굴 인식 시스템에서 각 얼굴을 나타내는 수많은 픽셀 값을 처리하기 전에, 특징의 수를 줄이는 데 사용된다. Fisher의 선형 판별을 사용하여 얻은 선형 결합은 ''피셔 얼굴''이라고 불린다.
- 마케팅: 로지스틱 회귀 분석이 보편화되기 이전에는 설문 조사 데이터를 기반으로 고객 또는 제품을 구별하는 요소를 결정하는 데 사용되었다.
- 의학: 환자의 질병 중증도를 평가하고 예후를 예측하는 데 사용된다. 예를 들어, 환자를 질병 중증도에 따라 그룹으로 나누고, 임상 및 실험실 분석 결과를 통해 각 그룹을 구별하는 변수를 찾아 판별 함수를 구축한다. 또한, 데이터 증강을 위해 더 차별적인 샘플을 선택하여 분류 성능을 향상시키는 데에도 활용된다.[30]
- 생물학: 생물학적 객체의 그룹을 분류하고 정의하는 데 사용된다. 예를 들어, 푸리에 변환 적외선 스펙트럼을 기반으로 살모넬라 엔테리티디스의 파지 유형을 정의하거나,[31] 독성 인자를 연구하여 ''대장균''의 동물 기원을 탐지하는 데 사용된다.[32]
- 지구과학: 변질대를 분리하는 데 사용될 수 있다. 다양한 구역의 데이터를 분석하여 패턴을 찾고 효과적으로 분류한다.[33]
이 외에도 LDA는 포지셔닝 및 제품 관리에도 적용된다.
10. 로지스틱 회귀와의 비교 (Comparison to Logistic Regression)
로지스틱 회귀와 선형 판별 분석(LDA)은 모두 같은 문제 해결에 사용될 수 있다는 점에서 매우 유사하다.[10] 로지스틱 회귀는 판별 분석에 비해 가정과 제약 조건이 적다. 하지만 판별 분석의 가정이 충족된다면 로지스틱 회귀보다 더 강력한 성능을 낸다.[34] 또한, 판별 분석은 로지스틱 회귀와 달리 적은 표본 크기에도 사용 가능하다. 표본 크기가 같고 분산, 공분산의 동질성이 유지되는 경우 판별 분석이 더 정확하다는 것이 입증되었다.[8] 이러한 장점에도 불구하고, 실제로는 판별 분석의 가정이 충족되지 않는 경우가 많아 로지스틱 회귀가 더 일반적으로 사용된다.[9][8]
11. 고차원에서의 선형 판별 (Linear Discriminant in High Dimensions)
LDA는 조건부 확률 밀도 함수 및 이 모두 평균 및 공분산을 갖는 정규 분포라고 가정한다. 이 가정을 통해 베이즈 최적 솔루션을 도출할 수 있다.[11] 추가적인 가정이 없으면, 결과 분류기는 2차 판별 분석 (QDA)이 된다. LDA는 클래스 공분산이 동일하다는 등분산성 가정을 통해 단순화한다.
고차원 데이터에서는 차원의 저주 문제가 발생할 수 있다. 하지만, 적절한 측도의 집중 현상을 활용하면 계산이 더 쉬워질 수 있다.[35] 도노호와 태너는 샘플이 본질적으로 고차원이라면, 각 점이 선형 부등식에 의해 나머지 샘플과 분리될 수 있음을 보였다.[36] 이는 지수적으로 큰 샘플에서도 높은 확률로 성립한다. 이러한 선형 부등식은 다양한 확률 분포에 대해 선형 판별 분석의 표준 형태로 선택될 수 있다.[37] 특히, 로그 오목 측도를 포함하는 다변량 정규 분포[38]와 다차원 큐브에 대한 곱 측도에 대해 증명되었다. 이러한 데이터 분리 특성은 고차원 인공지능 시스템의 오류 보정 문제를 단순화한다.[39]
참조
[1]
웹사이트
Linear Discriminant Analysis (LDA) Can Be So Easy
https://towardsdatas[...]
2023-02-20
[2]
논문
The Use of Multiple Measurements in Taxonomic Problems
https://digital.libr[...]
[3]
서적
Discriminant Analysis and Statistical Pattern Recognition
Wiley Interscience
[4]
간행물
Analyzing Quantitative Data: An Introduction for Social Researchers
[5]
논문
PCA versus LDA
http://www.ece.osu.e[...]
2010-06-30
[6]
간행물
"Discriminant correspondence analysis."
http://www.utdallas.[...]
Sage
2007
[7]
논문
Use of Correspondence Discriminant Analysis to predict the subcellular location of bacterial proteins
[8]
간행물
Discriminant function analysis: Concept and application
https://ejer.com.tr/[...]
[9]
서적
Applied Multiple Regression/Correlation Analysis for the Behavioural Sciences
Taylor & Francis Group
[10]
논문
Using SPSS for Windows and Macintosh: Analyzing and Understanding Data
https://www.tandfonl[...]
2005
[11]
서적
Modern Applied Statistics with S
Springer Verlag
[12]
서적
Discriminant analysis
Hafner
[13]
서적
Discriminant analysis
Sage Publications
[14]
서적
Applied Multivariate Statistical Analysis
Springer Berlin Heidelberg
[15]
웹사이트
Discriminant function analysis
https://web.archive.[...]
[16]
서적
Applied Multivariate Statistical Analysis
https://pdfs.semanti[...]
Springer Berlin Heidelberg
[17]
논문
Performance Metrics: How and When
2006-06
[18]
웹사이트
PA 765: Discriminant Function Analysis
http://www2.chass.nc[...]
2008-03-04
[19]
논문
The utilization of multiple measurements in problems of biological classification
[20]
논문
Fast incremental LDA feature extraction
2015-06-01
[21]
논문
On self-organizing algorithms and networks for class-separability features
1997-05-01
[22]
논문
Online Local Learning Algorithms for Linear Discriminant Analysis
2005-03-01
[23]
논문
A direct LDA algorithm for high-dimensional data — with application to face recognition
[24]
논문
Regularized Discriminant Analysis
http://www.slac.stan[...]
[25]
논문
Feature selection in omics prediction problems using cat scores and false nondiscovery rate control
[26]
논문
Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy
[27]
웹사이트
Twenty-five years of z-scores in the UK: do they really work?
https://efmaefm.org/[...]
[28]
논문
Twenty-Five Years of the Taffler Z-Score Model: Does It Really Have Predictive Ability?
[29]
논문
Assessing Predictive Power and Earnings Manipulations. Applied Study on Listed Consumer Goods and Service Companies in Ghana Using 3 Z-Score Models
https://finance.expe[...]
[30]
논문
Alzheimer’s disease classification using 3D conditional progressive GAN-and LDA-based data selection
[31]
논문
Application of Fourier transform infrared spectroscopy and chemometrics for differentiation of Salmonella enterica serovar Enteritidis phage types
[32]
논문
Evaluation of virulence factor profiling in the characterization of veterinary Escherichia coli isolates
[33]
논문
Application of discriminant analysis for alteration separation; sungun copper deposit, East Azerbaijan, Iran. Australian
http://ajbasweb.com/[...]
[34]
서적
The Elements of Statistical Learning. Data Mining, Inference, and Prediction
Springer
[35]
간행물
Utilizing geometric anomalies of high dimension: When complexity makes computation easier
https://web.archive.[...]
Springer
[36]
논문
Observed universality of phase transitions in high-dimensional geometry, with implications for modern data analysis and signal processing
https://arxiv.org/ab[...]
Phil. Trans. R. Soc. A
2009
[37]
논문
Correction of AI systems by linear discriminants: Probabilistic foundations
[38]
논문
Interpolating thin-shell and sharp large-deviation estimates for isotropic log-concave measures
https://arxiv.org/ab[...]
Geom. Funct. Anal.
2011
[39]
논문
The unreasonable effectiveness of small neural ensembles in high-dimensional brain
2019-07
[40]
저널
The Use of Multiple Measurements in Taxonomic Problems
https://digital.libr[...]
[41]
서적
Discriminant Analysis and Statistical Pattern Recognition
https://archive.org/[...]
Wiley Interscience
[42]
문서
Analyzing Quantitative Data: An Introduction for Social Researchers
[43]
저널
PCA versus LDA
https://web.archive.[...]
2010-06-30
[44]
논문
"Discriminant correspondence analysis."
http://www.utdallas.[...]
Encyclopedia of Measurement and Statistic, Sage
2007
[45]
저널
Use of Correspondence Discriminant Analysis to predict the subcellular location of bacterial proteins
[46]
논문
Discriminant function analysis: Concept and application
https://ejer.com.tr/[...]
Egitim Arastirmalari - Eurasian Journal of Educational Research
2008
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com