원형 공산 오차

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 개념
3. CEP와 다른 백분위수 간의 변환
4. 대한민국 국군의 활용
참조

1. 개요

원형 공산 오차(CEP)는 탄착군의 정확도를 나타내는 지표로, 평균 착탄 지점으로부터 50%의 탄착군이 위치하는 원의 반지름을 의미한다. CEP는 원형 이변량 정규 분포를 따르는 탄약의 경우 유용하며, 그렇지 않은 경우 정확도 측정에 적합하지 않을 수 있다. CEP는 평균 제곱 오차(MSE)의 제곱근으로 정의될 수 있으며, 탄착 데이터로부터 CEP를 추정하기 위한 다양한 방법이 존재한다. CEP는 50% 백분위수를 기준으로 하지만, 다른 백분위수로 표현될 수 있으며, 특정 공식을 통해 서로 변환이 가능하다.

더 읽어볼만한 페이지

확률 - 불확실성
불확실성이란 현재나 미래를 정확히 예측할 수 없는 상태를 말하며, 확률을 알 수 없는 근본적인 불확실성도 존재하고, 바람직하지 않은 결과를 초래할 수 있는 위험과는 구별되며, 과학, 경제, 철학 등 다양한 분야에서 다뤄지는 중요한 개념이다.
확률 - 유의 확률
유의 확률은 통계적 가설 검정에서 귀무 가설이 참일 때 관측된 결과의 극단성을 나타내는 확률값으로, 귀무 가설 기각 여부를 판단하는 기준이 되지만 오용될 수 있어 다른 통계적 추론 방법이 대안으로 제시된다.
항공기용 무장 - 어뢰
어뢰는 수중에서 스스로 움직여 목표물을 공격하는 유도 무기로, 다양한 유도 및 추진 방식과 플랫폼을 통해 해상 전투에서 중요한 역할을 수행하며, 각국 해군에서 개발 및 운용하고 있다.
항공기용 무장 - 하드포인트
하드포인트는 항공기, 특히 군용 항공기의 외부 무장 및 장비 장착을 위해 항공기 프레임에 설치된 특정 지점으로, 파일런을 통해 다양한 무기류 및 장비를 장착하며, 항공기의 성능, 스텔스 기능, 가변익기 활용 등 다양한 요소를 고려하여 설계 및 운용된다.
응용확률론 - 자급자족
자급자족은 개인이 스스로 생산한 것만 소비하며 자립적 건축, 지속 가능한 농업, 재생 에너지 등을 통해 실현되는 지속 가능한 삶의 방식이다.
응용확률론 - 진폭 편이 방식
진폭 편이 방식(ASK)은 반송파의 진폭을 변화시켜 데이터를 표현하는 변조 방식이며, 온오프 변조와 다치 ASK가 있으며, 오류 확률은 다양한 요인에 의해 영향을 받는다.

원형 공산 오차
개요
정의	무기 시스템의 정밀도를 나타내는 탄도학적 측정
설명	탄착군 중심과 목표 지점 사이의 거리가 해당 반경 내에 있을 확률이 50%임을 의미함 원형 공산 오차(CEP) 값은 탄착군 중심과 목표 지점 사이의 거리를 나타내는 척도
중요도	핵무기 정확도에 중요한 사양 핵탄두가 목표물을 파괴할 확률을 결정하는 데 중요한 요소
활용	핵무기 외에도 재래식 무기 시스템의 정확도를 평가하는 데 사용 가능 탄도 미사일, 포병, 소형 무기 등 다양한 무기 시스템에 적용 가능
관련 개념	DRMS (Distance Root Mean Square) 2DRMS (2 times Distance Root Mean Square) R95
계산 및 확률
가정	탄착군이 2차원 정규 분포를 따름 탄착군의 x축, y축 오차가 독립적이고 동일한 분산을 가짐
계산식	CEP = r (여기서 r은 반경)
확률	탄착군 중심이 CEP 반경 내에 있을 확률은 50%
핵무기 관련
중요성	핵탄두가 목표물을 파괴할 확률을 결정하는 데 중요한 요소 CEP가 작을수록 파괴 확률이 높아짐
파괴 확률 계산	파괴 확률은 CEP, 탄두 위력, 목표물의 경도 등을 고려하여 계산
기타
주의사항	CEP는 무기 시스템의 정확도를 나타내는 하나의 척도일 뿐이며, 실제 전투 상황에서는 다양한 요인이 영향을 미칠 수 있음 탄착군이 반드시 원형이 아닐 수 있으며, 2차원 정규 분포를 따르지 않을 수도 있음

2. 개념

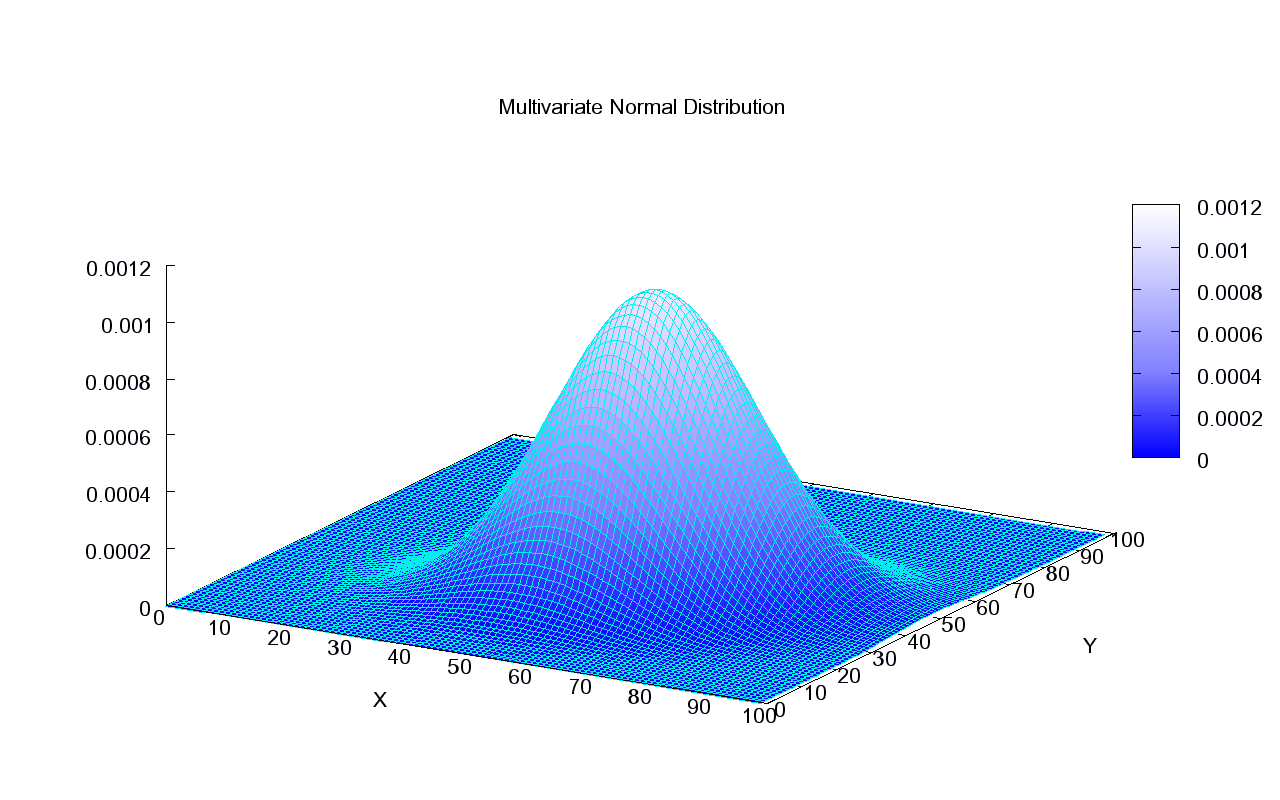
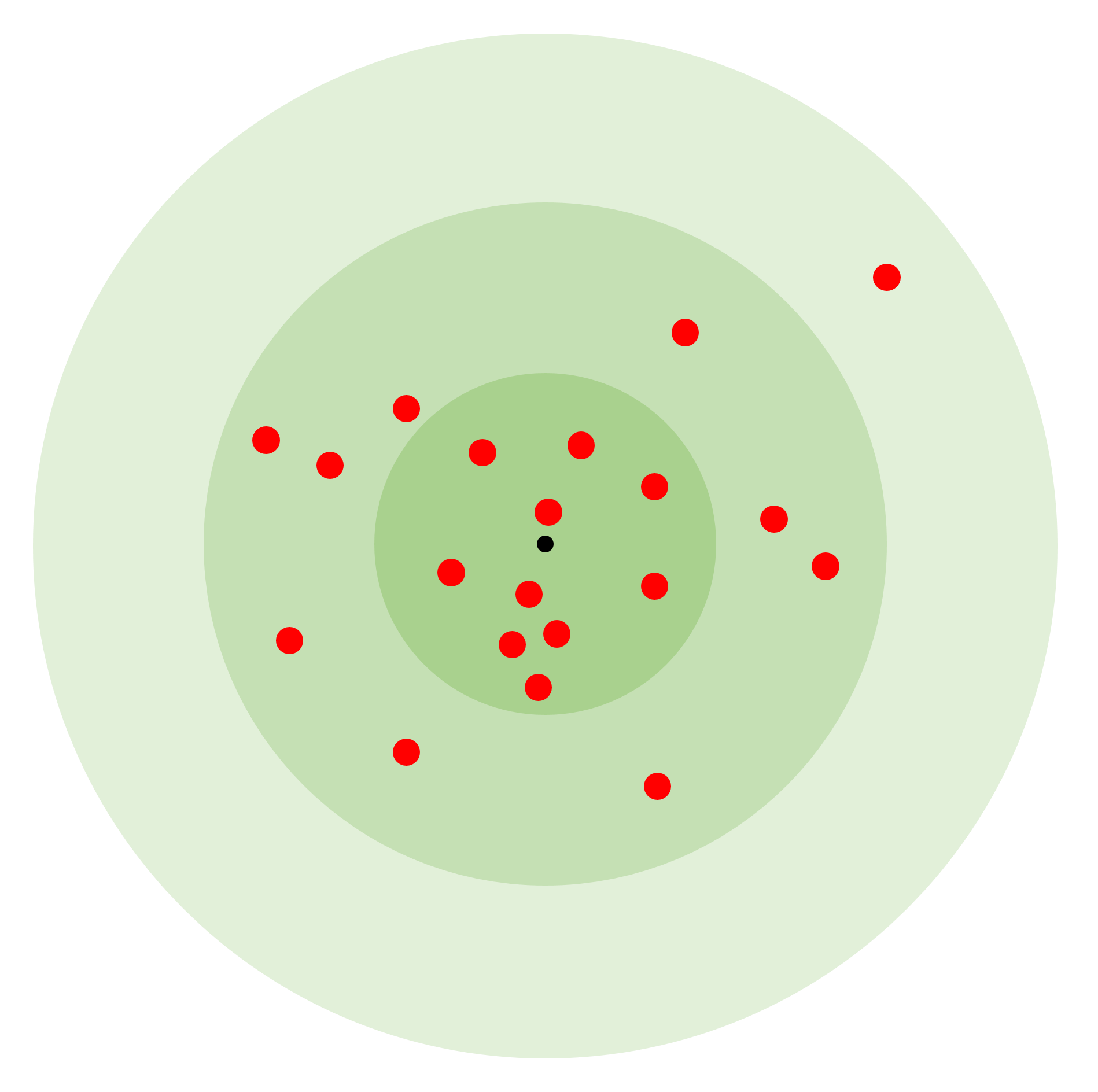
원형 공산 오차(CEP)는 평균 착탄 지점을 중심으로 탄약의 탄착군이 어떻게 분포하는지를 나타내는 개념이다. CEP 값이 ''n'' 미터라면, 발사된 탄약의 50%는 평균 착탄 지점 ''n'' 미터 반경 내에 떨어진다.

CEP는 탄착 분포가 원형 이변량 정규 분포(CBN)를 따른다고 가정한다. 하지만 실제로는 탄착 분포가 항상 원형 정규 분포를 따르지는 않으며, 사거리 오차나 방위각 오차의 편차, 또는 편향 등이 발생할 수 있다. 이러한 한계점을 극복하기 위해 평균 제곱 오차(MSE)의 제곱근으로 CEP를 정의하는 방법이 사용된다.

2. 1. 원형 이변량 정규 분포 가정

원형 공산 오차(CEP)의 원래 개념은 CEP를 원형 이변량 정규 분포(CBN)의 모수, 즉 μ와 σ처럼 사용하는 것이었다. 이러한 분포를 보이는 탄약은 평균 탄착점 주변에 모이는 경향이 있으며, 대부분은 비교적 가깝게, 점점 더 적은 수가 멀리 떨어져 있고, 매우 적은 수가 멀리 떨어진 곳에 떨어진다. 즉, CEP가 ''n'' 미터인 경우, 50%의 탄착군은 평균 탄착점으로부터 ''n'' 미터 이내에, 43.7%는 ''n''과 ''2n'' 미터 사이에, 6.1%는 ''2n''과 ''3n'' 미터 사이에 떨어지며, 평균에서 CEP의 3배 이상 떨어진 곳에 떨어지는 탄착군의 비율은 0.2%에 불과하다.

이러한 분포를 보이지 않는 경우 CEP는 정확도를 측정하는 데 적합하지 않다. 탄약은 또한 방위각(편향) 오차의 표준 편차보다 사거리 오차의 더 큰 표준 편차를 가질 수 있으며, 결과적으로 타원형 신뢰 영역을 초래할 수 있다. 탄약 표본이 정확하게 목표 지점에 있지 않을 수 있는데, 즉, 평균 벡터가 (0,0)이 아닐 수 있다. 이를 편향이라고 한다.

2. 2. 한계 및 추가 고려 사항

CEP는 원래 원형 이변량 정규 분포를 따르는 탄착군에 대해 정의되었으나, 실제로는 탄착 분포가 항상 원형 정규 분포를 따르지는 않는다. 예를 들어, 사거리 오차의 표준 편차가 방위각 오차의 표준 편차보다 큰 경우, 탄착군은 타원형 신뢰 영역을 형성할 수 있다. 또한, 평균 탄착 지점이 목표 지점과 일치하지 않는 편향이 발생할 수도 있다.^[1]

이러한 한계를 극복하기 위해, 평균 제곱 오차(MSE)의 제곱근으로 CEP를 정의하는 방법이 사용된다. MSE는 사거리 오차의 분산, 방위각 오차의 분산, 사거리 오차와 방위각 오차의 공분산, 그리고 편향의 제곱을 모두 합한 값이다. 따라서 MSE는 다양한 오차 요인을 종합적으로 고려하여, 50%의 탄착군이 포함되는 원의 반지름을 나타낸다.^[1]

탄착 데이터로부터 CEP를 추정하기 위한 다양한 방법들이 개발되었다. Blischke와 Halpin(1966)은 플러그인 방식을, Spall과 Maryak(1992)은 베이즈 방식을, Winkler와 Bickert(2012)는 최대 우도 방식을 제안했다. 특히, Spall과 Maryak의 방식은 여러 종류의 탄약이나 여러 위치에서 발사된 탄착 데이터가 혼합된 경우에 유용하다.^[1]

2. 3. CEP 추정 방법

탄착 데이터로부터 CEP를 추정하기 위해 여러 방법이 도입되었다. 이러한 방법에는 다음이 포함된다.

Blischke와 Halpin(1966)의 플러그인 접근 방식
Spall과 Maryak(1992)의 베이즈 접근 방식
Winkler와 Bickert(2012)의 최대 우도 접근 방식

Spall과 Maryak의 접근 방식은 탄착 데이터가 서로 다른 발사체 특성(예: 여러 탄약 유형 또는 여러 위치에서 하나의 표적을 향해 발사된 탄)의 혼합을 나타낼 때 적용된다.

3. CEP와 다른 백분위수 간의 변환

CEP는 50% 백분위수를 기준으로 하지만, DRMS, R95, 2DRMS 등 다른 백분위수로도 표현될 수 있다. 이러한 백분위수 간에는 특정 공식을 통해 변환할 수 있다.^[5]^[6]

3. 1. 백분위수 정의

수평 위치 오차는 각 축에 대해 표준 편차 σ를 갖는 2개의 직교하는 가우스 확률 변수로 정의된다. 거리 오차는 해당 벡터의 크기이며, 이는 레일리 분포를 따른다.

레일리 분포의 속성에 따라, 수준

F \in [0\%, 100\%]

에서의 백분위수는 다음 공식으로 주어진다.

:

Q(F, \sigma) = \sigma \sqrt{-2\ln(1 - F/100\%)}

DRMS로 표현하면 다음과 같다.

:

Q(F, \sigma_d) = \sigma_d \frac{\sqrt{-2\ln(1 - F/100\%)}}{\sqrt{2}}

Q

와

F

사이의 관계는 다음 표와 같다. DRMS 및 2DRMS (거리 제곱 평균 제곱근의 두 배)에 대한

F

값은 레일리 분포에 특화되어 수치적으로 구해지며, CEP, R95 (95% 반경) 및 R99.7 (99.7% 반경) 값은 68–95–99.7 규칙을 기반으로 정의된다.

$Q$ 의 척도	확률 $F \, (\%)$
DRMS	63.213...
CEP	50
2DRMS	98.169...
R95	95
R99.7	99.7

어떤 백분위 수준으로 표현된 값을 다른 백분위 수준으로 변환하는 변환 표를 만들 수 있다.^[5]^[6] $X$ 를 $Y=\alpha.X$ 로 변환하기 위한 계수 $\alpha$ 는 다음 표와 같다.

$X \downarrow$ 에서 $Y \rightarrow$ 로	RMS ( $\sigma$ )	CEP	DRMS	R95	2DRMS	R99.7
RMS ( $\sigma$ )	1.00	1.18	1.41	2.45	2.83	3.41
CEP	0.849	1.00	1.20	2.08	2.40	2.90
DRMS	0.707	0.833	1.00	1.73	2.00	2.41
R95	0.409	0.481	0.578	1.00	1.16	1.39
2DRMS	0.354	0.416	0.500	0.865	1.00	1.21
R99.7	0.293	0.345	0.415	0.718	0.830	1.00

예를 들어, 1.25m DRMS를 갖는 GPS 수신기는 1.25m × 1.73 = 2.16m 95% 반경을 갖는다.

3. 2. 백분위수 공식

백분위수는 수평 위치 오차가 각 축에 대해 표준 편차

\sigma

를 갖는 두 개의 직교하는 가우스 확률 변수(각각의 축에 대해 하나씩)인 2D 벡터로 정의된다는 것을 인식함으로써 결정될 수 있다. "거리 오차"는 해당 벡터의 크기이다. 이는 2D 가우스 벡터의 속성이며, 크기는 척도 인자

\sigma

를 갖는 레일리 분포를 따른다. "거리 제곱 평균 제곱근(DRMS)"은

\sigma_d=\sqrt{2}\sigma

이고, 이 값 내의 오차가 이변량 원형 분포에 의해 표현된 표본의 63%를 차지하므로 일종의 표준 편차로 두 배가 된다. 반대로, 레일리 분포의 속성은 수준

F \in [0\%, 100\%]

에서의 백분위수가 다음 공식에 의해 주어진다는 것이다.

:

Q(F, \sigma) = \sigma \sqrt{-2\ln(1 - F/100\%)}

또는 DRMS로 표현하면 다음과 같다.

:

Q(F, \sigma_d) = \sigma_d \frac{\sqrt{-2\ln(1 - F/100\%)}}{\sqrt{2}}

Q

와

F

사이의 관계는 아래 표와 같으며, 여기서 DRMS 및 2DRMS (거리 제곱 평균 제곱근의 두 배)에 대한

F

값은 레일리 분포에 특화되어 수치적으로 구해지는 반면, CEP, R95 (95% 반경) 및 R99.7 (99.7% 반경) 값은 68–95–99.7 규칙을 기반으로 정의된다.

$Q$ 의 척도	확률 $F \, (\%)$
DRMS	63.213...
CEP	50
2DRMS	98.169...
R95	95
R99.7	99.7

그 후, 한 백분위 수준에 대해 표현된 값을 다른 백분위 수준으로 변환하는 변환 표를 파생할 수 있다.^[5]^[6] $X$ 를 $Y=\alpha.X$ 로 변환하기 위한 계수 $\alpha$ 를 제공하는 해당 변환 표는 아래와 같다.

$X \downarrow$ 에서 $Y \rightarrow$ 로	RMS ( $\sigma$ )	CEP	DRMS	R95	2DRMS	R99.7
RMS ( $\sigma$ )	1.00	1.18	1.41	2.45	2.83	3.41
CEP	0.849	1.00	1.20	2.08	2.40	2.90
DRMS	0.707	0.833	1.00	1.73	2.00	2.41
R95	0.409	0.481	0.578	1.00	1.16	1.39
2DRMS	0.354	0.416	0.500	0.865	1.00	1.21
R99.7	0.293	0.345	0.415	0.718	0.830	1.00

3. 3. 변환표

다른 백분위수 수준 간의 변환을 위한 계수 표는 다음과 같다.^[5]^[6] X를 Y=αX로 변환하기 위한 계수 α를 제공한다.

$X \downarrow$ 에서 $Y \rightarrow$ 로	RMS ( $\sigma$ )	CEP	DRMS	R95	2DRMS	R99.7
RMS ( $\sigma$ )	1.00	1.18	1.41	2.45	2.83	3.41
CEP	0.849	1.00	1.20	2.08	2.40	2.90
DRMS	0.707	0.833	1.00	1.73	2.00	2.41
R95	0.409	0.481	0.578	1.00	1.16	1.39
2DRMS	0.354	0.416	0.500	0.865	1.00	1.21
R99.7	0.293	0.345	0.415	0.718	0.830	1.00

예를 들어, 1.25m DRMS를 갖는 GPS 수신기는 1.25m × 1.73 = 2.16m의 R95(95% 반경)를 갖는다.

4. 대한민국 국군의 활용

대한민국 국군은 CEP를 무기 시스템 정확도 평가에 활용한다.

참조

_[1] 간행물 Circular Error Probable (CEP) Air Force Operational Test and Evaluation Center 1987-07
_[2] 웹사이트 Use of Circular Error Probability in Target Detection https://apps.dtic.mi[...] The MITRE Corporation; United States Air Force
_[3] 서적 Waging Nuclear Peace: The Technology and Politics of Nuclear Weapons State University of New York Press
_[4] 서적 Principles of Naval Weapon Systems Naval Institute Press
_[5] 뉴스 GPS Accuracy: Lies, Damn Lies, and Statistics http://gpsworld.com/[...] GPS World 1998-01
_[6] 뉴스 GNSS Accuracy – Lies, Damn Lies and Statistics http://www.gpsworld.[...] GPS World 2007-01
_[7] 논문 大陸の目標に対する核攻撃：物理的可能性の検討

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com