꼬인 위치

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

꼬인 위치는 3차원 공간에서 두 직선이 동일 평면상에 존재하지 않는 상태를 의미한다. 꼬인 위치에 있는 두 직선은 평행하지도 않고 교차하지도 않으며, 삼각뿔의 변이나 입체 교차하는 도로와 같은 예시가 있다. 꼬인 위치에 있는 두 직선 사이의 거리는 두 직선 모두에 수직인 선분의 길이로 정의되며, 벡터를 사용하여 계산할 수 있다. 꼬인 위치는 유선면과 기하학적 구조를 형성하는 데 활용되며, 고차원 공간에서는 평면 간에도 엇갈린 위치 관계가 존재한다. 대한민국 중학교 수학 교육과정에서 꼬인 위치를 다루며, 공간 감각을 키우는 데 기여한다.

더 읽어볼만한 페이지

다중선형대수학 - 아인슈타인 표기법
아인슈타인 표기법은 수식에서 중복된 첨자를 사용하여 합을 간결하게 표현하는 방법으로, 동일한 항에 위첨자와 아래첨자로 반복되는 지표가 나타날 경우 해당 지표에 대한 모든 가능한 값에 대한 합을 의미하는 것으로 간주하며, 일반 상대성 이론, 텐서 대수 등에서 복잡한 수식을 단순화하는 데 사용된다.
다중선형대수학 - 외대수
외대수는 가환환 위의 가군에 대해 정의되는 텐서 대수의 몫환으로, 선형대수학, 미분기하학, 물리학 등에서 응용되며 단위 결합 대수이자 등급 대수 구조를 갖는 대수 구조이다.
유클리드 공간기하학 - 원기둥
원기둥은 밑면이 원인 3차원 도형으로, 직사각형을 회전시켜 만들 수 있으며, 부피는 밑면의 면적과 높이의 곱으로, 겉넓이는 밑넓이와 측면적의 합으로 계산한다.
유클리드 공간기하학 - 입체각
입체각은 3차원 공간에서 한 점을 기준으로 물체가 보이는 범위를 나타내는 각도의 일반화된 개념으로, 구의 중심에서 바라본 물체의 겉넓이와 구 반지름의 제곱의 비율로 정의되며 스테라디안 단위를 사용하고, 천문학, 물리학, 컴퓨터 그래픽스 등 다양한 분야에서 활용된다.
초등 기하학 - 대원
구면기하학에서 대원은 구의 중심을 지나는 평면과 구의 교선으로, 유클리드 공간의 직선에 대응하며, 서로 대극점이 아닌 두 점을 잇는 최단 거리인 대원 거리를 정의하고, 자오선이나 적도처럼 항해, 천문학 등 다양한 분야에서 응용된다.
초등 기하학 - 현 (기하학)
현은 원 둘레를 두 호로 나누는 선분으로, 원에 내접하는 정다각형의 변이 될 수 있으며, 원의 중심을 지나는 가장 긴 현은 지름이라고 한다.

꼬인 위치
개요
정의	3차원 공간에서 만나지도 않고 평행하지도 않은 두 직선의 관계
다른 이름	비공면선
관련 개념	평행선 교차 수직
특징
동일 평면	두 직선은 동일 평면 위에 존재하지 않음
교점	두 직선은 교점을 가지지 않음
평행	두 직선은 평행하지 않음
판별법
벡터 이용	두 직선의 방향 벡터와 한 직선 위의 점을 지나고 다른 직선에 평행한 평면 사이의 거리를 이용하여 판별 가능
행렬식 이용	두 직선의 방정식을 이용하여 행렬식을 만들고, 행렬식의 값이 0이 아니면 꼬인 위치에 있음
예시
공간도형	정육면체에서 모서리 AB와 모서리 CD (단, AB와 CD는 평행하지 않고 만나지 않음)
현실	고가도로와 일반 도로, 철길과 도로

2. 정의 및 성질

3차원 공간에서 두 직선이 꼬인 위치에 있다는 것은, 두 직선을 포함하는 평면이 존재하지 않는다는 것을 의미한다.

공간 기하학에서 "특정 두 직선 , 가 동일 평면상에 존재하지 않는" 상태, 즉 "특정 두 직선 , 에 의해 하나의 평면이 결정되지 않는" 상태에 있을 때, "두 직선 , 는 꼬인 위치에 있다"라고 말한다.^[6]。

; 꼬인 위치의 구체적인 예

예를 들어, "삼각형 BCD를 밑면으로 하는 삼각뿔 A-BCD"의 변 AB와 변 CD는 꼬인 위치에 있다.
예를 들어, 입체 교차하는 두 노선 (두 개의 도로, 혹은 두 개의 철로, 혹은 "도로와 철로" 등)은 꼬인 위치에 있다.

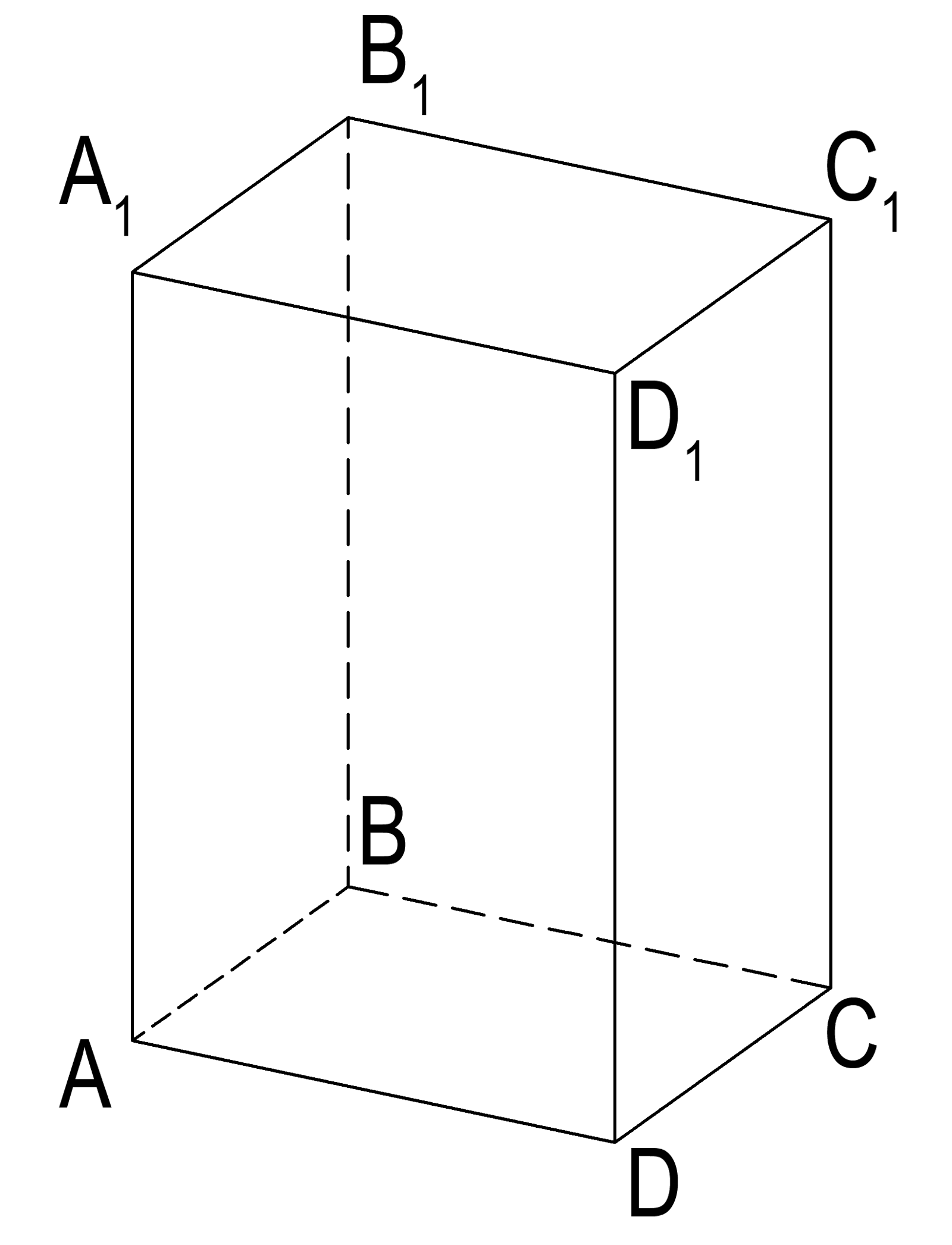
; 꼬인 위치에 있는 두 직선의 거리

꼬인 위치에 있는 두 직선 、의 거리란, 、에 모두 수직인 선분의 길이를 말한다.^[6]。（다른 말로 하면, 에 대해서도 수직이며 또한에 대해서도 수직인 선분의 길이이다）。

; 공간 내 두 직선에 관한 지식

공간 내 두 직선의 위치 관계는 다음 세 가지 중 하나이다.

평행
교차
꼬인 위치

; 꼬인 위치에 있는 두 직선이 등장하지 않는 기하학

꼬인 위치에 있는 두 직선은 3차원 이상의 "공간"에서만 존재한다. 공간 기하학에는 등장하지만, 평면 기하학에는 등장하지 않는다.

평면 기하학에서 등장하는 직선은, 임의의 두 직선을 선택해도 "꼬인 위치"에 있지 않다.

어떤 입체물이라도 그것을 평면으로 절단한 단면 위에 나타나는 직선에 한정하면, 이는 "평면 기하학"으로 다룰 수 있는 범위가 되므로, 거기에 꼬인 위치에 있는 두 직선은 절대 등장하지 않는다.

==== 일반적인 위치 ====

단위 정육면체 내에서 무작위로 네 점을 균등하게 선택하면, 거의 확실하게 꼬인 위치에 있는 두 직선을 정의한다. 처음 세 점을 선택한 후, 네 번째 점은 처음 세 점과 동일 평면 상에 있을 때에만 꼬이지 않은 선을 정의한다. 그러나 처음 세 점을 지나는 평면은 정육면체의 측도 영의 부분 집합을 형성하며, 네 번째 점이 이 평면 위에 놓일 확률은 0이다. 만약 그렇지 않다면, 점에 의해 정의된 선은 꼬인 위치에 있게 된다.

마찬가지로, 3차원 공간에서 두 개의 평행선 또는 교차하는 선을 아주 약간만 변동시켜도 거의 확실하게 꼬인 위치의 선으로 바뀔 것이다. 그러므로 일반적인 위치에 있는 임의의 네 점은 항상 꼬인 위치의 선을 형성한다.

이런 의미에서 꼬인 위치의 선은 "일반적인" 경우이고, 평행선 또는 교차선은 특수한 경우이다.

==== 꼬임 판별 ====

두 직선이 꼬인 위치에 있는지 판별하기 위해, 각 직선을 정의하는 두 점, 총 네 점으로 구성된 사면체의 부피를 계산할 수 있다. 만약 꼬인 두 직선 쌍의 각 선이 지나는 두 개의 점으로 정의된다면, 이 네 점은 공면 상에 있지 않아야 하므로, 비부피의 사면체의 꼭짓점이 되어야 한다. 반대로, 비 부피의 사면체를 정의하는 두 쌍의 점은 꼬인 두 직선 쌍을 정의한다.

'''a'''와 '''b'''를 통과하는 선이 '''c'''와 '''d'''를 통과하는 선과 꼬여 있는지 확인하기 위한 방법은 다음과 같다. 점을 세 개의 요소가 점의 세 좌표 값인 1×3 벡터로 표현하여, '''a''', '''b''', '''c''', '''d'''로 나타낸다. 이 때, 사면체 부피 공식이 0이 아닌 결과를 제공하는지 확인하면 된다.

사면체의 부피 공식은 다음과 같다.

:

V=\frac{1}{6}\left|\det\left[\begin{matrix}\mathbf{a}-\mathbf{b} \\ \mathbf{b}-\mathbf{c} \\ \mathbf{c}-\mathbf{d} \end{matrix}\right]\right|.

사면체의 부피가 0이 아니라면, 네 점은 동일 평면 상에 있지 않으므로 두 직선은 꼬인 위치에 있다.

2. 1. 일반적인 위치

단위 정육면체 내에서 무작위로 네 점을 균등하게 선택하면, 거의 확실하게 꼬인 위치에 있는 두 직선을 정의한다. 처음 세 점을 선택한 후, 네 번째 점은 처음 세 점과 동일 평면 상에 있을 때에만 꼬이지 않은 선을 정의한다. 그러나 처음 세 점을 지나는 평면은 정육면체의 측도 영의 부분 집합을 형성하며, 네 번째 점이 이 평면 위에 놓일 확률은 0이다. 만약 그렇지 않다면, 점에 의해 정의된 선은 꼬인 위치에 있게 된다.

마찬가지로, 3차원 공간에서 두 개의 평행선 또는 교차하는 선을 아주 약간만 변동시켜도 거의 확실하게 꼬인 위치의 선으로 바뀔 것이다. 그러므로 일반적인 위치에 있는 임의의 네 점은 항상 꼬인 위치의 선을 형성한다.

이런 의미에서 꼬인 위치의 선은 "일반적인" 경우이고, 평행선 또는 교차선은 특수한 경우이다.

2. 2. 꼬임 판별

두 직선이 꼬인 위치에 있는지 판별하기 위해, 각 직선을 정의하는 두 점, 총 네 점으로 구성된 사면체의 부피를 계산할 수 있다. 만약 꼬인 두 직선 쌍의 각 선이 지나는 두 개의 점으로 정의된다면, 이 네 점은 공면 상에 있지 않아야 하므로, 비부피의 사면체의 꼭짓점이 되어야 한다. 반대로, 비 부피의 사면체를 정의하는 두 쌍의 점은 꼬인 두 직선 쌍을 정의한다.

한 점을 세 개의 요소가 점의 세 좌표 값인 1×3 벡터 '''a'''로 나타내고, 마찬가지로 다른 점에 대해 '''b''', '''c''', '''d'''로 나타내면, '''a'''와 '''b'''를 통과하는 선이 '''c'''와 '''d'''를 통과하는 선과 꼬여 있는지 사면체 부피 공식이 0이 아닌 결과를 제공하는지 확인하여 확인할 수 있다.

사면체의 부피 공식은 다음과 같다.

:

V=\frac{1}{6}\left|\det\left[\begin{matrix}\mathbf{a}-\mathbf{b} \\ \mathbf{b}-\mathbf{c} \\ \mathbf{c}-\mathbf{d} \end{matrix}\right]\right|.

사면체의 부피가 0이 아니라면, 네 점은 동일 평면 상에 있지 않으므로 두 직선은 꼬인 위치에 있다.

3. 꼬인 위치의 두 직선 사이의 거리

PQ, 두 꼬인선 AB와 CD 사이의 최단 거리는 AB와 CD 모두에 수직이다

꼬인 위치에 있는 두 직선 사이의 거리는, 두 직선 모두에 수직인 선분의 길이로 정의된다.

벡터 표현을 이용하여 두 직선 사이의 최단 거리를 계산할 수 있다. 두 직선의 방향 벡터의 외적은 두 직선 모두에 수직인 벡터를 제공하며, 이를 이용하여 최단 거리를 구하는 공식을 유도할 수 있다.

두 선을 벡터로 표현하면 다음과 같다.

:선 1: '''v₁'''='''p₁'''+''t₁'''''d₁'''

:선 2: '''v₂'''='''p₂'''+''t₂'''''d₂'''

'''d₁'''과 '''d₂'''의 외적은 두 선에 수직이다.

:'''n'''= '''d₁''' × '''d₂'''

'''n'''을 따라 선 2를 평행 이동하여 형성된 평면은 점 '''p₂'''를 포함하며 '''n₂'''= '''d₂''' × '''n'''에 수직이다.

선 1과 위에서 언급한 평면의 교차점, 즉 선 2에 가장 가까운 선 1 위의 점은 다음과 같다.

:'''c₁'''='''p₁'''+ (('''p₂'''-'''p₁''')·'''n₂'''/'''d₁'''·'''n₂''') '''d₁'''

마찬가지로, 선 1에 가장 가까운 선 2 위의 점은 다음과 같다 (여기서 '''n₁'''= '''d₁''' × '''n''').

:'''c₂'''='''p₂'''+ (('''p₁'''-'''p₂''')·'''n₁'''/'''d₂'''·'''n₁''') '''d₂'''

두 꼬인 선에서 가장 가까운 점 '''c₁'''과 '''c₂'''는 선 1과 선 2를 연결하는 가장 짧은 선분을 형성한다.

: ''d'' = ∥ '''c₁''' - '''c₂''' ∥.

두 꼬인 선에서 가장 가까운 점 사이의 거리는 다른 벡터를 사용하여 나타낼 수도 있다.

:'''x''' = '''a''' + ''λ'' '''b''';

:'''y''' = '''c''' + ''μ'' '''d'''.

여기서 1×3 벡터 '''x'''는 특정 점 '''a'''를 지나고 선의 방향을 나타내는 '''b'''를 가지며, 실수 ''λ''의 값은 선상의 점의 위치를 결정하는 임의의 점을 나타내고, '''d''' 방향으로 특정 점 '''c'''를 지나는 선상의 임의의 점 '''y'''에 대해서도 마찬가지이다.

'''b'''와 '''d'''의 외적은 선에 수직이며, 단위 벡터도 마찬가지이다.

:'''n''' = '''b''' × '''d'''/|'''b''' × '''d'''|

그런 다음 선 사이의 수직 거리는 다음과 같다.

:''d'' = |'''n''' · ('''c''' - '''a''')|.

(|'''b''' × '''d'''|가 0이면 선은 평행하며 이 방법을 사용할 수 없다.)

3. 1. 최단 거리 계산

벡터 표현을 이용하여 두 직선 사이의 최단 거리를 계산할 수 있다. 두 직선의 방향 벡터의 외적은 두 직선 모두에 수직인 벡터를 제공하며, 이를 이용하여 최단 거리를 구하는 공식을 유도할 수 있다.

두 선을 벡터로 표현하면 다음과 같다.

:

\text{선 1:} \; \mathbf{v_1}=\mathbf{p_1}+t_1\mathbf{d_1}

:

\text{선 2:} \; \mathbf{v_2}=\mathbf{p_2}+t_2\mathbf{d_2}

\mathbf{d_1}

과

\mathbf{d_2}

의 외적은 두 선에 수직이다.

:

\mathbf{n}= \mathbf{d_1} \times \mathbf{d_2}

\mathbf{n}

을 따라 선 2를 평행 이동하여 형성된 평면은 점

\mathbf{p_2}

를 포함하며

\mathbf{n_2}= \mathbf{d_2} \times \mathbf{n}

에 수직이다.

선 1과 위에서 언급한 평면의 교차점, 즉 선 2에 가장 가까운 선 1 위의 점은 다음과 같다.

:

\mathbf{c_1}=\mathbf{p_1}+ \frac{(\mathbf{p_2}-\mathbf{p_1})\cdot\mathbf{n_2}}{\mathbf{d_1}\cdot\mathbf{n_2}} \mathbf{d_1}

마찬가지로, 선 1에 가장 가까운 선 2 위의 점은 다음과 같다 (여기서

\mathbf{n_1}= \mathbf{d_1} \times \mathbf{n}

).

:

\mathbf{c_2}=\mathbf{p_2}+ \frac{(\mathbf{p_1}-\mathbf{p_2})\cdot\mathbf{n_1}}{\mathbf{d_2}\cdot\mathbf{n_1}} \mathbf{d_2}

두 꼬인 선에서 가장 가까운 점

\mathbf{c_1}

과

\mathbf{c_2}

는 선 1과 선 2를 연결하는 가장 짧은 선분을 형성한다.

:

d = \Vert \mathbf{c_1} - \mathbf{c_2} \Vert.

두 꼬인 선에서 가장 가까운 점 사이의 거리는 다른 벡터를 사용하여 나타낼 수도 있다.

:

\mathbf{x} = \mathbf{a} + \lambda \mathbf{b};

:

\mathbf{y} = \mathbf{c} + \mu \mathbf{d}.

여기서 1×3 벡터 는 특정 점 를 지나고 선의 방향을 나타내는 를 가지며, 실수

\lambda

의 값은 선상의 점의 위치를 결정하는 임의의 점을 나타내고, 방향으로 특정 점 를 지나는 선상의 임의의 점 에 대해서도 마찬가지이다.

'''b'''와 '''d'''의 외적은 선에 수직이며, 단위 벡터도 마찬가지이다.

:

\mathbf{n} = \frac{\mathbf{b} \times \mathbf{d}}

그런 다음 선 사이의 수직 거리는 다음과 같다.

:

d = |\mathbf{n} \cdot (\mathbf{c} - \mathbf{a})|.

(|'''b''' × '''d'''|가 0이면 선은 평행하며 이 방법을 사용할 수 없다.)

4. 꼬인 위치의 활용

4. 1. 유선면

한 직선 ''L''을 이와 꼬인 관계에 있지만 수직하지는 않은 다른 직선 ''M'' 주위로 회전시키면 ''L''이 쓸고 지나가는 회전면은 일엽 쌍곡면이 된다. 예를 들어, 그림에 보이는 세 개의 쌍곡면은 직선 ''L''을 중앙의 흰색 수직선 ''M'' 주위로 회전시켜서 만들 수 있다. 이 표면 내의 ''L'' 사본은 규칙을 형성하며, 쌍곡면은 또한 ''M''과 같은 거리에 있지만 반대 각도를 이루는 두 번째 직선군을 포함하며, 이들은 반대 규칙을 형성한다. 두 규칙은 쌍곡면을 유선면으로 나타낸다.

쌍곡 포물면은 꼬인 두 직선군을 가지는 유선면이다. 일엽 쌍곡면과 마찬가지로 쌍곡 포물면은 꼬인 두 개의 직선군을 가지며, 두 군 각각에서 직선들은 서로 평행하지는 않지만 공통 평면에 평행하다. '''R'''³에서 꼬인 세 개의 직선은 이러한 유형 중 하나인 정확히 하나의 유선면에 놓인다.

4. 2. 기하학적 구조

꼬인 위치의 ''구성''은 모든 쌍이 꼬인 선의 집합이다. 두 구성은 변환 전체에서 모든 선의 쌍이 꼬인 상태를 유지하면서, 한 구성을 다른 구성으로 지속적으로 변환할 수 있다면 ''동위''라고 한다. 두 선의 모든 두 구성은 쉽게 동위인 것으로 보이며, 3차원보다 높은 차원에서의 동일한 수의 선 구성은 항상 동위이지만, 3차원에서는 세 개 이상의 선에 대한 여러 개의 비동위 구성이 존재한다. '''R'''³에서 ''n''개의 선에 대한 비동위 구성의 수는 ''n'' = 1부터 시작하여 1, 1, 2, 3, 7, 19, 74, ... 순서로 증가한다.

5. 꼬인 위치와 관련된 정리

세 개의 꼬인 직선이 다른 세 개의 꼬인 직선과 모두 만나는 경우, 첫 번째 세 직선 집합의 임의의 횡단선은 두 번째 집합의 임의의 횡단선과 만난다.

5. 1. 갈루치의 정리

세 개의 꼬인 직선이 다른 세 개의 꼬인 직선과 모두 만나는 경우, 첫 번째 세 직선 집합의 임의의 횡단선은 두 번째 집합의 임의의 횡단선과 만난다.

6. 고차원 공간에서의 꼬인 위치

고차원 공간에서 차원 ''k''의 평면은 ''k''-평면이라고 하며, 선은 1-평면이라고 할 수 있다.

''엇갈린 선''의 개념을 ''d''차원 공간으로 일반화하면, ''i''-평면과 ''j''-평면은 ''i'' + ''j'' < ''d''인 경우 '''엇갈릴''' 수 있다. 3차원 공간의 꼬인 직선과 마찬가지로 엇갈린 평면은 평행하지도 않고 교차하지도 않는 평면을 말한다.

아핀 ''d''-공간에서 임의의 차원을 가진 두 평면은 평행할 수 있지만, 사영 공간에서는 평행이 존재하지 않으므로 두 평면은 교차하거나 엇갈려야 한다.

''I''를 ''i''-평면상의 점의 집합, ''J''를 ''j''-평면상의 점의 집합이라고 할 때, 사영 ''d''-공간에서 ''i'' + ''j'' ≥ ''d''이면 ''I''와 ''J''의 교집합은 (''i''+''j''−''d'')-평면을 포함해야 한다. (''0''-평면은 점이다.)

어떤 기하학에서든 ''I''와 ''J''가 ''k'' ≥ 0에 대해 ''k''-평면에서 교차하면 ''I'' ∪ ''J''의 점들은 (''i''+''j''−''k'')-평면을 결정한다.

6. 1. 꼬인 평면

고차원 공간에서 차원 ''k''의 평면은 ''k''-평면이라고 하며, 선은 1-평면이라고 할 수 있다.

''엇갈린 선''의 개념을 ''d''차원 공간으로 일반화하면, ''i''-평면과 ''j''-평면은 ''i'' + ''j'' < ''d''인 경우 '''엇갈릴''' 수 있다. 3차원 공간의 꼬인 직선과 마찬가지로 엇갈린 평면은 평행하지도 않고 교차하지도 않는 평면을 말한다.

아핀 ''d''-공간에서 임의의 차원을 가진 두 평면은 평행할 수 있지만, 사영 공간에서는 평행이 존재하지 않으므로 두 평면은 교차하거나 엇갈려야 한다.

''I''를 ''i''-평면상의 점의 집합, ''J''를 ''j''-평면상의 점의 집합이라고 할 때, 사영 ''d''-공간에서 ''i'' + ''j'' ≥ ''d''이면 ''I''와 ''J''의 교집합은 (''i''+''j''−''d'')-평면을 포함해야 한다. (''0''-평면은 점이다.)

어떤 기하학에서든 ''I''와 ''J''가 ''k'' ≥ 0에 대해 ''k''-평면에서 교차하면 ''I'' ∪ ''J''의 점들은 (''i''+''j''−''k'')-평면을 결정한다.

7. 한국의 교육과정 및 사회적 맥락

7. 1. 교육과정

대한민국에서는 중학교 1학년 수학 교육과정에서 꼬인 위치를 다룬다.^[7] 이는 공간 감각을 키우는 데 중요한 역할을 한다. 대학수학능력시험에서도 꼬인 위치와 관련된 문제가 출제될 수 있다.

공간 기하학에서 "특정 두 직선 a, b가 동일 평면상에 존재하지 않는" 상태, 즉 "특정 두 직선 a, b에 의해 하나의 평면이 결정되지 않는" 상태에 있을 때, "두 직선 a, b는 꼬인 위치에 있다"라고 말한다.^[6]

꼬인 위치의 구체적인 예는 다음과 같다.

예를 들어, "삼각형 BCD를 밑면으로 하는 삼각뿔 A-BCD"의 변 AB와 변 CD는 꼬인 위치에 있다.
예를 들어, 입체 교차하는 두 노선 (두 개의 도로, 혹은 두 개의 철로, 혹은 "도로와 철로" 등)은 꼬인 위치에 있다.

꼬인 위치에 있는 두 직선 a, b의 거리란, a, b에 모두 수직인 선분의 길이를 말한다.^[6]

7. 2. 예시

8. 추가 정보

8. 1. 공간 내 두 직선의 위치 관계

8. 2. 꼬인 위치가 등장하지 않는 기하학

참조

_[1] 서적 Introduction to Geometry John Wiley & Sons
_[2] 논문 Studio della figura delle otto rette e sue applicazioni alla geometria del tetraedro ed alla teoria della configurazioni
_[3] 서적 Geometry and the Imagination Chelsea
_[4] 웹사이트 Line-Line Distance
_[5] 논문 Configurations of skew lines http://www.math.uu.s[...] 2006-10-24
_[6] 간행물 『ブリタニカ国際大百科事典小項目事典』【ねじれの位置】
_[7] 뉴스 今年､京大も阪大も｢ねじれの位置｣出題で衝撃の訳 https://toyokeizai.n[...] 東洋経済オンライン 2024-02-29

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com