정투상도

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 기하학
3. 종류
- 3.1. 다중 투영 (Multiview projection)
  - 3.1.1. 제1각법 (First-angle projection)
  - 3.1.2. 제3각법 (Third-angle projection)
- 3.2. 축측 투영 (Axonometric projection)
4. 지도 제작
참조

1. 개요

정투상도는 3차원 객체를 2차원 평면에 투영하는 방법 중 하나이다. 기하학에서 정사영은 평면 z=0으로 정의되는 행렬을 통해 표현되며, 컴퓨터 그래픽스에서는 클리핑 평면을 정의하는 6-튜플을 사용하여 정사영 변환을 수행한다. 정투상도는 시야의 각도에 따라 등각 투상도, 이등각 투상도, 삼등각 투상도로 나뉘며, 엔지니어링 도면에는 등각 투상도가 주로 사용된다. 또한 정투상도는 지도 제작에도 활용되며, 지구의 반구를 외계에서 보는 듯한 형태로 묘사한다.

더 읽어볼만한 페이지

사영기하학 - 무한원점
무한원점은 사영평면에서 z=0인 동차좌표로 표현되는 점들의 집합으로 무한원직선을 구성하며, 유클리드 기하학에는 없지만 사영기하학 등에서 평행선의 교점으로 정의되고 투영기하학에서 소실점과 관련되어 응용되지만 교육적 어려움을 야기한다는 비판도 있다.
사영기하학 - 동차좌표
동차좌표는 $(n+1)$ 개의 수로 이루어진 순서쌍 집합에서 0이 아닌 원소를 제외하고 동치관계를 정의하여 얻는 $n$ 차원 사영 공간의 좌표이며, 데카르트 좌표와 달리 단일 점을 무한히 많은 좌표로 표현하고 컴퓨터 그래픽스, 컴퓨터 비전 등에 응용된다.
유클리드 기하학 - 결정계
결정계는 결정 구조의 대칭성에 따라 7가지(삼사, 단사, 사방, 정방, 삼방, 육방, 입방)로 분류되며, 각 결정계는 고유한 대칭 요소와 점군의 대칭성을 갖는다.
유클리드 기하학 - 퐁슬레-슈타이너 정리
퐁슬레-슈타이너 정리는 자와 주어진 원(중심 포함)만 사용하여 자와 컴퍼스로 작도 가능한 모든 것을 작도할 수 있다는 기하학적 정리이다.

정투상도

2. 기하학

thumb

간단한 정사영 투영은 평면 ''z'' = 0으로 다음 행렬로 정의할 수 있다.

:

P =\begin{bmatrix}1 & 0 & 0  \\0 & 1 & 0  \\0 & 0 & 0  \\\end{bmatrix}

각 점 ''v'' = (''v''_''x'', ''v''_''y'', ''v''_''z'')에 대해 변환된 점 ''Pv''는 다음과 같다.

:

Pv =\begin{bmatrix}1 & 0 & 0  \\0 & 1 & 0  \\0 & 0 & 0  \\\end{bmatrix}\begin{bmatrix}v_x \\ v_y \\ v_z\end{bmatrix}=\begin{bmatrix}v_x \\ v_y \\ 0\end{bmatrix}

종종, 동차 좌표를 사용하는 것이 더 유용하다. 위의 변환은 동차 좌표에 대해 다음과 같이 표현될 수 있다.

:

P =\begin{bmatrix}1 & 0 & 0 & 0 \\0 & 1 & 0 & 0 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 1\end{bmatrix}

각 동차 벡터 ''v'' = (''v''_''x'', ''v''_''y'', ''v''_''z'', 1)에 대해 변환된 벡터 ''Pv''는 다음과 같다.

:

Pv =\begin{bmatrix}1 & 0 & 0 & 0 \\0 & 1 & 0 & 0 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}v_x \\ v_y \\ v_z \\ 1\end{bmatrix}=\begin{bmatrix}v_x \\ v_y \\ 0 \\ 1\end{bmatrix}

컴퓨터 그래픽스에서, 정사영 투영에 사용되는 가장 일반적인 행렬 중 하나는 6-튜플 (''left'', ''right'', ''bottom'', ''top'', ''near'', ''far'')로 정의할 수 있으며, 이는 클리핑 평면을 정의한다. 이러한 평면은 최소 모서리가 (''left'', ''bottom'', -''near'')이고 최대 모서리가 (''right'', ''top'', -''far'')인 상자를 형성한다.^[3]

상자는 중심이 원점에 오도록 평행 이동된 다음, 최소 모서리가 (−1,−1,−1)이고 최대 모서리가 (1,1,1)인 단위 입방체로 크기가 조정된다.

정사영 변환은 다음 행렬로 주어질 수 있다.

:

P =\begin{bmatrix}\frac{2}{\text{right}-\text{left}} & 0 & 0 & -\frac{\text{right}+\text{left}}{\text{right}-\text{left}} \\0 & \frac{2}{\text{top}-\text{bottom}} & 0 & -\frac{\text{top}+\text{bottom}}{\text{top}-\text{bottom}} \\0 & 0 & \frac{-2}{\text{far}-\text{near}} & -\frac{\text{far}+\text{near}}{\text{far}-\text{near}} \\0 & 0 & 0 & 1\end{bmatrix}

이는 형태의 크기 변환 ''S''와 이동 ''T''의 조합으로 주어질 수 있다.

:

P = ST =\begin{bmatrix}\frac{2}{\text{right}-\text{left}} & 0 & 0 & 0 \\0 & \frac{2}{\text{top}-\text{bottom}} & 0 & 0 \\0 & 0 & \frac{2}{\text{far}-\text{near}} & 0 \\0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0 & 0 & -\frac{\text{left}+\text{right}}{2} \\0 & 1 & 0 & -\frac{\text{top}+\text{bottom}}{2} \\0 & 0 & -1 & -\frac{\text{far}+\text{near}}{2} \\0 & 0 & 0 & 1\end{bmatrix}

투영 행렬 ''P⁻¹''의 역행렬은 역투영 행렬로 사용할 수 있으며, 다음과 같이 정의된다.

P^{-1} =\begin{bmatrix}\frac{\text{right}-\text{left}}{2} & 0 & 0 & \frac{\text{left}+\text{right}}{2} \\0 & \frac{\text{top}-\text{bottom}}{2} & 0 & \frac{\text{top}+\text{bottom}}{2} \\0 & 0 & \frac{\text{far}-\text{near}}{-2} &  -\frac{\text{far}+\text{near}}{2} \\0 & 0 & 0 & 1\end{bmatrix}

다중 투영에서는 최대 6개의 물체 그림이 생성되며, 이를 ''주 투영''이라고 하며, 각 투영 평면은 물체의 좌표축 중 하나에 평행하다. 뷰는 ''제1각법'' 또는 ''제3각법'' 투영의 두 가지 방식 중 하나에 따라 서로 상대적으로 배치된다. 각 방식에서 뷰의 모양은 물체 주위에 6면 상자를 형성하는 평면에 ''투영''된 것으로 생각할 수 있다. 6개의 서로 다른 면을 그릴 수 있지만 일반적으로 그림의 세 가지 뷰만으로도 3차원 물체를 만드는 데 충분한 정보를 제공한다. 이러한 뷰는 정면도((''입면도''라고도 함), 평면도((''평면''이라고도 함) 및 측면도((''단면''이라고도 함)로 알려져 있다. 묘사된 물체의 평면 또는 축이 투영 평면에 ''평행하지 않''고, 물체의 여러 면이 동일한 이미지에 보이는 경우 이를 ''보조 뷰''라고 한다. 따라서 등각 투영, 이등각 투영 및 삼각 투영은 다중 투영에서 ''보조 뷰''로 간주된다. 다중 투영의 일반적인 특징은 공간의 한 축이 일반적으로 수직으로 표시된다는 것이다.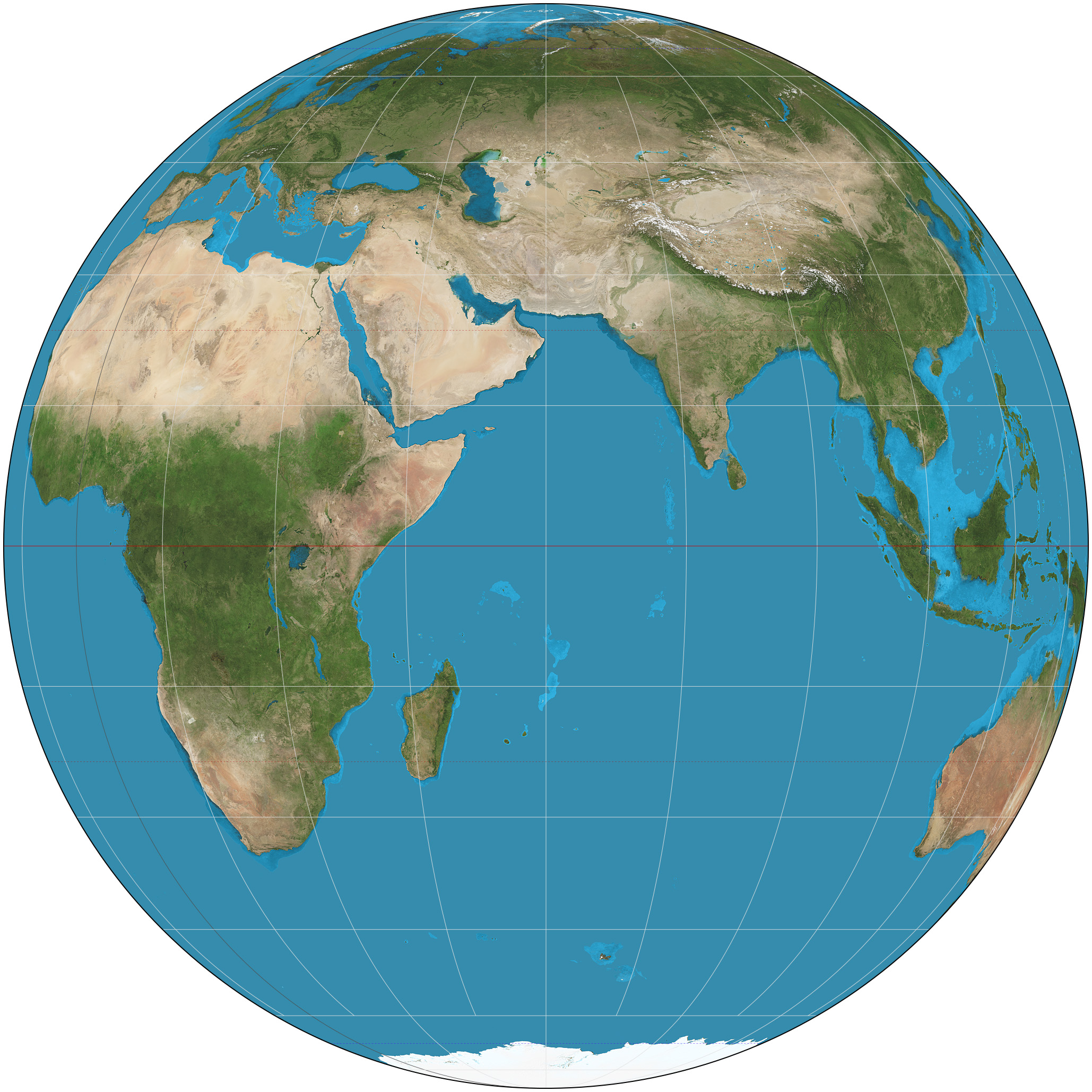

지도 제작법의 정투상도법은 지도 투영법의 한 종류이며, 지도 제작법에서 사용된다. 스테레오 투영법 및 정거 투영법과 마찬가지로, 정투상도법은 구를 접평면 또는 할선 평면에 투영하는 원근 (또는 방위) 투영법이다. 정투상도법의 '원근점'은 무한대에 있다. 이 투영법은 지구의 구의 반구를 외계에서 보이는 것처럼 묘사하며, 여기서 지평선은 대원이다. 모양과 면적은 특히 가장자리 근처에서 왜곡된다.^[6]^[7]

정투상도법은 고대부터 알려져 왔으며, 지도 제작에서의 사용이 잘 기록되어 있다. 히파르코스는 기원전 2세기에 이 투영법을 사용하여 별의 돋음과 짐을 결정했다. 기원전 14년경, 로마의 기술자 마르쿠스 비트루비우스 폴리오는 이 투영법을 사용하여 해시계를 제작하고 태양의 위치를 계산했다.^[7]

비트루비우스는 또한 이 투영법에 대해 그리스어 'orthos'("곧은")와 'graphē'("그림")에서 유래한 'orthographic'이라는 용어를 고안한 것으로 보인다. 그러나, 위도와 경도를 나타내는 해시계를 의미하는 이름인 '아날렘마'가 앤트워프의 프랑수아 다귈론이 1613년에 현재의 이름을 널리 사용하기 전까지 일반적인 이름이었다.^[7]

이 투영법으로 제작된 가장 오래된 현존하는 지도는 1509년 (익명), 1533년 및 1551년 (요하네스 쇠너), 그리고 1524년 및 1551년 (아피안)의 지구본의 목판 그림으로 나타난다.^[7]

3. 종류

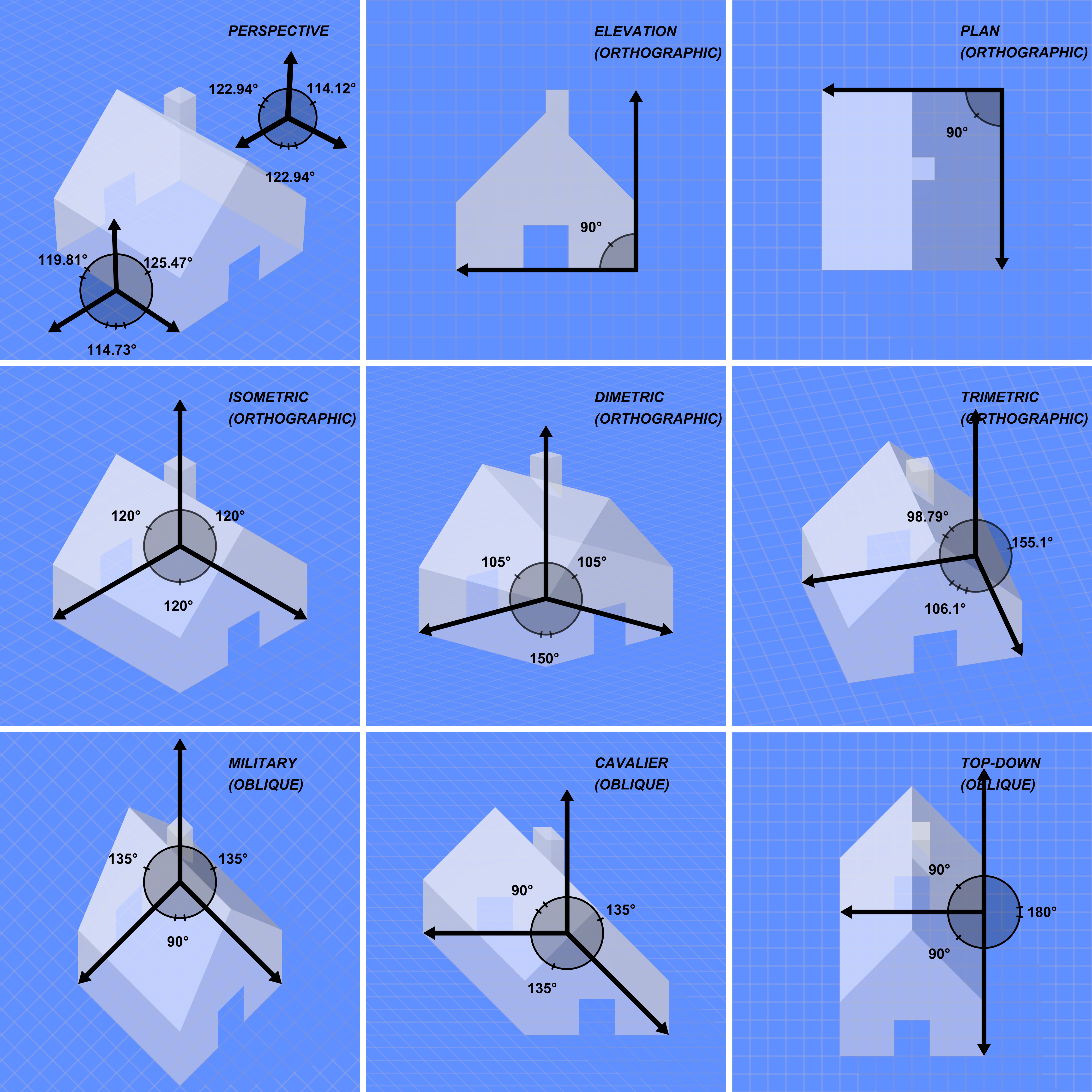
정투상도는 3차원 물체를 2차원으로 표현하는 주요 방법 중 하나로, 크게 '''다중 투영'''과 '''축측 투영''' 두 가지 방식으로 나눌 수 있다.

'''다중 투영'''은 물체를 여러 방향 (주로 정면, 평면, 측면)에서 바라본 모습을 각각 별도의 2차원 그림으로 나타내는 방식이다. 각 그림은 투영 평면에 평행한 물체의 한 면을 보여주며, 제1각법과 제3각법이라는 표준화된 배치 규칙에 따라 배열된다. 건축, 공학 등에서 물체의 정확한 치수와 형태를 전달하는 데 주로 사용된다.

'''축측 투영'''은 물체를 비스듬히 바라본 모습을 하나의 2차원 그림으로 표현하여 3차원 형태를 시각적으로 쉽게 이해하도록 돕는 방식이다. 투영 시 공간의 세 축이 얼마나 짧아져 보이는지에 따라 '''등각 투영''', '''이등각 투영''', '''삼등각 투영'''으로 세분화된다.^[2]^[4]

3. 1. 다중 투영 (Multiview projection)

'''다중 투영'''(Multiview projection|다중 투영^영어)은 정투상도 기법 중 하나로, 3차원 물체를 여러 방향에서 본 2차원 그림으로 나타내는 방식이다. 대상 물체를 90도 간격으로 회전시키거나 관찰자의 시점을 90도씩 바꾸어 가며 여러 개의 그림을 그린다. 이렇게 생성된 각 그림을 '''주 투영'''(principal view|주 투영^영어)이라고 하며, 최대 6개까지 만들 수 있다. 각 주 투영은 물체의 주요 좌표축 중 하나와 평행한 평면에 투영된 모습이다.

일반적으로 물체의 형태를 표현하는 데는 정면도(입면도), 평면도, 측면도의 세 가지 뷰만으로도 충분한 경우가 많다. 이 세 가지 뷰를 조합하여 표현하는 방식을 삼면도라고 한다. 하지만 원기둥처럼 특정 뷰가 불필요한 경우 생략하기도 하며, 제품의 의장권 등록 등 특수한 목적을 위해서는 정면도, 배면도, 좌측면도, 우측면도, 평면도, 저면도의 6면 전체를 요구하기도 한다.

다중 투영에서 각 뷰를 배치하는 방식에는 제1각법과 제3각법의 두 가지 표준이 있다. 이 두 방식은 각 뷰를 도면 상에 어떻게 배치하는지에 따라 구분된다.^[9]^[10] 어떤 방식을 사용하는지에 따라 도면 상에서 각 뷰의 상대적인 위치가 달라진다. (자세한 내용은 제1각법 및 제3각법 섹션 참조)

만약 물체의 면이나 축이 투영 평면과 평행하지 않아서 하나의 그림에 여러 면이 동시에 보이는 경우, 이를 '''보조 뷰'''(auxiliary view|보조 뷰^영어)라고 한다. 등각 투영, 이등각 투영, 삼각 투영 등이 보조 뷰에 해당하며, 다중 투영의 범주 안에서 특수한 경우로 다루어진다. 다중 투영 방식은 주로 건축, 공학, 디자인 분야에서 물체의 정확한 형태와 치수를 전달하기 위해 널리 사용된다.

3. 1. 1. 제1각법 (First-angle projection)

'''제1각법'''(第一角法, first angle projection method^영어)은 대상물의 여러 정투영을 정해진 배치로 나열한 투영도이다.^[10] 그림 이론에서는 제1사분면에 입체물을 놓고 이를 투영하는 방식으로 설명된다.

제3각법과 비교했을 때, 각 면도(평면도, 하면도, 배면도, 좌우 측면도)의 형태는 숨은 선을 포함하여 동일하다. 그러나 각 그림의 배치가 다르다. 제1각법에서는 좌측면도를 정면도의 오른쪽에 배치하고, 평면도를 정면도의 아래에 배치한다. 이는 입체의 뒤쪽에 투영면을 놓고, 앞에서 본 입체의 모습을 투영면에 그린 후, 이를 펼쳐서 배치하는 방식이다. 다른 관점에서는 투영면 위에 놓인 입체를 굴렸을 때 보이는 면을 그리는 방법이라고도 설명할 수 있다.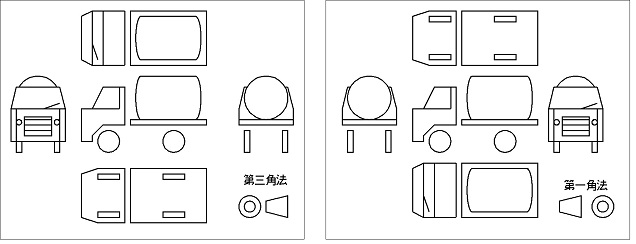

일본에서는 JIS에 따라 제3각법 사용이 규정되어 있지만, 여러 외국에서는 제1각법을 전통적으로 사용해왔으며 현재도 사용하는 국가들이 있다. 이에 따라 ISO 표준에서는 제1각법과 제3각법 두 가지 방식 모두를 인정하고 있다. 한국에서는 특히 조선 분야에서 제1각법이 많이 사용된다.

3. 1. 2. 제3각법 (Third-angle projection)

'''제3각법'''(third angle projection method^영어)은 대상물의 여러 정투상도를 정해진 배치로 배열한 투영도이다.^[9] 기하학적 이론상으로는 물체를 제3사분면에 놓고 투영하는 방식이다.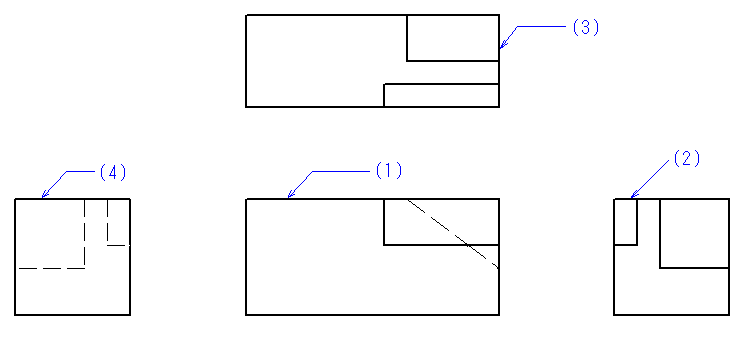

구체적인 배치 방법은 다음과 같다.

물체의 정면도(입면도) (그림 중 (1))를 중앙에 놓는다.
원칙적으로 우측면도(그림 중 (2))를 정면도의 오른쪽에 배치한다.
평면도(윗면도) (그림 중 (3))를 정면도의 위에 배치한다.
좌측면도(그림 중 (4))는 정면도의 왼쪽에, 저면도는 정면도의 아래쪽에 배치한다.
배면도는 우측면도의 오른쪽에 배치한다.

도면을 작성할 때는 제작에 필요한 만큼의 그림으로 물체의 형태를 나타내도록 규정되어 있다. 예를 들어, 위 해설도에서 좌측면도(그림 중 (4))는 물체의 형태를 이해하는 데 반드시 필요하지 않다면 생략할 수 있다. 저면도나 배면도 역시 필요에 따라 생략 가능하다.

따라서 도면을 그릴 때는 물체의 특징을 가장 잘 나타내는 면이나 가공상 중요도가 높은 면을 주투영도(주로 정면도)로 선택하고, 주투영도만으로 표현하기 어려운 부분을 다른 투영도로 보충한다. 예를 들어, 선반을 이용한 절삭 가공에서는 가공의 기준이 되는 중심선을 수평으로 하여 주투영도를 그리는 경우가 많다.

일본에서는 JIS에 따라 제3각법 사용이 규정되어 있다. 하지만 여러 외국에서는 전통적으로 제1각법을 사용해 왔으며 현재도 사용하는 나라들이 있다. 이 때문에 ISO 표준에서는 제1각법과 제3각법 두 가지 방식 모두를 인정하고 있다. 한국에서는 특히 조선 분야에서 제3각법이 많이 사용된다.

3. 2. 축측 투영 (Axonometric projection)

축측 투영은 정투상도의 한 종류로, 시야가 기준 축에 직교하는 방향에서 얼마나 벗어났는지에 따라 세 가지 하위 유형으로 나뉜다. 이들은 각각 '''등각 투상도'''(Isometric projection^eng), '''이등각 투상도'''(Dimetric projection^eng), '''삼등각 투상도'''(Trimetric projection^eng)이다.^[2]^[4] 일반적으로 축측 투상도에서는 공간의 세 축 중 하나를 수직으로 표시하는 경우가 많다.

'''등각 투상도''': 공간의 세 축이 모두 동일한 비율로 단축되어 보이며, 축 사이의 각도는 모두 120°가 된다. 기술 도면에서 가장 흔하게 사용된다.^[5]
'''이등각 투상도''': 세 축 중 두 축만 동일한 비율로 단축되어 보인다. 나머지 한 축의 단축률과 축 간 각도는 시점 방향에 따라 달라진다.
'''삼등각 투상도''': 세 축 모두 서로 다른 비율로 단축되어 보인다. 각 축의 축척과 축 간 각도가 모두 다르다. 기술 도면에서는 거의 사용되지 않는다.^[4]

3. 2. 1. 등각 투영 (Isometric projection)

'''등각 투상도'''는 기술 도면에서 가장 일반적으로 사용되는 축측 투상도 형태이다.^[5] 등각 투상도에서는 공간의 세 축이 동일하게 짧아져 보이도록 시점 방향을 정하며, 세 축 사이의 각도는 모두 120°가 된다.

이렇게 축이 짧아지는 왜곡이 균일하게 일어나기 때문에, 그려진 대상의 각 부분 길이 간의 비례 관계가 그대로 유지된다. 또한 세 축은 모두 동일한 축척을 공유하므로, 도면에서 직접 길이를 측정하기 쉽다는 장점이 있다. 더불어 120° 각도는 컴퍼스와 자 작도만으로도 비교적 쉽게 그릴 수 있다는 편리함도 있다.

3. 2. 2. 이등각 투영 (Dimetric projection)

'''이등각 투상도'''에서는 시점의 방향에 따라 공간의 세 축 중 두 축만이 동일하게 단축되어 보인다.^[2]^[4] 이 두 축에 적용되는 축척과 화면상에 표시되는 각도는 시점에 따라 결정되며 서로 동일하다. 나머지 세 번째 축의 축척은 앞선 두 축과는 다르게 별도로 결정된다.

3. 2. 3. 삼등각 투영 (Trimetric projection)

'''삼등각 투영'''은 시점 방향에 따라 공간의 세 축이 모두 서로 다른 비율로 단축되어 보이는 투영법이다. 세 축 각각의 축척과 축 사이의 각도는 시점에 따라 개별적으로 결정된다. 삼등각 투영은 기술 도면에서는 거의 사용되지 않는다.^[4]

4. 지도 제작

정투상도법 지도는 지도 투영법의 한 종류이며, 지도 제작법에서 사용된다. 스테레오 투영법 및 정거 투영법과 마찬가지로, 정투상도법은 구를 접평면 또는 할선 평면에 투영하는 원근 (또는 방위) 투영법이다. 정투상도법의 '원근점'은 무한대에 있다. 이 투영법은 지구의 구의 반구를 외계에서 보이는 것처럼 묘사하며, 여기서 지평선은 대원이다. 모양과 면적은 특히 가장자리 근처에서 왜곡된다.^[6]^[7]

정투상도법은 고대부터 알려져 왔으며, 지도 제작에서의 사용이 잘 기록되어 있다. 히파르코스는 기원전 2세기에 이 투영법을 사용하여 별의 돋음과 짐을 결정했다. 기원전 14년경, 로마의 기술자 마르쿠스 비트루비우스 폴리오는 이 투영법을 사용하여 해시계를 제작하고 태양의 위치를 계산했다.^[7]

비트루비우스는 또한 이 투영법에 대해 그리스어 'orthos'("곧은")와 'graphē'("그림")에서 유래한 'orthographic'이라는 용어를 고안한 것으로 보인다. 그러나, 위도와 경도를 나타내는 해시계를 의미하는 이름인 '아날렘마'가 앤트워프의 프랑수아 다귈론이 1613년에 현재의 이름을 널리 사용하기 전까지 일반적인 이름이었다.^[7]

이 투영법으로 제작된 가장 오래된 현존하는 지도는 1509년 (익명), 1533년 및 1551년 (요하네스 쇠너), 그리고 1524년 및 1551년 (아피안)의 지구본의 목판 그림으로 나타난다.^[7]

참조

_[1] 논문 Of Analemmas, Mean Time and the Analemmatic Sundial http://citeseerx.ist[...]
_[2] 서적 Drawing Distinctions: The Varieties of Graphic Expression https://books.google[...] Cornell University Press
_[3] 웹사이트 Graphics Programming – Cameras: Parallel Projection – Part 6, Chapter 2 https://www.mathemat[...] 2021-11-26
_[4] 서적 Advanced graphics programming using openGL https://books.google[...] Elsevier
_[5] 서적 Computer graphics https://books.google[...] Technical Publications
_[6] 서적 Map Projections—A Working Manual (US Geologic Survey Professional Paper 1395) US Government Printing Office
_[7] 서적 Flattening the Earth: Two Thousand Years of Map Projections The University of Chicago Press
_[8] 간행물 正投影法正座標面に一致又は平行な一つ以上の投影面平上に，座標面に対して平行なその主要平面に直角に置いた対象物の正投影。... orthographical representation ... 正投影図正投影法によって描いた図。 orthographical drawing JIS
_[9] 간행물 第三角法 하나의 대상물의 주투영도의 주위에, 그 대상물의 다른 다섯 개의 투영도의 일부 또는 전부를 배치하여 그리는 정투영법 .... third angle projection (method) JIS
_[10] 간행물 第一角法 하나의 대상물의 주투영도의 주위에, 그 대상물의 다른 다섯 개의 투영도의 일부 또는 전부를 배치하여 그리는 정투영법 .... first angle projection (method) JIS

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com