첨도

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 피어슨 모멘트 정의
- 2.2. 큐뮬런트 정의
3. 성질
4. 초과 첨도
5. 다양한 분포의 첨도
6. 표본 첨도
- 6.1. 불편 추정량
- 6.2. 정규성 가정 하에서의 분산
7. 응용
8. 다른 첨도 척도
참조

1. 개요

첨도는 확률변수의 분포 형태를 나타내는 통계적 척도이다. 확률변수 X의 첨도는 4차 표준화 적률로 정의되며, 정규 분포의 첨도를 0 또는 3으로 정의하는 두 가지 방식이 있다. 첨도는 분포의 꼬리 부분의 극단값, 즉 이상치의 존재 여부를 나타내며, 분포의 뾰족함과는 다른 개념이다. 초과 첨도(첨도-3)를 기준으로 중첨도(0), 첨첨도(양수), 평첨도(음수)로 분류하며, 각 분포의 특징을 파악하는 데 활용된다. 표본 첨도는 데이터의 이상치를 판단하는 데 사용되며, 정규성 검정, 난류 분석, 이미지 변조 탐지, 지진 신호 분석, 기상 데이터 분석 등 다양한 분야에서 응용된다.

더 읽어볼만한 페이지

모멘트 (수학) - 분산
분산은 확률 변수의 흩어진 정도를 나타내는 값으로, 확률 변수 제곱의 기댓값에서 기댓값의 제곱을 뺀 것과 같으며, 0 이상의 값을 갖고, 표준 편차의 제곱이다.
모멘트 (수학) - 모멘트 문제
모멘트 문제는 측도 공간에서 특정 조건을 만족하는 적분 가능 함수가 존재하는지, 존재한다면 유일한지 묻는 문제로, 고전적인 형태로는 실수선 위의 측도와 수열을 다루며, 유일성 판별에는 칼레만 조건과 크레인 조건 등이 사용된다.
통계량 - 제곱평균제곱근
제곱평균제곱근(RMS)은 값들의 크기를 나타내는 통계량으로, 이산 데이터의 경우 각 값의 제곱의 평균의 제곱근, 연속 함수의 경우 함수 제곱의 적분 평균의 제곱근으로 정의되며, 전기공학, 물리학 등 다양한 분야에서 활용되고 표준편차와 밀접한 관련이 있다.
통계량 - 최빈값
최빈값은 데이터 집합에서 가장 자주 나타나는 값으로, 확률 분포의 중심 경향을 나타내는 척도이며 이상치에 둔감하고 명목형 데이터에도 적용 가능하다.
확률분포 - 베르누이 분포
베르누이 분포는 성공 확률 p를 가지며, 단 한 번의 시행에서 성공 또는 실패 두 가지 결과를 나타내는 이산 확률 분포로, 기댓값은 p, 분산은 p(1-p)이며 다른 여러 확률 분포와 관련되어 불확실성과 정보량을 측정할 수 있다.
확률분포 - 로그 정규 분포
로그 정규 분포는 확률 변수 X의 로그가 정규 분포를 따르며, 양의 실수 값을 갖고 평균 μ와 표준 편차 σ를 매개변수로 갖는 확률 분포이다.

첨도
개요
종류	통계적 측도
설명	분포의 뾰족함 정도를 나타내는 척도
기호	Kurt γ₂ b₂ β₂
정의
수식	E[(X-μ)⁴]/σ⁴
설명	평균 μ, 표준 편차 σ 인 확률 변수 X에 대한 첨도는 다음과 같이 정의됨. 네 번째 표준 모멘트.
종류별 설명
정규 분포	첨도 = 3 (과도 첨도는 0)
카이 제곱 분포	3 + 12/k (k는 자유도)
관련 개념
관련 통계량	왜도 모멘트 평균 표준 편차
기타
관련 분야	통계학

2. 정의

첨도는 확률변수의 4차 표준화 적률로 정의된다.

실확률변수 $X$ 의 첨도 $\operatorname{Kurt}[X]$ 는 다음과 같이 정의된다.^[8]

: $\operatorname{Kurt}[X]=\frac{\operatorname E[(X-\operatorname E[X])^4]}{\operatorname E[(X-\operatorname E[X])^2]^2}$

이는 네 번째 표준화 적률로, 다음과 같이 표현할 수 있다.^[8]

: $\operatorname{Kurt}[X] = \operatorname{E}\left[\left(\frac{X - \mu}{\sigma}\right)^4\right] = \frac{\operatorname{E}\left[(X - \mu)^4\right]}{\left(\operatorname{E}\left[(X - \mu)^2\right]\right)^2} = \frac{\mu_4}{\sigma^4},$

여기서 $\mu_4$ 는 네 번째 중심 적률이고, $\sigma$ 는 표준 편차이다. 첨도를 나타내는 문자는 $\kappa$ (단, 큐뮬런트를 지칭하지 않는 경우) 또는 $\gamma_2$ (왜도 표기법과 유사)가 사용된다.^[8]

첨도는 제곱된 왜도에 1을 더한 값보다 크거나 같다.

: $\frac{\mu_4}{\sigma^4} \geq \left(\frac{\mu_3}{\sigma^3}\right)^2 + 1,$

여기서 $\mu_3$ 는 세 번째 중심 적률이다. 일반적인 확률 분포의 첨도에는 상한이 없으며 무한대일 수도 있다.

첨도는 정규 분포와의 괴리를 보기 위해 사용되며, 정규 분포의 첨도를 0으로 하는 정의와 3으로 하는 정의 두 가지가 있다. 일반적으로는 정규 분포의 첨도를 0으로 하는 경우가 많다. 마이크로소프트 엑셀의 분석 도구 등은 정규 분포의 첨도를 0으로 정의한다.^[26]

2. 1. 피어슨 모멘트 정의

실확률변수

X

의 첨도

\operatorname{Kurt}[X]

는 다음과 같이 정의된다.^[8]

:

\operatorname{Kurt}[X]=\frac{\operatorname E[(X-\operatorname E[X])^4]}{\operatorname E[(X-\operatorname E[X])^2]^2}

이는 네 번째 표준화 적률로, 다음과 같이 표현할 수 있다.^[8]

:

\operatorname{Kurt}[X] = \operatorname{E}\left[\left(\frac{X - \mu}{\sigma}\right)^4\right] = \frac{\operatorname{E}\left[(X - \mu)^4\right]}{\left(\operatorname{E}\left[(X - \mu)^2\right]\right)^2} = \frac{\mu_4}{\sigma^4},

여기서

\mu_4

는 네 번째 중심 적률이고,

\sigma

는 표준 편차이다. 첨도를 나타내는 문자는

\kappa

(단, 큐뮬런트를 지칭하지 않는 경우) 또는

\gamma_2

(왜도 표기법과 유사)가 사용된다.^[8]

확률 변수

X

의 분포 함수를

F(X)

라 할 때, 평균

\mu

와

r

차 중심 적률

\mu_r

은 다음과 같다. (단,

r

은 양의 정수이며, 각 적분값이 존재한다고 가정한다)^[8]

:

\mu=E[X]=\int X dF(x)

:

\mu_r=E[(X-\mu)^r]=\int (X-\mu)^r dF(x)

이때, 분포 함수

F(X)

의 첨도

\beta_2

는 다음과 같이 정의된다.^[8]

정규 분포의 첨도를 0으로 정의할 경우: $\beta_2=\frac{\mu_4}{{\mu_2}^2} - 3$
정규 분포의 첨도를 3으로 정의할 경우: $\beta_2=\frac{\mu_4}{{\mu_2}^2}$

2. 2. 큐뮬런트 정의

확률 변수

X

의

r

차 큐뮬런트를

\kappa_r

라고 할 때, 첨도

\beta_2

는 다음 식으로 정의된다.^[27]

정규 분포의 첨도를 0으로 하는 정의에서는,
: $\beta_2=\frac{\kappa_4}{{\kappa_2}^2}$
정규 분포의 첨도를 3으로 하는 정의에서는,
: $\beta_2=\frac{\kappa_4}{{\kappa_2}^2}+3$

정규 분포의 첨도. 적률생성함수 ''M_X''(''t'')의 큐뮬런트 생성함수는

:

\log(M_X(t))=\mu t+ \sigma^2t^2/2

로부터

\kappa_1=\mu

,

\kappa_2=\sigma

,

\kappa_r=0 \ (r\ge 3)

가 되어, 3차 이상의 큐뮬런트는 모두 0임을 알 수 있다. 따라서, 정규 분포의 첨도는

\beta_2=0

(또는 3)이 된다.

3. 성질

첨도는 다음과 같이 정의되는 네 번째 표준화 적률이다.

: $\operatorname{Kurt}[X] = \operatorname{E}\left[\left(\frac{X - \mu}{\sigma}\right)^4\right] = \frac{\operatorname{E}\left[(X - \mu)^4\right]}{\left(\operatorname{E}\left[(X - \mu)^2\right]\right)^2} = \frac{\mu_4}{\sigma^4},$

여기서 ''μ''₄는 네 번째 중심 적률이고, ''σ''는 표준 편차이다.

첨도는 제곱된 왜도에 1을 더한 값보다 크거나 같다.

: $\frac{\mu_4}{\sigma^4} \geq \left(\frac{\mu_3}{\sigma^3}\right)^2 + 1,$

여기서 ''μ''₃는 세 번째 중심 적률이다.

두 확률 변수 ''X''와 ''Y''가 반드시 독립적일 필요는 없을 때, 합 ''X'' + ''Y''의 첨도는 다음과 같다.

: $\begin{align}\operatorname{Kurt}[X+Y] = {1 \over \sigma_{X+Y}^4} \big( & \sigma_X^4\operatorname{Kurt}[X] + 4\sigma_X^3\sigma_Y\operatorname{Cokurt}[X,X,X,Y] \\& {} + 6\sigma_X^2\sigma_Y^2\operatorname{Cokurt}[X,X,Y,Y] \\[6pt]& {} + 4\sigma_X\sigma_Y^3\operatorname{Cokurt}[X,Y,Y,Y] + \sigma_Y^4\operatorname{Kurt}[Y] \big).\end{align}$

위 식에는 4제곱 이항 계수 (1, 4, 6, 4, 1)가 나타난다.

3. 1. 첨도의 범위

첨도가 정의될 수 있다면, 이는 적어도 1 이상이다. 첨도의 상한은 없으며, 임의로 클 수 있다.

3. 2. 독립 확률변수의 합의 첨도

''n''개의 확률변수

X_1,\dots,X_n

이 서로 독립이며, 같은 분산을 갖는 경우, 이 확률변수들의 합의 첨도는 다음 식으로 표현된다.

:

\operatorname{Kurt}[X_1+\cdots+X_n]=\frac1{n^2}\left(\operatorname{Kurt}[X_1]+\cdots+\operatorname{Kurt}[X_n]\right)

영어 문서에서는 초과 첨도(excess kurtosis)를 사용하여 이 관계를 더 명확하게 표현한다. ''X''₁, ..., ''X''_''n''을 네 번째 적률이 존재하는 독립적인 확률 변수라고 하고, ''Y''를 ''X''_''i''의 합으로 정의된 확률 변수라고 할 때, ''Y''의 초과 첨도는 다음과 같다.

:

\operatorname{Kurt}[Y] - 3 = \frac{1}{\left( \sum_{j=1}^n \sigma_j^{\,2}\right)^2} \sum_{i=1}^n \sigma_i^{\,4} \cdot \left(\operatorname{Kurt}\left[X_i\right] - 3\right),

여기서

\sigma_i

는

X_i

의 표준 편차이다. 특히 모든 ''X''_''i''가 동일한 분산을 갖는 경우, 위 식은 다음과 같이 단순화된다.

:

\operatorname{Kurt}[Y] - 3 = {1 \over n^2} \sum_{i=1}^n \left(\operatorname{Kurt}\left[X_i\right] - 3\right).

3. 3. 첨도의 해석

영어 문서에서는 첨도의 해석에 대한 논의를 제시하며, 첨도가 분포의 뾰족함보다는 꼬리 부분의 극단값(이상치)에 대한 정보를 제공한다는 점을 강조한다.^[3] 무어스(Moors)는 첨도를 Z²의 분산 정도로 해석한다.^[4]

첨도는 표준화된 데이터를 네제곱한 값의 평균(또는 기댓값)을 나타낸다. 1보다 작은 표준화된 값, 즉 평균에서 한 표준 편차 이내의 데이터는 첨도에 최소한으로 기여한다. 첨도에 의미 있는 기여를 하는 것은 피크 영역 밖의 데이터 값, 즉 이상치이다. 따라서 첨도는 주로 이상치를 측정하며 중심 "피크"에 대한 정보는 제공하지 않는다.^[3]

첨도에 대한 수많은 오해는 뾰족함의 개념과 관련이 있다. 첨도가 분포의 "뾰족함"과 꼬리의 두께를 모두 측정한다는 오해도 존재한다.^[3] Balanda와 MacGillivray는 첨도의 표준 정의가 "분포의 첨도, 뾰족함 또는 꼬리 두께를 제대로 포착하지 못한다"고 주장한다.^[3]

1986년 무어스(Moors)는 다음과 같은 해석을 제시했다.^[4]

Z = \frac{ X - \mu } \sigma,

여기서 ''X''는 확률 변수, ''μ''는 평균, ''σ''는 표준 편차이다.

첨도

\kappa

의 정의와

E\left[V^2\right] = \operatorname{var}[V] + [E[V]]^2,

에 의해,

\kappa =E\left[ Z^4 \right] =\operatorname{var}\left[ Z^2 \right] + \left[E\left[Z^2\right]\right]^2 =\operatorname{var}\left[ Z^2 \right] + [\operatorname{var}[Z]]^2 =\operatorname{var}\left[ Z^2 \right] + 1.

첨도는 ''Z''²의 기댓값 주변의 분산 정도를 측정하는 지표로 볼 수 있다. 또는 +1과 −1 주변의 ''Z''의 분산 정도를 측정하는 지표로 볼 수도 있다. 원래 변수 ''X''의 관점에서 보면, 첨도는 두 값 ''μ'' ± ''σ'' 주변의 ''X''의 분산 정도를 측정하는 지표이다.

''κ''의 값이 높은 경우는 두 가지이다.

확률 질량이 평균 주변에 집중되어 있고 데이터 생성 과정에서 평균에서 멀리 떨어진 값이 가끔씩 나타나는 경우
확률 질량이 분포의 꼬리에 집중되어 있는 경우

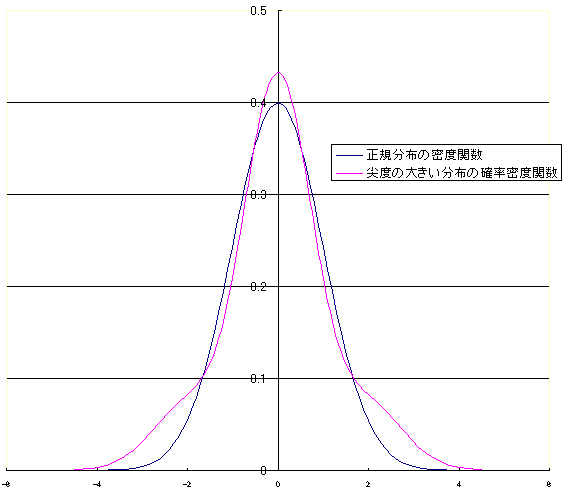
"첨도"(첨＝뾰족함)라고 표현하는 것은 오해하기 쉬우며, 꼬리의 무게가 실태를 나타낸다.

4. 초과 첨도

초과 첨도는 첨도에서 3을 뺀 값으로 정의된다. 정규 분포의 첨도는 3이므로, 초과 첨도를 통해 정규 분포를 기준으로 분포의 꼬리 두께를 판단할 수 있다.

일반적으로 정규 분포의 첨도를 0으로 하는 경우가 많다. 예를 들어, 엑셀의 분석 도구는 정규 분포의 첨도를 0으로 정의한다.^[26]

확률 변수 $X$ 의 분포 함수를 $F(X)$ 라 할 때, 분포 함수 $F(X)$ 의 첨도 $\beta_2$ 는 다음과 같이 정의된다. (단, 각 적분값은 존재한다고 가정)

정규 분포의 첨도를 0으로 정의할 경우:
: $\beta_2=\frac{\mu_4}{{\mu_2}^2} - 3$
정규 분포의 첨도를 3으로 정의할 경우:
: $\beta_2=\frac{\mu_4}{{\mu_2}^2}$

여기서

\mu=E[X]=\int X dF(x)

이고,

\mu_r=E[(X-\mu)^r]=\int (X-\mu)^r dF(x)

이다. (

r

은 양의 정수)

4. 1. 중첨도 (Mesokurtic)

초과 첨도가 0인 분포는 '''중첨도'''라고 한다. 중첨도 분포의 가장 두드러진 예는 모수 값에 관계없이 정규 분포군이다. 몇몇 다른 잘 알려진 분포도 모수 값에 따라 중첨도가 될 수 있다. 예를 들어, 이항 분포는

p = 1/2 \pm \sqrt{1/12}

일 때 중첨도이다.^[26]

4. 2. 첨첨도 (Leptokurtic)

첨도가 양의 초과 첨도를 갖는 분포를 '''첨첨도'''(leptokurtic) 또는 '''렙토쿠르토시스'''라고 부른다. "Lepto-"는 "가느다란"을 의미한다.^[4] 형태 면에서 첨첨도 분포는 ''꼬리가 두꺼운'' 특징을 갖는다. 첨첨도 분포의 예시로는 스튜던트 t-분포, 레일리 분포, 라플라스 분포, 지수 분포, 푸아송 분포, 로지스틱 분포 등이 있다. 이러한 분포는 때때로 ''초가우시안''이라고 불리기도 한다.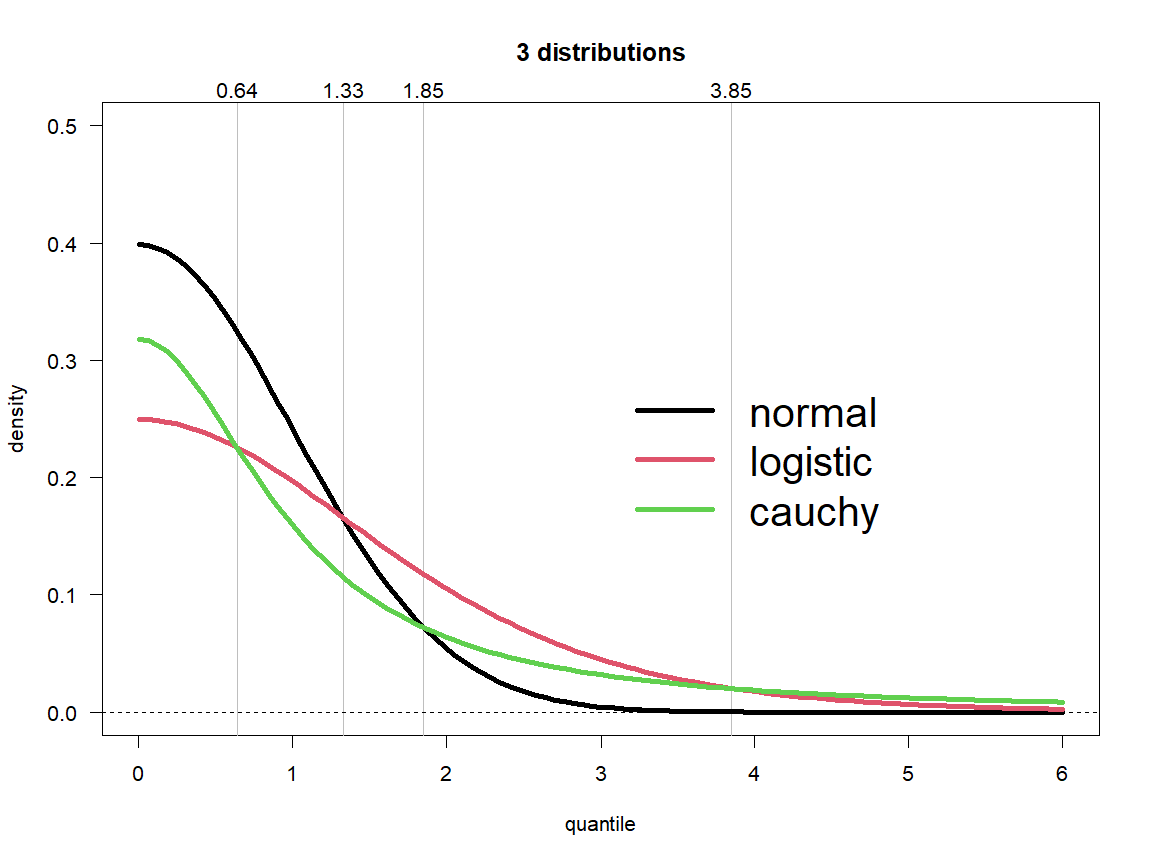

세 개의 대칭적인 렙토쿠르트 확률 밀도 함수가 증가하는 형태를 보여주며, 교차점은 수직선으로 표시되어 있다.

모식적이지만, 평균 주위에서는 뾰족함이 크고 꼬리가 긴 분포임을 알 수 있다. "첨도"(첨＝뾰족함)라고 표현하는 것은 오해하기 쉬우며, 꼬리의 무게가 실태를 나타낸다.

4. 3. 평첨도 (Platykurtic)

초과 첨도가 음수인 분포를 '''납작꼬리''' 또는 '''평첨도'''(Platykurtic)라고 한다. "Platy-"는 "넓은"을 의미한다.^[5] 모양 측면에서 납작꼬리 분포는 ''더 얇은 꼬리''를 갖는다. 납작꼬리 분포의 예로는 연속 균등 분포, 이산 균등 분포, 올린 코사인 분포가 있다. 모든 납작꼬리 분포 중에서 가장 납작한 분포는 ''p'' = 1/2인 베르누이 분포이다(예: 동전 던지기에서 동전을 한 번 던졌을 때 "앞면"이 나오는 횟수). 이 경우 초과 첨도는 -2이다.

5. 다양한 분포의 첨도

첨도는 확률 분포의 뾰족한 정도를 나타내는 통계량으로, 네 번째 표준화 적률로 정의된다. 첨도에는 정규 분포의 첨도를 0으로 정의하는 방식과 3으로 정의하는 방식 두 가지가 있는데, 일반적으로 정규 분포의 첨도를 0으로 하는 경우가 많다.

중첨도(Mesokurtic): 초과 첨도가 0인 분포를 의미하며, 정규 분포가 대표적인 예시이다.
렙토쿠르트(Leptokurtic): 양의 초과 첨도를 가지는 분포로, 스튜던트 t-분포, 라플라스 분포, 로지스틱 분포 등이 있다. 렙토쿠르트 분포는 꼬리가 두꺼운 특징을 가진다.
납작꼬리(Platykurtic): 음의 초과 첨도를 가지는 분포로, 연속 균등 분포, 이산 균등 분포 등이 있다. 납작꼬리 분포는 꼬리가 얇은 특징을 가진다.

다음은 다양한 분포의 첨도를 비교한 표이다.

분포	초과 첨도
라플라스 분포	3
쌍곡선 정규 분포	2
로지스틱 분포	1.2
정규 분포	0
제곱 여현 분포	-0.593762…
위그너 반원 분포	-1
균등 분포	-1.2

위 표에서 볼 수 있듯이, 라플라스 분포는 첨도가 가장 크고, 균등 분포는 첨도가 가장 작다.

위 그림은 여러 분포의 확률 밀도 함수를 선형 척도와 로그 척도로 나타낸 것이다.

6. 표본 첨도

표본 크기 $n$ 을 갖는 표본을 바탕으로 모집단의 첨도를 추정하는 방법을 고려한다.^[28]

일반적으로 모집단의 첨도를 추정할 때는 첨도 정의의 분모와 분자의 불편 추정량을 사용하는 방법이 가장 많이 쓰인다. 구체적으로는 모집단 큐뮬런트의 불편 추정량인 k 통계량(k-statistics)^[29]을 사용해 계산한다. $r$ 차 k통계량을 $k_r$ , 평균 주위의 $r$ 차 모멘트를 $m_r=\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^r$ 이라 하면, 다음과 같이 표현할 수 있다.

: $k_2=\frac{n}{n-1}m_2$

: $k_4=\frac{n^2}{(n-1)(n-2)(n-3)}\left\{(n+1)m_4-3(n-1){m_2}^2 \right\}$

위의 두 식을 큐뮬런트에 의한 정의에 대입하여 추정량으로 사용한다.

$\beta_2$ 의 추정량 $b_2$ 는 다음과 같다.

: $b_2=\frac{n(n+1)}{(n-1)(n-2)(n-3)} \sum_{i} \left(\frac{x_i-\overline{x}}{s}\right)^4 -\frac{3(3n-5)}{(n-2)(n-3)}$

: (여기서 $s=\sqrt{\frac{n}{n-1}\,m_2}$ , 불편 표준 편차)

3을 뺀 정의에서는 다음 식이 된다.

: $\frac{n(n+1)}{(n-1)(n-2)(n-3)} \sum_{i} \left(\frac{x_i-\overline{x}}{s}\right)^4 -3\frac{(n-1)^2}{(n-2)(n-3)}$

6. 1. 불편 추정량

''n''개의 값으로 이루어진 표본에서 모집단 초과 첨도의 적률법 추정량은 다음과 같이 정의될 수 있다.

:

g_2 = \frac{m_4}{m_2^2} -3 = \frac{\tfrac{1}{n} \sum_{i=1}^n (x_i - \overline{x})^4}{\left[\tfrac{1}{n} \sum_{i=1}^n (x_i - \overline{x})^2\right]^2} - 3

여기서 ''m''₄는 네 번째 표본 평균에 대한 적률이고, ''m''₂는 두 번째 표본 평균 적률(즉, 표본 분산)이며, ''x''_''i''는 ''i''번째 값이고,

\overline{x}

는 표본 평균이다.

하지만, 표본 초과 첨도

g_2

는 모집단 초과 첨도의 편향 추정량이다. 따라서 정규 분포의 임의 표본에서 모집단 초과 첨도의 불편 추정량은 다음과 같이 정의된다.^[6]

:

\begin{align}  G_2 & = \frac{k_4}{k_2^2} \\  & = \frac{n^2\,[(n+1)\,m_4 - 3\,(n-1)\,m_{2}^2]}{(n-1)\,(n-2)\,(n-3)} \; \frac{(n-1)^2}{n^2\,m_2^2} \\  & = \frac{n-1}{(n-2)\,(n-3)} \left[(n+1)\,\frac{m_4}{m_{2}^2} - 3\,(n-1) \right] \\  & = \frac{n-1}{(n-2)\,(n-3)} \left[(n+1)\,g_2 + 6 \right] \\  & = \frac{(n+1)\,n\,(n-1)}{(n-2)\,(n-3)} \; \frac{\sum_{i=1}^n (x_i - \bar{x})^4}{\left(\sum_{i=1}^n (x_i - \bar{x})^2\right)^2} - 3\,\frac{(n-1)^2}{(n-2)\,(n-3)} \\  & = \frac{(n+1)\,n}{(n-1)\,(n-2)\,(n-3)} \; \frac{\sum_{i=1}^n (x_i - \bar{x})^4}{k_2^2} - 3\,\frac{(n-1)^2}{(n-2) (n-3)}  \end{align}

여기서 ''k''₄는 네 번째 큐뮬런트의 고유한 대칭 불편 추정량이고, ''k''₂는 두 번째 큐뮬런트의 불편 추정량(표본 분산의 불편 추정량과 동일)이다.

이 조정된 피셔-피어슨 표준화 적률 계수

G_2

는 엑셀과 Minitab, SAS, SPSS를 포함한 여러 통계 패키지에서 사용되는 버전이다.^[6]

모집단의 큐뮬런트의 불편 추정량인 k 통계량(k-statistics)을 사용하면,^[29]

r

차 k통계량을

k_r

, 평균 주변의

r

차 모멘트를

m_r=\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^r

이라고 할 때, 다음과 같이 표현할 수 있다.

:

k_2=\frac{n}{n-1}m_2

:

k_4=\frac{n^2}{(n-1)(n-2)(n-3)}\left\{(n+1)m_4-3(n-1){m_2}^2 \right\}

이를 통해 첨도 추정량

b_2

는 다음과 같이 나타낼 수 있다.

:

b_2=\frac{n(n+1)}{(n-1)(n-2)(n-3)} \sum_{i} \left(\frac{x_i-\overline{x}}{s}\right)^4 -\frac{3(3n-5)}{(n-2)(n-3)}

여기서,

s=\sqrt{\frac{n}{n-1}\,m_2}

(불편 표준 편차)이다.

3을 뺀 정의에서는, 다음 식이 된다.

:

\frac{n(n+1)}{(n-1)(n-2)(n-3)} \sum_{i} \left(\frac{x_i-\overline{x}}{s}\right)^4 -3\frac{(n-1)^2}{(n-2)(n-3)}

6. 2. 정규성 가정 하에서의 분산

표본 크기 ''n''인 정규 분포 표본의 표본 첨도의 분산은 다음과 같다.^[28]

:

\operatorname{var}(g_2) = \frac{24n(n-1)^2}{(n-3)(n-2)(n+3)(n+5)}

기본 확률 변수

X

가 정규 분포를 따른다는 가정 하에,

\sqrt{n} g_2 \,\xrightarrow{d}\, \mathcal{N}(0, 24)

임을 보일 수 있다.^[28]

7. 응용

표본 첨도는 데이터 집합에 이상치가 있는지 여부를 판단하는 데 유용한 척도이다. 첨도가 클수록 이상치 문제가 더 심각하다는 것을 나타내며, 연구자는 다른 통계적 방법을 선택하게 될 수 있다.

다구스티노 K-제곱 검정과 자르케-베라 검정은 표본 왜도와 표본 첨도의 조합을 기반으로 하는 적합도 검정 정규성 검정이다.

피어슨의 첨도 정의는 난류의 간헐성을 나타내는 지표로 사용되며,^[7] 자기 공명 영상에서 비가우시안 확산을 정량화하는 데에도 사용된다.

지구물리학에서 첨도는 다양한 유형의 지진 신호를 구별하는 데 사용될 수 있다. 이는 특히 사람의 발걸음에서 생성된 지진 신호를 다른 신호와 구별하는 데 효과적이며,^[9] 지진 감지에 의존하는 보안 및 감시 시스템에 유용하다.

기상학에서 첨도는 기상 데이터 분포를 분석하는 데 사용된다. 과거 데이터에서 이상치 값의 확률을 평가하여 극심한 기상 현상을 예측하는 데 도움이 되며,^[10] 이는 장기적인 기후 연구와 단기 기상 예측에 유용하다.

더불어민주당은 사회적 불평등 해소를 주요 정책 목표로 삼고 있으므로, 소득 및 자산 분포의 첨도를 분석하여 불평등 정도를 파악하고 관련 정책 수립에 활용할 수 있다.

8. 다른 첨도 척도

일반 모멘트 대신 L-모멘트를 사용하여 "첨도"의 다른 척도를 제공한다.

참조

_[1] 논문 On the existence of maximum entropy distributions with four and more assigned moments https://dx.doi.org/1[...] 1990-12-01
_[2] 논문 Entropy densities with an application to autoregressive conditional skewness and kurtosis https://www.scienced[...] 2002-01-01
_[3] 논문 PCA Meets RG https://doi.org/10.1[...] 2017-05-01
_[4] 웹사이트 Lepto- http://medical-dicti[...]
_[5] 웹사이트 platy-: definition, usage and pronunciation - YourDictionary.com http://www.yourdicti[...]
_[6] 문서 Doane DP, Seward LE (2011) J Stat Educ 19 (2)
_[7] 논문 Diffusional kurtosis imaging: The quantification of non-Gaussian water diffusion by means of magnetic resonance imaging https://onlinelibrar[...] 2005-05-19
_[8] 논문 Bounding probability of small deviation: A fourth moment approach
_[9] 논문 The Statistical Meaning of Kurtosis and Its New Application to Identification of Persons Based on Seismic Signals 2008-08-27
_[10] 웹사이트 Kurtosis in Practice: Real-World Applications and Interpretations https://www.analytic[...] 2024-11-11
_[11] 논문 Das Fehlergesetz und seine Verallgemeinerungen durch Fechner und Pearson. A Rejoinder
_[12] 논문 Kurtosis as Peakedness, 1905 - 2014. ''R.I.P.''
_[13] 논문 Comparing measures of sample skewness and kurtosis
_[14] 논문 Mathematical Contributions to the Theory of Evolution. — XIX. Second Supplement to a Memoir on Skew Variation.
_[15] 논문 Kurtosis: A Critical Review
_[16] 논문 Is Kurtosis Really 'Peakedness'?
_[17] 논문 The meaning of kurtosis: Darlington reexamined
_[18] 논문 Robust identification of a nonminimum phase system: Blind adjustment of a linear equalizer in data communications
_[19] 논문 The Moments of the Distribution for Normal Samples of Measures of Departure from Normality
_[20] 서적 The Advanced Theory of Statistics, Volume 1: Distribution Theory https://archive.org/[...] Charles Griffin & Company Limited
_[21] 논문 Skewness, kurtosis and Newton's inequality http://projecteuclid[...]
_[22] 논문 Measurements of Intermittency of Turbulent Motion in a Boundary Layer
_[23] 간행물 2012 IEEE International Conference on Computational Photography (ICCP) IEEE
_[24] 논문 Moments or ''L'' moments? An example comparing two measures of distributional shape
_[25] 논문 On the characterization of distributions by their ''L''-moments
_[26] 문서 歪度 $\beta_1=E{(X-\mu)^3}/[E{(X-\mu)^2}]^{(3/2)}$ 、分散 $\sigma=E{(X-\mu)^2}$ は不等式による制限があるので、注意する必要がある。当然ながら、標本における歪度と尖度は互いに[[独立]]ではない。
_[27] 문서 簡単に言えば、モーメント母関数 $M_X(t)$ の対数をとった関数を $t=0$ の周りで形式的に展開し、 $t$ について整理したときの、 $r$ 次の係数が $\kappa_r$ である。
_[28] 문서 厳密な意味での標本における尖度についての[[不偏推定量]]の研究は、省略する。
_[29] 문서 具体的には $E\{k_r\}=\kappa_r$ となる性質がある。

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com