초기하 분포

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

초기하 분포는 N개의 요소 중 K개의 성공 상태를 가진 모집단에서 n개의 요소를 비복원 추출했을 때 k개의 성공 상태가 포함될 확률을 나타내는 이산 확률 분포이다. 확률 질량 함수를 통해 확률을 계산하며, N이 커지면 이항 분포에, K/N이 작고 추출 횟수 n이 클 때는 푸아송 분포에 가까워진다. 기댓값, 분산, 최빈값, 대칭성 등의 성질을 가지며, 비복원 추출, 텍사스 홀덤 포커, 키노, 피셔의 정확 검정, 선거 감사, 품질 관리, 생태학적 개체 수 추정 등 다양한 분야에 응용된다.

더 읽어볼만한 페이지

이산분포 - 푸아송 분포
푸아송 분포는 주어진 시간 안에 특정 사건이 일어날 횟수를 나타내는 이산 확률 분포이며, 사건 발생 횟수가 많고 각 사건이 드문 시스템에 적용되고 이항 분포의 극한 사례로 볼 수 있다.
이산분포 - 베르누이 시행
베르누이 시행은 '성공' 또는 '실패' 두 가지 결과만 존재하는 독립적인 시행을 반복하는 실험으로, 각 시행의 성공 확률 $p$ 와 실패 확률 $q$ 의 합은 1이며, 확률 변수와 이항 분포, 음이항 분포, 포아송 분포 등 다른 확률 분포와 관련된다.

초기하 분포
분포 정보
이름	초기하 분포
종류	이산 확률 분포
모수	N ∈ {0, 1, 2, ...} K ∈ {0, 1, 2, ..., N} n ∈ {0, 1, 2, ..., N}
지지 집합	{max(0, n+K-N), ..., min(n, K)}
확률 질량 함수	(K choose k) * (N-K choose n-k) / (N choose n)
누적 분포 함수	확률 질량 함수의 합
평균	n * K / N
중앙값	해당 없음
분산	n * (K / N) * ((N - K) / N) * ((N - n) / (N - 1))
왜도	((N - 2K) * (N - 1)^(1/2) * (N - 2n)) / (n * K * (N - K) * (N - n) * (N - 2))^(1/2)
첨도	복잡한 표현식
모멘트 생성 함수	복잡한 표현식
관련 분포
관련 분포	N이 무한대로 갈 때 이항 분포로 수렴 n=1일 때 베르누이 분포로 수렴

2. 정의

초기하 분포는 ''N''개의 요소 중 ''K''개의 성공 상태를 가진 모집단에서 ''n''개의 요소를 비복원 추출했을 때 ''k''개의 성공 상태가 포함될 확률을 나타내는 이산 확률 분포의 일종이다.

초기하 분포는 ''N''이 커지면 이항 분포에 가까워진다. 또한 K/N^영어가 작고 추출 횟수 ''n''이 클 때 푸아송 분포에 가까워진다.

속성이 1 ≤ ''i'' ≤ ''c''^영어인 요소를 ''K''_''i''개 포함하는 ''N'' = ''K''₁ + … + ''K''_''c''^영어개의 요소로 이루어진 모집단에서 ''n''개의 요소를 비복원 추출했을 때, 속성이 ''i''인 요소를 ''k''_''i''개 포함할 확률을 주는 분포를 '''다변량 초기하 분포'''라고 한다. 초기하 분포와 다변량 초기하 분포의 관계는 이항 분포와 다항 분포의 관계에 해당한다.

2. 1. 확률 질량 함수

확률 변수

X

가 초기하 분포를 따를 때,

X = k

(n번의 추출에서 k번 성공)일 확률은 다음과 같은 확률 질량 함수(pmf)로 주어진다.^[1]

:

p_X(k) = \Pr(X = k)= \frac{\binom{K}{k} \binom{N - K}{n-k}}{\binom{N}{n}},

여기서

$N$ 은 모집단 크기,
$K$ 는 모집단 내 성공 상태의 수,
$n$ 은 추출 횟수 (각 시행에서 추출된 수량),
$k$ 는 관찰된 성공 횟수,
$\textstyle {a \choose b}$ 는 이항 계수이다.

확률 질량 함수는

\max(0, n+K-N) \leq k \leq \min(K,n)

일 때 양수이다.

이 공식은 조합론의 반데르몽드 항등식에 의해 다음과 같이 나타낼 수 있다.

:

\sum_{0\leq k\leq \textrm{min}(n,K)} { {K \choose k} { N-K \choose n-k} \over {N \choose n} }= 1,

또한, 다음과 같이 표현할 수 있다.

:

=;

3. 성질

초기하 분포는 다음과 같은 성질을 가진다.

최빈값: $\left\lfloor \frac{(n+1)(K+1)}{N+2} \right\rfloor$
대칭성:
$f_X (k;N,K,n) = f_X (k;N,n,K)$
$f_X (k;N,K,n) = f_X (n-k;N,N-K,n)$
$f_X (k;N,K,n) = f_X (K-k;N,K,N-n)$
꼬리 경계: $X \sim \operatorname{Hypergeometric}(N,K,n)$ 이고 $p=K/N$ 일 때, $0 < t < K/N$ 범위에서 다음 경계가 성립한다.^[3]
$\Pr[X\le (p - t)n] \le e^{-n\text{D}(p-t\parallel p)} \le e^{-2t^2n}$
$\Pr[X\ge (p+t)n] \le e^{-n\text{D}(p+t\parallel p)} \le e^{-2t^2n}$
여기서 $D(a\parallel b)=a\log\frac{a}{b}+(1-a)\log\frac{1-a}{1-b}$ 는 쿨백-라이블러 발산이며, $D(a\parallel b) \ge 2(a-b)^2$ 가 사용된다.^[4]
''n''이 ''N''/2보다 크면, 대칭성을 적용해 경계를 "반전"하는 것이 유용할 수 있으며, 다음을 얻는다.^[4]^[5]
$\Pr[X\le (p - t)n] \le e^{-(N-n)\text{D}(p+\tfrac{tn}{N-n}||p)} \le e^{-2 t^2 n \tfrac{n}{N-n}}$
$\Pr[X\ge (p+t)n] \le e^{-(N-n)\text{D}(p-\tfrac{tn}{N-n}||p)} \le e^{-2 t^2 n \tfrac{n}{N-n}}$

다변량 초기하 분포를 따르는 확률 변수를 (''X'''')}}라고 하면, 다음과 같은 성질을 갖는다.

확률 질량 함수: $\operatorname{P} (X_1 =k_1 ,\dots ,X_c =k_c )=\frac{1}{\binom{N}{n}} \prod_{i=1}^c \binom{K_i}{k_i}$
공분산: $\operatorname{Cov} [X_i ,X_j ]=-\frac{(N-n)nK_i K_j}{(N-1)N^2}$

3. 1. 기댓값

:

E(X)=n \cdot \frac{K}{N}

3. 2. 분산

\operatorname{Var} (X)=n \cdot \frac{K}{N} \cdot \frac{N-K}{N} \cdot \frac{N-n}{N-1}

3. 3. 최빈값

초기하 분포의 최빈값은

\left\lfloor \frac{(n+1)(K+1)}{N+2} \right\rfloor

이다.

3. 4. 대칭성

초기하 분포는 다음과 같은 대칭성을 갖는다.

:

=;

이 항등식은 이항 계수를 팩토리얼로 표현하고 후자를 재정렬하여 나타낼 수 있다. 또한, 두 가지 다르게 표현되지만 상호 교환 가능한 방식으로 설명되는 문제의 대칭성에서 따른다.

예를 들어, 복원하지 않고 두 라운드의 추첨을 생각해 볼 수 있다. 첫 번째 라운드에서 *N*개의 중립 구슬 중 *K*개를 복원하지 않고 항아리에서 꺼내 녹색으로 칠한다. 그런 다음 색칠된 구슬을 다시 넣는다. 두 번째 라운드에서 *n*개의 구슬을 복원하지 않고 꺼내 빨간색으로 칠한다. 그런 다음 두 가지 색상이 모두 있는 구슬의 수(즉, 두 번 추첨된 구슬의 수)는 초기하 분포를 갖는다. *K*와 *n*의 대칭성은 두 라운드가 독립적이라는 사실에서 비롯되며, 먼저 *n*개의 공을 꺼내 빨간색으로 칠하는 것으로 시작할 수 있다.

이러한 대칭성은 다음과 같이 요약할 수 있다.

녹색 구슬과 빨간 구슬의 역할 바꾸기:

:

f(k;N,K,n) = f(n-k;N,N-K,n)

뽑힌 구슬과 뽑히지 않은 구슬의 역할 바꾸기:

:

f(k;N,K,n) = f(K-k;N,K,N-n)

녹색 구슬과 뽑힌 구슬의 역할 바꾸기:

:

f(k;N,K,n) = f(k;N,n,K)

이러한 대칭은 이산면체군

D_4

를 생성한다.

3. 5. 꼬리 경계

X \sim \operatorname{Hypergeometric}(N,K,n)

이고

p=K/N

일 때,

0 < t < K/N

범위에서 다음 경계가 성립한다.^[3]

:

\begin{align}\Pr[X\le (p - t)n]&\le e^{-n\text{D}(p-t\parallel p)} \le e^{-2t^2n}\\\Pr[X\ge (p+t)n]&\le e^{-n\text{D}(p+t\parallel p)} \le e^{-2t^2n}\\\end{align}\!

여기서

:

D(a\parallel b)=a\log\frac{a}{b}+(1-a)\log\frac{1-a}{1-b}

는 쿨백-라이블러 발산이며,

D(a\parallel b) \ge 2(a-b)^2

가 사용된다.^[4]

위 경계를 유도하기 위해

X = \frac{\sum_{i=1}^n Y_i}{n}

임을 관찰하는데, 여기서

Y_i

는 특정 분포

D

를 따르는 종속 확률 변수이다. 확률 변수 합에 대한 경계 관련 정리 대부분은 독립 시퀀스에 대한 것이므로, 먼저 동일한 분포

D

를 따르는 독립 확률 변수

Z_i

시퀀스를 생성하고

X' = \frac{\sum_{i=1}^{n}Z_i}{n}

에 정리를 적용한다. 이후 이 과정으로 얻은 결과와 경계가

X

에도 적용됨이 호프딩(Hoeffding)에 의해 증명되었다.^[3]

''n''이 ''N''/2보다 크면, 대칭성을 적용해 경계를 "반전"하는 것이 유용할 수 있으며, 다음을 얻는다.^[4]^[5]

:

\begin{align}\Pr[X\le (p - t)n]&\le e^{-(N-n)\text{D}(p+\tfrac{tn}{N-n}||p)} \le e^{-2 t^2 n \tfrac{n}{N-n}}\\\\\Pr[X\ge (p+t)n]&\le e^{-(N-n)\text{D}(p-\tfrac{tn}{N-n}||p)} \le e^{-2 t^2 n \tfrac{n}{N-n}}\\\end{align}\!

4. 예시

예를 들어, 빨간 공 10개와 흰 공 20개가 섞여 총 30개의 공이 들어있는 항아리에서 5개의 공을 꺼낼 때, 빨간 공이 정확히 1개일 확률은 다음과 같다.

: $\frac{\binom{10}{1} \binom{30-10}{5-1}}{\binom{30}{5}} =\frac{8075}{23751} \approx 0.34$

빨간 공 개수의 기댓값은 다음과 같다.

: $\frac{5\times 10}{30} \approx 1.67$

검은 구슬 5개, 흰 구슬 10개, 빨간 구슬 15개가 있는 항아리에서 6개의 구슬을 꺼낼 때, 각 색깔별로 2개씩 꺼낼 확률은 다음과 같다.

: $\frac{\binom{5}{2} \binom{10}{2} \binom{15}{2}}{\binom{30}{6}} \approx 0.0796$

4. 1. 항아리 문제

초기하 분포의 고전적인 적용 사례는 '''비복원 추출'''이다. 예를 들어 빨간색과 녹색 구슬 두 가지 색깔이 섞여 있는 구슬 단지를 생각해 볼 수 있다. 녹색 구슬을 뽑는 것을 성공, 빨간색 구슬을 뽑는 것을 실패라고 정의한다. 이때, ''N''을 '''단지 안의 모든 구슬'''의 수, ''K''를 '''녹색 구슬'''의 수라고 하면, ''N'' − ''K''는 '''빨간색 구슬'''의 수가 된다.

이제 구슬 단지에서 눈을 감고 비복원 추출로 n개의 구슬을 뽑는다고 가정하자. ''X''를 실험에서 뽑힌 녹색 구슬의 수인 ''k''를 결과로 갖는 확률 변수라고 정의하면, 이 상황은 다음 분할표로 나타낼 수 있다.

	뽑힘	안 뽑힘	합계
녹색 구슬	k	K − k	K
빨간색 구슬	n − k	N + k − n − K	N − K
합계	n	N − n	N

예를 들어 단지 안에 '''5'''개의 녹색 구슬과 '''45'''개의 빨간색 구슬이 있고, 비복원 추출로 '''10'''개의 구슬을 뽑는다고 가정하자. 이때 정확히 '''10'''개 중 '''4'''개가 녹색일 확률은 다음과 같이 계산할 수 있다.

	뽑힘	안 뽑힘	합계
녹색 구슬	k = 4	K − k = 1	K = 5
빨간색 구슬	n − k = 6	N + k − n − K = 39	N − K = 45
합계	n = 10	N − n = 40	N = 50

'''총 N번의 추출 중 정확히 n번의 추출에서 k개의 녹색 구슬을 뽑을''' 확률은 다음 공식을 사용하여 계산한다.

:

5개의 녹색 구슬을 모두 뽑을 확률은 다음과 같이 4개를 뽑을 확률보다 약 35배 낮다.

:

다른 예로, 빨간 공 10개와 흰 공 20개가 들어있는 항아리에서 5개의 공을 꺼낼 때, 빨간 공이 정확히 1개일 확률은 다음과 같다.

이때 빨간 공 개수의 기댓값은 다음과 같다.

또 다른 예로, 검은 구슬 5개, 흰 구슬 10개, 빨간 구슬 15개가 있는 항아리에서 6개의 구슬을 꺼낼 때, 각 색깔별로 2개씩 꺼낼 확률은 다음과 같이 계산할 수 있다.

:

4. 2. 텍사스 홀덤 포커

텍사스 홀덤 포커에서 플레이어는 손에 든 두 장의 카드와 테이블에 공개된 5장의 카드(커뮤니티 카드)를 조합하여 가능한 최고의 패를 만든다. 카드 덱은 52장이며 각 무늬는 13장이다.

이 예시에서는 플레이어가 손에 클럽 2장을 가지고 있고, 테이블에 클럽 2장을 포함한 3장의 카드가 공개되어 있다고 가정한다. 플레이어는 다음 2장의 카드 중 한 장이 클럽이 나와 플러시를 완성할 확률을 알고 싶어한다. (이 예시에서 계산된 확률은 다른 플레이어의 손에 있는 카드에 대한 정보가 없다고 가정한다. 그러나 경험이 많은 포커 플레이어는 각 시나리오의 확률을 고려할 때 다른 플레이어의 베팅(체크, 콜, 레이즈 또는 폴드) 방식을 고려할 수 있다. 엄밀히 말해, 여기에 설명된 성공 확률 계산 방식은 테이블에 한 명의 플레이어만 있는 시나리오에서 정확하다. 멀티플레이어 게임에서는 상대방의 베팅 플레이에 따라 이 확률이 다소 조정될 수 있다.)

클럽 4장이 공개되었으므로 아직 보이지 않은 클럽은 9장이다. 5장의 카드(손에 2장, 테이블에 3장)가 공개되었으므로 아직 보이지 않은 카드는 47장이다.

다음 두 장의 카드 중 한 장이 클럽일 확률, 다음 두 장의 카드 모두 클럽일 확률, 다음 두 장의 카드 중 클럽이 없을 확률은 각각 초기하 분포를 사용하여 계산할 수 있다.

경우	초기하 분포 변수	확률
다음 두 장의 카드 중 한 장이 클럽일 확률	$k=1, n=2, K=9$ 및 $N=47$	약 31.64%
다음 두 장의 카드 모두 클럽일 확률	$k=2, n=2, K=9$ 및 $N=47$	약 3.33%
다음 두 장의 카드 중 클럽이 없을 확률	$k=0, n=2, K=9$ 및 $N=47$	약 65.03%

4. 3. 키노(Keno)

키노는 80개의 번호가 매겨진 공이 들어 있는 용기에서 무작위로 20개의 공을 뽑는 게임으로, 미국식 빙고와 유사하다. 각 추첨 전에 플레이어는 1에서 80까지의 숫자 중 원하는 만큼 숫자를 선택한다. 예를 들어, 6개의 숫자를 선택하는 것을 "6-스폿을 플레이"한다고 한다. 20개의 공이 추첨된 후, 플레이어가 선택한 숫자와 일치하는 공("히트")의 개수에 따라 상금을 받는다. 일반적으로 "히트"가 많을수록 지급액이 커진다.^[1]

예를 들어, 6-스폿에 1달러를 베팅하고 6개 중 4개를 맞히면 카지노는 보통 4달러를 지급한다. 이 확률은 다음과 같이 계산된다.^[1]

:

마찬가지로, 6개 중 5개를 맞힐 확률은 다음과 같다.^[1]

:

6개를 모두 맞힐 확률은 약 0.000128985 (7752 대 1)이며, 이 경우 지급액은 약 1500USD이다. 3개의 숫자를 맞히면 베팅한 금액과 동일한 1달러를 받으며, 이 확률은 약 0.129819548이다.^[1]

각 지급액과 해당 확률을 곱한 값의 합계를 구하면 6-스폿의 예상 수익률은 약 71%가 되고, 카지노의 이점은 29%가 된다. 다른 스폿 게임도 비슷한 예상 수익률을 보인다. 이러한 낮은 수익률은 게임 운영에 필요한 큰 간접비(바닥 공간, 장비, 인력) 때문으로 설명된다.^[1]

5. 관련 분포

$X \sim \operatorname{Hypergeometric}(N, K, n)$ 이고 $p = K/N$ 이라고 하자.

$n=1$ 이면, $X$ 는 베르누이 분포(파라미터 $p$ )를 따른다.
$N$ 과 $K$ 가 $n$ 에 비해 크고, $p$ 가 0 또는 1에 가깝지 않다면, $X$ 는 이항 분포(파라미터 $n$ 과 $p$ )와 유사한 분포를 갖는다. ( $P(X \le k) \approx P(Y \le k)$ ).
만약 $n$ 이 크고, $N$ 과 $K$ 가 $n$ 에 비해 크며, $p$ 가 0 또는 1에 가깝지 않다면,

:

P(X \le k) \approx \Phi \left( \frac{k-n p}{\sqrt{n p (1-p)}} \right)

여기서

\Phi

는 표준 정규 분포 함수이다.

녹색 또는 빨간색 구슬을 뽑을 확률이 같지 않다면 (예: 녹색 구슬이 빨간색 구슬보다 크거나 잡기 쉽기 때문), $X$ 는 비중심 초 기하 분포를 따른다.
베타-이항 분포는 초기하 분포에 대한 켤레 사전 분포이다.

다음 표는 일련의 추출에서 성공 횟수와 관련된 네 가지 분포를 설명한다.

	복원 추출	비복원 추출
주어진 추출 횟수	이항 분포	초기하 분포
주어진 실패 횟수	음이항 분포	음의 초 기하 분포

5. 1. 이항 분포

Y

가 매개변수

n

과

p

를 갖는 이항 분포를 따른다고 가정하면, 이는 복원 추출을 통해 이루어지는 유사한 표본 추출 문제에서 성공 횟수를 모델링한다.^[1] 모집단 크기

N

과 모집단 내 성공 상태의 수

K

가 표본 크기

n

에 비해 크고, 성공 확률

p=K/N

가 0 또는 1에 가깝지 않다면, 초기하 분포를 따르는 확률 변수

X

와

Y

는 유사한 분포를 가지며,

P(X \le k) \approx P(Y \le k)

이다.^[1]

다음 표는 일련의 추출에서 성공 횟수와 관련된 네 가지 분포를 설명한다.

	복원 추출	비복원 추출
주어진 추출 횟수	이항 분포	초기하 분포
주어진 실패 횟수	음이항 분포	음의 초 기하 분포

5. 2. 푸아송 분포

Poisson distribution|푸아송 분포^영어는 성공 확률

\frac{K}{N}

이 작고 추출 횟수

n

이 클 때 초기하 분포가 근사하는 분포이다.

5. 3. 다변량 초기하 분포

모집단이 3개 이상의 범주로 구성될 때, 초기하 분포를 확장할 수 있는데, 이를 다변량 초기하 분포라고 한다. 다변량 초기하 분포는 각 범주에서 추출되는 요소의 수를 고려한다.^[8]

항아리 모델에서 구슬의 색상이 2가지 이상인 경우로 확장할 수 있다. 항아리에 색상 ''i''의 구슬이 ''K''_''i''개 있고, 무작위로 비복원 추출을 통해 ''n''개의 구슬을 꺼낼 경우, 표본에서 각 색상의 구슬 수 (''k''₁, ''k''₂,..., ''k''_''c'')는 다변량 초기하 분포를 따른다.

:

\Pr(X_1 = k_1, \ldots, X_c = k_c) = \frac{\prod\limits_{i=1}^c \binom{K_i}{k_i}}{\binom{N}{n}}

이 분포는 초기하 분포가 이항 분포와 갖는 관계와 동일한 관계를 다항 분포와 갖는다. 즉, 다항 분포는 "복원 추출" 분포이고 다변량 초기하는 "비복원 추출" 분포이다.^[8]

이 분포의 특성은 ''c''는 서로 다른 색상의 수이고,

N=\sum_{i=1}^c K_i

는 항아리 안에 있는 구슬의 총 개수일 때 다음과 같다.

특성	값
확률 질량 함수	$\operatorname{P} (X_1 =k_1 ,\dots ,X_c =k_c )=\frac{1}{\binom{N}{n}} \prod_{i=1}^c \binom{K_i}{k_i}$
기댓값	$E[X_i ]=\frac{nK_i}{N}$
분산	$\operatorname{Var} [X_i ]=\frac{(N-n)n(N-K_i )K_i}{(N-1)N^2}$
공분산	$\operatorname{Cov} [X_i ,X_j ]=-\frac{(N-n)nK_i K_j}{(N-1)N^2}$

예를 들어 항아리에 검은 구슬 5개, 흰 구슬 10개, 빨간 구슬 15개가 들어있다고 가정하고 비복원 추출로 6개의 구슬을 뽑을 때, 각 색깔별로 정확히 2개씩 뽑힐 확률은 다음과 같다.

: $\frac{\binom{5}{2} \binom{10}{2} \binom{15}{2}}{\binom{30}{6}} \approx 0.0796$

6. 응용

초기하 분포는 모집단에서 비복원 추출을 할 때 특정 속성을 가진 표본이 나올 확률을 계산하는 데 사용된다. 항아리에서 구슬을 꺼내는 문제를 예로 들 수 있다. N개의 구슬 중 K개가 녹색이고 나머지가 빨간색일 때, n개를 비복원 추출하여 k개의 녹색 구슬을 얻을 확률은 다음과 같다.^[6]

: $P(X=k) = f(k;N,K,n) = .$

이 확률은 가설 검정에서 사용되는 p값과는 다르다. p값을 구하려면 실제 관측값보다 극단적인 경우도 고려해야 한다. 또한, 각 시행에서 성공 확률이 일정하지 않기 때문에 이항 분포로 정확하게 모델링할 수 없다.
사분할표 예시초기하 분포 문제는 사분할표를 사용하여 나타낼 수 있다. N, n, K가 고정되면 주변 빈도수는 모두 고정되며, O11을 확정하면 나머지 값들도 확정된다. O11=X=k라고 하면, 사분할표의 모든 값이 결정된다.

	녹색 구슬(성공)	빨간색 구슬(실패)	Row Total
항아리에서 꺼낸 것	O11=k	O12=n − k	n
항아리에 남은 것	O21=K − k	O22=N + k − n − K	N − n
Column Total	K	N − K	N

N=50, K=5, n=10인 경우를 생각해보자. k=4이면, P(X=4)는 다음과 같다.

: $P(X=4) = f(4;50,5,10) = = {5\cdot 8145060\over 10272278170} = 0.003964583\dots.$

이때 사분할표는 다음과 같다.

	녹색 구슬(성공)	빨간색 구슬(실패)	Row Total
항아리에서 꺼낸 것	4	6	10
항아리에 남은 것	1	39	40
Column Total	5	45	50

k=5인 경우, P(X=5)는 다음과 같다.

: $P(X=5) = f(5;50,5,10) = = {1\cdot 1221759\over 10272278170} = 0.0001189375\dots,$

녹색 구슬이 5개 나올 확률은 4개 나올 확률보다 약 35배 낮다.

6. 1. 피셔의 정확 검정

피셔의 정확 검정과 동일한 초기하 분포 기반 검정(초기하 검정)은, 표본에서 어떤 하위 집단이 과다 또는 과소 대표되는지 식별하는 데 자주 사용된다.^[6]

이 검정은 2x2 분할표에서 두 범주형 변수 간의 연관성을 검정하는 데 사용된다. 예를 들어, 마케팅 그룹은 알려진 고객 집합을 검사하여 다양한 인구 통계학적 하위 그룹이 과다 대표되는지 확인하고 고객 기반을 이해하는 데 초기하 검정을 사용할 수 있다.

초기하 p-값은 모집단에서 무작위로

n

번 추출하여

k

번 또는 그 이상 성공할 확률로 계산된다. 과소 표현에 대한 검정에서 p-값은 무작위로

k

번 또는 그 미만의 성공을 추출할 확률이다. 양측 피셔의 정확 검정의 p-값은 두 개의 적절한 초기하 검정의 합으로 계산할 수 있다.^[7]

사분할표에 대한 독립성 검정과 비교하기 위해 이 문제를 사분할표로 표현할 수 있다. N, m, n이 고정되면 주변 빈도수 (제3열 및 제3행의 값)는 모두 고정되며, O11을 확정하면 나머지 O12, O21, O12가 확정된다. O11=X=k라고 하면, 사분할표의 값이 모두 확정된다.

	녹색 구슬(성공)	빨간색 구슬(실패)	Row Total
항아리에서 꺼낸 것	O11=k	O12=n − k	n
항아리에 남은 것	O21=K − k	O22=N + k − n − K	N − n
Column Total	K	N − K	N

6. 2. 선거 감사 (한국 사례)

선거 감사는 기계로 집계된 투표 결과와 수작업 재검표 결과가 일치하는지 확인하기 위해 투표구 표본을 검사한다. 불일치가 발생하면 보고서를 발행하거나 더 큰 규모의 재검표를 진행한다. 일반적으로 법률에 따라 표본 크기가 정해지는데, $N$개의 투표구에서 $Hack$개의 투표구에 해킹이나 버그와 같은 문제가 발생했을 때 이를 놓칠 확률은 초기하 분포를 통해 계산할 수 있다.^[9]^[10]^[11]

예를 들어, 100개의 투표구 중 5개에 문제가 있는 경우, 3% 표본(3개 투표구)을 추출하여 검사했을 때 문제가 발견되지 않을 확률(k=0일 확률)은 86%이다. 반면, 문제가 표본에 나타날 확률(k>0)은 14%에 불과하다.

:

\begin{align}\operatorname{\boldsymbol\mathcal P}\{\ X = 0\ \} & = \frac{\ \left[\ \binom{100-5}{3}\ \right]\ }{\ \left[\ \binom{100}{3}\ \right]\ } = \frac{\ \left[\ \frac{(100-5)!}{(100-5-3)!}\ \right]\ }{\left[\ \frac{100!}{(100-3)!}\ \right]} = \frac{\ \left[\ \frac{95!}{92!}\ \right]\ }{\ \left[\ \frac{100!}{97!}\ \right]\ } = \frac{\ 95\times94\times93\ }{100\times99\times98} = 86\%\end{align}

표본에서 문제를 발견할 확률을 95% 이상(k=0일 확률 5% 미만)으로 높이려면 45개의 투표구를 표본으로 추출해야 한다.

:

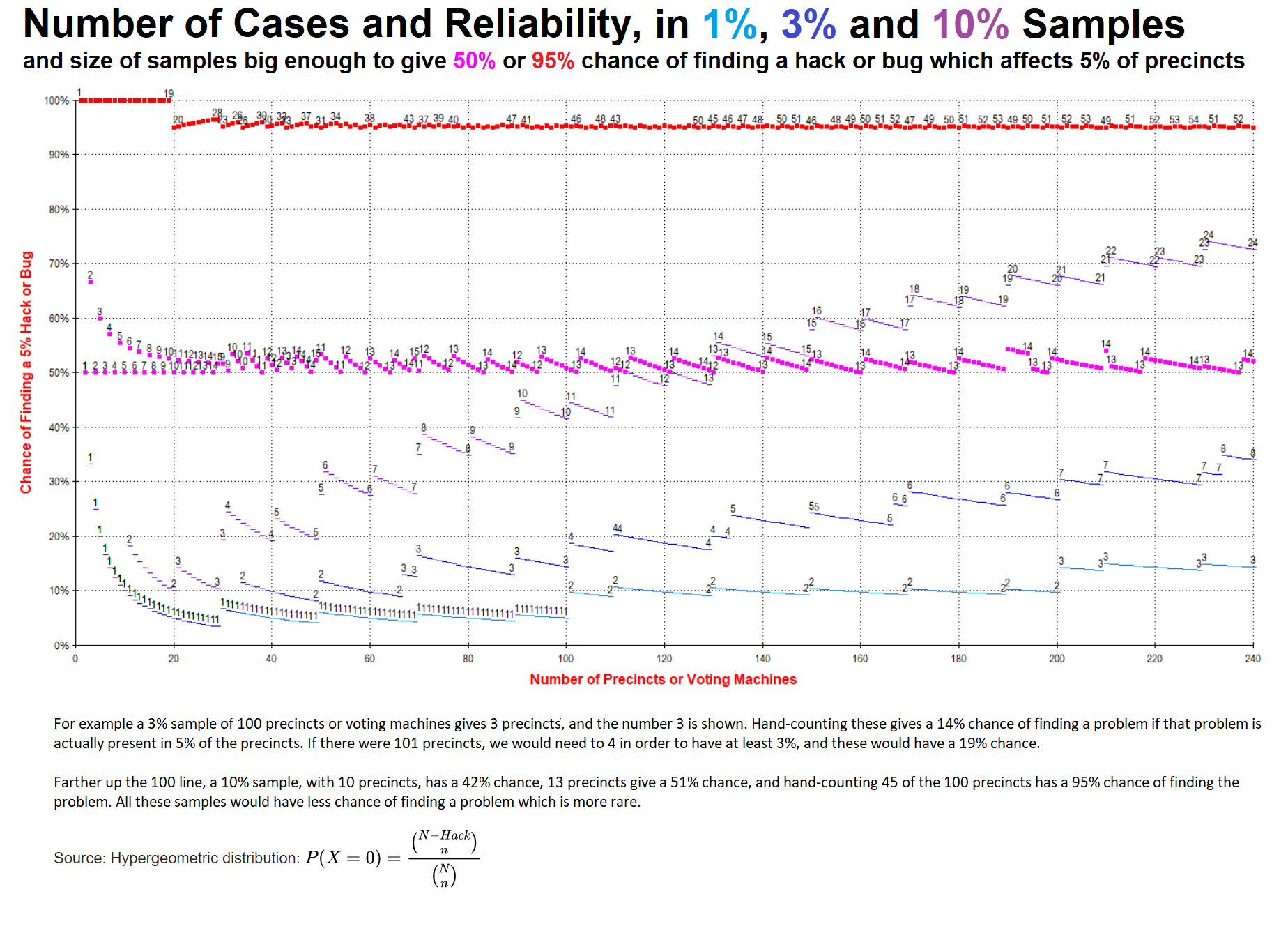
\operatorname{\boldsymbol\mathcal P}\{\ X = 0\ \} =  \frac{\ \left[\ \binom{100-5}{45}\ \right]\ }{\left[\  \binom{100}{45}\ \right]} = \frac{\ 55\times 54\times 53\times 52\times 51\ }{\ 100\times 99\times 98\times 97\times 96\ } = 4.6\% ~.

참조

_[1] 서적 Mathematical Statistics and Data Analysis Duxbury Press
_[2] URL http://www.stat.yale[...] 2022-03
_[3] 간행물 Probability inequalities for sums of bounded random variables http://repository.li[...]
_[4] 웹사이트 Another Tail of the Hypergeometric Distribution https://ahlenotes.wo[...] 2015-12-08
_[5] 간행물 Probability inequalities for the sum in sampling without replacement
_[6] 학술지 Enrichment or depletion of a GO category within a class of genes: which test? https://hal-espci.ar[...]
_[7] 웹사이트 Calculation for Fisher's Exact Test: An interactive calculation tool for Fisher's exact probability test for 2 x 2 tables (interactive page) http://quantpsy.org/[...]
_[8] 학술지 Better understanding of the multivariate hypergeometric distribution with implications in design-based survey sampling 2021
_[9] white paper Start spreading the news: New York's post-election audit has major flaws https://papers.ssrn.[...] Elsevier 2020-02-10
_[10] 웹사이트 State audit laws https://www.verified[...] 2017-02-10
_[11] 웹사이트 Post-election audits http://www.ncsl.org/[...] National Conference of State Legislatures
_[12] 문서 二項分布は超幾何分布の定義における「非復元抽出」を「復元抽出」に置き換えたものに相当する。

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com