쿨백-라이블러 발산
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
쿨백-라이블러 발산(KL 발산)은 두 확률 분포의 차이를 측정하는 비대칭적인 척도로, 정보 이론, 통계학, 기계 학습 등 다양한 분야에서 활용된다. 이 척도는 두 확률 분포 P와 Q 간의 차이를 나타내며, Q에서 P로의 발산으로 표현된다. 이산 확률 변수와 연속 확률 변수의 경우, 적분 또는 합을 통해 정의되며, 확률 측도를 이용한 일반적인 정의도 존재한다. 쿨백-라이블러 발산은 항상 0 이상의 값을 가지며, P와 Q가 동일할 때만 0이 된다. 이 발산은 부호화, 추론, 베이즈 추론, 최우추정, 사노프 정리 등 다양한 관점에서 해석될 수 있으며, 정보 이론의 여러 다른 개념들과 밀접한 관련을 맺고 있다. 또한, 쿨백-라이블러 발산은 모델과 현실 간의 관계를 평가하고 모델의 학습 정도를 파악하는 데 사용될 수 있으며, 제프리스 발산, 젠센-섀넌 발산 등과 같은 대칭 발산과 다른 확률 거리 측정과도 관련이 있다.
더 읽어볼만한 페이지
- 정보 엔트로피 - 최대 엔트로피 원리
최대 엔트로피 원리는 주어진 제약 조건에서 정보 엔트로피를 최대화하는 확률 분포를 선택하는 원리로, 불완전한 정보나 불확실성 하에서 시스템의 확률 분포를 추정하거나 최적의 결정을 내리는 데 활용되며 다양한 분야에 응용된다. - 정보 엔트로피 - 교차 엔트로피
교차 엔트로피는 동일한 이벤트 공간에서 정의된 두 확률 분포 간의 차이를 측정하는 척도로, 한 확률 분포 p에 대해 다른 확률 분포 q를 사용하여 특정 사건을 식별하는 데 필요한 평균 비트 수를 나타내며, 기계 학습에서 손실 함수를 정의하고 분류 문제에서 모델 성능 평가 및 개선에 활용된다. - 통계 이론 - 로지스틱 회귀
로지스틱 회귀는 범주형 종속 변수를 다루는 회귀 분석 기법으로, 특히 이항 종속 변수에 널리 사용되며, 오즈에 로짓 변환을 적용하여 결과값이 0과 1 사이의 값을 가지도록 하는 일반화 선형 모형의 특수한 경우이다. - 통계 이론 - 정보 엔트로피
정보 엔트로피는 확률 변수의 불확실성을 측정하는 방법으로, 사건 발생 가능성이 낮을수록 정보량이 커진다는 원리에 기반하며, 데이터 압축, 생물다양성 측정, 암호화 등 다양한 분야에서 활용된다.
| 쿨백-라이블러 발산 | |
|---|---|
| 개요 | |
| 이름 | 쿨백-라이블러 발산 |
| 다른 이름 | 정보 획득 (information gain) 상대 엔트로피 (relative entropy) 정보 발산 (information divergence) |
| 분야 | 확률론, 정보 이론 |
| 정의 | |
| 확률 분포 | P (실제 분포) Q (근사 분포) |
| 이산 확률 변수 | D(P||Q) = Σ P(i) log(P(i) / Q(i)) |
| 연속 확률 변수 | D(P||Q) = ∫ p(x) log(p(x) / q(x)) dx |
| 성질 | |
| 비대칭성 | D(P||Q) ≠ D(Q||P) |
| 음이 아닌 값 | D(P||Q) ≥ 0 |
| 최소값 | P = Q 일 때 0 |
| 활용 | |
| 통계적 추론 | 모델 간의 차이 측정 |
| 기계 학습 | 손실 함수, 특징 선택 |
| 신경 과학 | 신경 코딩의 효율성 측정 |
| 관련 개념 | |
| 교차 엔트로피 | P와 Q의 교차 엔트로피 |
| 정보 엔트로피 | 확률 변수의 불확실성 측정 |
| 참고 문헌 | |
| 참고 문헌 | Csiszar, I. (1975). I-Divergence Geometry of Probability Distributions and Minimization Problems. Ann. Probab., 3(1), 146–158. Kullback, S., & Leibler, R. A. (1951). On information and sufficiency. Annals of Mathematical Statistics, 22(1), 79–86. |
2. 정의
쿨백-라이블러 발산은 두 확률분포의 차이를 나타내는 척도이다. 일반적으로 P는 실제 데이터 분포를, Q는 이론적 분포, 모델, 또는 P의 근사치를 나타낸다. 쿨백-라이블러 발산은 Q에 최적화된 코드를 사용하여 P의 샘플을 인코딩할 때 추가로 필요한 평균 비트 수를 나타낸다.[4]
두 확률변수에 대한 확률분포 P, Q가 있을 때, 쿨백-라이블러 발산은 다음과 같이 정의된다.
- 이산확률변수의 경우:
:
- 연속확률변수의 경우:
:
여기에서 p, q는 두 확률분포의 확률 밀도 함수를 의미한다.
일반적으로, 측도를 사용하여 더 일반적인 표현을 사용할 수 있다. 두 확률측도 P, Q가 있고 Q가 P에 대해 절대수렴할 경우, 두 분포의 쿨백-라이블러 발산은 다음과 같이 정의된다.
:
여기에서 는 라돈-니코딤 도함수이다.[7]
는 'P에서 Q로의 발산'으로 표현될 수 있는데, 이는 베이즈 추론에서의 비대칭성을 반영한다. 즉, 사전 확률 Q에서 시작하여 사후 확률 P로 업데이트된다. 또는 'Q에 대한 P의 상대 엔트로피' 또는 'Q보다 P에서 얻는 정보 이득'으로 표현되기도 한다.
쿨백[4]은 다음과 같은 예시를 제시한다(표 2.1, 예시 2.1).

| x | 0 | 1 | 2 |
|---|---|---|---|
| 분포 P(x) | |||
| 분포 Q(x) |
P는 그림의 왼쪽에 있는 분포로, N = 2이고 p = 0.4인 이항 분포이다. Q는 그림의 오른쪽에 있는 분포로, 가능한 세 가지 결과 x = 0, 1, 2 (즉, )를 가지는 이산 균등 분포이며, 각 결과는 확률 p = 1/3을 가진다.
자연 로그를 밑수 e로 사용하여, nat 단위로 계산하면 다음과 같다.
:
:
이러한 공식의 로그는 정보가 비트 단위로 측정되는 경우 일반적으로 밑 2를 사용하고, 정보가 냇 단위로 측정되는 경우 밑 e를 사용한다.
2. 1. 이산 확률 변수
확률 분포 ''P''와 ''Q''가 동일한 표본 공간 에서 정의될 때, ''Q''에서 ''P''로의 상대 엔트로피는 다음과 같이 정의된다.[4]:
이는 확률 ''P''를 사용하여 계산된, 확률 ''P''와 ''Q'' 사이의 로그 차이의 기대값이다.
다시 말해, 다음 식과 동일하다.
:
상대 엔트로피는 모든 ''x''에 대해 일 때 이 성립하는 경우(절대 연속)에만 이러한 방식으로 정의된다. 그렇지 않은 경우 [1]로 정의되는 경우가 많지만, 이 모든 곳에서 성립하더라도, 의 범위가 무한하다면 의 값을 가질 수 있다.[5][6]
가 0일 때는 해당 항은 0으로 계산되는데, 이는 다음 극한값 때문이다.
:
이산 확률 분포 ''P''와 ''Q''를 따르는 확률 변수의 값이 가 될 확률을 각각 , 라고 할 때, 쿨백-라이블러 발산은 다음과 같이 정의된다.
:
2. 2. 연속 확률 변수
연속확률변수의 경우 쿨백-라이블러 발산은 다음과 같이 정의된다.:
여기에서 는 두 확률분포의 확률 밀도 함수를 의미한다.
2. 3. 확률 측도를 이용한 일반적인 정의
두 확률측도 , 가 있고 가 에 대해 절대수렴할 경우, 두 분포의 쿨백-라이블러 발산은 다음과 같이 정의된다.[7]:
여기서 는 에 대한 의 라돈-니코딤 도함수이다. 즉, 를 만족하는 상에서 거의 모든 곳에서 정의되는 유일한 함수 이며, 이는 가 에 대해 절대 연속이므로 존재한다.
동등하게 ( 연쇄 법칙에 의해), 이것은 다음과 같이 쓸 수 있다.
:
이는 를 기준으로 한 의 엔트로피이다.
만약 가 밀도 와 를 갖는 에 대한 측도이며, 및 가 존재하는 경우 (즉, 와 가 모두 에 대해 절대 연속인 경우), 에서 로의 상대 엔트로피는 다음과 같다.
:
는 로 설정할 수 있기 때문에, 밀도를 정의할 수 있는 측도는 항상 존재한다.[4][5][6]
3. 어원
솔로몬 쿨백과 리처드 라이블러는 1951년에 상대 엔트로피를 "μ1으로부터의 관찰당 H1과 H2 간의 차별을 위한 평균 정보"로 소개하였다.[3] 여기서 H1과 H2는 각각 두 확률 측정 μ1과 μ2에서 선택하는 가설이다. 쿨백과 라이블러는 이를 I(1:2)로 표기했으며, 해럴드 제프리스가 1948년에 이미 정의하고 사용했던 대칭화된 양 J(1,2) = I(1:2) + I(2:1)을 "μ1과 μ2 간의 '발산'"으로 정의했다. 쿨백은 1959년에 대칭화된 형태를 다시 "발산"으로 언급했고, 각 방향의 상대 엔트로피는 두 분포 간의 "방향성 발산"으로 언급했다. 쿨백은 '차별 정보'라는 용어를 선호했다. "발산"이라는 용어는 대칭화된 발산이 삼각 부등식을 만족하지 않기 때문에 거리(메트릭)와는 대조적이다. 비대칭 "방향성 발산"은 쿨백-라이블러 발산으로 알려지게 되었고, 대칭화된 "발산"은 현재 '''제프리스 발산'''이라고 불린다.
4. 직관적 의미
쿨백-라이블러 발산(KL 발산)은 확률분포 를 근사적으로 표현하는 확률분포 를 대신 사용할 때 발생하는 엔트로피 변화를 의미한다. 이는 의 엔트로피 와 대신 를 사용할 때의 교차 엔트로피 의 차이로 계산된다.[12]
:
:
일반적으로 는 실제 데이터, 는 이론 또는 의 근사치를 나타낸다. KL 발산은 에 최적화된 코드로 의 샘플을 부호화할 때 필요한 평균 비트 수의 차이로 해석된다.[16][17][18]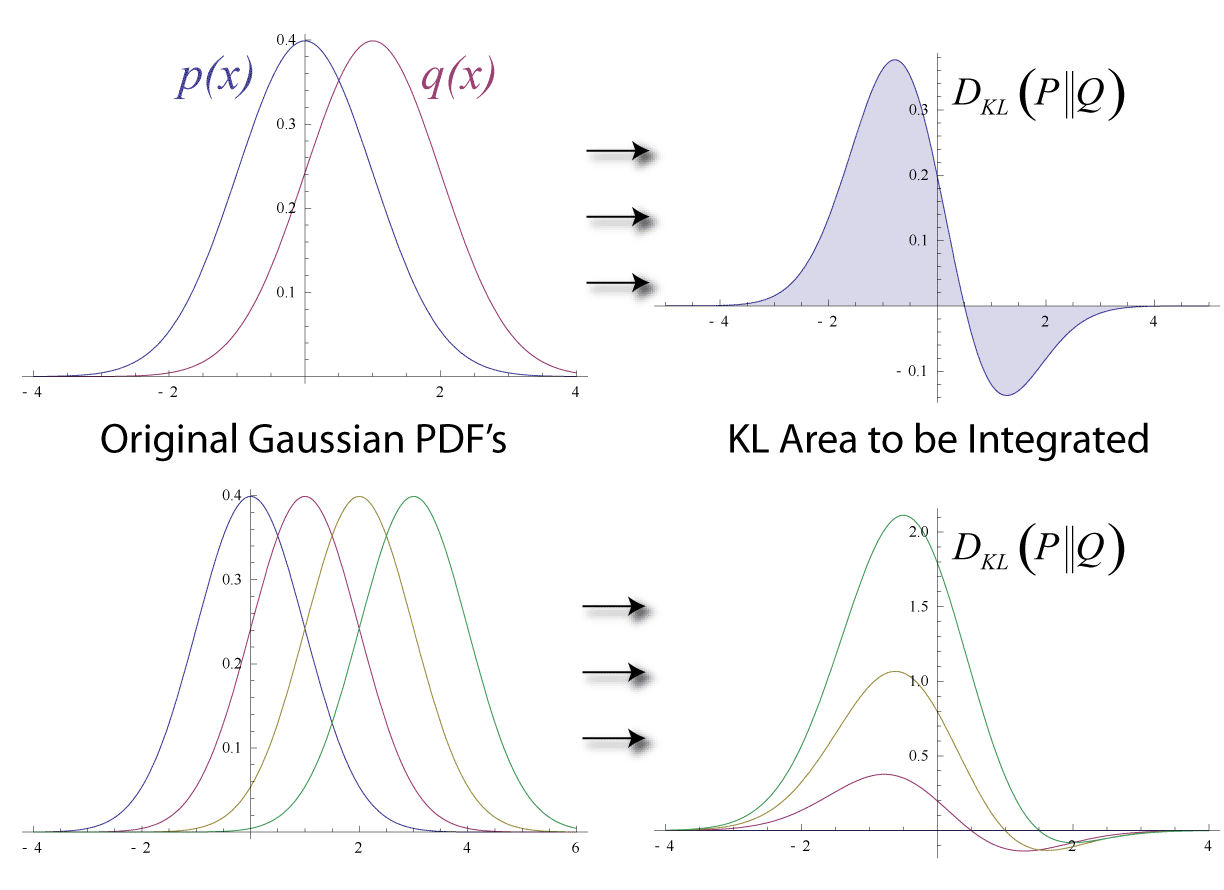
KL 발산은 통계적 거리로 생각할 수 있으며, 분포 가 에서 얼마나 떨어져 있는지 측정한다. 이는 발산의 일종으로, 비대칭적이다.[12]
아서 홉슨은 KL 발산이 확률 분포 간 차이를 측정하는 유일한 방법이며, 엔트로피의 특징에 나타나는 속성의 확장임을 증명했다.[18]
4. 1. 통계학적 해석
통계학 분야에서, 네이만-피어슨 보조정리는 관측값 Y|영어 (두 분포 중 하나에서 추출)을 기반으로 두 분포 P|영어와 Q|영어를 구별하는 가장 강력한 방법은 해당 우도 비율의 로그 를 사용하는 것이라고 명시한다. KL 발산은 실제로 Y|영어가 P|영어에서 추출된 경우 이 통계량의 기대값이다. 쿨백은 이 통계량을 기대 로그 우도비로 설명했다.유한 차원의 파라미터 θ|영어로 특징지어지는 확률 밀도 함수를 사용하여 를 추정하는 맥락에서, 쿨백-라이블러 정보량의 경험량 최소화
:
는 (로그 변환된) 최우도법
:
와 동일한 문제가 된다. 즉, 최우도 추정량은 쿨백-라이블러 정보량을 경험적으로 최소화하는 추정 방법으로 생각할 수 있다.
4. 2. 부호화 관점
부호 이론의 맥락에서, 에 최적화된 코드가 아닌 에 최적화된 코드를 사용하여 에서 추출한 샘플을 부호화하는 데 필요한 추가 비트의 예상 수를 측정하여 쿨백-라이블러 발산을 구성할 수 있다.[16][17][18]정보 이론에서, 크라프트-맥밀란 정리는 집합 의 가능성 중 하나의 값 를 식별하기 위해 메시지를 코딩하기 위한 직접 해독 가능한 코딩 방식은 에 대한 코드의 길이 가 비트 단위일 때, 에 대한 암묵적인 확률 분포 를 나타내는 것으로 볼 수 있음을 확립한다. 따라서 상대 엔트로피는 주어진 (잘못된) 분포 에 최적인 코드를 사용했을 때, 참 분포 를 기반으로 한 코드를 사용하는 것과 비교하여 통신해야 하는 데이터당 예상 추가 메시지 길이로 해석될 수 있다. 즉, ''초과'' 엔트로피이다.
:
여기서 는 에 대한 의 교차 엔트로피이고 는 의 엔트로피이다 (이는 P와 자체의 교차 엔트로피와 동일하다).
정보 엔트로피가 ''H''인 확률 변수 ''X''는 평균 비트 수가 (거의) ''H''인 비트열로 부호화할 수 있지만(허프만 부호), 평균 비트 수가 ''H'' 미만이 되도록 부호화할 수 없다는 것이 알려져 있다(정보원 부호화 정리). 즉, 확률 변수 ''X''를 부호화하려 할 때, ''H''가 비트 수의 최소값이다. 이제 확률 변수 ''X''가 실제로는 분포 ''P''를 따르는데, 잘못하여 분포 ''Q''를 따른다고 판단한 경우, 원래의 최소값보다 더 많은 비트 수가 필요하게 된다. 쿨백-라이블러 정보량은 이러한 오류를 범했을 때 추가로 소요되는 비트 수의 평균값을 나타낸다.
4. 3. 추론 관점
쿨백-라이블러 발산은 현재 사용 중인 확률 분포 Q 대신 실제 확률 분포 P를 사용했을 때 얻을 수 있는 정보 이득을 나타낸다. 정보 이론과의 유추를 통해, P의 Q에 대한 ''상대 엔트로피''라고도 불린다.[8]베이즈 추론 관점에서 보면, 쿨백-라이블러 발산은 사전 확률 분포 Q에서 사후 확률 분포 P로 신념을 수정함으로써 얻는 정보의 양을 측정한다. 다시 말해, Q를 사용하여 P를 근사할 때 손실되는 정보량을 나타낸다.[8]
좀 더 구체적으로 설명하면, 확률 변수 X에 대해, 어떤 값 x를 가질 확률이 Q(x)라고 가정한다 (베이즈 확률에서 사전 분포). 이후 새로운 데이터 I를 얻게 되어, X가 x일 확률이 P(x)로 바뀌었다고 가정한다 (베이즈 확률에서 사후 분포).
이때, I는 X에 대해 어느 정도의 정보를 제공했는지 알 수 있다. 정보량은 사건의 불확실성을 측정하는 척도이다. I를 알기 전 X의 불확실성(자기 정보량)은 -logQ(x)이지만, I를 알게 되면서 -logP(x)로 감소한다. 따라서 I를 통해 X에 대해 다음과 같은 자기 정보량을 얻게 된다.
:
x는 X에 따라 변하므로, 이 값의 평균을 (사후 확률 분포에 의해) 구하면 다음과 같다.
:
이는 쿨백-라이블러 정보량과 일치한다.
결론적으로, 쿨백-라이블러 정보량은 X에 대해 데이터 I로부터 얻어지는 정보량의 평균값을 나타내며, 정보 획득(Information gain)이라고도 불린다.
4. 4. 최우추정량에 의한 설명
확률 밀도 함수 `p(x)`를, 유한 차원의 파라미터 `θ`로 특징지어지는 확률 밀도 함수 `q(x|θ)`를 사용하여 추정하는 상황을 생각해 보자. 이 경우, 쿨백-라이블러 정보량의 경험량을 최소화하는 식은 다음과 같다.:
이는 로그 변환된 최우추정법과 동일한 문제이며, 식은 다음과 같다.
:
즉, 최우추정량은 쿨백-라이블러 정보량을 경험적으로 최소화하는 추정 방법으로 생각할 수 있다.
4. 5. 베이즈 확률에 의한 설명
확률 변수 ''X''에 대해, ''X''가 ''x''일 확률 Pr[''X''=''x'']가 ''Q''(''x'')였다고 가정하자(베이즈 확률에서 말하는 사전 분포). 이제 ''X''에 관한 새로운 데이터 ''I''를 알게 되었고, 그 결과 ''X''가 따르는 (조건부) 확률 Pr[''X''=''x''|''I'']가 ''P''(''x'')가 되었다고 가정한다(베이즈 확률에서 말하는 사후 분포).[8]이때, ''I''는 ''X''에 관해 어느 정도의 정보를 제공했다고 할 수 있을까? 정보량이 사건의 불확실성을 측정하는 척도였음을 떠올려보자. ''I''를 알기 전의 ''X''의 불확실성(즉, 자기 정보량)은 −log''Q''(''x'')이지만, ''I''를 알게 됨으로써 −log''P''(''x'')로 줄어든다. 따라서 ''I''에 의해 ''X''에 관해
:
만큼의 자기 정보량을 얻게 된다. ''x''는 ''X''에 따라 바뀌므로, 이 값의 (사후 확률 분포에 의한) 평균값을 취하면,
:
가 된다. 이것은 쿨백-라이블러 정보량과 일치한다.
즉, 쿨백-라이블러 정보량은 ''X''에 관해 데이터 ''I''로부터 얻어지는 정보량의 평균값을 나타낸다. 이상의 이유로, 쿨백-라이블러 정보량은 정보 획득(Information gain)이라고도 불린다.[8]
4. 6. 사노프 정리(Sanov's theorem)에 의한 설명
쿨백-라이블러 정보량은 대편차 이론의 일부로, 사노프 정리를 통해 이해할 수 있다. 집합 {1, 2, ..., ''r''} 위의 확률 분포 전체의 집합을 ''P''라 하고, ''K''⊂''P''를 콤팩트 집합으로 한다. 이때, 확률 분포 ''p ∈ P''에서 독립적으로 동일하게 분포된 확률 변수 열 ''x''1, ''x''2, ..., ''xN''로부터 유도되는 경험 분포가 ''K''에 포함될 확률의 레이트 함수는 쿨백-라이블러 정보량으로 주어진다.[41]간단히 말해, 확률 분포 ''p''의 제비를 반복적으로 뽑았을 때 경험 분포 ''q''가 얻어질 확률은, ''p''에서 ''q''로의 쿨백-라이블러 정보량 ''D''(''q''||''p'')을 레이트 함수로 하여 시행 횟수의 증가와 함께 감소한다는 것을 의미한다.[41]
앞면과 뒷면이 같은 확률로 나오는 동전 던지기를 100번 반복하여 앞면이 1번만 나올 확률이, 1/100의 확률로 앞면이 나오는 동전 던지기를 100번 반복하여 앞면과 뒷면이 정확히 50번씩 나올 확률보다 높다는 것은 쿨백-라이블러 정보량이 대칭성을 갖지 않는다는 것을 직관적으로 보여준다.
5. 동기
정보 이론에서 크라프트-맥밀란 정리는 집합의 가능성 중 하나의 값 를 식별하기 위해 메시지를 코딩하기 위한 직접 해독 가능한 코딩 방식은 에 대한 코드의 길이 가 비트 단위일 때, 암묵적인 확률 분포 를 나타내는 것으로 볼 수 있음을 확립한다. 따라서 쿨백-라이블러 발산은 주어진 (잘못된) 분포 에 최적인 코드를 사용했을 때, 참 분포 를 기반으로 한 코드를 사용하는 것과 비교하여 통신해야 하는 데이터당 예상 추가 메시지 길이로 해석될 수 있다. 즉, ''초과'' 엔트로피이다.[16][17][18]
:
여기서 는 에 대한 의 교차 엔트로피이고 는 의 엔트로피이다 (이는 P와 자체의 교차 엔트로피와 동일하다).
6. 속성
쿨백-라이블러 발산은 다음과 같은 중요한 속성들을 가진다.
- 음이 아닌 값: 쿨백-라이블러 발산은 항상 0보다 크거나 같다. 즉, 이다. 이는 깁스 부등식으로 알려져 있으며, 는 인 경우에만 0이 된다.[19] 자세한 내용은 #음이 아닌 값 문단을 참조하라.
- 상한의 부재: 일반적인 경우 쿨백-라이블러 발산에 상한은 존재하지 않는다.[19] 그러나 P와 Q가 동일한 이산량을 분배하여 생성된 두 개의 이산 확률 분포인 경우에는 의 최댓값을 계산할 수 있다.[19] 자세한 내용은 #상한의 부재 문단을 참조하라.
- 변수 변환 불변성: 쿨백-라이블러 발산은 변수 변환에 대해 불변한다.[20] 즉, 변수 x를 로 변환해도 쿨백-라이블러 발산의 값은 변하지 않는다. 자세한 내용은 #변수 변환 불변성 문단을 참조하라.
- 독립 확률 변수에 대한 가법성: 가 독립 분포이고 이며, 마찬가지로 가 독립 분포이고 이면, 다음이 성립한다.
:
- 볼록 함수: 쿨백-라이블러 발산 는 확률 측정 쌍 에 대해 볼록 함수이다. 즉, 과 가 확률 측정 쌍이면, 다음 부등식이 성립한다.
:
- 테일러 전개: 쿨백-라이블러 발산은 최솟값()에 대해 다음과 같이 테일러 전개될 수 있다.[19]
:
이는 거의 확실하게 인 경우에만 수렴한다.[19]
6. 1. 음이 아닌 값
쿨백-라이블러 발산은 항상 음수가 아닌 값이며, 이는 깁스 부등식으로 알려져 있다.[19] 즉, 다음이 성립한다.:
여기서 가 0이 되는 경우는 일 때뿐이다.
특히, 이고 인 경우, 는 -거의 어디에서나이다. 따라서 엔트로피 는 교차 엔트로피 의 최솟값을 설정하며, 이는 가 아닌 를 기반으로 하는 코드를 사용할 때 필요한 비트의 기대값이다. 쿨백-라이블러 발산은 "진실된" 분포 가 아닌 확률 분포 에 해당하는 코드를 사용하는 경우, 에서 추출된 값 를 식별하기 위해 전송해야 하는 추가 비트의 기대값을 나타낸다.[19]
쿨백-라이블러 정보량은 항상 음이 아닌 값을 갖는다.
:
이는 깁스 부등식으로 알려져 있으며, ''D''KL(''P''||''Q'')가 0이 되는 것은 ''P'' = ''Q''일 때뿐이다. 따라서, 엔트로피 ''H(P)''는 교차 엔트로피 ''H(P,Q)''의 하한값이 된다. 이 교차 엔트로피는 ''P''가 아닌 ''Q''에 기반한 부호를 사용했을 때 예상되는 비트 수를 나타낸다. 따라서, KL 발산은 ''X''에서 ''x''라는 값을 특정하는 정보를 얻기 위해, ''P''라는 참 분포가 아닌 ''Q''라는 확률 분포에 대응하는 부호를 사용했을 때 추가로 예상되는 비트 수를 나타내는 것이다.
6. 2. 상한의 부재
일반적인 경우에는 상한이 존재하지 않는다.[19] 그러나 P와 Q가 동일한 이산량을 분배하여 생성된 두 개의 이산 확률 분포인 경우, 의 최대값을 계산할 수 있다.[19]6. 3. 변수 변환 불변성
상대 엔트로피는 변수 변환에 불변한다. 예를 들어, 변수 x에서 변수 로 변환이 이루어지는 경우, 이고 이며, 여기서 는 도함수의 절댓값 또는 일반적으로 야코비안이므로 상대 엔트로피는 다음과 같이 다시 작성할 수 있다.[20]여기서 이고 이다. 변환이 연속적이라고 가정했지만, 반드시 그럴 필요는 없다.
이는 또한 상대 엔트로피가 차원 분석적으로 일관된 양을 생성한다는 것을 보여주는데, 만약 x가 차원 변수이면 가 무차원이므로 와 도 차원을 갖는다. 로그 항의 인수는 무차원이며, 반드시 그래야 한다. 따라서 이는 비이산 확률에 대해 정의되지 않거나 음수가 될 수 있는 자기 정보 또는 섀넌 엔트로피와 같은 다른 정보 이론 속성보다 어떤 면에서는 더 기본적인 양으로 볼 수 있다.[20]
6. 4. 독립 확률 변수에 대한 가법성
가 독립 분포이고, 이며, 마찬가지로 가 독립 분포인 경우 이면, 다음이 성립한다.[20]:
즉, 독립 확률 변수에 대한 쿨백-라이블러 발산은 각 독립 변수에 대한 쿨백-라이블러 발산의 합으로 표현된다. 이는 쿨백-라이블러 발산이 독립 확률 변수에 대해 가법적(additive)임을 의미한다.
6. 5. 볼록 함수
상대 엔트로피 는 확률 측정 쌍 에 대해 볼록 함수이다. 즉, 과 가 확률 측정 쌍이면, 다음 부등식이 성립한다.6. 6. 테일러 전개
Taylor expansion영어는 최소값()에 대해 다음과 같이 전개될 수 있다.[19]:
이는 거의 확실하게 인 경우에만 수렴한다.[19]
7. 변분 추론을 위한 이중성 공식
다음 결과는 돈스커(Donsker)와 바라단(Varadhan)에 의한 것으로,[21] '''돈스커-바라단 변분 공식'''으로 알려져 있다.
:가 적절한 -체 를 갖는 집합이고, 두 확률 측도 와 가 있어 두 확률 공간 와 를 구성하며, 라고 하자. (는 가 에 대해 절대적으로 연속임을 나타낸다.) 가 에서 실수 값을 갖는 적분 가능한 확률 변수라고 하자. 그러면 다음 등식이 성립한다.
:
:또한, 우변의 상한은 다음이 성립하는 경우에만 달성된다.
:
:확률 측도 에 대해 거의 확실하며, 여기서 는 에 대한 의 라돈-니코딤 도함수를 나타낸다.
:에 대해 의 적분 가능성을 가정하는 간단한 증명을 위해, 가 밀도 를 갖는다고 하자. 즉, 이다. 그러면
:
:따라서,
:
:마지막 부등식은 에서 비롯되며, 이는 인 경우에만 등식이 성립한다. 결론이 따른다.
8. 예시
쿨백[24]은 다음과 같은 예시를 제시한다(표 2.1, 예시 2.1). 와 를 표와 그림에 나타난 분포라고 하자. 는 그림의 왼쪽에 있는 분포로, 이고 인 이항 분포이다. 는 그림의 오른쪽에 있는 분포로, 가능한 세 가지 결과 0, 1, 2 (즉, )를 가지는 이산 균등 분포이며, 각 결과는 확률 을 가진다.
| 0 | 1 | 2 | |
| 분포 | |||
| 분포 |
자연 로그를 밑 e로 사용하여 nat 단위의 결과를 얻는다. (정보 단위 참조)
와 는 다음과 같이 계산된다.
:
:
8. 1. 다변량 정규 분포
평균이 이고, 공분산 행렬 을 갖는 두 다변량 정규 분포가 있다고 가정한다. 두 분포의 차원이 로 동일하다면, 두 분포 간의 상대 엔트로피는 다음과 같다.[22]:
마지막 항의 로그는 밑이 e여야 한다. 이는 마지막 항을 제외한 모든 항이 밀도 함수의 요소이거나 자연적으로 발생하는 식의 밑-e 로그이기 때문이다. 따라서 이 방정식은 nat 단위로 측정된 결과를 제공한다. 위의 전체 식을 로 나누면 비트 단위의 발산이 된다.
수치 구현에서는 촐레스키 분해 을 사용하여 결과를 표현하는 것이 유용하다. 여기서 및 이다. 그런 다음 과 는 삼각 선형 시스템 과 의 해이다.
:
8. 1. 1. 대각 다변량 정규 분포와 표준 정규 분포
다변량 정규 분포가 대각 다변량 정규 분포이고 표준 정규 분포(평균 0, 분산 1)인 특수한 경우, 상대 엔트로피는 다음과 같이 표현된다.[22]:
두 개의 일변량 정규 분포 p영어 및 q영어의 경우, 위 식은 다음과 같이 단순화된다.[23]
:
중심이 같은 정규 분포에서 인 경우, 다음과 같이 단순화된다.[24]
:
8. 2. 균등 분포
쿨백[24]은 다음과 같은 예시를 제시했다. ''P''와 ''Q''를 표와 그림에 나타난 분포라고 하자. ''P''는 그림의 왼쪽에 있는 분포로, N = 2이고 p = 0.4인 이항 분포이다. ''Q''는 그림의 오른쪽에 있는 분포로, 가능한 세 가지 결과 x = 0, 1, 2 (즉, )를 가지는 이산 균등 분포이며, 각 결과는 확률 p = 1/3을 가진다.
| x | 0 | 1 | 2 |
|---|---|---|---|
| 분포 | |||
| 분포 |
상대 엔트로피 와 는 다음과 같이 계산된다.
:
:
두 개의 균등 분포에서 p=[A,B]의 지지 집합이 q=[C,D] (
9. 메트릭과의 관계
쿨백-라이블러 발산(KL 발산)은 미터법이 아니라 발산의 일종이다.[9] 미터법은 대칭적이며 삼각 부등식을 만족하는 '선형' 거리를 일반화하는 반면, 발산은 비대칭적이며 경우에 따라 일반화된 피타고라스 정리를 만족하는 '제곱' 거리를 일반화한다. 일반적으로
상대 엔트로피의 무한소 형태, 특히 그 헤시안은 피셔 정보 메트릭과 같은 계량 텐서를 제공한다. 핀스커 부등식에 따르면 쿨백-라이블러 발산이 0으로 수렴하면, 전체 변동에서 일반적인 수렴을 의미한다.
9. 1. 피셔 정보량 척도
쿨백-라이블러 발산은 피셔 정보량 척도와 밀접하게 관련되어 있다. 상대 엔트로피의 헤세 행렬은 피셔 정보 메트릭과 같은 계량 텐서를 제공하며, 이는 정보 기하학적 최적화 알고리즘에서 자연스러운 기울기를 결정하는 데 사용될 수 있다.[9]9. 1. 1. 피셔 정보량 척도 정리
상대 엔트로피는 피셔 정보량 척도와 직접적인 관련이 있다. 확률 분포1차까지는 (아인슈타인 합 표기법을 사용하여) 다음이 성립한다.
:
여기서
상대 엔트로피는
:
테일러 전개에 의해 2차까지는 다음과 같다.
:
여기서 발산의 헤세 행렬
:
은 양의 준정부호여야 한다.
:
:
\left|\frac{\partial p}{\partial \rho}\right| &< F(x): \int_{x=0}^\infty F(x)\,dx < \infty, \\
\left|\frac{\partial^2 p}{\partial \rho^2}\right| &< G(x): \int_{x=0}^\infty G(x)\,dx < \infty \\
\left|\frac{\partial^3 \log(p)}{\partial \rho^3}\right| &< H(x): \int_{x=0}^\infty p(x, 0)H(x)\,dx < \xi < \infty
\end{align}
여기서
:
\left.\int_{x=0}^\infty \frac{\partial p(x, \rho)}{\partial \rho}\right|_{\rho=0}\, dx =
\left.\int_{x=0}^\infty \frac{\partial^2 p(x, \rho)}{\partial \rho^2}\right|_{\rho=0}\, dx = 0
그러면:
:
9. 2. 정보 변동
또 다른 정보 이론적 척도는 정보의 변동인데, 이는 조건부 엔트로피의 대칭화이다. 이것은 이산 확률 공간의 분할 집합에 대한 척도이다.9. 3. MAUVE 메트릭
MAUVE는 모델이 생성한 텍스트와 사람이 작성한 텍스트 간의 차이와 같이, 두 텍스트 분포 간의 통계적 격차를 측정하는 척도이다. 이 척도는 파운데이션 모델의 양자화된 임베딩 공간에서 두 분포 간의 쿨백-라이블러 발산을 사용하여 계산된다.10. 정보 이론의 다른 양과의 관계
크라프트-맥밀란 정리에 따르면, 특정 집합의 값
:
D_\text{KL}(P\parallel Q) &= \sum_{x\in\mathcal{X}} p(x) \log \frac{1}{q(x)} - \sum_{x\in\mathcal{X}} p(x) \log \frac{1}{p(x)} \\[5pt]
&= \Eta(P, Q) - \Eta(P)
\end{align}
위 식에서
쿨백-라이블러 발산
상대 엔트로피는 대편차 이론에서 "율 함수"와 관련이 있으며,[16][17] 아서 홉슨은 상대 엔트로피가 엔트로피의 특징에 나타나는 속성의 표준적인 확장이면서, 확률 분포 간 차이를 측정하는 유일한 값임을 증명했다.[18] 결과적으로, 상호 정보는 특정 관련 조건을 따르는 유일한 상호 의존성 측정값이며, 쿨백-라이블러 발산의 측면에서 정의될 수 있다.
자기 정보, 상호 정보, 섀넌 엔트로피, 조건부 엔트로피 등 정보 이론의 여러 다른 양들은 쿨백-라이블러 발산의 특수한 경우를 응용한 것으로 해석할 수 있다.
10. 1. 자기 정보
정보 이론에서 자기 정보는 신호, 확률 변수, 또는 사건의 정보 내용이라고도 하며, 주어진 결과가 발생할 확률의 음의 로그로 정의된다.이산 확률 변수에 적용할 때, 자기 정보는 다음과 같이 나타낼 수 있다.
:
여기서
10. 2. 상호 정보
상호 정보량은 두 주변 확률 분포의 곱인:
\operatorname{I}(X; Y)
&= D_\text{KL}(P(X, Y) \parallel P(X)P(Y)) \\[5pt]
&= \operatorname{E}_X \{D_\text{KL}(P(Y \mid X) \parallel P(Y))\} \\[5pt]
&= \operatorname{E}_Y \{D_\text{KL}(P(X \mid Y) \parallel P(X))\}
\end{align}
이는 주변 분포만 사용하여 코딩하는 경우 X와 Y를 식별하기 위해 전송해야 하는 추가 비트의 예상 수이다. 결합 분포 대신 주변 분포를 사용할 때의 추가 비트 수로 해석할 수 있다. 혹은, 결합 확률
10. 3. 섀넌 엔트로피
섀넌 엔트로피(Shannon entropy영어)는 다음과 같이 나타낼 수 있다.:
\Eta(X) &= \operatorname{E}\left[\operatorname{I}_X(x)\right] \\
&= \log(N) - D_\text{KL}\left(p_X(x) \parallel P_U(X)\right)
\end{align}
여기서 ''N''은 확률 변수 ''X''가 가질 수 있는 값의 개수이고,
조건부 엔트로피는 다음과 같이 나타낼 수 있다.
:
H(X|Y) & = \log N - D_{\mathrm{KL}}(P(X,Y) \| P_U(X) P(Y) ) \\
& = \log N - D_{\mathrm{KL}}(P(X,Y) \| P(X) P(Y) ) - D_{\mathrm{KL}}(P(X) \| P_U(X)) \\
& = H(X) - I(X;Y) \\
& = \log N - \mathbb{E}_Y \{ D_{\mathrm{KL}}(P(X|Y) \| P_U(X)) \}
\end{align}
10. 4. 조건부 엔트로피
조건부 엔트로피는 다음과 같이 나타낼 수 있다.[1]:
H(X \mid Y)
&= \log(N) - D_\text{KL}(P(X, Y) \parallel P_U(X) P(Y)) \\[5pt]
&= \log(N) - D_\text{KL}(P(X, Y) \parallel P(X) P(Y)) - D_\text{KL}(P(X) \parallel P_U(X)) \\[5pt]
&= H(X) - I(X;Y) \\
&= \log(N) - \mathbb{E}_Y \{ D_\text{KL}(P(X|Y) \parallel P_U(X)) \}
\end{align}
이는 ''N''개의 동일한 가능성 중에서 ''X''를 식별하기 위해 전송해야 하는 비트 수에서, 실제 결합 분포
10. 5. 교차 엔트로피
쿨백-라이블러 발산은 확률분포:
:
크라프트-맥밀란 정리에 따르면, 집합에서 값
:
D_\text{KL}(P\parallel Q) &= \sum_{x\in\mathcal{X}} p(x) \log \frac{1}{q(x)} - \sum_{x\in\mathcal{X}} p(x) \log \frac{1}{p(x)} \\[5pt]
&= \Eta(P, Q) - \Eta(P)
\end{align}
여기서
쿨백-라이블러 발산(
상대 엔트로피는 대편차 이론에서 "율 함수"와 관련이 있다.[16][17]
아서 홉슨(Arthur Hobson)은 상대 엔트로피가 확률 분포 간 차이를 측정하는 유일한 값이며, 엔트로피의 특징에 나타나는 속성의 확장임을 증명했다.[18] 상호 정보는 특정 조건을 따르는 유일한 상호 의존성 측정값이며, 쿨백-라이블러 발산으로 정의될 수 있다.
두 확률 분포
:
상대 엔트로피(KL-발산)는
11. 베이즈 업데이트
베이즈 통계학에서 상대 엔트로피는 사전 확률 분포에서 사후 확률 분포:
:
이 분포는 새로운 엔트로피를 갖는다.
:
이는 원래 엔트로피
:
이것은 메시지 길이에 유용한 정보의 양 또는
만약 추가 데이터
:
따라서 결합된 정보 획득은 삼각 부등식을 따르지 않는다.
:
말할 수 있는 모든 것은
12. 베이즈 실험 설계
베이즈 실험 설계에서 흔한 목표는 사전 확률과 사후 확률 사이의 기대 상대 엔트로피를 최대화하는 것이다.[25] 사후 확률이 가우시안 분포로 근사될 때, 기대 상대 엔트로피를 최대화하는 설계를 베이즈 d-최적 설계라고 부른다.
13. 판별 정보
상대 엔트로피
:
두 양 중 하나는 베이즈 실험 설계에서 다음으로 조사할 최적의 질문을 선택하기 위한 효용 함수로 사용될 수 있다. 그러나 일반적으로 상당히 다른 실험 전략으로 이어진다.
''정보 이득''의 엔트로피 척도에서 거의 확실성과 절대적인 확실성 사이에는 거의 차이가 없다. 거의 확실성에 따라 코딩하는 것은 절대적인 확실성에 따라 코딩하는 것보다 거의 더 많은 비트가 필요하지 않다. 반면에, 증거의 가중치에 의해 암시되는 로짓 척도에서 둘 사이의 차이는 엄청나다. 즉, 무한할 수 있다. 이는, 예를 들어, 리만 가설이 옳다는 것을 (확률적 수준에서) 거의 확신하는 것과 수학적 증명이 있기 때문에 그것이 옳다고 확신하는 것의 차이를 반영할 수 있다. 불확실성에 대한 이러한 두 가지 다른 손실 함수 척도는 각 척도가 문제의 특정 상황을 얼마나 잘 반영하는지에 따라 ''모두'' 유용하다.
14. 최소 판별 정보 원리
쿨백은 상대 엔트로피를 차별 정보로 간주하여 '''최소 차별 정보 원리(MDI)'''를 제안했다. 새로운 사실이 주어지면, 새로운 분포는 원래 분포
예를 들어, x와 a에 대한 사전 분포
:
즉, 업데이트된 분포
MDI는 라플라스의 무차별 원리와 E.T. 제인스의 최대 엔트로피 원리의 확장으로 볼 수 있다. 특히, 섀넌 엔트로피가 더 이상 유용하지 않게 되는 연속 분포에 대한 최대 엔트로피 원리의 자연스러운 확장이다(''미분 엔트로피'' 참조).
공학 문헌에서 MDI는 때때로 '''최소 교차 엔트로피 원리'''(MCE) 또는 간단히 '''민센트'''라고 불린다.
15. 사용 가능한 작업과의 관계
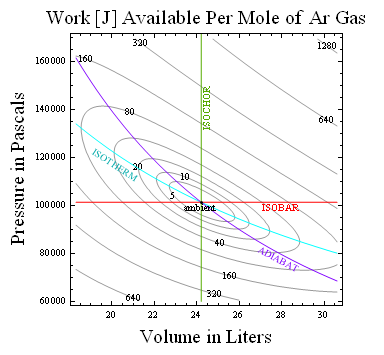
어떤 주변 환경에 대한 사용 가능한 일은 주변 온도
:
예를 들어, 표준 온도와 압력에서 아르곤 1몰에 대해 오른쪽에 표시된 일정한 상대 엔트로피의 결과 등고선은 화염으로 구동되는 에어컨이나 끓는 물을 얼음물로 변환하는 전원이 없는 장치에서와 같이 뜨거운 것을 차가운 것으로 변환하는 데 한계를 둔다.[33] 따라서 상대 엔트로피는 열역학적 가용성을 비트 단위로 측정한다.
16. 양자 정보 이론
힐베르트 공간에 대한 밀도 행렬 ''P''와 ''Q''에 대해 ''Q''에서 ''P''로의 양자 상대 엔트로피는 다음과 같이 정의된다.
:
양자 정보 과학에서 모든 분리 가능한 상태 ''Q''에 대한
17. 모델과 현실 간의 관계
"주변 환경으로부터 실제"의 상대 엔트로피가 열역학적 가용성을 측정하는 것과 마찬가지로, "모델로부터 현실"의 상대 엔트로피는 현실에 대한 유일한 단서가 몇 가지 실험 측정값뿐일 때에도 유용하다. 전자의 경우 상대 엔트로피는 ''평형으로부터의 거리'' 또는 (주변 온도와 곱해질 때) ''가용 작업량''을 설명하는 반면, 후자의 경우 현실이 숨겨둔 놀라움, 즉 ''모델이 얼마나 더 배워야 하는지''를 알려준다.[34][35]
실험적으로 접근 가능한 시스템에 대한 모델을 평가하는 이 도구는 어떤 분야에도 적용될 수 있지만, 아카이케 정보 기준을 통해 통계 모델을 선택하는 데 적용하는 것은 특히 잘 설명되어 있다. 간단히 말해서, 모델로부터 현실의 상대 엔트로피는 데이터와 모델의 예측 간에 관찰된 편차(예: 평균 제곱 편차)의 함수에 의해 상수 가산 항 내에서 추정될 수 있다. 동일한 가산 항을 공유하는 모델에 대한 이러한 발산 추정치는 차례로 모델 간의 선택에 사용될 수 있다.
매개변수화된 모델을 데이터에 맞추려고 할 때 최대 우도 및 최대 간격 추정 추정치와 같이 상대 엔트로피를 최소화하려는 다양한 추정기가 있다.
18. 대칭 발산
솔로몬 쿨백과 리처드 라이블러는 1951년에 쿨백-라이블러 발산을 처음 소개하면서, '발산'이라는 용어를 사용하여 대칭화된 형태인
쿨백-라이블러 발산의 비대칭성은 때때로 문제가 될 수 있다. 이러한 문제를 해결하기 위해 다음과 같은 대칭화된 발산들이 사용된다.
- 제프리스 발산: 쿨백과 라이블러가 "발산"으로 정의했던 함수로, 다음과 같이 정의된다.
:
:이 함수는 대칭적이고 항상 0 이상의 값을 가진다. 제프리스가 이미 사용했던 함수이므로 제프리스 발산이라고 불린다.
- 람다 발산: 또 다른 대안으로, 다음과 같이 정의된다.
:
:이는 어떤 확률 분포에서 표본을 추출했을 때, 그 분포가 P인지 Q인지를 알아내는 데 필요한 예상 정보 이득으로 해석할 수 있다.
- 젠센-섀넌 발산: 람다 발산에서
\lambda = 0.5 인 경우로, 다음과 같이 정의된다.
:
:여기서
19. 다른 확률 거리 측정과의 관계
다른 많은 중요한 확률 거리 척도가 있다. 이 중 일부는 상대 엔트로피와 특히 관련이 있다. 예를 들어:
- 전변동 거리
\delta(p,q) 는 핀스커 부등식을 통해 발산과 연결된다:\delta(P, Q) \le \sqrt{\frac{1}{2} D_\text{KL}(P \parallel Q)}. 핀스커 부등식은D_{\mathrm{KL}}(P\parallel Q)>2 인 모든 분포에 대해 무의미한데, 전변동 거리가 최대 1이기 때문이다. 이러한 분포에 대해서는 브르타뇰-후버 부등식[38](또한, Tsybakov[39] 참조)에 의한 대체 경계를 사용할 수 있다:\delta(P,Q) \le \sqrt{1-e^{ -D_{\mathrm{KL}}(P\parallel Q) }}. - 레니 발산 계열은 상대 엔트로피를 일반화한다. 특정 매개변수
\alpha 의 값에 따라 다양한 부등식을 유추할 수 있다.
다른 주목할 만한 거리 척도에는 헬링거 거리, 히스토그램 교차, 카이제곱 통계량, 이차 형식 거리, 매치 거리, 콜모고로프-스미르노프 거리, 어스 무버 거리가 있다.[40]
20. 데이터 차분
절대 엔트로피가 데이터 압축의 이론적 배경 역할을 하는 것처럼, 상대 엔트로피는 데이터 차분의 이론적 배경 역할을 한다. 이러한 맥락에서 데이터 집합의 절대 엔트로피는 데이터를 재구성하는 데 필요한 데이터(최소 압축 크기)이고, 소스 데이터 집합이 주어졌을 때 대상 데이터 집합의 상대 엔트로피는 소스를 '주어진' 대상을 재구성하는 데 필요한 데이터(패치의 최소 크기)이다.[1]
참조
[1]
논문
I-Divergence Geometry of Probability Distributions and Minimization Problems
1975-02
[2]
논문
On information and sufficiency
[3]
논문
Letter to the Editor: The Kullback–Leibler distance
[4]
서적
Information Theory, Inference, and Learning Algorithms
https://books.google[...]
Cambridge University Press
[5]
웹사이트
What's the maximum value of Kullback-Leibler (KL) divergence?
https://stats.stacke[...]
[6]
웹사이트
In what situations is the integral equal to infinity?
https://math.stackex[...]
[7]
서적
Pattern recognition and machine learning
http://worldcat.org/[...]
[8]
서적
Model Selection and Multi-Model Inference
https://archive.org/[...]
Springer
[9]
논문
Survey of Optimization Algorithms in Modern Neural Networks
2023-01
[10]
논문
Fubini-Study metrics and Levi-Civita connections on quantum projective spaces
https://linkinghub.e[...]
2021-12
[11]
논문
Policy mirror descent for reinforcement learning: linear convergence, new sampling complexity, and generalized problem classes
https://link.springe[...]
2023-03
[12]
논문
A New Interpretation of Information Rate
[13]
논문
Economics of Disagreement—Financial Intuition for the Rényi Divergence
[14]
논문
Information Geometry of Risks and Returns
[15]
논문
Flow Rider: Tradable Ecosystems' Relative Entropy of Flows As a Determinant of Relative Value
2024-09-30
[16]
논문
On the probability of large deviations of random magnitudes
[17]
서적
Extreme Value Methods with Applications to Finance
Chapman & Hall
[18]
서적
Concepts in statistical mechanics.
Gordon and Breach
1971
[19]
arXiv
Kullback-Leibler divergence between quantum distributions, and its upper-bound
[20]
문서
Relative Entropy video lecture
http://videolectures[...]
[21]
논문
Asymptotic evaluation of certain Markov process expectations for large time. IV.
[22]
웹사이트
Derivations for Linear Algebra and Optimization
https://web.stanford[...]
[23]
논문
Distributions of the Kullback-Leibler divergence with applications
http://dx.doi.org/10[...]
2011-04-15
[24]
서적
An intuition for physicists: information gain from experiments
http://worldcat.org/[...]
2022-04-29
[25]
논문
Bayesian experimental design: a review
[26]
서적
Numerical Recipes: The Art of Scientific Computing
Cambridge University Press
[27]
서적
Elements of Information Theory
John Wiley & Sons
1991
[28]
서적
Thermostatics and Thermodynamics: An Introduction to Energy, Information and States of Matter, with Engineering Applications
https://books.google[...]
Van Nostrand
1959
[29]
논문
Information theory and statistical mechanics
http://bayes.wustl.e[...]
[30]
논문
Information theory and statistical mechanics II
http://bayes.wustl.e[...]
[31]
서적
A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces
https://books.google[...]
The Academy
1871
[32]
논문
Energy and information
[33]
논문
Thermal roots of correlation-based complexity
http://www3.intersci[...]
[34]
논문
Kullback–Leibler information as a basis for strong inference in ecological studies
[35]
서적
Model selection and multimodel inference : a practical information-theoretic approach
http://worldcat.org/[...]
Springer
2010-12
[36]
논문
On the Jensen–Shannon Symmetrization of Distances Relying on Abstract Means
[37]
논문
On a Generalization of the Jensen–Shannon Divergence and the Jensen–Shannon Centroid
[38]
서적
Séminaire de Probabilités XII
http://dx.doi.org/10[...]
Springer Berlin Heidelberg
2023-02-14
[39]
서적
Introduction to nonparametric estimation
http://worldcat.org/[...]
Springer
2010
[40]
논문
The earth mover's distance as a metric for image retrieval
[41]
서적
Information, physics, and computation
https://www.worldcat[...]
Oxford University Press
2009
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com