추아 회로
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
추아 회로는 혼돈 현상을 보이는 간단한 전자 회로이다. 이 회로는 비선형 요소, 국소 활성 저항기, 3개 이상의 에너지 저장 요소를 포함하며, 두 개의 축전기, 하나의 인덕터, 그리고 추아 다이오드로 구성된다. 추아 회로는 복잡한 상미분 방정식으로 표현되며, 매개변수 값에 따라 다양한 형태의 혼돈 끌개를 나타낸다. 특히 "이중 두루마리" 끌개가 대표적이다. 쉬운 설계와 이론적 분석의 용이성으로 인해 혼돈 이론 연구에 널리 활용되며, 셀룰러 신경망 구현에도 사용된다. 또한, 자려 끌개 뿐만 아니라 숨겨진 끌개도 발견되었으며, 실험적으로도 혼돈 현상이 검증되었다.
더 읽어볼만한 페이지
| 추아 회로 | |
|---|---|
| 개요 | |
 | |
 | |
| 유형 | |
| 종류 | 전자 회로 |
| 개발 | |
| 발명가 | 레온 추아 |
| 발명 연도 | 1983년 |
| 발표 연도 | 1984년 |
| 특성 | |
| 동작 | 혼돈적 |
| 구성 요소 | 축전기 (2개) 저항 (1개) 인덕터 (1개) 추아 다이오드(비선형 저항 소자) (1개) |
2. 혼돈의 기준
자율 회로가 혼돈 행동을 보이기 위해서는 다음 세 가지 기준을 만족해야 한다.[3]
- 하나 이상의 비선형 요소
- 하나 이상의 저항
- 세 개 이상의 에너지 저장 장치
추아 회로는 이러한 기준을 만족하는 가장 간단한 회로이다.[3] 에너지 저장 장치는 두 개의 축전기(C1, C2)와 하나의 인덕터(L)이다.[4] 추아 회로는 저항, 두 개의 선형 저항, 두 개의 다이오드로 이루어진 비선형 저항을 포함한다. 가장 오른쪽에는 세 개의 선형 저항과 연산 증폭기 하나로 만들어진 부성 임피던스 변환기가 있는데, 이는 추아 다이오드를 구현한 것이다. 추아 다이오드는 상업적으로 판매되지 않지만, 간단한 부품들로 직접 만들 수 있다.

3. 회로 구성 및 분석
추아 회로는 혼돈 행동을 보이는 가장 간단한 회로로, 다음 세 가지 기준을 만족한다.[3]
# 하나 이상의 비선형 요소
# 하나 이상의 저항
# 세 개 이상의 에너지 저장 장치
에너지를 저장하는 장치는 두 개의 축전기(C1, C2)와 하나의 인덕터(L)이며,[4] 저항과 두 개의 다이오드로 구성된 비선형 저항이 있다. 비선형 저항은 '''''N''R''', 즉 "추아 다이오드"라는 장치에 결합되어 있는데, 이는 상업적으로 판매되지 않지만 능동 회로에서 다양한 방식으로 구현된다. 비선형 저항은 두 개의 선형 저항과 두 개의 다이오드로 구현된다. 맨 오른쪽에는 세 개의 선형 저항과 연산 증폭기로 만들어진 부성 임피던스 변환기가 있으며, 이는 국소 활성 저항(부성 저항)을 구현한다.
추아 회로는 쉬운 설계와 간단하고도 확실한 이론적 분석 덕분에 혼돈 이론의 근본과 최근 이슈를 연구하기 좋은 시스템이 되었다. 이로 인해 많은 연구의 대상이 되었으며, 넓은 범위의 논문에서도 등장한다.[18] 더욱이, 추아 회로는 다층 셀룰러 신경망(CNN)을 통해 쉽게 구현할 수 있다. 셀룰러 신경망은 1988년 리언 추아가 발명했다. 현재까지 많은 종류의 혼돈 끌개들이 추아 회로 속에서 발견되었으며,[18] 이들은 상대적으로 쉽게 계산을 통해 얻을 수 있다. 최근에는 숨겨진 추아 끌개가 전통적인 추아 회로에서 발견되었고,[19][20] 나중에 매끈하고 불연속적인 변수들이 특정되었다.[21][22]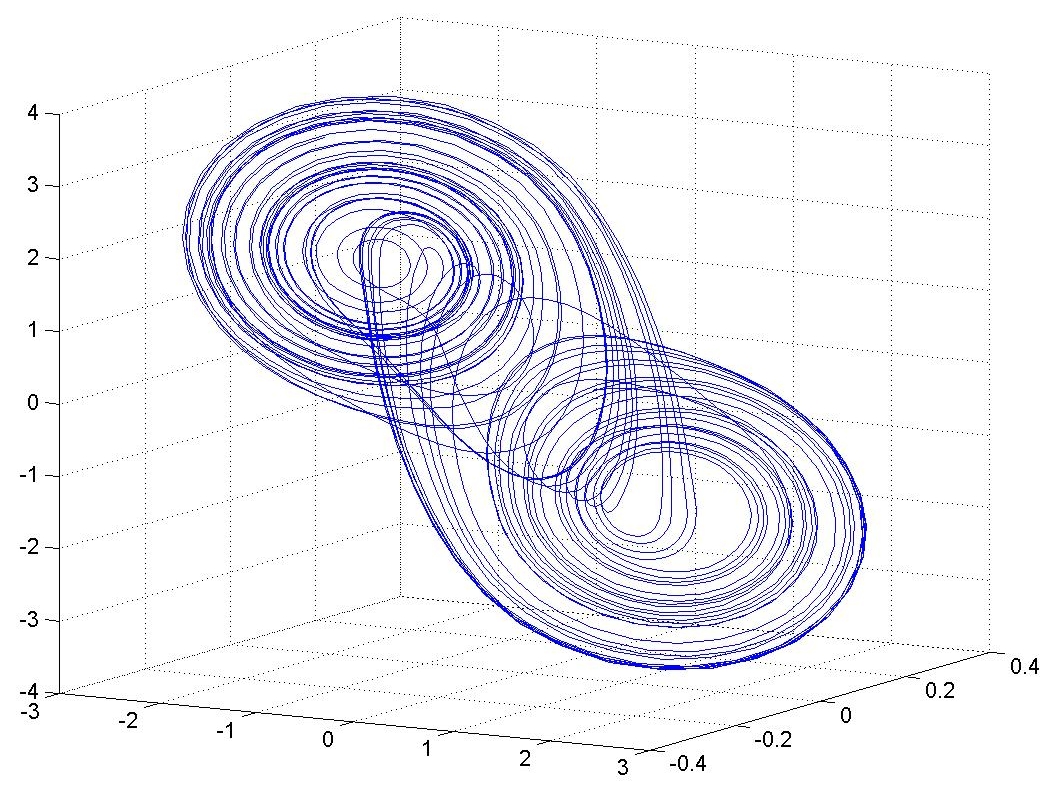


3. 1. 회로 방정식
전자기학의 법칙이나 키르히호프 회로 법칙을 적용하면, 추아 회로는 세 개의 비선형 상미분 방정식으로 정확히 설명할 수 있다. 이 방정식들은 축전기 C1, C2에 걸리는 전압과 코일 L1에 흐르는 전류의 세기를 각각 변수 x(t), y(t), z(t)로 나타낸다.[17][5]:
:
:
혹은
:
:
:
함수 f(x)는 비선형 저항에 걸리는 전압과 흐르는 전류의 관계이며, 이는 구성요소의 배치에 따라 달라질 수 있다. 계수 α, β는 회로 구성 부품의 특성에 의해 결정된다.[17]
4. 동역학 및 끌개
추아 회로는 키르히호프 회로 법칙을 사용하여 분석할 수 있으며, 이 회로의 동역학은 세 개의 비선형 상미분 방정식 시스템으로 정확하게 모델링할 수 있다. 이 방정식들은 커패시터 C1과 C2의 전압(각각 ''x''(''t''), ''y''(''t'')) 및 인덕터 L1의 전류(''z''(''t''))를 나타낸다.[5]
:
:
:
여기서 함수 ''f''(''x'')는 비선형 저항의 전기적 응답을 나타내며, 매개변수 α와 β는 회로 구성 요소의 값에 의해 결정된다.
1997년에는 추아 회로의 혼돈적 거동(보다 정확하게는 양의 위상 엔트로피)에 대한 컴퓨터 지원 증명이 발표되었다.[6] (< *x*, *y*, *z* ) 공간에서 그 형태 때문에 "더블 스크롤"로 알려진 자려 혼돈 어트랙터는 ''f''(''x'')가 3개 구간별 선형 함수인 비선형 요소를 포함하는 회로에서 처음 관찰되었다.[7]
추아 회로는 설계가 쉽고, 이론적 분석이 간단하며 확실하다는 장점 덕분에 혼돈 이론의 근본적인 문제와 최근 이슈들을 연구하기에 좋은 시스템이다. 이러한 이유로 추아 회로는 많은 연구의 대상이 되었고, 다양한 논문에서 널리 인용된다. 또한, 추아 회로는 1988년 리언 추아가 발명한 다층 셀룰러 신경망(CNN)으로 쉽게 구현할 수 있다.
현재까지 추아 시스템에서 다양한 유형의 자가 여기 카오스성 끌개가 다수 발견되었다.[9]
4. 1. 자려 끌개와 숨겨진 끌개

초기에는 0 근처의 초기 조건에서 시작하는 자려(self-excited) 끌개만 관찰되었다.[5] 이 경우, 수학적 모델에서 카오스성 끌개는 표준 계산 절차를 통해 비교적 쉽게 얻을 수 있는데, 과도 현상 후 불안정한 0 평형점의 작은 이웃 내에서 불안정한 매니폴드의 한 점에서 시작된 궤도가 자가 여기 어트랙터에 도달하여 계산된다.[5] 현재까지 추아 시스템에서 다양한 유형의 자가 여기 카오스성 끌개가 다수 발견되었다.[9]
그러나 2009년 N. 쿠즈네초프는 안정적인 0 평형과 공존하는 숨겨진 추아 끌개를 발견했고,[10][11] 이후 숨겨진 어트랙터의 발생에 대한 다양한 시나리오가 설명되었다.[12][5] 숨겨진 끌개는 초기 조건에 따라 다른 궤적을 보이며, 그 존재는 시스템의 안정성 및 예측 가능성에 대한 새로운 관점을 제시한다.
5. 실험적 검증
1985년, 캘리포니아 대학교 버클리 전자 연구소에서 추아 회로의 자가 여기 카오스에 대한 첫 번째 실험적 확인이 보고되었다.[13] 2022년 러시아 과학 아카데미 전파 공학 및 전자 공학 연구소의 이론적 비선형 역학 연구소에서 은닉 카오스의 첫 번째 확인이 보고되었다.[5][14]
6. 의의 및 활용
쉬운 설계와 간단하고도 확실한 이론적 분석 덕분에 추아 회로는 혼돈 이론의 근본과 최근 이슈를 연구하기 좋은 시스템으로 평가받는다. 이로 인해 많은 연구의 대상이 되었으며, 넓은 범위의 논문에서도 등장한다.[17] 더욱이, 추아 회로는 다층 셀룰러 신경망(cellular neural network, CNN)을 통해 쉽게 구현할 수 있다. 셀룰러 신경망은 1988년 리언 추아가 발명하였다. 현재까지 많은 종류의 혼돈 끌개들이 추아 회로 속에서 발견되었다.[18]
참조
[1]
논문
A Chaotic Attractor from Chua's Circuit
https://eecs.berkele[...]
IEEE
2008-05-01
[2]
서적
Chua's circuit: a paradigm for chaos
World Scientific Publishing Company
[3]
논문
Three steps to chaos – Part 1: Evolution
https://eecs.berkele[...]
Institute of Electrical and Electronics Engineers
2014-02-06
[4]
논문
Three steps to chaos – Part 2: A Chua's circuit primer
https://eecs.berkele[...]
Institute of Electrical and Electronics Engineers
2014-02-06
[5]
논문
Hidden attractors in Chua circuit: mathematical theory meets physical experiments
https://link.springe[...]
[6]
간행물
Positive topological entropy of Chua's circuit: a computer-assisted proof
https://eecs.berkele[...]
[7]
논문
The Double Scroll
IEEE
1985-08
[8]
간행물
Implementing memristor based chaotic circuits
http://harpgroup.org[...]
World Scientific Publishing Company
[9]
서적
Gallery of Chua Attractors
World Scientific
[10]
논문
Localization of hidden Chua's attractors
http://www.math.spbu[...]
[11]
논문
Hidden attractors in dynamical systems. From hidden oscillations in Hilbert–Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits
[12]
논문
Scenario of the birth of hidden attractors in the Chua circuit
[13]
논문
Experimental confirmation of chaos from Chua's circuit
http://doi.wiley.com[...]
1985-01
[14]
웹사이트
Mathematicians prove the existence of hidden attractors in an electrical circuit
https://phys.org/new[...]
2023-01-25
[15]
논문
A Chaotic Attractor from Chua's Circuit
http://www.eecs.berk[...]
IEEE
1984-12
[16]
서적
Chua's circuit: a paradigm for chaos
World Scientific Publishing Company
[17]
논문
The Double Scroll
http://ieeexplore.ie[...]
IEEE
1985-08
[18]
서적
Gallery of Chua Attractors
https://archive.org/[...]
World Scientific
[19]
논문
Localization of hidden Chua's attractors
http://www.math.spbu[...]
[20]
논문
Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits
http://www.worldscie[...]
[21]
논문
Hidden attractor in smooth Chua systems
http://www.math.spbu[...]
[22]
논문
Analytical-numerical localization of hidden attractor in electrical Chua’s circuit
http://www.math.spbu[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
