펜로즈 그림

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 기본 원리 및 특징
3. 주요 시공간의 펜로즈 그림
4. 펜로즈 그림의 활용
- 4.1. 블랙홀 연구
5. 역사
참조

1. 개요

펜로즈 그림은 점근적으로 평탄한 시공간의 인과 구조를 보존하면서 무한대를 유한한 영역으로 사상하는 등각 변환을 기반으로 한다. 펜로즈 그림은 시공간의 무한대 구조를 시각화하여 블랙홀, 웜홀, 우주론 연구 등 다양한 분야에 활용되며, 로저 펜로즈와 브랜든 카터에 의해 1960년대에 처음 소개되었다. 펜로즈 그림은 시공간의 인과 구조를 유계 영역으로 표현하여, 45° 각도로 그려진 두 선은 실제 시공간에서 해당 두 광선이 교차하는 경우에만 도표에서 교차하도록 설계된다.

더 읽어볼만한 페이지

로런츠 다양체 - 중력 특이점
중력 특이점은 일반 상대성이론에서 시공간이 정의되지 않고 물리량이 무한대로 발산하는 지점으로, 다양한 형태로 나타나며 이론에 따라 존재가 부정되거나 사건 지평선 뒤에 숨겨져 있다고 여겨지기도 하고 블랙홀의 엔트로피와 관련된 호킹 복사 이론과도 관련된다.
로런츠 다양체 - 크리스토펠 기호
크리스토펠 기호는 미분기하학에서 미분 다양체 위의 계량 텐서와 좌표계를 사용하여 정의되는 기호로, 제1종과 제2종으로 나뉘며 레비-치비타 접속의 접속 계수를 나타내고, 일반 상대성 이론에서 시공간의 기하학 기술 및 측지선 방정식 계산, 고전 역학에서 가상적인 힘 설명에 활용되며 1869년 엘빈 브루노 크리스토펠에 의해 도입되었다.
다이어그램 - 회로도
회로도는 전기 또는 전자 회로의 구성 요소와 연결을 기호와 선으로 나타낸 도식적 표현으로, 표준화된 기호와 규칙을 따르며 전자 제품 설계 및 교육에 필수적인 도구이지만 표기법 통일은 아직 완벽하지 않다.
다이어그램 - 헤르츠스프룽-러셀 도표
헤르츠스프룽-러셀 도표(HR도표)는 항성의 광도와 표면 온도 관계를 나타내는 그래프로, 항성의 분류, 진화 단계, 물리적 특성을 이해하는 데 필수적인 도구이며, 주계열성, 거성, 초거성 등 다양한 항성의 종류와 분포를 보여주며 항성물리학 발전에 기여한다.
일반 상대성이론 - 양자 중력
양자 중력은 양자역학과 일반 상대성이론을 통합하여 중력이 강한 극한 조건에서 발생하는 이론적 모순을 해결하려는 시도로, 재규격화 불능성과 시공간 배경 의존성 차이 등의 난제 해결을 위해 끈 이론, 루프 양자 중력 등 다양한 접근 방식이 연구되고 있으며, 우주 마이크로파 배경 데이터 등을 이용한 실험적 검증이 시도되고 있다.
일반 상대성이론 - 중력 특이점
중력 특이점은 일반 상대성이론에서 시공간이 정의되지 않고 물리량이 무한대로 발산하는 지점으로, 다양한 형태로 나타나며 이론에 따라 존재가 부정되거나 사건 지평선 뒤에 숨겨져 있다고 여겨지기도 하고 블랙홀의 엔트로피와 관련된 호킹 복사 이론과도 관련된다.

펜로즈 그림
개요
유형	2차원 다이어그램
목적	시공간 내의 다른 지점들 간의 인과 관계를 나타냄
관련 개념	인과 구조
고안자	로저 펜로즈
다른 이름	컨포멀 다이어그램 펜로즈-카터 다이어그램 (브랜든 카터의 공헌을 기리기 위해)
상세 정보
특징	시공간의 인과 구조를 나타내는 다이어그램 무한한 시공간 영역을 유한한 크기로 표현 광선의 궤적은 45도 각도의 선으로 표현
사용 예시	블랙홀의 사건 지평선, 특이점 등의 시공간 구조 분석
주의 사항	거리 정보는 보존되지 않음 (등각 변환 사용)

2. 기본 원리 및 특징

펜로즈 도표는 브랜든 카터와 로저 펜로즈의 이름을 따서 펜로즈-카터 도표 또는 카터-펜로즈 도표라고도 불리며, 등각 도표 또는 시공간 도표라고도 불린다.^[2] 펜로즈 도표는 점근적으로 평탄한 시공간과 같은 좌표 벡터 시스템을 공유하지만, 멀리 떨어진 거리를 축소하여 무한대를 유한한 영역으로 사상(mapping)하는 등각 변환을 기반으로 한다.^[1]

펜로즈 도표에서 일정한 시간의 직선과 일정한 공간 좌표의 직선은 쌍곡선이 되어 도표의 모서리에서 수렴하는 것처럼 보인다. 이 점과 경계는 시공간의 등각 무한대를 나타낸다. 45° 각도로 그려진 두 선은 실제 시공간에서 해당 두 광선이 교차하는 경우에만 도표에서 교차하며, 펜로즈 도표의 대각선 경계선은 "영 무한대" 또는 광선이 끝나야 하는 특이점에 해당한다.^[1]

무한 정적 민코프스키 우주는 좌표 $(x, t)$ 가 펜로즈 좌표 $(u, v)$ 와 $\tan(u \pm v) = x \pm t$ 의 관계를 가지며, 시공간 및 시간형 등각 무한대를 나타내는 펜로즈 도표의 모서리는 원점에서 $\pi /2$ 이다.

2. 1. 등각 변환

등각 변환은 각도를 보존하는 변환이다. 펜로즈 그림에서 빛의 경로는 항상 45° 각도로 유지되는데, 이는 시공간의 계량(metric)에 특정 함수(등각 인자)를 곱하는 방식으로 이루어진다. 이러한 변환을 통해 시공간의 무한대가 유한한 점 또는 선으로 표현된다.^[1]

45° 각도로 그려진 두 선은 실제 시공간에서 해당 두 광선이 교차하는 경우에만 펜로즈 그림에서 교차한다. 펜로즈 그림의 대각선 경계선은 "영 무한대"라고 불리는 영역 또는 광선이 끝나야 하는 특이점에 해당한다. 따라서 펜로즈 그림은 시공간의 점근적 특성과 특이점 연구에 유용하다.^[2]

민코프스키 공간과 반 더 시터르 공간의 등각 무한대는 다음과 같이 분류된다.

공간	공간 무한대	미래 무한대	과거 무한대	미래 영벡터 무한대	과거 영벡터 무한대
민코프스키 공간	$(u,v)=(\pi/2,0)$ 에 붙어 있는 $d-1$ 차원 초구	$(u,v)=(0,\pi/2)$ 에 붙어 있는 점	$(u,v)=(0,\pi/2)$ 에 붙어 있는 점	\{(u,v)>u+v=\pi/2\}에 붙어 있는 점들 (밑이 초구 $S^{d-1}$ 인 초구뿔 모양)	\{(u,v)>u-v=\pi/2\}에 붙어 있는 점들 (밑이 초구 $S^{d-1}$ 인 초구뿔 모양)
반 더 시터르 공간	$S^{d-1}\times\mathbb R$	하나의 점	하나의 점	해당사항 없음	해당사항 없음

2. 2. 인과 구조

펜로즈 도표는 블랙홀을 포함하는 시공간의 인과적 구조를 설명하는 데 자주 사용된다. 슈바르츠실트 블랙홀에서 특이점은 일반적인 시공간 도표와는 다르게 공간꼴 경계로 나타나는데, 이는 블랙홀의 지평선 안에서 시간꼴 좌표와 공간꼴 좌표가 서로 바뀌기 때문이다.^[10]^[11] 물체가 지평선을 통과하면 특이점을 피할 수 없다는 것을 명확하게 보여주기 위해 특이점은 공간꼴 경계로 표현된다.

펜로즈 도표는 종종 최대로 확장된 슈바르츠실트 해에서 두 개의 분리된 우주를 연결하는 가상의 아인슈타인-로젠 다리(웜홀)를 설명하는 데 사용된다. 크러스컬-세케레스 좌표를 전신으로 하며, 구멍에서 멀리 떨어진 평평한 시공간 영역을 등각 수축하여 표현한다. 사건의 지평선은 45° 각도로 정렬되며, 수학적 특이점은 과거 및 미래의 수평선으로 나뉜다. 아인슈타인-로젠 다리는 매우 빠르게 닫히기 때문에 두 개의 점근적으로 평평한 외부 영역 사이를 통과하려면 빛보다 빠른 속도가 필요하여 통과가 불가능하다. 또한, 매우 청색 편이된 광선(청색 시트)은 통과를 불가능하게 한다.

최대로 확장된 해는 별의 붕괴로 생성된 전형적인 블랙홀을 설명하지 않는다. 붕괴된 별의 표면은 과거를 향한 ''백색 왜성'' 기하학 및 다른 우주를 포함하는 해의 영역을 대체한다. 정적 블랙홀의 기본 공간꼴 통로는 통과할 수 없지만, 케르 계량 및/또는 라이스너-노르드스트룀 계량을 나타내는 해에 대한 펜로즈 도표는 내부 사건 지평선(미래에 위치)과 수직으로 향하는 특이점을 보여준다. 이는 시간꼴 "웜홀"을 통해 미래 우주로 통과할 수 있음을 보여준다. 회전하는 구멍의 경우, 고리 모양의 특이점을 통과하여 "음"의 우주로 들어갈 수도 있다. 그러나 이러한 해의 특징은 섭동에 대해 안정적이지 않으며, 그러한 블랙홀 내부의 현실적인 묘사로 여겨지지 않는다. 우주 검열 가설에 따르면 그들의 내부의 진정한 특성은 아직 밝혀지지 않았다.

공형 변환은 시공간의 인과 구조를 보존하므로, 펜로즈 그림은 원래 시공간의 인과 구조를 정확하게 재현한다. 민코프스키 시공간의 시간 좌표 및 공간 좌표를 각각

T

,

R

로 표현하면, 이들은 좌표

( U, V )

와 다음 관계를 가진다.

:

U = T - R , \ \ V = T + R

펜로즈 그림은 시공간의 인과 구조를 유계 영역으로 표현하여, 원래 시공간의 무한대 구조를 시각화할 수 있다.

모든 공간적 측지선 $t = \mathrm{Const.}$ 는 점 $( T, R ) = \left( 0, \frac{ \pi }{ 2 } \right)$ 를 지나는 공간적 곡선으로 표현된다. 이 점은 공간적 무한대 $i^0$ 라고 불린다.
모든 시간적 측지선 $r = \mathrm{Const.}$ 는 두 점 $( T, R ) = \left( \pm \frac{ \pi }{ 2 }, 0 \right)$ 을 잇는 시간적 곡선으로 표현된다. 이 두 점은 시간적 무한대 $i^\pm$ 라고 불린다.
모든 널 측지선 $t \mp r = \mathrm{Const.}$ 는 공간적 무한대 $i^0$ 와 시간적 무한대 $i^\pm$ 를 잇는 널 곡선과 교차한다. 이 곡선은 널 무한대 $\mathcal{I}^\pm$ 라고 불린다.

2. 3. 무한대의 표현

펜로즈 그림에서 시공간의 무한대는 유한한 경계로 표현된다. 이를 통해 시공간의 전체적인 구조를 한눈에 파악할 수 있다.^[10]^[11]

공간 무한대 ( $i^0$ ): 모든 공간적 측지선( $t = \mathrm{Const.}$ )이 지나는 점으로, $( T, R ) = \left( 0, \frac{ \pi }{ 2 } \right)$ 로 표현된다.
시간꼴 무한대 ( $i^\pm$ ): 모든 시간적 측지선( $r = \mathrm{Const.}$ )이 지나는 두 점으로, $( T, R ) = \left( \pm \frac{ \pi }{ 2 }, 0 \right)$ 으로 표현된다.
영벡터 무한대 ( $\mathcal{I}^\pm$ ): 모든 영벡터 측지선( $t \mp r = \mathrm{Const.}$ )이 지나는 곡선으로, 공간 무한대 ( $i^0$ )와 시간꼴 무한대 ( $i^\pm$ )를 잇는다.

3. 주요 시공간의 펜로즈 그림

펜로즈 도표는 블랙홀을 포함하는 시공간의 인과적 구조를 설명하는 데 유용하게 사용된다. 특히 슈바르츠실트 블랙홀의 경우, 특이점은 일반적인 시공간 도표에서 시간꼴 경계로 표시되는 것과 달리 공간꼴 경계로 나타난다. 이는 블랙홀의 지평선 안쪽에서는 시간꼴 좌표와 공간꼴 좌표가 서로 바뀌기 때문이다.^[13] 이러한 특성 때문에, 물체가 지평선을 통과하면 특이점을 피할 수 없게 된다.

펜로즈 도표는 종종 최대로 확장된 슈바르츠실트 해에서 두 개의 개별 우주를 연결하는 가상의 아인슈타인-로젠 다리(웜홀)를 묘사하는 데에도 사용된다. 펜로즈 도표는 크러스컬-세케레스 좌표를 기반으로 만들어졌는데, 사건의 지평선을 45° 각도로 정렬하고 수학적 특이점을 과거와 미래의 수평선으로 분할하는 방식이 도입되었다.

하지만 아인슈타인-로젠 다리는 매우 빠르게 닫히기 때문에 두 외부 영역 사이를 통과하려면 빛보다 빠른 속도가 필요하며, 이는 불가능하다. 또한, "청색 시트"라고 불리는 매우 청색 편이된 광선이 통과를 방해한다.

최대로 확장된 해는 별의 붕괴로 생성된 전형적인 블랙홀을 설명하지 않는다. 붕괴된 별의 표면은 과거를 향한 백색 왜성 기하학 및 다른 우주를 포함하는 해의 영역을 대체한다.

정적 블랙홀의 기본 공간꼴 통로는 통과할 수 없지만, 회전하거나 대전된 블랙홀을 나타내는 케르 계량 및 라이스너-노르드스트룀 계량의 펜로즈 도표에서는 내부 사건 지평선과 수직으로 향하는 특이점이 나타난다. 이는 시간꼴 "웜홀"을 통해 미래 우주로 이동할 수 있게 한다. 회전하는 블랙홀의 경우, 고리 모양의 특이점을 통해 "음"의 우주로 들어갈 수도 있다. 그러나 이러한 특징들은 섭동에 대해 안정적이지 않으며, 실제 블랙홀 내부를 묘사하는 것으로 여겨지지 않는다.

3. 1. 민코프스키 공간

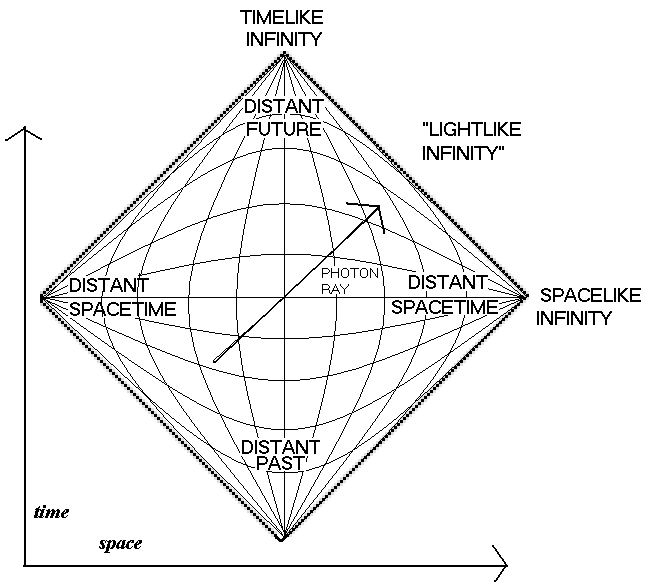
특수 상대성 이론의 배경이 되는 평탄한 시공간인 민코프스키 공간의 펜로즈 그림은 마름모꼴로 표현된다. 2차원 민코프스키 공간의 펜로즈 그림에서, 시간꼴 무한대는 위아래 두 점으로, 공간꼴 무한대는 오른쪽 한 점으로 나타나며, 영벡터 무한대는 마름모의 경계를 이루는 선분으로 표현된다.^[1]^[2]

시간 1차원, 공간 3차원의 4차원 민코프스키 시공간의 점(사건)은 시각

t

, 공간 좌표

(x, y, z)

의 조합

(t, x, y, z)

로 표현된다.^[5] 이 계량은 다음과 같다.

:

ds^2 = - dt^2 + dx^2 + dy^2 + dz^2

구 좌표

(r, \theta, \phi)

를 사용하면 다음과 같다.

:

ds^2 = - dt^2 + dr^2 + r^2 d\Omega^2 , \ \ d \Omega^2 = d\theta^2 + \sin^2 \theta d\phi^2

시각

t

와 동경 좌표

r

은 각각

- \infty < t < \infty

,

0 \leq r < \infty

라는 범위의 값을 가지므로, 이 좌표계에서는 민코프스키 시공간은

(t, r)

-평면상의 비유계 영역으로 도식화된다.

시공간의 인과 구조를 논의할 때는 다음 좌표 변환

(t, x) \mapsto (u, v)

에 의해 널 좌표

(u, v)

를 도입하는 것이 편리하다.^[6]

:

u = t - r, \ \ v = t + r

이 새로운 좌표

(u, v)

에서 계량은

:

ds^2 = - du \, dv + r^2 d\Omega^2

로 표현된다.^[6]

좌표

(u, v)

에 대해 다음 변환

(u, v) \mapsto (U, V)

를 적용한다.^[7]

:

U = \arctan u , \ \ V = \arctan v

:

ds^2 = - \frac{ 1 }{ \cos^2 U \cos^2 V } dU \, dV + r^2 d\Omega^2

이 좌표는

- \frac{ \pi }{ 2 } < U < \frac{ \pi }{ 2 }

,

- \frac{ \pi }{ 2 } < V < \frac{ \pi }{ 2 }

를 만족한다. 그러므로, 등각 변환

dS^2 = \cos^2 U \cos^2 V ds^2

에 의해 좌표

(U, V)

가 나타내는 시공간 영역은 평탄한 2차원 민코프스키 시공간의 유계 영역으로 매립할 수 있다.^[8] 이렇게 얻어지는 원래의 민코프스키 시공간의 유계 표현이 펜로즈 그림이다.^[9]

매립 대상인 민코프스키 시공간의 시간 좌표 및 공간 좌표를 각각

T

,

R

로 표현할 때, 이는 좌표

( U, V )

와

:

U = T - R , \ \ V = T + R

라는 관계에 있다.

펜로즈 그림은 원래 시공간의 무한대 구조를 시각화할 수 있다.^[10]^[11]

모든 공간적 측지선 $t = \mathrm{Const.}$ 는 점 $( T, R ) = \left( 0, \frac{ \pi }{ 2 } \right)$ 을 지나는 공간적 곡선으로 표현된다. 이 점은 공간적 무한대 $i^0$ 라고 불린다.
모든 시간적 측지선 $r = \mathrm{Const.}$ 는 두 점 $( T, R ) = \left( \pm \frac{ \pi }{ 2 }, 0 \right)$ 을 잇는 시간적 곡선으로 표현된다. 이 두 점은 시간적 무한대 $i^\pm$ 라고 불린다.
모든 널 측지선 $t \mp r = \mathrm{Const.}$ 는 공간적 무한대 $i^0$ 와 시간적 무한대 $i^\pm$ 를 잇는 널 곡선과 교차한다. 이 곡선은 널 무한대 $\mathcal{I}^\pm$ 라고 불린다.

3. 2. 더 시터르 공간

더 시터르 공간의 펜로즈 그림. 왼쪽 변은 공간의 북극, 오른쪽 변은 공간의 남극을 나타낸다. 윗변은 무한 미래, 아랫변은 무한 과거를 나타낸다.

더 시터르 공간의 펜로즈 그림은 정사각형이다. 더 시터르 공간은 위상학적으로

S^3\times\mathbb R

이므로, 펜로즈 그림에서 오른쪽 변과 왼쪽 변은 실제 공간에서 각각 하나의 점을 나타낸다. (그러나 무한한 미래와 과거를 나타내는 윗변과 아랫변은 그렇지 않다.)

3. 3. 반 더 시터르 공간

d^영어+1차원 반 더 시터르 공간의 펜로즈 그림은 더 시터르 공간의 펜로즈 그림과 유사하지만, 윗변·아랫변이 한 점만을 포함하며 오른·왼변의 각 점은 초구

S^{d-1}

를 나타낸다. 즉, 그 등각 경계는

S^{d-1}\times\mathbb R

이며, 이는 원점을 제거한 민코프스키 공간

\mathbb R^d\setminus\{0\}

과 바일 변환으로 동치이다.

종류	내용
공간 무한대	$S^{d-1}\times\mathbb R$
미래 무한대	하나의 점
과거 무한대	하나의 점

3. 4. 블랙홀

슈바르츠실트 계량이나 커 계량의 펜로즈 그림은 매우 복잡한 형상을 보인다. 블랙홀 밖 실제 우주의 등각 무한대 외에도, 블랙홀 내부 반대편에 화이트홀 등의 등각 확장이 존재한다.

실재하는 (유한한 과거에서 생성된) 블랙홀은 이러한 복잡한 구조를 갖지 않는다. 펜로즈 도표는 블랙홀을 포함하는 시공간의 인과적 구조를 설명하는 데 사용된다.

펜로즈 도표는 최대로 확장된 슈바르츠실트 해에서 두 개의 개별 우주를 연결하는 가상의 아인슈타인-로젠 다리를 설명하는 데 사용되기도 한다. 펜로즈 도표의 전신은 크러스컬-세케레스 좌표였다. 이는 사건의 지평선을 과거 및 미래 지평선에 45° 각도로 정렬하고, 수학적 특이점을 과거 및 미래의 수평선으로 향하는 선으로 분할하는 방법을 도입했다.

아인슈타인-로젠 다리는 매우 빠르게 닫히기 때문에("미래" 특이점을 형성) 두 개의 점근적으로 평평한 외부 영역 사이를 통과하려면 빛보다 빠른 속도가 필요하여 불가능하다. 또한 매우 청색 편이된 광선('청색 시트'라고 함)은 통과를 불가능하게 한다.

블랙홀 시공이란 시간적 무한원점

i^+

으로부터 인과적으로 도달 불가능한 영역이 존재하는 시공을 말하며, 그러한 영역의 경계를 사상의 지평선이라고 부른다.

3. 4. 1. 슈바르츠실트 블랙홀

슈바르츠실트 해는 질량

M

의 질점이 만드는 중력장을 나타내는 아인슈타인 방정식의 엄밀해로, 가장 단순한 블랙홀 시공간이다.^[12] 슈바르츠실트 시공간의 펜로즈 그림은 사건의 지평선과 특이점을 포함하여 여러 영역으로 구성된다. 펜로즈 도표에서 특이점은 일반적인 시공간 도표와 달리 공간꼴 경계로 표시되는데, 이는 블랙홀의 지평선 내에서 시간꼴 좌표와 공간꼴 좌표가 서로 바뀌기 때문이다.^[13]

최대 확장된 슈바르츠실트 시공간의 펜로즈 도표는

:

\tilde{U} = \arctan U , \ \ \tilde{V} = \arctan V

에 의해 도입할 수 있다.^[17] 이 펜로즈 도표에서 슈바르츠실트 시공간에는 시간적 무한대

i^+

와 인과적으로 연결되지 않은 영역이 존재하며, 이를 블랙홀이라고 부른다.^[18]

3. 4. 2. 커 블랙홀

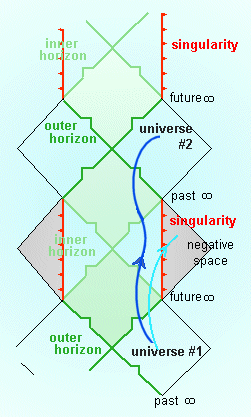
커 블랙홀의 펜로즈 그림은 슈바르츠실트 블랙홀보다 복잡하다. 내부 사건의 지평선과 고리 모양의 특이점을 포함하며, 수직으로 향하는 특이점은 시간꼴 "웜홀"을 통해 미래 우주로 이동할 수 있게 한다. 또한, 고리 모양의 특이점을 통해 "음"의 우주로 들어갈 수도 있다. 그러나 이러한 특징은 섭동에 대해 안정적이지 않아 실제 블랙홀 내부를 묘사하는 것으로 여겨지지 않는다.

3. 4. 3. 중력 붕괴

실제 별의 중력 붕괴로 형성되는 블랙홀의 펜로즈 그림은 점근적으로 평탄한 외부 영역과 블랙홀 내부 영역으로 구성된다.^[19]

4. 펜로즈 그림의 활용

펜로즈 그림은 블랙홀, 웜홀, 우주론 등 다양한 상대론적 천체 물리학 연구에 활용된다.^[10]^[11]

4. 1. 블랙홀 연구

펜로즈 그림은 블랙홀의 인과 구조, 사건의 지평선, 특이점 등을 분석하는 데 사용된다. 특히, 블랙홀 내부의 구조와 진화를 이해하는 데 중요한 역할을 한다.^[10]^[11]

펜로즈 도표는 블랙홀을 포함하는 시공간의 인과적 구조를 설명하는 데 사용된다. 슈바르츠실트 블랙홀에서의 특이점은 일반적인 시공간 도표와 달리 공간꼴 경계로 표시되는데, 이는 블랙홀의 지평선 내에서 시간꼴 좌표와 공간꼴 좌표가 서로 바뀌기 때문이다.^[12]

슈바르츠실트 계량이나 커 계량의 펜로즈 그림은 매우 복잡하다. 블랙홀 밖의 실제 우주 외에도 블랙홀 내부의 반대편에 존재하는 화이트홀 등의 등각 확장이 존재한다. 그러나 실제로 유한한 과거에서 생성된 블랙홀은 이러한 복잡한 구조를 갖지 않는다.

펜로즈 도표는 최대로 확장된 슈바르츠실트 해에서 두 개의 개별 우주를 연결하는 가상의 아인슈타인-로젠 다리를 설명하는 데에도 사용된다. 하지만 아인슈타인-로젠 다리는 매우 빠르게 닫히기 때문에 두 영역 사이를 통과하는 것은 불가능하다.

정적 블랙홀의 기본 공간꼴 통로는 통과할 수 없지만, 케르 계량 및/또는 라이스너-노르드스트룀 계량을 나타내는 해에 대한 펜로즈 도표는 내부 사건 지평선과 수직으로 향하는 특이점을 보여준다. 그러나 이러한 특징은 섭동에 대해 안정적이지 않으며, 블랙홀 내부를 현실적으로 묘사한다고 보기 어렵다. 우주 검열 가설에 따르면, 블랙홀 내부의 진정한 특성은 아직 밝혀지지 않은 문제이다.

5. 역사

로저 펜로즈^[21]^[22]가 1960년대에 브랜든 카터(Brandon Carter|브랜든 카터^영어)^[20]와 함께 도입하였다.

참조

_[1] 논문 Asymptotic proprierties of fields and space-times 1963-01-15
_[2] 서적 Spacetime and Geometry – An Introduction to General Relativity Addison Wesley
_[3] 문서 Poisson, p. 129
_[4] 웹사이트 大学院一般相対論講義マスターファイル https://research.kek[...] 2020-10-01
_[5] 문서 本記事では[[光速]] $c$ および[[重力定数]] $G$ を 1 とする単位系を用いる。従って時間 $t$ と空間座標 $x$ はどちらも距離の次元を持つ。
_[6] 문서 Hawking & Ellis, p. 118
_[7] 문서 Hawking & Ellis, pp. 120-121
_[8] 문서 Hawking & Ellis, pp. 121-122
_[9] 문서 Hawking & Ellis, p. 123
_[10] 문서 Hawking & Ellis, pp. 121-123
_[11] 문서 Poisson, p. 130
_[12] 문서 Poisson, p. 125
_[13] 문서 Poisson, p. 126
_[14] 문서 Poisson, pp. 126-127
_[15] 문서 Poisson, pp. 127-128
_[16] 문서 Hawking & Ellis, pp. 154-156
_[17] 문서 Poisson, pp. 129-130
_[18] 문서 Poisson, pp. 130-131
_[19] 문서 Hawking & Ellis, p. 309
_[20] 논문
_[21] 저널 https://archive.org/[...]
_[22] 논문

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com