폴리아몬드
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
폴리아몬드는 "많은"을 뜻하는 접두사 "poly-"와 다이아몬드를 의미하는 "iamond"의 합성어이다. 이는 2개의 삼각형이 연결된 형태의 다이아몬드를 구성하는 삼각형을 의미한다. 폴리아몬드는 정삼각형의 수에 따라 모니아몬드, 다이아몬드 등으로 분류되며, 주어진 개수의 셀을 가진 서로 다른 폴리아몬드의 개수를 세는 조합 문제가 존재한다. 폴리아몬드는 자유형과 일면형으로 구분되며, 8차 이하의 모든 폴리아몬드는 평면 타일링이 가능하다. 또한, 폴리헥스와 대응되며, 보드 게임 블로커스 트리곤의 말 모양으로 사용된다.
더 읽어볼만한 페이지
- 폴리폼 - 테트로미노
테트로미노는 4개의 정사각형이 변끼리 연결된 폴리오미노로, 회전 및 반사 고려 방식에 따라 자유, 단면, 고정 테트로미노로 나뉘며, 직사각형 채우기 퍼즐과 테트리스 게임에 활용된다. - 폴리폼 - 폴리오미노
폴리오미노는 n개의 정사각형을 변으로 연결하여 만든 도형으로, 평행이동, 회전, 반사를 통해 겹쳐지는지에 따라 분류되며, 테트리스와 같은 게임에 활용된다. - 다각형 - 대각선
대각선은 다각형이나 다면체에서 서로 인접하지 않은 꼭짓점을 연결하는 선분이며, 다각형은 변의 개수에 따라, 다면체는 면의 위치에 따라 대각선의 개수와 종류가 달라지고, 기하학에서는 데카르트 곱의 부분 집합으로 정의되기도 한다. - 다각형 - 내접원
내접원은 다각형의 모든 변에 접하는 원으로, 중심을 내심이라 하고, 내접원을 갖는 다각형을 외접 다각형이라 하며, 모든 삼각형은 내접원을 가지고, 사각형의 내접원 조건, 쌍심사각형 등의 개념이 있으며, 반지름은 면적과 둘레로 계산 가능하다.
| 폴리아몬드 | |
|---|---|
| 정의 | |
| 설명 | 폴리아몬드는 정삼각형을 기본 단위로 하는 폴리폼이다. 폴리아몬드는 각 변이 다른 폴리아몬드와 완전히 일치하도록 변끼리 연결된 하나 이상의 동일한 정삼각형으로 구성된 평면 도형이다. 폴리아몬드는 폴리오미노의 삼각형 유사체이다. |
| 명칭 | |
| 어원 | "폴리-"와 "다이아몬드"의 합성어이다. 여기서 "다이아몬드"는 정삼각형 두 개가 합쳐진 모양에서 유래했다. |
| 폴리아몬드 종류 및 개수 | |
| 모노아몬드 | 1개 (정삼각형) |
| 다이아몬드 | 1개 (두 개의 정삼각형이 평행사변형을 이룸) |
| 트리아몬드 | 3개 |
| 테트라아몬드 | 4개 |
| 펜타아몬드 | 12개 |
| 헥사아몬드 | 24개 (6개의 폴리아몬드가 육각형을 이룸) |
| 헵타아몬드 | 82개 |
| 옥타아몬드 | 333개 |
| 노나아몬드 | 1448개 |
| 데카아몬드 | 6226개 |
| 운데카아몬드 | 26660개 |
| 도데카아몬드 | 114679개 |
2. 명칭
'''폴리아몬드'''라는 명칭은 "많은"을 의미하는 접두사 ''poly-''와 ''iamond''에서 유래되었다.
폴리아몬드는 정삼각형 여러 개를 이어 붙여 만든 평면도형이다. 기본적인 조합 문제는 주어진 개수의 정삼각형으로 만들 수 있는 서로 다른 폴리아몬드가 몇 가지인지 묻는 것이다. 폴리오미노와 마찬가지로, 폴리아몬드는 자유형, 일면형, 고정형으로 분류할 수 있다. 자유 폴리아몬드는 평행이동, 회전, 반사에 대해 모두 같은 모양으로 취급하며, 일면 폴리아몬드는 반사된 모양을 다른 모양으로 취급한다.
''iamond''는 2개의 삼각형이 연결된 형태의 다이아몬드 ''diamond''를 ''d-''와 ''iamond''로 분해하여 만든 조어이며, 다이아몬드를 구성하는 삼각형을 의미한다.
3. 종류 및 개수
''n'' = 1, 2, 3, ...일 때, 자유 ''n''-아몬드의 개수는 다음과 같다.
: 1, 1, 1, 3, 4, 12, 24, 66, 160, ...
일부 저자는 다이아몬드 (60° 각도의 마름모)를 프랑스 과자와 비슷한 모양을 따서 ''칼리송''이라고도 부른다.[2][3]
3. 1. 폴리아몬드의 종류
폴리아몬드는 사용되는 정삼각형의 수에 따라 다음과 같이 불린다.
| n | 명칭 | 종류 | 종류(한 면) | 종류(유향) |
|---|---|---|---|---|
| 1 | 모니아몬드 | 1 | 1 | 2 |
| 2 | 다이아몬드 | 1 | 1 | 3 |
| 3 | 트리아몬드 | 1 | 1 | 6 |
| 4 | 테트라아몬드 | 3 | 4 | 14 |
| 5 | 펜타아몬드 | 4 | 6 | 36 |
| 6 | 헥사아몬드 | 12 | 19 | 94 |
| 7 | 헵타아몬드 | 24 | 43 | 250 |
| 8 | 옥타아몬드 | 66 | 120 | 675 |
| 9 | 노니아몬드 | 160 | 307 | 1838 |
| 10 | 데시아몬드 | 448 | 866 | 5053 |





3. 2. 폴리아몬드의 개수 세기
기본적인 조합 문제는 주어진 개수의 셀을 가진 서로 다른 폴리아몬드가 몇 개나 존재하는가이다. 폴리오미노와 마찬가지로, 폴리아몬드는 자유형 또는 일면형일 수 있다. 자유 폴리아몬드는 평행 이동 및 회전뿐만 아니라 반사에 대해서도 불변이다. 일면 폴리아몬드는 반사를 구별한다.''n'' = 1, 2, 3, ...에 대한 자유 ''n''-아몬드의 수는 다음과 같다.
: 1, 1, 1, 3, 4, 12, 24, 66, 160, ...
폴리아몬드는 사용되는 정삼각형의 수에 따라 다음과 같이 불린다.
| 명칭 | 종류 | 종류(한 면) | 종류(유향) | |
|---|---|---|---|---|
| 1 | 모니이아몬드 | 1 | 1 | 2 |
| 2 | 다이아몬드 | 1 | 1 | 3 |
| 3 | 트리아몬드 | 1 | 1 | 6 |
| 4 | 테트라아몬드 | 3 | 4 | 14 |
| 5 | 펜타아몬드 | 4 | 6 | 36 |
| 6 | 헥사아몬드 | 12 | 19 | 94 |
| 7 | 헵타아몬드 | 24 | 43 | 250 |
| 8 | 옥타아몬드 | 66 | 120 | 675 |
| 9 | 노니아몬드 | 160 | 307 | 1838 |
| 10 | 데시아몬드 | 448 | 866 | 5053 |
일부 저자는 다이아몬드 (60° 각도의 마름모)를 비슷한 모양의 프랑스 과자를 따라 ''칼리송''이라고도 부른다.[2][3]
| 이름 | 형태의 수 | 형태 |
|---|---|---|
| 모나이아몬드 | 1 |  |
| 다이아몬드 | 1 |  |
| 트라이아몬드 | 1 |  |
| 테트라아몬드 | 3 |    |
| 펜타이아몬드 | 4 |     |
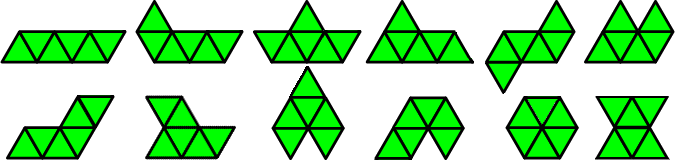
| 헥사이아몬드 | 12 |             |
4. 대칭
폴리아몬드는 거울 대칭, 2-회전 대칭, 3-회전 대칭, 6-회전 대칭이 가능하며, 각각은 거울 대칭과 결합될 수 있다.
거울 대칭 유무에 따른 2-회전 대칭은 각각 최소 2개 및 4개의 삼각형을 필요로 한다. 거울 대칭 유무에 따른 6-회전 대칭은 각각 최소 6개 및 18개의 삼각형을 필요로 한다. 비대칭은 최소 5개의 삼각형을 필요로 한다. 거울 대칭이 없는 3-회전 대칭은 최소 7개의 삼각형을 필요로 한다.
거울 대칭만 있는 경우, 대칭축이 격자에 맞춰져 있는지 또는 30° 회전되어 있는지 구별할 수 있다(각각 최소 4개 및 3개의 삼각형이 필요함). 3-회전 대칭의 경우도 마찬가지이며, 거울 대칭과 결합된 경우(각각 최소 18개 및 1개의 삼각형이 필요함)도 마찬가지이다.
5. 테셀레이션
8차 이하의 모든 폴리아몬드는 평면을 타일링할 수 있으며, V-헵타이아몬드는 예외이다.
6. 폴리헥스와의 관계
모든 폴리아몬드는 오른쪽 그림과 같이 폴리헥스에 대응된다. 반대로, 모든 폴리헥스는 또한 폴리아몬드인데, 이는 폴리헥스의 각 육각형 셀이 여섯 개의 인접한 정삼각형의 합집합이기 때문이다. 어느 쪽의 대응도 일대일은 아니다.
7. 대중문화
1차부터 6차까지의 폴리아몬드 22개는 보드 게임 블로커스 트리곤에서 게임 말로 사용된다. 플레이어들은 게임 규칙에 따라 가능한 한 많은 폴리아몬드로 평면을 채워야 한다.[1] 블로커스・트라이곤은 폴리아몬드-헥사몬드 22개 조각을 판에 놓는 보드 게임이다.[1]
참조
[1]
웹사이트
A000577
https://oeis.org/A00[...]
The OEIS Foundation Inc.
2021-07-09
[2]
서적
A Mathematical Space Odyssey: Solid Geometry in the 21st Century
https://books.google[...]
2015-12-31
[3]
학술지
The Problem of the Calissons
http://jstor.org/sta[...]
[4]
웹사이트
All of the polyiamonds of order eight or less, with the exception of one of the heptiamonds will tessellate the plane. The exception is the V-shaped heptiamond. Gardner (6th book p.248) posed the problem of identifying this heptiamond and reproduced an impossibilty proof of Gregory. However, in combination with other heptiamonds or other polyiamonds, tesselations using this V-shaped heptiamond can be achieved.
http://www.mathpuzzl[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

