1/2

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 수학적 성질
3. 언어적 표현
4. 기타 1/2 관련 내용
5. 컴퓨터에서의 표현
참조

1. 개요

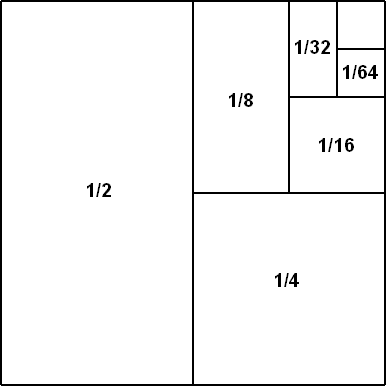
1/2는 0과 1의 산술 평균이며, 1을 2로 나눈 값으로, 다양한 수학적 성질을 갖는다. 0.5 또는 0.4999...로 표현되며, 짝수 진법에서는 유한 소수, 홀수 진법에서는 순환 소수로 나타난다. 삼각 함수, 감마 함수, 리만 가설 등에서 중요한 역할을 하며, 삼각형 면적 계산, 반올림, 2로 나누는 연산 등 여러 수학적 상황에서 활용된다. 언어적으로는 "절반"과 같이 표현되며, 양자역학, 스포츠, 식품 등 다양한 분야에서도 사용된다.

2. 수학적 성질

1/2는 수직선에서 0과 1 사이에 있는 유리수이다. 1/2을 곱하는 것은 2로 나눗셈하는 것과 같으며, 이는 "반으로 나누는 것"과 같다. 반대로, 1/2로 나누는 것은 2를 곱하는 것과 같으며, 이는 "두 배로 하는 것"과 같다.

한 변의 길이가 1인 정사각형으로, 여기서는 면적이 1/2의 연속적인 지수인 직사각형으로 구성되어 있다.

삼각형의 면적은 (밑변) × (높이) × 1/2로 구할 수 있다. 또한, 삼각형의 두 변의 길이를 ''a'', ''b''라고 하고, 그들이 이루는 각을 ''θ''라고 하면, 면적 ''S''는

S=\frac{1}{2} ab \sin\theta

로 나타낼 수 있다.

1부터 ''n''까지의 자연수의 합은

\frac{1}{2}n(n+1)

이 된다 (→삼각수).

그 외, 사다리꼴의 면적, 부정 적분

\int x\,dx

, 어떤 두 점의 중점의 좌표, 중점 연결 정리 등, 다양한 공식에 1/2가 등장한다.

\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}

(

\Gamma

는 감마 함수)

리만 가설에서는, "제타 함수 ''ζ''(''s'')의 자명하지 않은 영점 ''s''는, 모두 실수부가 1/2인 직선상에 존재한다"고 추측된다.

\dfrac{1}{2}=\dfrac{\dfrac{1}{6}}{1-\dfrac{2}{3}}=\sum\limits_{n=1}^\infty \dfrac{1}{6}\left(\dfrac{2}{3}\right)^n.

다음은 여러 진법에서의 1/2 표현을 나타낸 표이다.

진법	표현
이진법	0.1
삼진법	0.1111…
사진법	0.2
오진법	0.2222…
육진법	0.3
팔진법	0.4
구진법	0.4444…
십진법	0.5
십이진법	0.6
십오진법	0.7777…
십육진법	0.8
십팔진법	0.9
이십진법	0.A

2. 1. 기본 연산

0과 1의 산술 평균이다.
이진법으로는 0.1, 십진법으로는 0.5로 표기된다.
1/2 + 1/2 = 1
1/2 × 1/2 = 1/4
√(1/2) ≈ 0.707107
짝수의 1/2는 정수이고, 홀수의 1/2은 반정수이다.
정수를 1/2로 나누면 짝수이고, 반정수를 1/2로 나누면 홀수이다.
어떤 수를 정수로 반올림할 때 소수 부분이 0.5 미만일 때는 버림, 0.5 이상은 올림한다. 예를 들어 2.5는 3으로 반올림한다. 다만, 이보다 더 정확한 '짝수 반올림'에서는 0.5에 딱 걸쳤을 때 가장 가까운 짝수로 버림 또는 올림한다. 이때의 2.5는 2로 반올림한다.
1/2는 각도가 0° 이상 90° 이하(0 이상 π|파이^영어/2 이하)인 범위 내에서 sin 30°(= sin π|파이^영어/6) = cos 60°(= cos π|파이^영어/3)의 값이며, tan 26.6°(≈ tan 0.464)의 값과 비슷하다.
1/2를 곱하는 것은 2로 나눗셈하는 것과 같으며, 이는 "반으로 나누는 것"과 같다. 반대로, 1/2로 나누는 것은 2를 곱하는 것과 같으며, 이는 "두 배로 하는 것"과 같다.
1/2의 지수로 거듭제곱된 숫자는 그 숫자의 제곱근과 같다.
십진법에서 익숙한 0.5와 순환 소수 0.49의 두 가지 다른 소수 표현을 가지며, 모든 짝수 수 체계에서도 비슷한 쌍의 전개가 존재한다. 홀수 진법에서는 1/2가 순환 소수 표현을 갖지 않는다.
1 ÷ 2와 같다.
사칙 연산에서 "2로 나누는 것"은 "1/2을 곱하는 것"과 동치이다.
는 | $x^{frac{1}{2}}$ }}와 같다.

2. 2. 정수 및 반정수와의 관계

짝수의 1/2는 정수이고, 홀수의 1/2은 반정수이다. 정수를 1/2로 나누면 짝수이고, 반정수를 1/2로 나누면 홀수이다. 단짝수에 1/2을 곱한 값은 홀수이다.

2. 3. 반올림

어떤 수를 정수로 반올림할 때 소수 부분이 0.5 미만이면 버리고, 0.5 이상이면 올린다. 예를 들어 2.5는 3으로 반올림한다. 다만, 이보다 더 정확한 '짝수 반올림'에서는 0.5에 딱 걸렸을 때 가장 가까운 짝수로 버림 또는 올림한다. 이때의 2.5는 2로 반올림한다.

2. 4. 삼각 함수

2. 5. 기타 수학적 성질

1/2의 지수로 거듭제곱된 숫자는 그 숫자의 제곱근과 같다.

삼각형의 면적은 밑변과 높이의 절반이다.

1/2에서 평가된 감마 함수는 원주율의 제곱근이다.

리만 가설은 리만 제타 함수의 모든 비자명한 복소근의 실수부가 1/2^영어와 같다는 추측이다.

1 ÷ 2와 같다.
0과 1의 산술 평균과 같다.
짝수에 1/2을 곱한 값은 정수이고, 홀수에 1/2을 곱한 값은 반정수이다. 또한, 단짝수에 1/2을 곱한 값은 홀수이다.
사칙 연산에서 "2로 나누는 것"은 "1/2을 곱하는 것"과 동치이다.
$\sqrt{x}$ 는 $x^1/2$ ^영어와 같다.
삼각 함수에서, $\sin\frac{\pi}{6} = \sin\frac{5}{6}\pi = \frac{1}{2}, \cos\frac{\pi}{3} = \cos\frac{5}{3}\pi = \frac{1}{2}$ 이다. 따라서,

\sin^{-1}\frac{1}{2}  = \frac{\pi}{6} , \cos^{-1}\frac{1}{2} = \frac{\pi}{3}

이다. 또한

\tan^{-1}\frac{1}{2} = 0.463\ 647\ 609\ 000\ 806\ 116\ 21 \cdots

이다.

1부터 n까지의 자연수의 합은 $\frac{1}{2}n(n+1)$ 이 된다 (→삼각수).
삼각형의 면적은 (밑변) × (높이) × 1/2로 구할 수 있다. 또한, 삼각형의 두 변의 길이를 a, b라고 하고, 그들이 이루는 각을 θ라고 하면, 면적 S는 $S=\frac{1}{2} ab \sin\theta$ 로 나타낼 수 있다.

$\Gamma\left(1/2$ ^영어\right)=\sqrt{\pi} ( $\Gamma$ 는 감마 함수)
그 외, 사다리꼴의 면적, 부정 적분 $\int x\,dx$ , 어떤 두 점의 중점의 좌표, 중점 연결 정리 등, 다양한 공식 중에 1/2가 등장한다.
리만 가설에서는, "제타 함수 ''ζ''(''s'')의 자명하지 않은 영점 ''s''는, 모두 실수부가 1/2인 직선상에 존재한다"고 생각되고 있다.
$\dfrac{1}{2}=\dfrac{\dfrac{1}{6}}{1-\dfrac{2}{3}}=\sum\limits_{n=1}^\infty \dfrac{1}{6}\left(\dfrac{2}{3}\right)^n.$

2. 6. 다른 진법에서의 표현

이진법에서는 0.1, 십진법에서는 0.5로 표기된다. 짝수 진법에서는 1/2가 나누어 떨어지는 소수가 되지만, 삼진법 등 홀수 진법에서는 나누어 떨어지지 않는 순환 소수가 된다. 다음은 여러 진법에서의 1/2 표현을 나타낸 표이다.

진법	표현
이진법	0.1
삼진법	0.1111…
사진법	0.2
오진법	0.2222…
육진법	0.3
팔진법	0.4
구진법	0.4444…
십진법	0.5
십이진법	0.6
십오진법	0.7777…
십육진법	0.8
십팔진법	0.9
이십진법	0.A

3. 언어적 표현

1/2는 자연 언어에서 일반적인 파생 대신 보충법으로 표현되는 몇 안 되는 분수 중 하나이다. 예를 들어, 영어에서는 "one half"라는 표현을 쓴다. 한국어에서는 "절반"이라는 표현을 사용한다. 부모 중 한 명이 외국인인 사람을 하프라고 부르는데, 이는 1/2에서 유래했다.

4. 기타 1/2 관련 내용

양자역학에서 전자의 스핀 양자수는 +1/2 또는 -1/2이다.
FIFA 월드컵 예선에서는 6개의 FIFA 산하 지역 연맹 중 힘이 떨어진다고 생각되는 연맹의 예선에 관해서 1/2장의 티켓이 배분되는 경우가 있다. 이 경우, 해당 연맹 내 예선에서 승리해도 그 후에 개최되는 대륙간 플레이오프를 통과하지 않으면 본선에 출전할 수 없다.
큐피 하프는 큐피의 마요네즈 브랜드이다. 패키지에 1/2라고 적혀 있다.
1/2는 카와모토 마코토의 1997년 곡이다.
구약 성서에서는 4곳에서 "이분의 일"이라는 표현이 사용되고 있다.

성경 구절	내용
민수기 15장 9절	"젊은 수소에 더하여, 십분의 삼 에바의 고운 밀가루에 이분의 일 힌의 올리브 기름을 섞은 곡식 제물과"
민수기 15장 10절	"이분의 일 힌의 포도주를 포도주 제물로 바쳐라. 그것은 불태워 여호와께 드리는 위로의 향기이다."
민수기 28장 14절	"그것에 곁들일 포도주 제물은, 수소 한 마리에 포도주 이분의 일 힌, 숫양 한 마리에 삼분의 일 힌, 어린 양 한 마리에 사분의 일 힌으로 하라. 이상이 일 년 내내 매달 바치는 번제물이다."
에스겔서 43장 17절	"이것을 받치는 중간 단의 네 변은 길이가 열네 암마, 너비가 열네 암마이다. 그 주위의 가장자리는 높이가 이분의 일 암마, 주위의 도랑의 너비는 일 암마이다. 제단의 계단은 동쪽을 향하고 있다."

5. 컴퓨터에서의 표현

유니코드에서 ½는 숫자 형태 블록에 있는 미리 조합된 문자로서 자체 코드 포인트를 가지며, U+00BD로 표현된다.

기호	유니코드	JIS X 0213	문자 참조	명칭
½	U+00BD	1-9-20	½	2분의 1

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com