B+ 트리
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
B+ 트리는 자료구조의 한 종류로, 대용량 데이터를 효율적으로 저장하고 검색하기 위해 사용된다. B-트리의 변형으로, 루트, 내부, 리프 노드로 구성되며 모든 리프 노드는 같은 레벨에 위치한다. B+ 트리는 삽입, 삭제 연산 시 자동 균형을 유지하며, 리프 노드가 연결 리스트로 연결되어 있어 순차 접근에 효율적이다. 파일 시스템, 데이터베이스 시스템 등 다양한 분야에서 인덱싱을 위해 활용되며, 비휘발성 메모리에서도 사용된다.
더 읽어볼만한 페이지
- 1972년 컴퓨팅 - 프롤로그 (프로그래밍 언어)
프롤로그는 알랭 콜메로에르가 개발한 논리 프로그래밍 언어로, 사실과 규칙 기반 데이터베이스에 대한 질의를 통해 프로그램을 실행하며, 단일화, 백트래킹, 논리 변수 바인딩을 핵심 특징으로 인공지능, 자연어 처리 등에 활용된다. - 1972년 컴퓨팅 - 레드-블랙 트리
레드-블랙 트리는 각 노드가 색상 속성을 가지는 이진 탐색 트리로, 삽입, 삭제, 검색 연산에서 일정한 실행 시간을 보장하며 트리의 균형을 유지하고 효율적인 탐색 성능을 제공하는 특징을 가진다. - 트리 구조 - 덴드로그램
덴드로그램은 데이터 분석에서 데이터 포인트 간 계층적 관계를 시각적으로 표현하는 나무 형태의 다이어그램으로, 군집 분석에서 클러스터 간 유사성을 나타내기 위해 활용되며 다양한 분야에 응용된다. - 트리 구조 - 프림 알고리즘
프림 알고리즘은 그래프의 최소 비용 신장 트리를 찾는 탐욕 알고리즘으로, 최소 가중치를 가진 간선을 선택하여 트리를 확장하며, 시간 복잡도는 사용되는 자료 구조에 따라 달라진다.
| B+ 트리 | |
|---|---|
| 일반 정보 | |
| 자료 구조 유형 | 트리 (자료 구조) |
| 종류 | m-원 루트 트리 |
| 공간 복잡도 | |
| 평균 | O(n) |
| 최악 | O(n) |
| 탐색 | |
| 평균 | O(log n) |
| 최악 | O(log n) |
| 삽입 | |
| 평균 | O(log n) |
| 최악 | O(log n) |
| 삭제 | |
| 평균 | O(log n) |
| 최악 | O(log n) |
2. 역사
B+ 트리의 개념을 소개하는 단일 논문은 없다. 대신, 모든 데이터를 리프 노드에 유지하는 개념은 루돌프 바이어(R. Bayer)와 에드워드 맥크레이트(E. McCreight)가 소개한 B-트리의 흥미로운 변형으로 반복적으로 언급되었다.[2] 더글러스 코머(Douglas Comer)는 B-트리에 대한 초기 조사(B+ 트리도 포함)에서 B+ 트리가 IBM의 VSAM 데이터 액세스 소프트웨어에 사용되었으며 1973년 IBM에서 발행한 논문을 언급하고 있다.[3]
B+ 트리는 그래프의 일종인 트리 형태의 자료 구조로, 데이터베이스 및 파일 시스템에서 널리 사용된다. B+ 트리는 루트 노드, 내부 노드, 리프 노드로 구성되며, 모든 리프 노드는 같은 레벨에 위치하여 균형 잡힌 트리 구조를 유지한다.
3. 구조
B+ 트리의 차수는 트리 구조 내 노드의 용량을 나타내는 척도이다. 차수를 ''d''라고 할 때, 각 내부 노드는 ''d''개 이상 2''d''개 이하의 키를 저장할 수 있다. ( ''d'' <= ''m'' <= 2''d'', ''m''은 노드의 키 개수) 예를 들어 차수가 7인 B+ 트리에서 루트 노드를 제외한 내부 노드는 7개에서 14개의 키를 저장한다. 루트 노드는 1개에서 14개의 키를 저장할 수 있다.
또한 각 내부 노드는 최소 ''d''+1개, 최대 2''d''+1개의 자식 노드를 갖는다.
3. 1. 노드 구조
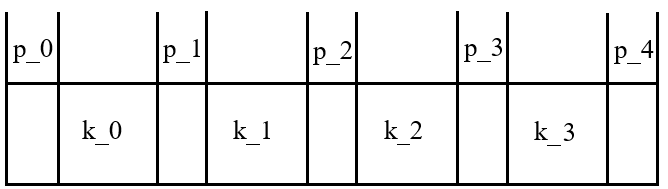
B+ 트리는 '루트', '내부'(내부 또는 내장), '리프'의 세 가지 유형의 노드로 구성된다. B+ 트리에서 이러한 노드들에 대해 다음 속성이 유지된다.
노드의 포인터 속성은 다음 표에 요약되어 있다.
| 이(가) 존재하는 경우 | 및 이(가) 존재하는 경우 | 이(가) 존재하고, 이(가) 존재하지 않는 경우 | 및 이(가) 존재하지 않는 경우 |
|---|---|---|---|
| 모든 검색 키가 보다 작은 서브트리를 가리킨다. | 모든 검색 키가 보다 크거나 같고 보다 작은 서브트리를 가리킨다. | 모든 검색 키가 보다 크거나 같은 서브트리를 가리킨다. | 여기서 는 비어 있다. |
| 이(가) 존재하는 경우 | 이(가) 존재하지 않고 인 경우 | |
|---|---|---|
| 와 동일한 값을 가진 레코드를 가리킨다. | 여기서 는 비어 있다. | 트리의 다음 리프를 가리킨다. |
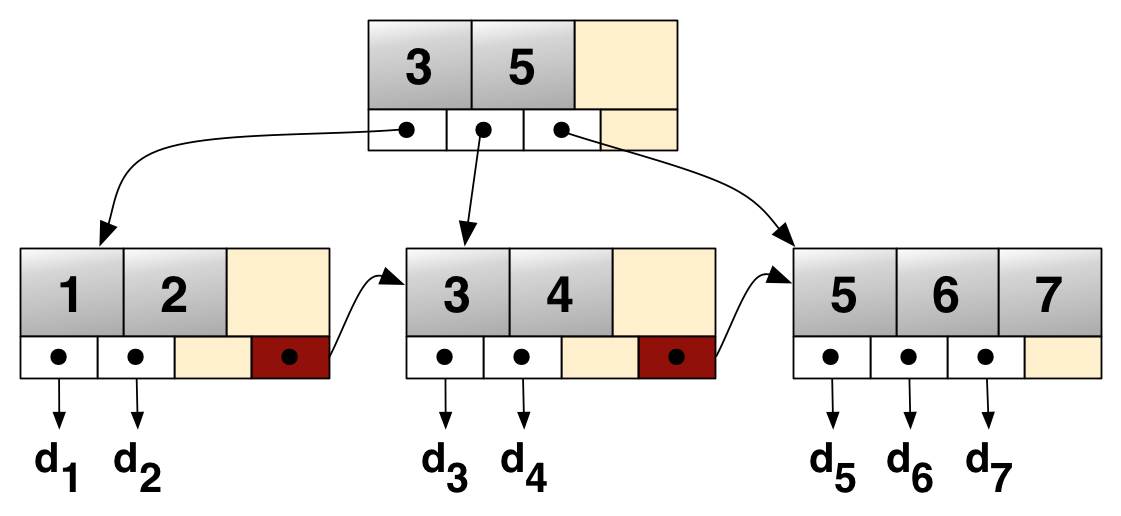
B+ 트리에 포함된 각 값은 정확히 하나의 리프 노드에 포함된 키이다. 각 키는 모든 다른 키와 직접 비교 가능해야 하며, 이는 전순서를 형성한다.[5] 이를 통해 각 리프 노드는 항상 모든 키를 정렬된 상태로 유지할 수 있으며, 각 내부 노드는 특정 리프에 포함된 값의 연속 범위를 나타내는 정렬된 구간 모음을 구성할 수 있다. 트리의 상위 내부 노드는 자체 자식 내부 노드에 포함된 구간을 재귀적으로 집계하여 자체 구간을 구성할 수 있다. 결국, B+ 트리의 루트는 트리의 전체 값 범위를 나타내며, 여기서 모든 내부 노드는 하위 구간을 나타낸다.
내부 노드는 인덱스 i를 가진 자식(내부 노드 또는 리프일 수 있음)이 포함하는 구간 내에서 최소 요소를 나타내는 m - 1개의 키 li 사본을 추가로 포함해야 한다. 여기서 m은 주어진 내부 노드에 대한 ''실제'' 자식 수를 나타낸다.
3. 2. 노드 제약 조건
B+ 트리의 차수는 트리 구조 내 노드의 용량을 나타내는 척도이다. 차수를 ''d''라고 할 때, 각 노드는 ''d'' <= ''m'' <= 2''d''를 만족하는 ''m''개의 항목을 가진다. 예를 들어 차수가 7인 B+ 트리가 있다면, 루트 노드를 제외한 내부 노드는 7개에서 14개의 키를 저장할 수 있다. 루트 노드는 1개에서 14개의 키를 저장할 수 있다.[1]각 내부 노드는 최소 ''d''+1개, 최대 2''d''+1개의 자식 노드를 갖는다.
노드 경계는 다음 표와 같이 요약할 수 있다.
| 노드 유형 | 최소 키 개수 | 최대 키 개수 | 최소 자식 노드 개수 | 최대 자식 노드 개수 |
|---|---|---|---|---|
| 루트 노드 (리프 노드인 경우) | 0 | 0 | 0 | |
| 루트 노드 (내부 노드인 경우) | 1 | 2 | ||
| 내부 노드 | ||||
| 리프 노드 | 0 | 0 |
4. 특징
B+ 트리는 삽입, 삭제 연산 시 자동으로 균형을 유지하여 검색 성능을 보장하는 균형 트리이다.[6] 모든 리프 노드가 같은 레벨에 위치하므로, 최악의 경우에도 검색 시간이 O(log n)으로 제한된다. (n은 레코드 수)[6]
리프 노드가 연결 리스트로 연결되어 있어 순차 접근에 효율적이며, 트리 구조를 통해 임의 접근도 빠르게 수행할 수 있다. 모든 데이터는 리프 노드에만 저장되므로, 내부 노드의 크기를 줄여 더 많은 분기를 가질 수 있고, 이는 트리의 높이를 낮추는 효과를 가져온다.[7] 레코드 수의 증가/감소에 따라 트리가 동적으로 확장/축소되므로, 대용량 데이터 처리에 적합하다.
차수 ''b'', 높이 ''h''인 B+ 트리의 특징은 다음과 같다.
| 특징 | 설명 |
|---|---|
| 최대 레코드 수 | |
| 최소 키 수 | |
| 저장 공간 | |
| 레코드 삽입 연산 횟수 (최악의 경우) | |
| 레코드 검색 연산 횟수 (최악의 경우) | |
| 레코드 삭제 연산 횟수 (최악의 경우, 위치를 아는 경우) | |
| 범위 질의에서 k개 요소 검색 연산 횟수 (최악의 경우) |
5. 알고리즘
B+ 트리의 알고리즘은 검색, 삽입, 삭제, 벌크 로딩(대량 적재)으로 구성된다.
검색B+ 트리에서 검색은 루트 노드에서 시작하여 리프 노드에 도달할 때까지 수행된다. 각 노드에서는 찾고자 하는 값을 포함하는 하위 노드를 가리키는 포인터를 따라간다. 리프 노드에 도달하면, 해당 노드 내에서 원하는 키를 찾는다. 총 키 수가 N개일 때, 검색에는 O(log N)영어의 시간이 걸린다.[8]
삽입삽입을 위해서는 먼저 검색을 통해 새 레코드가 들어갈 위치를 찾는다. 해당 리프 노드(버킷)에 공간이 있으면 레코드를 추가하고, 공간이 없으면 노드를 분할한다. 노드 분할은 부모 노드에도 영향을 미치며, 필요한 경우 루트 노드까지 분할이 반복될 수 있다. B+ 트리는 루트에서부터 증가한다.[1]
삭제삭제는 루트에서 시작하여 해당 엔트리가 있는 리프 노드를 찾은 후 엔트리를 제거하는 방식으로 진행된다. 리프 노드의 엔트리가 절반 이하로 줄어들면, 형제 노드에서 엔트리를 빌려오거나(재분배) 형제 노드와 병합한다. 병합은 루트까지 전파될 수 있으며, 트리의 높이를 감소시킬 수 있다.[10]
벌크 로딩 (대량 적재)대량의 데이터를 B+ 트리에 한 번에 효율적으로 삽입하는 방법이다. 데이터 엔트리들을 검색 키를 기준으로 정렬한 후, 리프 레벨 바로 위 가장 오른쪽 인덱스 페이지에 순차적으로 삽입한다. 페이지가 가득 차면 분할이 발생하며, 이는 루트까지 연쇄적으로 일어날 수 있다.[9]
5. 1. 검색
루트 노드에서 시작하여 검색을 수행한다. 찾고자 하는 값 k를 포함하는 리프 노드를 찾을 때까지 각 노드에서 어떤 포인터를 따라갈지 결정해야 한다. 내부 B+ 트리 노드는 최대 개의 자식을 가지며, 각 자식은 서로 다른 하위 간격을 나타낸다. 내부 노드의 개의 항목을 선형 검색하여 해당 자식을 선택하고, 리프 노드에 도달하면 원하는 키에 대한 개 요소의 선형 검색을 수행한다. 트리의 각 단계에서 모든 자식 중 하나만 탐색하므로, B+ 트리의 리프에 저장된 총 키 수가 일 때 의 런타임을 가진다.[8]아래는 검색 및 리프 검색 함수의 의사 코드이다.
'''function''' search(''k'', ''root'') '''is'''
'''let''' leaf = leaf_search(k, root)
'''for''' leaf_key '''in''' leaf.keys():
'''if''' k = leaf_key:
'''return''' true
'''return''' false
'''function''' leaf_search(''k'', ''node'') '''is'''
'''if''' node is a leaf:
'''return''' node
'''let''' p = node.children()
'''let''' l = node.left_sided_intervals()
'''assert'''
'''let''' m = p.len()
'''for''' i '''from''' 1 '''to''' m - 1:
'''if''' :
'''return''' leaf_search(k, p[i])
'''return''' leaf_search(k, p[m])
위 의사 코드는 1 기반 배열 인덱싱을 사용한다.
레코드 r을 탐색하는 알고리즘은 리프 노드에 도달할 때까지 올바른 자식 노드에 대한 포인터를 따라간다. 리프 노드에 도달하면 해당 노드 내에서 찾고 있는 레코드를 찾는다(찾을 수 없는 경우에는 실패한다). 아래는 의사 코드이다.
```
'''function''' search(record r)
u := 루트 노드
'''while''' (u는 잎이 아님) '''do'''
그 노드 내의 올바른 포인터를 선택
포인터를 따라간 다음 노드로 이동
u := 현재 노드
scan u for r
```
이 의사 코드는 반복이 없다고 가정한다.
5. 2. 삽입
먼저 검색을 통해 새 레코드를 삽입할 버킷(공간)을 결정한다.[1]- 버킷에 공간이 있다면 (삽입 후 최대 b-1개의 엔트리) 레코드를 추가한다.[1]
- 버킷이 꽉 찼다면, 버킷을 쪼갠다.[1]
- * 새로운 단말 노드를 위한 메모리를 확보하고, 버킷에 있던 요소의 절반을 새 노드로 옮긴다.[1]
- * 새 단말 노드의 최소 키를 부모 노드에 삽입한다.[1]
- * 부모 노드가 꽉 찼다면, 부모 노드도 쪼갠다.[1]
- ** 부모 노드에 중간 키를 추가한다.[1]
- * 쪼개지지 않는 부모 노드를 찾을 때까지 반복한다.[1]
- 루트가 쪼개졌다면, 새 루트를 만드는데, 이 루트는 1개의 키와 2개의 포인터를 가진다. (새 루트로 올라간 값은 기존 노드에서 사라진다.)[1]
- 새 레코드를 넣을 노드를 찾기 위해 다시 검색을 수행한다.[1]
- 노드가 가득 차지 않았다면 ( b - 1개의 항목 이하) 레코드를 추가한다.[1]
- 그렇지 않은 경우, 새 레코드를 삽입하기 ''전''에 노드를 분할한다.[1]
- * 기존 노드는 ⌈(K+1)/2⌉|올림(K+1)/2영어개의 항목을 가진다.[1]
- * 새 노드는 ⌊(K+1)/2⌋|내림(K+1)/2영어개의 항목을 가진다.[1]
- * ⌈(K+1)/2⌉|올림(K+1)/2영어번째 키를 부모 노드에 복사하고, 새 노드를 부모 노드에 삽입한다.[1]
- * 분할할 필요가 없는 부모 노드를 찾을 때까지 반복한다.[1]
- * 새 레코드를 새 노드에 삽입한다.[1]
- 루트가 분할되는 경우, 빈 부모 노드가 있는 것처럼 처리하고 위에서 설명한 대로 분할한다.[1]
B+ 트리는 잎 노드가 아닌 루트에서 증가한다.[1]
5. 3. 삭제
루트에서 시작하여, 엔트리가 속한 단말노드 L을 찾는다. 엔트리를 삭제한다.- L이 절반 이상 차 있다면 종료한다.
- L이 절반 이하라면,
- 형제(L과 동일한 부모를 가진 인접노드)가 절반 초과라면, 재분배하고 엔트리를 빌려온다.
- 형제의 엔트리들이 정확히 절반일 경우에는 L과 형제를 병합한다.
- 병합이 일어났다면, L의 부모로부터 삭제된 노드를 가리키는 포인터를 삭제한다.
- 병합은 루트까지 전파되어, 트리의 높이를 감소시킬 가능성이 있다.[10]
삭제 알고리즘의 목적은 트리 구조에서 원하는 항목 노드를 제거하는 것이다. 우리는 노드를 찾을 때까지 적절한 노드에 대해 재귀적으로 삭제 알고리즘을 호출한다. 각 함수 호출에 대해 인덱스를 사용하여 노드를 찾고, 삭제한 다음, 루트로 다시 올라간다.
삭제하려는 항목 L에서:
- L이 적어도 절반 이상 채워져 있으면 완료
- L에 d-1개의 항목만 있는 경우, 형제 노드(L과 동일한 부모를 가진 인접 노드)에서 빌려와 재분배를 시도한다.
두 개의 형제 노드의 재분배가 발생한 후, 부모 노드는 이 변경 사항을 반영하도록 업데이트되어야 한다. 두 번째 형제 노드를 가리키는 인덱스 키는 해당 노드의 가장 작은 값을 인덱스 키로 사용해야 한다.
- 재분배에 실패하면 L과 형제 노드를 병합한다. 병합 후, 부모 노드는 삭제된 항목을 가리키는 인덱스 키를 삭제하여 업데이트된다. 즉, 병합이 발생한 경우 L 또는 형제 노드를 가리키는 항목을 L의 부모에서 삭제해야 한다.
참고: 병합은 루트까지 전파될 수 있으며, 이는 높이가 감소함을 의미한다.[10]
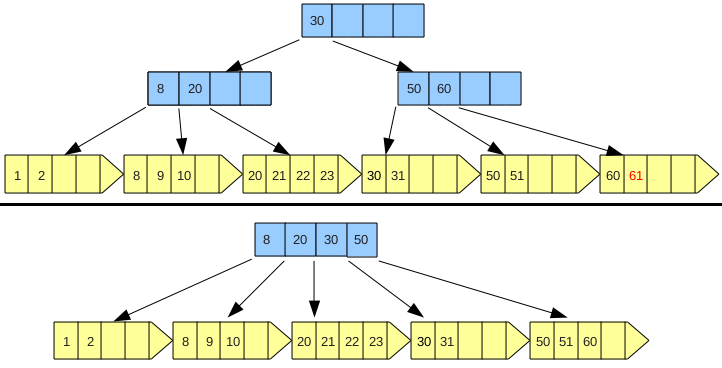
5. 4. 벌크 로딩 (대량 적재)
대량의 데이터를 이용하여 B+ 트리 인덱스를 생성할 때, 각 레코드를 빈 트리에 하나씩 삽입하는 방식은 비용이 많이 든다. 각 엔트리를 루트 노드에서 시작하여 올바른 위치까지 찾아가야 하기 때문이다.[9] 이를 해결하기 위한 효율적인 대안이 벌크 로딩(bulk-loading)이다.[9]벌크 로딩의 단계는 다음과 같다.[9]
1. 데이터 정렬: 검색 키를 기준으로 데이터 엔트리들을 오름차순으로 정렬한다.
2. 루트 생성: 빈 페이지를 할당하여 루트로 만들고, 첫 번째 페이지를 가리키는 포인터를 삽입한다.
3. 루트 분할: 루트가 가득 차면 루트를 분할하고 새로운 루트 페이지를 만든다.
4. 엔트리 삽입: 모든 엔트리가 인덱싱될 때까지 리프 레벨 바로 위에 있는 가장 오른쪽에 있는 인덱스 페이지에 엔트리를 계속 삽입한다.
참고 사항:[9]
- 리프 레벨 바로 위에 있는 가장 오른쪽에 있는 인덱스 페이지가 가득 차면 분할된다.
- 이 분할은 연쇄적으로 루트에 더 가까운 인덱스 페이지의 분할을 일으킬 수 있다.
- 분할은 루트에서 리프 레벨까지의 가장 오른쪽 경로에서만 발생한다.
6. 구현
B+ 트리의 리프 노드(가장 아래쪽의 색인 블록)는 종종 연결 리스트로 서로 연결되어 있다. 이렇게 하면 범위 쿼리나 블록을 통한 (정렬된) 반복이 더 간단하고 효율적이다.[13] 이는 B-트리에 비해 B+ 트리의 중요한 장점 중 하나인데, B-트리에서는 모든 키가 잎 노드에 존재하지 않으므로 이러한 정렬된 연결 리스트를 구성할 수 없기 때문이다. 따라서 B+ 트리는 데이터가 일반적으로 디스크에 저장되는 데이터베이스 시스템 색인으로 특히 유용하다.
저장 시스템의 블록 크기가 B 바이트이고 저장할 키의 크기가 k인 경우, 가장 효율적인 B+ 트리는 이다. 이론적으로는 1을 뺄 필요는 없지만, 실제로는 인덱스 블록에 어떤 여분의 공간이 필요한 경우가 많다(예를 들어, 잎 블록에서의 연결 리스트용 참조).
B+ 트리의 노드가 배열로 구성되는 경우, 삽입이나 삭제 시 배열의 요소를 이동해야 하므로 성능이 나빠진다. 따라서 노드 내의 요소는 이진 트리나 B+ 트리로 구성하는 것이 바람직하다.
B+ 트리는 메모리상의 데이터 저장에도 사용된다. 그 경우, 블록 크기는 프로세서의 캐시 라인에 맞추는 것이 좋다.
B+ 트리의 공간 효율은 특정 종류의 압축 기법을 사용하여 개선할 수 있다. 예를 들어, 각 블록에 저장하는 키에 차분 부호화를 적용하는 것을 고려할 수 있다. 내부 블록의 경우, 공간을 절약하려면 키 또는 포인터를 압축하면 된다. 문자열 키의 경우, 내부 블록의 ''i'' 번째 엔트리에는 i+1 번째 블록의 첫 번째 키가 저장되는데, 키 전체를 저장하는 대신 바로 앞의 i 번째 블록의 마지막 키보다 확실히 크다는 것을 알 수 있는, i+1 번째 블록의 첫 번째 키의 가장 짧은 접두사를 저장한다. 포인터에도 간단한 압축 방법이 있는데, 몇 개의 블록이 연속된 위치에 순서대로 배치되어 있는 경우, 선두 블록에 대한 포인터와 연속된 블록 수를 저장하면 된다.
하지만 이러한 압축 기법에는 블록 전체를 해제해야 하나의 요소를 꺼낼 수 있다는 등의 문제가 존재한다. 이러한 문제를 해결하기 위해 블록을 서브 블록으로 나누어 서브 블록 단위로 압축하는 방법이 고려될 수 있다.
7. 응용
B+ 트리는 ReiserFS, XFS, JFS, NTFS, ReFS 등 여러 파일 시스템에서 메타데이터 인덱싱에 사용된다.[11] EXT4는 파일 익스텐트 인덱싱을 위해 수정된 B+ 트리인 익스텐트 트리를 사용한다.[11] APFS는 B+ 트리를 사용하여 파일 시스템 객체 ID를 디스크 상의 위치에 매핑하고 파일 시스템 레코드를 저장한다.[12]
IBM Db2[13], Informix[13], Microsoft SQL Server[13], Oracle 8[13], Sybase ASE[13], SQLite[14]와 같은 대부분의 관계형 데이터베이스 관리 시스템과 CouchDB[15], Tokyo Cabinet[16]과 같은 일부 NoSQL 데이터베이스 시스템도 테이블 인덱스에 B+ 트리 유형의 트리를 지원한다.
비휘발성 랜덤 액세스 메모리(NVRAM)는 사물 인터넷(IoT) 시스템의 주요 메모리 접근 기술로 B+ 트리 구조를 사용해 왔으며, 데이터베이스 시스템의 내구성을 높이는 데 상당한 결과를 보여준다.[19]
7. 1. 파일 시스템
ReiserFS, XFS, JFS, NTFS, ReFS는 모두 메타데이터 인덱싱에 B+ 트리를 사용한다. JFS와 NTFS는 디렉토리 저장에도 B+ 트리를 사용한다. NTFS는 보안 관련 메타데이터 인덱싱에도 B+ 트리를 사용한다. EXT4는 파일 익스텐트 인덱싱을 위해 수정된 B+ 트리 데이터 구조인 익스텐트 트리를 사용한다.[11] APFS는 파일 시스템 객체 ID를 디스크 상의 해당 위치에 매핑하고, 파일 시스템 레코드(디렉토리 포함)를 저장하기 위해 B+ 트리를 사용하지만, 이러한 트리의 리프 노드는 형제 포인터를 가지고 있지 않다.[12]7. 2. 데이터베이스 시스템
IBM Db2[13], Informix[13], Microsoft SQL Server[13], Oracle 8[13], Sybase ASE[13], SQLite[14]와 같은 대부분의 관계형 데이터베이스 관리 시스템과 CouchDB[15], Tokyo Cabinet[16]과 같은 일부 NoSQL 데이터베이스 시스템은 테이블 인덱스에 B+ 트리 유형의 트리를 지원하며, 각 시스템은 기본 B+ 트리 구조에 변형과 확장을 적용하여 구현한다.7. 3. 비휘발성 메모리 (NVRAM)
비휘발성 랜덤 액세스 메모리(NVRAM)는 정적 전력 소비가 없고 셀 메모리의 높은 견고성으로 인해 사물 인터넷(IoT) 시스템의 주요 메모리 접근 기술로 B+ 트리 구조를 사용해 왔다. B+ 트리는 메모리로의 데이터 트래픽을 효율적으로 조절할 수 있다. 또한, 일부 고도로 사용되는 리프 또는 참조 지점의 빈도에 대한 고급 전략을 통해 B+ 트리는 데이터베이스 시스템의 내구성을 높이는 데 상당한 결과를 보여준다.[19]8. 다른 자료 구조와의 관계
B+ 트리는 B 트리에서 파생된 것으로, B 트리는 내부 노드에도 키와 레코드를 저장할 수 있다. B+ 트리는 (a,b)-트리를 특수화한 것이다. ((a,b)-트리는 최대 및 최소를 ''a''와 ''b''로 명시적으로 지정한 트리 구조이다.) 어떤 의미에서는 B 트리가 B+ 트리를 특수화한 것으로 볼 수도 있다.
B# 트리는 B+ 트리에 추가적인 제한을 가한 것이다.
참조
[1]
서적
Fundamentals of database systems
Pearson Education
[2]
서적
Proceedings of the 1970 ACM SIGFIDET (Now SIGMOD) Workshop on Data Description, Access and Control - SIGFIDET '70
1970-11
[3]
간행물
Ubiquitous B-Tree
[4]
서적
Database system concepts
McGraw-Hill Education
2020
[5]
웹사이트
"Tree-Structured Indexing: ISAM and B+-trees"
https://db.inf.uni-t[...]
2013-07
[6]
서적
Database Systems for Advanced Applications
2010
[7]
서적
Database Systems for Advanced Applications
2010
[8]
웹사이트
"B+ trees"
https://www.cs.helsi[...]
[9]
웹사이트
ECS 165B: Database System Implementation Lecture 6
http://web.cs.ucdavi[...]
2010-04-09
[10]
서적
Database management systems
McGraw-Hill
2003
[11]
서적
Practical File System Design with the Be File System
http://www.nobius.or[...]
Morgan Kaufmann
2014-07-29
[12]
웹사이트
Apple File System Reference
https://developer.ap[...]
Apple Inc.
2020-06-22
[13]
서적
Database Management Systems
McGraw-Hill Higher Education
[14]
웹사이트
SQLite Version 3 Overview
http://sqlite.org/ve[...]
[15]
웹사이트
CouchDB Guide (see note after 3rd paragraph)
http://guide.couchdb[...]
[16]
웹사이트
Tokyo Cabinet reference
http://1978th.net/to[...]
[17]
서적
Database Systems for Advanced Applications
[18]
간행물
iDistance: An adaptive B+-tree based indexing method for nearest neighbor search
https://dl.acm.org/d[...]
2005-06
[19]
간행물
Beyond Write-Reduction Consideration: A Wear-Leveling-Enabled B⁺-Tree Indexing Scheme Over an NVRAM-Based Architecture
https://ieeexplore.i[...]
2021-12
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com