XOR 게이트

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 기호
3. 구현
4. 3개 이상 입력으로의 확장
5. 응용
6. 표준 칩 패키지
7. 해석적 표현
참조

1. 개요

XOR 게이트는 두 개의 입력이 서로 다를 경우에만 참(1)을 출력하는 디지털 논리 게이트이다. XOR 게이트는 다양한 기호로 표현되며, MOSFET을 사용하여 구현할 수 있다. XOR 게이트는 AND, OR, NOT 게이트를 조합하거나 NAND 또는 NOR 게이트만 사용하여 구성할 수 있다. XOR 게이트는 가산기, 의사 난수 생성기, 위상 검출기, 신호 버퍼링, 상관 관계 및 시퀀스 감지 등 다양한 응용 분야에서 활용된다. 7486, 4070, 4030과 같은 표준 칩 패키지로도 제공되며, 해석적 표현식으로도 나타낼 수 있다.

더 읽어볼만한 페이지

논리 게이트 - NAND 게이트
NAND 게이트는 모든 입력이 1일 때 0을 출력하고 그 외에는 1을 출력하는 논리 게이트로서, 다양한 기호로 표현되며, AND 연산의 결과를 부정하는 연산을 수행하고, 여러 방식으로 구현될 수 있으며, 기능적으로 완전하여 디지털 회로 설계에 필수적이다.
논리 게이트 - AND 게이트
AND 게이트는 모든 입력이 참일 때만 참을 출력하고 하나라도 거짓이면 거짓을 출력하는 논리 게이트로, 논리곱으로 표현되며 다양한 방식으로 구현되어 디지털 시스템의 핵심 구성 요소로 사용된다.

XOR 게이트
기본 정보
종류	논리 회로
기능	배타적 논리합
진리표	A B 출력 거짓 거짓 거짓 참 거짓 참 거짓 참 참 참 참 거짓
다양한 표현
XOR 게이트 (ANSI)
XOR 게이트 (IEC)
불 대수식	A ⊕ B = A'B + AB'
간략화된 불 대수식	A ⊕ B = (A + B)(A' + B')
드 모르간의 법칙	A ⊕ B = (A'B')' (AB)'
NAND 게이트만을 사용한 표현	A ⊕ B = (A NAND (A NAND B)) NAND (B NAND (A NAND B))
응용
주요 응용 분야	암호학 오류 검출 부호 의사 난수 생성기
관련 정보
관련 논리 게이트	AND 게이트 OR 게이트 NOT 게이트 NAND 게이트 NOR 게이트 XNOR 게이트

2. 기호

XOR 게이트를 나타내는 기호는 여러 가지가 있다. 크게 전통적인 기호와 IEEE 기호 두 가지로 나뉜다. 더 자세한 정보는 논리 게이트 기호에서 확인할 수 있다.


전통적인 XOR 기호		IEEE XOR 기호

논리 기호에서는 ⊕, J''pq'', ⊻ 기호를 사용하여 XOR 연산을 나타낸다.

C 계열 언어에서는 캐럿(^) 기호를 사용하여 비트 단위 XOR 연산을 표현한다. 여기서 캐럿 기호는 논리곱(AND)을 의미하지 않는다.

XOR 게이트에는 세 가지 회로 기호가 사용된다. 여기에는 전통적인 ANSI 및 DIN 기호와 IEC 기호가 포함된다. DIN 기호의 경우, ≢ 대신 ⊕를 사용하는 경우도 있다. IEC 기호에서 "=1"은 출력이 하나의 활성 입력에 의해서만 활성화됨을 나타낸다.

ANSI XOR 회로 기호

IEC XOR 회로 기호

DIN XOR 회로 기호

3. 구현

XOR 게이트는 MOSFET을 사용하여 구성할 수 있으며, 패스 트랜지스터 로직 구현도 가능하다.^[18]^[19]^[20]^[21]^[22]^[23]

특정 종류의 게이트를 사용할 수 없는 경우에는 사용 가능한 다른 게이트들을 조합하여 XOR 기능을 구현할 수 있다. 예를 들어, XNOR 게이트에 NOT 게이트를 연결하거나,

(A \cdot \overline{B}) + (\overline{A} \cdot B)

식을 이용해 AND 게이트, OR 게이트, NOT 게이트를 조합할 수 있다.

부울 대수를 활용하고 드 모르간의 법칙을 적용하면, 4개의 NAND 게이트만으로 XOR 게이트를 구현할 수도 있다. NAND 게이트와 NOR 게이트는 "범용 게이트"라고 불리며, 이들만으로도 모든 논리 함수를 구성할 수 있다. 5개의 NOR 게이트나 NAND 게이트를 사용하는 방법도 있다.

회로도	설명
200px	NAND 게이트만 사용하여 구성한 XOR 게이트 회로
200px	NOR 게이트만 사용하여 구성한 XOR 게이트 회로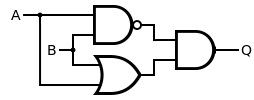
200px	3개의 게이트를 혼합하여 만든 XOR 게이트 회로

TTL이나 CMOS 논리의 범용 로직 IC에는 XOR 게이트가 포함된 제품군(7486, 4070(4030의 대체))이 있으며, DIP 패키지나 플랫 패키지 형태로 제공된다.

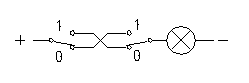
3로 스위치를 사용한 배선 방법도 XOR 게이트의 일종이다.

3. 1. AND-OR-Invert (AOI)

XOR 게이트는 AND-OR-Invert (AOI, AOI) 또는 OR-AND-Invert (OAI) 로직을 사용하여 구현할 수 있다.^[4]

금속-산화물-반도체(CMOS) XOR 게이트의 구현은 위의 AOI 논리에 해당한다.

왼쪽에서, nMOS 및 pMOS 트랜지스터는 입력 쌍

A \cdot \overline{B}

및

\overline{A} \cdot B

가 각각 왼쪽 상단의 두 pMOS 트랜지스터 또는 오른쪽 상단의 두 pMOS 트랜지스터를 활성화하여 논리 하이를 위해 Vdd를 출력에 연결하도록 배열되어 있다. 나머지 입력 쌍

A \cdot B

및

\overline{A} \cdot \overline{B}

는 논리 로우를 위해 하단의 두 nMOS 경로 중 하나를 Vss에 활성화한다.^[5]

반전된 입력(예: 플립플롭)을 사용할 수 있는 경우 이 게이트를 직접 사용할 수 있다. 그렇지 않은 경우

\overline{A}

및

\overline{B}

를 생성하기 위해 각각 두 개의 트랜지스터가 있는 두 개의 추가 인버터가 필요하며, 총 트랜지스터 수는 12개가 된다.

반전된 입력이 없는 AOI 구현은 예를 들어 인텔 386 CPU에서 사용되었다.^[6]

3. 2. CMOS

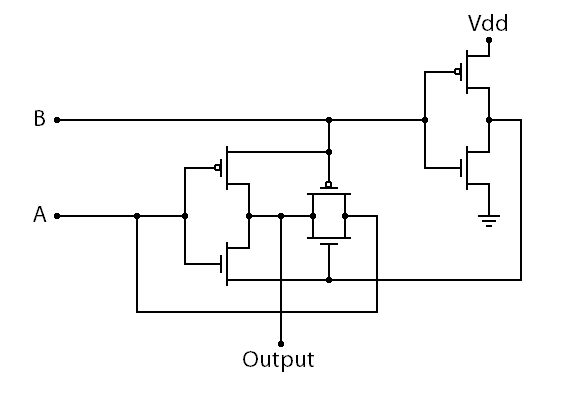
MOSFET 회로를 사용하여 구현되는 금속-산화물-반도체(CMOS) XOR 게이트는 AOI 로직을 기반으로 한다.

nMOS 및 pMOS 트랜지스터는 입력 쌍

A \cdot \overline{B}

및

\overline{A} \cdot B

가 각각 왼쪽 상단의 두 pMOS 트랜지스터 또는 오른쪽 상단의 두 pMOS 트랜지스터를 활성화하여 논리 하이를 위해 Vdd를 출력에 연결하도록 배열되어 있다. 나머지 입력 쌍

A \cdot B

및

\overline{A} \cdot \overline{B}

는 논리 로우를 위해 하단의 두 nMOS 경로 중 하나를 Vss에 활성화한다.^[5]

반전된 입력(예: 플립플롭)을 사용할 수 있는 경우 이 게이트를 직접 사용할 수 있다. 그렇지 않은 경우

\overline{A}

및

\overline{B}

를 생성하기 위해 각각 두 개의 트랜지스터가 있는 두 개의 추가 인버터가 필요하며, 총 트랜지스터 수는 12개가 된다. 반전된 입력이 없는 AOI 구현은 인텔 386 CPU에서 사용되었다.^[6]

CMOS에서는 NOR 게이트와 AND-OR-Invert(:en:AND-OR-invert) 복합 게이트에 의한 10 트랜지스터 구현도 가능하다.

XOR with NOR gate and AND-OR-Invert comp. gate

일반적인 구성의 게이트가 아니라, 논리값이 "통과하는" 게이트(자세한 내용은 영어판 :en:Pass transistor logic 및 :en:Transmission gate 참조)를 사용하면, 보다 효율적으로 구현할 수 있다. 6개의 트랜지스터에 의한 CMOS IC 구현의 한 예시는 다음과 같다 (그림 속의 4개와, 입력의 한쪽 반전을 위한 2개).

Transmission Gate Logic wiring of an XOR gate

3. 3. 패스 트랜지스터 로직

패스 트랜지스터 로직을 사용하면 더 적은 수의 트랜지스터로 XOR 게이트를 구현할 수 있다.^[18]^[19]^[20]^[21]^[22]^[23]

이 구현 방식은 전송 게이트 두 개와,

\overline{A}

와

\overline{B}

를 생성하는 인버터 두 개(다이어그램에 표시되지 않음)를 사용하여 총 8개의 트랜지스터를 사용한다. 이는 이전 설계보다 트랜지스터 4개를 절약한다. XOR 기능은 B가 높을 때 A의 반전된 값을 출력으로 전달하고, B가 낮을 때 A의 값을 전달하는 방식으로 구현된다.

하지만 전송 게이트는 이상적인 스위치가 아니므로 저항이 발생하며, 입력 신호 강도에 따라 출력이 저하될 수 있다.^[8]

일반적인 구성의 게이트가 아니라, 논리값이 "통과하는" 게이트(패스 트랜지스터 로직 및 전송 게이트 참조)를 사용하면 더 효율적으로 구현할 수 있다. 다음은 6개의 트랜지스터를 사용한 CMOS IC 구현의 한 예이다 (그림 속 4개와 입력 한쪽의 반전을 위한 2개).

3. 4. 최적화된 패스 게이트 로직 배선

이전의 전송 게이트 구현은 인버터^영어와 하단 통과 게이트의 기능을 인버터처럼 배열된 단 두 개의 트랜지스터로 구현하여 8개에서 6개의 트랜지스터로 더 최적화할 수 있다. 이때 pMOS의 소스는 Vdd 대신

B

에 연결되고, nMOS의 소스는 GND 대신

\overline{B}

에 연결된다.^[8]

위에 언급된 가장 왼쪽의 두 트랜지스터는 통과 트랜지스터 논리를 사용하여 트랜지스터 수를 줄이기 위해 B가 로직 하이일 때 A의 최적화된 조건부 반전을 수행하고, B가 로직 로우일 때 이들의 출력은 높은 임피던스 상태에 있다. 중간에 있는 두 트랜지스터는 B가 로직 로우일 때 출력을 A의 값으로 구동하는 전송 게이트이며, 가장 오른쪽에 있는 두 트랜지스터는 전송 게이트와 통과 트랜지스터 논리 회로에서 사용되는

\overline{B}

를 생성하는 데 필요한 인버터를 형성한다.^[9]

이전 구현과 마찬가지로, 통과 게이트 트랜지스터 또는 가장 왼쪽의 두 트랜지스터를 통해 입력과 출력을 직접 연결하는 것을 특히 계단식으로 연결할 때 고려해야 한다.^[8]

4. 3개 이상 입력으로의 확장

XOR 연산은 3개 이상의 입력에 대해서도 확장할 수 있다. 일반적인 확장 방식은 2입력 XOR 게이트를 직렬로 연결하는 것이다. 처음 두 신호는 XOR 게이트에 공급된 다음, 해당 게이트의 출력은 세 번째 신호와 함께 두 번째 XOR 게이트에 공급되며, 나머지 신호에 대해서도 동일하게 반복된다.^[12] 이렇게 하면 입력 중 1의 개수가 홀수일 때 1을 출력하고, 짝수일 때 0을 출력하는 회로가 된다.^[12] 이러한 회로는 패리티 발생기나 모듈로-2 가산기로 활용된다.^[12]

예를 들어, 74LVC1G386 마이크로칩은 세 개의 입력 논리 게이트로 광고되며 패리티 발생기를 구현한다.^[13]^[17]

대규모 패리티 생성 등에서는 지연 시간을 줄이기 위해 병렬 처리 방식(토너먼트 방식)을 사용하기도 한다.

5. 응용

XOR 게이트와 AND 게이트는 VLSI 응용 분야에서 가장 많이 사용되는 두 가지 구조이다.^[14] XOR 게이트는 디지털 회로에서 다음과 같은 다양한 용도로 활용된다.

가산기: XOR 게이트는 두 비트를 더하여 하나의 비트를 출력하는 1비트 가산기로 사용할 수 있다.
의사 난수 생성기: LFSR을 이용한 의사 난수(PRN) 생성기는 XOR 연산으로 정의된다. 따라서 XOR 게이트를 적절히 설정하면 난수를 생성하기 위해 LFSR을 모델링할 수 있다.^[1]
위상 검출기: XOR 게이트는 가장 간단한 위상 검출기 회로 구성에 사용될 수 있다.^[15]
신호 버퍼링 또는 반전: XOR 게이트는 신호를 버퍼링하거나 반전시키는 것을 쉽게 전환하는 데 사용될 수 있다.
상관 관계 및 시퀀스 감지: XOR 게이트는 두 입력이 서로 다를 때 1을 출력하고, 같을 때 0을 출력하는 특징을 갖는다. 이러한 특성을 이용하여, 매우 긴 데이터 시퀀스에서 특정 비트 패턴이나 PRN 시퀀스를 검색하는 데 XOR 게이트를 활용할 수 있다.^[1]

5. 1. 가산기

XOR 논리 게이트는 두 비트를 더하여 하나의 비트를 출력하는 1비트 가산기로 사용할 수 있다. 예를 들어, 이진법에서 1과 1을 더하면 10 (즉, 십진법으로 2)의 2비트 답을 얻게 된다. 이 출력의 뒤쪽 '합' 비트는 XOR로 얻어지므로, 앞쪽 '자리올림' 비트는 AND 게이트로 계산된다. 이것이 반가산기의 주요 원리이다. 더 큰 전가산기 회로는 더 긴 이진수를 더하기 위해 함께 연결될 수 있다.^[16]

XOR 게이트는 1비트 가산기의 기능을 한다. 즉, 두 비트를 더한 결과의 1비트가 얻어진다. 2비트째의 올림수(캐리)는 더하는 두 비트가 모두 1일 때이므로 AND 게이트를 통해 얻을 수 있다. 따라서 XOR 게이트와 AND 게이트를 사용하여 반가산기를 구성할 수 있다.

5. 2. 의사 난수 생성기

LFSR을 이용한 의사 난수(PRN) 생성기는 XOR 연산으로 정의된다. 따라서 XOR 게이트를 적절히 설정하면 난수를 생성하기 위해 LFSR을 모델링할 수 있다.^[1]

5. 3. 위상 검출기

XOR 게이트는 가장 간단한 위상 검출기 회로 구성에 사용될 수 있다.^[15]

5. 4. 신호 버퍼링 또는 반전

XOR 게이트는 신호를 버퍼링하거나 반전시키는 것을 쉽게 전환하는 데 사용될 수 있다. 예를 들어, XOR 게이트는 세븐 세그먼트 디스플레이 디코더 회로의 출력에 추가하여 사용자가 액티브 로우 또는 액티브 하이 출력을 선택할 수 있도록 할 수 있다.

5. 5. 상관 관계 및 시퀀스 감지

XOR 게이트는 두 입력이 서로 다를 때 1을 출력하고, 같을 때 0을 출력하는 특징을 갖는다. 이러한 특성을 이용하여, 매우 긴 데이터 시퀀스에서 특정 비트 패턴이나 PRN 시퀀스를 검색하는 데 XOR 게이트를 활용할 수 있다. 일련의 XOR 게이트를 사용하여 데이터 시퀀스와 찾고자 하는 대상 시퀀스를 병렬로 비교하고, 그 결과로 나오는 0의 개수를 세어 데이터 시퀀스와 대상 시퀀스가 얼마나 일치하는지 확인할 수 있다.

이러한 상관기는 CDMA 수신기, 오류 정정 및 채널 코드를 위한 디코더 등 다양한 통신 장치에 사용된다. 특히 CDMA 수신기에서는 여러 PRN 시퀀스 중에서 특정 PRN 시퀀스의 극성(polarity)을 추출하는 데 XOR 게이트를 이용한 상관기가 활용된다.^[1]

예를 들어, 데이터 시퀀스 `1110100101`에서 `11010` 패턴을 찾는 경우를 생각해보자. 상관기는 대상 시퀀스를 가능한 모든 오프셋에서 데이터 비트와 비교하여 일치하는 횟수(0의 개수)를 계산한다.

데이터	대상	XOR 연산 결과	0의 개수
1110100101	11010	00111	2
1110100101	11010	00000	5
1110100101	11010	01110	2
1110100101	11010	10011	2
1110100101	11010	01000	4
1110100101	11010	11111	0

위 표에서 볼 수 있듯이, 대상 시퀀스가 1비트만큼 오프셋되었을 때 5개의 비트가 모두 일치하여 0의 개수가 5개로 가장 많다. 반면, 5비트만큼 오프셋된 경우에는 모든 비트가 달라 0의 개수가 0개이다. 이처럼 XOR 게이트의 출력을 통해 시퀀스가 어디에서 나타나고, 반전되었는지 여부를 쉽게 확인할 수 있다. 일반적으로 긴 시퀀스일수록 짧은 시퀀스보다 감지하기가 더 쉽다.^[1]

6. 표준 칩 패키지

XOR 칩은 쉽게 구할 수 있다. 가장 일반적인 표준 칩 코드는 다음과 같다.

4070: CMOS 쿼드 듀얼 입력 XOR 게이트.^[10]
4030: CMOS 쿼드 듀얼 입력 XOR 게이트.^[11]
7486: TTL 쿼드 듀얼 입력 XOR 게이트.^[10]

CMOS 논리에서는 2입력 NAND 게이트나 NOR 게이트는 4개의 트랜지스터로 간단하게 구현할 수 있지만, XOR를 4개의 트랜지스터로 구현하는 것은 어렵다. 하지만 기본 논리의 조합으로 만드는 것은 약간 번거로우며, 회로적인 궁리도 있기 때문에, TTL이나 CMOS 논리의 범용 로직 IC에는 XOR 게이트가 포함되어 있다. 74 시리즈에서는 7486, 4000 시리즈에서는 4070 (4030의 대체)에 2입력 XOR 게이트가 4개 들어있다. 핀 배치는 모두 동일하다. DIP 패키지 제품이나 플랫 패키지 제품이 있다.

7. 해석적 표현

XOR^영어 게이트는 수식으로 표현될 수 있다.

: $f(a,b)=a+b-2ab$ 는 XOR 게이트의 해석적 표현이다.

:* $f(0,0)=0+0-2\cdot 0\cdot 0=0$

:* $f(0,1)=0+1-2\cdot 0\cdot 1=1$

:* $f(1,0)=1+0-2\cdot 1\cdot 0=1$

:* $f(1,1)=1+1-2\cdot 1\cdot 1=0$

: $f(a,b)=|a-b|$ 는 또 다른 해석적 표현이다.

참조

_[1] 서적 Practical Programmable Circuits: A Guide to PLDs, State Machines, and Microcontrollers https://books.google[...] Elsevier Science
_[2] 서적 Crypto 101 https://github.com/c[...]
_[3] 서적 An engineering approach to digital design https://archive.org/[...] Prentice-Hall 1980
_[4] 웹사이트 Aussagenlogik und Gatter https://sus.ziti.uni[...] University of Heidelberg 2024-01-21
_[5] 서적 Digital Electronics and Design with VHDL https://books.google[...] Morgan Kaufmann 2008-01-25
_[6] 웹사이트 Two interesting XOR circuits inside the Intel 386 processor http://www.righto.co[...] 2024-01-14
_[7] 서적 The Computer Engineering Handbook https://books.google[...] CRC Press 2001-12-26
_[8] 서적 Designing combinational logic gates in CMOS http://bwrcs.eecs.be[...]
_[9] 서적 Digital CMOS Circuit Design https://books.google[...] Springer Science & Business Media 2012-12-06
_[10] 서적 Introduction to Digital Systems: Modeling, Synthesis, and Simulation Using VHDL https://books.google[...] John Wiley & Sons 2011-06-15
_[11] 서적 Electronics All-in-One For Dummies - UK https://books.google[...] John Wiley & Sons 2013-09-24
_[12] 웹사이트 The "XOR" versus "Sum modulo 2" https://www.edn.com/[...] 2023-07-04
_[13] 간행물 74LVC1G386 http://www.nxp.com/d[...]
_[14] 웹사이트 Comparison of different design techniques of XOR & AND gate using EDA simulation tool https://www.research[...]
_[15] 서적 Digital integrated circuits : a design perspective Prentice-Hall
_[16] 문서 doi 10.1155/2009/803974,[...]
_[17] 간행물 74LVC1G386 http://www.nxp.com/d[...]
_[18] 웹사이트 A comparative performance analysis of various CMOS design techniques for XOR and XNOR circuits: Fig. 7. High performance transmission gate XOR, XNOR circuits http://researchtrend[...]
_[19] 웹사이트 Designing combinational logic gates in CMOS http://bwrcs.eecs.be[...]
_[20] 웹사이트 Transmission Gate XOR http://gram.eng.uci.[...]
_[21] 웹사이트 transmission-gate XOR (tiny XOR) https://tams-www.inf[...]
_[22] 웹사이트 Figure 3, Exclusive OR and XNOR gate https://wiki.analog.[...]
_[23] 웹사이트 Pass-Transistor Logic: Transmission Gate XOR https://ece.uwaterlo[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com