모딜리아니-밀러 정리

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사적 배경
3. 주요 명제 (1958년 무세금 모형)
4. 주요 명제 (1963년 수정 모형, 법인세 고려)
5. MM 이론의 가정
6. MM 이론에 대한 비판
7. 경제적 귀결
참조

1. 개요

모딜리아니-밀러 정리(MM 정리)는 기업의 자본 구조가 기업 가치에 미치는 영향에 대한 이론으로, 1958년 머튼 밀러와 프랑코 모딜리아니에 의해 처음 제시되었다. 이 정리는 세금과 거래 비용이 없는 완전 자본 시장을 가정하여, 기업의 가치는 자본 구조와 무관하며, 부채 사용 여부와 관계없이 동일한 영업 위험을 가진 기업의 가중 평균 자본 비용은 같다고 주장한다. MM 정리는 1963년 법인세를 고려한 수정 모형으로 확장되었으며, 부채 사용에 따른 이자 비용 절세 효과를 반영하여 최적 자본 구조의 존재 가능성을 제시했다. MM 이론은 현실적인 가정의 부족으로 비판받지만, 자본 구조 이론 발전에 기여했으며, 경제학 분야에서 재무의 중요성을 강조하는 데 영향을 미쳤다.

더 읽어볼만한 페이지

1958년 경제 - 필립스 곡선
필립스 곡선은 실업률과 인플레이션 간의 관계를 설명하는 경제 이론으로, 단기적으로는 역의 상관관계를 보이나 장기적으로는 자연실업률 개념에 따라 상충관계가 성립하지 않을 수 있으며, 현대 경제학에서는 기대인플레이션을 고려한 수정된 형태로 사용된다.
1958년 경제 - 풍요한 사회
풍요한 사회는 과잉 생산과 소비주의, 공공 부문 부족, 소득 불균형, 환경 문제 등 다양한 문제점을 안고 있으며, GDP 중심의 경제 평가가 삶의 질과 사회적 형평성을 간과한다는 비판을 받는 존 케네스 갤브레이스의 저서에서 유래한 개념이다.
경제학 정리 - 애로의 불가능성 정리
애로의 불가능성 정리는 3개 이상의 선택지에서 약한 파레토, 무관한 대안으로부터의 독립성, 비독재성을 모두 만족하는 사회 후생 함수는 존재하지 않음을 증명한 정리이다.
경제학 정리 - 후생경제학의 기본 정리
후생경제학의 기본 정리는 완전 경쟁 시장의 균형이 파레토 효율적임을 보이는 제1정리와, 특정 조건 하에 파레토 효율적인 자원 배분이 경쟁 균형으로 달성될 수 있음을 설명하는 제2정리로 구성되어, 자유 시장 경제의 이론적 기반을 강화하고 시장 실패 가능성과 정부 개입 필요성에 대한 논의를 낳는다.

모딜리아니-밀러 정리
개요
이름	모딜리아니-밀러 정리
다른 이름	자본 구조 무관련성 원리
주요 내용	완전 시장 하에서 기업의 가치는 자본 구조에 영향을 받지 않음
가정
완전 시장	정보의 비대칭성이 없음 거래 비용이 없음 세금이 없음 파산 비용이 없음 모든 투자자는 동일한 기대를 가짐
명제 1 (세금 없음)
내용	기업의 가치는 자본 구조와 무관하며, 미래 이익에 의해 결정됨
수식	VL = VU (VL: 레버리지 기업 가치, VU: 언레버리지 기업 가치)
명제 2 (세금 없음)
내용	자기자본 비용은 부채 비율에 따라 증가하며, 부채 비율이 높을수록 자기자본 비용이 증가함
수식	rE = r0 + (r0 - rD) * (D/E) (rE: 자기자본 비용, r0: 부채가 없는 기업의 자기자본 비용, rD: 부채 비용, D: 부채, E: 자기자본)
명제 1 (법인세 존재)
내용	기업의 가치는 법인세로 인해 부채를 사용할수록 증가함
수식	VL = VU + t * D (t: 법인세율)
명제 2 (법인세 존재)
내용	자기자본 비용은 법인세로 인해 부채 비율에 따라 증가하며, 그 증가폭은 세금이 없는 경우보다 작음
수식	rE = r0 + (r0 - rD) * (1-t) * (D/E)
비판 및 한계
현실과의 괴리	완전 시장이라는 가정은 현실과 동떨어져 있으며, 세금, 파산 비용, 정보 비대칭성 등이 존재함
수정 모형	이러한 한계를 극복하기 위해 다양한 수정 모형이 제시되었음 (예: 트레이드오프 이론, Pecking Order 이론)
관련 연구
주요 연구자	프랑코 모딜리아니 머튼 밀러
관련 학문	재무 경제학 기업 재무

2. 역사적 배경

머튼 밀러와 프랑코 모딜리아니는 카네기 멜론 대학교 산업 행정 대학원(GSIA) 교수 시절 이 정리를 도출하고 발표했다. 기업 금융에 대한 경험이 부족했음에도 불구하고, 이들은 재학생들에게 해당 과목을 가르치도록 배정되었다. 이 주제에 대한 기존 자료가 부족하다고 판단한 두 교수는 자체 연구를 바탕으로 정리를 만들었다. 그 결과는 ''American Economic Review''에 게재된 논문이었고, 이후 M&M 정리로 알려지게 되었다.

이 정리는 1958년 F. 모딜리아니와 M. 밀러에 의해 처음 제안되었으며,^[6] 같은 해 머튼 밀러와의 공동 저술 논문을 통해 발표되었다.^[7]

1963년에는 법인세를 고려한 모델로 수정되었다.^[8] 이는 MM의 수정 명제(tax correction of MM proposition)라고 불리며, 세후 영업 이익(NOPAT)을 사용하고, 법인세를 고려하면 레버리지를 올릴 때 자본 비용(가중 평균 자본 비용(WACC))이 하락하므로 주식 비용이 감소한다. 이 사실은 자금 조달에 있어 부채의 우위를 나타내고 있다. 밀러와 모딜리아니는 이러한 문제들을 논의하는 후속 논문을 여러 편 발표했다.

3. 주요 명제 (1958년 무세금 모형)

모딜리아니-밀러 정리(MM 정리)는 1958년 발표된 무세금 모형에서 다음과 같은 주요 명제를 제시했다.

MM 이론은 완전 시장을 가정할 때, 기업의 자본 구조와 배당 정책이 기업 가치에 영향을 미치지 않는다는 것을 보여준다. 그러나 현실에서는 완전 시장이 아니기 때문에 자본 구조나 배당 정책이 기업 가치에 영향을 미친다고 여겨진다.

제1 명제: 기업의 가치는 자본 구조와 무관하며, 동일한 영업위험을 가진 기업들의 가중평균자본비용은 모두 같다.
제2 명제: 기업의 이익 배분과 기업 가치는 무관하다. (주가 수익)
제3 명제: 자본 비용은 자본 구성에 의존하지 않는다.

3. 1. 제1 명제: 기업 가치와 자본 구조

MM이론의 기본적인 가정을 바탕으로 부채사용기업의 가치(

V^L

)와 무부채기업의 가치(

V^U

)가 동일하다는 것을 무위험차익거래의 논리로 증명하였다. 제1 명제에 따르면 자본구조의 변경, 즉 부채의 차입 여부는 기업가치와 가중평균자본비용에 아무런 영향을 미치지 못한다. 즉, 동일한 영업위험을 부담하는 기업집단의 가중평균자본비용(

k_0

)은 서로 같으며 단 하나의 자본비용이 존재한다(

k_0 = \rho

).^[4]

무부채기업의 경우 주식을 통해 자금을 조달한 경우의 자본비용인 자기자본비용이 가중평균자본비용과 일치한다. 따라서 무부채기업의 주주는 동일 영업집단의 영업위험만을 부담하므로 영업위험 프리미엄(Business Risk Premium, BRP)만을 기업에 요구하게 된다.

:

(k^U_0 = k_e^U = R_f + {\rm BRP})

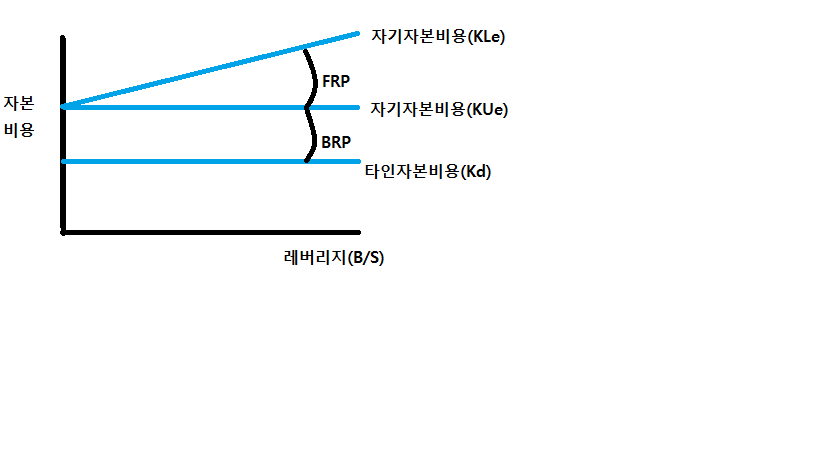
부채사용기업의 자기자본비용은 무부채기업의 자기자본비용에 재무위험 프리미엄을 더한 것이며, 재무위험 프리미엄은 부채비율(

B/S

)에 비례하여 증가한다.

:

k^L_e = \rho + (\rho - k_d)\frac{B}{S}

무부채기업과 달리 부채사용기업의 주주는 영업위험뿐만 아니라 부채 사용에 따라 채무를 불이행할 위험, 즉 재무위험을 부담하게 된다. 따라서 주주는 기업에게 영업위험 프리미엄뿐만 아니라 재무위험 프리미엄(Financial Risk Premium, FRP)을 추가로 요구하게 된다. 이때 자기자본비용과 타인자본비용의 가중평균인 가중평균자본비용은 달라지지 않는다.

재무 구조를 제외하고는 동일한 두 회사 U(무차입 회사)와 L(차입 회사)를 가정할 때, 모딜리아니-밀러 정리는 두 회사의 기업 가치가 동일하다고 말한다. 이는 차익 거래를 통해 시각화할 수 있는데, 투자자는 더 높은 가치의 회사 지분을 매각하고 낮은 가치의 회사 지분을 구매하여 더 적은 자본 지출로 동일한 수익을 올릴 수 있다. 이러한 차익 거래는 시장 왜곡을 수정하며, 궁극적으로 두 회사의 가치를 동일하게 만든다.

MM 가설에 따르면, 차입 회사의 가치는 무차입 회사의 가치보다 높을 수 없다. 두 가치는 같아야 한다. 회사의 자본 구조에서 부채를 사용하는 데에는 이점도 불이익도 없다.

:

V_U = V_L

여기서

V_U

는 무차입 기업의 가치(지분으로만 구성된 기업을 구매하는 가격),

V_L

은 차입 기업의 가치(부채와 지분이 혼합된 기업을 구매하는 가격)이다.

이것이 사실인 이유는 다음과 같이 설명할 수 있다. 투자자가 두 기업 U 또는 L 중 하나를 구매하는 것을 고려할 때, 차입 기업 L의 주식을 구매하는 대신, 그는 기업 U의 주식을 구매하고 기업 L이 가진 것과 동일한 금액 B를 차입할 수 있다. 이러한 두 투자에 대한 최종 수익은 동일할 것이다. 따라서 L의 가격은 U의 가격에서 차입한 금액 B를 뺀 것과 같아야 하며, 이는 L의 부채 가치이다.

이 논의는 또한 이 정리의 몇 가지 가정의 역할을 명확히 한다. 투자자의 차입 비용이 기업의 차입 비용과 동일하다고 가정했는데, 비대칭 정보가 존재하거나, 효율적인 시장이 부재하거나, 투자자가 기업과 다른 위험 프로필을 가진 경우에는 반드시 사실일 필요는 없다.

3. 2. 제2 명제: 자기자본비용과 부채비율

MM이론의 기본적인 가정을 바탕으로 부채사용기업의 가치와 무부채기업의 가치가 동일하다는 것을 무위험차익거래의 논리로 증명하였다. 주로 3가지 명제로 요약된다. 기업의 가치는 그 기업의 자본구조와 무관하며, 동일한 영업위험을 부담하는 기업집단의 가중평균자본비용(

k_0

)은 서로 같으며 단 하나의 자본비용이 존재한다.

:

( k_0 = \rho )

MM의 제1명제에 의하면 자본구조의 변경, 즉 부채의 차입여부는 기업가치와 가중평균자본비용에 아무런 영향을 미치지 못한다. 즉 동질적 영업집단은 단 하나의 자본비용만이 존재하는데 그것이

\rho

이다. 무부채기업의 경우 주식을 통해 자금을 조달한 경우의 자본비용인 자기자본비용이 가중평균자본비용과 일치한다. 따라서 무부채기업의 주주는 동일 영업집단의 영업위험만을 부담하므로 영업프리미엄(Business Risk Premium)만을 기업에 요구하게 된다.

:

(k^U_0 = k_e^U = R_f + {\rm BRP})

부채사용기업의 자기자본비용은 무부채기업의 자기자본비용에 재무위험프리미엄을 더한 것이며, 재무위험프리미엄은 부채비율(

B/S

)에 비례하여 증가한다.

:

k^L_e = \rho  + (\rho-k_d)\frac{B}{S}

무부채기업과 달리 부채사용기업의 주주는 영업위험뿐만 아니라 부채사용에 따라 채무를 불이행할 위험, 즉 재무위험을 부담하게 된다. 따라서 주주는 기업에게 영업위험 프리미엄뿐만 아니라 재무위험프리미엄(FRP:Financial Risk Premium)을 추가로 요구하게 된다. 이때 자기자본비용과 타인자본비용의 가중평균인 가중평균자본비용은 달라지지 않는다.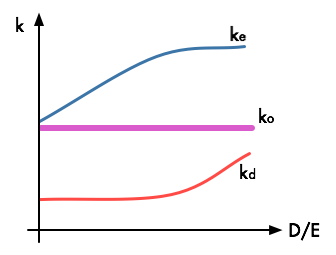

위험 부채를 포함한 명제 II. 레버리지(D/E)가 증가함에 따라 WACC(k0)는 일정하게 유지된다.

:

r_E = r_0 + \frac{D}{E}(r_0 - r_D)

여기서

$r_E$ 는 레버리지된 기업의 자기자본에 대한 예상 수익률 또는 자기자본 비용이다.
$r_0$ 는 레버리지가 없는 기업의 자기자본 비용 (레버리지 없는 자기자본 비용 또는 D/E = 0인 자산 수익률)이다.
$r_D$ 는 차입금에 대한 예상 수익률 또는 부채 비용이다.
$\frac{D}{E}$ 는 부채 자본 비율이다.

부채 자본 비율이 높을수록 부채가 있는 회사의 주주가 부담하는 위험이 커지므로 자기자본에 대한 요구 수익률이 높아진다. 이 공식은 가중 평균 자본 비용(WACC) 이론에서 파생되었다.

이러한 명제는 다음 가정을 따를 때 유효하다.

거래 비용이 존재하지 않으며,
개인과 기업은 동일한 금리로 차입한다.

이러한 결과는 무관해 보일 수 있지만 (결국 현실 세계에서는 이러한 조건 중 어느 것도 충족되지 않는다), 이 정리는 여전히 가르치고 연구되고 있는데, 이는 매우 중요한 점을 시사하기 때문이다. 즉, 자본 구조는 이러한 가정 중 하나 이상이 위반되기 때문에 중요하다는 것이다. 최적 자본 구조의 결정 요인을 어디에서 찾아야 하는지, 그리고 이러한 요인이 최적 자본 구조에 어떤 영향을 미칠 수 있는지 알려준다.

제3 명제: 자본 비용은 자본 구성에 의존하지 않는다.
* 자금 조달은 주가 또는 부채의 조달 방법과 무관하다.
* 기업의 투자 삭감률은 부채 미사용 기업의 자기 자본의 자본 비용이며, 이는 자본 구성과 완전히 무관하게 결정된다.

3. 3. 제3 명제: 투자 결정과 자본 조달

MM이론의 제1 명제와 제2 명제를 신규 투자안 의사결정에 적용한 것이다. 투자안 의사결정에 사용되는 적절한 할인율은 기업의 자본조달 방법과 무관하게 결정되며, 기업의 자본조달에 관한 의사결정과 투자안에 대한 의사결정은 무관하게 이루어진다.^[9]

자금 조달은 주가 또는 부채의 조달 방법과 무관하다.
기업의 투자 삭감률은 부채 미사용 기업의 자기 자본의 자본 비용이며, 이는 자본 구성과 완전히 무관하게 결정된다.

"만약 클래스

K

의 기업이 주주에게 가장 잘 부합하도록 의사 결정을 한다면, 그 기업은 투자 수익률

\rho

가

\rho K

와 같거나 클 경우에 한해서 투자를 진행할 것이다. 즉, 그 기업의 투자 [컷오프 레이트/할증률](cut off point)은 항상

\rho K

이며, 이 컷오프 레이트가 투자 자금을 조달하기 위해 사용되는 증권의 종류에 의해 영향을 받는 일은 전혀 없다. 다시 말해, 자금 조달 방식에 관계없이 기업의 한계 자본 비용은 가중 평균 자본 비용과 같으며, 또한 가중 평균 자본 비용은 그 기업이 속한 클래스에서 자기자본만으로 구성된 기업의 순 영업 이익 흐름(unlevered stream)에 대한 자본화율과 같다."^[9]

4. 주요 명제 (1963년 수정 모형, 법인세 고려)

1963년 수정 모형에서는 법인세가 존재할 때의 가정을 추가하여, 부채 사용 시 발생하는 이자비용 절세 효과를 고려하였다. 그 결과 최적 자본 구조가 존재한다는 수정된 결론을 내렸다. 수정 모형은 1958년 모형과 마찬가지로 제1, 2, 3 명제로 구성된다.^[8]

이 개념은 미국의 경제학자 프랑코 모딜리아니가 카네기 멜론 대학교 교수 시절 기본 아이디어를 제창하고^[6], 1958년 머튼 밀러와의 공동 저술 논문을 통해 발표하였다.^[7]

4. 1. 제1 명제: 기업 가치와 절세 효과

1963년의 수정 모형에서는 법인세가 존재할 때의 가정을 추가하여, 부채 사용 시 발생하는 이자비용 절세 효과를 고려하였다. 그 결과 최적 자본 구조가 존재한다는 수정된 결론을 내렸다.

법인세를 고려하는 경우 부채 사용 기업의 가치는 무부채 기업의 가치보다 절세 효과(

Bt

)만큼 더 크다. 부채 사용 기업의 경우 이자비용을 지출한 것에 대한 절세 효과가 존재하기 때문에 무부채 기업보다 기업 가치가 더 크다. 이러한 이자비용 절세 효과의 크기를 '''레버리지 이득'''이라고 한다. 주주가 부담해야 하는 위험을 과세 당국인 정부가 나누어 부담하므로 주주가 요구하는 자본 비용이 감소한다고 이해해도 무방하다.^[8]

:

V_L = V_U + T_C D\,

여기서

$V_L$ 는 "차입 기업의 가치"이다.
$V_U$ 는 "무차입 기업의 가치"이다.
$T_C D$ 는 "세율( $T_C$ ) x 부채의 가치(D)"이다.
$T_C D$ 의 유도:
연간 이자 금액 = 부채 x 이자율
연간 절세 효과 = 부채 x 이자율 x 세율
자본화 가치(영구 기업) = (부채 × 이자율 x 세율) ÷ 부채 비용
$T_C D$ 라는 용어는 부채가 영구적임을 가정한다.

이는 기업이 이자 지급액을 공제할 수 있으므로 차입에 대한 이점이 있음을 의미한다. 따라서 레버리지는 세금 지급액을 낮춘다. 배당금 지급액은 공제 대상이 아니다.^[6]^[7]

4. 2. 제2 명제: 자기자본비용과 법인세

1963년, 모딜리아니와 밀러는 법인세가 존재할 때의 가정을 추가하여 기존 모형을 수정했다. 법인세가 존재하면 부채 사용 시 발생하는 이자비용 절세효과를 고려해야 한다. 그 결과, 최적자본구조가 존재한다는 수정된 결론을 내렸다. 수정 모형도 1958년 모형과 마찬가지로 제1, 2, 3 명제로 구성된다.

법인세를 고려하는 경우, 부채사용기업의 자기자본비용은 다음과 같다.

:

r_E = r_0 + \frac{D}{E}(r_0 - r_D)(1-T_C)

여기서:

$r_E$ 는 자기 자본에 대한 요구 수익률 또는 레버리지 자기 자본 비용 (무레버리지 자기 자본 + 자금 조달 프리미엄)이다.
$r_0$ 는 레버리지가 없는 회사의 자기 자본 비용(무레버리지 자기 자본 비용 또는 D/E = 0일 때 자산 수익률)이다.
$r_D$ 는 차입에 대한 요구 수익률 또는 부채 비용이다.
${D}/{E}$ 는 부채/자기 자본 비율이다.
$T_c$ 는 세율이다.

위 식에서 볼 수 있듯이, 법인세를 받는 정부도 재무위험을 부담하게 되어 재무위험프리미엄이 (

1-t

)의 비율로 감소한다. 자기자본비용은 레버리지가 증가함에 따라 증가하며, 자기자본에 대한 위험이 증가한다는 이전과 동일한 관계가 여전히 유효하다. 그러나 이 공식은 WACC와의 차이점에 대한 함의를 갖는다. 세금을 포함하여 싼 부채로 자기자본을 대체하여 레버리지를 높이면 WACC가 감소하고 부채가 100%인 지점에서 최적의 자본 구조가 실제로 존재한다는 점을 확인했다.^[8]

세금이 있는 명제에서는 다음과 같은 가정이 이루어진다.

법인은 이자 지급 후 소득에 대해 $T_C$ 세율로 과세된다.
거래 비용은 존재하지 않는다.
개인과 법인은 동일한 금리로 차입한다.

1963년에 법인세를 고려한 모델로 수정되었다.^[8] 이는 MM의 수정 명제(tax correction of MM proposition)라고 불리며, 세후 영업 이익(NOPAT)을 사용하고, 법인세를 고려하면 레버리지를 올릴때 자본 비용(가중 평균 자본 비용(WACC))이 하락하므로, 주식 비용이 감소한다. 이 사실은 자금 조달에 있어서 부채의 우위를 나타내고 있다.

4. 3. 제3 명제: 투자 결정과 법인세

MM의 1963년 수정 모형에서는 법인세가 존재할 때의 가정을 추가하여, 이자비용 절세효과를 고려한 최적자본구조가 존재한다는 결론을 내렸다. 이 수정 모형도 1958년 모형과 마찬가지로 제1, 2, 3 명제로 구성된다.

법인세를 고려하는 경우, 부채사용기업의 가치는 무부채기업의 가치보다 절세 효과(tax shield^영어)만큼 더 크다. 이를 '''레버리지 이득'''이라고 한다. 이는 주주가 부담해야 할 위험을 정부가 나누어 부담하여 주주의 요구 자본비용이 감소하는 것으로 이해할 수 있다.^[9]

수정 제3 명제는 신규 투자안에 수정 제1 명제와 제2 명제를 적용한 것이다. 자금 조달은 주가 또는 부채의 조달 방법과 무관하며, 기업의 투자 삭감률은 부채 미사용 기업 자기자본의 자본 비용이며, 이는 자본 구성과 완전히 무관하게 결정된다.^[9]

"만약 클래스

K

의 기업이 주주에게 가장 잘 부합하도록 의사 결정을 한다면, 그 기업은 투자 수익률

\rho

가

\rho K

와 같거나 클 경우에 한해서 투자를 진행할 것이다. 즉, 그 기업의 투자 [컷오프 레이트/할증률](cut off point)은 항상

\rho K

이며, 이 컷오프 레이트가 투자 자금을 조달하기 위해 사용되는 증권의 종류에 의해 영향을 받는 일은 전혀 없다. 다시 말해, 자금 조달 방식에 관계없이 기업의 한계 자본 비용은 가중 평균 자본 비용과 같으며, 또한 가중 평균 자본 비용은 그 기업이 속한 클래스에서 자기자본만으로 구성된 기업의 순 영업 이익 흐름(unlevered stream)에 대한 자본화율과 같다."^[9]

5. MM 이론의 가정

MM이론은 다음과 같은 기본적인 가정을 전제로 한다.^[4]

완전자본시장: 거래 비용이나 세금이 없고, 정보에 제한이 없는 시장이다.
단순화된 증권: 기업은 주식과 무위험 영구 부채만 발행한다. 현실에서는 부채에 만기가 있지만, 만기가 도래하면 새로운 부채를 발행하여 부채액을 유지할 수 있다고 가정한다.
동일한 차입/대출 금리: 개인 투자자는 기업과 같은 이자율로 돈을 빌리거나 빌려줄 수 있다.
동질적 위험 집단: 기업은 영업 위험이 동일한 집단으로 분류할 수 있다.

이러한 가정 하에, 모딜리아니-밀러 정리는 기업 가치가 자본 구조(부채와 자기자본의 비율)와 무관하다는 것을 보여준다. 즉, 부채를 전혀 사용하지 않는 기업(무차입 기업)과 부채를 사용하는 기업(차입 기업)의 가치는 동일하다.

이는 차익 거래를 통해 설명할 수 있다. 두 기업이 자본 구조만 다르고 모든 면에서 동일하다고 가정할 때, 가치가 더 높은 기업의 투자자는 자신의 지분을 팔고 가치가 낮은 기업의 지분을 구매하여 더 적은 돈으로 같은 수익을 얻을 수 있다. 이러한 차익 거래는 시장 왜곡을 수정하여 결국 두 기업의 가치를 동일하게 만든다.

투자자가 차입 기업의 주식을 사는 대신, 무차입 기업의 주식을 사고 차입 기업과 같은 금액을 빌릴 수 있다. 두 경우의 최종 수익은 같으므로, 차입 기업의 가격은 무차입 기업의 가격에서 빌린 금액(부채 가치)을 뺀 것과 같아야 한다.

이러한 논의는 투자자의 차입 비용이 기업의 차입 비용과 같다는 가정이 중요함을 보여준다. 만약 비대칭 정보, 비효율적인 시장, 또는 투자자와 기업 간 위험 프로필 차이가 존재하면 이 가정은 성립하지 않을 수 있다.

6. MM 이론에 대한 비판

MM의 이론은 자본구조이론에 있어 큰 공헌을 했지만, 이론의 가정이 비현실적이라는 비판이 있었다.^[1] 주요 내용은 다음과 같다.

현실에는 법인세가 존재한다.
현실에는 시장불완전 요소가 존재한다.
개인과 기업의 차입 능력은 현저히 다르다.
거래 비용 등 마찰적 요인이 존재한다.

MM 이론에 따르면 주가와 배당 간의 무관련성이 증명된다.^[1] 또한 완전 시장의 전제를 완화하여 세금과 파산 비용을 도입한다.^[1] 자기자본이익률(ROE, 주주 자본 이익률)과의 비교도 이루어졌다.^[1]

MM 이론은 경제학 내에 재무 분야를 위치시켰다는 점에서 중요한 업적을 남겼으며, 많은 경제학자를 재무 분야로 이끌어 발전시키는 계기를 만들었다.^[1]

이 이론이 자본 시장에 영향을 미친 정확한 범위를 결정하기는 어렵지만, 인수가 레버리지 이용을 촉진하거나 확대하는 데 사용되고 있다.^[1] 이 이론의 주요 문제는 주주가 공기업의 소유주라고 가정하는 것이다. 이 가정은 벌 앤 민스(Berle and Means, 1932년) 이래 법학자들에 의해 논파되어 왔다. 99.9%가 유통 시장인데, 주주는 소유주(잔여 청구권자)도, 투자자도 아니다.^[1]

EBIT(기업 가치) 계산을 위한 자본 비용 계산식 사용은 극히 제한적이다.^[1]

법인세 도입에 따른 MM이론(MM의 수정 명제)은 자금 조달의 부채 우위를 보여주었지만, 부채에 의존하면 재무적 파산(financial distress)이 발생하여 파산이나 채무 불이행에 이를 위험성이 있으며, 비용으로 인식해야 한다.^[1]

MM이론이 발표된 이후, 최적 자본 구성에 관한 일반 공식이나 실무 해답은 아직 제시되지 않았으며, 연구 논문 등에서는 "실무에서의 검증이 요구된다"는 결론이 많다.^[1]

7. 경제적 귀결

모딜리아니-밀러 정리에 따르면, 완벽한 시장에서 기업의 가치는 자금 조달 방법에 영향을 받지 않는다. 즉, 빚을 내서 자금을 마련하든, 자기 자본으로 자금을 마련하든 기업의 가치는 동일하다는 것이다.^[4]

이는 차익 거래를 통해 설명할 수 있다. 두 회사가 똑같은 사업을 하고 있지만, 한 회사는 빚이 있고(차입 기업) 다른 회사는 빚이 없다(무차입 기업)고 가정해 보자. 만약 두 회사의 가치가 다르다면, 투자자들은 더 싼 회사의 주식을 사서 더 비싼 회사의 주식을 팔아 차익을 얻을 수 있다. 이러한 차익 거래는 결국 두 회사의 가치를 같게 만든다.

MM 가설에 따르면, 차입 기업의 가치는 무차입 회사의 가치보다 높을 수 없다. 두 가치는 같아야 한다. 회사의 자본 구조에서 부채를 사용하는 데에는 이점도 불이익도 없다.

: $V_U = V_L \,$

여기서 $V_U$ 는 ''무차입 기업의 가치'' (지분으로만 구성된 기업을 구매하는 가격)이고, $V_L$ 은 ''차입 기업의 가치'' (부채와 지분이 혼합된 기업을 구매하는 가격)이다. 차입(levered)의 다른 말은 ''기어드(geared)''이며, 동일한 의미를 갖는다.^[4]

이는 투자자가 차입 기업의 주식을 사는 대신, 무차입 기업의 주식을 사고 돈을 빌려 같은 효과를 낼 수 있기 때문이다. 따라서 차입 기업의 주식 가격은 무차입 기업의 주식 가격에서 빌린 돈을 뺀 값과 같아야 한다.

이러한 논리는 투자자가 기업과 같은 비용으로 돈을 빌릴 수 있다는 가정을 전제로 한다. 하지만 현실에서는 정보 비대칭, 비효율적인 시장, 투자자와 기업 간의 위험 프로필 차이 등으로 인해 이 가정이 항상 성립하지는 않는다.

: $r_E = r_0 + \frac{D}{E}(r_0 - r_D)$

여기서

$r_E$ ''는 레버리지된 기업의 자기자본에 대한 예상 수익률 또는 자기자본 비용이다.''
$r_0$ ''는 레버리지가 없는 기업의 자기자본 비용 (레버리지 없는 자기자본 비용 또는 D/E = 0인 자산 수익률)이다.''
$r_D$ ''는 차입금에 대한 예상 수익률 또는 부채 비용이다.''
$\frac{D}{E}$ ''는 부채 자본 비율이다.''

부채 비율이 높을수록 주주들이 더 큰 위험을 부담해야 하므로, 자기자본에 대한 요구 수익률이 높아진다. 이 공식은 가중 평균 자본 비용(WACC) 이론에서 파생되었다.

이러한 명제는 거래 비용이 없고, 개인과 기업이 같은 금리로 돈을 빌릴 수 있다는 가정을 전제로 한다.

하지만 현실에서는 이러한 가정이 항상 성립하지 않기 때문에 자본 구조가 중요해진다. 모딜리아니-밀러 정리는 최적 자본 구조를 결정하는 요인이 무엇인지, 그리고 이러한 요인이 최적 자본 구조에 어떤 영향을 미칠 수 있는지 알려준다.

:

V_L =V_U + T_C D\,

여기서

$V_L$ 는 "차입 기업의 가치"이다.
$V_U$ 는 "무차입 기업의 가치"이다.
$T_C D$ 는 "세율( $T_C$ ) x 부채의 가치(D)"이다.

T_C D

의 유도 -

연간 이자 금액 = 부채 x 이자율
연간 절세 효과 = 부채 x 이자율 x 세율
자본화 가치(영구 기업) = (부채 × 이자율 x 세율) ÷ 부채 비용
$T_C D$ 라는 용어는 부채가 영구적임을 가정한다.

이는 기업이 이자 지급액을 공제받을 수 있어 빚을 내는 것이 유리하다는 것을 의미한다. 즉, 빚을 내면 세금을 줄일 수 있다. 배당금 지급액은 공제 대상이 아니다.

:

r_E = r_0 + \frac{D}{E}(r_0 - r_D)(1-T_C)

여기서:

$r_E$ 는 ''자기 자본에 대한 요구 수익률 또는 레버리지 자기 자본 비용 = 무레버리지 자기 자본 + 자금 조달 프리미엄''이다.
$r_0$ 는 ''레버리지가 없는 회사의 자기 자본 비용(무레버리지 자기 자본 비용 또는 D/E = 0일 때 자산 수익률)''이다.
$r_D$ 는 ''차입에 대한 요구 수익률 또는 부채 비용''이다.
${D}/{E}$ 는 ''부채/자기 자본 비율''이다.
$T_c$ 는 ''세율''이다.

자기 자본 비용은 레버리지가 증가함에 따라 증가하며, 자기 자본에 대한 위험이 증가한다는 이전과 동일한 관계가 여전히 유효하다. 그러나 이 공식은 WACC와의 차이점에 대한 함의를 갖는다. 자본 구조에 대한 두 번째 시도는 세금을 포함하여 싼 부채로 자기 자본을 대체하여 레버리지를 높이면 WACC가 감소하고 부채가 100%인 지점에서 최적의 자본 구조가 실제로 존재한다는 점을 확인했다.

세금이 있는 명제에서는 다음과 같은 가정이 이루어진다.

법인은 이자 지급 후 소득에 대해 $T_C$ 세율로 과세된다.
거래 비용은 존재하지 않으며,
개인과 법인은 동일한 금리로 차입한다.

MM 이론은 주가와 배당 간의 무관련성을 증명하고, 완전 시장의 가정을 완화하여 세금과 파산 비용을 고려한다. 또한 자기자본이익률(ROE)과의 비교를 통해 이론의 의미를 설명한다.

MM 이론은 경제학 내에 재무를 위치시켰다는 점에서 중요한 업적을 남겼으며, 재무 분야에 많은 경제학자를 이끌어 발전시키는 계기를 만들었다.

참조

_[1] 논문 The Modigliani and Miller Theorem and the Integration of Financial Markets
_[2] 강연 MIT Sloan Lecture Notes, Finance Theory II
_[3] 서적 Finance for Executives: A Practical Guide for Managers NPV Publishing
_[4] 문서
_[5] 서적 現代経済学のフロンティア日本経済新聞社
_[6] 서적 現代経済学の巨人たち:20世紀の人・時代・思想日本経済新聞出版社
_[7] 논문 "The Cost of Capital, Corporation Finance and the Theory of Investment（邦題：資本コスト、企業金融、および投資理論）" 1958-06
_[8] 논문 "Corprate Income Taxes and the Cost of Capital: A Correction（邦題：法人税と資本コスト）" 1963-06
_[9] 논문 "The Cost of Capital, Corporation Finance and the Theory of Investment"

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com