변위장
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
변위장은 전기장과 전기 편극 밀도 사이의 관계를 나타내는 벡터장으로, 유전체의 전기적 특성을 설명하는 데 사용된다. 변위장 D는 진공 유전율과 전기장의 곱에 전기 편극 밀도를 더한 값으로 정의되며, 가우스 법칙을 만족한다. 선형 매질에서는 전기장과 비례하며, 유전율을 통해 표현된다. 변위장은 맥스웰 방정식에서 중요한 역할을 하며, 축전기 내의 전하 분포와 전기장 관계를 설명하는 데 사용된다.
더 읽어볼만한 페이지
| 변위장 | |
|---|---|
| 개요 | |
| 이름 | 전기 변위장 전기 선속 밀도 |
| 영어 이름 | Electric displacement field Electric flux density |
| 기호 | D |
| 차원 | T I L |
| SI 단위 | 쿨롱/제곱미터 (C/m²) |
| 일반적인 관계 | |
| 구성 방정식 | D = ε₀ E + P |
| 여기서 | E는 전기장 P는 분극 밀도 ε₀는 진공 유전율 |
| 맥스웰 방정식과의 관계 | |
| 가우스 법칙 | ∇ ⋅ D = ρ |
| 앙페르 회로 법칙 | ∇ × H = J + ∂D/∂t |
| 여기서 | ρ는 자유 전하 밀도 J는 전류 밀도 H는 자기장 t는 시간 |
2. 정의
유전체인 매질이 전기장에 놓이면, 매질 고유의 전기 쌍극자 모멘트가 발생한다. 이 밀도를 '''전기 편극 밀도'''(electric polarization density|전기 편극 밀도영어) 로 정의한다.
전기 변위장 '''D'''는 다음과 같이 정의된다.
유전체인 매질에서 전기장은 매질 고유의 전기 쌍극자 모멘트를 생성하는데, 그 밀도를 '''전기 편극 밀도'''(electric polarization density영어) 라고 한다.
변위장 는 전기장 와 편극 밀도 사이의 관계를 나타내며, 다음과 같이 표현된다.
:.
여기서 은 진공의 유전율이다.
선형 매질에서 편극 밀도는 외부 전기장에 비례한다.
:.
여기서 는 비례 상수인 '''감수율'''(susceptibility|감수율영어)이다. 매질의 유전율 을 다음과 같이 정의하면,
:
변위장은 다음과 같이 나타낼 수 있다.
:.
가우스 법칙에 따르면, 변위장의 발산은 자유 전하 밀도 와 같다.
:.
스토크스 정리를 이용하면, 폐곡면에서의 변위장 선속은 폐곡면 내 총 자유 전하량 와 같다.
:.
전기 변위장 '''D'''는 다음과 같이 정의된다.
:
여기서 는 진공 유전율이며, '''P'''는 분극 밀도를 나타낸다.
변위장은 유전체 내에서 가우스 법칙을 만족한다.
:
여기서 는 단위 부피당 자유 전하의 수 (때로는 공간 전하)이다. '''D'''의 선속선이 자유 전하에서 시작하고 끝나야 함을 의미한다. 는 중성인 각 쌍극자의 일부인 모든 전하의 밀도이다.
'''D'''는 자유 전하에 의해서만 결정되지 않는데, '''E'''는 정전기적 상황에서 컬이 0이므로, 다음이 따른다.
:
선형, 균질, 등방성 유전체에서, '''P'''는 전기장에 선형적으로 의존한다.
:
여기서 는 전기 감수율이다. 따라서
:
여기서 는 상대 유전율이고 는 유전율이다.
선형적이고 균질하며 등방성인 매질에서, ''ε''는 상수이나, 선형 이방성 매질에서는 텐서이고, 비균질 매질에서는 매질 내부의 위치에 대한 함수이다. 선형 시불변 매질에 대한 다음 관계를 얻는다.
:
여기서 는 인가된 전장의 주파수이다. 인과율의 제약은 크라머스-크로니히 관계로 이어진다.
경계에서, , 여기서 ''σ''f는 자유 전하 밀도이고 단위 법선 는 매질 2에서 매질 1의 방향을 가리킨다.[1]
전속 밀도는 가우스 법칙에 의해 정의된다. 어떤 영역 를 생각하고, 그 경계를 로 한다. 영역 내부의 전하를 라고 할 때, 전속 밀도 는
:
를 만족하는 벡터장으로 정의된다. 유리화 계수 는 국제량계 (ISQ)에 대표되는 유리계에서 , 가우스 단위계에 대표되는 비유리계에서는 이다.
발산 정리에 의해
:
로 변형되어
:
가 된다. 여기서 영역을 작게 하는 극한 을 고려하면
:
가 되어 가우스 법칙을 미분으로 나타낼 수 있다. 여기서 전하 밀도는
:
이다.
3. 가우스 법칙
:
여기서 는 진공 유전율(자유 공간의 유전율이라고도 함)이고, '''P'''는 물질 내의 영구적 및 유도된 전기 쌍극자 모멘트의 (거시적) 밀도이며, 이를 분극 밀도라고 한다.
변위장은 유전체 내에서 가우스 법칙을 만족한다.
:
이 식에서 는 단위 부피당 자유 전하의 수이다. 이러한 전하는 부피를 중성 상태가 아닌 상태로 만들고, 때로는 공간 전하라고도 한다. 이 방정식은 실제로 '''D'''의 선속선이 자유 전하에서 시작하고 끝나야 함을 말한다. 반대로 는 중성인 각 쌍극자의 일부인 모든 전하의 밀도이다. 금속 콘덴서 판 사이의 절연 유전체의 예에서, 유일한 자유 전하는 금속 판에 있으며, 유전체는 쌍극자만 포함한다. 유전체가 도핑된 반도체 또는 이온화된 가스 등으로 대체되면, 전자는 이온에 대해 이동하고, 시스템이 유한하면 두 전하 모두 가장자리에서 에 기여한다.
'''D'''는 자유 전하에 의해서만 결정되지 않는다. '''E'''는 정전기적 상황에서 컬이 0이므로, 다음이 따른다.
:
이 방정식의 효과는 막대 자석의 전기적 유사물인 막대 일렉트릿과 같이 "고정된" 분극을 가진 물체의 경우에 볼 수 있다. 이러한 물질에는 자유 전하가 없지만, 고유한 분극은 전기장을 발생시켜 '''D'''장이 완전히 자유 전하에 의해 결정되지 않음을 보여준다. 전기장은 위의 관계와 분극 밀도에 대한 다른 경계 조건을 사용하여 결합 전하를 생성하고, 이는 다시 전기장을 생성한다.
전기장에 대한 즉각적인 응답을 보이는 선형, 균질, 등방성 유전체에서, '''P'''는 전기장에 선형적으로 의존한다.
:
여기서 비례 상수 는 물질의 전기 감수율이라고 한다. 따라서
:
여기서 는 물질의 상대 유전율이고 는 유전율이다.
선형적이고 균질하며 등방성인 매질에서, ''ε''는 상수이다. 그러나 선형 이방성 매질에서는 텐서이고, 비균질 매질에서는 매질 내부의 위치에 대한 함수이다. 또한 전기장에 따라 달라질 수 있으며 (비선형 물질) 시간 의존적인 응답을 가질 수 있다. 명시적인 시간 의존성은 물질이 물리적으로 움직이거나 시간에 따라 변하는 경우 (예: 움직이는 경계면에서의 반사로 인해 도플러 이동이 발생) 발생할 수 있다. 다른 형태의 시간 의존성은 시간 불변 매질에서 발생할 수 있으며, 전기장 인가와 물질의 결과적인 분극 사이에는 시간 지연이 있을 수 있다. 이 경우 '''P'''는 임펄스 응답 감수율 ''χ''와 전기장 '''E'''의 컨볼루션이다. 이러한 컨볼루션은 주파수 영역에서 더 간단한 형태를 취한다. 관계를 푸리에 변환하고 컨볼루션 정리를 적용하여, 선형 시불변 매질에 대한 다음 관계를 얻는다.
:
여기서 는 인가된 전장의 주파수이다. 인과율의 제약은 크라머스-크로니히 관계로 이어지며, 이는 주파수 의존성의 형태에 제한을 둔다. 주파수 의존 유전율의 현상은 물질 분산의 예이다. 사실, 모든 물리적 물질은 인가된 전장에 즉시 응답할 수 없기 때문에 물질 분산을 가지고 있지만, 많은 문제 (충분히 좁은 대역폭)의 경우, ''ε''의 주파수 의존성은 무시될 수 있다.
경계에서, 이고, 여기서 ''σ''f는 자유 전하 밀도이고 단위 법선 는 매질 2에서 매질 1의 방향을 가리킨다.[1]
전속 밀도는 가우스 법칙에 의해 정의된다. 즉, 어떤 영역 V를 생각하고, 그 경계를 ∂V로 한다. 영역 V 내부의 전하를 QV라고 할 때, 전속 밀도 '''D'''는
를 만족하는 벡터장으로 정의된다. 유리화 계수 λ는 국제량계 (ISQ)에 대표되는 유리계에서 λ = 1, 가우스 단위계에 대표되는 비유리계에서는 λ = 4π이다.
발산 정리에 의해 좌변은
로 변형되어
가 된다. 여기서 영역을 작게 하는 극한 V → 0을 고려하면
가 되어 가우스 법칙을 미분으로 나타낼 수 있다. 여기서 전하 밀도는
이다.
4. 전속 밀도와 전장(전기장)의 세기의 관계
변위장 는 전기장 와 편극 밀도 와 다음과 같은 관계를 가진다.
:.
여기서 은 진공 유전율이다.
가우스 법칙에 따라, 변위장의 발산은 그 자유 전하 밀도 와 같다.
:.
스토크스 정리에 따라, 폐곡면에 대한 변위장의 선속은 폐곡면 속에 든 총 자유 전하량 와 같다.
:.
전기 변위장 '''D'''는 다음과 같이 정의된다.
:
여기서 는 진공 유전율(자유 공간의 유전율이라고도 함)이고, '''P'''는 물질 내의 영구적 및 유도된 전기 쌍극자 모멘트의 (거시적) 밀도이며, 이를 분극 밀도라고 한다.
변위장은 유전체 내에서 가우스 법칙을 만족한다.
:
이 식에서 는 단위 부피당 자유 전하의 수이다. 이러한 전하는 부피를 중성 상태가 아닌 상태로 만들고, 때로는 공간 전하라고도 한다. 이 방정식은 실제로 '''D'''의 선속선이 자유 전하에서 시작하고 끝나야 함을 말한다. 반대로 는 중성인 각 쌍극자의 일부인 모든 전하의 밀도이다. 금속 콘덴서 판 사이의 절연 유전체의 예에서, 유일한 자유 전하는 금속 판에 있으며, 유전체는 쌍극자만 포함한다. 유전체가 도핑된 반도체 또는 이온화된 가스 등으로 대체되면, 전자는 이온에 대해 이동하고, 시스템이 유한하면 두 전하 모두 가장자리에서 에 기여한다.
'''D'''는 자유 전하에 의해서만 결정되지 않는다. '''E'''는 정전기적 상황에서 컬이 0이므로, 다음이 따른다.
:
이 방정식의 효과는 막대 자석의 전기적 유사물인 막대 일렉트릿과 같이 "고정된" 분극을 가진 물체의 경우에 볼 수 있다. 이러한 물질에는 자유 전하가 없지만, 고유한 분극은 전기장을 발생시켜 '''D'''장이 완전히 자유 전하에 의해 결정되지 않음을 보여준다. 전기장은 위의 관계와 분극 밀도에 대한 다른 경계 조건을 사용하여 결합 전하를 생성하고, 이는 다시 전기장을 생성한다.
전속 밀도 '''D'''와 전장의 세기 '''E'''의 관계는
:
로 주어진다. 비례 계수 는 전기 상수라고 불리는 물리 상수이다. 두 양은 유전체의 물성을 반영한 유전 분극 '''P'''에 의해 관계 지어진다.
자유 공간에서는 유전 분극이 생기지 않으며, 전속 밀도 '''D'''와 전장의 세기 '''E'''는
:
에 의해 관계 지어진다.
미분을 통해 나타낸 가우스 법칙에 진공에서의 전속 밀도와 전장의 세기의 관계를 대입하면
:
이 된다. 전하 밀도의 아래첨자 0은 진공에 분포하는 전하 밀도임을 의미한다.
한편, 유전체가 존재하는 경우 유전 분극의 정의식을 대입하면
:
:
가 되어, 진공에서의 관계식과 비교하면
:
이다. 여기서 도입한 유전 분극 에 의한 전하 밀도
:
는 분극 전하 밀도라고 불린다. 분극 전하 밀도와 대비하여 는 진전하 밀도라고 불린다.
유전체도 원자핵이나 전자 등의 하전 입자로 구성되어 있으며, 을 사용하는 것은 유전체를 진공에 분포하는 하전 입자의 집합이라고 생각하는 것에 상당한다. 현실적으로 모든 원자핵이나 전자의 운동 모습을 아는 것은 불가능하다. 가령 모든 운동을 안다고 해도, 거기에서 유전체로서의 성질을 아는 것은 역시나 어렵다.
진전하 밀도 는 유전체를 유전체로서 취급할 수 있는 정도의 스케일에서의 평균값, 즉
:
이다. 체적 는 충분히 작지만, 유전체가 유전체로서 행동할 정도로 원자핵이나 전자를 포함한다. 전도를 담당하는 자유 전자가 없고, 전자가 원자핵에 속박되어 있는 유전체의 내부에서는, 통상적으로는 양과 음의 전하가 상쇄되어 진전하 밀도는 존재하지 않는다. 분극 전하 밀도는 보다 작은 스케일에서의 전하 밀도이며, 유전 분극에 의해 생기는 미세한 전하의 분포 편향을 나타낸다.
경계에서, 이며, 여기서 는 자유 전하 밀도이고 단위 법선 는 매질 2에서 매질 1의 방향을 가리킨다.[1]
4. 1. 선형 매질
매질이 선형이면, 편극 밀도는 외부 전기장에 비례한다.
:.
여기서 는 감수율(susceptibility영어)이라는 비례 상수이다. 따라서 매질의 유전율 을
:
으로 정의하면 변위장은 다음과 같다.
:.
선형, 균질, 등방성 유전체에서, '''P'''는 전기장에 선형적으로 의존한다.[1]
:
여기서 비례 상수 는 물질의 전기 감수율이다. 따라서
:
여기서 은 물질의 상대 유전율이고 는 유전율이다.
선형적이고 균질하며 등방성인 매질에서, ''ε''는 상수이다. 그러나 선형 이방성 매질에서는 텐서이고, 비균질 매질에서는 매질 내부의 위치에 대한 함수이다. 또한 전기장에 따라 달라질 수 있으며(비선형 물질) 시간 의존적인 응답을 가질 수 있다.
4. 2. 비선형 매질
선형, 균질, 등방성 유전체가 아닌 비선형 매질의 경우, 분극 밀도 '''P'''는 전기장에 선형적으로 의존하지 않는다. 따라서 비선형 매질에서 유전율 ''ε''는 상수가 아니라 텐서이거나, 매질 내부의 위치에 대한 함수이거나, 전기장에 따라 달라질 수 있다. 또한, 시간 의존적인 응답을 가질 수 있다.
일반적으로 유전체가 선형성을 가정할 수 없는 경우에는 적분에 의해
로 나타낼 수 있다. 여기서 D는 변위장이다. 더 일반적으로는 자기장과의 교차항이나 히스테리시스를 고려해야 한다.
5. 유전체
매질이 유전체라면 전기장에 의하여 매질 고유의 전기 쌍극자 모멘트가 생기게 된다. 그 밀도를 '''전기 편극 밀도'''(electric polarization density|일렉트릭 폴러리제이션 덴시티영어) 라고 한다.
변위장 는 전기장 와 편극 밀도 와 다음과 같은 관계를 가진다.
:.
여기서 은 진공 유전율이다.
선형 매질에서는 편극 밀도는 외부 전기장에 다음과 같이 비례한다.
:.
여기서 는 '''감수율'''(susceptibility|서셉티빌리티영어)이라고 불리는 비례 상수이다. 따라서 매질의 유전율 을
:
으로 정의하면 변위장은 다음과 같다.
:.
가우스 법칙에 따라, 변위장의 발산은 그 자유 전하 밀도 와 같다.
:.
스토크스 정리에 따라, 폐곡면에 대한 변위장의 선속은 폐곡면 속에 든 총 자유 전하량 와 같다.
:.
전기 변위장 '''D'''는 다음과 같이 정의된다.
:
여기서 는 진공 유전율 (자유 공간의 유전율이라고도 함)이고, '''P'''는 물질 내의 영구적 및 유도된 전기 쌍극자 모멘트의 (거시적) 밀도이며, 이를 분극 밀도라고 한다.
변위장은 유전체 내에서 가우스 법칙을 만족한다.
:
이 식에서 는 단위 부피당 자유 전하의 수이다. 반대로 는 중성인 각 쌍극자의 일부인 모든 전하의 밀도이다.
'''D'''는 자유 전하에 의해서만 결정되지 않는다. '''E'''는 정전기적 상황에서 컬이 0이므로, 다음이 따른다.
:
전기장에 대한 즉각적인 응답을 보이는 선형, 균질, 등방성 유전체에서, '''P'''는 전기장에 선형적으로 의존한다.
:
여기서 비례 상수 는 물질의 전기 감수율이라고 한다. 따라서
:
여기서 은 물질의 상대 유전율이고, 는 유전율이다.
선형적이고 균질하며 등방성인 매질에서, ''ε''는 상수이다. 그러나 선형 이방성 매질에서는 텐서이고, 비균질 매질에서는 매질 내부의 위치에 대한 함수이다. 또한 전기장에 따라 달라질 수 있으며 (비선형 물질) 시간 의존적인 응답을 가질 수 있다.
경계에서, 이다. 여기서 ''σ''f는 자유 전하 밀도이고 단위 법선 는 매질 2에서 매질 1의 방향을 가리킨다.[1]
유전체가 존재하는 경우 유전 분극의 정의식을 대입하면 다음과 같다.
:
:
여기서 도입한 유전 분극 에 의한 전하 밀도
:
는 분극 전하 밀도라고 불린다. 분극 전하 밀도와 대비하여 는 진전하 밀도라고 불린다.
전도를 담당하는 자유 전자가 없고, 전자가 원자핵에 속박되어 있는 유전체의 내부에서는, 통상적으로는 양과 음의 전하가 상쇄되어 진전하 밀도는 존재하지 않는다. 분극 전하 밀도는 보다 작은 스케일에서의 전하 밀도이며, 유전 분극에 의해 생기는 미세한 전하의 분포의 편향을 나타낸다.
6. 역사
1864년 제임스 클러크 맥스웰의 논문 ''전자기장의 동역학 이론''에서 이 용어가 처음 사용된 것으로 알려져 있다. 맥스웰은 현대적이고 익숙한 표기법과는 다른 형태로 유전율을 나타내는 '''D'''라는 용어를 도입했다.[2]
올리버 헤비사이드는 복잡한 맥스웰 방정식을 현대적인 형태로 재구성했다. 1884년 헤비사이드가 윌러드 기브스, 하인리히 헤르츠와 함께 방정식을 별개의 집합으로 묶었다. 이 네 개의 방정식 집합은 헤르츠-헤비사이드 방정식과 맥스웰-헤르츠 방정식으로 다양하게 알려졌으며, 때로는 맥스웰-헤비사이드 방정식으로도 알려져 있다. 따라서 현재의 의미를 갖게 된 '''D'''의 중요성을 헤비사이드가 부여했을 가능성이 크다.
7. 예시: 축전기 내의 변위장
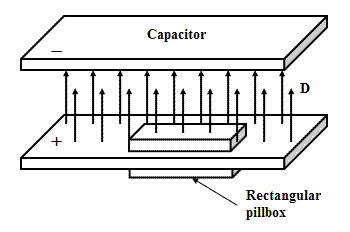
무한 평행판 축전기를 가정하면, 판 사이는 비어 있거나 중성 절연 매질로 채워져 있다. 두 경우 모두 자유 전하는 금속 축전기 판에만 존재한다. SI 단위에서 판의 전하 밀도는 판 사이의 변위장 '''D'''의 값과 같다. 이는 가우스 법칙을 통해 유도된다. 축전기 판 하나를 가로지르는 작은 직사각형 상자에 대해 가우스 법칙을 적분하면 다음과 같다.
상자 측면에서 d'''A'''는 장에 수직이므로 이 부분의 적분은 0이고, '''D'''가 0인 축전기 바깥쪽 면의 적분도 0이다. 따라서 적분에 기여하는 유일한 표면은 축전기 내부 상자의 윗면이며, 다음 식이 성립한다.
여기서 ''A''는 상자 윗면의 면적이고, 는 양전하 판의 자유 표면 전하 밀도이다. 축전기 판 사이가 유전율 인 선형 균질 등방성 유전체로 채워져 있다면, 매질에 분극이 유도되어 가 되고, 판 사이의 전압 차이는 다음과 같다.
여기서 ''d''는 두 판 사이의 간격이다.
유전체를 넣으면 ''ε''가 배 증가하고, 전압 차이는 같은 비율로 작아지거나, 전하가 더 커져야 한다. 유전체 내에서 장이 부분적으로 상쇄되면, 판이 진공 상태일 때보다 단위 전위 강하 당 축전기 두 판에 더 많은 자유 전하가 존재할 수 있다.
유한 평행판 축전기에서 판 사이 거리 ''d''가 측면 치수보다 훨씬 작으면, 무한 평행판 축전기의 경우로 근사하여 정전 용량을 다음과 같이 구할 수 있다.
참조
[1]
서적
Introduction to Electrodynamics
[2]
문서
A Dynamical Theory of the Electromagnetic Field PART V. — THEORY OF CONDENSERS
[3]
웹사이트
한국물리학회 물리학용어집
https://www.kps.or.k[...]
[4]
웹사이트
한국물리학회 물리학용어집
https://www.kps.or.k[...]
[5]
웹사이트
한국물리학회 물리학용어집
https://www.kps.or.k[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com