텐서

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

텐서는 다차원 배열, 다중선형 사상, 텐서곱을 이용하여 정의되는 수학적 객체로, 기하학적 개념을 설명하며, 물리학, 공학, 컴퓨터 과학 등 다양한 분야에서 활용된다. 다차원 배열로서의 텐서는 기저의 선택에 따라 성분 값이 변하지만, 다중선형 사상이나 텐서곱을 이용한 정의는 기저 독립적인 특성을 갖는다. 텐서는 스칼라, 벡터, 행렬 등을 포함하며, 응력 텐서, 리만 곡률 텐서 등 다양한 예시가 존재한다. 텐서의 변환 법칙은 좌표계 변환에 따른 성분의 변화를 나타내며, 공변성과 반변성으로 구분된다. 텐서 연산에는 텐서곱, 텐서 축약, 지수 올리기와 내리기가 있으며, 텐서 분해는 머신 러닝 분야에서 고차원 데이터 처리에 사용된다. 텐서의 개념은 가우스의 미분기하학 연구에서 시작되어, 20세기 초 아인슈타인의 일반 상대성 이론을 통해 널리 알려졌으며, 현재는 무한 차원, 텐서 밀도 등으로 일반화되어 사용된다.

더 읽어볼만한 페이지

텐서 - 맥스웰 변형력 텐서
맥스웰 변형력 텐서는 전자기장의 변형력을 나타내는 텐서로, 전기장과 자기장의 함수로 정의되며 힘, 압력, 전자기장의 운동량과 관련된다.
텐서 - 변형력
변형력은 물체가 외부 힘에 저항하여 형태를 유지하려는 힘으로, 단위 면적당 작용하는 힘(응력)으로 정의되며, 수직 응력과 전단 응력으로 나뉘고, 재료의 강도 한계를 초과하면 변형이나 파괴를 일으킬 수 있으며, 구조물 안전성 평가에 사용된다.
물리학 개념 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다.
물리학 개념 - 전기 전도체
전기 전도체는 전기를 잘 통하는 물질로, 금속, 전해질, 초전도체, 반도체 등이 있으며, 구리, 은, 알루미늄 등 다양한 재료가 전선 등에 사용된다.

텐서
기본 정보
영어	tensor
독일어	Tensor
개요
종류	벡터 공간 선형대수학 다중선형대수학 미분기하학
특징	대수학적 객체로서 기하학적 응용 가능
수학적 개념	다중선형 사상의 일반화
수학적 정의
정의	벡터 공간의 텐서곱 다중선형 사상 (multilinear map)
유형	(p, q)형 텐서 (p번의 쌍대 공간과 q번의 벡터 공간의 텐서곱) 쌍대 공간의 원소 (1, 0)형 텐서 = 코벡터 벡터 공간의 원소 (0, 1)형 텐서 = 벡터 (0, 2)형 텐서 = 쌍선형 형식
변환 규칙
텐서의 성분	좌표 변환에 따른 특정 변환 규칙을 따름
변환 규칙 예시	회전 변환 로렌츠 변환
불변량	스칼라 텐서 축약 (tensor contraction)
사용 분야
주요 분야	물리학 기하학
세부 분야	상대성 이론 응력과 변형률 해석 미분기하학 다양체 텐서 해석학 리만 기하학 수학 머신 러닝
역사
기원	미분기하학 선형대수학
발전	19세기 말: 그라스만의 연구 20세기 초: 리치와 레비치비타의 연구
추가 정보
참고 문헌	\|date=1990\|publisher=Oxford University Press \|isbn= 978-0-19-506137-6}}

2. 정의

텐서는 벡터 공간 $V$와 그 쌍대 공간 $V^*$를 이용하여 정의할 수 있다. 음이 아닌 정수 ''m'', ''n''에 대해, ''(m, n)''형 텐서는 다음과 같은 벡터 공간의 원소로 정의된다.^[45]

: $T^m_n(V) = \underbrace{V\otimes \dots \otimes V}_{m} \otimes \underbrace{ V^*\otimes \dots \otimes V^*}_{n}$

여기서 $\otimes$은 텐서곱을 나타내며, 외적의 일반화된 형태로 볼 수 있다. 예를 들어, 2차원 행렬 두 개의 텐서곱은 다음과 같이 4차원 행렬로 표현된다.

: $\begin{bmatrix}a_{1,1} & a_{1,2} \\a_{2,1} & a_{2,2} \\\end{bmatrix}\otimes\begin{bmatrix}b_{1,1} & b_{1,2} \\b_{2,1} & b_{2,2} \\\end{bmatrix}=\begin{bmatrix}a_{1,1} b_{1,1} & a_{1,1} b_{1,2} & a_{1,2} b_{1,1} & a_{1,2} b_{1,2} \\a_{1,1} b_{2,1} & a_{1,1} b_{2,2} & a_{1,2} b_{2,1} & a_{1,2} b_{2,2} \\a_{2,1} b_{1,1} & a_{2,1} b_{1,2} & a_{2,2} b_{1,1} & a_{2,2} b_{1,2} \\a_{2,1} b_{2,1} & a_{2,1} b_{2,2} & a_{2,2} b_{2,1} & a_{2,2} b_{2,2} \\\end{bmatrix}$

일반적으로, $ A_{ij} \otimes B_{kl} = T_{ijkl} $ 와 같이 표현할 수 있다.

벡터 공간이 주어지면 그 쌍대 공간과 텐서곱은 유일하게 정의된다. 스칼라는 (0, 0)형 텐서이며, 텐서곱을 반복하여 다양한 텐서 공간을 만들 수 있다. 따라서 모든 텐서는 어떤 벡터 공간의 스칼라 또는 벡터라고 할 수 있다.

텐서는 다중선형 사상으로도 정의할 수 있다.^[45] (p, q)형 텐서 T는 다음과 같은 함수로 정의된다.

: $T\colon \underbrace{ V^* \times\dots\times V^*}_{p \text{ copies}} \times \underbrace{ V \times\dots\times V}_{q \text{ copies}} \to \mathbb{R}$

이 함수는 각 인수에 대해 선형이다. V의 기저 $\mathbf{e}_{j}$와 그 쌍대 기저 $\boldsymbol{\varepsilon}^{i}$를 이용하면, T의 성분은 다음과 같이 (p + q)차원 배열로 표현된다.

: $T^{i_1\dots i_p}_{j_1\dots j_q} \equiv T(\boldsymbol{\varepsilon}^{i_1},\ldots,\boldsymbol{\varepsilon}^{i_p},\mathbf{e}_{j_1},\ldots,\mathbf{e}_{j_q})$

기저가 바뀌면 성분도 바뀌지만, T의 선형성 때문에 이 성분들은 다차원 배열로서 텐서의 변환 법칙을 만족한다. 따라서 다중선형 사상 T의 성분으로 이루어진 다차원 배열은 텐서를 이룬다고 할 수 있다.

텐서를 다중선형 사상으로 볼 때는, 벡터 공간 V를 그 이중 쌍대 공간 $V^{}$와 동일시하는 것이 일반적이다. 유한 차원 벡터 공간의 경우, V에서 $V^{}$로의 자연스러운 선형 동형 사상이 존재한다.

벡터 공간의 텐서곱의 보편성을 이용하여 텐서를 정의할 수도 있다.^[46] (p, q)형 텐서는 다음과 같은 벡터 공간 텐서곱의 원소로 정의된다.

: $T\in \underbrace{V \otimes\dots\otimes V}_{p\text{ copies}} \otimes \underbrace{V^* \otimes\dots\otimes V^*}_{q \text{ copies}}$

$V$의 기저 ${v_i}$와 $W$의 기저 ${w_j}$가 주어지면, 텐서곱 공간 $V \otimes W$는 자연스러운 기저 ${v_i \otimes w_j}$를 갖는다. 텐서 $T$의 성분은 $V$의 기저 ${e_i}$와 그 쌍대 기저 $\{\varepsilon^j\}$에 대한 계수로 표현된다.

: $T = T^{i_1\dots i_p}_{j_1\dots j_q}\; e_{i_1}\otimes\cdots\otimes e_{i_p}\otimes \varepsilon^{j_1}\otimes\cdots\otimes \varepsilon^{j_q}$

텐서곱의 성질과 보편성에 의해, 이 정의는 다중선형 사상으로 정의된 텐서와 일대일 대응된다.

텐서는 이처럼 다양한 방식으로 정의될 수 있지만, 결국 같은 기하학적 개념을 표현하는 서로 다른 방법이다.

2. 1. 다차원 배열로서의 텐서

텐서는 기저에 대한 임의의 다차원 배열로 표현될 수 있다. 예를 들어, 선형 작용소는 기저에서 2차원 정방 배열로 표현된다. 다차원 배열의 숫자는 텐서의 ''성분''으로 알려져 있으며, 배열에서의 위치를 나타내는 첨자와 지수로 텐서의 기호 이름 다음에 표시된다.^[2]^[3]^[4] 예를 들어, 차수 2 텐서

T

의 성분은

T_{ij}

(

i

와

j

는 1부터

n

까지) 또는

T^i_j

로 표시될 수 있다.

각 성분을 고유하게 식별하는 데 필요한 색인의 총 수(

m

)는 배열의 ''차원'' 또는 ''방법''의 수와 같으며, 텐서가 때때로

m

-차원 배열 또는

m

-방법 배열이라고 불리는 이유이다. 색인의 총 수는 텐서의 ''차수'', ''차원'' 또는 ''계수''라고도 하지만, "계수"라는 용어는 일반적으로 행렬 및 텐서의 맥락에서 다른 의미를 갖는다.

벡터의 성분이 벡터 공간의 기저를 변경할 때 변경되는 것과 마찬가지로, 텐서의 성분도 그러한 변환 하에서 변경된다. 각 유형의 텐서는 텐서의 성분이 기저 변환에 어떻게 반응하는지 설명하는 ''변환 법칙''을 갖추고 있다. 벡터의 성분은 벡터의 공변성과 반공변성에 따라 두 가지 방식으로 변환될 수 있다.

반공변 변환 법칙: 새로운 기저 벡터 $\mathbf{\hat{e}}_i$ 가 이전 기저 벡터 $\mathbf{e}_j$ 로 표현될 때 ( $\mathbf{\hat{e}}_i = \mathbf{e}_j R^j_i$ , $R$ 은 기저 변환 행렬), 열 벡터 $\mathbf{v}$ 의 성분 $v^i$ 는 행렬 $R$ 의 역행렬로 변환된다 ( $\hat{v}^i = \left(R^{-1}\right)^i_j v^j$ ).^[5]
공변 변환 법칙: 코벡터(또는 행 벡터) $\mathbf{w}$ 의 성분 $w_i$ 는 행렬 $R$ 자체로 변환된다 ( $\hat{w}_i = w_j R^j_i$ ).

일반적인 텐서의 성분은 각 색인에 대해 하나의 변환 법칙을 사용하여 공변 및 반공변 변환의 조합으로 변환된다. 색인의 변환 행렬이 기저 변환의 역행렬인 경우 해당 색인을 ''반공변''이라고 하며 위첨자(지수)로 표시되고, 기저 변환 자체인 경우 ''공변''이라고 하며 아래첨자(첨자)로 표시된다.

예를 들어, 선형 작용소의 행렬은

R = \left(R^j_i\right)

의 기저 변환 행렬에 따라

\hat{T} = R^{-1}TR

로 변환되는 직사각형 배열

T

이다. 개별 행렬 항목에 대한 변환 법칙은

\hat{T}^{i'}_{j'} = \left(R^{-1}\right)^{i'}_i T^i_j R^j_{j'}

의 형태를 가지므로, 선형 작용소의 행렬에 해당하는 텐서는 하나의 공변 색인과 하나의 반공변 색인을 갖는 (1,1) 유형이다.

같은 색인을 가진 공변 및 반공변 성분의 조합을 통해 기하학적 불변량을 표현할 수 있다. 예를 들어, 벡터가 다른 좌표계에서 동일한 객체라는 사실은 다음 방정식으로 표현될 수 있다.

:

\mathbf{v} = \hat{v}^i \,\mathbf{\hat{e}}_i = \left( \left(R^{-1}\right)^i_j {v}^j \right) \left( \mathbf{e}_k R^k_i \right) = \left( \left(R^{-1}\right)^i_j R^k_i \right) {v}^j \mathbf{e}_k = \delta_j^k {v}^j \mathbf{e}_k = {v}^k \,\mathbf{e}_k = {v}^i \,\mathbf{e}_i

여기서

\delta^k_j

는 크로네커 델타이며, 단위 행렬과 유사하게 작동한다.

p

개의 반공변 색인과

q

개의 공변 색인을 가진 차수

p + q

텐서의 변환 법칙은 다음과 같다.

:

\hat{T}^{i'_1, \ldots, i'_p}_{j'_1, \ldots, j'_q} = \left(R^{-1}\right)^{i'_1}_{i_1} \cdots \left(R^{-1}\right)^{i'_p}_{i_p}T^{i_1, \ldots, i_p}_{j_1, \ldots, j_q}R^{j_1}_{j'_1}\cdots R^{j_q}_{j'_q}.

이러한 텐서는 차수 또는 ''유형''

(p, q)

라고 하며, 간단히

(p, q)

-텐서라고도 한다.^[6]^[7]

텐서는 변환 법칙을 만족하는 다차원 배열로 정의될 수 있다. 이 정의는 Ricci의 연구로 거슬러 올라간다.^[1] 텐서는 일반 선형 군의 표현을 사용하여 정의될 수도 있다.^[8]^[6]

2. 2. 다중선형 사상으로서의 텐서

텐서는 다중선형 사상으로 정의할 수 있다. 벡터 공간의 쌍대 공간은 그 벡터 공간 위의 선형 범함수 전체의 집합이다. 유한 차원 벡터 공간 V의 경우, V를 그 이중 쌍대 공간 V^**와 동일시하는 것이 일반적이다.

(p, q)형 텐서 T는 다음과 같은 함수로 정의된다.^[45]

:T:\underbrace{V^* \times\dots\times V^*}_{p \text{ copies}} \times \underbrace{V \times\dots\times V}_{q \text{ copies}} \to \mathbb{R}

이는 각 인수에 대해 선형이다.

(p, q)형 다중선형 사상 T를 V의 기저 {e_j}와 V^*에서의 표준적인 쌍대 기저 {εⁱ}에 대해 적용하면, 다음과 같이 (p + q)차원 배열을 얻을 수 있다.

:T^{i_1\dots i_p}_{j_1\dots j_q} \equiv T(\boldsymbol{\varepsilon}^{i_1},\ldots,\boldsymbol{\varepsilon}^{i_p},\mathbf{e}_{j_1},\ldots,\mathbf{e}_{j_q})

기저를 변경하면 다른 성분을 얻지만, T는 각 인수에 대해 선형이므로, 성분들은 다차원 배열로서의 텐서의 변환 법칙을 만족한다. 따라서 T의 성분으로 구성된 다차원 배열은 텐서를 이룬다. 또한, 이러한 성질을 갖는 다차원 배열은 다중선형 사상 T의 성분으로 표현될 수 있다. 이러한 이유로 다중선형 사상은 텐서의 본질적인 대상으로 간주된다.

2. 3. 텐서곱을 이용한 정의

벡터 공간 $V$와 그 쌍대 공간 $V^*$에 대하여, 음이 아닌 정수 ''m'', ''n''마다 ''(m, n)''형의 텐서는 다음 벡터 공간의 원소로 정의된다.

:

T^m_n(V) = \underbrace{V\otimes \dots \otimes V}_{m} \otimes \underbrace{ V^*\otimes \dots \otimes V^*}_{n}

여기서 텐서곱 $\otimes$은 외적의 일반화로, 다음과 같은 연산으로 생각할 수 있다.

:

\begin{bmatrix}a_{1,1} & a_{1,2} \\a_{2,1} & a_{2,2} \\\end{bmatrix}\otimes\begin{bmatrix}b_{1,1} & b_{1,2} \\b_{2,1} & b_{2,2} \\\end{bmatrix}=\begin{bmatrix}a_{1,1}  \begin{bmatrix}b_{1,1} & b_{1,2} \\b_{2,1} & b_{2,2} \\\end{bmatrix} & a_{1,2}  \begin{bmatrix}b_{1,1} & b_{1,2} \\b_{2,1} & b_{2,2} \\\end{bmatrix} \\& \\a_{2,1}  \begin{bmatrix}b_{1,1} & b_{1,2} \\b_{2,1} & b_{2,2} \\\end{bmatrix} & a_{2,2}  \begin{bmatrix}b_{1,1} & b_{1,2} \\b_{2,1} & b_{2,2} \\\end{bmatrix} \\\end{bmatrix}=\begin{bmatrix}a_{1,1} b_{1,1} & a_{1,1} b_{1,2} & a_{1,2} b_{1,1} & a_{1,2} b_{1,2} \\a_{1,1} b_{2,1} & a_{1,1} b_{2,2} & a_{1,2} b_{2,1} & a_{1,2} b_{2,2} \\a_{2,1} b_{1,1} & a_{2,1} b_{1,2} & a_{2,2} b_{1,1} & a_{2,2} b_{1,2} \\a_{2,1} b_{2,1} & a_{2,1} b_{2,2} & a_{2,2} b_{2,1} & a_{2,2} b_{2,2} \\\end{bmatrix}

:

A_{ij} \otimes B_{kl} = T_{ijkl}

하나의 벡터 공간이 주어지면 그 쌍대 벡터 공간과 텐서곱 연산은 유일하게 정의된다. (0, 0)형의 텐서인 스칼라를 포함하여, 텐서곱을 반복하여 얻을 수 있는 벡터 공간들의 벡터를 단순히 텐서라고 한다. 따라서 모든 텐서는 어떤 벡터 공간의 스칼라 혹은 벡터이다.

체 $F$ 위의 벡터 공간 $V,\ W,\ V \otimes W$에 대하여 쌍선형 변환 $\varphi:V \times W \to V \otimes W$는 아래의 보편 성질을 갖는다.

:임의의 벡터 공간 $Z$에 대하여 임의의 쌍선형 변환 $h: V \times W \to Z$은 선형 변환 $\bar{h}: V \otimes W \to Z$이 유일하게 존재하여 $h = \bar{h} \circ \varphi$이다.

이 조건으로 텐서곱 $\otimes$이 유일하게 정의되며, 따라서 유한 차원 벡터 공간 $V$에 대하여 텐서의 벡터 공간은 다중선형 공간과 자연 동형이다.

:

T^m_n(V) \cong L^{m+n}\left(\underbrace{V^*\times \dots \times V^*}_{m} \times \underbrace{ V\times \dots \times V}_{n} \to F \right)

여기에서 $V \cong V^{**}$이다.

텐서는 (다차원일 수 있는) 배열로 표현될 수 있다. n-차원 공간의 벡터가 주어진 기저에 대해 n개의 성분을 갖는 일차원 배열로 표현되는 것과 마찬가지로, 기저에 대한 임의의 텐서는 다차원 배열로 표현된다. 예를 들어, 선형 작용소는 기저에서 2차원 정방 n × n 배열로 표현된다. 다차원 배열의 숫자는 텐서의 성분으로 알려져 있다. 이들은 배열에서의 위치를 나타내는 색인, 즉 첨자와 지수로 텐서의 기호 이름 다음에 표시된다. 예를 들어, 차수 2 텐서 T의 성분은 $T_{ij}$ 로 표시될 수 있으며, 여기서 i와 j는 1부터 n까지 실행되는 색인이거나, $T^i_j$로도 표시될 수 있다. 색인이 지수로 표시될지 첨자로 표시될지는 아래에 설명된 텐서의 변환 특성에 따라 달라진다. 따라서 $T_{ij}$ 와 $T^i_j$는 모두 n × n 행렬로 표현될 수 있으며, 색인 조작을 통해 수치적으로 관련되어 있지만, 변환 법칙의 차이는 이들을 더하는 것이 부적절함을 나타낸다.

각 성분을 고유하게 식별하는 데 필요한 색인의 총 수(m)는 배열의 차원 또는 방법의 수와 같으며, 이것이 텐서가 때때로 m-차원 배열 또는 m-방법 배열이라고 불리는 이유이다. 색인의 총 수는 텐서의 차수, 차원 또는 계수라고도 하지만,^[2]^[3]^[4] "계수"라는 용어는 일반적으로 행렬 및 텐서의 맥락에서 다른 의미를 갖는다.

벡터의 성분이 벡터 공간의 기저를 변경할 때 변경되는 것과 마찬가지로, 텐서의 성분도 그러한 변환 하에서 변경된다. 각 유형의 텐서는 텐서의 성분이 기저 변환에 어떻게 반응하는지 자세히 설명하는 변환 법칙을 갖추고 있다. 벡터의 성분은 기저 변환에 두 가지 고유한 방식으로 반응할 수 있다(''벡터의 공변성과 반공변성'' 참조). 여기서 새로운 기저 벡터 $\mathbf{\hat{e}}_i$는 이전 기저 벡터 $\mathbf{e}_j$로 다음과 같이 표현된다.

:

\mathbf{\hat{e}}_i = \sum_{j=1}^n \mathbf{e}_j R^j_i = \mathbf{e}_j R^j_i .

여기서 $R^{ j}_{ i}$는 기저 변환 행렬의 항목이며, 가장 오른쪽 표현식에서는 합산 기호가 생략되었다. 이것은 이 글 전체에서 사용될 아인슈타인 합산 규칙이다.^[5] 열 벡터 '''v'''의 성분 $v^{i}$는 행렬 $R$의 역행렬로 변환된다.

:

\hat{v}^i = \left(R^{-1}\right)^i_j v^j,

여기서 모자는 새로운 기저에서의 성분을 나타낸다. 이것은 벡터 성분이 기저 변환의 역행렬로 변환되기 때문에 반공변 변환 법칙이라고 한다. 반대로, 코벡터(또는 행 벡터) '''w'''의 성분 $w_{i}$는 행렬 $R$ 자체로 변환된다.

:

\hat{w}_i = w_j R^j_i .

이것은 코벡터 성분이 기저 변환 행렬과 같은 행렬로 변환되기 때문에 공변 변환 법칙이라고 한다. 보다 일반적인 텐서의 성분은 각 색인에 대해 하나의 변환 법칙을 사용하여 공변 및 반공변 변환의 조합으로 변환된다. 색인의 변환 행렬이 기저 변환의 역행렬인 경우 해당 색인을 반공변이라고 하며 일반적으로 위첨자(지수)로 표시된다. 색인의 변환 행렬이 기저 변환 자체인 경우 해당 색인을 공변이라고 하며 아래첨자(첨자)로 표시된다.

간단한 예로, 기저에 대한 선형 작용소의 행렬은 $R = \left(R^j_i\right)$의 기저 변환 행렬에 따라 $\hat{T} = R^{-1}TR$로 변환되는 직사각형 배열 $T$이다. 개별 행렬 항목에 대해 이 변환 법칙은 $\hat{T}^{i'}_{j'} = \left(R^{-1}\right)^{i'}_i T^i_j R^j_{j'}$의 형태를 가지므로 선형 작용소의 행렬에 해당하는 텐서는 하나의 공변 색인과 하나의 반공변 색인을 갖는다. 이는 (1,1) 유형이다.

같은 색인을 가진 공변 및 반공변 성분의 조합을 통해 기하학적 불변량을 표현할 수 있다. 예를 들어, 벡터가 다른 좌표계에서 동일한 객체라는 사실은 위에서 정의된 공식을 사용하여 다음 방정식으로 나타낼 수 있다.

:

\mathbf{v} = \hat{v}^i \,\mathbf{\hat{e}}_i =\left( \left(R^{-1}\right)^i_j v^j \right) \left( \mathbf{e}_k R^k_i \right) =\left( \left(R^{-1}\right)^i_j R^k_i \right) v^j \mathbf{e}_k =\delta_j^k v^j  \mathbf{e}_k = v^k \,\mathbf{e}_k = v^i \,\mathbf{e}_i

,

여기서 $\delta^k_j$는 크로네커 델타이며, 단위 행렬과 유사하게 작동하며, 이 예에서 색인 (j를 k로)을 바꾸는 효과를 갖는다. 이것은 성분 표기법의 여러 특징을 보여준다. 즉, 원하는 대로 항을 재배열하는 능력(교환 법칙), 동일한 표현식에서 여러 객체를 사용할 때 다른 색인을 사용해야 할 필요성, 색인을 바꾸는 능력, 그리고 반공변 및 공변 텐서가 결합하여 기저 변환 행렬과 그 역행렬의 모든 인스턴스가 상쇄되어 ${v}^i \,\mathbf{e}_i$와 같은 표현식이 모든 좌표계에서 기하학적으로 동일하다는 것을 즉시 알 수 있는 방식이다.

마찬가지로, 기하학적 객체로 간주되는 선형 작용소는 실제로 기저에 의존하지 않는다. 그것은 단지 인수로 벡터를 받아 다른 벡터를 생성하는 선형 사상일 뿐이다. 선형 작용소의 성분 행렬이 기저에 따라 어떻게 변하는지에 대한 변환 법칙은 반공변 벡터의 변환 법칙과 일치하므로 선형 작용소의 반공변 벡터에 대한 작용은 좌표에서 각각의 좌표 표현의 행렬 곱으로 표현된다. 즉, 성분 $(Tv)^i$는 $(Tv)^i = T^i_j v^j$로 주어진다. 이러한 성분은 다음과 같이 반공변으로 변환된다.

:

\left(\widehat{Tv}\right)^{i'} = \hat{T}^{i'}_{j'} \hat{v}^{j'} = \left[ \left(R^{-1}\right)^{i'}_i T^i_j R^j_{j'} \right] \left[ \left(R^{-1}\right)^{j'}_k v^k \right] = \left(R^{-1}\right)^{i'}_i (Tv)^i .

p개의 반공변 색인과 q개의 공변 색인을 가진 차수 (p + q) 텐서의 변환 법칙은 다음과 같이 주어진다.

:

\hat{T}^{i'_1, \ldots, i'_p}_{j'_1, \ldots, j'_q} = \left(R^{-1}\right)^{i'_1}_{i_1} \cdots \left(R^{-1}\right)^{i'_p}_{i_p}T^{i_1, \ldots, i_p}_{j_1, \ldots, j_q}R^{j_1}_{j'_1}\cdots R^{j_q}_{j'_q}.

여기서 소수점이 있는 색인은 새로운 좌표에서의 성분을 나타내고, 소수점이 없는 색인은 이전 좌표에서의 성분을 나타낸다. 이러한 텐서는 차수 또는 유형 (p, q)라고 한다. "차수", "유형", "계수", "원자가" 및 "차수"라는 용어는 모두 때때로 동일한 개념에 사용된다. 여기서는 "차수" 또는 "총 차수"라는 용어가 배열의 총 차원(또는 다른 정의에서의 일반화), 앞의 예에서 (p + q)에 사용되고, "유형"이라는 용어가 반공변 및 공변 색인의 수를 제공하는 쌍에 사용된다. (p, q) 유형의 텐서는 간단히 (p, q)-텐서라고도 한다.

이러한 논의는 다음과 같은 공식적인 정의를 유도한다.^[6]^[7]

: (p, q) 유형의 텐서는 다차원 배열 $T^{i_1\dots i_p}_{j_{1}\dots j_{q}}[\mathbf{f}]$를 n차원 벡터 공간의 각 기저 $\mathbf{f} = (\mathbf{e}_1, \dots, \mathbf{e}_n)$에 대해 할당하는 것이다. 기저 변환 $\mathbf{f}\mapsto \mathbf{f}\cdot R = \left( \mathbf{e}_i R^i_1, \dots, \mathbf{e}_i R^i_n \right)$을 적용하면 다차원 배열은 다음 변환 법칙을 따른다.

:

T^{i'_1\dots i'_p}_{j'_1\dots j'_q}[\mathbf{f} \cdot R] = \left(R^{-1}\right)^{i'_1}_{i_1} \cdots \left(R^{-1}\right)^{i'_p}_{i_p}T^{i_1, \ldots, i_p}_{j_1, \ldots, j_q}[\mathbf{f}]R^{j_1}_{j'_1}\cdots R^{j_q}_{j'_q} .

변환 법칙을 만족하는 다차원 배열로서의 텐서의 정의는 Ricci의 연구로 거슬러 올라간다.^[1]

텐서의 동등한 정의는 일반 선형 군의 표현을 사용한다. 일반 선형 군의 작용은 n차원 벡터 공간의 모든 순서 기저 집합에 있다. $\mathbf{f} = (\mathbf{f}_1, \dots, \mathbf{f}_n)$이 순서 기저이고 $R = \left(R^i_j\right)$가 가역적인 $n\times n$ 행렬이면 작용은 다음과 같이 주어진다.

:

\mathbf{f}R = \left(\mathbf{f}_i R^i_1, \dots, \mathbf{f}_i R^i_n\right).

$F$를 모든 순서 기저의 집합이라고 하자. 그러면 $F$는 GL(n)에 대한 주동차 공간이다. $W$를 벡터 공간이라고 하고 $\rho$를 GL(n)의 $W$에 대한 표현(즉, 군 준동형 사상 $\rho: \text{GL}(n) \to \text{GL}(W)$)이라고 하자. 그러면 $\rho$ 유형의 텐서는 동변 사상 $T: F \to W$이다. 여기서 동변성은 다음을 의미한다.

:

T(FR) = \rho\left(R^{-1}\right)T(F).

$\rho$가 일반 선형 군의 텐서 표현인 경우 이것은 다차원 배열로서의 텐서의 일반적인 정의를 제공한다. 이 정의는 종종 다양체의 텐서를 설명하는 데 사용되며,^[8] 다른 군으로 쉽게 일반화된다.^[6]

지금까지 텐서에 대한 논의는 관련 공간의 유한 차원을 가정했으며, 이러한 구성 각각으로 얻어진 텐서 공간은 자연스럽게 동형이다.^[13] 텐서곱과 다중선형 사상을 기반으로 한 텐서 공간의 구성은 본질적으로 수정 없이 벡터 번들 또는 결합층으로 일반화될 수 있다.^[14] 무한 차원 벡터 공간의 경우, 동등하지 않은 위상은 동등하지 않은 텐서 개념으로 이어지며, 이러한 다양한 동형 사상은 텐서의 정확한 의미에 따라 성립할 수도 있고 성립하지 않을 수도 있다(위상적 텐서곱 참조). 어떤 응용 분야에서는 힐베르트 공간의 텐서곱이 의도된 것으로, 그 특성은 유한 차원의 경우와 가장 유사하다. 보다 현대적인 관점에서는 특정 모델이 아니라 대칭 모노이드 범주로서의 텐서의 구조가 가장 중요한 특성을 나타낸다는 것이다.^[15]

텐서의 정의, 표현 및 다루는 방법에는 여러 가지 동등한 방법이 있다. 특히, 고전적인 접근 방식에서는 텐서를 다차원 배열로 간주하며, 0계 스칼라, 1계 벡터, 2계 행렬 등의 n계로 일반화한 것으로 본다. 텐서의 "성분"은 배열 요소의 값으로 주어진다. 이 개념은 텐서장으로 일반화되어 텐서의 성분으로 함수나 그 미분이 다루어진다.

텐서라고 불리려면 배열은 기준으로 삼는 좌표계가 바뀔 때 일정한 변환을 받아야 한다. 이 변환은 벡터 요소에 대한 관계를 일반화한 것이며, 벡터의 경우와 마찬가지로 나타내는 양이 본질적으로는 표시를 위한 좌표계의 선택에 의존하지 않음을 보여준다.

물리학에서 일반적인 텐서의 정의는 특정 규칙에 따라 성분이 변환되는 대상이라는 표현을 사용하며, 공변 변환과 반변 변환의 개념이 사용된다.

현대적인 (성분을 사용하지 않는) 접근 방식에서는 텐서가 먼저 추상적으로 다중선형성 개념에 기초한 수학적 대상으로 정의된다. 잘 알려진 여러 가지 성질이 선형 사상으로서 (혹은 더 일반적인 부분에 대한) 정의로부터 유도된다. 텐서의 연산 규칙은 선형대수학에서 다중선형대수학으로의 확장에서 자연스럽게 나타난다.

수학에서는 어떤 종류의 벡터 공간을 사용하여, 필요할 때까지 기저를 생각하지 않고 특히 좌표계를 지정하지 않는다. 예를 들어 공변 벡터는 일차 미분 형식으로 설명할 수 있고, 또는 반변 벡터 공간의 쌍대 공간의 원소로 설명할 수도 있다.

현대적인 성분에 의존하지 않는 벡터의 개념에 의해, 성분 표시에 기초한 전통적인 취급이 대체될 수 있듯이, 이 취급은 성분에 기초한 취급을 더 고차원적인 사고방식으로 대체하는 것을 목적으로 한다.

물리학자와 기술자들은 임의로 선택 가능한 좌표계에 좌우되지 않는 개념으로서의 벡터와 텐서의 중요성을 인식했다. 마찬가지로, 수학자들은 좌표 표시로 유도하는 것이 더 간편한 텐서 관계도 있음을 알게 되었다.

수학적 응용에 있어서는 보다 추상적인 방법이 효과적인 경우도 있다. 이는 보편성을 통해 정의할 수 있는 벡터 공간의 텐서곱의 원소로서 텐서를 정의함으로써 이루어진다. 이러한 맥락에서, (p, q)-형 텐서는 벡터 공간의 텐서곱의 원소

:

T\in \underbrace{V \otimes\dots\otimes V}_{p\text{ copies}} \otimes \underbrace{V^* \otimes\dots\otimes V^*}_{q \text{ copies}}

로 정의된다.^[46]

일반적으로, $v_i$가 $V$의 기저를 이루고, $w_j$가 $W$의 기저를 이룰 때, 텐서곱 공간 $V \otimes W$는 자연스러운 기저 ${v_i \otimes w_j}$를 갖는다. 텐서 $T$의 성분은 $V$의 기저 ${e_i}$와 그 쌍대 기저 $\{\varepsilon^j\}$로부터 얻어지는 기저에 대한 텐서의 계수

:

T = T^{i_1\dots i_p}_{j_1\dots j_q}\; e_{i_1}\otimes\cdots\otimes e_{i_p}\otimes \varepsilon^{j_1}\otimes\cdots\otimes \varepsilon^{j_q}

와 같다. 텐서곱의 성질을 이용하여, 이 성분이 (p, q)-형 텐서의 변환 규칙을 만족함을 보일 수 있다. 더 나아가, 텐서곱의 보편성에 의해, 지금 정의한 의미에서의 텐서와 다중선형 사상으로서 정의한 의미에서의 텐서가 일대일 대응함을 말할 수 있다.

텐서는 매우 일반적으로 (예를 들어 임의의 환 위의 가군까지 포함하여) 정의할 수 있다. 하나의 원리로서 ‘텐서란 단지 임의의 텐서곱 공간의 원소이다’라고 정의할 수 있지만, 수학 문헌에서는 “텐서”란 위와 같이 하나의 공간 $V$와 그 쌍대에서 얻어지는 텐서곱(텐서 공간)의 원소에 대해 사용하는 것이 일반적이다.

3. 변환 법칙

아인슈타인 표기법을 사용하면 ''(m, n)''형 텐서는 기저를 선택하여 ''m+n''차원 배열

: $T^{i_1\dots i_m}_{j_{1}\dots j_{n}}[\mathbf{f}]$

와 같이 나타낼 수 있다. 다른 기저 $\mathbf{f}\cdot R = \left( \mathbf{e}_i R^i_1, \dots, \mathbf{e}_i R^i_k \right)$ 를 선택하면 기저에 의존하지 않는 변환 법칙

: $T^{i'_1\dots i'_m}_{j'_1\dots j'_n}[\mathbf{f} \cdot R] = \left(R^{-1}\right)^{i'_1}_{i_1} \cdots \left(R^{-1}\right)^{i'_m}_{i_m}$ $T^{i_1, \ldots, i_m}_{j_1, \ldots, j_n}[\mathbf{f}]$ $R^{j_1}_{j'_1}\cdots R^{j_n}_{j'_n} .$

을 적용할 수 있다. 여기서 ''m''을 이 텐서의 반변 계수(contravariant rank), ''n''을 공변 계수(covariant rank)라 하며, ''m+n''을 총 계수(total rank)라 한다.

기저의 선택에 의존하는 행렬, 위치벡터, 유사텐서 등은 텐서의 표현 방식이며, 기저의 선택이 없으면 텐서가 아니다. 마찬가지로 위치벡터 또한 기저의 선택이 없으면 벡터가 아니기 때문에, 모든 벡터 공간의 스칼라 혹은 벡터가 어떤 텐서라는 사실은 변하지 않는다.

유사텐서인 3차원 레비치비타 기호를 다차원 배열로 나타낸 모습. 이는 ''(0, 3)''형의 치환 텐서로 대체할 수 있고, 이를 통해 벡터곱도 ''(1, 2)''형의 텐서처럼 다룰 수 있다.

3. 1. 공변성과 반변성

벡터의 공변성과 반변성은 기저 변환에 따른 벡터 성분의 변환 규칙을 설명하는 개념이다.

좌표 변환

\bar{x}^i\left(x^1, \ldots, x^n\right),

이 주어지면, 텐서의 변환 법칙은 다음과 같이 좌표 함수의 편도함수로 표현된다.^[1]

:

\hat{T}^{i'_1\dots i'_p}_{j'_1\dots j'_q}\left(\bar{x}^1, \ldots, \bar{x}^n\right) =\frac{\partial \bar{x}^{i'_1}}{\partial x^{i_1}}\cdots\frac{\partial \bar{x}^{i'_p}}{\partial x^{i_p}}\frac{\partial x^{j_1}}{\partial \bar{x}^{j'_1}}\cdots\frac{\partial x^{j_q}}{\partial \bar{x}^{j'_q}}T^{i_1\dots i_p}_{j_1\dots j_q}\left(x^1, \ldots, x^n\right).

그레고리오 리치-쿠르바스트로는 그의 표기법에서 공변 및 반변 성분을 가진 "계"를 언급했는데, 이는 현대적 의미로는 텐서장으로 알려져 있다.^[19]

3. 2. 텐서의 변환 법칙

아인슈타인 표기법을 사용하면, (m, n)형 텐서는 기저 를 선택하여 ''m+n''차원 배열

:

T^{i_1\dots i_m}_{j_{1}\dots j_{n}}[\mathbf{f}]

와 같이 나타낼 수 있다. 다른 기저

\mathbf{f}\cdot R = \left( \mathbf{e}_i R^i_1, \dots, \mathbf{e}_i R^i_k \right)

를 선택하면, 기저 에 의존하지 않는 변환 법칙

:

T^{i'_1\dots i'_m}_{j'_1\dots j'_n}[\mathbf{f} \cdot R] = \left(R^{-1}\right)^{i'_1}_{i_1} \cdots \left(R^{-1}\right)^{i'_m}_{i_m}

T^{i_1, \ldots, i_m}_{j_1, \ldots, j_n}[\mathbf{f}]

R^{j_1}_{j'_1}\cdots R^{j_n}_{j'_n} .

을 적용할 수 있다. 여기서 ''m''을 이 텐서의 반변 계수(contravariant rank), ''n''을 공변 계수(covariant rank)라 하며, ''m+n''을 총 계수(total rank)라 한다.

많은 응용 분야, 특히 미분 기하학과 물리학에서 공간의 점의 함수인 성분을 가진 텐서를 고려하는 것이 자연스럽다. 이것은 Ricci의 초기 연구의 배경이었다. 현대 수학 용어에서 이러한 대상을 텐서 필드라고 하며, 종종 간단히 텐서라고 한다.^[1]

이러한 맥락에서 접 벡터 공간에 대해 좌표 기저가 종종 선택된다. 그러면 변환 법칙을 좌표 함수의 편도함수로 표현할 수 있다.

:

\bar{x}^i\left(x^1, \ldots, x^n\right),

좌표 변환을 정의한다.^[1]

:

\hat{T}^{i'_1\dots i'_p}_{j'_1\dots j'_q}\left(\bar{x}^1, \ldots, \bar{x}^n\right) =\frac{\partial \bar{x}^{i'_1}}{\partial x^{i_1}}\cdots\frac{\partial \bar{x}^{i'_p}}{\partial x^{i_p}}\frac{\partial x^{j_1}}{\partial \bar{x}^{j'_1}}\cdots\frac{\partial x^{j_q}}{\partial \bar{x}^{j'_q}}T^{i_1\dots i_p}_{j_1\dots j_q}\left(x^1, \ldots, x^n\right).

4. 예시

텐서는 스칼라, 벡터, 행렬 등을 일반화한 개념이다.

다음은 텐서의 몇 가지 예시이다.

스칼라: 크기만 있고 방향이 없는 양이다. 온도, 질량, 압력 등이 그 예시이다. 스칼라는 0차 텐서이다.
벡터: 크기와 방향을 모두 가지는 양으로, 힘, 속도 등이 있다. 벡터는 1차 텐서이다.
응력 텐서: 3차원 물체 내의 응력을 나타내는 2차 텐서로, 3차 정방행렬로 표현할 수 있다. 물체 내의 정육면체 모양의 무한소 체적 요소에 작용하는 힘을 9개의 성분(3x3 행렬)으로 나타낸다.
변형률 텐서: 물체의 변형 정도를 나타내는 2차 텐서이다.
탄성률 텐서: 응력 텐서와 변형률 텐서를 연결하는 4차 텐서이다.
확산텐서영상: 뇌의 장기에서 물의 확산 정도를 나타내는 텐서를 이용하여 뇌의 영상을 구성한다.
에너지-운동량 텐서, 관성 텐서: 물리학에서 사용되는 텐서이다.

텐서는 물리학과 공학에서 중요한 개념으로 사용된다. 예를 들어, 응력 텐서와 변형률 텐서는 고체역학에서 물체의 변형과 파괴를 분석하는 데 사용된다.

다중선형대수는 추상적인 텐서 이론을 다루는 선형대수의 한 분야이다.

4. 1. 벡터 공간의 텐서

벡터 공간 $V$와 그 쌍대 공간 $V^*$에 대하여, 음이 아닌 정수 $m$, $n$에 대해 $(m, n)$형 텐서는 다음 벡터 공간의 원소로 정의된다.

:$T^m_n(V) = \underbrace{V\otimes \dots \otimes V}_{m} \otimes \underbrace{ V^*\otimes \dots \otimes V^*}_{n}$

여기서 $\otimes$은 텐서곱을 나타내며, 외적의 일반화로 생각할 수 있다. 예를 들어 다음과 같은 연산이다.

:$ A_{ij} \otimes B_{kl} = T_{ijkl} $

하나의 벡터 공간이 주어지면 그 쌍대 벡터 공간과 텐서곱 연산은 유일하게 정의된다. $(0, 0)$형 텐서인 스칼라를 포함하여, 텐서곱을 반복하여 얻을 수 있는 벡터 공간들의 벡터를 단순히 텐서라고 한다. 따라서 모든 텐서는 어떤 벡터 공간의 스칼라 혹은 벡터이다.

행렬, 위치벡터, 유사텐서 등은 기저를 선택하여 텐서를 표현 하는 방식이며, 기저를 선택하지 않으면 텐서가 아니다. 마찬가지로 위치벡터 또한 기저를 선택하지 않으면 벡터가 아니기 때문에, 모든 벡터 공간의 스칼라 혹은 벡터가 어떤 텐서라는 사실은 변하지 않는다.

하나의 벡터 공간에서 얻을 수 있는 벡터 공간들의 원소는 다음과 같이 분류할 수 있다. 물리학과 공학 등에서는 각 점마다 텐서가 하나씩 붙어 있는 공간, 즉 텐서장을 텐서라고 부르기도 한다.

colspan=2 rowspan=2 \|	n
0	1	2	3	⋯	p	⋯
m	0	스칼라 (예: 스칼라 곡률)	기울기	쌍선형 형식 (예: 스칼라곱, 계량 텐서), 리치 곡률, 심플렉틱 형식			p-형식 (예: 부피 형식), 2^p중극자 모멘트
	1	벡터 (예: 1-벡터)	선형 변환 (예: 크로네커 델타)		리만 곡률 텐서
	2	푸아송 구조		탄성 텐서
	⋮
	q	q-벡터
	⋮

4. 2. 다양체의 텐서장

다양체의 각 점에 텐서를 부여한 것을 텐서장이라고 한다. 다양체 위에 정의되는 텐서장의 예시는 다음과 같다.

계량 텐서
리만 곡률 텐서: 일반 상대성이론에서 사용되는 텐서로, 4차원(공간 3차원+시간 1차원)의 4계 텐서이다. 256(=4×4×4×4)개의 성분을 가지지만, 실제로 독립적인 성분은 20개이다.^[48]

5. 텐서 연산

아인슈타인 합 규약은 합 기호를 생략하고 합을 암시적으로 나타내는 표기법이다. 텐서 표현식에서 동일한 인덱스 기호가 두 번 나타나면, 해당 항은 모든 가능한 인덱스 값에 대해 합산된다는 것을 의미한다. 이러한 방식을 통해 여러 쌍의 인덱스에 대한 합을 간결하게 표현할 수 있다.^[1]

텐서에 대한 주요 연산에는 텐서곱, 텐서 축약, 지수 올리기와 내리기가 있다. 텐서 축약과 지수 올리기/내리기는 서로 연관되어 있으며, 계량 텐서를 통해 텐서의 유형(반변, 공변)을 변환하는 역할을 한다.

5. 1. 텐서곱

체

F

위의 벡터 공간

V,\ W,\ V \otimes W

에 대하여 쌍선형 변환

\varphi:V \times W \to V \otimes W

는 아래의 보편 성질을 갖는다.

:임의의 벡터 공간

Z

에 대하여 임의의 쌍선형 변환

h: V \times W \to Z

은 선형 변환

\bar{h}: V \otimes W \to Z

이 ''유일하게'' 존재하여

h = \bar{h} \circ \varphi

이다.

이 조건으로 텐서곱

\otimes

이 유일하게 정의되며, 따라서 유한 차원 벡터 공간

V

에 대하여 텐서의 벡터 공간은 다중선형 공간과 자연 동형이다.

:

T^m_n(V) \cong L^{m+n}\left(\underbrace{V^*\times \dots \times V^*}_{m} \times \underbrace{ V\times \dots \times V}_{n} \to F \right)

여기에서

V \cong V^{**}

이다.

펜로즈 그래프 표기법은 텐서의 기호를 도형으로, 그리고 텐서의 인덱스를 선과 곡선으로 대체하는 도식적 표기법이다. 이는 기저 원소와 무관하며, 인덱스를 위한 기호가 필요하지 않다.

5. 2. 텐서 축약

텐서 축약은 (''n'', ''m'')형 텐서를 (''n'' − 1, ''m'' − 1)형 텐서로 축소하는 연산으로, 추적이 특수한 경우이다. 이를 통해 텐서의 전체 차수가 2만큼 감소한다. 이 연산은 하나의 지정된 반변 인덱스와 하나의 지정된 공변 인덱스가 동일한 성분들을 합산하여 새로운 성분을 생성함으로써 수행된다. 두 인덱스가 다른 성분들은 버려진다. 예를 들어, (1, 1)-텐서

T_i^j

는

T_i^i

를 통해 스칼라로 축약될 수 있으며, 여기서 합산은 다시 암시적으로 이루어진다. (1, 1)-텐서가 선형 사상으로 해석될 때, 이 연산은 추적으로 알려져 있다.

축약은 텐서 곱과 함께 사용되어 각 텐서에서 인덱스를 축약하는 경우가 많다.

축약은 또한 텐서를 공간 ''V''의 복사본과 공간 ''V''^∗의 텐서곱의 원소로 정의하여 이해할 수 있다. 먼저 텐서를 단순 텐서의 선형 결합으로 분해한 다음, ''V''^∗의 인수를 ''V''의 인수에 적용한다. 예를 들어, 텐서

T \in V\otimes V\otimes V^*

는 다음과 같은 선형 결합으로 쓸 수 있다.

:

T = v_1\otimes w_1\otimes \alpha_1 + v_2\otimes w_2\otimes \alpha_2 +\cdots + v_N\otimes w_N\otimes \alpha_N.

그러면 첫 번째와 마지막 슬롯에서 ''T''의 축약은 다음과 같은 벡터이다.

:

\alpha_1(v_1)w_1 + \alpha_2(v_2)w_2 + \cdots + \alpha_N(v_N)w_N.

내적(또는 계량) ''g''가 있는 벡터 공간에서, 축약이라는 용어는 계량 텐서 또는 그 역행렬을 사용하여 추적을 형성함으로써 두 개의 반변 인덱스 또는 두 개의 공변 인덱스를 제거하는 데 사용된다. 예를 들어, (2, 0)-텐서

T^{ij}

는

T^{ij} g_{ij}

를 통해 스칼라로 축약될 수 있다(다시 합산 규약을 가정한다).

5. 3. 지수 올리기와 내리기

벡터 공간에 비퇴화 이중 선형 형식(이 맥락에서는 종종 ''계량 텐서''라고 부름)이 주어지면, 반변(위첨자) 지수를 공변(아래첨자) 지수로 변환하고 그 반대로 변환하는 연산을 정의할 수 있다. 계량 텐서는 (대칭) (0, 2)-텐서이므로, 곱에서 텐서의 위첨자 지수 하나를 계량 텐서의 아래첨자 지수 중 하나와 축약할 수 있다. 이렇게 하면 이전 텐서와 같은 지수 구조를 갖지만, 일반적으로 축약된 위첨자 지수의 위치에 아래첨자 지수가 있는 새로운 텐서가 생성된다. 이 연산은 매우 직관적인 방법으로 ''지수 내리기''라고 한다.

반대로, 역연산을 정의할 수 있으며, 이를 ''지수 올리기''라고 한다. 이것은 (2, 0)-텐서와의 곱에 대한 유사한 축약과 같다. 이 ''역 계량 텐서''는 계량 텐서의 성분의 역행렬인 성분을 갖는다.

6. 응용

텐서는 공학, 연속체 역학, 물리학 등 다양한 분야에서 널리 응용된다.

연속체 역학에서 고체나 유체 내부의 응력은 텐서장으로 설명된다. 응력 텐서와 변형률 텐서는 모두 2차 텐서이며, 탄성 텐서는 4차 텐서이다.

물리학에서 텐서는 여러 분야에서 중요한 역할을 한다.

전자기 텐서는 전자기장을 나타낸다.
유한 변형 텐서와 변형률 텐서는 물체의 변형을 설명한다.
비등방성 매질에서 유전율과 전기 감수율은 텐서로 표현된다.
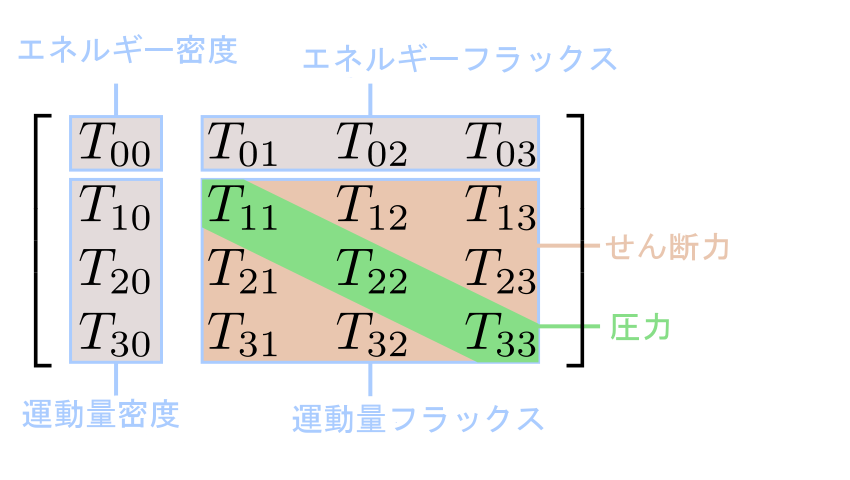
일반 상대성 이론에서 응력-에너지 텐서는 운동량 플럭스를 나타낸다.^[48]
양자 역학 및 양자 컴퓨팅에서 텐서 곱은 양자 상태 결합에 사용된다.
확산 텐서 영상에서 확산 텐서는 뇌 영상 구성에 활용된다.

컴퓨터 비전 분야에서 삼초점 텐서는 기본 행렬을 일반화한다.^[2] 비선형 광학에서 분극파는 비선형 감수율 텐서를 통해 생성되는 전기장과 관련된다.^[2]

머신 러닝에서 텐서 분해를 활용하여 고차원 데이터를 인공 신경망에 임베딩한다.^[1]

6. 1. 연속체 역학

연속체 역학에서 텐서는 중요한 역할을 한다. 고체나 유체^[30] 내부의 응력은 텐서장으로 설명된다. 응력 텐서와 변형률 텐서는 모두 2차 텐서장이며, 일반적인 선형 탄성 재료에서는 4차 탄성 텐서장과 관련이 있다. 3차원 고체 물체의 응력을 정량화하는 텐서는 그 구성 요소를 3×3 배열, 즉 9개의 구성 요소로 나타낼 수 있다. 이는 고체 내부의 다양한 응력량 각각을 설명하는 데 9개의 양이 필요하기 때문이다.

재료 내부에서 특정 표면 요소가 선택되면, 표면 한쪽의 재료가 다른 쪽에 힘을 가한다. 이 힘은 일반적으로 표면에 직교하지 않지만, 표면의 방향에 따라 선형적으로 변한다. 이는 2, 0형 텐서장으로 설명된다. 응력은 지점마다 달라질 수 있기 때문이다.

공학에서 강체나 유체 내의 응력은 텐서로 설명된다. "텐서"라는 단어는 라틴어의 "늘어나는 것", 즉 응력을 발생시키는 것을 의미한다. 물체 내의 특정 면 요소에 주목하면, 면의 한쪽 측에 있는 물질이 반대쪽에 대해 힘을 미치고 있다고 생각할 수 있다. 이 힘은 (2,0)형 텐서장으로 기술된다.

6. 2. 물리학에서의 응용

물리학에서 텐서는 여러 분야에 걸쳐 중요한 역할을 한다. 몇 가지 예시는 다음과 같다.

전자기학: 전자기 텐서(패러데이 텐서)는 전자기장을 나타내는 데 사용된다.
연속체 역학: 유한 변형 텐서와 변형률 텐서는 물체의 변형과 변형률을 설명하는 데 사용된다.
유전율 및 전기 감수율: 비등방성 매질에서 유전율과 전기 감수율은 텐서로 표현된다.
일반 상대성 이론: 응력-에너지 텐서와 같은 4차 텐서는 운동량 플럭스를 나타내는 데 사용된다.^[48]
양자 역학 및 양자 컴퓨팅: 텐서 곱은 양자 상태의 결합을 표현하는 데 사용된다.
확산 텐서 영상: 확산 텐서는 생물 환경, 특히 뇌에서 물의 확산 속도를 나타내어 뇌 영상 구성에 활용된다.
응력 텐서: 강체나 유체 내의 응력은 텐서로 설명되며, "텐서"라는 단어는 라틴어의 "늘어나는 것"(tendere|텐데레^la)에서 유래했다. 물체 내의 특정 면에 작용하는 힘은 면의 방향에 선형적으로 의존하며, (2,0)형 텐서(또는 텐서장)로 기술된다.

이 외에도 관성 텐서, 편극 텐서 등 다양한 물리량들이 텐서로 표현된다.

6. 3. 컴퓨터 비전과 광학

컴퓨터 비전 분야에서 삼초점 텐서는 기본 행렬을 일반화한다.^[2]

비선형 광학 분야는 극한 전기장 하에서 물질의 분극 밀도 변화를 연구한다.^[2] 생성된 분극파는 비선형 감수율 텐서를 통해 생성되는 전기장과 관련이 있다.^[2] 분극 '''P'''가 전기장 '''E'''에 선형적으로 비례하지 않으면 매질은 비선형으로 여겨진다.^[2] (영구 쌍극자 모멘트가 존재하지 않는다고 가정하고, 충분히 약한 장에 대해) 좋은 근사치로 '''P'''는 '''E'''의 테일러 급수로 주어지며, 그 계수는 비선형 감수율이다.^[2]

:

\frac{P_i}{\varepsilon_0} = \sum_j \chi^{(1)}_{ij} E_j  +  \sum_{jk} \chi_{ijk}^{(2)} E_j E_k + \sum_{jk\ell} \chi_{ijk\ell}^{(3)} E_j E_k E_\ell + \cdots. \!

여기서

\chi^{(1)}

은 선형 감수율이고,

\chi^{(2)}

는 포켈스 효과와 제2차 고조파 발생을 나타내며,

\chi^{(3)}

는 커 효과를 나타낸다.^[2]

6. 4. 머신 러닝

텐서 분해의 특성을 가진 텐서는 머신 러닝에서 고차원 데이터를 인공 신경망에 임베딩하는 데 활용되어 왔다.^[1] 수학 및 물리학의 다른 분야에서의 텐서 개념과는 상당히 다르게, 텐서는 일반적으로 고정된 기저에서의 수치적 양으로 간주되며, 텐서의 서로 다른 축을 따라 공간의 차원이 동일할 필요는 없다.^[1]

7. 역사

텐서라는 용어는 1846년 윌리엄 로언 해밀턴(William Rowan Hamilton)이 특정 종류의 대수계(훗날 클리포드 대수(Clifford algebra)로 알려지게 됨)에서 노름(norm) 연산을 설명하기 위해 도입했다.^[47] 현재와 같은 의미로 사용되기 시작한 것은 1899년 볼데마르 포크트(Waldemar Voigt)부터이다.

1890년경 그레고리오 리치-쿠르바스트로(Gregorio Ricci-Curbastro)는 텐서의 기호법을 발전시켰고, 투리오 레비-치비타(Tullio Levi-Civita)의 저술을 통해 많은 수학자들에게 알려지게 되었다. 20세기에 들어 이 분야는 텐서 해석(tensor analysis)으로 알려지게 되었고, 1915년경 알베르트 아인슈타인(Albert Einstein)이 일반 상대성 이론을 공식화하고 기술하는 데 사용하면서 더욱 널리 알려지게 되었다.^[47] 텐서는 연속체 역학 등 다른 분야에서도 사용된다.

7. 1. 초기 연구

텐서라는 용어는 1846년 윌리엄 로언 해밀턴(William Rowan Hamilton)이 특정 종류의 대수계(훗날 클리포드 대수(Clifford algebra)로 알려지게 됨)에서 노름(norm) 연산을 설명하기 위해 도입하였다. 현재와 같은 의미로 사용되기 시작한 것은 1899년 볼데마르 포크트(Waldemar Voigt)부터이다. 텐서의 기호법은 1890년경 그레고리오 리치-쿠르바스트로(Gregorio Ricci-Curbastro)에 의해 절대 미분 기하학이라는 이름으로 발전되었고, 투리오 레비-치비타(Tullio Levi-Civita)의 1900년 동명의 고전적인 저술을 통해 많은 수학자들에게 알려지게 되었다.^[47]

7. 2. 텐서 미적분학의 발전

1890년경 그레고리오 리치-쿠르바스트로(Gregorio Ricci-Curbastro)는 절대 미분 기하학이라는 이름으로 텐서의 기호법을 발전시켰고, 투리오 레비-치비타(Tullio Levi-Civita)의 1900년 동명의 고전적인 저술을 통해 많은 수학자들에게 알려지게 되었다.^[47]

20세기에 들어 이 분야는 텐서 해석(tensor analysis)으로 알려지게 되었다. 1915년경 알베르트 아인슈타인(Albert Einstein)이 일반 상대성 이론을 공식화하고 기술하는 데 사용하면서 더욱 널리 알려지게 되었다. 일반 상대성 이론은 텐서를 사용하여 완벽하게 공식화된다. 아인슈타인은 고심 끝에 마르셀 그로스만(Marcel Grossmann)에게 텐서 이론을 배운 것으로 알려져 있다.^[47] 텐서는 연속체 역학 등 다른 분야에서도 사용된다.

8. 일반화

텐서 개념은 여러 방식으로 확장될 수 있다. 유한 차원 벡터 공간뿐만 아니라 무한 차원 벡터 공간에서도 텐서를 정의할 수 있다. 예를 들어, 힐베르트 공간의 텐서곱을 이용하여 텐서를 정의하거나,^[51] 바나흐 공간과 그 연속 쌍대 공간 위에서의 다중선형 사상을 통해 텐서를 정의할 수 있다.^[52] 이러한 텐서는 바나흐 다양체 위에 존재한다고 생각할 수 있다.^[53]

또한, 텐서는 밀도라는 개념을 가질 수 있다. 밀도 r을 가지는 텐서는 좌표 변환 시 일반적인 텐서처럼 행동하는 것에 더해, 변환 함수의 야코비 행렬의 행렬식의 r승이 곱해진다.^[33]

8. 1. 벡터 공간의 텐서곱

체

F

위의 벡터 공간

V,\ W,\ V \otimes W

에 대하여 쌍선형 변환

\varphi:V \times W \to V \otimes W

는 아래의 보편 성질을 갖는다.

:임의의 벡터 공간

Z

에 대하여 임의의 쌍선형 변환

h: V \times W \to Z

은 선형 변환

\bar{h}: V \otimes W \to Z

이 ''유일하게'' 존재하여

h = \bar{h} \circ \varphi

이다.

이 조건으로 텐서곱

\otimes

이 유일하게 정의되며, 따라서 유한 차원 벡터 공간

V

에 대하여 텐서의 벡터 공간은 다중선형 공간과 자연 동형이다.

:

T^m_n(V) \cong L^{m+n}\left(\underbrace{V^*\times \dots \times V^*}_{m} \times \underbrace{ V\times \dots \times V}_{n} \to F \right)

여기에서

V \cong V^{**}

이다.

반드시 같은 벡터 공간일 필요는 없고 텐서곱을 취할 수 있으며, 그러한 더 일반적인 텐서곱의 원소를 "텐서"라고 부르는 경우도 있다. 예를 들어 텐서곱 공간의 원소는 이러한 더 일반적인 의미에서 2계 "텐서"이며^[49], 마찬가지로 d계 텐서를 d개의 서로 다른 벡터 공간의 텐서곱의 원소로 정의할 수 있다.^[50] 일반적인 (n, m)형 텐서는 이 더 일반적인 의미에서도 (n + m)계 텐서가 된다.

8. 2. 무한 차원 텐서

지금까지 텐서에 대한 논의는 유한 차원을 가정하였으며, 이러한 구성으로 얻어진 텐서 공간은 자연스럽게 동형이다.^[13] 텐서곱과 다중선형 사상을 기반으로 한 텐서 공간의 구성은 벡터 번들 또는 결합층으로 일반화될 수 있다.^[14] 무한 차원 벡터 공간의 경우, 동등하지 않은 위상은 동등하지 않은 텐서 개념으로 이어지며, 이러한 다양한 동형 사상은 텐서의 정확한 의미에 따라 성립할 수도 있고 성립하지 않을 수도 있다(위상적 텐서곱 참조). 어떤 응용 분야에서는 힐베르트 공간의 텐서곱이 의도된 것으로, 그 특성은 유한 차원의 경우와 가장 유사하다.

텐서의 개념은 여러 가지 방법으로 무한 차원으로 일반화될 수 있다. 텐서곱을 통해 힐베르트 공간을 일반화하거나,^[33] 비선형 분석에서 흔히 사용되는 다중선형 사상 정의를 통해 유한 차원 벡터 공간과 그 대수적 쌍대 공간 대신 무한 차원 바나흐 공간과 그 연속 쌍대 공간을 사용할 수 있다.^[34] 따라서 텐서는 바나흐 다양체^[35]와 프레셰 다양체에 자연스럽게 존재한다.

텐서의 개념은 기저 공간이 무한 차원인 경우로 일반화할 수 있는데, 그 중 하나는 힐베르트 공간에 대한 tensor product of Hilbert spaces|힐베르트 공간의 텐서곱^영어을 통해 정의하는 것이다.^[51] 비선형 해석에서 자주 사용되는 텐서 개념의 일반화로서, 유한 차원 공간과 그 대수적 쌍대 공간 위의 다중선형 사상을 고려하는 대신, 무한 차원 바나흐 공간과 그 연속적 쌍대 공간 위의 다중선형 사상으로 대체할 수도 있다.^[52] 이러한 텐서는 바나흐 다양체 위에 있다고 생각할 수 있다.^[53]

8. 3. 텐서 밀도

텐서장은 밀도를 가질 수 있다. 밀도 r을 가지는 텐서는 좌표변환에 대해서 일반적인 텐서처럼 행동하는 것 외에 변환 함수의 야코비 행렬의 행렬식의 r승이 곱해진다. 이러한 상황은 벡터다발을 생각함으로써 설명할 수 있다. 접다발의 행렬식 다발은 직선다발이지만, 이것의 r승을 다른 벡터다발에 텐서곱함으로써 비틀림을 표현할 수 있다.^[33]

9. 같이 보기

카르테시안 텐서
섬유 다발
텐서 이론 용어집
다중선형 투영
1-형식
모듈의 텐서곱

참조

_[1] 서적 Mathematical Thought From Ancient to Modern Times https://books.google[...] Oxford University Press 1990
_[2] 논문 A Multilinear Singular Value Decomposition https://alterlab.org[...] 2000
_[3] 서적 Computer Vision — ECCV 2002 https://web.archive.[...] 2022-12-29
_[4] 논문 Tensor Decompositions and Applications https://www.kolda.ne[...] 2009
_[5] 문서 The Einstein summation convention
_[6] 서적 Differential Geometry: Cartan's Generalization of Klein's Erlangen Program https://books.google[...] Springer 2000
_[7] 서적 Tensor analysis for physicists https://archive.org/[...] Courier Corporation
_[8] 서적 Foundations of Differential Geometry Wiley Interscience
_[9] 서적 Introduction to smooth manifolds https://books.google[...] Springer
_[10] 서적 Tensor geometry: The Geometric Viewpoint and Its Uses Springer 2013
_[11] Springer Affine tensor
_[12] 웹사이트 Why are Tensors (Vectors of the form a⊗b...⊗z) multilinear maps? https://math.stackex[...] 2021-06-05
_[13] 문서 The double duality isomorphism
_[14] 서적 Algebra I: Chapters 1-3 Springer 1998
_[15] 논문 Braided tensor categories
_[16] 서적 Die Entwicklung des Tensorkalküls https://books.google[...] Birkhäuser
_[17] 논문 On some Extensions of Quaternions http://www.emis.de/c[...]
_[18] 문서 the norm operation
_[19] 서적 What Are Tensors Exactly? https://books.google[...] World Scientific 2021-06-16
_[20] 서적 Die fundamentalen physikalischen Eigenschaften der Krystalle in elementarer Darstellung https://books.google[...] Von Veit
_[21] 논문 Résumé de quelques travaux sur les systèmes variables de fonctions associés à une forme différentielle quadratique https://books.google[...]
_[22] 서적 Subtle Is the Lord: The Science and the Life of Albert Einstein https://books.google[...] Oxford University Press
_[23] 논문 The Italian Mathematicians of Relativity
_[24] 서적 Algebraic Topology https://books.google[...] Springer 2012
_[25] 서적 Algebra https://books.google[...] Springer 2003
_[26] 서적 Categories for the Working Mathematician https://books.google[...] Springer 2013
_[27] 서적 A Course in Mathematics for Students of Physics Cambridge University Press
_[28] 서적 The Road to Reality Vintage
_[29] 서적 Gravitation https://books.google[...] W.H. Freeman
_[30] 서적 Fluid Mechanics for Engineers Springer 2021
_[31] 서적 Geometry of the Fundamental Interactions: On Riemann's Legacy to High Energy Physics and Cosmology https://books.google[...] Springer
_[32] 서적 Handbook of Linear Algebra https://books.google[...] CRC Press
_[33] 논문 Tensor Algebras Over Hilbert Spaces. I 1956-01
_[34] 서적 Manifolds, Tensor Analysis and Applications Springer 1988-02
_[35] 서적 Differential manifolds https://books.google[...] Addison-Wesley
_[36] 서적 Tensor analysis for physicists
_[37] 서적 Applications of tensor analysis https://books.google[...] Dover 2014
_[38] 서적 Equivalence, invariants, and symmetry https://books.google[...] Cambridge University Press
_[39] 저널 On the definition of geometric objects. I 1953
_[40] 논문 Proc. Internat. Congress Math.(Edinburgh, 1958) Cambridge University Press 2017-10-26
_[41] 저널 On the theory of geometric objects https://projecteucli[...]
_[42] 서적 The road to reality: a complete guide to the laws of our universe https://books.google[...] Knopf
_[43] 서적 Clifford Algebras and Lie Theory Springer
_[44] 서적 Wave Equations in Higher Dimensions Springer
_[45] 서적 Introduction to smooth manifolds Springer
_[46] 백과사전 Affine tensor
_[47] 서적 Subtle is the Lord: The Science and the Life of Albert Einstein
_[48] 서적 一般相対性理論筑摩書房
_[49] 서적 Geometry of the Fundamental Interactions: On Riemann's Legacy to High Energy Physics and Cosmology https://books.google[...] Springer Science & Business Media
_[50] 서적 Handbook of Linear Algebra, Second Edition https://books.google[...] CRC Press
_[51] 저널 Tensor Algebras Over Hilbert Spaces. I American Mathematical Society 1956-01
_[52] 서적 Manifolds, Tensor Analysis and Applications Springer-Verlag 1988-02
_[53] 서적 Differential manifolds Addison-Wesley Pub. Co.
_[54] 저널 占領期の日本数学界 https://www2.tsuda.a[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com