상 (수학)

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
4. 예시
5. 표기법
참조

1. 개요

상(image)은 수학에서 함수와 관련된 개념으로, 정의역의 원소나 부분 집합에 함수를 적용하여 얻는 결과물을 의미한다. 함수 f: X → Y가 주어졌을 때, X의 원소 x의 상은 f(x)이며, X의 부분 집합 A의 상은 f(A) = {f(x) | x ∈ A}로 정의된다. 함수의 상은 함수의 치역과 동일하며, 공역의 원소 y의 원상(역상)은 f⁻¹(y) = {x ∈ X | f(x) = y}로 정의된다. 상과 원상은 집합의 포함 관계를 보존하는 단조성을 가지며, 합성 함수에서의 상과 원상은 각각 g(f(A))와 f⁻¹(g⁻¹(C))로 표현된다. 상과 원상은 다양한 표기법으로 표현될 수 있으며, 집합족에 대한 교집합과 합집합에 대한 불 대수를 잘 생각할 수 있게 해준다.

더 읽어볼만한 페이지

집합론의 기본 개념 - 치역
치역은 함수에서 정의역의 모든 원소에 대한 함숫값들의 집합으로, 공역의 부분집합이며, 함수의 상을 의미하거나 공역 전체를 의미하기도 한다.
집합론의 기본 개념 - 항등 함수
항등 함수는 집합 X의 각 원소를 자기 자신에게 대응시키는 함수로서, 정의역과 공역이 같은 집합 X에서 단사 함수이자 전사 함수이며, 함수 합성에서 항등원의 역할을 수행하는 중요한 개념이다.
함수와 사상 - 적분
적분은 아르키메데스가 고안하고 앙리 르베그가 완성한 미적분학의 핵심 개념으로, 도형의 면적과 부피를 구하는 데 사용되며 미분과 역의 관계를 갖고, 확률, 넓이, 부피 계산 등 다양한 분야에서 활용된다.
함수와 사상 - 지수 함수
지수 함수는 양의 상수 *a*를 밑으로 하는 *y = a^x* 형태의 함수이며, 특히 자연로그의 역함수인 *e^x*는 다양한 정의와 응용을 가지며 복소수로 확장될 수 있다.

상 (수학)
일반 정보
정의	어떤 함수의 모든 출력 값들의 집합
다른 이름	치역
기호	Im(f) 또는 f(A)
예시
함수 f(x) = x^2	정의역 A = {1, 2, 3}일 때, 상은 {1, 4, 9}이다. 실수 전체의 집합에서 정의된 함수 f(x) = x^2의 상은 0 이상의 실수 집합이다.
성질
전사 함수	함수의 상이 공역과 같으면 전사 함수이다.
역함수	전단사 함수는 역함수를 가지며, 역함수의 정의역은 원래 함수의 상이다.
관련 개념
역상	공역의 부분집합에 대응하는 정의역의 부분집합
핵	선형대수학에서, 선형 변환의 핵은 영벡터로 변환되는 벡터들의 집합

2. 정의

정의역이 $X$ , 공역이 $Y$ 인 함수 $f\colon X\to Y$ 를 생각하자.

정의역의 원소 $x\in X$ 의, 함수 $f$ 에 대한 '''상'''은 공역의 원소 $f(x)\in Y$ 이다.
정의역의 부분 집합 $A\subseteq X$ 의, 함수 $f$ 에 대한 '''상'''은 공역의 부분 집합

:

f(A)=\{f(x)\colon x\in A\}\subseteq Y

이다.

공역의 원소 $y\in Y$ 의, 함수 $f$ 에 대한 '''원상'''은 정의역의 부분 집합

:

f^{-1}(y)=\{x\in X\colon f(x)=y\}\subseteq X

이다. 이는 정의역의 원소가 아니라, 정의역의 부분 집합이라는 데 주의해야 한다.

공역의 부분 집합 $B\subseteq Y$ 의, 함수 $f$ 에 대한 '''원상'''은 정의역의 부분 집합

:

f^{-1}(B)=\{x\in X\colon f(x)\in B\}\subseteq X

이다.

정의역의 상을 '''치역'''이라고 한다.

상과 원상의 표기는 다음과 같이 여러 가지가 있다.

상	원상
$f(A)$	$f^{-1}(B)$
$f[A]$	$f^{-1}[B]$
$f_*(A)$	$f^*(B)$
$f^\rightarrow(A)$	$f^\leftarrow(B)$

2. 1. 원소의 상

정의역이

X

, 공역이

Y

인 함수

f\colon X\to Y

를 생각하자. 정의역의 원소

x\in X

의, 함수

f

에 대한 '''상'''은 공역의 원소

f(x)\in Y

이다.

f(x)

는

x

에 함수

f

를 적용했을 때의 값을 의미하며, 인자

x

에 대한

f

의 출력값으로도 불린다.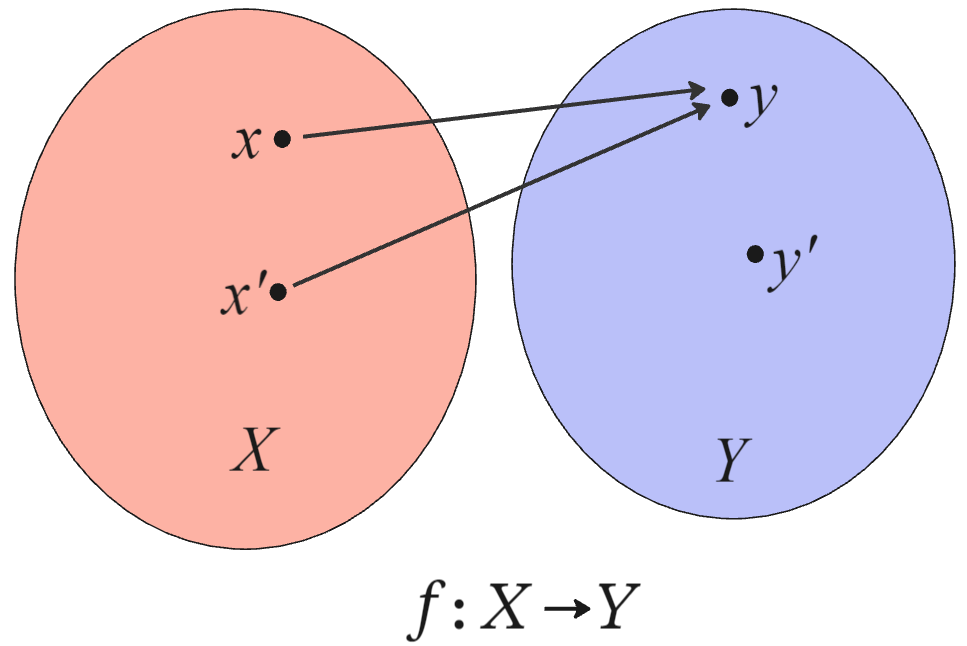

$f$ 는 정의역 $X$ 에서 공역 $Y$ 로의 함수이다. 원소 $x$ 의 상은 원소 $y$ 이다.

2. 2. 부분 집합의 상

정의역이

X

, 공역이

Y

인 함수

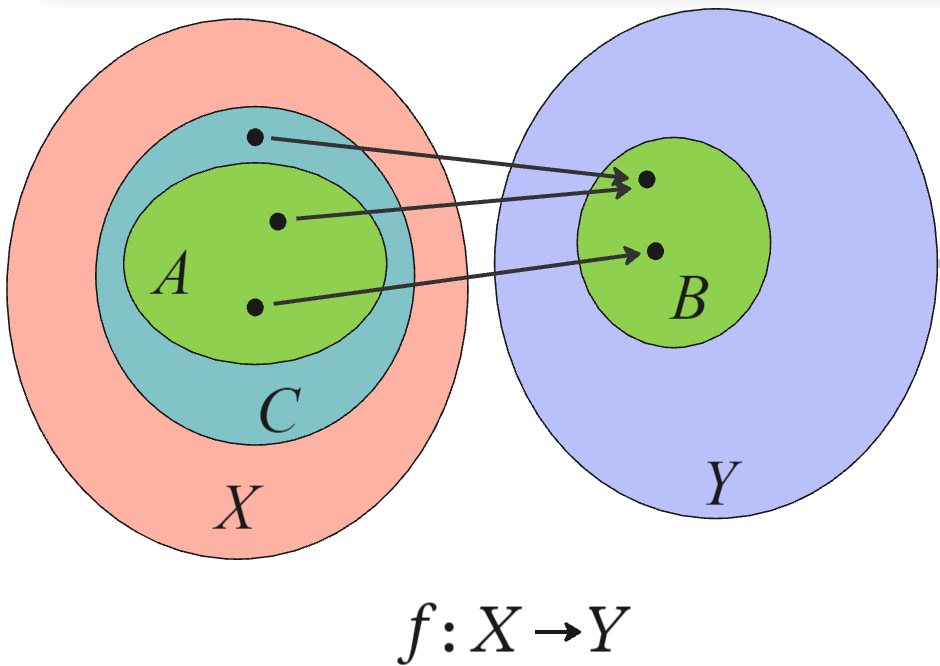
f\colon X\to Y

를 생각하자. 정의역의 부분 집합

A\subseteq X

의, 함수

f

에 대한 '''상'''은 공역의 부분 집합

:

f(A)=\{f(x)\colon x\in A\}\subseteq Y

이다.^[1]^[2]

이는 함수

f[\,\cdot\,] : \mathcal P(X) \to \mathcal P(Y)

를 유도하며, 여기서

\mathcal P(S)

는 집합

S

의 모든 부분 집합의 집합인

S

의 멱집합을 나타낸다.

부분 집합 ''A'' ⊆ ''X''의 ''f''에 의한 상 ''f''[''A''] ⊆ ''Y''는 (집합의 내포적 표기법으로)

:

f[A] := \{f(x) \in Y \mid x \in A\} = \{y \in Y \mid \exists x \in A : y=f(x)\}

:로 정의된다. 후자가 더 엄밀한 표현이다. 혼동될 우려가 없을 경우, ''f''[''A'']는 간단히 ''f''(''A'')라고도 표기한다.

$f$ 는 정의역 $X$ 에서 공역 $Y$ 로의 함수이다. 부분집합 $A$ 의 모든 원소의 상은 부분집합 $B$ 이다. $B$ 의 역상은 부분집합 $C$ 이다.

2. 3. 함수의 상 (치역)

정의역이

X

, 공역이

Y

인 함수

f\colon X\to Y

에서, 정의역 전체의 상

f(X)

를 '''치역'''이라고 부른다.^[3] 함수의 '''상'''은 함수의 전체 정의역의 상이며, 함수의 치역이라고도 한다.

$f$ 는 정의역 $X$ 에서 공역 $Y$ 로의 함수이다. $Y$ 내부의 노란색 타원은 $f$ 의 상이다.

사상 ''f''의 시역 ''X'' 전체에 관한 부분 집합으로서의 상 ''f''[''X'']를 단순히 사상 ''f''의 상이라고 부르며, im ''f'' 등으로 나타낸다.

2. 4. 원상 (역상)

정의역이

X

, 공역이

Y

인 함수

f\colon X\to Y

를 생각하자. 공역의 원소

y\in Y

의, 함수

f

에 대한 '''원상'''(preimage)은 정의역의 부분 집합

:

f^{-1}(y)=\{x\in X\colon f(x)=y\}\subseteq X

이다. 이는 정의역의 원소가 아니라, 정의역의 부분 집합이라는 데 주의해야 한다. 공역의 부분 집합

B\subseteq Y

의, 함수

f

에 대한 '''원상'''은 정의역의 부분 집합

:

f^{-1}(B)=\{x\in X\colon f(x)\in B\}\subseteq X

이다.

원상은 올(fiber) 또는 레벨 집합(level set)이라고도 불린다.

상과 원상의 표기는 다음과 같다.

상	원상
$f(A)$	$f^{-1}(B)$
$f[A]$	$f^{-1}[B]$
$f_*(A)$	$f^*(B)$
$f^\rightarrow(A)$	$f^\leftarrow(B)$

예를 들어, 함수 $f(x) = x^2$ 에 대해, $\{ 4 \}$ 의 역상은 $\{ -2, 2 \}$ 이다.

$f^{-1}[B]$ 는 $f^{-1}(B)$ 로 표시될 수 있으며, $f^{-1}$ 는 $Y$ 의 멱집합에서 $X$ 의 멱집합으로 가는 함수로 생각할 수도 있다. 표기법 $f^{-1}$ 은 역함수에 대한 표기법과 혼동해서는 안 되지만, $f$ 에 대한 $B$ 의 역상이 $f^{-1}$ 에 대한 $B$ 의 이미지라는 점에서 전단사 함수에 대한 일반적인 표기법과 일치한다.

''f''가 ''X''에서 ''Y''로의 사상일 때, 부분 집합 ''B'' ⊆ ''Y''의 ''f''에 의한 원상은

: $f^{-1}[ B ] := \{x \in X \mid f(x) \in B\}$

로 정의되는 ''X''의 부분 집합이다. ''f''에 의한 '''당겨올림'''(pull-back^영어)이라고도 불린다.^[2]

3. 성질

함수 $f : X \to Y$ 와 모든 부분 집합 $A \subseteq X$ , $B \subseteq Y$ 에 대해 다음 성질들이 성립한다.^[7]^[8]

이미지	역상
$f(X) \subseteq Y$	$f^{-1}(Y) = X$
$f(A) = \varnothing$ (iff) $A = \varnothing$	$f^{-1}(B) = \varnothing$ (iff) $B \subseteq Y \setminus f(X)$
$f(X \setminus A) \supseteq f(X) \setminus f(A)$	$f^{-1}(Y \setminus B) = X \setminus f^{-1}(B)$ ^[7]
$f(A) \cap B = \varnothing$ (iff) $A \cap f^{-1}(B) = \varnothing$

$f$ 가 전사 함수인 경우, $f(f^{-1}(B)) = B$ 이다. $f$ 가 단사 함수인 경우, $f^{-1}(f(A)) = A$ 이다.

함수 $f : X \to Y$ 와 부분 집합 $A, B \subseteq X$ 및 $S, T \subseteq Y$ 에 대해 다음이 성립한다.

상(Image)	역상(Preimage)
$A \subseteq B$ 이면 $f(A) \subseteq f(B)$	$S \subseteq T$ 이면 $f^{-1}(S) \subseteq f^{-1}(T)$
$f(A \cup B) = f(A) \cup f(B)$ ^[9]^[10]	$f^{-1}(S \cup T) = f^{-1}(S) \cup f^{-1}(T)$
$f(A \cap B) \subseteq f(A) \cap f(B)$ ( $f$ 가 단사 함수인 경우 등호 성립)^[9]^[10]^[11]	$f^{-1}(S \cap T) = f^{-1}(S) \cap f^{-1}(T)$
$f(A \setminus B) \supseteq f(A) \setminus f(B)$ ( $f$ 가 단사 함수인 경우 등호 성립)^[9]^[11]	$f^{-1}(S \setminus T) = f^{-1}(S) \setminus f^{-1}(T)$ ^[9]

상과 역상은 불 대수의 교집합 및 합집합과 관련하여 부분 집합 쌍뿐만 아니라 모든 부분 집합 모음에 대해 다음 관계가 성립한다.

$f\left(\bigcup_{s\in S}A_s\right) = \bigcup_{s\in S} f\left(A_s\right)$
$f\left(\bigcap_{s\in S}A_s\right) \subseteq \bigcap_{s\in S} f\left(A_s\right)$
$f^{-1}\left(\bigcup_{s\in S}B_s\right) = \bigcup_{s\in S} f^{-1}\left(B_s\right)$
$f^{-1}\left(\bigcap_{s\in S}B_s\right) = \bigcap_{s\in S} f^{-1}\left(B_s\right)$

(여기서

S

는 무한집합일 수 있으며, 심지어 비가산 무한집합일 수도 있다.)

이에 따라, 역상 함수는 격자 준동형사상이지만, 상 함수는 세미격자 준동형사상이다 (항상 교집합을 보존하지는 않는다).

3. 1. 합성 함수에서의 상과 원상

임의의 함수

f\colon X\to Y

및

g\colon Y\to Z

에 대하여, 그 합성

g\circ f\colon X\to Z

의 상과 원상은 다음과 같다.

$(g\circ f)(A)=g(f(A))\qquad(A\subseteq X)$
$(g\circ f)^{-1}(C)=f^{-1}(g^{-1}(C))\qquad(C\subseteq Z)$

즉, 상은 함자

:

\operatorname{Set}\to\operatorname{Set}

:

X\to\mathcal P(X)

:

(f\colon X\to Y)\mapsto(f\colon\mathcal P(X)\to\mathcal P(Y))

를 정의하며, 원상은 함자

:

\operatorname{Set}^{\operatorname{op}}\to\operatorname{Set}

:

X\to\mathcal P(X)

:

(f\colon X\to Y)\mapsto(f^{-1}\colon\mathcal P(Y)\to\mathcal P(X))

를 정의한다.

함수

f : X \to Y

와

g : Y \to Z

에 대해,

A \subseteq X

와

C \subseteq Z

가 주어지면 다음이 성립한다.

$(g \circ f)(A) = g(f(A))$
$(g \circ f)^{-1}(C) = f^{-1}(g^{-1}(C))$

3. 2. 단조성

함수

f\colon X\to Y

에 대하여, 다음이 성립한다.

만약 $A\subseteq A'\subseteq X$ 라면, $f(A)\subseteq f(A')$
만약 $B\subseteq B'\subseteq Y$ 라면, $f^{-1}(B)\subseteq f^{-1}(B')$

즉, 임의의 함수

f\colon X\to Y

에 대하여,

:

f\colon\mathcal P(X)\to\mathcal P(Y)

:

f^{-1}\colon\mathcal P(Y)\to\mathcal P(X)

는 (범주로 본) 멱집합 격자 사이의 두 함자를 이룬다.

함수

f : X \to Y

와 부분 집합

A, B \subseteq X

및

S, T \subseteq Y

에 대해 다음 속성이 적용된다.

상(Image)	역상(Preimage)
$A \subseteq B$ 이면 $f(A) \subseteq f(B)$	$S \subseteq T$ 이면 $f^{-1}(S) \subseteq f^{-1}(T)$

상과 역상을 불 대수의 교집합 및 합집합과 관련된 결과는 부분 집합의 쌍뿐만 아니라 모든 부분 집합 모음에 적용된다.

$f\left(\bigcup_{s\in S}A_s\right) = \bigcup_{s\in S} f\left(A_s\right)$
$f\left(\bigcap_{s\in S}A_s\right) \subseteq \bigcap_{s\in S} f\left(A_s\right)$
$f^{-1}\left(\bigcup_{s\in S}B_s\right) = \bigcup_{s\in S} f^{-1}\left(B_s\right)$
$f^{-1}\left(\bigcap_{s\in S}B_s\right) = \bigcap_{s\in S} f^{-1}\left(B_s\right)$

(여기서

S

는 무한할 수 있으며, 심지어 비가산 무한일 수도 있다.)

위에서 설명한 부분 집합 대수와 관련하여 역상 함수는 격자 준동형사상인 반면, 상 함수는 단지 세미격자 준동형사상이다 (즉, 항상 교집합을 보존하지는 않는다).

사상 ''f'': ''X'' → ''Y'' 와 ''X''의 임의의 부분 집합 ''A''₁, ''A''₂ 및 ''Y''의 임의의 부분 집합 ''B''₁, ''B''₂에 관하여

''B''₁ ⊆ ''B''₂ ⇒ ''f''^-1(''B''₁) ⊆ ''f''^-1(''B''₂)

등이 성립한다. 상 및 역상에 관한 이 결과는 임의의 부분 집합족에 대하여 교집합과 합집합에 관한 불 대수를 잘 생각할 수 있다는 것을 의미하며, 부분 집합의 쌍뿐만 아니라 더 일반적으로

$f^{-1}\!\left(\bigcup_{s\in S}A_s\right) = \bigcup_{s\in S} f^{-1}(A_s)$
$f^{-1}\!\left(\bigcap_{s\in S}A_s\right) = \bigcap_{s\in S} f^{-1}(A_s)$

등도 성립한다. 여기서 ''S''는 무한 집합이어도 (물론 비가산 무한이어도) 좋다.

이러한 사실로부터 부분 집합의 불 대수에 관하여 역상은 격자 준동형이 되지만, 상의 경우에는 반격자 준동형에 지나지 않음(상은 교집합을 보존한다는 보장이 없음)을 알 수 있다.

3. 3. 상과 원상 사이의 관계

임의의 함수

f\colon X\to Y

에 대하여, 다음 성질들이 성립한다.

임의의 $A\subseteq X$ 에 대하여,
* $f^{-1}(f(A))\supseteq A$
* 만약 $f$ 가 단사 함수라면, $f^{-1}(f(A))=A$
임의의 $B\subseteq Y$ 에 대하여,
* $f(f^{-1}(B))\subseteq B$
* 만약 $f$ 가 전사 함수라면, $f(f^{-1}(B))=B$
임의의 $A\subseteq X$ 및 $B\subseteq Y$ 에 대하여, 다음 두 조건이 서로 동치이다.
* $f(A)\subseteq B$
* $A\subseteq f^{-1}(B)$

이에 따라, 임의의 함수

f\colon X\to Y

에 대하여,

f\colon\mathcal P(X)\to\mathcal P(Y)

와

f^{-1}\colon\mathcal P(Y)\to\mathcal P(X)

는 서로 수반 함자이다.

:

f\dashv f^{-1}

함수

f : X \to Y

와 부분 집합

A, B \subseteq X

및

S, T \subseteq Y

에 대해 다음 속성이 적용된다.

상(Image)	역상(Preimage)
$A \subseteq B$ 이면, $f(A) \subseteq f(B)$	$S \subseteq T$ 이면, $f^{-1}(S) \subseteq f^{-1}(T)$
$f(A) \supseteq B$ (동치) $C \subseteq A$ 이고 $f(C) = B$ 인 $C$ 가 존재	$f^{-1}(B) \supseteq A$ (동치) $f(A) \subseteq B$

3. 4. 기타 성질

임의의 함수

f\colon X\to Y

에 대해, 다음 성질들이 성립한다.

정의역 속의 집합족 $(A_i)_{i\in I}\subseteq\mathcal P(X)$ 에 대하여,

::

f\biggl(\bigcup_{i\in I}A_i\biggr)=\bigcup_{i\in I}f(A_i)

::

f\biggl(\bigcap_{i\in I}A_i\biggr)\subseteq\bigcap_{i\in I}f(A_i)

공역 속 집합족 $(B_j)_{j\in J}\subseteq\mathcal P(Y)$ 에 대하여,

::

f^{-1}\biggl(\bigcup_{j\in J}B_j\biggr)=\bigcup_{j\in J}f^{-1}\left(B_j\right)

::

f^{-1}\biggl(\bigcap_{j\in J}B_j\biggr)=\bigcap_{j\in J}f^{-1}\left(B_j\right)

정의역의 두 부분 집합 $A,A'\subseteq X$ 에 대하여,

::

f(A\setminus A')\supseteq f(A)\setminus f(A')

공역의 두 부분 집합 $B,B'\subseteq Y$ 에 대하여,

::

f^{-1}(B\setminus B')=f^{-1}(B)\setminus f^{-1}(B')

f : X \to Y

를 함수라고 할 때,

X

의 부분 집합

A

에 대한

f

아래에서의 상(image)은 모든

a\in A

에 대한

f(a)

의 집합이다. 이는

f[A]

또는

f(A)

로 표기한다. 집합-생성 표기법을 사용하여, 다음과 같이 쓸 수 있다.^[1]^[2]

:

f[A] = \{f(a) : a \in A\}.

이는 함수

f[\,\cdot\,] : \mathcal P(X) \to \mathcal P(Y)

를 유도하며, 여기서

\mathcal P(S)

는 집합

S

의 모든 부분 집합의 집합인

S

의 멱집합을 나타낸다.

만약

R

이

X \times Y

에 대한 임의의 이항 관계라면, 집합

\{ y \in Y : x R y \text{ for some } x \in X \}

를

R

의 상(image) 또는 치역이라고 부른다. 이와 대칭적으로, 집합

\{ x \in X : x R y \text{ for some } y \in Y \}

는

R

의 정의역이라고 부른다.

함수

f : X \to Y

와 모든 부분 집합

A \subseteq X

및

B \subseteq Y

에 대해 다음 속성이 적용된다.

이미지	역상
$f(X) \subseteq Y$	$f^{-1}(Y) = X$
$f\left(f^{-1}(Y)\right) = f(X)$	$f^{-1}(f(X)) = X$
$f\left(f^{-1}(B)\right) \subseteq B$ ( $B \subseteq f(X)$ 인 경우 등식 성립; 예를 들어, $f$ 가 전사 함수인 경우)^[7]^[8]	$f^{-1}(f(A)) \supseteq A$ ( $f$ 가 단사 함수인 경우 등식 성립)^[7]^[8]
$f(f^{-1}(B)) = B \cap f(X)$	$\left(f \vert_A\right)^{-1}(B) = A \cap f^{-1}(B)$
$f\left(f^{-1}(f(A))\right) = f(A)$	$f^{-1}\left(f\left(f^{-1}(B)\right)\right) = f^{-1}(B)$
$f(A) = \varnothing \,\text{ if and only if }\, A = \varnothing$	$f^{-1}(B) = \varnothing \,\text{ if and only if }\, B \subseteq Y \setminus f(X)$
$f(A) \supseteq B \,\text{ if and only if } \text{ there exists } C \subseteq A \text{ such that } f(C) = B$	$f^{-1}(B) \supseteq A \,\text{ if and only if }\, f(A) \subseteq B$
$f(A) \supseteq f(X \setminus A) \,\text{ if and only if }\, f(A) = f(X)$	$f^{-1}(B) \supseteq f^{-1}(Y \setminus B) \,\text{ if and only if }\, f^{-1}(B) = X$
$f(X \setminus A) \supseteq f(X) \setminus f(A)$	$f^{-1}(Y \setminus B) = X \setminus f^{-1}(B)$ ^[7]
$f\left(A \cup f^{-1}(B)\right) \subseteq f(A) \cup B$ ^[9]	$f^{-1}(f(A) \cup B) \supseteq A \cup f^{-1}(B)$ ^[9]
$f\left(A \cap f^{-1}(B)\right) = f(A) \cap B$ ^[9]	$f^{-1}(f(A) \cap B) \supseteq A \cap f^{-1}(B)$ ^[9]

또한, 다음이 성립한다.

$f(A) \cap B = \varnothing \,\text{ if and only if }\, A \cap f^{-1}(B) = \varnothing$

함수

f : X \to Y

와 부분 집합

A, B \subseteq X

및

S, T \subseteq Y

에 대해 다음 속성이 적용된다.

상(Image)	역상(Preimage)
$A \subseteq B \,\text{ implies }\, f(A) \subseteq f(B)$	$S \subseteq T \,\text{ implies }\, f^{-1}(S) \subseteq f^{-1}(T)$
$f(A \cup B) = f(A) \cup f(B)$ ^[9]^[10]	$f^{-1}(S \cup T) = f^{-1}(S) \cup f^{-1}(T)$
$f(A \cap B) \subseteq f(A) \cap f(B)$ ( $f$ 가 단사 함수인 경우 등식 성립)^[9]^[10]^[11]	$f^{-1}(S \cap T) = f^{-1}(S) \cap f^{-1}(T)$
$f(A \setminus B) \supseteq f(A) \setminus f(B)$ ( $f$ 가 단사 함수인 경우 등식 성립)^[9]^[11]	$f^{-1}(S \setminus T) = f^{-1}(S) \setminus f^{-1}(T)$ ^[9]
$f\left(A \triangle B\right) \supseteq f(A) \triangle f(B)$ (단사 함수인 경우 등식 성립)	$f^{-1}\left(S \triangle T\right) = f^{-1}(S) \triangle f^{-1}(T)$

상과 역상을 불 대수의 교집합 및 합집합과 관련된 결과는 부분 집합의 쌍뿐만 아니라 모든 부분 집합 모음에 적용된다.

$f\left(\bigcup_{s\in S}A_s\right) = \bigcup_{s\in S} f\left(A_s\right)$
$f\left(\bigcap_{s\in S}A_s\right) \subseteq \bigcap_{s\in S} f\left(A_s\right)$
$f^{-1}\left(\bigcup_{s\in S}B_s\right) = \bigcup_{s\in S} f^{-1}\left(B_s\right)$
$f^{-1}\left(\bigcap_{s\in S}B_s\right) = \bigcap_{s\in S} f^{-1}\left(B_s\right)$

(여기서

S

는 무한할 수 있으며, 심지어 비가산 무한일 수도 있다.)

부분 집합 대수와 관련하여 역상 함수는 격자 준동형사상인 반면, 상 함수는 세미격자 준동형사상이다 (즉, 항상 교집합을 보존하지는 않는다).

4. 예시

함수 f^영어 : {1, 2, 3} → {a, b, c, d}는 다음과 같이 정의된다.

:

1 ↦ a

2 ↦ a

3 ↦ c

:집합 {2, 3}의 상은 }이다. 함수 f^영어의 상은 {a, c}이다. a의 원상은 }이다. {a, b}의 원상 또한 }이다. f^영어에 대한 {b, d}의 원상은 공집합(∅)이다.

함수 f^영어 : ℝ → ℝ는 f(x) = x²^영어로 정의된다.

:f^영어에 대한 {-2, 3}의 상은 }이고, f^영어의 상은 ℝ⁺(모든 양의 실수와 0의 집합)이다. f^영어에 대한 {4, 9}의 원상은 }이다. 집합 N = {n ∈ R : n < 0^영어}에 대한 f^영어의 원상은 공집합인데, 음수는 실수 집합에서 제곱근이 없기 때문이다.

함수 f^영어 : ℝ² → ℝ는 f(x, y) = x² + y²^영어로 정의된다.

:는 a > 0, a = 0, 또는 a < 0 (각각)에 따라 동심원, 원점, 그리고 공집합이다. (만약 a ≥ 0이라면, 올 는 방정식 x² + y² = a^영어를 만족하는 모든 (x, y) ∈ ℝ²의 집합, 즉 반지름이 √a인 원점을 중심으로 하는 원이다.)

M이 다양체이고 π : TM → M이 접다발 TM에서 M으로의 정규 사영이라면, π의 올은 접공간 T_x(M) for x ∈ M^영어이다. 이것은 올다발의 한 예이다.
몫군은 준동형 상이다.
사상 f: {1, 2, 3} → {a, b, c, d}는 f(1)=f(2)=a, f(3)=c^영어로 정의된다.

:부분 집합 {2, 3}의 f에 의한 상은 f({2, 3}) = {a, c}이다. 또한, 원소 a의 역상은 }이며, {a, b}의 역상도 마찬가지로 {1, 2}이다. {b, d}의 역상은 공집합 {}이다.

사상 f: ℝ → ℝ는 f(x) = x²^영어로 정의된다.

:부분 집합 {-2, 3}의 f에 의한 상은 f({-2, 3}) = {4, 9}이며, 사상 f의 상은 비음수 실수 전체 ℝ₊이다. 한편 {4, 9}의 f에 의한 역상은 }이며, 또한 음의 실수의 제곱근은 실수 범위에는 존재하지 않으므로, N = {n ∈ ℝ | n < 0}의 f에 의한 역상은 공집합이다.

사상 f: ℝ² → ℝ는 f(x, y) = x² + y²^영어로 정의된다.

:파이버 는 (a > 0, a = 0, a < 0에 따라 각각) 원점을 중심으로 하는 동심원, 원점, 공집합이 된다.

M이 미분 다양체이고 π: TM → M이 접다발 TM에서 M으로의 표준 사영이라면, 점 x ∈ M상의 π에 관한 파이버는 x에서의 접공간 T_x(M)이다. 이것은 파이버 다발의 예이다.

5. 표기법

혼동의 우려가 없을 경우, ''f''[''A'']는 간단히 ''f''(''A'')로 표기한다. 이는 일반적으로 많이 사용되는 표기법이지만, 그 의미는 문맥에서 추측해야 한다. 이 표기법은 사상 ''f'': ''X'' → ''Y''의 시역 ''X''를 ''X''의 멱집합으로 바꾸고, 종역 ''Y''를 ''Y''의 멱집합으로 바꿔 얻을 수 있는 부분 집합 간의 사상 (''f''가 유도하는 사상)으로 보는 관점을 제공한다.

수학적 논리나 집합론에서 사용되는 ''f''[''A'']''의 다른 표기로서 ''f'' ''A''가 있다.^[4]^[5]

사상 ''f''의 상을 ''f''의 치역 (range)^영어이라고 부르는 문헌도 있다. ''f''의 공역 (codomain)^영어과의 구별을 해두어야 한다.

부분 집합의 상과 역상에 관한 관습적인 표기법은 종종 혼란을 야기할 가능성이 있다. 이를 명시적으로 대체하는 표기로서, 멱집합 간의 사상으로서의 상과 원상에 대해서는, 다음과 같은 표기가 제안되었다.^[12]

화살표 표기법
$f^\to\colon \mathfrak{P}(X)\to\mathfrak{P}(Y);\; A\mapsto f^\to(A) = \{ f(a)\mid a \in A\}.$
$f^\gets\colon \mathfrak{P}(Y)\to\mathfrak{P}(X);\; B\mapsto f^\gets(B) = \{ a \in X \mid f(a) \in B\}.$
별 표기법
$f_\star\colon \mathfrak{P}(X)\to\mathfrak{P}(Y)\quad (=f^\to).$
$f^\star\colon \mathfrak{P}(Y)\to\mathfrak{P}(X)\quad (=f^\gets).$
기타 다른 표기법
$f^\rightarrow : \mathcal{P}(X) \to \mathcal{P}(Y)$ 로 $f^\rightarrow(A) = \{ f(a)\;|\; a \in A\}$
$f^\leftarrow : \mathcal{P}(Y) \to \mathcal{P}(X)$ 로 $f^\leftarrow(B) = \{ a \in X \;|\; f(a) \in B\}$
$f_\star : \mathcal{P}(X) \to \mathcal{P}(Y)$ 대신 $f^\rightarrow$
$f^\star : \mathcal{P}(Y) \to \mathcal{P}(X)$ 대신 $f^\leftarrow$

참조

_[1] 웹사이트 5.4: Onto Functions and Images/Preimages of Sets https://math.librete[...] 2020-08-28
_[2] 서적 Naive Set Theory Nostrand
_[3] 웹사이트 Image https://mathworld.wo[...] 2020-08-28
_[4] 서적 Set Theory for the Mathematician https://archive.org/[...] Holden-Day
_[5] 간행물 Inhomogeneity of the urelements in the usual models of NFU https://web.archive.[...] Semantic Scholar 2005-12-29
_[6] 서적 Linear Algebra Prentice-Hall
_[7] 문서
_[8] 문서
_[9] 문서
_[10] 문서
_[11] 문서
_[12] 문서
_[13] 서적 Set Theory for the Mathematician Holden-Day
_[14] 문서
_[15] 문서
_[16] 문서

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com