이항 관계
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
이항 관계는 두 집합 간의 원소들 사이의 관계를 나타내는 수학적 개념이다. 집합 R이 이항 관계이면, R의 모든 원소는 순서쌍으로 구성된다. 집합 X와 Y의 데카르트 곱의 부분 집합으로 정의되며, 순서쌍 (x, y)가 R에 속할 경우 x와 y 사이에 관계 R이 성립한다고 표현한다. 이항 관계는 연산, 종류, 성질 등을 가지며, 함수, 동차 관계, 이종 관계 등 다양한 형태로 분류될 수 있다.
더 읽어볼만한 페이지
| 이항 관계 | |
|---|---|
| 개요 | |
| 정의 | 두 집합의 원소 간의 관계 |
| 다른 이름 | 이항 관계 (二項關係) 2항 관계 다이애딕 관계 (dyadic relation) |
| 상세 정보 | |
| 예시 | '보다 큼' (>) '와 같다' (=) '의 약수이다' |
| 표현 | 집합의 데카르트 곱의 부분집합 |
| 형식적 정의 | 임의의 두 집합 A와 B의 데카르트 곱 A × B의 부분집합 R ⊆ A × B |
| n항 관계 | 'n'개의 집합 A1, ..., An의 데카르트 곱 A1 × ... × An의 부분집합 R ⊆ A1 × ... × An |
| 성질 | |
| 종류 | 대칭적 반대칭적 연결적 정초적 합류를 가짐 교차를 가짐 반사적 비반사적 비대칭적 |
| 관련 개념 | 동치 관계 준순서 부분 순서 전순서 엄격한 부분 순서 약한 순서 엄격한 전순서 격자 합류 반격자 교차 반격자 |
2. 정의
이항 관계는 집합(또는 클래스) 와 의 데카르트 곱 의 부분집합으로 정의된다.[56][57] 은 가 와 관계 을 가짐을 의미하며, 로 표기하기도 한다.[4][5][6]
이항 관계는 집합 연산(합집합, 교집합)과 합성, 역관계 등의 연산을 할 수 있다.
와 가 같은 집합일 때, 이항 관계는 동차 관계(또는 내부 관계)라고 불린다.[12][13] 와 가 다른 집합일 때, 이항 관계는 '''이종 관계'''라고도 불린다.[12][13][14]
이항 관계에서 원소의 순서는 중요하며, 만약 이면, 는 와 독립적으로 참 또는 거짓일 수 있다. 예를 들어, 3은 9를 나누지만, 9는 3을 나누지 않는다.
3. 연산
만약 과 가 집합 와 에 대한 이항 관계라면, 는 와 에 대한 과 의 합 관계이다. 항등원은 공집합 관계이다. 예를 들어, 는 <와 =의 합이고, 는 >와 =의 합이다.
만약 과 가 집합 와 에 대한 이항 관계라면, 는 와 에 대한 과 의 교집합 관계이다. 항등원은 전체 관계이다. 예를 들어, "6으로 나누어떨어진다"라는 관계는 "3으로 나누어떨어진다"와 "2로 나누어떨어진다"라는 관계의 교집합이다.
3. 1. 합성
이항 관계 와 의 '''합성''' 는 다음과 같이 정의된다.
:
즉, 은 이고 인 가 존재할 때 를 원소로 갖는 관계이다.
이항 관계의 합성은 결합 법칙을 만족시킨다.
:
이에 따라, 범주 을 다음과 같이 정의할 수 있다.
집합과 이항 관계의 범주 은 모든 작은 곱과 쌍대곱을 가지며, 둘 모두 분리합집합으로 주어진다.
또한, 이항 관계 의 거듭제곱을 다음과 같이 정의할 수 있다.
:
이에 대하여 다음 항등식들이 성립한다.
:
:
그 밖에도, 다음 항등식들이 성립한다.
:
:
만약 이 집합 와 에 대한 이항 관계이고, 가 집합 와 에 대한 이항 관계라면, (또한 로 표기)는 와 에 대한 과 의 합성 관계이다.
여기서 사용된 표기에서 과 의 순서는 함수의 합성에 대한 표준 표기 순서와 일치한다. 예를 들어, 합성 (부모이다)(어머니이다)는 (외조부모이다)를 생성하며, 반면 합성 (어머니이다)(부모이다)는 (할머니이다)를 생성한다. 전자의 경우, 만약 가 의 부모이고 가 의 어머니라면, 는 의 외조부모이다.
3. 2. 역관계
이항 관계 의 '''역관계''' 는 속 순서쌍의 두 성분을 뒤바꾼 이항 관계이다.
:
역관계는 자명하게 대합을 이룬다.
:
역관계와 합성은 다음과 같이 호환된다.
:
특히,
:
이다.
만약 이 집합 와 에 대한 이항 관계라면, 는 의 역관계이며, 이는 와 에 대한 관계이다.
예를 들어, 는 자기 자신의 역관계이며, 도 마찬가지이다. 그리고 와 는 서로의 역관계이며, 와 도 마찬가지이다. 이항 관계는 만약 대칭 관계일 때에만 역관계와 같다.
이 와 위의 이항 관계라면, 다음과 같은 와 위의 이항 관계가 정해진다.
; 역관계 inverse|인버스영어, converse|컨버스영어
: 어떤 집합 위의 이항 관계가 그 역관계와 일치하는 것은, 그 관계가 대칭적인 것과 동치이다.
3. 3. 정의역과 치역
이항 관계 R의 정의역(dom R)은 R에 속하는 순서쌍의 첫 번째 원소들의 집합이다.[57] 이항 관계 R의 치역(ran R)은 R에 속하는 순서쌍의 두 번째 원소들의 집합이다.[57]
정의역과 치역은 다음과 같이 표현된다.
여기서,
상(image)과 원상(preimage)은 정의역과 치역 개념의 확장이다.
임의의 이항 관계 에 대하여 다음이 성립한다.
:
:
:
:
:
4. 종류
이항 관계는 다양한 종류가 있으며, 크게 동차 관계와 이종 관계로 나눌 수 있다.
- 동차 관계: 반사 관계, 비반사 관계, 대칭 관계, 반대칭 관계, 비대칭 관계, 추이 관계, 연결 관계, 강한 연결 관계, 조밀 관계 등이 있다.
- 이종 관계: 단사, 함수 관계, 일대일, 일대다, 다대일, 다대다, 전체 관계, 전사 함수 등이 있다.
함수는 이항 관계의 중요한 유형 중 하나이지만, 모든 이항 관계가 함수는 아니다. 예를 들어, 약수 관계에서 5로 나누어지는 정수는 유일하지 않다.[23]
4. 1. 함수
함수는 이항 관계의 중요한 유형이다. 이항 관계 가 함수 일 필요충분조건은 다음 두 조건을 만족시키는 것이다.이항 관계는 일반적으로 함수가 아니다. 예를 들어 약수 관계에서, 5로 나누어지는 정수는 유일하지 않다.[23]
집합 와 에 대한 몇 가지 중요한 유형의 이항 관계 은 다음과 같다.
고유성 속성:
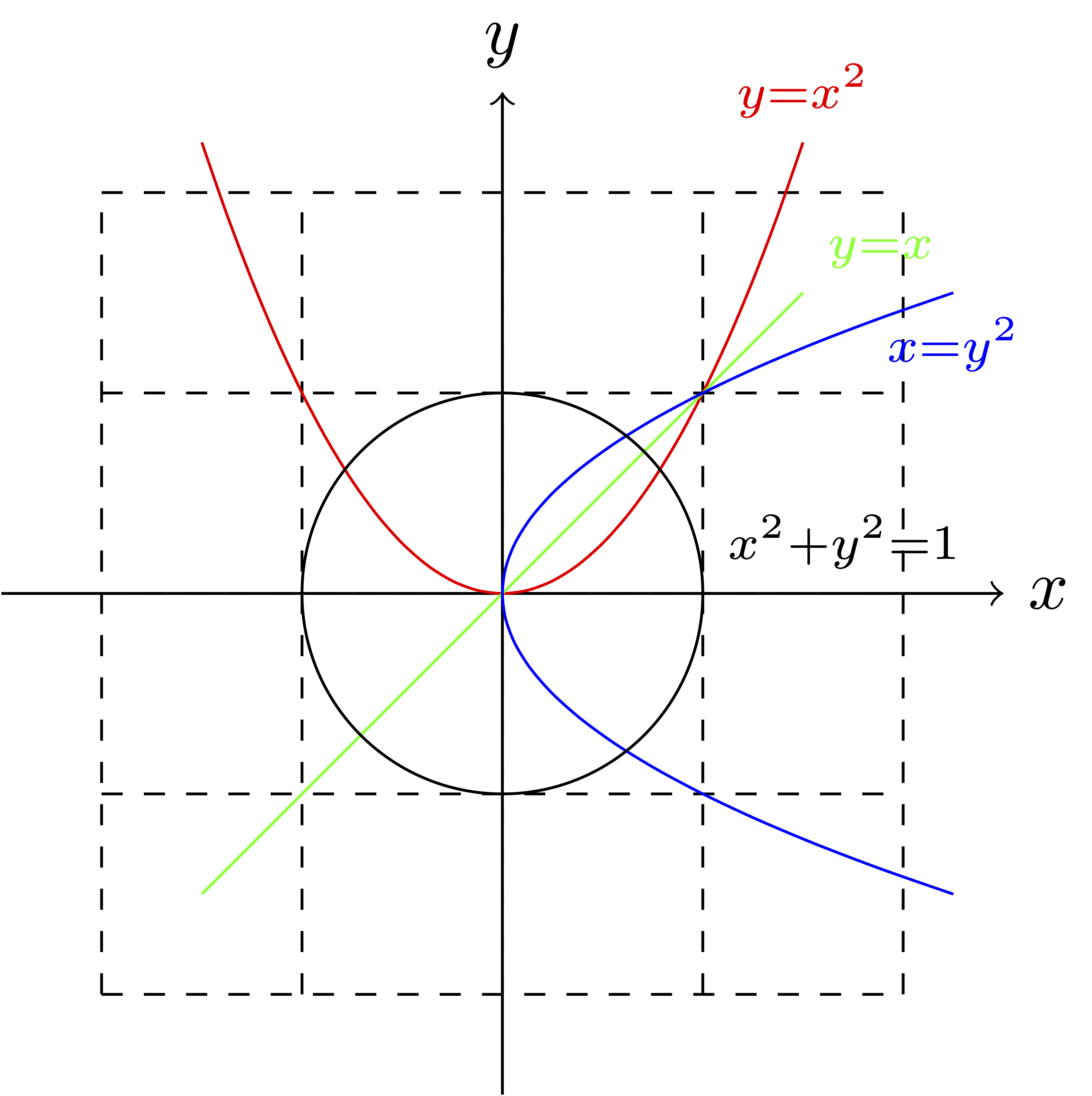
- '''함수 관계'''[23][25][26] ('''오른쪽 고유'''[24] 또는 '''단가'''[27]): 모든 와 모든 에 대해, 이고 이면 이다. 즉, 정의역의 모든 요소는 ''최대'' 하나의 상 요소를 갖는다. 이러한 이항 관계를 부분 함수 또는 부분 매핑이라고 한다.[28] 이러한 관계에 대해 는 의 기본 키라고 한다.[2] 예를 들어, 그림의 빨간색과 녹색 이항 관계는 함수 관계이지만, 파란색 관계는 (을 과 에 모두 연결하므로) 그렇지 않으며, 검은색 관계도 (을 과 에 모두 연결하므로) 그렇지 않다.
전체성 속성 (정의역 와 공역 가 지정된 경우에만 정의 가능):
- '''전체'''[23] ('''왼쪽 전체'''[24]): 모든 에 대해, 인 가 존재한다. 즉, 정의역의 모든 요소는 ''최소'' 하나의 상 요소를 갖는다. 즉, 의 정의역은 와 같다. 이 속성은 연결 관계의 정의와는 다르다(일부 저자는 전체라고도 함).[29] 이러한 이항 관계를 다중 값 함수라고 한다. 예를 들어, 그림의 빨간색과 녹색 이항 관계는 전체이지만, 파란색 관계는 (을 어떤 실수에도 연결하지 않으므로) 그렇지 않으며, 검은색 관계도 (를 어떤 실수에도 연결하지 않으므로) 그렇지 않다. 또 다른 예로, 는 정수에 대한 전체 관계이다. 그러나 양의 정수에는 인 가 없으므로, 양의 정수에 대한 전체 관계는 아니다.
고유성 및 전체성 속성 (정의역 와 공역 가 지정된 경우에만 정의 가능):
- '''함수''' ('''매핑'''[24]): 함수 관계이고 전체적인 이항 관계이다. 즉, 정의역의 모든 요소는 ''정확히'' 하나의 상 요소를 갖는다. 예를 들어, 그림의 빨간색과 녹색 이항 관계는 함수이지만, 파란색과 검은색 관계는 그렇지 않다.
4. 2. 동차 관계의 종류
- '''반사적''' 관계: 모든 에 대해 인 관계이다. 예를 들어, 는 반사 관계이지만, >는 그렇지 않다.
- '''비반사적''' 관계: 모든 에 대해 가 성립하지 않는 관계이다. 예를 들어, 는 비반사 관계이지만, 는 그렇지 않다.
- '''대칭적''' 관계: 모든 에 대해, 이면 인 관계이다. 예를 들어, "는 의 혈족이다"는 대칭 관계이다.
- '''반대칭적''' 관계: 모든 에 대해, 이고 이면 인 관계이다. 예를 들어, 는 반대칭 관계이다.[34]
- '''비대칭적''' 관계: 모든 에 대해, 이면 가 성립하지 않는 관계이다. 관계가 비대칭적일 필요충분조건은 반대칭적이면서 비반사적이어야 한다.[35] 예를 들어, >는 비대칭 관계이지만, 는 그렇지 않다.
- '''추이적''' 관계: 모든 에 대해, 이고 이면 인 관계이다. 추이 관계가 비반사적일 필요충분조건은 비대칭적이어야 한다.[36] 예를 들어, "는 의 조상이다"는 추이 관계인 반면, "는 의 부모이다"는 그렇지 않다.
- '''연결적''' 관계: 모든 에 대해, 이면 또는 인 관계이다.
- '''강하게 연결적''' 관계: 모든 에 대해, 또는 인 관계이다.
- '''조밀한''' 관계: 모든 에 대해, 이면, 이고 인 가 존재하는 관계이다.
4. 3. 이종 관계의 종류
집합 와 에 대한 이항 관계 은 다음과 같은 고유성 속성을 가질 수 있다.- '''단사'''(왼쪽 고유라고도 함): 의 임의의 원소 , 와 의 임의의 원소 에 대해, 이고 이면 이다. 즉, 공역의 모든 요소는 ''최대'' 하나의 원상 요소를 갖는다.[23] 이러한 관계에 대해 는 의 ''기본 키''라고 한다.[2]
- '''함수 관계'''(오른쪽 고유 또는 단가라고도 함): 의 임의의 원소 와 의 임의의 원소 , 에 대해, 이고 이면 이다. 즉, 정의역의 모든 요소는 ''최대'' 하나의 상 요소를 갖는다. 이러한 이항 관계를 부분 함수라고도 한다.[23][25][26][27][28] 이러한 관계에 대해 는 의 기본 키라고 한다.[2]
- '''일대일''': 단사이고 함수 관계이다.
- '''일대다''': 단사이지만 함수 관계는 아니다.
- '''다대일''': 함수 관계이지만 단사는 아니다.
- '''다대다''': 단사도 아니고 함수 관계도 아니다.
또한, 다음과 같은 전체성 속성을 가질 수 있다. (정의역 와 공역 가 지정된 경우에만 정의 가능)
- '''전체'''(왼쪽 전체라고도 함): 의 모든 원소 에 대해, 인 가 에 존재한다. 즉, 정의역의 모든 요소는 ''최소'' 하나의 상 요소를 갖는다. 이러한 이항 관계를 다중 값 함수라고 한다.[23]
- '''전사'''(오른쪽 전체라고도 함): 의 모든 원소 에 대해, 인 가 에 존재한다. 즉, 공역의 모든 요소는 ''최소'' 하나의 원상 요소를 갖는다.[23][24]
고유성과 전체성 속성을 조합하여 다음과 같은 관계를 정의할 수 있다.
- '''함수''': 함수 관계이고 전체인 이항 관계이다. 즉, 정의역의 모든 요소는 ''정확히'' 하나의 상 요소를 갖는다.
- '''단사 함수''': 단사인 함수이다.
- '''전사 함수''': 전사인 함수이다.
- '''전단사 함수''': 단사이고 전사인 함수이다. 즉, 정의역의 모든 요소는 ''정확히'' 하나의 상 요소를 가지며, 공역의 모든 요소는 ''정확히'' 하나의 원상 요소를 갖는다.
5. 성질
집합론적 관점에서 특정 관계(같음, 부분집합, 원소)는 이항 관계로 정의될 수 없는 경우가 있다. 왜냐하면 그들의 정의역과 공역이 일반적인 공리적 집합론 체계에서 집합으로 간주될 수 없기 때문이다. 예를 들어, 일반적인 "같음"의 개념을 이항 관계 로 모델링하려면, 정의역과 공역을 "모든 집합의 클래스"로 설정해야 하는데, 이것은 일반적인 집합론에서는 집합이 아니다.[31] 이 문제에 대한 일반적인 해결책은 "충분히 큰" 집합 를 선택하고, 대신 제한된 를 사용하는 것이다.
동차 관계는 유향 그래프로 표현될 수 있다.
관계 미적분은 이항 관계의 연산을 다루는 수학 분야이다. 관계의 합성과 역관계의 사용으로 확장된다.
유도된 개념 격자는 이항 관계를 분석하는 데 사용된다. 주어진 관계 에 대해, 조인과 만남에 의해 확장된 개념 집합은 "유도된 개념 격자"를 형성하며, 포함 은 전순서를 형성한다.
디펑셔널 관계, 페레 타입 관계, 접촉 관계 등 특수한 관계들이 존재한다.
- '''디펑셔널 관계''': 동치 관계의 일반화로서, 구별되는 속성으로 객체를 분할한다. 자크 리게는 이 관계들을 '''디펑셔널'''이라고 명명했다.[41]
- '''페레 타입 관계''': 자크 리고는 일반적인 이진 관계로 순서를 확장하기 위해 페르 다이어그램이라고 하는 정수 분할의 순서를 채택했다.[47]
- '''접촉 관계''': 게오르그 아우만에 의해 도입되었다.[49][50]
이항 관계의 종류와 그 성질은 다음 표와 같다.
| 이항 관계 | 반사적 | 대칭적 | 추이적 | 자주 사용되는 기호 | 예 |
|---|---|---|---|---|---|
| 유향 그래프 | → | ||||
| 무향 그래프 | |||||
| 토너먼트 | 상하 관계 (찌르기 순서) | ||||
| dependency relation|종속 관계영어 | |||||
| weak order|약한 순서영어 | ≤ | ||||
| 전순서 | ≤ | 선호 순서 (선호 관계의 일종) | |||
| 반순서 | ≤ | 포함 관계 | |||
| partial equivalence relation|반동치영어 | |||||
| 동치 관계 | ∼, ≅, ≈, ≡ | 항등 관계 | |||
| strict partial order|강한 반순서영어 | < | 진 부분 집합 관계 |
참조
[1]
웹사이트
MIT 6.042J Math for Computer Science, Lecture 3T, Slide 2
https://ocw.mit.edu/[...]
2021-11-17
[2]
논문
A Relational Model of Data for Large Shared Data Banks
https://www.seas.upe[...]
2020-04-29
[3]
웹사이트
Relation definition – Math Insight
https://mathinsight.[...]
2019-12-11
[4]
서적
Algebra und Logic der Relative
https://archive.org/[...]
Internet Archive
1895
[5]
서적
A Survey of Symbolic Logic
https://archive.org/[...]
internet Archive
1918
[6]
서적
Relational Mathematics
Cambridge University Press
2010
[7]
서적
1977
[8]
서적
Introduction to Mathematical Logic
Springer
[9]
서적
Axiomatic Set Theory
https://archive.org/[...]
Dover
[10]
서적
Set Theory and the Continuum Problem
Dover
[11]
서적
Basic Set Theory
Dover
[12]
서적
Relations and Graphs: Discrete Mathematics for Computer Scientists
https://books.google[...]
Springer Science & Business Media
2012
[13]
서적
Encyclopedia of Optimization
https://books.google[...]
Springer Science & Business Media
[14]
서적
Goguen Categories: A Categorical Approach to L-fuzzy Relations
Springer
[15]
서적
Heterogeneous relation algebra
Springer books
1997
[16]
서적
Basic Algebra II (2nd ed.)
https://books.google[...]
2009
[17]
서적
Modern Applied Algebra
McGraw-Hill
1970
[18]
서적
Modern Algebra: Structure and Method
Houghton Mifflin
1962
[19]
뉴스그룹
quantum mechanics over a commutative rig
https://groups.googl[...]
2018-11-25
[20]
간행물
Semirings and Formal Power Series
2009
[21]
위키북스
Relative simultaneity
https://en.wikibooks[...]
[22]
서적
Design Theory
Cambridge University Press
[23]
서적
1990
[24]
서적
2000
[25]
웹사이트
Functional relation - Encyclopedia of Mathematics
https://encyclopedia[...]
2024-06-13
[26]
웹사이트
functional relation in nLab
https://ncatlab.org/[...]
2024-06-13
[27]
서적
2010
[28]
서적
2000
[29]
논문
Generalization of rough sets using relationships between attribute values
http://www2.cs.uregi[...]
[30]
서적
Set theory: an introduction to independence proofs
https://archive.org/[...]
North-Holland
[31]
서적
A formalization of set theory without variables
https://archive.org/[...]
American Mathematical Society
[32]
서적
Relational Knowledge Discovery
Cambridge University Press
[33]
서적
Mathematical Foundations of Computational Engineering: A Handbook
Springer Science & Business Media
[34]
서적
A Transition to Advanced Mathematics
Brooks/Cole
[35]
서적
Foundations of Logic and Mathematics: Applications to Computer Science and Cryptography
https://books.google[...]
Springer-Verlag
[36]
서적
Transitive Closures of Binary Relations I
https://web.archive.[...]
School of Mathematics – Physics Charles University
[37]
서적
Linear orderings
Academic Press
[38]
간행물
Decomposition of relations on concept lattices
[39]
서적
Boolean Matrix Theory and Applications
Marcel Dekker
[40]
서적
Data mining, reasoning and incremental information retrieval through non enlargeable rectangular relation coverage
Springer
[41]
논문
Quelques proprietes des relations difonctionelles
https://gallica.bnf.[...]
1950-01
[42]
서적
Finite Automata, Their Algebras and Grammars: Towards a Theory of Formal Expressions
Springer Science & Business Media
[43]
논문
Ranks of ideals in inverse semigroups of difunctional binary relations
2018-02
[44]
서적
Relational Methods in Computer Science
Springer Science & Business Media
[45]
서적
Databases
Springer Science & Business Media
[46]
서적
Coalgebraic Methods in Computer Science
[47]
논문
Les relations de Ferrers
[48]
서적
Relations and Graphs: Discrete Mathematics for Computer Scientists
https://books.google[...]
Springer Science & Business Media
[49]
논문
Kontakt-Relationen
https://www.zobodat.[...]
[50]
리뷰
Review: Kontakt-Relationen
https://mathscinet.a[...]
[51]
문서
[52]
서적
Relational Mathematics
Cambridge University Press
[53]
논문
The theory of generalised heaps and generalised groups
[54]
서적
Wagner's Theory of Generalised Heaps
Springer books
[55]
서적
Mathematics across the Iron Curtain: a history of the algebraic theory of semigroups
American Mathematical Society
[56]
서적
Set theory
https://archive.org/[...]
Springer
2003
[57]
서적
Set theory
College Publications
2011
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com