정상파

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정상파의 특징
- 2.1. 공간적 특징
- 2.2. 시간적 특징
3. 정상파의 발생 조건
4. 정상파의 수학적 표현
- 4.1. 진행파의 표현
- 4.2. 정상파의 표현
5. 정상파의 종류 및 활용
참조

1. 개요

정상파는 동일한 진동수, 파장, 진폭을 가진 두 파동이 서로 반대 방향으로 진행하면서 중첩되어 형성되는 파동이다. 정상파는 각 지점이 같은 위상과 주기로 진동하며, 마디(진폭 0)와 배(진폭 최대)가 파장의 절반 간격으로 나타난다. 정상파는 반사, 제한된 공간, 폐곡선 등 다양한 조건에서 발생하며, 현의 진동, 관악기의 공명, 2차원 표면에서의 파동, 3차원 광학 매질 등 다양한 물리적 현상에서 관찰된다. 정상파는 악기 제작, X선 현미경, 기상 현상, 강 서핑 등 다양한 분야에 활용된다.

더 읽어볼만한 페이지

파동 - 진동수
진동수는 주기적인 현상이 단위 시간당 반복되는 횟수를 나타내는 물리량으로, 주기와 역수 관계를 가지며 소리의 높낮이, 빛의 색깔 등을 결정하는 중요한 요소이다.
파동 - 전파
전파는 전기장과 자기장의 결합으로 공간을 통해 이동하는 전자기파의 일종으로, 통신, 방송 등 다양한 분야에서 활용되며, 파장에 따라 분류되고, 열적 및 비열적 효과를 가지며 생물학적 영향을 미칠 수 있다.
표시 이름과 문서 제목이 같은 위키공용분류 - 라우토카
라우토카는 피지 비치레부섬 서부에 위치한 피지에서 두 번째로 큰 도시이자 서부 지방의 행정 중심지로, 사탕수수 산업이 발달하여 "설탕 도시"로 알려져 있으며, 인도에서 온 계약 노동자들의 거주와 미 해군 기지 건설의 역사를 가지고 있고, 피지 산업 생산의 상당 부분을 담당하는 주요 기관들이 위치해 있다.
표시 이름과 문서 제목이 같은 위키공용분류 - 코코넛
코코넛은 코코넛 야자나무의 열매로 식용 및 유지로 사용되며, 조리되지 않은 과육은 100g당 354kcal의 열량을 내는 다양한 영양 성분으로 구성되어 있고, 코코넛 파우더의 식이섬유는 대부분 불용성 식이섬유인 셀룰로오스이며, 태국 일부 지역에서는 코코넛 수확에 훈련된 원숭이를 이용하는 동물 학대 문제가 있다.
한국어 위키백과의 링크가 위키데이터와 같은 위키공용분류 - 라우토카
라우토카는 피지 비치레부섬 서부에 위치한 피지에서 두 번째로 큰 도시이자 서부 지방의 행정 중심지로, 사탕수수 산업이 발달하여 "설탕 도시"로 알려져 있으며, 인도에서 온 계약 노동자들의 거주와 미 해군 기지 건설의 역사를 가지고 있고, 피지 산업 생산의 상당 부분을 담당하는 주요 기관들이 위치해 있다.
한국어 위키백과의 링크가 위키데이터와 같은 위키공용분류 - 코코넛
코코넛은 코코넛 야자나무의 열매로 식용 및 유지로 사용되며, 조리되지 않은 과육은 100g당 354kcal의 열량을 내는 다양한 영양 성분으로 구성되어 있고, 코코넛 파우더의 식이섬유는 대부분 불용성 식이섬유인 셀룰로오스이며, 태국 일부 지역에서는 코코넛 수확에 훈련된 원숭이를 이용하는 동물 학대 문제가 있다.

정상파
파동의 종류
분야	물리학
매질의 유무	무관
파동의 진행	진행하지 않음 (정지)
에너지 전달	에너지 전달 없음
특징
진동	특정 위치에서 진폭이 최대 또는 최소인 점이 존재함.
마디	진폭이 항상 0인 지점 (변위가 없는 곳)
배	진폭이 최대인 지점
파장	인접한 두 마디 사이의 거리의 2배
발생 조건	양 끝이 고정된 줄 관악기 내부
간섭 현상	진행 방향이 반대인 두 파동의 간섭에 의해 발생
활용
악기	현악기, 관악기
통신	마이크로파 공진기

2. 정상파의 특징

동일한 진폭과 주파수를 가진 두 파동이 서로 반대 방향으로 진행하며 중첩될 때, 파동이 마치 공간적으로 이동하지 않고 제자리에서 진동하는 것처럼 보이는 현상을 정상파라고 한다. 이는 주로 파동이 매질의 경계면에서 반사되어 되돌아오는 파동과 원래 진행하던 파동이 간섭을 일으킬 때 발생한다.

정상파의 가장 두드러진 특징은 공간적으로 고정된 지점들이 나타난다는 것이다. 매질 내에서 전혀 진동하지 않아 변위가 항상 0인 지점을 '''마디(node)'''라 하고, 진폭이 최대가 되어 가장 크게 진동하는 지점을 '''배(antinode)'''라고 한다.^[36] 마디와 배는 서로 엇갈려 나타나며, 인접한 마디 사이 또는 인접한 배 사이의 거리는 원래 파동의 파장 (λ)의 절반(λ/2)이다. 또한 인접한 마디와 배 사이의 거리는 파장의 1/4(λ/4)이다.

정상파가 형성되면 매질의 각 점은 그 위치에 따라 정해진 고유한 진폭으로 단진동하며, 모든 점(마디 제외)은 같은 주기로 진동한다. 인접한 마디 사이의 모든 점들은 같은 위상으로 진동하지만, 마디를 건너뛰면 위상이 180° 반대가 된다.

이상적인 순수 정상파는 에너지를 한 지점에서 다른 지점으로 전달하지 않는다.^[17] 파동 에너지는 마디와 배 사이에 갇혀 진동하는 형태로 존재한다. 그러나 실제 상황에서는 매질의 손실이나 불완전한 반사 등으로 인해 완벽한 정상파가 형성되기 어렵다. 이 경우 진행파 성분이 일부 남아있는 '''부분 정상파'''가 형성되며, 진행파와 정상파의 비율은 정재파비(SWR, Standing Wave Ratio)라는 값으로 나타낸다.^[9] SWR이 무한대에 가까우면 순수 정상파에 가깝고, SWR이 1이면 순수 진행파를 의미한다.^[16]

정상파는 다양한 물리 현상에서 관찰된다. 예를 들어, 악기의 현이나 관 내부의 공기 기둥에서 발생하는 소리, 전송선로에서의 전자기파^[8], 레이저 광 공진기 내부의 빛^[20], 특정 조건 하의 강 급류^[7], 호수의 잔잔호^[28]^[29] 등이 정상파의 예이다. 심지어 X선 간섭을 이용한 원자 규모 측정^[21]에도 정상파 원리가 활용된다.

카멜 강의 하구 - 카멜 강이 태평양과 만나는 곳에서 정상파가 형성된다.

2. 1. 공간적 특징

정상파에서 매질의 각 지점은 시간에 따라 진동하지만, 그 진폭은 위치에 따라 다르게 나타난다. 이러한 공간적인 진폭 분포가 정상파의 중요한 특징을 만든다.

'''마디(Node)''': 매질에서 전혀 진동하지 않아 변위가 항상 0인 지점을 마디라고 한다.^[36] 마디는 파동의 간섭 결과 진폭이 상쇄되어 0이 되는 곳이다. 마디는 일정한 간격으로 나타나며, 그 간격은 파동의 반 파장(λ/2)과 같다. 수학적으로 마디의 위치 ''x''는 다음과 같은 조건을 만족한다. (단, 파동이 $y(x,t) = 2y_\text{max}\sin \left({2\pi x \over \lambda} \right) \cos(\omega t)$ 형태로 표현될 경우)

:

x = \ldots, -{3\lambda \over 2}, \; -\lambda, \; -{\lambda \over 2}, \; 0, \; {\lambda \over 2}, \; \lambda, \; {3\lambda \over 2}, \ldots = \frac{n\lambda}{2}

(여기서 ''n''은 정수)

'''배(Antinode)''': 매질에서 진폭이 최대가 되어 가장 크게 진동하는 지점을 배라고 한다.^[36] 배는 파동의 보강 간섭이 최대로 일어나는 곳이다. 배 역시 반 파장(λ/2) 간격으로 나타나며, 위치상으로는 마디와 마디 사이에 존재한다. 배의 위치 ''x''는 다음과 같은 조건을 만족한다.

:

x = \ldots, -{5\lambda \over 4}, \; -{3\lambda \over 4}, \; -{\lambda \over 4}, \; {\lambda \over 4}, \; {3\lambda \over 4}, \; {5\lambda \over 4}, \ldots = \frac{(2n+1)\lambda}{4}

(여기서 ''n''은 정수)

'''진폭의 공간적 변화''': 정상파가 형성된 매질 내의 각 점은 그 위치에 따라 고유한 진폭을 가지고 단진동한다. 마디에서는 진폭이 0이고, 배에서는 진폭이 최대가 된다. 배에서의 최대 진폭은 정상파를 만든 원래 두 파동의 진폭(''y''_max 또는 ''A'')을 합한 값, 즉 2''y''_max (또는 2''A'')가 된다. 위치 ''x''에서의 진폭 ''A_x''는 일반적으로 다음과 같이 표현될 수 있다. (파동 형태와 위상차 $\delta_1, \delta_2$ 에 따라 sin 또는 cos 함수로 표현됨)

:

A_x = \left| 2y_\text{max}\sin \left({2\pi x \over \lambda} \right) \right|

또는

A_x = \left| 2A\cos\left(kx-\frac{\delta_1-\delta_2}{2}\right) \right|

(여기서

k = 2\pi/\lambda

는 파수)

'''마디와 배의 간격''':
인접한 마디와 마디 사이의 거리는 반 파장(λ/2)이다.
인접한 배와 배 사이의 거리도 반 파장(λ/2)이다.
인접한 마디와 배 사이의 거리는 1/4 파장(λ/4)이다.

'''위상 관계''': 정상파 내에서 진동하는 모든 점들은 (마디를 제외하고) 같은 위상 또는 정반대의 위상으로 진동한다. 즉, 모든 점들은 동시에 평형점(변위 0)을 지나고, 동시에 최대 변위에 도달한다. 인접한 두 마디 사이의 모든 점들은 같은 위상으로 진동하며, 한 마디를 건너뛴 다음 영역의 점들과는 반대 위상으로 진동한다. 각 점의 진동 주기는 원래 파동의 주기와 같다.

2. 2. 시간적 특징

정상파를 구성하는 매질의 각 점은 같은 위상과 주기를 가지고 단진동한다. 이는 정상파의 방정식

y(x,t) = 2y_\text{max}\sin \left({2\pi x \over \lambda} \right) \cos(\omega t)

또는 보다 일반적인 형태인

y=2A\sin\left(\omega t+\dfrac{\delta_1+\delta_2}{2}\right)\cos\left(kx-\dfrac{\delta_1-\delta_2}{2}\right)

에서 시간 항

\sin\left(\omega t+\dfrac{\delta_1+\delta_2}{2}\right)

또는

\cos(\omega t)

가 위치 x에 의존하지 않기 때문이다. 따라서 모든 점은 동시에 같은 움직임을 보인다.

이러한 동위상 진동 때문에 모든 점의 변위가 동시에 0이 되는 시각과, 모든 점의 변위가 동시에 각자의 최대값(위치에 따라 다름)에 도달하는 시각이 존재한다.

또한, 각 점의 진동 주기 τ는 정상파를 만드는 원래 진행파의 주기 T와 같다. 이는 정상파의 각 주파수 ω가 원래 파동의 각 주파수와 동일하기 때문이다 (

\tau = 2\pi/\omega = T

).

3. 정상파의 발생 조건

정상파는 서로 반대 방향으로 진행하는 동일한 주파수와 진폭을 가진 두 파동이 중첩될 때 발생하는 현상으로, 파동이 마치 이동하지 않고 제자리에서 진동하는 것처럼 보인다. 이러한 정상파는 다양한 조건과 상황에서 발생할 수 있다.

주요 발생 조건 및 예시는 다음과 같다.

반사: 파동이 매질의 경계면이나 장애물에서 반사될 때, 입사파와 반사파의 간섭으로 형성된다. (하위 섹션에서 상세 설명)
제한된 공간: 현이나 관과 같이 경계가 있는 매질 내에서 파동이 반복적으로 반사되며 형성된다. (하위 섹션에서 상세 설명)
폐곡선 경로: 닫힌 경로를 따라 파동이 반대 방향으로 진행하여 만날 때 특정 조건에서 형성된다. (하위 섹션에서 상세 설명)
자연 현상:
대기: 특정 기상 조건 하에서 산맥의 리 지역 대기 중에 정상파가 형성될 수 있으며, 이는 글라이더 조종사들이 상승 기류로 활용하기도 한다.
수면파: 급류나 솔트스트라우멘과 같은 강한 조류가 흐르는 곳에서 수리 수면 도약과 함께 정상파가 형성될 수 있다. 이는 물의 흐름이 특정 속도(프루드 수 1.7–4.5 이상^[7]) 이상으로 빠르게 흐르다가 장애물을 만나거나 속도가 변할 때 발생한다. 이러한 강의 정상파는 강 서핑 장소로 이용되기도 한다.

해양파: 바다에서는 폭풍 중심 근처나 해안에서 파도가 반사되어 서로 반대 방향으로 진행하는 파동이 중첩되면서 정상파가 형성될 수 있다. 이는 미소기압이나 미소지진의 원인이 되기도 한다.
전송선로: 전기 신호가 전송선로를 따라 진행하다가 끝부분에서 임피던스 불일치(예: 개방 회로 또는 단락 회로)로 인해 반사될 때, 전류, 전압, 또는 전계 세기의 정상파가 발생할 수 있다.^[8] 실제로는 전송선로나 부품의 손실 때문에 완벽한 반사가 일어나기 어려워, 순수한 정상파보다는 진행파 성분이 일부 섞인 '부분 정상파'가 형성되는 경우가 많다. 이러한 정상파의 정도는 정재파비(SWR)로 측정한다.^[9]

이처럼 정상파는 파동의 반사, 매질의 경계 조건, 특정 자연 현상 등 다양한 원인에 의해 발생하며, 물리학의 여러 분야와 실생활에서 관찰될 수 있다.

3. 1. 반사파

정상파를 발생시키는, 서로 다른 방향으로 진행하는 두 개의 파동은 대부분 동일한 파원에서 나온다.^[36] 이는 자연적으로 같은 진폭과 진동수를 가진 두 개의 독립된 파원이 존재하기 어렵고, 설령 존재하더라도 두 파원으로부터 거리가 다른 지점에서는 파동의 감쇠 때문에 진폭이 달라져 정상파가 만들어지기 어렵기 때문이다.

하나의 파원에서 나온 파동이 정상파를 만드는 일반적인 방법은 반사를 이용하는 것이다. 파동이 진행 방향에 수직인 면(예: 벽)에서 반사되면, 원래의 파동인 '''입사파'''와 진행 방향이 반대인 '''반사파'''가 생긴다. 이 입사파와 반사파가 간섭하여 중첩되면 정상파가 발생한다. 여기서 파동의 진행 방향에 수직인 면은 곧 파면을 의미하므로, 파면과 같은 형태의 반사면을 만들면 정상파를 효과적으로 생성할 수 있다.

반사를 이용하면 1차원 파동이나 평면파뿐만 아니라 다른 형태의 파동으로도 정상파를 만들 수 있다. 예를 들어, 3차원 구면파의 경우 파원을 중심으로 하는 구면 형태의 벽을 이용하고, 3차원 원통파는 파원 축을 중심으로 하는 원통면을, 2차원의 원형파는 파원을 중심으로 하는 원형 울타리를 이용하여 각각 정상파를 생성할 수 있다.

3. 2. 제한된 공간

파동이 현악기의 줄이나 관악기의 관 내부처럼 제한된 공간을 진행할 때, 파동은 공간의 경계(끝)에서 반사된다. 이렇게 서로 반대 방향으로 진행하는 동일한 두 파동이 간섭하여 중첩되면, 파동의 특정 지점은 전혀 움직이지 않고 다른 지점은 최대로 진동하는 것처럼 보이는 정상파가 만들어진다. 이때 매질의 분자가 정지해 있는 것처럼 보이는 지점을 마디(node)라 하고, 가장 크게 진동하는 지점을 배(antinode)라고 한다.^[36] 정상파가 형성될 수 있는 조건은 매질의 경계 조건에 따라 결정된다.

=== 1차원 정상파: 현 ===

길이가 ''L''인 팽팽한 현에서의 정상파를 생각해 보자.

==== 양 끝이 고정된 현 ====

기타나 바이올린의 줄처럼 양 끝($x=0$ 및 $x=L$)이 고정된 현의 경우, 파동은 양 끝에서 반사된다. 정상 상태에 도달하면, 현의 양 끝은 움직일 수 없으므로 항상 마디가 되어야 한다. 즉, 변위 ''y''는 $x=0$과 $x=L$에서 항상 0이어야 한다 ($y(0,t)=0$, $y(L,t)=0$).

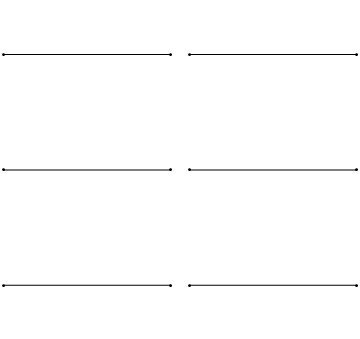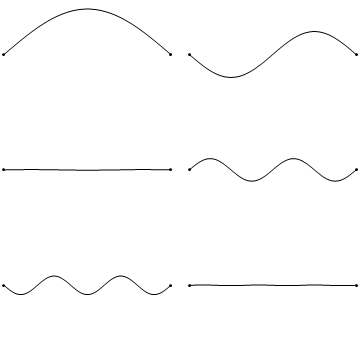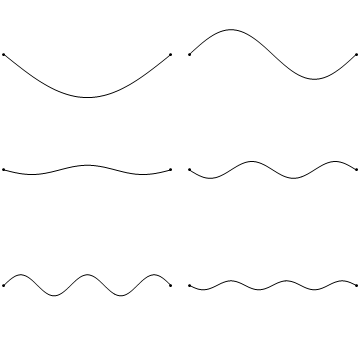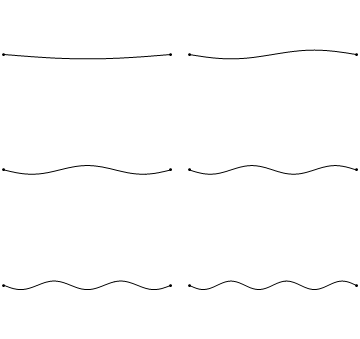
이 경계 조건을 만족시키기 위해서는 현의 길이 ''L''이 반파장($\lambda/2$)의 정수배가 되어야 한다.

:

L = n \frac{\lambda}{2}, \quad n = 1, 2, 3, \ldots

따라서 정상파를 형성할 수 있는 파장 ''λ''는 다음과 같이 제한된다.

:

\lambda_n = \frac{2L}{n}

파동의 속도를 ''v''라고 할 때, 허용되는 진동수 ''f'' (고유진동수)는 다음과 같다.

:

f_n = \frac{v}{\lambda_n} = \frac{nv}{2L}, \quad n = 1, 2, 3, \ldots

여기서 ''n''은 양의 정수이다.

''n'' = 1일 때 가장 낮은 진동수 $f_1 = v/2L$를 기본 진동수 또는 기본음이라고 하며, 이때 파장은 $\lambda_1 = 2L$이다. 이 모드에서는 양 끝만 마디이고 중앙이 배가 된다.
''n'' = 2, 3, ... 일 때의 진동수 $f_n = n f_1$는 배음 또는 배진동이라고 한다. ''n''차 배음의 정상파는 양 끝을 포함하여 총 ''n''+1개의 마디와 ''n''개의 배를 가진다.

이러한 특정 진동수에서만 정상파가 안정적으로 형성되는데, 이를 공진이라고 하며 해당 진동수를 공진 주파수라고 한다.^[10]

==== 한쪽 끝은 고정, 다른 쪽 끝은 자유로운 현 ====

한쪽 끝($x=0$)은 고정되어 마디가 되고, 다른 쪽 끝($x=L$)은 자유롭게 움직일 수 있어 배가 되는 경우를 생각해 보자. 예를 들어, 현의 한쪽 끝이 마찰 없이 움직이는 고리에 연결된 경우이다.

이 경우 경계 조건은 $y(0,t)=0$이고, $x=L$에서는 변위가 최대가 되어야 한다(배). 즉, $x=L$에서 변위 곡선의 기울기가 0이어야 한다 ($\partial y / \partial x = 0$ at $x=L$).

이 경계 조건을 만족시키려면 현의 길이 ''L''이 1/4 파장($\lambda/4$)의 홀수배가 되어야 한다.

:

L = n \frac{\lambda}{4}, \quad n = 1, 3, 5, \ldots

따라서 허용되는 파장 ''λ''는 다음과 같다.

:

\lambda_n = \frac{4L}{n}, \quad n = 1, 3, 5, \ldots

허용되는 진동수 ''f''는 다음과 같다.

:

f_n = \frac{v}{\lambda_n} = \frac{nv}{4L}, \quad n = 1, 3, 5, \ldots

이 경우 ''n''은 홀수만 가능하다.

''n'' = 1일 때 기본 진동수는 $f_1 = v/4L$이고, 파장은 $\lambda_1 = 4L$이다. 이 모드는 고정된 끝($x=0$)에서 마디, 자유로운 끝($x=L$)에서 배를 가진다.
''n'' = 3, 5, ... 일 때의 진동수는 홀수 배음만 존재하며, $f_n = n f_1$이다. 예를 들어, 첫 번째 배음(n=3)은 $f_3 = 3v/4L$이다.

=== 1차원 정상파: 관 (음파) ===

관 속의 공기 기둥에서도 음파 (종파)의 정상파가 형성될 수 있다. 이때는 공기 분자의 변위 또는 압력 변화를 기준으로 정상파를 기술할 수 있다. 일반적으로 압력 변화를 기준으로 설명하는 것이 편리하다.

관의 열린 끝: 외부 대기와 연결되어 압력이 대기압으로 거의 일정하게 유지되므로 압력 마디(pressure node)가 된다. (공기 분자의 움직임은 자유로우므로 변위 배(displacement antinode)가 된다.)
관의 닫힌 끝: 공기 분자의 움직임이 막혀 변위가 0이 되므로 변위 마디(displacement node)가 된다. 이곳에서는 공기가 최대로 압축되거나 팽창하므로 압력 배(pressure antinode)가 된다.^[11]

==== 양 끝이 열린 관 ====

플루트나 리코더처럼 양 끝($x=0$ 및 $x=L$)이 모두 열린 관의 경우, 양 끝 모두 압력 마디가 된다. 이는 양 끝이 고정된 현의 경우와 수학적으로 동일한 경계 조건이다.

따라서 허용되는 파장과 진동수는 다음과 같다.

:

\lambda_n = \frac{2L}{n}, \quad f_n = \frac{nv}{2L}, \quad n = 1, 2, 3, \ldots

여기서 ''v''는 관 속에서의 음속이다. 양 끝이 열린 관은 기본 진동수와 모든 정수배의 배음을 가진다.

==== 한쪽 끝은 닫히고 다른 쪽 끝은 열린 관 ====

클라리넷이나 한쪽 끝을 막은 병과 같이 한쪽 끝($x=0$)은 열려 있고 다른 쪽 끝($x=L$)은 닫힌 관의 경우, 열린 끝은 압력 마디, 닫힌 끝은 압력 배가 된다. 이는 한쪽 끝은 고정되고 다른 쪽 끝은 자유로운 현의 경우와 유사한 경계 조건이다.

따라서 허용되는 파장과 진동수는 다음과 같다.

:

\lambda_n = \frac{4L}{n}, \quad f_n = \frac{nv}{4L}, \quad n = 1, 3, 5, \ldots

이 경우 ''n''은 홀수만 가능하므로, 기본 진동수($f_1 = v/4L$)와 홀수 배음만 존재한다.

==== 양 끝이 닫힌 관 ====

양 끝이 모두 닫힌 관의 경우, 양 끝 모두 압력 배가 된다 (변위 마디). 이 경우 허용되는 파장과 진동수는 양 끝이 열린 관과 동일하다.

:

\lambda_n = \frac{2L}{n}, \quad f_n = \frac{nv}{2L}, \quad n = 1, 2, 3, \ldots

다만 마디와 배의 위치가 양 끝이 열린 관과 비교하여 $\lambda/4$만큼 이동한다. 예를 들어, 기본 모드($n=1$)에서는 양 끝이 압력 배이고 관의 중앙($x=L/2$)에 압력 마디가 생긴다. 루벤스 관은 이러한 관 속 정상파의 압력 변화를 시각적으로 보여주는 장치이다.^[13]

=== 고유진동수와 공진 ===

위에서 살펴본 것처럼, 현이나 관과 같이 경계가 있는 매질에서는 특정 파장과 진동수의 파동만이 안정적인 정상파를 형성할 수 있다. 이렇게 정상파를 형성할 수 있는 고유한 진동수를 고유진동수라고 한다. 고유진동수 중에서 가장 작은 값을 기본 진동수라고 하며, 악기 소리의 기본음을 결정한다.

외부에서 가해지는 진동수가 물체의 고유진동수와 일치할 때, 파동의 진폭이 매우 커지는 현상을 공진 또는 공명이라고 한다. 악기는 이러한 공진 현상을 이용하여 소리를 증폭시킨다. 고유진동수는 매질의 길이, 장력(현의 경우), 밀도, 온도(음속에 영향) 및 경계 조건(양 끝이 고정/자유/열림/닫힘)에 따라 달라진다.

3. 3. 폐곡선

정상파를 만드는, 서로 반대 방향으로 진행하는 두 파동은 보통 같은 파원에서 나온다. 자연적으로 동일한 진폭과 진동수를 가진 두 개의 다른 파원이 존재하기는 어렵고, 설령 존재하더라도 파원에서 거리가 달라지면 파동의 감쇠 정도가 달라져 진폭이 달라지기 때문에 일반적인 환경에서는 정상파가 잘 생기지 않는다.

하지만 특정한 조건에서는 하나의 파원에서 나온 파동이 반사되거나 경로가 나뉘어 다시 만나면서 정상파를 형성할 수 있다. 그중 하나가 폐곡선, 즉 원형처럼 닫힌 경로를 따라 파동이 진행하는 경우다.

예를 들어, 고무줄처럼 길고 가는 물체를 원형으로 연결한 폐곡선 위에서 파동을 만들면, 파동은 양방향으로 퍼져나간다. 이 두 파동은 폐곡선을 따라 계속 진행하다가 서로 반대 방향에서 만나 간섭하게 된다. 이때, 폐곡선의 전체 길이 ''L''이 파장 ''λ''의 자연수 배, 즉 ''n''배 (n = 1, 2, 3, ...)가 될 때, 각 지점에서 파동의 위상이 일정하게 유지되어 안정적인 정상파가 만들어진다. 이 조건을 만족하는 파장 ''λ_n''은 다음과 같다.

:

\lambda_n = \frac{L}{n}

(여기서 ''n''은 1 이상의 정수)

따라서 이 특정 파장 ''λ_n''을 가진 파동만이 폐곡선 위에서 정상파를 형성할 수 있다. 파동의 속도를 ''c'', 진동수를 ''ν''라고 할 때, 파동의 기본 관계식인 ''c'' = ''νλ''를 이용하면 정상파를 만드는 특정 진동수 ''ν_n''을 구할 수 있다.

:

\nu_n = \frac{c}{\lambda_n} = \frac{nc}{L}

이렇게 폐곡선 위에서 정상파를 형성할 수 있는 특정 진동수 ''ν_n''들을 그 시스템의 '''고유진동수'''라고 부른다. 만약 폐곡선의 길이 ''L''이 파장 ''λ''의 정수배가 되지 않으면, 서로 다른 위상으로 만나는 파동들이 상쇄되어 에너지가 소멸하므로 안정적인 정상파는 만들어지지 않는다.

4. 정상파의 수학적 표현

정상파는 같은 진동수, 파장, 진폭을 갖는 두 파동이 서로 마주보며 진행할 때 중첩되어 만들어진다. 예를 들어, 줄 위에서 서로 반대 방향으로 진행하는 두 조화파 $y_{1} = y_{0}\sin(kx-\omega t)$ 와 $y_{2} = y_{0}\sin(kx+\omega t)$ 가 합성되면, 삼각 함수 항등식을 이용하여 다음과 같은 정상파의 식을 얻을 수 있다.

: $y = y_{1} + y_{2} = 2y_{0} \sin(kx) \cos(\omega t)$

이 식에서 $y_0$ 는 각 파동의 진폭, $k = {2\pi \over \lambda}$ 는 파수, $\omega$ 는 각진동수, $\lambda$ 는 파장, ''x''는 위치, ''t''는 시간을 나타낸다. 이 식은 파동이 진행하지 않고 각 위치 ''x''에서 $2y_{0} \sin(kx)$ 를 진폭으로 하여 시간에 따라 $\cos(\omega t)$ 형태로 진동함을 보여준다.

정상파는 다양한 물리 현상에서 관찰된다. 예를 들어, 전송선로에서는 반대 방향으로 진행하는 동일한 주파수의 전자기파가 중첩되어 전류, 전압, 또는 전계 세기의 정상파 패턴을 형성할 수 있다. 이는 전송선로 끝에서의 임피던스 부정합으로 인한 반사 때문에 발생하며, 마디(진폭 0)와 배(최대 진폭) 지점이 고정되어 나타난다.^[8] 실제로는 손실 때문에 완벽한 정상파 대신 진행파 성분이 포함된 ''부분 정상파''가 형성되며, 이는 정재파비(SWR)로 측정된다.^[9]

열린 바다에서도 폭풍 중심 근처나 해안에서의 파동 반사로 인해 정상파가 형성될 수 있으며, 이는 미소기압과 미소지진의 원인이 되기도 한다.

정상파는 1차원뿐 아니라 2차원 또는 3차원 공진기에서도 발생한다. 2차원 막(예: 북의 가죽막)에서는 진동하지 않는 선인 마디선이 나타나며, 이 패턴을 클라드니 도형이라고 한다. 3차원 공진기(예: 악기의 울림통, 마이크로파 공진기)에서는 마디면이 존재한다.
1차원 정상파: 현

무한 길이 현: 경계 조건이 없으므로 어떤 진동수에서든 정상파가 형성될 수 있다. 마디는 $x = n\lambda/2$ (n은 정수)인 지점이며, 배는 $x = (n+1/2)\lambda/2$ 인 지점이다. 인접한 마디 또는 배 사이의 거리는 $\lambda/2$ 이다.

유한 길이 현 (길이 L):
양 끝 고정: 경계 조건( $y(0,t)=0, y(L,t)=0$ )을 만족해야 하므로, 허용되는 파장은 $\lambda_n = \frac{2L}{n}$ (n=1, 2, 3, ...)으로 양자화된다. 해당 공진 주파수는 $f_n = \frac{v}{\lambda_n} = \frac{nv}{2L}$ 이다. n=1일 때를 기본 진동수, n>1일 때를 배음이라 한다. 정상파는 n+1개의 마디와 n개의 배를 가진다.

한 끝 고정(x=0), 한 끝 자유(x=L): 경계 조건( $y(0,t)=0, \partial y/\partial x|_{x=L}=0$ , 즉 x=L에서 배)을 만족해야 하므로, 허용되는 파장은 $\lambda_n = \frac{4L}{n}$ (n=1, 3, 5, ...)이다. 해당 공진 주파수는 $f_n = \frac{nv}{4L}$ 이다. 이 경우 홀수 배음만 존재한다.

1차원 정상파: 관 속의 음파 (길이 L)종파인 소리에서도 정상파가 형성된다. 압력 변화(

\Delta p

) 또는 공기의 종방향 변위(''s'')로 기술할 수 있다. 압력과 변위는

\Delta p = -\rho v^2 \frac{\partial s}{\partial x}

(

\rho

는 공기 밀도) 관계를 가지며, 압력 마디는 변위 배, 압력 배는 변위 마디에 해당한다.

닫힌 끝: 압력 배 (변위 마디)
열린 끝: 압력 마디 (변위 배) ^[11] (실제로는 열린 끝 보정 필요)

양 끝 열린 관: 경계 조건( $\Delta p(0,t)=0, \Delta p(L,t)=0$ )은 양 끝 고정 현과 같다.
$\lambda_n = \frac{2L}{n}$ (n=1, 2, 3, ...)
$f_n = \frac{nv}{2L}$ ( $v$ 는 음속)
한 끝 열림(x=0), 한 끝 닫힘(x=L): 경계 조건( $\Delta p(0,t)=0, \partial(\Delta p)/\partial x|_{x=L}=0$ , 즉 x=L에서 압력 배)은 한 끝 고정 현과 같다.
$\lambda_n = \frac{4L}{n}$ (n=1, 3, 5, ...)
$f_n = \frac{nv}{4L}$

양 끝 닫힌 관: 경계 조건(양 끝에서 압력 배)을 만족해야 한다.
$\lambda_n = \frac{2L}{n}$ (n=1, 2, 3, ...)
$f_n = \frac{nv}{2L}$

루벤스 관은 닫힌 관 속 압력 변화를 시각화하는 장치이다.^[13]
2차원 정상파: 직사각형 경계 (L_x × L_y)2차원 표면(예: 막)에서의 횡파 변위 ''z''(''x'',''y'',''t'')는 파동 방정식

\frac{\partial^2 z}{\partial t^2} = c^2 \left(\frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2}\right)

를 따른다. 변수 분리법을 사용하여 해를 구하면, 경계 조건(예: 가장자리에서

z=0

)에 의해 허용되는 파수와 주파수가 결정된다.^[14]

직사각형 경계(0 ≤ x ≤ L_x, 0 ≤ y ≤ L_y)에서 모든 가장자리가 고정된 경우, 정상파 해는 다음과 같다.

:

z(x,y,t) = z_{\text{max}}\sin \left(\frac{n\pi x}{L_x}\right) \sin \left(\frac{m\pi y}{L_y}\right) \cos \left(\omega_{nm} t\right)

여기서 ''n'', ''m''은 1 이상의 정수이며, 공진 주파수는 다음과 같이 양자화된다.

:

\omega_{nm} = c \pi \sqrt{\left(\frac{n}{L_x}\right)^2 + \left(\frac{m}{L_y}\right)^2}

서로 다른 (n, m) 조합이 동일한 공진 주파수를 가질 수 있으며(축퇴), 이는 주파수의 중복도와 관련된다.^[15]
정재파비 (SWR)서로 반대 방향으로 진행하는 두 파동의 진폭이 같지 않으면, 마디에서 진폭이 0이 되지 않고 최솟값을 갖는 부분 정상파가 형성된다. 정재파비(SWR)는 배에서의 최대 진폭과 마디에서의 최소 진폭의 비율이다. 순수한 정상파는 SWR이 무한대이고, 순수한 진행파는 SWR이 1이다. SWR 값은 파동이 정상파와 진행파 중 어느 쪽에 더 가까운지를 나타낸다.^[16] 순수한 정상파는 에너지를 전달하지 않지만^[17], 매질의 손실이나 불완전한 반사로 인해 SWR이 유한해지면 에너지 전달이 발생할 수 있다.

4. 1. 진행파의 표현

x축을 따라 무한히 긴 현이 y방향으로 횡으로 움직일 수 있다고 가정하자.

오른쪽으로 진행하는 정현파의 경우, 위치 x와 시간 t의 함수로서 현의 y방향 변위는 다음과 같이 표현할 수 있다.

:

y_\text{R}(x,t) = y_\text{max}\sin \left({2\pi x \over \lambda} - \omega t \right)

파수 ''k'' (=

2\pi / \lambda

)를 사용하면 다음과 같이 더 간단하게 나타낼 수도 있다.

:

y_\text{R}(x,t) = y_\text{max}\sin(kx - \omega t)

왼쪽으로 진행하는 동일한 정현파의 y방향 변위는 다음과 같이 표현된다.

:

y_\text{L}(x,t) = y_\text{max}\sin \left({2\pi x \over \lambda} + \omega t \right)

마찬가지로 파수 ''k''를 사용하면 다음과 같다.

:

y_\text{L}(x,t) = y_\text{max}\sin(kx + \omega t)

여기서 각 기호는 다음을 의미한다.

''y''_max: 각 파동의 최대 변위인 진폭.
''ω'': 각진동수. 진동수 ''f''와의 관계는 ''ω'' = 2π''f'' 이다.
''λ'': 파동의 파장.
''k'': 파수. 파장과의 관계는 ''k'' = 2π/''λ'' 이다.
''x'': 위치.
''t'': 시간.

4. 2. 정상파의 표현

정상파는 파장, 주기, 진폭, 속도가 같고 서로 반대 방향으로 진행하는 두 개의 정현파가 중첩될 때 형성된다. 이 두 파동을 수학적으로 다음과 같이 표현할 수 있다.

$y_1(x,t)=A\sin\left\{\omega\left(t-\frac{x}{v}\right)+\delta_1\right\}=A\sin\left\{2\pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)+\delta_1\right\}=A\sin(\omega t-kx+\delta_1)$
$y_2(x,t)=A\sin\left\{\omega\left(t+\frac{x}{v}\right)+\delta_2\right\}=A\sin\left\{2\pi\left(\frac{t}{T}+\frac{x}{\lambda}\right)+\delta_2\right\}=A\sin(\omega t+kx+\delta_2)$

여기서 각 기호는 다음을 의미한다.

''A'': 진폭
''ω'': 각진동수
''v'': 전파 속도
''δ₁'', ''δ₂'': 각 파동의 초기 위상
''T'': 주기
''λ'': 파장
''k'': 파수 (''k'' = 2π/λ)
''x'': 매질 위의 위치
''t'': 시간

두 파동이 중첩된 결과인 정상파 ''y(x, t)''는 두 파동의 합으로 나타낼 수 있다.

:

y(x,t)=y_1+y_2

삼각 함수 항등식 중 합을 곱으로 바꾸는 공식을 이용하면 다음과 같이 정리된다.

:

\begin{align}y&=A\sin(\omega t-kx+\delta_1)+A\sin(\omega t+kx+\delta_2)\\&=2A\sin\left(\omega t+\dfrac{\delta_1+\delta_2}{2}\right)\cos\left(kx-\dfrac{\delta_1-\delta_2}{2}\right)\end{align}

이 식을 분석하면 정상파의 특징을 알 수 있다.
1. 위치 x를 고정하고 시간 t에 따른 변화 관찰:위 식에서 특정 위치 ''x''를 고정하면, ''y''는 시간에 대한 함수 ''y(t)''가 된다. 이때 위치에 따라 변하는 진폭 항을 다음과 같이 정의할 수 있다.

:

A_x=2A\cos\left(kx-\frac{\delta_1-\delta_2}{2}\right)

그러면 ''y(t)''는 다음과 같이 표현된다.

:

y(t)=A_x\sin\left(\omega t+\dfrac{\delta_1+\delta_2}{2}\right)

이는 진폭이 ''A_x''이고 각진동수가 ''ω''인 단진동을 나타낸다. 즉, 각 위치 ''x''의 매질은 진폭

A_x = 2A\cos\left(kx-\frac{\delta_1-\delta_2}{2}\right)

로 단진동한다. 이 단진동의 위상

\left(\omega t+\dfrac{\delta_1+\delta_2}{2}\right)

는 위치 ''x''에 의존하지 않으므로, 매질 각 점의 단진동은 모두 같은 위상으로 일어난다. 또한, 이 단진동의 각진동수가 ''ω=2π/T''이므로, 단진동의 주기 ''τ''는 원래 파동의 주기 ''T''와 같다.

:

\tau=\frac{2\pi}{\omega}=T

2. 시간 t를 고정하고 위치 x에 따른 변화 관찰:위 식에서 특정 시간 ''t''를 고정하면, ''y''는 위치에 대한 함수 ''y(x)''가 된다. 이때 시간에 따라 변하는 진폭 항을 다음과 같이 정의할 수 있다.

:

A_t=2A\sin\left(\omega t+\dfrac{\delta_1+\delta_2}{2}\right)

그러면 ''y(x)''는 다음과 같이 표현된다.

:

y(x)=A_t\cos\left(kx-\frac{\delta_1-\delta_2}{2}\right)

이는

\cos\left(kx-\frac{\delta_1-\delta_2}{2}\right)

형태의 파형을 ''y''축 방향으로 ''A_t''배 확대한 것과 같다. 이 파형은 시간에 따라 전체적인 진폭만 변할 뿐, 파형 자체가 x축 방향으로 진행하지 않는다. 따라서 진동하지 않는 지점인 마디와 진폭이 최대가 되는 지점인 배가 나타난다.
마디와 배의 특징:

배에서의 최대 진폭 (A_max): 배는 공간적 진폭 항 ''A_x''가 최댓값을 가지는 지점이므로, 최대 진폭은 ''2A''이다.

:

A _{\mathrm{max}}=\mbox{max}\left\

5. 정상파의 종류 및 활용

정상파는 다양한 자연 현상과 기술 분야에서 관찰되고 활용된다. 정상파를 이해하는 간단한 예로는 두 사람이 줄넘기의 양쪽 끝을 잡고 동시에 흔드는 경우를 들 수 있다. 이때 줄은 위아래로 진동하는 규칙적인 파형을 만들며, 거의 움직이지 않는 지점(마디)과 진폭이 최대인 지점(배)이 나타난다. 이처럼 파동이 이동하지 않고 제자리에 머물러 있는 것처럼 보이기 때문에 정상파(standing wave)라는 이름이 붙었다.자연에서 볼 수 있는 정상파의 예는 다음과 같다.

대기 중 정상파: 특정 기상 조건 하에서 산맥의 리 지역 대기 중에 정상파가 형성될 수 있다. 이는 글라이더 조종사들이 비행에 활용하기도 한다. (자세한 내용은 기타 정상파 현상 참조)
강과 조류의 정상파: 강 급류나 솔트스트라우멘 메일스트롬과 같은 강한 조류 지역에서도 특정 조건 하에 정상파나 수리 수면 도약이 형성된다.^[7] 이는 강 서핑 장소로 이용되기도 한다. (자세한 내용은 기타 정상파 현상 참조)
잔잔호: 호수와 같이 닫힌 수역에서 물 전체가 주기적으로 출렁이는 잔잔호 현상도 정상파의 일종이다.^[28]^[29] (자세한 내용은 기타 정상파 현상 참조)^[30]^[31]^[32]
지구 자유 진동: 지진 발생 시 지구 전체가 특정 주파수로 진동하는 현상으로, 이는 지구 표면의 거대한 정상파로 볼 수 있다. (지구의 자유 진동 및 기타 정상파 현상 참조)
파라데이 파동: 유체 표면에 수직으로 진동을 가할 때 유체-공기 경계면에서 발생하는 비선형 정상파이다. 이는 마이크로 크기 재료를 조립하는 틀(템플릿)로 활용될 수 있다.^[27] (자세한 내용은 기타 정상파 현상 참조)

정상파는 공진 현상을 통해 기술적으로도 응용된다. 예를 들어, 캔틸레버 보(한쪽 끝만 고정된 막대)에 진동을 가해 정상파를 만들 수 있다. 이때 보의 자유로운 끝은 다른 어떤 지점보다 크게 움직인다. 이러한 원리를 이용하여 물체의 공진 주파수나 위상 변화를 감지하는 센서를 만들 수 있으며, 차원 측정 장비 등에 응용된다.^[25]^[26] 이 외에도 음향학, 광학, 전자기학 등 다양한 분야에서 정상파의 원리가 중요하게 활용된다. (하위 섹션 참조)

5. 1. 1차원 정상파

1차원 정상파는 서로 반대 방향으로 진행하는 동일한 주파수와 진폭을 가진 두 파동이 중첩되어 만들어지는 파동이다. 이 파동은 진행하지 않고 제자리에서 진동하는 것처럼 보이며, 특정 지점에서는 진폭이 항상 0인 마디(node)가, 다른 지점에서는 진폭이 최대가 되는 배(antinode)가 나타난다. 1차원 정상파의 대표적인 예로는 현의 진동이나 관 속 공기의 진동이 있다.=== 무한 길이 현의 정상파 ===x축을 따라 무한히 긴 현이 y 방향으로 진동하는 경우를 생각해 보자. 오른쪽으로 진행하는 정현파의 변위는 다음과 같다.:

y_\text{R}(x,t) = y_\text{max}\sin \left({2\pi x \over \lambda} - \omega t \right)

왼쪽으로 진행하는 동일한 파동의 변위는 다음과 같다.

:

y_\text{L}(x,t) = y_\text{max}\sin \left({2\pi x \over \lambda} + \omega t \right)

여기서 ''y''_max는 각 파동의 최대 진폭, ''ω''는 각진동수, ''λ''는 파동의 파장이다.

두 파동이 중첩되면 현의 전체 변위 ''y''(''x'',''t'')는 두 파동의 합이 된다.

:

y(x,t) = y_\text{R} + y_\text{L} = y_\text{max}\sin \left({2\pi x \over \lambda} - \omega t \right) + y_\text{max}\sin \left({2\pi x \over \lambda} + \omega t \right)

삼각함수 합-곱 공식

\sin a + \sin b = 2\sin \left({a+b \over 2}\right)\cos \left({a-b \over 2}\right)

을 사용하면, 다음과 같이 정리할 수 있다.

:

y(x,t) = 2y_\text{max}\sin \left({2\pi x \over \lambda} \right) \cos(\omega t)

(식 1)

식 (1)은 파동이 진행하지 않고 각 위치 x에서

2y_\text{max}\sin \left({2\pi x \over \lambda}\right)

의 진폭으로 시간에 따라 진동함을 보여준다. 이것이 정상파이다.

현의 특정 위치에서는 진폭이 항상 0이 되는데, 이를 마디라고 한다. 마디의 위치는 다음과 같다.

:

x = \ldots, -{3\lambda \over 2}, \; -\lambda, \; -{\lambda \over 2}, \; 0, \; {\lambda \over 2}, \; \lambda, \; {3\lambda \over 2}, \ldots

(즉,

x = n \frac{\lambda}{2}

, n은 정수)

반대로 진폭이 최대(

2y_\text{max}

)가 되는 위치를 배라고 하며, 위치는 다음과 같다.

:

x = \ldots, -{5\lambda \over 4}, \; -{3\lambda \over 4}, \; -{\lambda \over 4}, \; {\lambda \over 4}, \; {3\lambda \over 4}, \; {5\lambda \over 4}, \ldots

(즉,

x = (n + \frac{1}{2}) \frac{\lambda}{2}

, n은 정수)

인접한 마디와 마디, 또는 배와 배 사이의 거리는 파장의 절반(

\lambda/2

)이다. 무한 길이의 현에서는 경계 조건이 없으므로 어떤 주파수의 파동이라도 정상파를 형성할 수 있다.

=== 유한 길이 현의 정상파 ===

==== 양 끝이 고정된 현 ====

길이가 L인 현의 양 끝(

x=0

과

x=L

)이 고정되어 있다고 가정하자. 이 경우 현의 변위는 양 끝에서 항상 0이어야 한다(

y(0,t)=0

,

y(L,t)=0

). 정상파의 일반식 식 (1)에 이 경계 조건을 적용하면,

x=0

에서는

\sin(0)=0

이므로 자동으로 만족된다.

x=L

에서는 다음 조건이 만족되어야 한다.

:

\sin \left({2\pi L \over \lambda} \right) = 0

이 조건은

{2\pi L \over \lambda}

가

\pi

의 정수배일 때 성립하므로, 허용되는 파장은 다음과 같이 제한된다.

:

\lambda_n = \frac{2L}{n}, \quad (n = 1, 2, 3, \ldots)

(식 2)

파동의 속도를 v라고 할 때, 정상파를 형성할 수 있는 고유진동수는 다음과 같다.

:

f_n = \frac{v}{\lambda_n} = \frac{nv}{2L}, \quad (n = 1, 2, 3, \ldots)

가장 낮은 진동수(

n=1

)를 기본 진동수(fundamental frequency)라 하고, 이때의 파장은

\lambda_1 = 2L

이다.

n=2, 3, \ldots

에 해당하는 더 높은 진동수들을 배음(overtones) 또는 배진동이라고 한다. n번째 배음의 정상파는 양 끝을 포함하여

n+1

개의 마디와

n

개의 배를 가진다. 이러한 특정 주파수에서만 정상파가 형성되는 현상을 공진(resonance)이라고 하며, 이때의 주파수를 공진 주파수라고 한다.^[10]

==== 한 끝 고정, 한 끝 자유인 현 ====

길이가 L인 현의 한쪽 끝(

x=0

)은 고정되어 있고 다른 쪽 끝(

x=L

)은 자유롭게 움직일 수 있다고 가정하자. 예를 들어,

x=L

지점이 마찰 없이 위아래로 움직일 수 있는 고리에 연결된 경우이다. 이 경우 경계 조건은

y(0,t)=0

이고,

x=L

에서는 변위가 최대가 되는 배가 형성되어야 한다. 정상파 식 (1)에서

x=L

일 때 진폭

2y_\text{max}\sin \left({2\pi L \over \lambda}\right)

이 최대가 되려면

\sin \left({2\pi L \over \lambda}\right)

의 절댓값이 1이어야 한다. 이는

\cos \left({2\pi L \over \lambda}\right) = 0

조건을 만족할 때 가능하다.

이 조건은

{2\pi L \over \lambda}

가

\frac{\pi}{2}

의 홀수배일 때 성립하므로, 허용되는 파장은 다음과 같다.

:

\lambda_n = \frac{4L}{n}, \quad (n = 1, 3, 5, \ldots)

따라서 고유진동수는 다음과 같다.

:

f_n = \frac{v}{\lambda_n} = \frac{nv}{4L}, \quad (n = 1, 3, 5, \ldots)

이 경우, 기본 진동수(

n=1

)는

f_1 = v/4L

이고, 홀수 배음만 존재한다. 기본 모드는 현의 길이가 파장의 1/4에 해당한다. 이 경우에도 특정 공진 주파수에서만 정상파가 형성된다.

=== 관 속 공기의 정상파 ===

관 속에서 소리파동은 공기의 압축과 팽창을 통해 전달되는 종파이다. 현의 횡파와 달리, 공기 입자는 파동의 진행 방향과 나란하게 진동하며, 이에 따라 공기 압력도 주기적으로 변한다. 관 속에서 오른쪽으로 진행하는 압력 변화 파동과 왼쪽으로 진행하는 압력 변화 파동이 중첩되면 정상파가 형성될 수 있다. 압력 변화

\Delta p

에 대한 정상파 식은 현의 변위 식과 유사하다.

:

\Delta p(x,t) = 2p_\text{max}\sin \left({2\pi x \over \lambda} \right) \cos(\omega t)

여기서

p_\text{max}

는 각 진행파의 최대 압력 변화 진폭이다.

관의 끝에서의 경계 조건은 끝이 열려 있는지 또는 닫혀 있는지에 따라 달라진다.

닫힌 끝: 공기 분자의 운동이 제한되므로 변위는 0(마디)이 된다. 반면, 공기가 벽에 부딪혀 압축되거나 팽창하므로 압력 변화는 최대(배)가 된다.
열린 끝: 공기 분자가 자유롭게 운동할 수 있으므로 변위는 최대(배)가 된다. 외부 대기와 압력이 거의 같아지므로 압력 변화는 0(마디)에 가깝다.^[11] (실제로는 열린 끝 약간 바깥쪽에 압력 마디가 형성되므로 끝 보정이 필요할 수 있다.)

==== 양 끝이 열린 관 ====

오르간 파이프나 리코더처럼 양 끝(

x=0

,

x=L

)이 모두 열린 관의 경우, 양 끝에서 압력 변화가 0(마디)이어야 한다. 이는 양 끝이 고정된 현의 경우와 동일한 경계 조건이다.

:

\Delta p(0,t) = 0, \quad \Delta p(L,t) = 0

따라서 허용되는 파장과 고유진동수는 다음과 같다.

:

\lambda_n = \frac{2L}{n}, \quad f_n = \frac{nv}{2L}, \quad (n = 1, 2, 3, \ldots)

여기서 v는 음속이다.

==== 한 끝 열림, 한 끝 닫힘 관 ====

병이나 클라리넷처럼 한쪽 끝(

x=0

)은 열려 있고 다른 쪽 끝(

x=L

)은 닫혀 있는 관의 경우, 열린 끝에서는 압력 마디(

\Delta p(0,t) = 0

), 닫힌 끝에서는 압력 배가 형성되어야 한다. 이는 한 끝 고정, 한 끝 자유인 현의 경우와 동일한 경계 조건이다. 따라서 허용되는 파장과 고유진동수는 다음과 같다.

:

\lambda_n = \frac{4L}{n}, \quad f_n = \frac{nv}{4L}, \quad (n = 1, 3, 5, \ldots)

이 경우에도 홀수 배음만 존재한다.

==== 양 끝이 닫힌 관 ====

양 끝이 모두 닫힌 관의 경우, 양 끝에서 압력 변화가 최대(배)가 되어야 한다. 이는 양 끝이 열린 관과 파장 및 주파수 공식은 동일하지만, 마디와 배의 위치가

\lambda/4

만큼 이동한 형태가 된다.

:

\lambda_n = \frac{2L}{n}, \quad f_n = \frac{nv}{2L}, \quad (n = 1, 2, 3, \ldots)

기본 모드(

n=1

)의 경우, 양 끝에 압력 배가 있고 관의 중앙(

x=L/2

)에 압력 마디가 존재한다. 루벤스 관은 이러한 관 내부의 압력 변화를 시각적으로 보여주는 장치이다.^[13]

=== 공진과 고유진동수 ===

thumb

현이나 관과 같이 경계가 있는 매질에서는 특정 주파수의 파동만이 안정적인 정상파를 형성하며 큰 진폭으로 진동하게 되는데, 이러한 현상을 공진(resonance) 또는 공명이라고 한다. 이때 정상파를 형성하는 특정 주파수를 고유진동수(natural frequency)라고 한다. 고유진동수 중 가장 작은 값을 기본 진동수(fundamental frequency)라고 하며, 소리의 경우 이를 기음(fundamental tone)이라고 부른다. 기본 진동수보다 높은 고유진동수들을 배음(overtones)이라고 한다.

고유진동수는 매질의 길이(L), 파동의 속도(c, 현의 경우

v = \sqrt{T/\mu}

, T는 장력, μ는 선밀도 / 관의 경우 음속 v), 그리고 양 끝의 경계 조건에 따라 결정된다.

양 끝이 고정단 또는 양 끝이 자유단인 경우: (예: 양 끝 고정 현, 양 끝 열린 관, 양 끝 닫힌 관)

양 끝이 모두 마디(고정단)이거나 모두 배(자유단, 압력 기준으로는 열린 관은 마디, 닫힌 관은 배)가 되는 조건이다.

:허용 파장:

\lambda_n = \frac{2L}{n}

:고유진동수:

f_n = \frac{c}{\lambda_n} = \frac{nc}{2L} \quad (n = 1, 2, 3, \ldots)

기본 진동수(

n=1

)는

f_1 = c/2L

이며, 모든 정수배의 배음이 존재한다.

한 끝이 고정단, 다른 끝이 자유단인 경우: (예: 한 끝 고정 현, 한 끝 열림-한 끝 닫힘 관)

한쪽 끝은 마디, 다른 쪽 끝은 배가 되는 조건이다.

:허용 파장:

\lambda_n = \frac{4L}{2n-1}

(n=1, 2, 3...)

:고유진동수:

f_n = \frac{c}{\lambda_n} = \frac{(2n-1)c}{4L} \quad (n = 1, 2, 3, \ldots)

기본 진동수(

n=1

)는

f_1 = c/4L

이며, 홀수배의 배음만 존재한다.

이러한 정상파와 공진 원리는 현악기와 관악기 등 다양한 악기의 소리를 만드는 기본 원리로 활용된다.

5. 2. 2차원 정상파

정상파는 1차원뿐만 아니라 2차원 또는 3차원 공진기에서도 발생할 수 있다. 예를 들어, 북 가죽막과 같은 2차원 막에서 정상파가 생기면, 진동하지 않는 지점들이 모여 선을 이루는데 이를 마디선이라고 한다. 마디선은 서로 반대 위상으로 진동하는 영역들을 구분하는 경계 역할을 한다. 이러한 마디선 패턴은 클라드니 도형이라고 불린다.^[15] 악기의 소리 상자나 마이크로파 공진기 같은 3차원 공진기에서는 마디선 대신 마디면이 형성된다.

직사각형 경계 내에서의 2차원 정상파를 살펴보자. 가로 길이가 ''L_x'', 세로 길이가 ''L_y''인 직사각형 표면 위를 움직이는 횡파를 생각할 수 있다. 수영장의 물결이나 팽팽하게 당겨진 사각형 모양의 천에서 관찰되는 파동이 이런 예시에 해당한다. 파동은 표면을 z 방향으로 변위시키며, ''z'' = 0은 표면이 정지했을 때의 높이를 의미한다.

2차원 데카르트 좌표계에서 파동 방정식은 다음과 같다.

:

\frac{\partial^2 z}{\partial t^2}  \;=\; c^2 \left(\frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2}\right)

여기서 ''z''(''x'',''y'',''t'')는 표면의 변위, ''c''는 파동의 속도이다.

이 방정식을 풀면, 정상파는 특정 공진 주파수에서만 형성될 수 있다는 것을 알 수 있다. 직사각형 경계의 네 변에서 변위가 0이어야 한다는 경계 조건을 적용하면, 허용되는 파수 ''k_x''와 ''k_y''는 다음과 같이 제한된다.

:

k_x = \frac{n \pi}{L_x}, \quad n = 1, 2, 3, \dots

:

k_y = \frac{m \pi}{L_y}, \quad m = 1, 2, 3, \dots

여기서 ''n''과 ''m''은 각각 x 방향과 y 방향의 모드를 나타내는 양의 정수이다.

이에 따라 허용되는 공진 각진동수 ''ω''도 다음과 같이 결정된다.

:

\omega = c \sqrt{k_x^2 + k_y^2} = c \pi \sqrt{\left(\frac{n}{L_x}\right)^2 + \left(\frac{m}{L_y}\right)^2}

적절한 초기 조건을 선택하면, 이 시스템의 정상파는 다음과 같은 형태로 표현될 수 있다.

:

z(x,y,t) = z_{\text{max}}\sin \left(\frac{n\pi x}{L_x}\right) \sin \left(\frac{m\pi y}{L_y}\right) \cos \left(\omega t\right)

이 식은 정상파가 시간에 따라 진동하지만 공간적으로 이동하지 않으며, x 방향과 y 방향으로 각각 사인파 형태의 공간적 변화를 가짐을 보여준다.

기본 모드: ''n'' = 1, ''m'' = 1인 경우로, 직사각형 중앙에 하나의 배(진폭이 최대인 지점)가 생긴다.
고차 모드: ''n'' 또는 ''m'' 값이 커지면, 직사각형 내부에 더 복잡하지만 예측 가능한 마디선과 배의 패턴이 만들어진다.^[15]

특정한 경우, 서로 다른 모드(''n'', ''m''의 다른 조합)가 동일한 주파수에서 공진할 수도 있다. 예를 들어, 경계가 정사각형이어서 ''L_x'' = ''L_y''일 경우, (''n''=1, ''m''=7), (''n''=7, ''m''=1), (''n''=5, ''m''=5) 모드는 모두 같은 주파수

\omega = \frac{c \pi}{L_x} \sqrt{50}

에서 공진한다. 이는 특정 주파수에 해당하는 모드가 여러 개 존재할 수 있음을 의미하며, 이를 주파수의 중복도라고 한다.

5. 3. 3차원 정상파

정상파는 2차원뿐만 아니라 3차원 공진기에서도 발생할 수 있다. 악기의 소리 상자나 마이크로파 공진기와 같은 3차원 공진기에서는 진동하지 않는 면인 마디면이 존재한다.

정상파는 광 도파로나 광 공진기와 같은 광학 매질에서도 관찰된다. 예를 들어, 레이저는 마주 보는 두 개의 거울로 이루어진 파브리-페로 간섭계 형태의 광 공진기를 사용한다. 공진기 내부의 이득 매질(예: 결정)은 빛을 결맞게 방출하여 공진기 안에 빛의 정상파를 만든다.^[20] 빛의 파장은 나노미터(10^-9 m) 단위로 매우 짧기 때문에, 이때 생기는 정상파의 크기는 미시적이다. 이러한 광학 정상파는 광학 평판을 이용하여 미세한 거리를 측정하는 데 활용되기도 한다.

X선 빔 사이의 간섭은 X선 정상파(XSW) 장을 형성할 수 있다.^[21] X선의 파장은 1 나노미터보다 짧아서, 이 현상을 이용하면 물질 표면에서 원자 수준의 현상을 측정하는 것이 가능하다. XSW는 X선 빔이 거의 완벽한 단결정 표면에서 회절된 빔 또는 X선 거울에서 반사된 빔과 간섭하는 영역에서 생성된다. 결정의 기하학적 구조나 X선 파장을 조절하면 XSW를 공간적으로 이동시킬 수 있는데, 이를 통해 표면 근처 원자에서 발생하는 X선 형광 또는 광전자 방출량의 변화를 관찰할 수 있다. 이 변화를 분석하면 기저 결정 구조나 거울 표면에 대한 특정 원자 종류의 정확한 위치를 파악할 수 있다. XSW 방법은 반도체 내 도펀트의 원자 규모 세부 사항 분석,^[22] 표면에서의 원자 및 분자 흡착 연구,^[23] 그리고 촉매 작용과 관련된 화학적 변환 과정을 밝히는 데 사용되어 왔다.^[24]

5. 4. 기타 정상파 현상

강의 정상파강 급류나 솔트스트라우멘 메일스트롬과 같은 조류에서도 정상파와 수리 수면 도약이 형성될 수 있다. 강 흐름에서 이러한 현상이 발생하려면, 얕은 수심에서 흐르는 물이 관성이 중력을 극복할 정도로 빠른 초임계류 속도(프루드 수: 1.7 – 4.5, 4.5를 초과하면 직접적인 정상파가 형성됨^[7])를 가져야 한다. 이 조건에서는 물의 흐름이 장애물에 의해 크게 속도가 줄거나 옆으로 밀리지 않는다. 많은 강의 정상파는 인기 있는 강 서핑 장소로 활용된다.
대기 중 정상파특정 기상 조건 하에서는 산맥의 리 지역 대기 중에 정상파가 형성되기도 한다. 이러한 파도는 종종 글라이더 조종사들이 비행에 활용한다.
해양 정상파와 관련 현상열린 바다에서는 동일한 파동 주기를 갖는 파동이 서로 반대 방향으로 이동하며 정상파를 형성할 수 있다. 이러한 정상파는 폭풍 중심 근처나 해안에서의 쇄파 반사에 의해 형성될 수 있으며, 미소기압과 미소지진의 원인이 되기도 한다. 또한, 지구 표면의 정상파는 지구의 자유 진동으로 관측된다.
전송선로의 정상파전송선로에서는 서로 반대 방향으로 진행하는 동일한 주파수를 가진 두 파동이 중첩되어 정상파가 형성될 수 있다. 이는 전류, 전압, 또는 전계 세기 분포로 나타나며, 전송선로를 따라 고정된 지점에 마디(변위 0)와 배(최대 변위)가 나타난다. 이러한 정상파는 파동이 전송선로 한쪽 끝에서 전송되고 다른 쪽 끝의 임피던스 불일치(개방 회로 또는 단락 회로 등)에 의해 반사될 때 형성된다.^[8] 전송선로가 정상파 주파수에서 전력을 제대로 전달하지 못하면 감쇠 왜곡이 발생할 수 있다. 실제로는 전송선로나 부품의 손실 때문에 완벽한 반사나 순수한 정상파는 드물며, 대개 정상파와 진행파가 중첩된 ''부분 정상파''가 발생한다. 파동이 정상파와 진행파 중 어느 쪽에 더 가까운지는 정재파비(SWR)로 측정한다.^[9]
기타 유체 현상파라데이 파동은 유체역학적 불안정성에 의해 유체-공기 계면에 발생하는 비선형 정상파이다. 이는 마이크로 스케일 재료를 조립하기 위한 액체 기반 템플릿으로 사용될 수 있다.^[27]

잔잔호는 호수와 같이 밀폐된 수역에서 발생하는 정상파의 한 예이다. 이는 수역 양쪽 끝에서 수위가 주기적으로 오르내리는 진동 현상으로, 일반적으로 수역 중앙 근처에는 수위 변화가 거의 없는 마디점이 존재한다. 이는 진동 없이 수위가 상승하는 폭풍 해일과는 구분된다. 큰 호수에서는 잔잔호의 주기가 수분에서 수 시간에 이를 수 있다. 예를 들어, 제네바 호의 종방향 주기는 73분, 횡방향 주기는 약 10분이며,^[28] 허론 호는 1~2시간 주기로 공진하는 것이 관측되었다.^[29] 호수 잔잔호 참조.^[30]^[31]^[32]
보어의 원자 모형보어의 원자 모형에서는 원자핵 주위를 도는 전자가 특정 원자 궤도 위에서 정상파 형태로 안정적으로 존재한다고 보았다. 보어의 양자 조건은

m_ev_nr_n=\frac{nh}{2\pi}

(단, ''m_e''는 전자의 질량, ''v_n''은 전자의 속도, ''r_n''은 궤도 반지름, ''h''는 플랑크 상수)

으로 나타내어지지만, 여기에 드 브로이 파장의 식

\lambda=\frac{h}{mv}

을 적용하면 다음 식이 얻어진다.

n\lambda_e=2\pi r_n

이 식에서 ''λ_e''는 전자의 물질파로서의 파장이다. 이것은 앞 절에서 언급한 폐곡선상의 정상파의 식을 만족하고 있으며, 즉 전자는 정상파로서 원자 궤도 위에 안정적으로 존재할 수 있음을 의미한다.

참조

_[1] 서적 Encyclopedia of Nonlinear Science Routledge
_[2] 서적 Nonlinear Instability of Nonparallel Flows: IUTAM Symposium Potsdam, New York Springer
_[3] 서적 Ueber einige krumme Flächen, welche von Ebenen, parallel einer bestimmten Ebene, durchschnitten, als Durchschnittsfigur einen Kegelschnitt liefern: Inaugural-Dissertation... Koch
_[4] 간행물 Ueber die Erregung stehender Wellen eines fadenförmigen Körpers
_[5] 서적 Die Lehre von den Schwingungscurven...: mit einem Atlas von 11 Tafeln in Steindruck JA Barth
_[6] 간행물 Akustische Experimentaluntersuchungen
_[7] 웹사이트 Surfbare Wechselsprünge {{!}} Espazium https://www.espazium[...] 2022-01-13
_[8] 웹사이트 Federal Standard 1037C https://www.its.bldr[...]
_[9] 서적 Fundamentals of Physical Acoustics Wiley–IEEE
_[10] 영상매체 String Resonance http://digitalsounda[...] Digital Sound & Music 2020-08-22
_[11] 웹사이트 Standing Waves http://hyperphysics.[...] Georgia State University 2020-08-23
_[12] 영상매체 Longitudinal Standing Waves Demonstration https://www.flipping[...] Flipping Physics 2020-08-23
_[13] 영상매체 A better description of resonance https://www.youtube.[...] YouTube 2020-08-23
_[14] 웹사이트 Helmholtz Differential Equation--Cartesian Coordinates https://mathworld.wo[...] 2021-01-02
_[15] 영상매체 2D Standing Wave Patterns (rectangular fixed boundaries) http://phys23p.sl.ps[...] Pennsylvania State University 2020-12-28
_[16] 서적 Microwave Engineering PHI Learning
_[17] 서적 Physics for the IB Diploma Cambridge University Press
_[18] 간행물 A Wave Dynamical Interpretation of Saturn's Polar Region http://pubs.giss.nas[...]
_[19] 간행물 A laboratory model of Saturn's North Polar Hexagon
_[20] 서적 Pedrottis' Introduction to Optics Cambridge University Press
_[21] 간행물 Dynamical Diffraction of X Rays by Perfect Crystals
_[22] 간행물 Detection of Foreign Atom Sites by Their X-Ray Fluorescence Scattering
_[23] 간행물 Solution to the Surface Registration Problem Using X-Ray Standing Waves https://dash.harvard[...]
_[24] 간행물 Direct Atomic-Scale Observation of Redox-Induced Cation Dynamics in an Oxide-Supported Monolayer Catalyst: WO_''x''/α-Fe₂O₃(0001)
_[25] 간행물 Development of a virtual probe tip with an application to high aspect ratio microscale features
_[26] 웹사이트 Precision Engineering and Manufacturing Solutions – IST Precision http://www.insitutec[...] 2018-04-28
_[27] 간행물 Microscale Assembly Directed by Liquid-Based Template
_[28] 백과사전 Surface Seiches Springer Netherlands
_[29] 웹사이트 Lake Huron Storm Surge July 13, 1995 https://web.archive.[...] NOAA 2023-01-01
_[30] 웹사이트 Bonanza for Lake Superior: Seiches Do More Than Move Water https://web.archive.[...] University of Minnesota Duluth 2000-02
_[31] 웹사이트 Seiche https://www.soest.ha[...] 2023-01-01
_[32] 웹사이트 Japanese earthquake literally made waves in Norway https://arstechnica.[...] 2023-01-01
_[33] 웹사이트 stationary wave https://www.kps.or.k[...]
_[34] 웹사이트 standing wave https://www.kps.or.k[...]
_[35] 웹사이트 standing wave https://new.kcsnet.o[...]
_[36] 위키소스 정상파 https://ko.wikisourc[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com