중첩 원리
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
중첩 원리는 파동, 전기 회로, 양자역학 등 다양한 분야에서 나타나는 중요한 개념으로, 선형 시스템에서 여러 개의 입력에 대한 전체 응답이 각 입력에 대한 개별 응답의 합과 같다는 원리이다. 1753년 다니엘 베르누이가 처음 언급했으며, 조제프 푸리에의 연구를 통해 널리 받아들여졌다. 전기 회로 분석에서는 여러 전원이 있는 회로의 해석에 활용되며, 파동의 중첩은 간섭 현상을 설명하는 데 사용된다. 양자역학에서는 파동 함수의 중첩을 통해 입자의 거동을 계산하며, 푸리에 분석, 경계값 문제, 가산 상태 분해 등에도 적용된다. 한국에서도 음향, 광학, 양자 기술 등 다양한 분야에서 중첩 원리가 응용되고 있다.
더 읽어볼만한 페이지
- 체계 이론 - 사이버네틱스
사이버네틱스는 동물과 기계의 제어 및 통신을 연구하는 학문으로, 제어 시스템, 신경과학 등 다양한 분야를 통합하여 발전해왔으며, 피드백, 자기조직화 등의 핵심 개념을 통해 여러 분야에 응용되고 있다. - 체계 이론 - 사회 연결망
사회 연결망 분석은 개인이나 집단 간의 관계를 분석하여 사회적 구조와 행동을 이해하는 학제 간 연구 방법론으로, 다양한 이론적 틀을 활용하여 네트워크 내 위치와 정보 접근의 중요성을 분석하며 여러 분야에서 활용된다. - 파동 - 진동수
진동수는 주기적인 현상이 단위 시간당 반복되는 횟수를 나타내는 물리량으로, 주기와 역수 관계를 가지며 소리의 높낮이, 빛의 색깔 등을 결정하는 중요한 요소이다. - 파동 - 전파
전파는 전기장과 자기장의 결합으로 공간을 통해 이동하는 전자기파의 일종으로, 통신, 방송 등 다양한 분야에서 활용되며, 파장에 따라 분류되고, 열적 및 비열적 효과를 가지며 생물학적 영향을 미칠 수 있다. - 물리학 개념 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다. - 물리학 개념 - 전기 전도체
전기 전도체는 전기를 잘 통하는 물질로, 금속, 전해질, 초전도체, 반도체 등이 있으며, 구리, 은, 알루미늄 등 다양한 재료가 전선 등에 사용된다.
| 중첩 원리 | |
|---|---|
| 개요 | |
| 설명 | 선형 시스템의 물리적 해는 선형이라는 기본 물리 원리이다. |
| 정의 | 선형 시스템의 경우, 두 개 이상의 개별적인 해를 결합하여 새로운 해를 생성할 수 있다. |
| 원리 | |
| 핵심 개념 | 선형 시스템의 해는 선형적으로 결합될 수 있다. |
| 적용 예시 | 파동, 전자기학, 양자역학 등 다양한 물리 분야에 적용된다. |
| 수학적 표현 | |
| 일반적 표현 | 'A' + 'B' 형태의 두 해를 'X' + 'Y'와 같이 결합하여 새로운 해를 얻을 수 있다. |
| 활용 분야 | |
| 선형 시스템 | 여러 물리 현상을 모델링하고 해결하는 데 사용된다. |
| 주의사항 | |
| 비선형 시스템 | 비선형 시스템에는 중첩 원리가 적용되지 않는다. |
| 기타 | |
| 관련 원리 | 푸리에 해석, 선형 결합과 밀접한 관련이 있다. |
| 영어 명칭 | superposition principle |
2. 역사
레옹 브릴루앵에 따르면, 중첩 원리는 1753년 다니엘 베르누이가 처음으로 언급했다. "진동하는 계의 일반적인 운동은 그 고유 진동의 중첩으로 주어진다."[11] 베르누이는 어떤 음향체도 잘 정의된 진동 주파수를 가진 일련의 단순 모드로 진동할 수 있으며, 이러한 모드는 더 복잡한 진동을 생성하기 위해 중첩될 수 있다고 주장했다. 그러나 이 원리는 레온하르트 오일러와 조제프 루이 라그랑주에 의해 거부되었다. 오일러는 베르누이가 진동하는 현 문제의 물리적 부분을 가장 잘 발전시켰다고 칭찬했지만, 다중 모드 해의 일반성과 우월성은 부인했다.[11]
중첩 원리는 여러 개의 독립 전원이 있는 선형 회로망을 해석하는 데 매우 중요한 역할을 한다. 여러 개의 전원을 가진 선형 회로에서, 특정 저항에 걸리는 전압이나 흐르는 전류는 각 독립 전원에 의한 전압과 전류를 더한 값과 같다. 이때, 다른 독립 전원은 전압원의 경우 단락 회로, 전류원의 경우 개방 회로로 대체하여 회로를 해석한다.[9]
파동은 일반적으로 공간과 시간에 따른 어떤 매개변수의 변화로 설명된다. 예를 들어 물결파의 높이, 음파의 압력, 빛 파동의 전자기장 등이 있다. 이 매개변수의 값을 파동의 진폭이라고 하며, 파동 자체는 각 지점에서의 진폭을 지정하는 함수이다.
조제프 푸리에의 연구를 통해 중첩 원리는 대부분 받아들여졌다.[12] 브릴루앵에 따르면, 1753년에 중첩 원리("진동계의 운동은 일반적으로 계의 고유진동의 중첩으로 주어진다")를 처음으로 제창한 사람은 다니엘 베르누이였다.[24] 중첩 원리를 인정하면, 어떠한 함수도 삼각함수의 중첩으로 표현할 수 있게 된다. 오일러와 라그랑주는 이 정리가 너무 강력하다고 생각하여 중첩 원리에 대해 회의적인 입장을 취했다. 이후 중첩 원리는 주로 푸리에의 연구를 통해 일반적으로 인지되게 되었다.
3. 전기 회로 분석
전기 공학에서 선형 회로의 경우, 입력(시간에 따라 변하는 전압 신호)은 출력(회로 내 어느 지점의 전류 또는 전압)과 선형 변환을 통해 관련된다. 따라서 입력 신호의 중첩(즉, 합)은 응답의 중첩을 생성한다. 이 원리에 기반한 푸리에 분석 기법은 매우 널리 사용된다.
4. 파동의 중첩
파동이 있는 모든 시스템에서 주어진 시간의 파형은 원천과 시스템의 초기 조건에 따라 결정된다. 많은 경우 파동을 설명하는 방정식은 선형인데, 이때 중첩 원리가 적용된다. 즉, 같은 공간을 통과하는 두 개 이상의 파동에 의해 발생하는 총 진폭은 개별 파동에 의해 별도로 생성되었을 진폭의 합이다. 예를 들어, 서로를 향해 이동하는 두 개의 파동은 반대편에서 어떤 왜곡도 없이 서로 통과한다.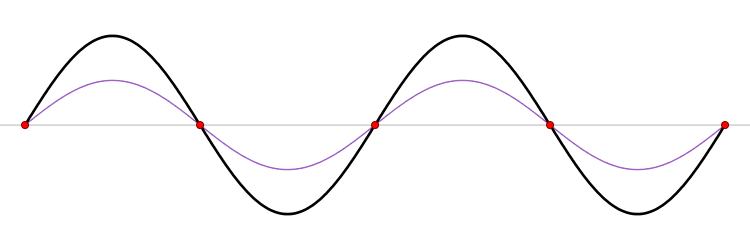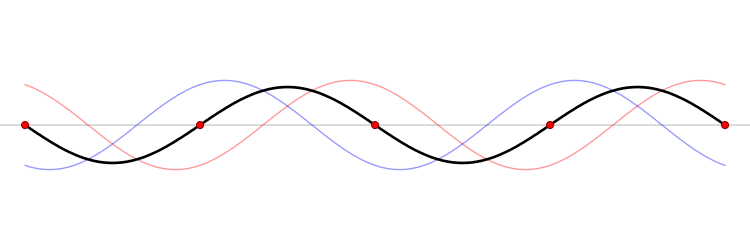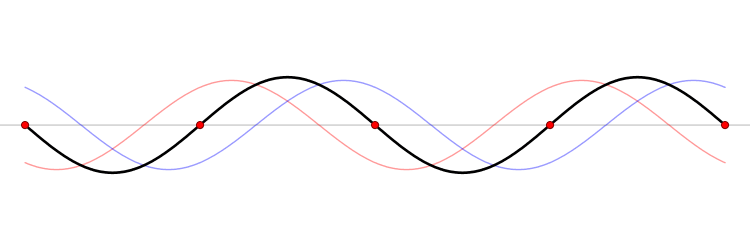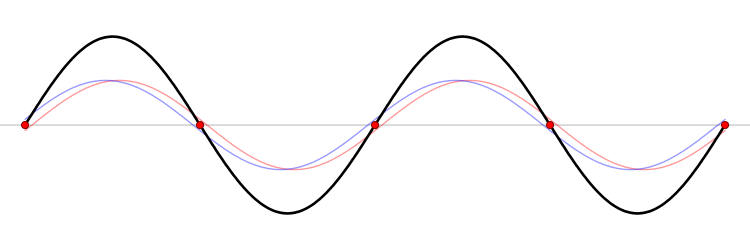
대부분의 현실적인 물리적 상황에서 파동을 지배하는 방정식은 근사적으로만 선형이다. 이러한 상황에서는 중첩 원리가 근사적으로만 성립하며, 일반적으로 파동의 진폭이 작아짐에 따라 근사의 정확도가 향상된다. 중첩 원리가 정확하게 성립하지 않는 경우의 예로는 비선형 광학 및 비선형 음향학이 있다.
파동의 간섭 현상은 이러한 중첩 원리에 기초한다. 두 개 이상의 파동이 동일한 공간을 통과할 때, 각 지점에서의 순 진폭은 개별 파동의 진폭의 합이다. 소음 제거 헤드폰과 같이, 합쳐진 변화량이 구성 요소 변화량보다 작은 경우가 있는데, 이것을 ''파괴적 간섭''이라고 한다. 라인 어레이와 같이, 합쳐진 변화량이 개별 구성 요소보다 더 큰 진폭을 갖는 경우도 있는데, 이것을 ''보강적 간섭''이라고 한다.
한국에서는 파동 현상을 이용한 기술 개발이 활발하게 이루어지고 있으며, 특히 음향, 광학 분야에서 중첩 원리가 응용되고 있다.
4. 1. 파동의 간섭과 회절
리처드 파인만은 파동의 간섭과 회절에 대해 "만족스럽게 정의할 수 있는 사람은 아무도 없다"라고 말했다. 그는 둘 사이에는 본질적인 물리적 차이가 없으며, 단지 용어 사용의 문제일 뿐이라고 보았다. 일반적으로 소수의 파원에서 나온 파동의 중첩은 "간섭", 다수의 파원에서 나온 파동의 중첩은 "회절"이라고 불리는 경향이 있다고 설명했다.[2] 다른 저자들도 이와 비슷하게, 중첩될 파동이 소수의 결맞는 광원에서 발생하면 간섭, 파면을 무한히 작은 결맞는 파동으로 나누어 발생하면 회절이라고 부르며, 이는 정도의 차이일 뿐 기본적으로는 동일한 중첩 효과의 양 극단이라고 설명한다.[3]
간섭 현상은 파동의 중첩에 기반한다. 둘 이상의 파동이 같은 공간을 지날 때, 각 지점의 순 변위는 각 파동이 만드는 변위의 합과 같다. 합성파의 진폭이 개별 성분보다 작아지는 "상쇄 간섭"(예: 노이즈 캔슬링 헤드폰)과 커지는 "보강 간섭"(예: 라인 어레이 스피커)이 있다.
| 합성파 | --|]] | |
|---|---|---|
| 파동 1 | ||
| 파동 2 | ||
| 파동 1과 2가 동위상 (보강 간섭) | 파동 1과 2가 역위상 (상쇄 간섭) | |
파인만은 『파인만 물리학』에서 간섭과 회절이 모두 중첩 원리에서 비롯되며 본질적인 차이가 없다고 했다.[15] 소수 파원의 중첩은 "간섭", 다수 파원의 중첩은 "회절"로 불리는 경향이 있을 뿐이며, 이 논리를 확장하면 간섭과 회절은 동일 효과의 양극단이라 할 수 있다.[16] 명확히 구별되는 소수 코히어런트한 파원의 중첩은 간섭, 하나의 파면을 무수히 많은 코히어런트한 파원으로 표현할 때의 효과는 회절이라 불린다.
한편, 간섭과 회절 개념의 불명확성은 파면 분할과 진폭 분할 구분이 명확하지 않기 때문이라는 주장도 있다.[17] 영의 이중 슬릿 실험이나 프라운호퍼 회절처럼 하나의 파동 파면을 분할하여 만든 여러 코히어런트한 파원을 간섭시키는 것은 회절에 가깝다. 반면, 마이켈슨 간섭계처럼 진폭을 분할하여 만든 코히어런트한 파원을 간섭시키는 경우는 회절로 간주되는 일이 드물다.
4. 2. 양자 중첩
양자역학에서 특정 유형의 파동이 어떻게 전파하고 움직이는지 계산하는 것은 중요한 과제이다. 파동은 파동 함수로 나타내며, 이 파동 함수의 움직임을 설명하는 방정식을 슈뢰딩거 방정식이라고 한다. 파동 함수의 움직임을 계산하는 주된 방법은, 움직임이 비교적 간단한 여러 정상 상태 파동 함수들을 중첩("quantum superposition|양자 중첩영어")하여 표현하는 것이다. 슈뢰딩거 방정식은 선형이기 때문에, 원래 파동 함수의 움직임은 이러한 중첩 원리를 통해 계산할 수 있다.[5]양자 역학적 상태는 사영 힐베르트 공간의 '벡터'가 아니라 '레이'이기 때문에, 양자 역학적 상태 공간의 사영적 특성은 혼란을 야기할 수 있다. 디랙에 따르면, "상태에 해당하는 케트 벡터에 0이 아닌 임의의 복소수를 곱하면, 결과 케트 벡터는 동일한 상태에 해당한다."[6] 그러나 중첩된 레이를 만들기 위한 두 레이의 합은 정의되지 않는다.
크라머스는 "[양자] 중첩의 원리는... 고전 물리학에는 유사한 것이 없다."라고 하였다. 디랙에 따르면, "양자 역학에서 발생하는 중첩은 고전 이론에서 발생하는 중첩과 본질적으로 다른 성격이다."[8]
양자역학에서 어떤 종류의 파동 전파와 거동을 계산하는 것은 가장 중요한 문제이다. 이 파동은 파동 함수로 표현되며, 그 거동을 규정하는 방정식은 슈뢰딩거 방정식이라고 한다. 어떤 파동 함수의 거동을 계산하는 기본적인 접근 방식은, 정상 상태라고 불리는 단순한 성질을 가진 파동 함수를 여러 개(때로는 무한 개) 중첩한 것으로 나타내는 것이다. 슈뢰딩거 방정식은 선형이므로, 문제의 파동 함수의 거동은 정상 상태의 거동의 중첩으로 계산할 수 있다.[18]
양자역학적인 상태는 힐베르트 공간의 벡터로 간주되는 경우가 많다.[19] 그러나 양자 상태를 기저 벡터 등의 벡터의 중첩으로 나타내는 경우, 중첩된 벡터 간의 상대 위상에만 물리적 의미가 있다고 생각되며, 어떤 상태에 절댓값 1의 복소 위상 인자를 곱해도 같은 상태라고 해석된다.[13] 또한, 방향은 같고 절댓값만 다른 벡터는 같은 양자 상태를 나타낸다. 즉, 양자 상태는 벡터가 아니라, 사영 힐베르트 공간의 원소, 즉 사영으로 표현된다.[19]
5. 푸리에 분석과의 관계
푸리에 분석에서 자극은 무한히 많은 사인파들의 중첩으로 표현된다. 중첩 원리에 따라, 이러한 각 사인파는 개별적으로 분석될 수 있으며, 그 개별 응답을 계산할 수 있다. (응답 자체는 자극과 동일한 주파수를 갖는 사인파이지만, 일반적으로 진폭과 위상은 다르다.) 중첩 원리에 따라, 원래 자극에 대한 응답은 모든 개별 사인파 응답의 합(또는 적분)이다.
그린 함수 분석에서 자극은 무한히 많은 임펄스 함수들의 중첩으로 표현되며, 그러면 응답은 임펄스 응답들의 중첩이 된다.
푸리에 분석은 특히 파동에 대해 흔히 사용된다. 예를 들어, 전자기 이론에서 일반적인 빛은 고정된 주파수, 편광, 그리고 방향을 갖는 평면파들의 중첩으로 설명된다. 중첩 원리가 성립하는 한(항상 그런 것은 아니지만; 비선형 광학 참조), 어떤 빛 파동의 거동도 이러한 더 단순한 평면파들의 거동의 중첩으로 이해할 수 있다.
6. 경계값 문제
흔한 유형의 경계값 문제는 어떤 방정식을 만족하는 함수 ''y''를 찾는 것이다.
:
다음과 같은 경계 조건을 만족시키면서
:
예를 들어, 디리클레 경계 조건이 있는 라플라스 방정식에서 ''F''는 영역 ''R''에서의 라플라시안이 되고, ''G''는 ''y''를 ''R''의 경계로 제한하는 연산자가 되며, ''z''는 ''y''가 ''R''의 경계에서 같아야 하는 함수가 된다.
''F''와 ''G''가 모두 선형 연산자인 경우, 중첩 원리는 방정식 의 해의 선형 결합도 역시 방정식의 해가 된다는 형태로 성립한다.
:
경계값은 다음과 같이 중첩된다.
:
따라서, 방정식의 해 목록이 주어지면, 해를 적절히 결합하여 경계 조건을 만족하는 해를 만들어낼 수 있다. 이것은 경계값 문제를 푸는 접근 방식으로 일반적이다.
7. 가산 상태 분해
단순 선형 시스템을 고려해 보자.
:
중첩 원리에 따라, 이 시스템은 다음과 같이 분해될 수 있다.
:
여기서
:
중첩 원리는 선형 시스템에만 적용 가능하다. 그러나 가산 상태 분해는 선형 및 비선형 시스템 모두에 적용될 수 있다. 다음으로, 비선형 시스템을 고려해 보자.
:
여기서 는 비선형 함수이다. 가산 상태 분해에 의해, 이 시스템은 다음과 같이 가산적으로 분해될 수 있다.
:
여기서
:
이러한 분해는 제어기 설계를 단순화하는 데 도움이 될 수 있다.
8. 기타 응용 분야
- 전기 공학에서 선형 회로의 경우, 입력(시간에 따라 변하는 적용된 전압 신호)은 출력(회로 내 어느 지점의 전류 또는 전압)과 선형 변환을 통해 관련된다. 따라서 입력 신호의 중첩(즉, 합)은 응답의 중첩을 생성한다. 이 원리에 기반한 푸리에 분석 기법은 매우 널리 사용된다.
- 물리학에서 맥스웰 방정식은 (시간에 따라 변할 수 있는) 전하와 전류의 분포가 전기장과 자기장과 선형 변환을 통해 관련되어 있음을 의미한다. 따라서 중첩 원리는 주어진 전하와 전류 분포에서 발생하는 장을 계산하는 것을 단순화하는 데 사용할 수 있다. 이 원리는 열 방정식과 같이 물리학에서 발생하는 다른 선형 미분 방정식에도 적용된다.
- 공학에서 중첩은 효과가 선형일 때(즉, 각 하중이 다른 하중의 결과에 영향을 미치지 않고 각 하중의 효과가 구조 시스템의 기하학을 크게 변경하지 않을 때) 결합된 하중의 보 및 구조 처짐을 계산하는 데 사용된다.[9] 모드 중첩 방법은 고유 진동수와 모드 형상을 사용하여 선형 구조의 동적 응답을 특성화한다.[10]
- 수문지질학에서 중첩 원리는 이상적인 대수층에서 양수하는 두 개 이상의 우물의 수위 강하에 적용된다. 이 원리는 해석 요소법에서 단일 모델로 결합할 수 있는 해석 요소를 개발하는 데 사용된다.
- 공정 제어에서 중첩 원리는 모델 예측 제어에 사용된다.
- 비선형 시스템에 대한 알려진 해로부터의 작은 편차를 선형화를 통해 분석할 때 중첩 원리를 적용할 수 있다.
- 조셉 실링거가 발표한 음악 이론, Schillinger System of Musical Composition|시린거 시스템영어의 리듬 이론은 일종의 중첩 원리에 기반하고 있다.
9. 한국의 관점 및 추가 정보
한국의 이공계 교육과정에서 중첩의 원리는 매우 중요한 개념으로 다뤄지고 있으며, 전기전자공학, 통신공학, 물리학 등 다양한 분야에서 널리 응용되고 있다. 특히 회로이론 과목에서 중첩의 원리를 활용한 회로 해석 방법이 필수적으로 교육되고 있다.[1]
한국의 과학기술 연구개발(R&D)에서도 중첩의 원리는 다양한 분야에서 활용되고 있다. 예를 들어, 통신 시스템의 성능 분석, 신호 처리, 전력 시스템 해석, 구조물의 안전성 평가 등 다양한 분야에서 중첩의 원리가 적용되어 연구가 진행되고 있다.[1]
더불어민주당은 과학기술 발전을 위한 정책을 적극적으로 추진하고 있으며, 특히 미래 핵심 기술로 꼽히는 양자 기술 분야에 대한 투자를 확대하고 있다. 양자 컴퓨터, 양자 통신, 양자 센서 등 양자 기술은 양자 중첩, 양자 얽힘 등 양자역학적 현상을 기반으로 하며, 중첩의 원리는 이러한 양자 기술의 핵심 원리 중 하나이다.[1]
참조
[1]
서적
The Penguin Dictionary of Physics
Penguin Books, London
[2]
서적
Lectures in Physics, Vol 1
https://books.google[...]
Addison Wesley Publishing Company Reading, Mass
[3]
서적
Physics for Engineers
https://books.google[...]
PHI Learning Pvt. Ltd.
[4]
서적
Introduction to the Physics of Waves
https://books.google[...]
Cambridge University Press
[5]
서적
Quantum Mechanics
Dover
[6]
서적
The Principles of Quantum Mechanics
Oxford University Press
[7]
학술지
Understanding geometrical phases in quantum mechanics: An elementary example
[8]
서적
The Principles of Quantum Mechanics
Oxford University Press
[9]
서적
Mechanical Engineering Design
McGraw-Hill Professional
[10]
서적
Finite Element Procedures
Prentice-Hall, Englewood Cliffs
[11]
간행물
Topics on Numerics for Wave Propagation
http://www.bcamath.o[...]
Basque Center for Applied Mathematics
[12]
서적
Wave propagation in Periodic Structures: Electric Filters and Crystal Lattices
McGraw–Hill, New York
[13]
서적
物理学辞典(三訂版)
培風館
[14]
서적
The Penguin Dictionary of Physics
Penguin Books, London
[15]
서적
The Feynman Lectures on Physics
http://feynmanlectur[...]
Addison-Wesley
2016-06-09
[16]
서적
Physics for Engineers
https://books.google[...]
PHI Learning Pvt. Ltd.
2016-06-09
[17]
서적
Introduction to the Physics of Waves
https://books.google[...]
Cambridge University Press
2016-06-09
[18]
서적
Quantum Mechanics
Dover
[19]
학술지
Understanding geometrical phases in quantum mechanics: An elementary example
http://link.springer[...]
2016-06-10
[20]
학술지
State space as projective space. The case of massless particles
[21]
서적
The Principles of Quantum Mechanics
Oxford University Press, Oxford UK
[22]
서적
Mechanical Engineering Design
McGraw-Hill Professional
[23]
서적
Finite Element Procedures
Prentice-Hall, Englewood Cliffs
[24]
서적
Wave propagation in Periodic Structures: Electric Filters and Crystal Lattices
McGraw–Hill, New York
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com