지평선

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 어원
3. 특징 및 용도
4. 지평선까지의 거리
5. 지평선 너머의 물체
6. 대기 굴절의 영향
- 6.1. 굴절 보정 계산법
7. 소실점
8. 군사적 응용
참조

1. 개요

지평선은 '경계 원'을 의미하는 고대 그리스어에서 유래된 단어로, 관찰자의 시야 범위와 통신 범위를 결정하는 데 중요한 역할을 해왔다. 천문학에서는 관찰자의 눈을 통과하는 수평면을 의미하며, 투시도에서는 지구의 곡률을 무시하고 수평면의 점들이 수렴하는 이론적인 선으로 간주되기도 한다. 지평선까지의 거리는 관측자의 높이와 지구 반지름에 따라 계산되며, 대기 굴절의 영향을 받는다. 또한 그림 과학에서 소실점과 밀접한 관련이 있으며, 군사적으로는 적을 조기에 발견하기 위한 감시 수단으로 활용되어 왔다.

더 읽어볼만한 페이지

천구좌표계 - 천정
천정은 관측자의 머리 바로 위 천구상의 점으로, 천정각 측정의 기준 방향으로 사용되며, 태양의 위치, 기블라 관측, 천정 망원경, 천체항해, 그리고 지심 천정과 측지 천정의 구분에 활용된다.
천구좌표계 - 황도
황도는 지구가 태양을 공전함에 따라 지구에서 보이는 태양의 연중 겉보기 운동 경로로, 천구 적도에 대해 약 23.4° 기울어져 천문학과 점성술에서 기준면으로 사용되며, 춘분점, 추분점 결정과 일식, 월식 이해에 중요한 역할을 한다.
그리스어계 외래어 - 리듬
리듬은 음악, 무용, 언어 등에서 나타나는 시간적 패턴으로, 음악에서는 펄스, 비트, 마디 등의 시간 단위가 결합하여 형성되며, 언어학에서는 강세, 음절 등을 기준으로 분류된다.
그리스어계 외래어 - 다이아몬드
다이아몬드는 높은 경도, 열전도율, 광학적 투명도, 굴절률을 지닌 탄소 동소체로 보석 및 산업용으로 사용되지만, 채굴 과정에서 윤리적 문제가 발생하기도 하며 최근에는 합성 다이아몬드가 대체재로 부상하고 있다.

지평선

2. 어원

"지평선"이라는 단어는 그리스어 ὁρίζων κύκλος|호리존 퀴클로스^grc '경계 원'에서 유래했는데,^[2] 여기서 ὁρίζων|호리존^grc은 동사 ὁρίζω(호리조) '나누다, 분리하다'^[3]에서 유래했고, 이는 다시 ὅρος|호로스^grc '경계, 랜드마크'에서 유래했습니다.^[4]

3. 특징 및 용도

역사적으로 수평선까지의 거리는 특히 바다에서 생존과 성공적인 항해에 매우 중요했다. 수평선은 관찰자의 시야 범위와 통신 범위를 결정했기 때문이다. 이 범위는 안전과 정보 전달에 분명한 영향을 미쳤다. 라디오와 전신의 발달로 그 중요성은 줄어들었지만, 오늘날에도 항공기를 계기비행규칙에 따라 비행할 때 자세비행이라는 기법을 사용한다. 조종사는 항공기의 기수와 수평선의 시각적 관계를 이용하여 항공기를 조종하며, 수평선을 참조하여 공간 착각을 유지할 수 있다.

많은 경우, 특히 투시도에서 지구의 곡률은 무시되고 수평선은 관찰자로부터의 거리가 증가함에 따라 모든 수평면의 점들이 (화면에 투영될 때) 수렴하는 이론적인 선으로 간주된다. 해수면 근처에 있는 관찰자에게는 ''기하학적 수평선''(완벽하게 평평하고 무한한 지면을 가정)과 ''진정한 수평선''(구형 지구 표면을 가정)의 차이는 육안으로는 감지할 수 없다. 그러나 1000m 높이의 언덕에서 바다를 바라보는 사람에게는 진정한 수평선이 수평선보다 약 1도 아래에 있을 것이다.

천문학에서 수평선은 관찰자의 눈을 통과하는 수평면이다. 기본면이며 수평 좌표계의 기준이 되는, 고도가 0도인 점들의 자취이다. 기하학적 수평선과 유사하지만, 이러한 맥락에서 수평선은 그림의 선이 아니라 공간의 면으로 간주될 수 있다.

4. 지평선까지의 거리

대기 굴절 효과를 무시하면, 지구 표면 근처의 관측자에게서 보이는 진정한 지평선까지의 거리는 다음과 같다.^[5]

: $d \approx \sqrt{2\,h\,R} \,,$

여기서 ''h''는 해발 고도이고 ''R''은 지구 반지름이다.

이 식은 다음과 같이 간략화할 수 있다.

: $d \approx k \sqrt{h} \,,$

여기서 상수 ''k''는 또는 이다. 이 방정식에서는 지구 표면이 완벽한 구형이며, ''R''이 약 라고 가정한다.

지구 표면을 구면이라고 가정하고, 지평선을 바라보는 시점의 지표면으로부터의 높이를 h, 지구의 반지름을 R, 시점에서 지평선까지의 직선 거리를 x라고 하면, 시점, 지평선, 지구 중심은 직각삼각형을 이룬다. 따라서 피타고라스 정리에 의해 다음과 같은 식을 얻을 수 있다.^[6]

:x²＋R²=(R+h)²

:x=√(2Rh+h²)

:x=√{2Rh(1+h/2R)}≒√(2Rh)

:（근사식은 h/2R≒0인 경우)

높은 곳일수록 보이는 지평선은 낮아지기 때문에, 해돋이를 해발 100m에서 보면 지표에서 볼 때보다 약 2분 정도 빠르게 볼 수 있다.^[12]

4. 1. 예시

대기 굴절을 고려하지 않고 반지름 R = 6371km인 구형 지구를 가정할 경우, 관찰자의 높이에 따라 수평선까지의 거리는 다음 표와 같다.

관찰 위치	높이(h)	수평선까지의 거리(x)
지면에 서 있는 관찰자	1.7m	4.7km
지면에 서 있는 관찰자	2m	5km
언덕이나 탑	30m	19.6km
언덕이나 탑	100m	36km
부르즈 할리파 꼭대기	지면으로부터 828m, 해발 약 834m	103km
에베레스트산 정상	8848m	336km
일반적인 상업용 여객기	약 10668.00m	369km
U-2 조종사 (운용 고도 상한)	21000m	517km

지구 표면을 구면이라고 가정하고, 지평선을 바라보는 시점의 지표면으로부터의 높이를 h, 지구의 반지름을 R, 시점에서 지평선까지의 직선 거리를 x라고 하면, 시점, 지평선, 지구 중심은 직각삼각형을 이루므로, 피타고라스 정리에 의해 다음 식이 성립한다.

:x²＋R²=(R+h)²

:x=√(2Rh+h²)

:x=√{2Rh(1+h/2R)}≒√(2Rh)

:(근사식은 h/2R≒0인 경우)

따라서 지름이 지구의 1/4 정도인 달에서는 지평선까지의 거리가 지구에서의 거리의 약 절반이 된다.^[12] 예를 들어 지구에서 높이 160cm인 사람이 지평선을 바라볼 때, 지평선까지의 거리는 약 4.5km이다. 달에서는 2.35km이다.

높은 곳일수록 보이는 지평선은 낮아지기 때문에, 해돋이를 해발 100미터의 위치에서 보면 지표에서 볼 때보다 약 2분 정도 빨리 볼 수 있다.^[12]

4. 2. 다른 행성

지구형 행성과 대기 효과가 무시할 만한 다른 고체 천체에서, "표준 관찰자"에게 지평선까지의 거리는 행성 반지름의 제곱근에 비례한다. 따라서 수성에서의 지평선은 지구에서의 지평선보다 관찰자로부터 62% 거리에 있고, 화성에서는 73%, 달에서는 52%, 미마스에서는 18% 등이다.

지구 표면을 구면이라고 가정하고, 지평선을 바라보는 시점의 지표면으로부터의 높이를 h, 지구의 반지름을 R, 시점에서 지평선까지의 직선 거리를 x라고 하면, 시점, 지평선, 지구 중심은 직각삼각형을 이루므로, 피타고라스 정리에 의해 다음과 같은 식이 성립한다.

:x²＋R²=(R+h)²

:x=√(2Rh+h²)

:x=√{2Rh(1+h/2R)}≒√(2Rh)

(근사식은 h/2R≒0인 경우)

따라서, 지름이 지구의 1/4 정도인 달에서는 지평선까지의 거리는 지구에서의 그것의 약 절반이 된다.^[12] 예를 들어 지구의 어떤 지점에서 지평선까지의 거리는, 높이 160cm에 시점이 있다면 약 4.5km가 된다. 달에서는 2.35km가 된다.

4. 3. 유도

대기 굴절 효과를 무시하면, 지구 표면 근처의 관측자에게서 보이는 진정한 지평선까지의 거리는 다음과 같다.^[5]

:

d \approx \sqrt{2\,h\,R} \,,

여기서 ''h''는 해발 고도이고 ''R''은 지구 반지름이다.

이 식은 다음과 같이 간략화할 수 있다.

:

d \approx k \sqrt{h} \,,

여기서 상수 ''k''는 또는 이다. 이 방정식에서는 지구 표면이 완벽한 구형이며, ''R''이 약 라고 가정한다.

4. 3. 1. 접선-할선 정리

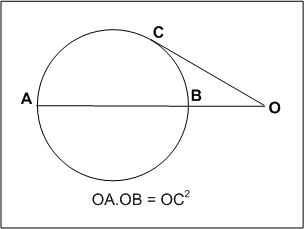
지구를 대기 굴절이 없는 특징 없는 구(지구 타원체가 아닌)로 가정하면 지평선까지의 거리를 쉽게 계산할 수 있다.^[6]

접선-할선 정리에 따르면 다음과 같다.

:OC² = OA × OB

다음과 같이 치환한다.

''d'' = OC = 지평선까지의 거리
''D'' = AB = 지구의 지름
''h'' = OB = 해발고도
''D+h'' = OA = 지구의 지름 + 해발고도

''d, D,'' 및 ''h''는 모두 같은 단위로 측정한다. 이제 공식은 다음과 같이 된다.

:d² = h(D+h)

또는

:d = √(h(D+h)) = √(h(2R+h))

여기서 ''R''은 지구의 반지름이다.

같은 방정식은 피타고라스 정리를 사용하여 유도할 수도 있다. 지평선에서 시선은 지구의 접선이며 지구 반지름에 수직이다. 이는 반지름과 높이의 합을 빗변으로 하는 직각삼각형을 만든다.

''d'' = 지평선까지의 거리
''h'' = 해발고도
''R'' = 지구의 반지름

위의 두 번째 그림을 참조하면 다음이 된다.

:(R+h)² = R² + d²

:R² + 2Rh + h² = R² + d²

:d = √(h(2R + h))

위의 정확한 공식은 다음과 같이 확장할 수 있다.

:d = √(2Rh + h²)

여기서 ''R''은 지구의 반지름이다(''R''과 ''h''는 같은 단위여야 한다). 예를 들어, 위성이 2000km의 고도에 있다면 지평선까지의 거리는 5430km이다. 괄호 안의 두 번째 항을 무시하면 5048km의 거리가 되는데, 이는 7%의 오차가 있다.

4. 3. 2. 피타고라스 정리

지구 표면을 구면이라고 가정하고, 지평선을 바라보는 시점의 지표면으로부터의 높이를 h, 지구의 반지름을 R, 시점에서 지평선까지의 직선 거리를 x라고 하면, 시점, 지평선, 지구 중심은 직각삼각형을 이룬다. 따라서 피타고라스 정리에 의해 다음과 같은 식을 얻을 수 있다.^[6]

:x²＋R²=(R+h)²

:x=√(2Rh+h²)

:x=√{2Rh(1+h/2R)}≒√(2Rh)

:（근사식은 h/2R≒0인 경우)

따라서, 지름이 지구의 1/4 정도인 달에서는 지평선까지의 거리는 지구에서의 절반 정도가 된다.^[12] 예를 들어 지구에서 높이 160cm에 시점이 있다면 지평선까지의 거리는 약 4.5km이고, 달에서는 2.35km이다.

높은 곳일수록 보이는 지평선은 낮아지기 때문에, 해돋이를 해발 100m에서 보면 지표에서 볼 때보다 약 2분 정도 빠르게 볼 수 있다.^[12]

4. 4. 근사

대기 굴절 효과를 무시하면, 지구 표면 근처의 관측자에게서 보이는 진정한 지평선까지의 거리는 다음과 같다.^[5]

:

d \approx \sqrt{2\,h\,R} \,,

여기서 ''h''는 해발 고도이고 ''R''은 지구 반지름이다.

이 식은 다음과 같이 간략화할 수 있다.

:

d \approx k \sqrt{h} \,,

여기서 상수 ''k''는 또는 이다. 이 방정식에서는 지구 표면이 완벽한 구형이며, ''R''이 약 6371km라고 가정한다.

지구상에서 특정 높이 ''h''에 대한 실제 지평선까지의 거리 그래프. ''s''는 지구 표면을 따라 측정한 거리이고, ''d''는 직선 거리이며, ''~d''는 ''h''가 지구 반지름 6371km보다 훨씬 작다고 가정할 때의 근사 직선 거리이다.

관측자가 지구 표면에 가까이 있다면, 항에서 ''h''를 무시하는 것이 타당하며, 공식은 다음과 같이 된다.

:

d = \sqrt{2Rh} \,.

''d''와 ''R''을 킬로미터 단위로, ''h''를 미터 단위로 사용하고 지구 반지름을 6371km로 하면 지평선까지의 거리는 다음과 같다.

:

d \approx \sqrt{2\cdot6371\cdot{h/1000}} \approx 3.570\sqrt{h} \,

.

야드·파운드법을 사용하여 ''d''와 ''R''을 법정 마일(육지에서 일반적으로 사용됨) 단위로, ''h''를 피트 단위로 하면 지평선까지의 거리는 다음과 같다.

:

d \approx \sqrt{2\cdot3963\cdot{h/5280}} \approx \sqrt{1.5h} \approx 1.22 \sqrt{h}

.

''d''를 해리 단위로, ''h''를 피트 단위로 하면 상수 계수는 약 1.06이며, 1에 충분히 가까워서 종종 무시하여 다음과 같이 된다.

:

d \approx \sqrt h

이러한 공식은 ''h''가 지구 반지름(6371km 또는 3959마일)보다 훨씬 작을 때 사용할 수 있으며, 산꼭대기, 비행기 또는 고고도 기구에서의 모든 시야를 포함한다. 주어진 상수를 사용하면 미터법 및 야드·파운드법 공식 모두 1% 이내의 정확도를 갖는다. ''h''가 ''R''에 비해 상당히 클 경우, 대부분의 위성과 같이 근사값은 더 이상 유효하지 않으며 정확한 공식이 필요하다.

지구 표면을 구면이라고 가정하고, 지평선을 바라보는 시점의 지표면으로부터의 높이를 h, 지구의 반지름을 R, 시점에서 지평선까지의 직선 거리를 x라고 하면, 시점, 지평선, 지구 중심은 직각삼각형을 이루므로, 피타고라스 정리에 의해,

:x²＋R²=(R+h)²

:x=√(2Rh+h²)

:x=√{2Rh(1+h/2R)}≒√(2Rh)

:（근사식은 h/2R≒0인 경우.）

따라서, 지름이 지구의 1/4 정도인 달에서는 지평선까지의 거리는 지구에서의 그것의 약 절반이 된다.^[12] 예를 들어 지구의 어떤 지점에서 지평선까지의 거리는, 높이 160cm에 시점이 있다면 약 4.5km가 된다. 달에서는 2.35km가 된다.

높은 곳일수록 보이는 지평선은 낮아지기 때문에, 해돋이를 해발 100미터의 위치에서 본 경우, 지표에서 본 경우와 비교하여 약 2분 정도 해돋이 시각이 빨라진다.^[12]

4. 5. 관련 측정

대기 굴절 효과를 무시하면, 지구 표면 근처의 관측자에게서 보이는 진정한 지평선까지의 거리는 다음과 같다.^[5]

:

d \approx \sqrt{2\,h\,R} \,,

여기서 ''h''는 해발 고도이고 ''R''은 지구 반지름이다.

이 식은 다음과 같이 간략화할 수 있다.

:

d \approx k \sqrt{h} \,,

여기서 상수 ''k''는 이다. 이 방정식에서는 지구 표면이 완벽한 구형이며, ''R''이 약 6371km라고 가정한다.

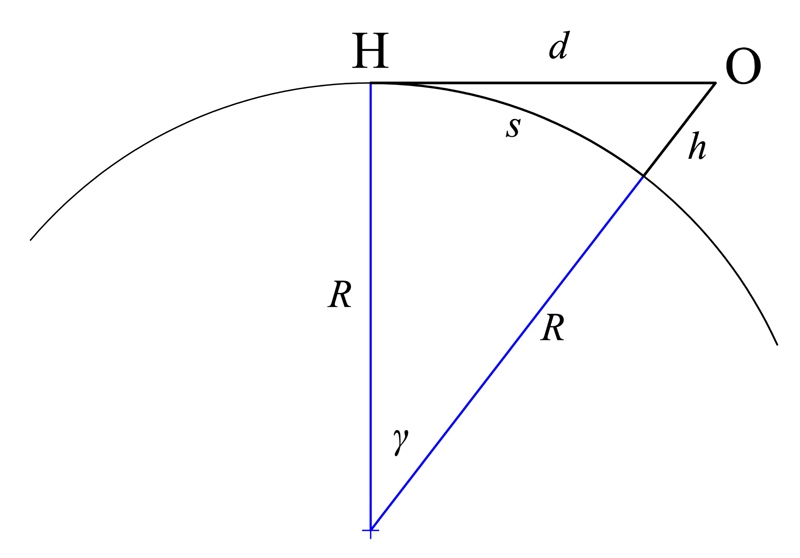
지구의 곡면을 따라 지평선까지의 호를 따라 측정한 대원거리 ''s''와의 관계는 다음과 같다. 이는 지도상의 지리적 거리와 더 직접적으로 비교할 수 있다.

라디안(radian) 단위의 ''γ''로 표현하면 다음과 같다.

:

s = R \gamma \,;

그러면

:

\cos \gamma = \cos\frac{s}{R}=\frac{R}{R+h}\,.

''s''에 대해 풀면 다음과 같다.

:

s=R\cos^{-1}\frac{R}{R+h} \,.

거리 ''s''는 시선 거리 ''d''로도 표현할 수 있다.

:

\tan \gamma = \frac {d} {R} \,;

''γ''를 대입하고 정리하면 다음과 같다.

:

s=R\tan^{-1}\frac{d}{R} \,.

물체의 높이가 반지름에 비해 무시할 수 있을 만큼 작을 때(즉, ''h'' ≪ ''R''), 거리 ''d''와 ''s''는 거의 같다.

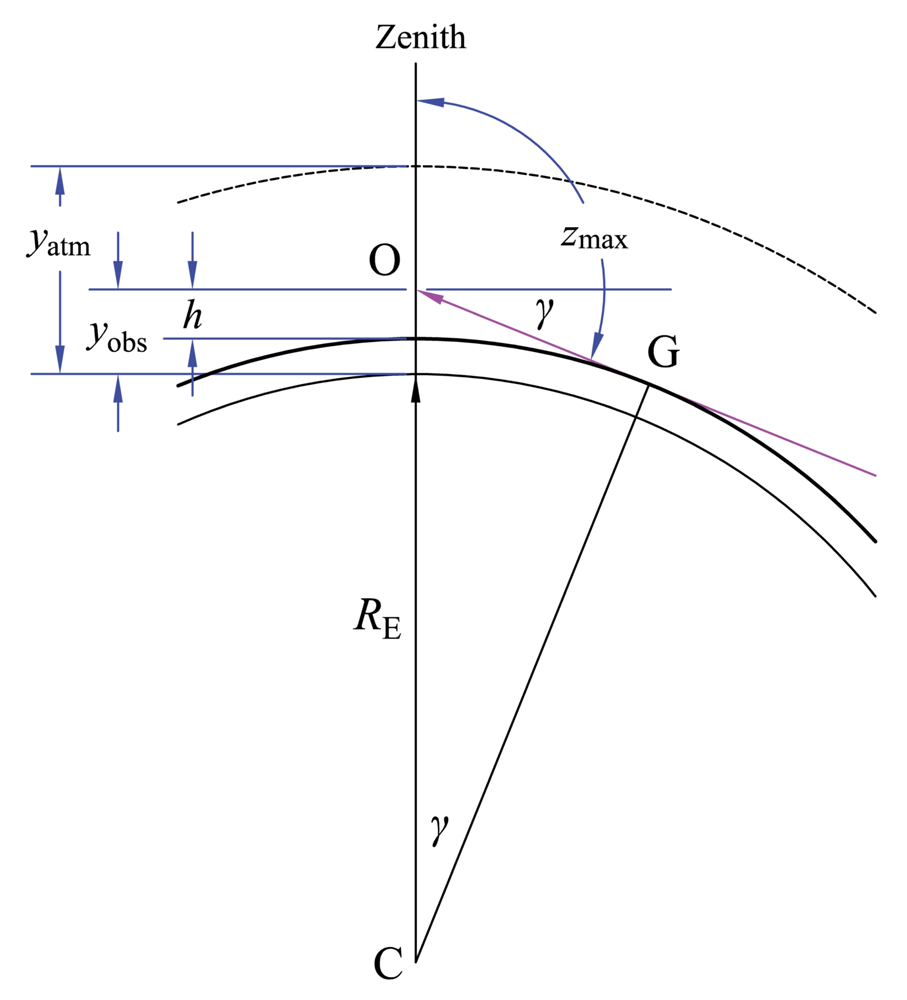
관측자가 고도에 있을 때, 지평선 천정각은 90°보다 클 수 있다. 최대 가시 천정각은 광선이 지구 표면에 접할 때 발생한다. 오른쪽 그림의 삼각형 OCG에서,

:

\cos \gamma =\frac{R}{R+h}

여기서

h

는 표면 위 관측자의 높이이고

\gamma

는 지평선의 각도 침강이다. 이것은 지평선 천정각

z

와 다음과 같은 관계가 있다.

:

z = \gamma +90{}^\circ

비음의 높이

h

에 대해 각도

z

는 항상 ≥ 90°이다.

지구 표면을 구면이라고 가정하고, 지평선을 바라보는 시점의 지표면으로부터의 높이를 h, 지구의 반지름을 R, 시점에서 지평선까지의 직선 거리를 x라고 하면, 시점, 지평선, 지구 중심은 직각삼각형을 이루므로, 피타고라스 정리에 의해,

:x²＋R²=(R+h)²

:x=√(2Rh+h²)

:x=√{2Rh(1+h/2R)}≒√(2Rh)

:（근사식은 h/2R≒0인 경우.）

따라서, 지름이 지구의 1/4 정도인 달에서는 지평선까지의 거리는 지구에서의 그것의 약 절반이 된다.^[12] 예를 들어 지구의 어떤 지점에서 지평선까지의 거리는, 높이 160cm에 시점이 있다면 약 4.5km가 된다. 달에서는 2.35km가 된다.

높은 곳일수록 보이는 지평선은 낮아지기 때문에, 해돋이를 해발 100미터의 위치에서 본 경우, 지표에서 본 경우와 비교하여 약 2분 정도 해돋이 시각이 빨라진다.^[12]

5. 지평선 너머의 물체

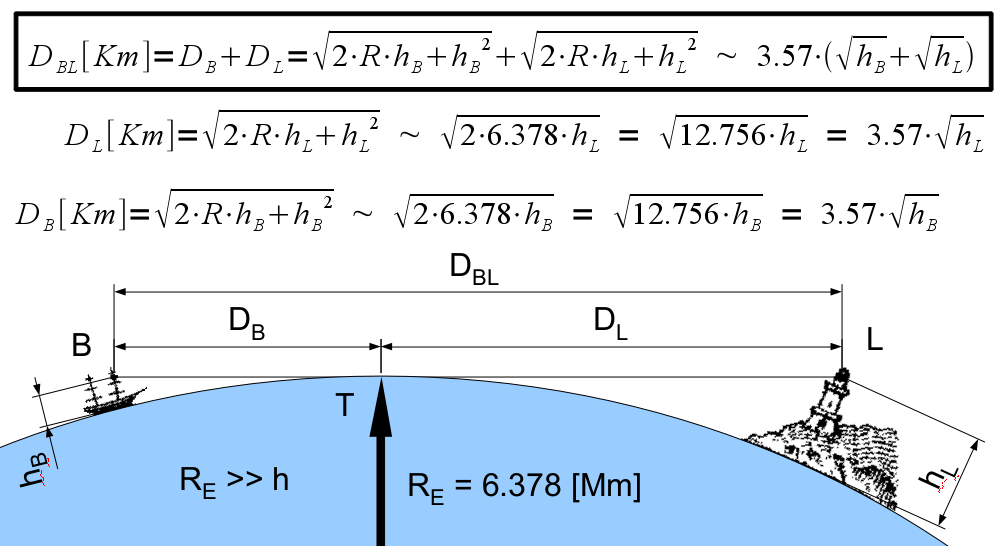
관측자 B가 지평선 위의 물체 L의 꼭대기를 볼 수 있는 최대 거리 ''D''_BL은 다음 공식으로 계산할 수 있다.

:''D''_BL = ''D''_B + ''D''_L

예를 들어, 키가 1.70m인 관측자 B가 지면에 서 있다면 지평선까지의 거리는 4.65km이다. 높이가 100m인 탑의 경우 지평선까지의 거리는 35.7km이다. 따라서 해변에 있는 관측자는 탑이 40.35km보다 멀리 떨어져 있지 않다면 탑의 꼭대기를 볼 수 있다. 반대로, 배 위에 있는 관측자(1.7m)가 근처 해안의 나무 꼭대기(10m)를 볼 수 있다면, 그 나무는 약 16km 떨어져 있을 것이다.

위의 그림을 참조하고 근사값을 사용하면, 배의 돛대 꼭대기에 있는 망대에 있는 관측자가 등대 꼭대기를 볼 수 있는지 여부를 판단할 수 있다.

:

D_\mathrm{BL} < 3.57\,(\sqrt{h_\mathrm{B}} + \sqrt{h_\mathrm{L}}) \,,

(여기서 ''D''_BL은 킬로미터, ''h''_B와 ''h''_L은 미터)

스페인 해안의 폭의 만을 가로지르는 전망. 지구의 곡률 때문에 멀리 있는 해안의 건물 기저부가 보이지 않는다.

다른 예로, 눈 높이가 지면에서 2미터인 관측자가 쌍안경으로 3.5미터 높이의 30층 건물을 볼 때, 보이는 층을 세어 10층만 있다는 것을 알게 된다. 이는 20층(70미터)이 지구 곡률 때문에 보이지 않기 때문이다. 이를 통해 건물까지의 거리를 계산할 수 있다.

:

D \approx 3.57(\sqrt{2}+\sqrt{70})

이는 약 35킬로미터이다.

마찬가지로, 지평선 위에 얼마나 많은 물체가 보이는지 계산할 수 있다. 관측자의 눈이 해수면 위 10미터에 있고 20km 떨어진 배를 보고 있다고 가정하면, 관측자의 지평선은 약 11.3km 떨어져 있다.

:

3.57 \sqrt{10}

배는 8.7km 더 멀리 있다. 관측자에게 겨우 보이는 배의 한 지점의 높이는 다음과 같다.

:

h\approx\left(\frac{8.7}{3.57}\right)^2

이는 약 6미터이다. 따라서 관측자는 수면보다 6미터 이상 높은 배의 부분만 볼 수 있고, 이보다 낮은 부분은 지구 곡률로 인해 보이지 않는다. 이러한 상황을 선체 잠복 상태라고 한다.

6. 대기 굴절의 영향

대기 굴절은 빛이 밀도가 다른 대기층을 통과하면서 휘어지는 현상이다. 이 때문에 우리가 보는 지평선은 실제 위치보다 더 멀리 있는 것처럼 보인다.

일반적으로 지구 표면 근처의 공기는 더 차갑고 밀도가 높아 빛이 아래쪽으로 휘어지면서 지구 표면을 따라 이동한다. 따라서 실제 지평선은 기하학적으로 계산된 거리보다 더 멀리 보이게 된다.^[7] 표준 대기 조건에서 이 차이는 약 8% 정도이다.

하지만 대기 조건에 따라 굴절 효과는 크게 달라진다. 예를 들어, 따뜻한 공기가 차가운 물 위에 있으면 빛이 수백 킬로미터까지 지구 표면을 따라 이동할 수 있다. 반대로 사막처럼 지표면이 매우 뜨거우면 빛이 위쪽으로 굴절되어 신기루 현상이 나타나기도 한다.^[5]

레이더의 경우에도 대기 굴절의 영향을 받지만, 시각적인 경우와는 다른 방식으로 계산된다.

6. 1. 굴절 보정 계산법

대기 굴절 때문에 보이는 지평선까지의 거리는 단순한 기하학적 계산에 의한 거리보다 더 멀다. 지표면이 위의 공기보다 차가우면, 차갑고 밀도가 높은 공기층이 형성되어 빛이 아래쪽으로 굴절되며 지구의 곡률을 어느 정도 따라간다.^[7] 반대로 지표면이 더 뜨거우면 신기루가 발생한다. 굴절에 대한 근사 보정으로, 측량사는 100미터보다 긴 거리를 측정할 때 계산된 곡률 오차에서 14%를 빼고, 시선이 지표면에서 최소 1.5미터 이상 떨어져 있도록 한다.

지구에는 대기가 있어, 밀도와 굴절률이 온도와 압력에 따라 달라진다. 이로 인해 공기가 빛을 굴절시켜 지평선의 모양에 영향을 준다. 일반적으로 지구 표면 바로 위의 공기 밀도는 고도가 높아짐에 따라 감소하여, 표면 근처의 굴절률이 커지고 빛이 아래쪽으로 굴절된다.^[7] 따라서 실제 지평선까지의 거리는 기하학적 공식으로 계산한 거리보다 멀며, 표준 대기 조건에서는 약 8%의 차이가 발생한다. 이는 미터법 공식의 3.57 계수를 약 3.86으로 변경하는 것과 같다. 예를 들어, 관측자의 눈높이가 해수면 위 1.70m라면, 대기 굴절로 인해 실제 지평선은 약 5km 떨어져 있게 된다.

이 보정은 대기 조건이 표준에 가까울 때 유효하지만, 조건이 비정상적일 경우 실패한다. 굴절은 온도 기울기에 크게 영향을 받으며, 특히 수면 위에서 날마다 다를 수 있다. 극단적인 경우, 따뜻한 공기가 차가운 물 위에 있으면 빛이 수백 킬로미터 동안 지구 표면을 따라 이동할 수 있다. 반대로 사막에서는 뜨거운 공기가 차가운 공기 아래에 있어 빛이 위쪽으로 굴절되어 신기루 효과를 일으킨다.^[5]

시각 파장 범위를 벗어나면 굴절이 달라진다. 레이더 (300~3mm 파장, 1~100GHz 주파수)의 경우 지구 반지름에 4/3을 곱하여 유효 반지름을 얻으며, 미터법 공식에서 4.12의 계수를 사용한다. 즉, 레이더 지평선은 기하학적 지평선보다 15%, 시각적 지평선보다 7% 더 멀리 있다.

대기의 밀도 프로파일을 알면, 지평선까지의 거리 ''d''는 다음과 같이 계산할 수 있다.^[8]

:

d=}\left( \psi +\delta \right) \,,

여기서 ''R''_E는 지구 반지름, ''ψ''는 지평선의 딥(dip), ''δ''는 지평선의 굴절이다. 딥은 다음과 같이 결정된다.

:

\cos \psi = \frac}}{\left( }+h \right)\mu } \,,

여기서 ''h''는 지구 위 관측자의 높이, ''μ''는 관측자 높이에서의 공기 굴절률, ''μ''₀는 지구 표면에서의 공기 굴절률이다. 굴절은 다음 적분으로 구한다.

:

\delta =-\int_{0}^{h}{\tan \phi \frac{\text{d}\mu }{\mu }} \,,

여기서

\phi\,\!

는 광선과 지구 중심을 통과하는 선 사이의 각도이며, ''ψ''와

\phi\,\!

는

\phi =90{}^\circ -\psi \,.

의 관계를 가진다.

더 간단한 방법으로, 기하학적 모델에서 반지름을 ''R′'' = 7/6 ''R''_E 로 사용하면, 지평선까지의 거리는 다음과 같다.^[5]

:

d=\sqrt{2 R^\prime h} \,.

지구 반지름을 6371km로 하면, ''d''는 km 단위, ''h''는 m 단위로,

:

d \approx 3.86 \sqrt{h} \,;

''d''는 mi 단위, ''h''는 ft 단위로,

:

d \approx 1.32 \sqrt{h} \,.

레이더의 경우 ''R′'' = 4/3 ''R''_E 를 사용하여 (''d''는 km 단위, ''h''는 m 단위로)

:

d \approx 4.12 \sqrt{h} \,;

Young 방법은 Sweer 방법과 매우 유사하며, 많은 경우에 충분히 정확하다.

7. 소실점

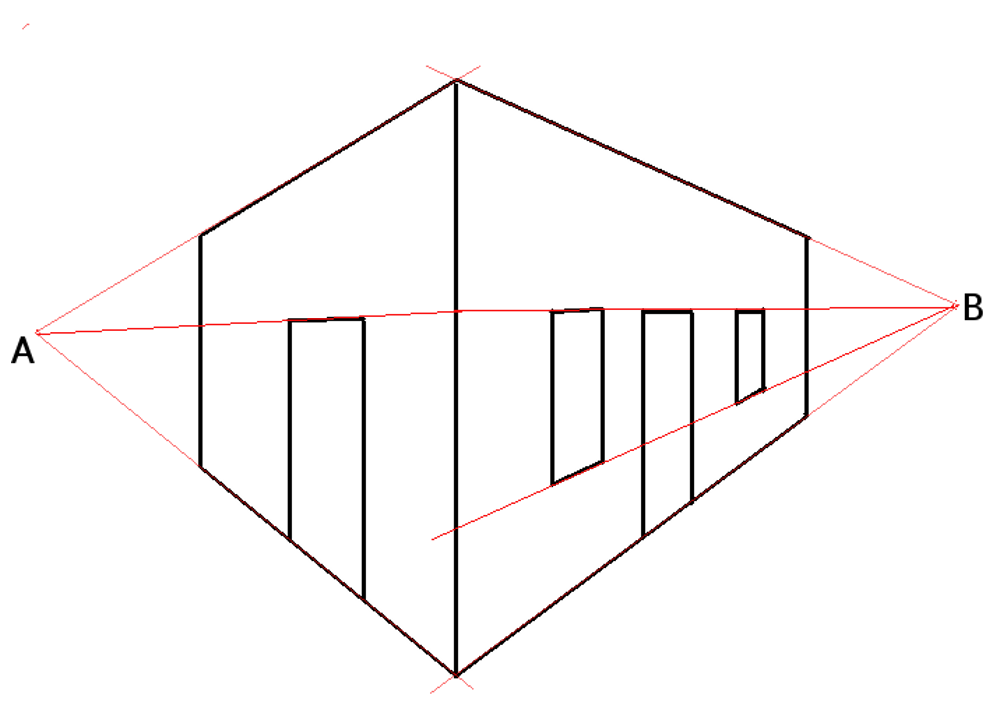
전경에 있는 건물 가장자리를 나타내는 선분을 연장한 선의 교차점에 지평선 위의 두 점이 있습니다. 여기서 지평선은 문과 창문 상단의 선과 일치합니다.

지평선은 그림면 과학에서 중요한 특징이다. 그림면이 지면에 수직으로 서 있다고 가정하고, ''P''가 시점 ''O''의 그림면에 대한 수직 투영이라고 하면, 지평선은 ''P''를 지나는 수평선으로 정의된다. 점 ''P''는 그림면에 수직인 선의 소실점이다. ''S''가 지평선상의 또 다른 점이라면, 그것은 ''OS''에 평행한 모든 선의 소실점이다. 그러나 브룩 테일러(1719)는 ''O''와 지평선에 의해 결정되는 지평면이 다른 어떤 평면과 같다고 지적했다.^[9]^[10]

평행선이 원근에서 수렴하는 투영 기하학의 특이한 기하학은 사영기하학의 발전을 자극했는데, 사영기하학은 평행선이 만나는 무한원점을 상정한다. 키르스티 안데르센은 ''기하학의 예술''(2007)이라는 책에서 1800년까지 투영 도면과 과학의 발전 과정을 설명하면서 소실점이 반드시 지평선에 있을 필요는 없다고 언급했다. 존 스틸웰은 "지평선"이라는 제목의 장에서 사영기하학이 입사기하학으로 이어졌으며, 이는 선 교차에 대한 현대적인 추상적 연구라고 설명했다. 스틸웰은 또한 "대수의 법칙은 무엇인가?"라는 제목의 섹션에서 수학의 기초로 나아갔다. 원래 칼 폰 슈타우트가 체의 공리를 유도한 "점의 대수"는 20세기에 해체되어 다양한 수학적 가능성을 제시했다. 스틸웰은 다음과 같이 말한다.^[11]

8. 군사적 응용

옛날부터 적을 조기에 발견하는 것이 중요시되어 왔기 때문에, 시점의 위치를 높이기 위해 감시탑을 건설하거나, 범선의 마스트 상부에 크로즈네스트(Crow's nest)라고 불리는 망루를 설치하거나, 정찰기, 함재 헬리콥터와 연계하게 되었다.

대함 미사일・대지 미사일 등이 실장되게 된 전투함은, 탐색뿐만 아니라 수평선 너머까지 공격하는 능력을 얻기 위해 정찰기나 미사일 등과 연계하는 시스템(예: TADIXS 등)을 개발했다.

참조

_[1] 뉴스 Offing
_[2] 뉴스 ὁρίζων https://www.perseus.[...] Perseus Digital Library 2011-04-19
_[3] 뉴스 ὁρίζω https://www.perseus.[...] Perseus Digital Library 2011-04-19
_[4] 뉴스 ὅρος https://www.perseus.[...] Perseus Digital Library 2011-04-19
_[5] 뉴스 Distance to the Horizon http://mintaka.sdsu.[...] San Diego State University Department of Astronomy 2011-04-16
_[6] 웹사이트 How far away is the horizon? http://blogs.discove[...] Kalmbach Publishing Co. 2009-01-15
_[7] 서적 Old and New Astronomy https://archive.org/[...] Longmans, Green and Company
_[8] 저널 The Path of a Ray of Light Tangent to the Surface of the Earth 1938
_[9] 서적 New Principles of Perspective
_[10] 뉴스 Brook Taylor's Work on Linear Perspective Springer 1991
_[11] 뉴스 Yearning for the Impossible https://archive.org/[...] A K Peters, Ltd. 2006
_[12] 서적 地球は本当に丸いのか？：身近に見つかる9つの証拠草思社
_[13] 뉴스 ὁρίζων http://www.perseus.t[...] Perseus Digital Library 2016-06-29

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com