척도 없는 네트워크

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 특징
4. 생성 모델
5. 척도 없는 이상적인 네트워크
6. 예시
7. 멱법칙 지수 추정
참조

1. 개요

척도 없는 네트워크는 노드의 연결 정도(차수)가 멱법칙 분포를 따르는 네트워크를 의미한다. 1965년 데릭 드 솔라 프라이스에 의해 처음 발견되었으며, 이후 알버트-라슬로 바라바시와 레카 앨버트가 월드 와이드 웹의 토폴로지를 분석하며 "척도 없는 네트워크"라는 용어를 사용했다. 이러한 네트워크는 허브 노드와 같은 특징을 가지며, 선호적 부착과 같은 생성 모델을 통해 설명된다. 척도 없는 네트워크는 소셜 네트워크, 인터넷, 생물학적 네트워크 등 다양한 분야에서 발견되며, 멱법칙 지수 추정을 통해 분석된다.

더 읽어볼만한 페이지

그래프족 - 정규 그래프
정규 그래프는 그래프 이론에서 모든 꼭짓점의 차수가 동일한 그래프를 의미하며, 각 꼭짓점이 k개의 변에 잇닿아 있는 그래프를 k-정규 그래프라고 하고, 여러 성질 및 다양한 분야에 응용된다.
그래프족 - 선 그래프
선 그래프는 주어진 그래프의 변을 정점으로, 원래 그래프에서 인접한 변들 사이의 관계를 변으로 나타내어 변들의 인접 관계를 정점 간의 관계로 표현한 그래프이다.
네트워크 - 신경망
신경망은 생물학적 뉴런과 인공 뉴런을 아우르는 개념으로, 생물학적 신경망은 전기화학적 신호 전달을 통해 근육 운동을 제어하고, 인공 신경망은 예측 모델링과 인공 지능 문제 해결에 활용된다.
네트워크 - 에티살랏
에티살랏은 1976년 설립된 아랍에미리트의 통신 회사로, 유무선 통신망 독점 운영 및 국제 통신 사업 확장, 중동 지역 경제 발전 기여, 정보 접근성 향상 등의 역할을 수행하고 있다.

척도 없는 네트워크
개요
척도 없는 네트워크의 예. 노드의 연결은 네트워크에서 노드의 순위와 거의 반비례한다.
유형	네트워크
연구 분야	네트워크 과학 그래프 이론
정의
정의	척도 없는 네트워크는 차수 분포가 멱법칙을 따르는 네트워크이다.
멱법칙 차수 분포	P(k) ~ k-γ
감마 (γ)	일반적으로 2 < γ < 3
특징
허브 노드	소수의 연결성이 높은 노드 (허브)가 존재한다.
평균 경로 길이	짧은 평균 경로 길이를 가진다.
클러스터링 계수	높은 클러스터링 계수를 가진다.
고유 경로 길이	대부분의 노드 쌍은 비교적 짧은 경로로 연결된다.
생성 모델
선호적 연결	새로운 노드가 네트워크에 연결될 때, 이미 연결성이 높은 노드에 연결될 확률이 높다.
바랍시-앨버트 (Barabási-Albert) 모델	가장 대표적인 척도 없는 네트워크 생성 모델이다.
예시
인터넷	인터넷의 라우터 연결망
월드 와이드 웹 (WWW)	웹 페이지 간의 하이퍼링크 연결망
사회 관계망	페이스북 트위터 인스타그램
생물학적 네트워크	단백질 상호작용 네트워크 유전자 조절 네트워크
분석 및 응용
네트워크 분석	네트워크의 구조와 기능 분석
전염병 확산 모델	척도 없는 네트워크에서의 전염병 확산 예측
정보 확산 모델	척도 없는 네트워크에서의 정보 확산 예측
추천 시스템	척도 없는 네트워크 기반 추천 시스템
주의 사항
주의 사항	실제 네트워크가 항상 완벽한 멱법칙을 따르지는 않으며, 척도 없는 네트워크로 간주하기 위해서는 신중한 분석이 필요하다.

2. 역사

데릭 드 솔라 프라이스는 1965년에 과학 논문 간의 인용 네트워크를 연구하면서, 논문에 대한 링크 수(즉, 인용 횟수)가 헤비 테일 분포를 가지며, 파레토 분포 또는 멱법칙을 따른다는 것을 발견했다. 이를 통해 인용 네트워크가 척도 없는 네트워크임을 밝혔다.^[9] 그러나 당시에는 "척도 없는 네트워크"라는 용어가 사용되지 않았다. 1976년, 프라이스는 인용 네트워크에서 멱법칙이 발생하는 메커니즘으로 "누적적 이점"을 제안했는데, 이는 오늘날 선호적 부착으로 더 잘 알려져 있다.

노트르담 대학교의 알버트-라슬로 바라바시와 레카 앨버트는 1999년에 월드 와이드 웹의 일부 토폴로지를 매핑하여 척도 없는 네트워크에 대한 연구를 다시 시작했다.^[9] 이들은 일부 노드("허브")가 다른 노드보다 훨씬 많은 연결을 가지며, 네트워크 전체가 노드에 연결된 링크 수에 대한 멱법칙 분포를 가진다는 것을 발견했다. 이들은 멱법칙 차수 분포를 나타내는 네트워크를 설명하기 위해 "척도 없는 네트워크"라는 용어를 만들었다. 그러나 아마랄 등은 사회, 경제, 기술, 생물학 및 물리적 시스템에서 7개의 네트워크 사례를 연구하면서 척도 없는 네트워크를 찾을 수 없었다. 이 중 영화 배우 네트워크만이 중간 ''k''에 대해 멱법칙 영역을 따르는 차수 분포 ''P''(''k'')를 가졌지만, 큰 ''k''에 대해서는 지수적 감쇠를 보여주는 컷오프로 이어졌다.^[10]

바라바시와 앨버트는 멱법칙 분포의 출현을 설명하기 위해 프라이스가 제안한 것과 본질적으로 동일한 "선호적 부착" 생성 메커니즘을 제안했다. 2000년에는 도로그프체프, 멘데스, 사무킨^[11], 그리고 크라피브스키, 레드너, 레이브라즈가 이 메커니즘에 대한 분석적 해를 제시했으며, 이는 나중에 수학자 벨라 볼로바스에 의해 엄밀하게 증명되었다.^[12] 그러나 이 메커니즘은 척도 없는 클래스의 특정 하위 집합의 네트워크만 생성하며, 이후 많은 대체 메커니즘이 발견되었다.^[13]

척도 없는 네트워크의 역사에는 몇 가지 논쟁도 있었다. 경험적 수준에서, 몇몇 네트워크의 척도 없는 특성에 대한 의문이 제기되었다. 예를 들어, 팔루토스 삼형제는 인터넷이 트레이스라우트 데이터를 기반으로 멱법칙 차수 분포를 가진다고 보았지만, 이는 라우터에 의해 생성된 3계층 착각이라는 주장이 제기되었다. 라우터는 고차수 노드로 나타나는 반면, 상호 연결되는 AS의 내부 2계층 구조를 숨긴다는 것이다.^[14]

이론적 수준에서는 척도 없는 네트워크의 추상적 정의에 대한 개선이 제안되었다. Li 등 (2005)은 더 정확한 "척도 없는 메트릭"을 제시했다. 간단히 말해, ''G''를 에지 집합 ''E''를 가진 그래프라고 하고, 정점 $v$ 의 차수 (즉, $v$ 에 인접한 에지의 수)를 $\deg(v)$ 로 나타낼 때, 다음을 정의한다.

: $s(G) = \sum_{(u,v) \in E} \deg(u) \cdot \deg(v).$

이는 고차수 노드가 다른 고차수 노드에 연결될 때 최대화된다. 그리고 다음을 정의한다.

: $S(G) = \frac{s(G)}{s_\max},$

여기서 ''s''_max는 ''G''와 동일한 차수 분포를 가진 모든 그래프 집합에서 ''H''에 대한 ''s''(''H'')의 최대 값이다. 이는 0과 1 사이의 메트릭을 제공하며, 작은 ''S''(''G'')를 가진 그래프 ''G''는 "척도 풍부"하고, 1에 가까운 ''S''(''G'')를 가진 그래프 ''G''는 "척도 없는"것으로 정의한다. 이 정의는 "척도 없는"이라는 이름에 내포된 자기 유사성의 개념을 포착한다.

3. 특징

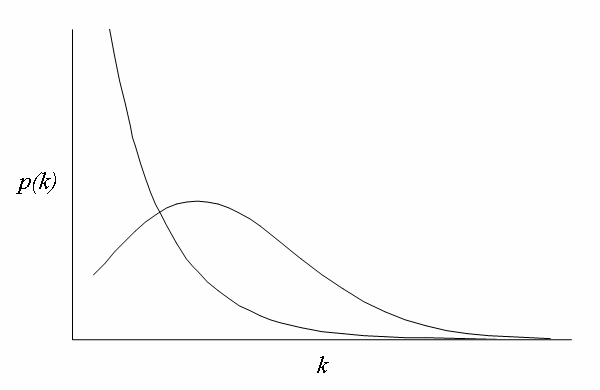
척도 없는 네트워크의 가장 두드러진 특징은 평균보다 훨씬 많은 연결을 가진 정점, 즉 "허브" 노드의 존재이다.^[18] 이러한 허브 노드는 네트워크에서 특정한 목적을 수행하는 것으로 여겨진다.

척도 없는 네트워크의 또 다른 중요한 특징은 클러스터링 계수 분포인데, 이는 노드의 차수(연결된 링크의 수)가 증가함에 따라 감소하며 멱법칙을 따른다. 이는 낮은 차수의 노드들이 매우 조밀한 서브 그래프를 형성하고, 이 서브 그래프들이 허브를 통해 서로 연결됨을 의미한다. 예를 들어, 소셜 네트워크에서 사람들은 모두가 서로를 아는 작은 커뮤니티(완전 그래프)를 형성하고, 일부 구성원은 커뮤니티 외부 사람들과도 관계를 맺는다. 이때, 많은 커뮤니티와 연결된 유명인이나 정치인 같은 사람들은 허브로 간주될 수 있으며, 이들은 스몰 월드 현상을 가능하게 한다.

선호적 부착으로 생성된 척도 없는 네트워크는 높은 차수의 정점이 네트워크 중심에 모여 코어를 형성하고, 낮은 차수의 노드들이 주변부를 구성하는 경향이 있다. 이러한 구조는 임의의 노드를 제거해도 네트워크 연결성에 큰 영향을 주지 않아 보안에 유용하지만, 허브 노드를 대상으로 하는 표적 공격에는 취약하다.

척도 없는 네트워크의 면역, 즉 인터넷 및 소셜 네트워크와 같은 현실적인 네트워크를 효율적으로 보호하는 방법에 대한 연구가 활발히 진행되고 있다.

4. 생성 모델

척도 없는 네트워크는 무작위로 생성되는 것이 아니라 특정한 생성 메커니즘을 따른다. 에르되시와 레니(1960)는 각 단계에서 두 노드를 무작위로 선택해 연결하는 그래프 성장 모델을 연구했지만, 이러한 무작위 그래프는 척도 없는 네트워크와 다른 속성을 가진다. 따라서 척도 없는 네트워크의 성장을 설명하는 모델이 필요하다.^[9]

척도 없는 네트워크의 하위 집합에 대해 가장 널리 알려진 생성 모델은 바라바시-앨버트 모델(BA 모델)이다. 이 모델은 선호적 부착을 통해 멱법칙 차수 분포를 생성한다. BA 모델 외에도 2단계 네트워크 모델, 중재 기반 부착 모델, 비선형 선호적 부착 모델, 계층적 네트워크 모델, 적합성 모델, 쌍곡 기하 그래프 등 다양한 생성 모델이 제안되었다.

척도 없는 네트워크의 역사에는 몇 가지 이견도 포함되어 있다. 경험적 수준에서, 몇몇 네트워크의 척도 없는 특성에 대해 의문이 제기되었다. 예를 들어, 팔루토스 삼형제는 인터넷이 트레이스라우트 데이터를 기반으로 멱법칙 차수 분포를 가진다고 믿었다. 그러나 이것은 라우터에 의해 생성된 3계층 착각이라는 주장이 제기되었으며, 라우터는 고차수 노드로 나타나는 반면, 상호 연결되는 AS의 내부 2계층 구조를 숨긴다.^[14]

이론적 수준에서, 척도 없는 네트워크의 추상적 정의에 대한 개선이 제안되었다. 예를 들어, Li 등 (2005)은 잠재적으로 더 정확한 "척도 없는 메트릭"을 제시했다.

4. 1. 바라바시-앨버트 모델 (BA 모델)

바라바시-앨버트 모델(BA 모델)은 척도 없는 네트워크를 만드는 데 사용되는 모델로, 성장과 선호적 부착이라는 두 가지 중요한 요소를 가지고 있다.

성장: 시간이 지남에 따라 새로운 노드(마디)가 네트워크에 추가된다.
선호적 부착: 새로운 노드는 이미 연결이 많은 노드에 연결될 확률이 더 높다.

이러한 특징은 부익부 빈익빈 현상을 만들어 내는데, 이미 연결이 많은 노드는 더 많은 연결을 얻게 되고, 연결이 적은 노드는 새로운 연결을 얻기 어려워진다.

BA 모델은 다음과 같은 방식으로 작동한다.

1. 처음에 m개의 노드로 시작한다.

2. 새로운 노드가 들어오면, 이 노드는 이미 존재하는 노드 중 m개의 노드에 연결된다.

3. 이때, 새로운 노드가 기존의 특정 노드에 연결될 확률은 그 노드의 차수(연결된 다른 노드의 수)에 비례한다. 즉, 연결이 많은 노드일수록 새로운 연결을 얻을 확률이 높아진다.^[29]

이 모델은 데릭 J. 드 솔라 프라이스가 1965년에 제안한 '누적적 이점' 모델과 본질적으로 동일하며,^[9] 1976년에는 "누적적 이점"이라고 불렀지만 오늘날에는 일반적으로 선호적 부착이라는 이름으로 알려져 있다. 프라이스 모형의 무방향 버전으로 볼 수 있다. 2000년에는 도로그프체프, 멘데스, 사무킨^[11]이 분석적 해를 제시했고, 크라피브스키, 레드너, 레이브라즈도 독립적으로 해를 발견했다. 이후 수학자 벨라 볼로바스가 이를 엄밀하게 증명했다.^[12]

BA 모델은 멱법칙 분포를 따르는 차수 분포를 가진 네트워크를 생성한다. 즉, 소수의 노드가 매우 많은 연결을 가지고 있고, 대다수의 노드는 적은 수의 연결을 가지는 형태이다. 이러한 특징은 실제 월드 와이드 웹을 비롯한 다양한 실제 네트워크에서 관찰되는 현상이다.^[9]

하지만 BA 모델이 척도 없는 네트워크의 유일한 생성 메커니즘은 아니다. 다른 많은 대체 메커니즘이 존재하며, 네트워크의 특성에 따라 다른 모델이 더 적합할 수 있다.^[13]

4. 2. 2단계 네트워크 모델

Dangalchev(^[1])는 선호적 연결에서 대상 노드의 각 이웃의 중요성을 고려하여 2-L 모델을 구축했다. 2-L 모델에서 노드의 매력도는 연결된 노드의 수뿐만 아니라 각 노드에 있는 링크의 수에 따라서도 달라진다.

:

\Pi(k_i)=\frac{k_i + C \sum_{(i,j)} k_j}{\sum_j k_j + C \sum_j k_j^2},

여기서 ''C''는 0과 1 사이의 계수이다.

2-L 모델의 변형인 k2 모델은 첫 번째 및 두 번째 이웃 노드가 대상 노드의 매력도에 동일하게 기여하며, 일시적인 척도 없는 네트워크의 출현을 보여준다.^[8] k2 모델에서 차수 분포는 네트워크가 비교적 작을 때는 대략 척도 없는 것으로 나타나지만, 네트워크가 커짐에 따라 척도 없는 체제에서 상당한 편차가 발생한다. 이는 서로 다른 차수를 가진 노드의 상대적인 매력도가 시간이 지남에 따라 변화하는 결과를 가져오며, 이는 실제 네트워크에서도 관찰되는 특징이다.

4. 3. 중재 기반 부착 모델 (MDA 모델)

중재 기반 부착(MDA) 모델에서, m개의 연결선을 가진 새로운 노드는 무작위로 기존에 연결된 노드를 선택한다. 그 후 해당 노드가 아닌 그 노드의 이웃 m개와 연결을 맺는데, 이웃 또한 무작위로 선택된다. 선택된 기존 노드 i일 확률 Π(i)는 다음과 같다.

:

\Pi(i) = \frac{k_i} N \frac{\sum_{j=1}^{k_i} \frac 1 {k_j} }{k_i}.

요인

\frac{\sum_{j=1}^{k_i} \frac 1 {k_j} }{k_i}

는 노드 i의 k개 이웃의 차수의 조화 평균의 역수(IHM)이다. 광범위한 수치 조사를 통해, 대략 m > 14일 경우, 큰 N 극한에서 평균 IHM 값은 상수가 되며, 이는 Π(i) ∝ k임을 의미한다. 이는 노드가 가진 연결선(차수)이 많을수록 중재자를 통해 더 많은 방식으로 연결될 기회가 높아진다는 것을 의미하며, 이는 본질적으로 부익부 현상(또는 바르바시-알버트 모델의 선호적 부착 규칙)의 직관적인 아이디어를 구현한다. 따라서 MDA 네트워크는 숨겨진 PA 규칙을 따른다고 볼 수 있다.^[39]

그러나, m=1일 경우, 거의 99%의 전체 노드가 차수 1을 가지고 하나의 노드가 차수에서 매우 풍부하다는 것을 알 수 있듯이, 승자 독식 메커니즘을 설명한다. m 값이 증가함에 따라 매우 풍부한 노드와 가난한 노드 사이의 불균형이 감소하고, m>14일 때 매우 풍부해지는 현상에서 부익부 현상으로의 전환을 발견한다.

4. 4. 비선형 선호적 부착 모델

바라바시-앨버트 모델은 노드가 노드

i

에 부착될 확률

\Pi(k)

가 노드

i

의 차수

k

에 비례한다고 가정한다. 이는

\Pi(k)

가

k

에 의존하며,

\Pi(k) = p

인 랜덤 그래프와 대조적이다. 또한,

\Pi(k)

의 함수 형태가

k

에 대해 선형이라는 가정을 포함한다.

비선형 선호적 부착에서

\Pi(k)

의 형태는 선형이 아니며, 최근 연구에 따르면 차수 분포는 함수

\Pi(k)

의 모양에 크게 의존하는 것으로 나타났다.

Krapivsky, Redner 및 Leyvraz^[34]는 비선형 선호적 부착의 경우 네트워크의 척도 없는 특성이 파괴된다는 것을 보여준다. 네트워크의 위상이 척도 없는 유일한 경우는 선호적 부착이 점근적으로 선형인 경우, 즉

k_i \to \infty

일 때

\Pi(k_i)  \sim a_\infty k_i

인 경우이다. 이 경우 율 방정식은 다음을 유도한다.

:

P(k) \sim k^{-\gamma}\text{ with }\gamma = 1 + \frac \mu {a_\infty}.

이러한 방식으로 차수 분포의 지수는 2에서

\infty

사이의 모든 값으로 조정될 수 있다.

4. 5. 계층적 네트워크 모델

반복적인 구성을 통해 척도 없는 네트워크를 생성하는 모델이다.^[40]

반복적 구성은 계층적 네트워크로 이어진다. 5개의 노드로 구성된 완전 연결 클러스터에서 시작하여, 각 클러스터의 주변 노드를 원래 클러스터의 중앙 노드에 연결하는 4개의 동일한 복제본을 생성한다. 이를 통해 25개 노드(''N'' = 25)의 네트워크를 얻는다.

같은 과정을 반복하면, 원래 클러스터의 복제본을 4개 더 만들 수 있는데, 각 복제본의 4개 주변 노드는 첫 번째 단계에서 생성된 노드의 중앙 노드에 연결된다. 이렇게 하면 ''N'' = 125가 되며, 이 과정은 무한정 계속될 수 있다.

4. 6. 적합성 모델

두 정점 간의 연결은 모든 정점 쌍에 대해 동일한 확률 ''p''로 무작위로 할당되지 않는다. 대신, 모든 정점 ''j''에는 고유한 ''적합도'' ''x''_''j''가 있으며, 정점 ''i''와 ''j'' 사이의 연결은 확률

p(x_i,x_j)

로 생성된다.^[41]

세계 무역 웹의 경우, 국가의 적합도로 GDP를 사용하며,

:

p(x_i,x_j)=\frac {\delta x_ix_j}{1+\delta x_ix_j}.

^[42]를 사용하여 모든 속성을 재구성할 수 있다.

4. 7. 쌍곡 기하 그래프

네트워크가 기저 쌍곡 기하학을 가지고 있다고 가정하면, 공간 네트워크의 프레임워크를 사용하여 척도 없는 차수 분포를 생성할 수 있다. 이러한 이질적인 차수 분포는 단순히 기저 쌍곡 기하학의 음의 곡률 및 메트릭 속성을 반영한다.^[43]

5. 척도 없는 이상적인 네트워크

네트워크 이론에서 '''척도 없는 이상적인 네트워크'''는 차수 분포가 척도 없는 이상 기체의 확률 밀도 함수를 따르는 랜덤 네트워크이다. 이러한 네트워크는 경쟁적인 클러스터 성장 과정이 네트워크에 적용될 때 복잡한 네트워크에 대한 정보 이론을 통해 사회 집단의 크기 분포를 풀어 설명할 수 있으며, 이를 통해 도시 크기 분포와 선거 결과를 재현할 수 있다.^[44]^[45] 척도 없는 이상적인 네트워크 모델에서는 던바의 수가 '여섯 단계의 분리' 현상의 원인임을 증명할 수 있다.

6. 예시

다양한 현실 세계의 네트워크가 척도 없는 네트워크로 간주된다. 몇 가지 예시는 다음과 같다.

소셜 네트워크: 영화 배우 협업, 논문 공동 저술 등^[10]
컴퓨터 네트워크: 인터넷, 월드 와이드 웹의 웹 그래프 등
금융 네트워크: 은행 간 지불 네트워크 등^[21]^[22]
생물학적 네트워크: 단백질-단백질 상호작용 네트워크 등
의미론적 네트워크^[23]
항공 네트워크

고온 초전도체에서도 척도 없는 토폴로지가 발견되었다.^[24]

7. 멱법칙 지수 추정

척도 없는 네트워크의 멱함수 지수 $\gamma$ 를 추정하는 것은 일반적으로 몇 개의 균일하게 샘플링된 노드의 차수를 사용하여 최대 우도 추정을 수행함으로써 이루어진다.^[3] 그러나 균일 샘플링은 멱함수 차수 분포의 중요한 헤비테일에서 충분한 표본을 얻지 못하므로, 이 방법은 큰 편향과 분산을 초래할 수 있다. 최근에는 우정의 역설의 결과로 차수 분포의 꼬리에서 나올 가능성이 더 높은 무작위 친구(즉, 무작위 링크의 무작위 끝)를 샘플링하는 방법이 제안되었다.^[47]^[48] 이론적으로, 무작위 친구를 이용한 최대 우도 추정은 균일 샘플링에 기반한 고전적인 접근 방식에 비해 더 작은 편향과 더 작은 분산을 보인다.^[48]

참조

_[1] 논문 Structure and tie strengths in mobile communication networks
_[2] 논문 Scale-Free Graph with Preferential Attachment and Evolving Internal Vertex Structure
_[3] 논문 Power-law distributions in empirical data
_[4] 논문 Scale-free networks are rare 2019-03-04
_[5] 논문 Rare and everywhere: Perspectives on scale-free networks 2019-12
_[6] 논문 Critical Truths About Power Laws 2012-02-10
_[7] 논문 Scale-free networks as preasymptotic regimes of superlinear preferential attachment 2008-08-21
_[8] 논문 Identifying time dependence in network growth 2020-06-18
_[9] 논문 Emergence of scaling in random networks 1999-10-15
_[10] 논문 Classes of small-world networks
_[11] 논문 Structure of Growing Networks with Preferential Linking
_[12] 논문 The degree sequence of a scale-free random graph process
_[13] 논문 Evolution of networks
_[14] 논문 Mathematics and the Internet: A Source of Enormous Confusion and Great Potential http://authors.libra[...] American Mathematical Society 2011-02-03
_[15] 논문 Emergence of scaling in random networks 1999-10-15
_[16] 서적 Statistical Field Theory: Volume 1, From Brownian Motion to Renormalization and Lattice Gauge Theory Cambridge University Press
_[17] 서적 Statistical Field Theory: Volume 2, Strong Coupling, Monte Carlo Methods, Conformal Field Theory and Random Systems Cambridge University Press
_[18] 논문 Scale-Free Networks beyond Power-Law Degree Distribution
_[19] 논문 Scale-Rich Metabolic Networks
_[20] 논문 Generating correlated networks from uncorrelated ones
_[21] 논문 Fitness model for the Italian interbank money market
_[22] 논문 The topology of interbank payment flows
_[23] 논문 The Large-Scale Structure of Semantic Networks: Statistical Analyses and a Model of Semantic Growth
_[24] 논문 Scale-free structural organization of oxygen interstitials in La2CuO4+y
_[25] 논문 Optimum inhomogeneity of local lattice distortions in La2CuO4+y
_[26] 논문 Scale-free network topology and multifractality in a weighted planar stochastic lattice
_[27] 논문 Scale-free coordination number disorder and multifractal size disorder in weighted planar stochastic lattice
_[28] 간행물 Stochastic Models for the Web Graph http://cs.brown.edu/[...] 2016-02-10
_[29] 논문 Network biology: understanding the cell's functional organization
_[30] 논문 Generation models for scale-free networks https://zenodo.org/r[...] 2004-07
_[31] 문서 Barabási, A.-L. and R. Albert, Science '''286''', 509 (1999).
_[32] 문서 R. Albert, and A.L. Barabási, Phys. Rev. Lett. '''85''', 5234(2000).
_[33] 문서 S. N. Dorogovtsev, J. F. F. Mendes, and A. N. Samukhim, cond-mat/0011115.
_[34] 문서 P.L. Krapivsky, S. Redner, and F. Leyvraz, Phys. Rev. Lett. '''85''', 4629 (2000).
_[35] 문서 B. Tadic, Physica A '''293''', 273(2001).
_[36] 논문 Scale-free behavior of networks with the copresence of preferential and uniform attachment rules
_[37] 문서 S. Bomholdt and H. Ebel, cond-mat/0008465; H.A. Simon, Bimetrika '''42''', 425(1955).
_[38] 논문 Scale-Free Networks beyond Power-Law Degree Distribution
_[39] 논문 Degree distribution, rank-size distribution, and leadership persistence in mediation-driven attachment networks
_[40] 논문 Hierarchical organization in complex networks
_[41] 논문 Scale-free networks from varying vertex intrinsic fitness http://eprints.imtlu[...]
_[42] 논문 Fitness-Dependent Topological Properties of the World Trade Web
_[43] 논문 Hyperbolic geometry of complex networks
_[44] arXiv Unravelling the size distribution of social groups with information theory on complex networks
_[45] 논문 Competitive cluster growth in complex networks
_[46] arXiv Distributed Maximal Independent Set on Scale-Free Networks
_[47] 논문 Tail-scope: Using friends to estimate heavy tails of degree distributions in large-scale complex networks 2015-05-11
_[48] 논문 Maximum Likelihood Estimation of Power-law Degree Distributions via Friendship Paradox-based Sampling 2021-05-19

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com