펜로즈 삼각형
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
펜로즈 삼각형은 고체 물체처럼 보이지만 실제로는 유클리드 공간에서 실현될 수 없는 불가능한 도형이다. 정사각형 단면을 가진 세 개의 빔이 삼각형의 꼭짓점에서 직각으로 만나 형성된 것처럼 보이며, 특정 각도에서 볼 때 2차원 묘사와 동일하게 보이는 3차원 조형물로도 제작된다. 펜로즈 삼각형을 따라 선을 그리면 4-루프 뫼비우스 띠가 형성된다. 펜로즈 삼각형은 M.C. 에셔의 석판화 '폭포'에 묘사되었으며, 오스트레일리아 퍼스, 오스트리아 고추첸, 독일 바서부르크 암 인 등 여러 지역에 조형물로 제작되었다. 펜로즈 삼각형과 유사하게 정사각형, 오각형, 육각형, 팔각형 등 다른 정다각형을 이용하여 펜로즈 다각형을 만들 수 있다.
더 읽어볼만한 페이지
- 불가능한 물체 - 조반니 바티스타 피라네시
이탈리아 출신 조반니 바티스타 피라네시는 판화 연작 "베두테"와 "가상의 감옥"으로 유명하며, 건축가, 고고학자, 미술 이론가로서 신고전주의 건축과 낭만주의 예술에 큰 영향을 미쳤다. - 불가능한 물체 - 펜로즈의 계단
펜로즈의 계단은 시각적 착시를 이용한 불가능한 도형으로, 끊임없이 오르내릴 수 있는 계단을 묘사하며, M.C. 에셔의 작품과 영화, 앨범 커버 등 대중문화에 영향을 미쳤다. - 위상수학 - 뫼비우스의 띠
"상상력" 한가 아닌 답변을 바랍니다. - 위상수학 - 공간
공간은 물체의 위치와 운동을 기술하는 배경으로, 시간과 함께 시공간을 구성하며, 학문 분야에 따라 정의와 관점이 다르지만, 현대 물리학에서는 고차원 공간을 가정하기도 한다. - 착시 - 달 착시
달 착시는 달이 지평선 근처에 있을 때보다 머리 위에 있을 때 더 작게 보이는 착시 현상으로, 대기 굴절, 겉보기 거리, 상대적 크기, 시선각 등 다양한 가설이 제시되었으나 아직 명확히 규명되지 않았다. - 착시 - 폰조 착시
폰조 착시는 길이가 동일한 두 선분을 수렴하는 선 위에 배치했을 때 위쪽 선분이 더 길어 보이는 착시 현상으로, 원근법에 기반한 깊이 인식 오류와 주변 시각 정보에 의해 발생하며, 시각적 경험이 없는 선천적 시각 장애인에게는 나타나지 않는다.
| 펜로즈 삼각형 | |
|---|---|
| 개요 | |
 | |
| 종류 | 불가능한 물체 |
| 다른 명칭 | 펜로즈 삼각형 펜로즈 삼각봉 |
| 상세 정보 | |
| 정의 | 시각적으로는 3차원 물체처럼 보이지만, 실제로는 존재할 수 없는 도형 |
| 착시 원리 | 3차원 공간에서의 투영으로 인해 착시가 발생함 |
| 관련 개념 | 불가능한 도형 착시 |
| 창시자 | 오스카르 로이터스베르트 (선구자) |
| 대중화 | 로저 펜로즈 |
| 특징 | 3개의 모서리가 각각 직각으로 연결된 삼각형 형태를 띔 각 모서리는 입체적인 사각 기둥처럼 보임 전체적으로는 닫힌 삼각형 형태를 이루지만, 실제로는 3차원 공간에서 연결될 수 없음 |
| 활용 | |
| 예술 | M. C. 에셔의 작품 "폭포"와 "오르막과 내리막" 등 |
| 건축 | 불가능한 건축 구조물의 표현 |
| 디자인 | 착시 효과를 활용한 디자인 요소 |
| 기타 | |
| 참고 문헌 | Pappas (1989) Brorub (2013) Zeng, Xu, Yang & Li (2021) Ernst (2012) Penrose & Penrose (1958) |
2. 특징
M.C. 에셔의 석판화 폭포(1961)는 두 개의 길쭉한 펜로즈 삼각형을 활용하여, 시작점보다 높은 곳에서 끝나는 수로를 묘사하고 있다. 폭포는 물레방아를 돌리는데, 에셔는 물레방아를 계속 돌리기 위해서는 때때로 증발을 보충하기 위해 물을 추가해야 한다고 설명한다.[2]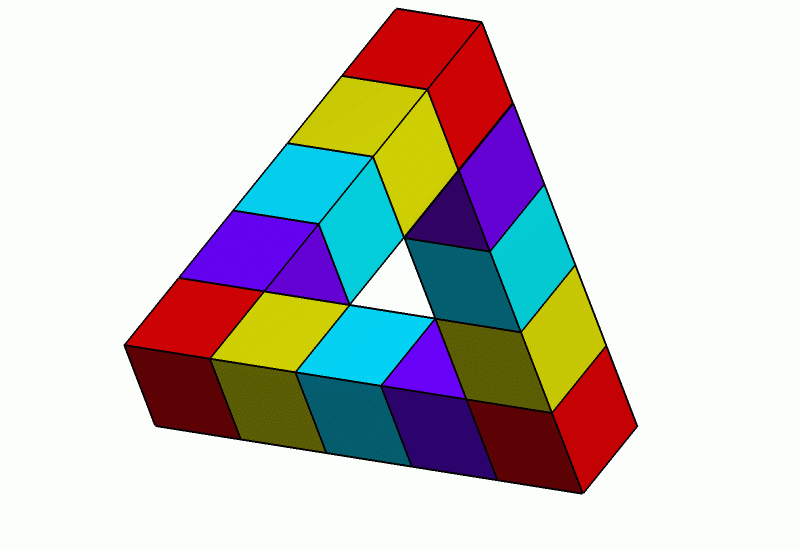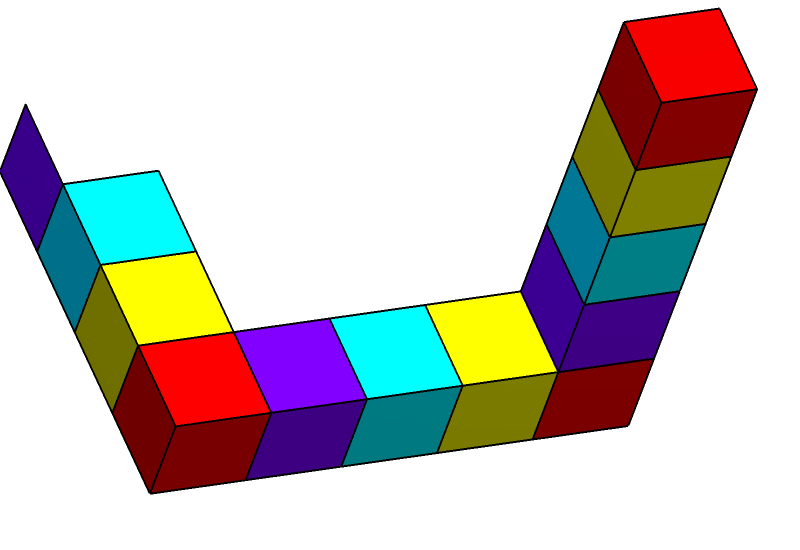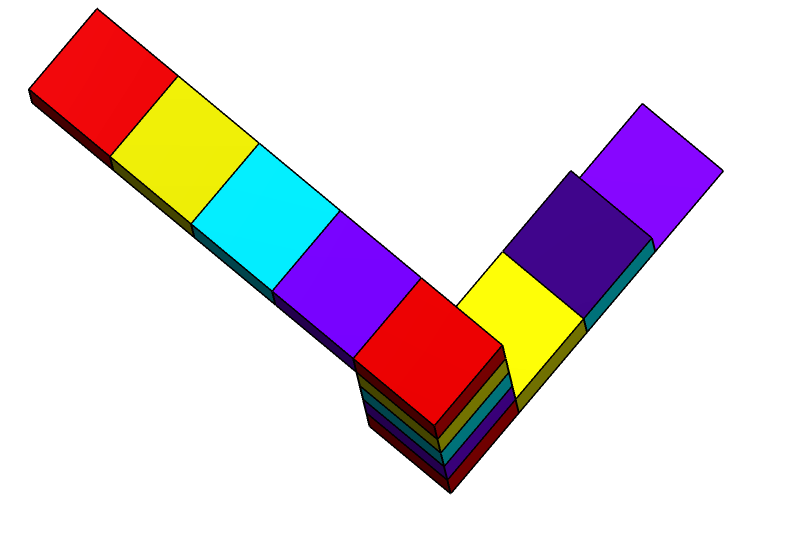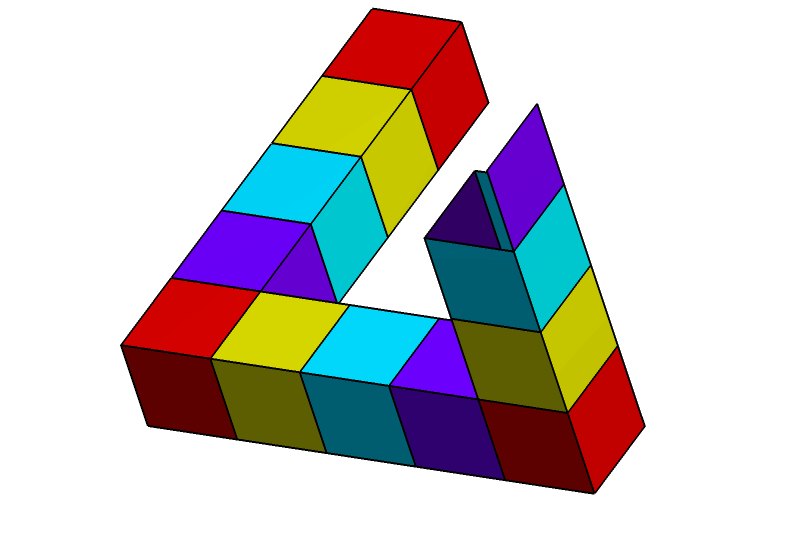
펜로즈 삼각형은 정사각형 단면을 가진 세 개의 직선 빔이 삼각형의 꼭짓점에서 쌍으로 직각으로 만나 형성되는 것처럼 보이는 고체 물체이다. 이 빔들은 잘려져서 정육면체 또는 직육면체를 형성할 수 있다.
이러한 속성의 조합은 일반적인 유클리드 공간에서는 3차원 물체로 실현될 수 없다. 그러나 이러한 물체는 특정 유클리드 3-다양체에서 존재할 수 있다.[1] 또한, 특정 각도에서 볼 때 이 페이지의 펜로즈 삼각형의 2차원 묘사와 동일하게 보이는 3차원 고체 모양이 존재한다 (예: 오스트레일리아 퍼스에 있는 조각상). "펜로즈 삼각형"이라는 용어는 2차원 묘사 또는 불가능한 물체 자체를 지칭할 수 있다.
펜로즈 삼각형을 따라 선을 그리면 4-루프 뫼비우스 띠가 형성된다.[4]
3. 묘사

펜로즈 삼각형은 2차원 그림뿐만 아니라, 특정 각도에서 볼 때 펜로즈 삼각형으로 보이는 3차원 조형물로도 제작된다. 펜로즈 삼각형의 면을 따라가면 4중의 뫼비우스의 띠가 된다.[4]
3. 1. 조형물
4. 다른 펜로즈 다각형
펜로즈 삼각형과 유사하게, 정사각형, 오각형, 육각형, 팔각형 등 다른 정다각형을 이용하여 펜로즈 다각형을 만들 수 있다. 그러나 각이 증가함에 따라 단순히 굽어 있거나 비틀려 보이는 경향이 있다.
참조
[1]
간행물
Maple in Mathematics Education and Research: 4th Maple Conference, MC 2020, Waterloo, Ontario, Canada, November 2–6, 2020, Revised Selected Papers
Springer International Publishing
[2]
서적
M. C. Escher: The Graphic Work
Taschen
[3]
서적
A topological picturebook
Springer
[4]
서적
별책 사이언스/수학 게임Ⅲ
일본경제신문사
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com




