평사 투영

2. 역사

평사 투영법의 기원은 정확하지 않지만, 고대 그리스 천문학자들로부터 발견되었고, 별과 행성들의 움직임을 평면 기하학으로 해석하기 위해 천구를 평면에 사영시킬 때 사용되었다고 알려져있다. 현존하는 가장 오래된 설명은 프톨레마이오스의 플라니스피어(기원전 2세기)에서 찾을 수 있지만, 시네시우스(기원전 400년경)가 히파르쿠스(기원전 2세기)에게 모호하게 기인했으며 아폴로니우스의 원뿔(기원전 200년경)에는 평사 투영법이 원과 원을 매핑한다는 특성을 증명하는 데 중요한 정리가 포함되어 있다.

알렉산드리아의 테온(4세기) 시기까지, 평사 투영도는 디옵트라와 결합되어 성반이라는 휴대 가능한 장치로 발전했다. 이 장치는 별의 위치를 측정하고 다양한 천문학적 계산을 수행할 수 있었다. 성반은 비잔티움 천문학자들에 의해 지속적으로 사용되었으며, 중세 이슬람 천문학자들에 의해 크게 발전되었다. 이 기술은 11세기에서 12세기에 아랍어 문서들이 라틴어로 번역되면서 서유럽으로 전해졌다.

16세기와 17세기에 이르러, 평사투영의 적도면 투영 방식은 동반구와 서반구의 지도를 제작하는 데 흔히 사용되었다. 1507년 발터리우스 루드(Gualterius Lud)가 제작한 지도가 평사 투영으로 그려졌을 가능성이 있으며, 이후 장 로제(Jean Roze, 1542), 루몰드 메르카토르(Rumold Mercator, 1595) 등의 지도에서도 사용되었다. 성도에서는 이미 고대 천문학자들, 예를 들어 프톨레마이오스 등이 이 적도 투영 방식을 사용했다.

3. 정의

3. 1. 첫번째 정의

삼차원 공간 '''R'''³에 있는 단위구 ''S''²는 ''x''² + ''y''² + ''z''² = 1이 되는 점 (''x'', ''y'', ''z'')의 집합이다. ''N'' = (0, 0, 1) 이 "북극"이라고 하고, ''M''은 구의 나머지 부분들이다. 평면 ''z'' = 0은 구의 중심을 뚫고 지나가며, 이 '적도'는 구와 이 평면의 교집합이다.

''M'' 위의 임의의 점 ''P'' 에 대하여 점 ''P'' 를 지나는 직선 ''N'' 은 항상 유일하게 존재한다. 그리고 이 직선 ''N'' 은 평면 z = 0 과 오로지 한 점 ''P''′ 에서 만나며, 이 점을 점 ''P'' 의 평면 z = 0 위로의 '''평사 투영'''이라고 한다.

데카르트 좌표계에서 구 위의 (''x'', ''y'', ''z'')와, 그를 평면 위로 사영 시킨 점 (''X'', ''Y'')에 대하여 둘의 관계는 다음과 같다.

:

(x, y, z) &= \left(\frac{2 X}{1 + X^2 + Y^2}, \frac{2 Y}{1 + X^2 + Y^2}, \frac{-1 + X^2 + Y^2}{1 + X^2 + Y^2}\right).\end{align}

구면좌표계에서 구 위의 점 (''φ'', ''θ'') (''φ''는 천정각, 0 ≤ ''φ'' ≤ π, ''θ''는 방위각, 0 ≤ ''θ'' ≤ 2π) 과 극좌표계에서 평면 위의 점 (''R'', ''Θ'')에 대하여 평사 투영과 그 역은 다음과 같다.

:

(\varphi, \theta) &= \left(2 \arctan \frac{1}{R}, \Theta\right).\end{align}

여기서, R = 0 일 때 φ = π 라고 이해된다. 그 뿐만 아니라 이 공식은 삼각함수 항등식에 의해 여러 다른 형태로 다시 표현할 수 있다. 원통 좌표계에서 구 위의 점 (''r'', ''θ'', ''z'') 과 극좌표계에서 평면 위의 점 (''R'', ''Θ'')에 대하여 평사 투영과 그 역은 다음과 같다.

:

(x, y, z) &= \left(\frac{2 \operatorname{Re} \xi}{1 + \bar \xi \xi}, \frac{-2 \operatorname{Im} \xi}{1 + \bar \xi \xi}, \frac{1 - \bar \xi \xi}{1 + \bar \xi \xi}\right)\end{align}

3. 2. 다른 협약들

몇몇 저자들은 평사 투영을 북극 (0, 0, 1)에서 단위구와 남극 (0, 0, -1)에서 접하는 평면 ''z'' = -1 위로의 투영으로 정의한다. 이는 위에서 설명한 적도면 위로 점을 투영시키는 함수와, 그것을 극좌표 평면 위로 중심 닮음 변환을 하는 함수의 합성으로 표현할 수 있다. 중심 닮은 변환은 상을 2배율로 키우므로(구의 반지름에 대한 지름의 비율), 이 투영을 통해 나온 ''X'' 와 ''Y''는 앞서 설명한 적도 투영법보다 정확히 2배의 값을 가지게 된다. 예를 들어서, 적도를 이 방법으로 투영하면 적도보다 2배의 반지름을 가지고 중심이 같은 축에 있는 원이 그려진다. 적도 투영은 적도에서 무한대 면적 왜곡을 생성하지 않지만, 이 극-접평면 투영은 대신 남극에서 무한대 면적 왜곡을 생성하지 않는다.

또 다른 저자들은 반지름이 1/2 인 구와 ''z'' = -1/2 인 평면을 사용하여 평사 투영을 정의하기도 한다.

일반적으로, 구 위의 임의의 점 ''Q'' 에 대해 아래 조건을 만족시키는 평면 ''E'' 로 투영 시키는 것을 "평사 투영"이라고 정의할 수 있다.

• ''E'' 는 ''Q'' 를 지나는 구의 반지름과 평행하다.
• ''E'' 는 ''Q'' 를 포함하고 있지 않다.

사영기하학상의 임의의 점 P에 대해서, N 과 P를 통과하는 고유한 선이 있으며, 이 선은 평면 z = 0과 오로지 한 점에서 교차한다. 이 점을 P의 평면 위로의 평사 투영이라고 정의한다.

3. 3. 일반화

더 일반적으로, 평사 투영은 $(n\; +\; 1)$차원 유클리드 공간 '''E'''^''n''+1의 $n$차원 단위 초구 에서 적용될 수 있다. 만일 가 과 차원의 초평면 위에 있는 점이라면, 점 }}$P\; \backslash in\; \backslash \{S^n\; -\; Q\; \backslash \}$의 평사 투영은 $\backslash overline\{QP\}$ 와 $E$ 의 교점 $P\text{'}$이다. 데카르트 좌표계로 정의된 위의 점 $x\_i$ ( from $0$ to $n$)과 에 대하여 점 $x\_i$를 $E$ 위로 평사 투영한 점 $X\_i$ ( from $1$ to $n$)은 다음과 같다.

:$$X\_i\; =\; \backslash frac\{x\_i\}\{1\; -\; x\_0\}\; \backslash quad\; (i\; =\; 1,\; \backslash dots,\; n).$$

이는 아래 식에서 다음을 정의하는데 사용된다.

:$$s^2=\backslash sum\_\{j=1\}^n\; X\_j^2\; =\; \backslash frac\{1+x\_0\}\{1-x\_0\},$$

역은 다음과 같다.

:$$x\_0\; =\; \backslash frac\{s^2-1\}\{s^2+1\}\; \backslash quad\; \backslash text\{과\}\; \backslash quad\; x\_i\; =\; \backslash frac\{2\; X\_i\}\{s^2+1\}\; \backslash quad\; (i\; =\; 1,\; \backslash dots,\; n).$$

더 일반화 하자면, 사영 공간 $P^\{n+1\}$ 에서 비단항 이차 초곡면 $S$ 를 생각할수 있다. 다시 표현하자면, $S$ 는 비단항 이차식 $f(x\_0,\; ...\; ,\; x\_\{n+1\})$ 이 0이 되는 동차좌표 $x\_i$ 의 자취이다. $S$ 위의 임의의 점 $Q$ 과 $Q$ 를 포함하지 않는 $P^\{n+1\}$ 안의 초평면 $E$ 를 고정하면, $\backslash \{S-Q\backslash \}$ 위에 있는 $P$의 평사 투영은 $\backslash overline\{QP\}$ 와 평면 $E$ 의 교점이고, 유일하다. 앞서 설명했듯, 평사 투영은 빽빽한 자리스키 열린 집합에서 등각성, 가역성을 만족한다. 평사 투영은 이차 초평면을 유리 다양체로 표현한다. 이 구조는 대수 기하학 및 등 공형 기하학에서 중요한 역할을 한다.

4. 특성

평사 투영은 등각 사상으로, 곡선이 교차하는 각도를 보존한다. 그러나 면적은 보존하지 않는데, 투영점 근처에서는 면적이 확대되고, 투영점에서 멀어질수록 축소된다. 투영점을 지나지 않는 구면 위의 원은 평면 위의 원으로, 투영점을 지나는 구면 위의 원은 평면 위의 직선으로 투영된다. 평면 위의 모든 직선은 투영점을 지나는 구면 위의 원으로 변환된다.

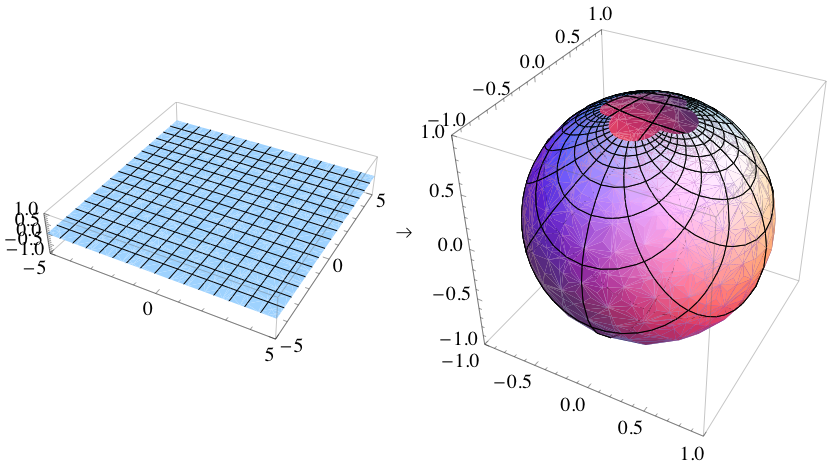
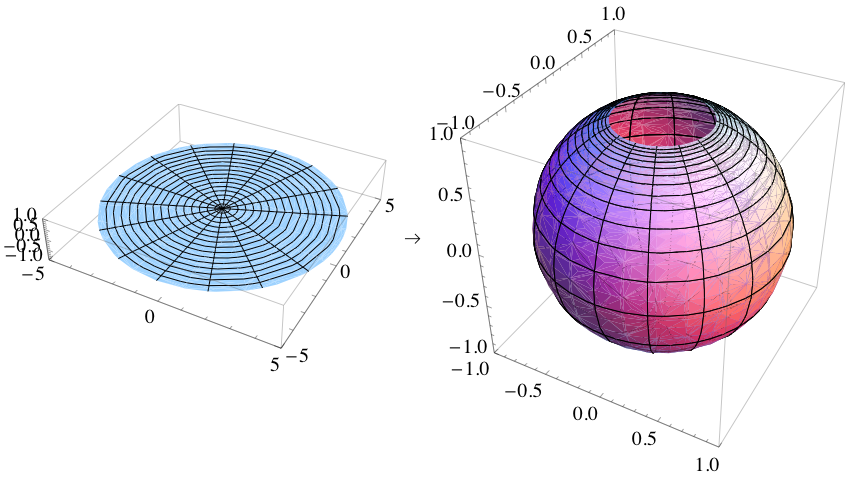
평사 투영법은 투영의 기준점인 N = (0, 0, 1)에서는 정의되지 않으며, 북극 근처의 점들은 투영 됐을 때 평면에서 (0, 0)으로부터 멀리 떨어지게 된다. 이러한 이유로 (0, 0, 1)을 평면에서 "무한"에 대응한다고 말하며, 구에 무한원점을 추가하여 평면을 완성한다고 말한다.

구면좌표계에서, 평사 투영은 곡선이 서로 교차하는 각도를 보존하는 등각성을 가진다. 반면에 면적은 보존하지 않아 구의 면적은 평면에 투영된 면적과 같지 않다. 단위 원을 따라서는 면적 팽창이 일어나지 않아 배율이 1이 된다. (0, 0) 근처에서 면적은 4배까지 팽창하고, 무한대에 가까운 영역에서는 미소하게 팽창한다.

구체를 만든 평면 지도는 등각성도, 면적보전성도 가지지 않는다. 구와 평면은 다른 가우스 곡률을 가지므로, 앞서 말한 기하적 특성이 구면에서와 일치하는 평면 지도는 불가능하다.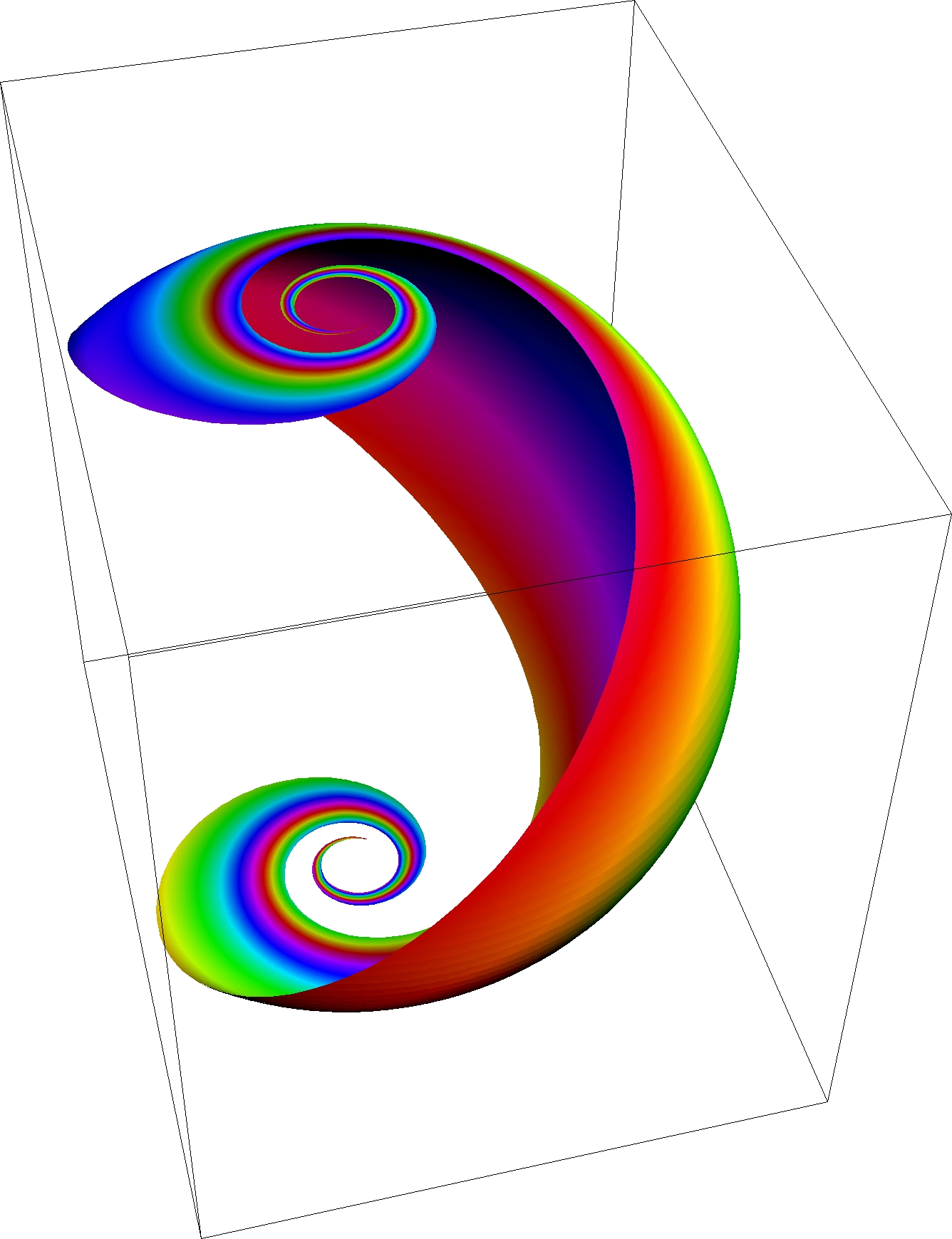

구의 록소드롬(항정선)은 평면에서 로그 나선 형태의 곡선에 매핑되며, 평면에서 방사형 선과 동일한 각으로 만난다.

평사 투영은 평면 반전과 관련이 있다. 구 위의 두 점 P와 Q를 평면에 사영시킨 점을 P', Q'이라고 할 때, P'과 Q'이 적도 원의 이미지에서 서로 역 이미지일 조건은 P와 Q가 적도면에서 대칭일 조건과 필요충분조건이다.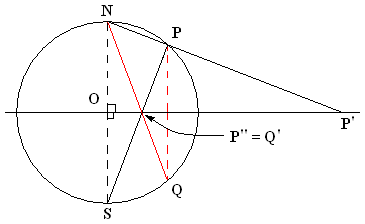

5. 수학에서의 사용

5. 1. 복소수 분석

평사 투영은 복소수 분석에서 특별한 의미를 갖는다. 실수 평면의 점 (X, Y)는 복소수 ''ξ'' = ''X'' + i''Y''로 식별할 수 있다. 북극에서 적도면으로의 평사 투영은 다음과 같이 표현된다.

:

\\

(x, y, z) &= \left(\frac{2 \operatorname{Re} \zeta}{1 + \bar \zeta \zeta}, \frac{2 \operatorname{Im} \zeta}{1 + \bar \zeta \zeta}, \frac{-1 + \bar \zeta \zeta}{1 + \bar \zeta \zeta}\right).\end{align}

마찬가지로, ''ξ'' = ''X'' - i''Y''를 또 다른 복소 좌표로 설정하면, 남극에서 적도면으로의 평사 투영을 정의할 수 있다.

:

(x, y, z) &= \left(\frac{2 \operatorname{Re} \xi}{1 + \bar \xi \xi}, \frac{-2 \operatorname{Im} \xi}{1 + \bar \xi \xi}, \frac{1 - \bar \xi \xi}{1 + \bar \xi \xi}\right)\end{align}

''ζ''-좌표와 ''ξ''-좌표 사이의 전환 맵은 ''ζ'' = 1/''ξ'' 이며, ξ가 무한대로 갈수록 ζ가 0에 가까워지고, 그 반대의 경우도 마찬가지이다. 이는 복소수에서의 무한대 개념을 다루는데 유용하며, 리만 구로 매핑되는 이형 함수 이론을 가능하게 한다. 단위 구에 대한 표준 메트릭은 리만 구에 대한 푸비니-스터디 메트릭과 일치한다.

5. 2. 선과 평면의 시각화

3차원 공간에서 원점을 통과하는 모든 선의 집합은 실제 투영 평면이라는 공간을 형성한다. 이 평면은 3차원 공간에 포함될 수 없기 때문에 시각화하기 어렵다. 하지만 다음과 같이 원판으로 시각화할 수 있다. 원점을 통과하는 모든 선은 한 점에서 남반구 z ≤ 0과 교차하며, 이를 XY 평면에서 디스크의 한 점에 입체적으로 투영할 수 있다. 원점을 통과하는 수평선은 적도를 따라 두 개의 대척점에서 남반구와 교차하여 디스크의 경계로 투영된다. 투영된 두 점 중 하나는 디스크의 일부로 간주할 수 있으며, 적도의 대척점은 3공간에서 하나의 선과 투영된 디스크의 경계에서 하나의 점을 나타낸다(몫 토폴로지 참조). 따라서 원점을 통과하는 모든 선 집합은 투영된 디스크의 점 집합으로 나타낼 수 있다. 그러나 경계점은 일반 2차원 디스크의 경계점과 다르게 동작하는데, 그 이유는 경계점 중 하나가 디스크의 반대편에 있는 내부 점과 동시에 가깝기 때문이다(원점을 통과하는 두 개의 거의 수평인 선이 디스크의 반대편에 있는 점으로 투영될 수 있는 것과 마찬가지로).

또한 원점을 통과하는 모든 평면은 단위 구와 큰 원으로 교차하는데, 이를 평면의 흔적이라고 한다. 이 원은 스테레오그래픽 투영에서는 원에 매핑된다. 따라서 투영을 통해 평면을 디스크에서 원호로 시각화할 수 있다. 컴퓨터가 등장하기 전에는 큰 원으로 입체 투영을 하려면 빔 컴퍼스를 사용해야 하는 큰 반경의 호를 그려야 하는 경우가 많았다. 이제 컴퓨터 덕분에 이 작업이 훨씬 쉬워졌다.

각 평면에는 원점을 통과하고 평면에 수직인 평면의 극이라고 하는 고유한 선이 있다. 이 선은 원점을 통과하는 모든 선과 마찬가지로 디스크에 점으로 그릴 수 있다. 따라서 입체 투영을 사용하면 평면을 디스크의 점으로 시각화할 수도 있다. 많은 평면을 포함하는 플롯의 경우, 극을 그리면 흔적을 그리는 것보다 덜 어수선한 그림을 만들 수 있다.

이 구조는 결정학 및 지질학에서 방향 데이터를 시각화하는 데 사용된다.

5. 3. 해석 기하학

초등 산술 기하학에서 단위 원으로부터의 평사 투영은 모든 원시 피타고라스 삼각형을 설명할 수 있는 수단을 제공한다. 특히, 북극 (0,1)에서 x축으로 평사 투영하면 단위 원의 유리수 점 (''x'', ''y'')과 x축의 유리점 (''y'' ≠ 1)이 일대일 대응을 이루게 된다. 만약 (, 0) 이 x축의 유리수 점이라면, 그 평사 투영의 역은 다음과 같다.

:$(\backslash frac\{2mn\}\{m^2\; +\; n^2\},\; \backslash frac\{m^2\; -\; n^2\}\{m^2\; +\; n^2\})$

이는 피타고라스 삼각형에 대한 유클리드의 공식을 제공한다.

5. 4. 반각 치환

두 삼각함수 (sin ''x'', cos ''x'') 는 단위 원의 매개변수로 작용할 수 있다. 평사 투영은 단위원의 매겨변수화에 아래와 같은 대안을 제공한다.

:$\backslash cos\; x\; =\; \backslash frac\{1\; -\; t^2\}\{1\; +\; t^2\},\backslash quad\; \backslash sin\; x\; =\; \backslash frac\{2\; t\}\{t^2\; +\; 1\}.$

이 재매개변수화에 의하면, 단위 원의 길이 ''dx'' 는 아래와 같이 표현된다.

:$dx\; =\; \backslash frac\{2\; \backslash ,\; dt\}\{t^2\; +\; 1\}.$

이 치환은 때때로 삼각함수를 포함한 적분을 간단하게 해준다.

6. 다른 분야에서의 적용

6. 1. 지도학

평사 투영은 각을 보존하는 등각 사상의 성질을 가지므로 항법에서 자주 사용된다. 극지방을 중심으로 투영하면 자오선은 방사형 직선, 위선은 동심원으로 나타난다.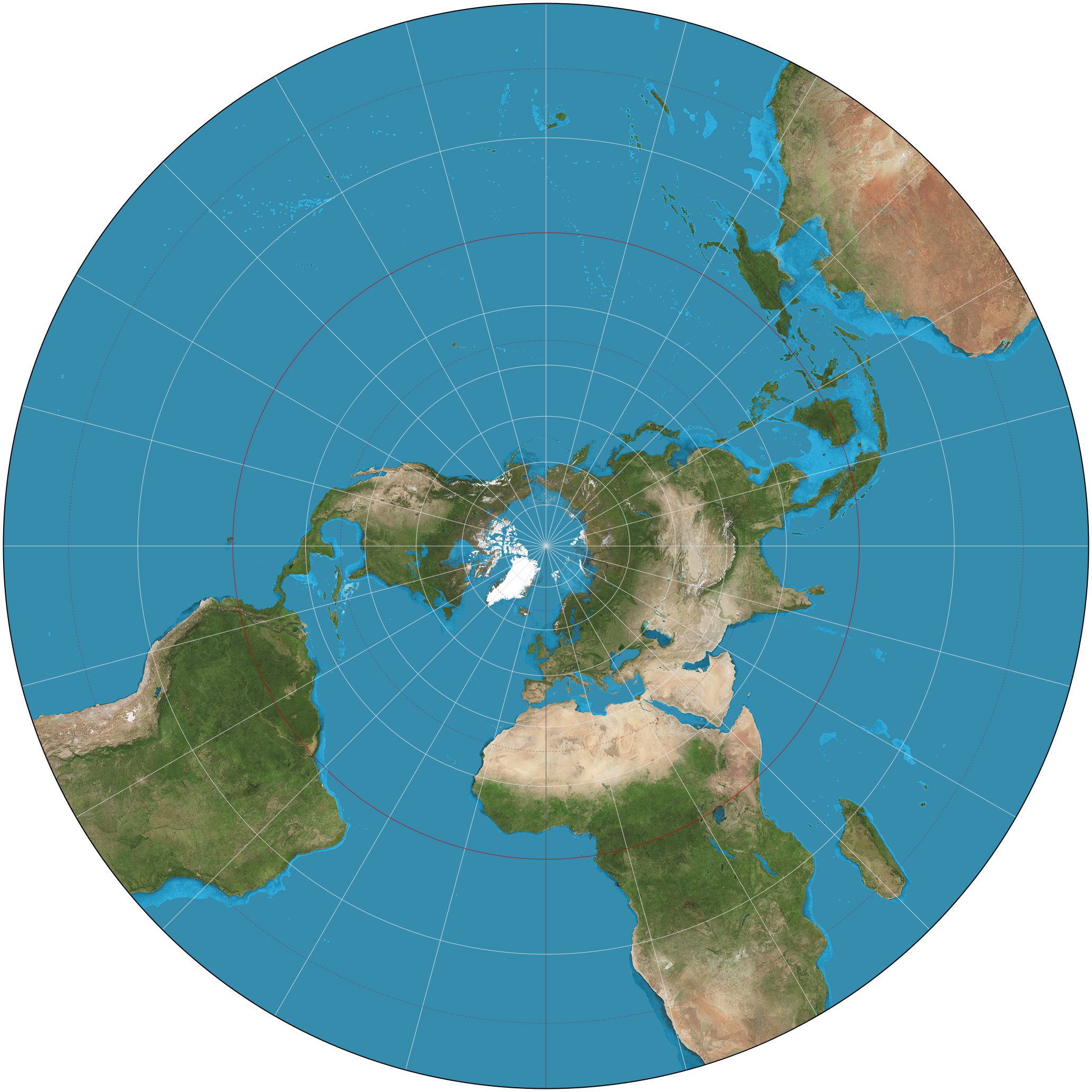

6. 2. 행성과학

평사 투영은 유일하게 구에 있는 원을 평면 위의 원으로 투영시키는 투영법이다. 이 특징은 행성학에서 천체의 크레이터를 관찰하기 위해 평면에 사상시킬 때 굉장히 유용하다. 투영점을 통과하는 원들은 무한한 반지름을 가져 선으로 변하게 된다.

6. 3. 결정학

결정학에서, 3차원 공간에서의 결정 축과 면의 방향은 엑스선과 전자의 회절 무늬 해석과 같은 기하학적 핵심 관심사이다. 이 방향들은 결정 축과 결정 면에 대한 극이 북반구와 교차하는 점들을 평사 투영을 사용하여 그래프로 표현하여 나타낼 수 있다. 극의 그래프는 극점도(pole figure)라고 한다.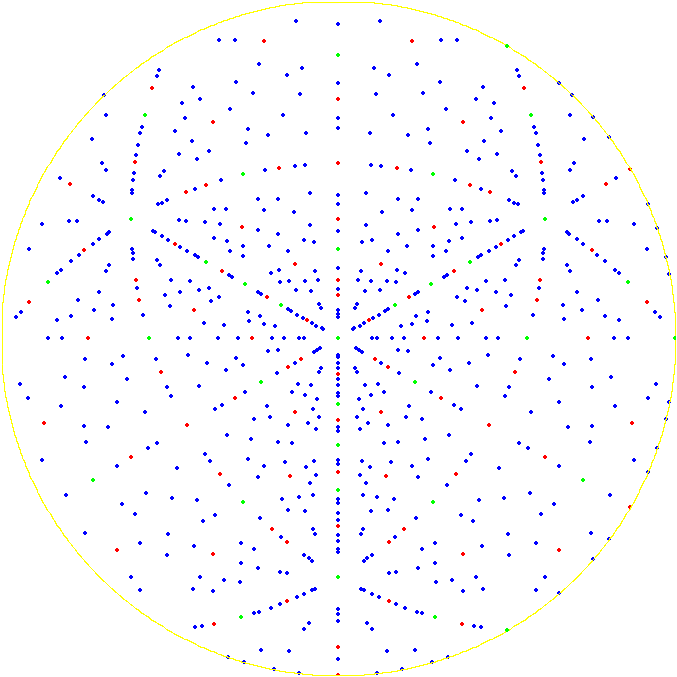

전자의 회절에서, 키쿠치선 쌍은 격자 평면과 에발트 구면의 교차점을 꾸미는 띠로 나타나므로, 결정의 평사 투영에 실험적 접근이 가능하도록 한다.

6. 4. 지질학

암석의 단층면은 평면적인 특징이며, 종종 선형이라고 하는 선형 특징을 포함한다. 마찬가지로 단층면은 슬릭사이드와 같은 선형 특징을 포함할 수 있는 평면적 특징이다.

이러한 다양한 축척의 선과 평면의 방향은 극을 기준으로 플롯될수 있으며, 이때 남반구가 사용된다. 평사 투영법은 종종 등각 하반구 투영법이라고도 하며, 램버트 방위각 등면적 하반구 투영법에 의해 정의된 등면적 하반구 투영법은 특히 밀도 윤곽과 같은 후속 통계 분석을 수행할 때 사용된다.

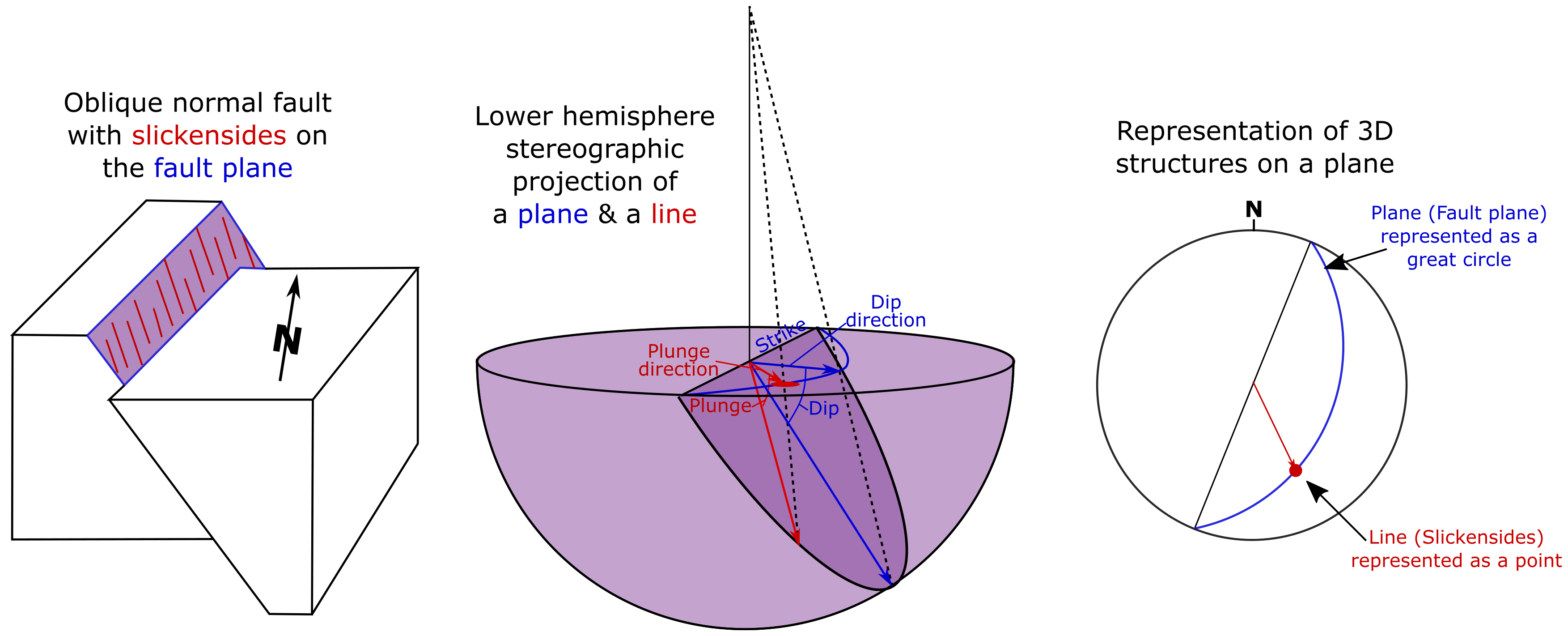
6. 5. 암반 역학

평사 투영은 암반 사면의 안정성을 평가하는 데 가장 널리 사용되는 방법 중 하나이다. 이를 통해 3차원 방향 데이터를 2차원으로 표현하고 분석할 수 있다. 평사 투영 내의 운동학 분석은 평면 파괴, 쐐기 파괴, 전도 파괴와 같은 다양한 암반 사면 파괴 모드의 잠재력을 평가하는 데 사용된다. 이 기술은 불연속성 세트와 관련하여 암반 사면의 방향을 시각화하여 가장 가능성이 높은 파괴 유형을 쉽게 평가하는 데 특히 유용하다. 예를 들어, 평면 파괴는 불연속성 세트의 타격이 사면과 평행하고 불연속성이 미끄러질 수 있을 만큼 가파른 각도로 사면 쪽으로 내려가지만 사면 자체보다 가파르지 않을 때 더 가능성이 높다.

또한 일부 연구자들은 경사 질량 등급(SMR) 및 암석 질량 등급 등 경사면의 암석 질량 분류를 위해 경사면과 불연속체 사이의 평행성, 불연속체의 기울기, 불연속체와 경사면 사이의 상대 각도 등 기하학적 보정 파라미터를 쉽게 계산하는 평사 투영 기반의 그래픽 방법을 개발하기도 한다.

6. 6. 사진술

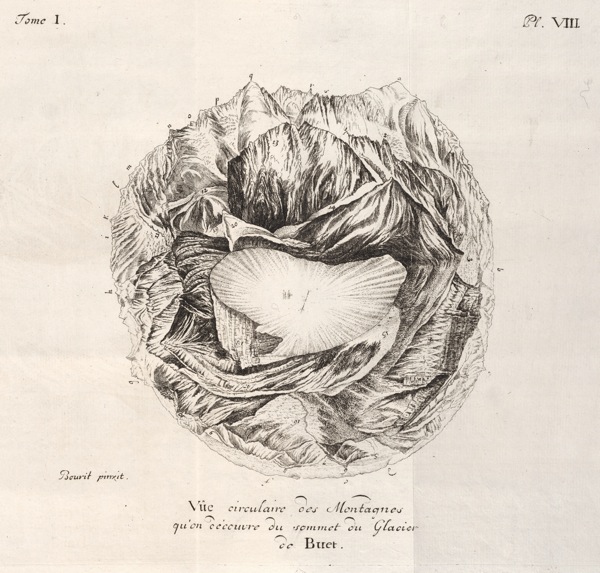
어안 렌즈는 넓은 시야를 담기 위해 평사 투영을 사용한다. 등면적 사영 방법인 전통 어안 렌즈와 비교했을 때, 폐곡선 면적은 더 잘 보존되며 선들도 덜 왜곡된다. Panotools와 같은 이미지 매핑 소프트웨어는 등면적 어안 렌즈를 다시 평사 투영화 시켜준다. 평사 투영은 구면 파노라마를 매핑하기 위해 사용되었으며, 1779년 Horace Bénédict de Saussure 가 처음 시작했다. "작은 행성(little planet)" (nadir가 투영의 중심) 효과나 "튜브" (zenith가 투영의 중심) 효과를 만드는 데 활용된다.

---

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com