헥소미노
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
헥소미노는 6개의 동일한 크기의 정사각형을 변끼리 연결하여 만들어지는 다각형으로, 총 35가지의 자유 헥소미노가 존재하며 대칭성에 따라 분류된다. 헥소미노는 반사 여부에 따라 총 60개의 단면 헥소미노로 확장될 수 있으며, 회전을 고려할 경우 216개의 고정 헥소미노가 생성된다. 헥소미노는 평면 채우기 문제와 관련이 있으며, 35개의 헥소미노는 콘웨이 기준을 만족하지만, 210개의 사각형으로 이루어진 직사각형을 채울 수는 없다. 하지만 중앙에 구멍이 있는 도형 등 다른 형태는 채울 수 있으며, 헥소미노는 정육면체의 전개도로도 활용된다.
더 읽어볼만한 페이지
| 헥소미노 |
|---|
2. 종류 및 대칭성
폴리오미노의 일종으로, 정사각형 6개를 변끼리 이어 붙여 만들 수 있는 도형인 헥소미노는 총 35가지의 서로 다른 모양(자유 헥소미노)이 존재한다.
이 35가지 헥소미노는 대칭성을 기준으로 여러 그룹으로 분류할 수 있다. 각 헥소미노가 가지는 대칭의 종류에 따라 대칭군이 결정되며, 자세한 분류 기준은 #대칭군 문단을 참고하라.
한편, 헥소미노를 뒤집어서(반사하여) 얻는 모양을 다른 것으로 간주하는 경우, 이를 단면 헥소미노라고 부른다. 단면 헥소미노는 총 60가지 종류가 있다. 자세한 내용은 #단면 헥소미노 문단을 참고하라.
또한, 회전하거나 뒤집어서 얻는 모양을 모두 다른 것으로 간주하는 경우, 이를 고정 헥소미노라고 하며, 총 216가지 종류가 존재한다.
2. 1. 대칭군
35개의 자유 헥소미노는 대칭군에 따라 다음과 같이 분류할 수 있다.- 대칭성이 없는 헥소미노 20개: 대칭군은 항등 사상만 원소로 가진다.
- 격자선과 평행한 거울 대칭 축을 갖는 헥소미노 6개: 대칭군은 항등 사상과 해당 축에 대한 반사로 구성된다.
- 격자선과 45° 각도를 이루는 거울 대칭 축을 갖는 헥소미노 2개: 대칭군은 항등 사상과 해당 대각선 반사로 구성된다.
- 점대칭(차수 2의 회전 대칭)을 갖는 헥소미노 5개: 대칭군은 항등 사상과 180° 회전으로 구성된다.
- 격자선과 평행한 두 개의 거울 대칭 축(수평축과 수직축)을 갖는 헥소미노 2개: 대칭군은 항등 사상, 수평 반사, 수직 반사, 180° 회전의 네 원소로 구성되며, 이는 이항군(차수 2) 또는 클라인 4군과 같다.
헥소미노의 반사된 모양을 다른 것으로 간주하는 경우(단면 헥소미노), 대칭성이 없는 헥소미노와 점대칭 헥소미노의 개수가 각각 두 배가 되어 총 (20 × 2) + 6 + 2 + (5 × 2) + 2 = 60개의 단면 헥소미노가 존재한다.
회전된 모양까지 다른 것으로 간주하는 경우(고정 헥소미노), 대칭성이 없는 헥소미노는 8가지, 평행선/대각선 반사 대칭 및 점대칭 헥소미노는 4가지, 두 축 반사 대칭 헥소미노는 2가지 방향으로 계산된다. 따라서 총 20 × 8 + (6 + 2 + 5) × 4 + 2 × 2 = 216개의 고정 헥소미노가 존재한다.
2. 2. 단면 헥소미노
자유 헥소미노는 회전하거나 뒤집어서(반사하여) 같은 모양이 되면 하나로 간주하지만, 단면 헥소미노는 반사하여 얻는 모양을 서로 다른 것으로 구별한다.35개의 자유 헥소미노 중 대칭성이 없는 20개와 점대칭만 가지는 5개는 반사를 통해 서로 다른 모양이 되므로, 단면 헥소미노에서는 각각 2가지로 계산된다. 반면, 반사 대칭 축을 가지는 나머지 10개(축이 격자선과 평행한 6개, 대각선인 2개, 두 축 모두 가진 2개)는 반사해도 모양이 변하지 않으므로 그대로 1가지로 계산된다.
따라서 단면 헥소미노의 총 개수는 (20 × 2) + (5 × 2) + 10 = 40 + 10 + 10 = 60개가 된다.
이 60개의 단면 헥소미노 중 18개는 조각을 구성하는 6개의 정사각형을 바둑판 무늬처럼 번갈아 칠했을 때, 두 색깔의 정사각형 개수가 서로 다르다.
단면 헥소미노 60개를 모두 사용하여, 짧은 변의 길이가 5 이상인 직사각형을 빈틈없이 채울 수 있으며[9][8], 크기는 다르지만 모양이 같은 임의의 데코미노 형태(상사 도형)도 만들 수 있다[8].
3. 채우기 및 타일링
각 35개의 헥소미노는 모두 콘웨이 기준을 만족하므로, 개별적으로는 평면을 타일링할 수 있다.[4]
하지만 35개의 서로 다른 헥소미노 전체(총 210칸)를 모아 직사각형을 만드는 것은 불가능하다. 이는 펜토미노 12개로는 여러 크기의 직사각형을 만들 수 있는 것과 대조된다. 직사각형 채우기가 불가능한 이유는 체커판 색칠을 이용한 패리티 논증으로 설명할 수 있는데, 35개 헥소미노가 덮는 각 색깔 칸의 총 개수는 항상 짝수이지만, 210칸 직사각형은 각 색깔 칸이 105개(홀수)이기 때문이다.
직사각형은 만들 수 없지만, 35개의 헥소미노로 210칸을 채울 수 있는 다른 형태는 존재한다. 예를 들어, 중앙에 3×5 크기의 구멍을 낸 15×15 정사각형[5]이나 20단 계단형[7] 등이 대표적이다.
또한, 헥소미노 두 세트(70개, 420칸)를 사용하거나, 좌우 대칭이 아닌 조각의 거울상을 별개로 취급하는 한 면 헥소미노(60개, 360칸)를 사용하면 직사각형을 만들 수 있다.[6][8]
3. 1. 콘웨이 기준
각 35개의 헥소미노는 모두 콘웨이 기준을 만족하므로, 모든 헥소미노는 평면을 타일링할 수 있다.[4]하지만 35개의 헥소미노 전체(총 210개의 사각형)를 사용하여 직사각형을 만드는 것은 불가능하다. 이는 12개의 펜토미노가 3 × 20, 4 × 15, 5 × 12, 6 × 10 크기의 직사각형을 만들 수 있는 것과는 대조적이다. 헥소미노로 직사각형을 만들 수 없는 이유는 패리티 논증으로 설명할 수 있다. 헥소미노를 체커판처럼 번갈아 색칠된 패턴 위에 놓는다고 가정해보자. 35개의 헥소미노 중 11개는 짝수 개의 검은색 사각형(흰색 2칸, 검은색 4칸 또는 그 반대)을 덮고, 나머지 24개는 홀수개의 검은색 사각형(흰색 3칸, 검은색 3칸)을 덮는다. 따라서 35개의 헥소미노를 어떻게 배열하든 전체적으로 덮이는 검은색 사각형의 개수는 항상 짝수가 된다. 그러나 총 210개의 사각형으로 이루어진 직사각형은 반드시 105개의 검은색 사각형과 105개의 흰색 사각형을 가지므로, 검은색 사각형의 개수가 홀수이다. 따라서 35개의 헥소미노로는 직사각형을 완전히 덮을 수 없다.
그렇지만 210개의 사각형으로 이루어진 다른 간단한 모양 중에는 헥소미노로 타일링이 가능한 것들이 있다. 예를 들어, 가운데에 3 × 5 크기의 직사각형 구멍이 뚫린 15 × 15 정사각형은 총 210개의 사각형으로 이루어져 있다. 이 도형을 체커판 무늬로 칠하면, 흰색 사각형 106개와 검은색 사각형 104개(또는 그 반대)를 가지게 되어 패리티 문제가 발생하지 않으며, 실제로 타일링이 가능하다.[5] 또한, 헥소미노 두 세트(총 70개, 420칸)를 사용하여 직사각형을 만들거나, 60개의 한 면 헥소미노(이 중 18개는 짝수 개의 검은색 사각형을 덮음)를 사용하여 360칸 크기의 직사각형을 만드는 것도 가능하다.[6]
한 면 헥소미노는 총 60개이며, 이들을 모두 사용하여 짧은 변의 길이가 5 이상인 모든 직사각형[9]을 만들 수 있다.[8] 또한, 임의의 데코미노 모양을 확대하여 헥소미노로 채우는 것도 가능하다.[8]
3. 2. 직사각형 채우기 문제
35개의 헥소미노 전체는 총 210개의 정사각형 칸으로 이루어져 있지만, 이 조각들을 모두 사용하여 직사각형을 만드는 것은 불가능하다. 이는 12개의 펜토미노 조각(총 60칸)으로는 3×20, 4×15, 5×12, 6×10 크기의 직사각형을 만들 수 있는 것과 대조적이다.헥소미노로 직사각형을 채울 수 없는 이유는 패리티 논증을 통해 간단히 증명할 수 있다. 만약 직사각형을 체커판처럼 흑백으로 번갈아 칠한다고 가정해 보자. 210칸짜리 직사각형은 정확히 105개의 검은색 칸과 105개의 흰색 칸을 가지게 된다. 이제 35개의 헥소미노를 이 체커판 위에 놓는다고 생각하면, 각 헥소미노는 6개의 칸을 덮는다. 헥소미노의 종류에 따라 덮는 흑백 칸의 수는 달라진다.
- 11종류의 헥소미노는 짝수 개의 검은색 칸(검은색 4칸, 흰색 2칸 또는 검은색 2칸, 흰색 4칸)을 덮는다.
- 나머지 24종류의 헥소미노는 홀수 개의 검은색 칸(검은색 3칸, 흰색 3칸)을 덮는다.
따라서 35개의 헥소미노를 어떻게 배열하든, 덮이는 검은색 칸의 총 개수는 (짝수 × 11) + (홀수 × 24) = 짝수 + 짝수 = 짝수가 된다. 그러나 목표인 직사각형은 105개(홀수)의 검은색 칸을 가지고 있으므로, 35개의 헥소미노 조각만으로는 직사각형을 완전히 덮을 수 없다는 결론에 이른다.
하지만 헥소미노로 채울 수 있는 210칸짜리 다른 간단한 도형은 존재한다. 예를 들어, 15×15 크기의 정사각형 중앙에 3×5 크기의 직사각형 구멍을 낸 도형은 총 210칸이다. 이 도형을 체커판 무늬로 칠하면, 106개의 한 색 칸과 104개의 다른 색 칸(예: 흰색 106칸, 검은색 104칸)을 가지게 된다. 이 경우 덮어야 할 각 색깔 칸의 개수가 짝수이므로 패리티 문제가 발생하지 않으며, 실제로 이 도형은 35개의 헥소미노로 채우는 것이 가능하다.[5] 다른 예로는 20단 계단형[7] 등이 있다. 또한, 헥소미노 세트 두 개(총 70개 조각, 420칸)로는 직사각형을 만들 수 있으며, 한 면만 사용하는 헥소미노(片면형 헥소미노) 60개(총 360칸)로도 직사각형을 만들 수 있다.[6]
만약 특정 헥소미노 조각을 추가하거나 중복해서 사용한다면 직사각형을 만들 수도 있다. 예를 들어, 흑백 칸 비율이 2:4(또는 4:2)인 11종류의 조각 중 하나를 골라 2개 사용하고 나머지 34개 조각을 사용하면 총 36개 조각(216칸)이 된다. 이 경우 패리티 문제가 해결되어 6×36 크기의 직사각형 등을 만들 수 있다. 또한, 11종류 중 어떤 조각을 추가하든 2개의 6×18 직사각형을 만들 수 있다.[7] 몇 종류의 조각을 더 추가하면 3개의 6×12 직사각형이나 4개의 6×9 직사각형을 만드는 것도 가능하다.[7]
한 면만 사용하는 헥소미노(片면형 헥소미노)는 총 60개가 존재한다. 이 60개의 조각을 모두 사용하여 짧은 변의 길이가 5 이상인 직사각형(예: 5x72, 6x60, 8x45, 9x40, 10x36, 12x30, 15x24, 18x20)은 모두 만들 수 있다.[8][9]
3. 3. 다른 형태 채우기
35개의 헥소미노 전체는 총 210개의 칸을 차지하지만, 이 조각들을 모두 사용하여 직사각형 모양을 만드는 것은 불가능하다. 이는 각 조각을 체커판처럼 번갈아 색칠했을 때 나타나는 패리티 문제 때문이다. 직사각형은 검은색 칸과 흰색 칸의 개수가 105개로 같아야 하지만, 35개의 헥소미노를 어떻게 배열하든 덮게 되는 검은색(또는 흰색) 칸의 총 개수는 항상 짝수가 되기 때문에 직사각형을 빈틈없이 채울 수 없다.그러나 직사각형이 아닌 다른 형태로는 210칸을 모두 채우는 것이 가능하다. 대표적인 예시는 다음과 같다:
- 구멍 뚫린 정사각형: 가운데에 3x5 크기의 직사각형 구멍이 뚫린 15x15 정사각형 형태이다. 이 도형은 총 210칸이며, 체커판 색상으로 칠했을 때 패리티 문제가 발생하지 않아 실제로 헥소미노로 채우는 것이 가능하다.[5]

이 외에도 다양한 방법으로 헥소미노를 배열할 수 있다. 예를 들어, 7개의 조각으로 구성된 5개의 합동 도형이나, 5개의 조각으로 구성된 7개의 합동 도형을 만들 수도 있다.[8] 특정 11개의 조각(흑백 칸 수가 다른 조각)만을 사용하여 면적비가 1:9:25인 닮은꼴 도형을 만드는 것도 가능하다.[8]
구멍이 뚫린 다른 형태들도 많이 연구되었다. 앞서 언급된 15x15 도형 외에도, 전체 면적과 구멍 면적의 비율이 224:14, 250:40, 280:70, 378:168 등이 되는 닮은꼴 도형[8], 15x17 직사각형 안에 펜토미노 모양의 구멍을 낸 도형(Jean Meeus)[8], 직사각형 안에 50개의 구멍을 낸 도형(Patrick Hamlyn)[8], 직사각형이 아닌 외형에 52개의 구멍을 낸 도형(Dominique Mallet)[8] 등이 발표되었다.
한편, 헥소미노 두 세트(총 70개, 420칸)를 사용하면 직사각형을 만들 수 있으며[6], 60개의 한 면 헥소미노(one-sided hexominoes) 세트를 사용하여 360칸 직사각형을 만드는 것도 가능하다.[6]
4. 정육면체 전개도
정육면체의 전개도는 정사각형 6개가 변으로 이어진 모양이므로 모두 헥소미노에 해당한다. 정육면체를 만들 수 있는 서로 다른 전개도는 총 11가지가 있다. 이 11가지 헥소미노는 자유 헥소미노(회전하거나 뒤집어서 같은 모양이 되는 것을 하나로 치는 헥소미노)에 해당한다.
정육면체의 전개도는 특정 모양의 폴리오미노를 포함할 수 없다. 예를 들어, O-테트로미노, I-펜토미노, U-펜토미노, V-펜토미노를 포함하는 모양으로는 정육면체를 접을 수 없다.
5. 기타
헥소미노는 펜토미노와 비슷하게 35개의 조각을 모두 사용해 직사각형을 만드는 퍼즐을 생각해 볼 수 있지만, 이는 해를 가지지 않는다. 이 사실은 조각을 체커무늬로 칠해보면 알 수 있다. 직사각형을 만들려면 흑백 칸이 각각 105개씩 필요하지만, 헥소미노 조각 중 흑백이 3:3으로 나뉘는 조각 24종과 2:4(또는 4:2)로 나뉘는 조각 11종을 합하면, 전체적으로 흑백 칸 수가 모두 짝수가 되어 105개씩 맞출 수 없기 때문이다.
단순한 직사각형 채우기가 불가능하기 때문에, 다른 형태로 배열하는 방법들이 고안되었다. 대표적인 예로는 20단 계단형[7]이나 15×15 크기의 정사각형 중앙에 3×5 크기의 구멍을 낸 형태[8] 등이 있다.
여러 조각을 조합하여 다른 도형을 만드는 것도 가능하다. 예를 들어, 7개의 헥소미노 조각으로 5개의 서로 합동인 도형을 만들거나, 5개의 조각으로 7개의 합동인 도형을 만들 수도 있다[8]. 또한, 흑백 칸 수가 다른 11개의 조각만 사용하여 면적비가 1:9:25인 닮은꼴 도형을 만드는 것도 가능하다[8].
구멍이 뚫린 도형으로는 앞서 언급된 15×15 도형(오른쪽 그림 참조) 외에도, 전체 면적과 구멍 면적의 비율이 224:14, 250:40, 280:70, 378:168이 되는 닮은꼴 도형들이 발표되었다[8]. Jean Meeus 등은 15×17 크기의 직사각형 안에 펜토미노 모양의 구멍을 낸 도형을 발표했으며[8], Patrick Hamlyn은 직사각형 안에 50개의 구멍을 낸 도형을, Dominique Mallet은 직사각형이 아닌 외형에 52개의 구멍을 낸 도형을 발표하기도 했다[8].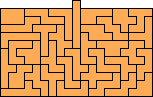
텐요(Tenyo)에서 발매한 플라스틱 퍼즐 시리즈 중에는 헥소미노 세트가 포함되어 있다. 이 퍼즐은 11×19 크기의 직사각형 외부에 정사각형 1개가 튀어나온 형태로 되어 있다. 이 형태의 퍼즐 해가 정확히 몇 개인지 알려져 있지는 않지만, 상품 설명에는 "10억 가지 이상의 조합이 있다"고 명시되어 있다. 실제로 컴퓨터를 이용한 탐색을 통해 200억 개 이상의 해가 발견되었으며, 전체 해의 개수는 1020에서 1025가지 사이일 것으로 추정된다.
참조
[1]
서적
Polyominoes
Princeton University Press
[2]
웹사이트
Hexomino
http://mathworld.wol[...]
From MathWorld – A Wolfram Web Resource
2008-07-22
[3]
논문
Counting polyominoes: yet another attack
[4]
서적
Planar Tilings and the Search for an Aperiodic Prototile
PhD dissertation, Rutgers University
[5]
웹사이트
Mathematische Basteleien: Hexominos
http://www.mathemati[...]
[6]
웹사이트
Hexomino Constructions
http://recmath.com/P[...]
[7]
웹사이트
The Poly Pages
http://www.recmath.o[...]
[8]
웹사이트
The Poly Pages のヘキソミノのページ
http://www.recmath.o[...]
[9]
문서
5×72, 6×60, 8×45, 9×40, 10×36, 12×30, 15×24, 18×20 の8種
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

