맨위로가기

버블 정렬

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

버블 정렬은 인접한 두 요소를 비교하여 정렬하는 알고리즘으로, 1956년 에드워드 해리 프렌드가 처음 설명했다. 배열의 두 수를 비교해 정렬되지 않았을 경우 교환하는 과정을 반복하며, 모든 요소에 대해 인접한 요소와 비교하여 순서가 역전되어 있으면 교환하는 방식으로 진행된다. 버블 정렬은 구현이 간단하지만, 시간 복잡도가 O(n2)로 비효율적이어서 실제 사용보다는 교육 목적으로 활용된다. 칵테일 정렬, 빗질 정렬과 같은 변형 알고리즘이 존재하며, '가라앉는 정렬'이라고 불리기도 한다.

더 읽어볼만한 페이지

  • 안정 정렬 - 합병 정렬
    합병 정렬은 분할 정복 알고리즘을 사용하여 리스트를 재귀적으로 분할하고 정렬된 부분 리스트를 병합하는 비교 기반 정렬 알고리즘으로, O(n log n)의 시간 복잡도를 가지며 안정 정렬에 속하고 연결 리스트 정렬 및 외부 정렬에 유용하다.
  • 안정 정렬 - 삽입 정렬
    삽입 정렬은 미정렬 부분의 원소를 정렬된 부분의 올바른 위치에 삽입하여 정렬을 완성하는 간단하고 효율적인 알고리즘이지만, 데이터 세트가 클수록 성능이 저하되어 이를 개선하기 위한 변형 알고리즘이 존재한다.
  • 비교 정렬 - 합병 정렬
    합병 정렬은 분할 정복 알고리즘을 사용하여 리스트를 재귀적으로 분할하고 정렬된 부분 리스트를 병합하는 비교 기반 정렬 알고리즘으로, O(n log n)의 시간 복잡도를 가지며 안정 정렬에 속하고 연결 리스트 정렬 및 외부 정렬에 유용하다.
  • 비교 정렬 - 퀵 정렬
    퀵 정렬은 토니 호어가 개발한 분할 정복 방식의 효율적인 정렬 알고리즘으로, 피벗을 기준으로 리스트를 분할하여 정렬하는 과정을 재귀적으로 반복하며 다양한 최적화 기법과 변형이 존재한다.
  • 정렬 알고리즘 - 합병 정렬
    합병 정렬은 분할 정복 알고리즘을 사용하여 리스트를 재귀적으로 분할하고 정렬된 부분 리스트를 병합하는 비교 기반 정렬 알고리즘으로, O(n log n)의 시간 복잡도를 가지며 안정 정렬에 속하고 연결 리스트 정렬 및 외부 정렬에 유용하다.
  • 정렬 알고리즘 - 퀵 정렬
    퀵 정렬은 토니 호어가 개발한 분할 정복 방식의 효율적인 정렬 알고리즘으로, 피벗을 기준으로 리스트를 분할하여 정렬하는 과정을 재귀적으로 반복하며 다양한 최적화 기법과 변형이 존재한다.
버블 정렬
개요
버블 정렬의 시각화
버블 정렬의 정적 시각화
분류정렬 알고리즘
자료 구조배열
최악 시간 복잡도O(n^2) 비교, O(n^2) 교환
평균 시간 복잡도O(n^2) 비교, O(n^2) 교환
최선 시간 복잡도O(n) 비교, O(1) 교환
공간 복잡도O(n) 총합, O(1) 보조 공간
최적화 여부아니오
명칭
영어Bubble sort
다른 영어 명칭Sinking sort (싱킹 소트)
상세 정보
시간 복잡도O(n^2)

2. 역사

버블 정렬 알고리즘에 대한 가장 초기의 설명은 수학자이자 보험 계리사인 에드워드 해리 프렌드(Edward Harry Friend)가 1956년에 발표한 논문[4] "전자 컴퓨터 시스템에서의 정렬"[5]에 담겨 있으며, 이는 ACM의 세 번째 권의 세 번째 호에 게재되었다. 프렌드는 이 알고리즘의 기본 원리를 설명했지만, 처음에는 주목받지 못하다가 몇 년 후 케네스 아이버슨을 비롯한 많은 컴퓨터 과학자들에 의해 재발견되었고, 현재의 이름이 붙여졌다.

3. 알고리즘

버블 정렬은 배열의 두 인접한 원소를 비교하여 정렬되지 않은 순서(오름차순의 경우 a > b, 내림차순의 경우 a < b)이면 두 원소의 위치를 서로 바꾸는 방식으로 동작한다. 이 과정을 배열의 처음부터 끝까지 반복하면, 가장 큰 값(오름차순) 또는 가장 작은 값(내림차순)이 배열의 끝으로 이동하게 된다. 이 과정을 배열에 아무 변화가 없을 때까지 반복한다.[4]

버블 정렬의 예시. 목록의 시작 부분부터 모든 인접한 쌍을 비교하고, 순서가 올바르지 않은 경우 위치를 바꾼다. 각 반복 후, 비교할 요소가 하나 줄어든다.


버블 정렬에서의 요소 이동 예시

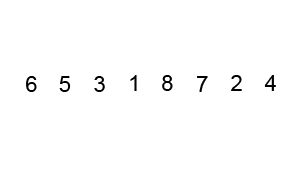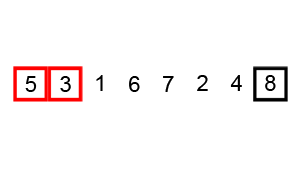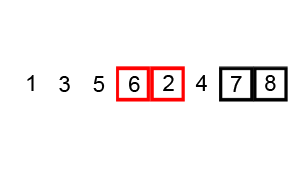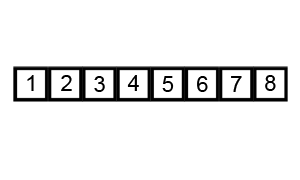
3. 1. 예시

정렬되지 않은 배열 [7, 2, 0, 1, 5, 6, 4]를 오름차순으로 정렬하는 과정은 다음과 같다.

알고리즘은 배열의 첫 두 숫자(7, 2)를 비교한다. 7 > 2 이므로 두 수를 바꾼다.

[2, 7, 0, 1, 5, 6, 4]

배열의 처음부터 끝까지 이 과정을 반복하면 다음과 같다.

[2, 0, 1, 5, 6, 4, 7][1]

가장 큰 수인 7이 정렬되었다. 이 과정을 여러 번 반복하면 다음과 같이 진행된다.

[0, 1, 2, 5, 4, 6, 7][2]

[0, 1, 2, 4, 5, 6, 7][3]

[0, 1, 2, 4, 5, 6, 7][4]

3회부터 4회까지는 아무 변화가 없으므로 모두 정렬된 것으로 정의한다.

초기 데이터: 8 4 3 7 6 5 2 1

결과가 확정된 부분을 굵게 표시하면 다음과 같다.

43765218(1번째 외부 루프 종료 시 교환 횟수: 7)
34652178(2번째 외부 루프 종료 시 교환 횟수: 5)
34521678(3번째 외부 루프 종료 시 교환 횟수: 3)
34215678(4번째 외부 루프 종료 시 교환 횟수: 2)
32145678(5번째 외부 루프 종료 시 교환 횟수: 2)
21345678(6번째 외부 루프 종료 시 교환 횟수: 2)
12345678(7번째 외부 루프 종료 시 교환 횟수: 1)



교환 횟수의 합계: 7+5+3+2+2+2+1=22

4. 분석

버블 정렬은 정렬되는 항목의 수 n에 대해 최악 및 평균 시간 복잡도가 O(n^2)이다. 퀵 정렬, 병합 정렬과 같은 대부분의 실용적인 정렬 알고리즘은 최악 또는 평균 시간 복잡도가 O(n \log n)으로 훨씬 더 효율적이다. 삽입 정렬과 같은 다른 O(n^2) 정렬 알고리즘도 버블 정렬보다 일반적으로 더 빠르게 실행되며, 복잡도도 더 높지 않다. 따라서 버블 정렬은 실제로 거의 사용되지 않는다.

버블 정렬은 적응형 정렬이므로, 이미 대부분 정렬된 목록(소수의 전위를 가짐)에서는 퀵 정렬과 같은 알고리즘보다 성능이 좋을 수 있다. 예를 들어, 버블 정렬은 이미 정렬된 목록에서 O(n) 시간이 걸리지만, 퀵 정렬은 여전히 O(n \log n) 시간이 걸린다.

버블 정렬은 모든 요소에 대해 인접한 요소와 비교하여 순서가 역전되어 있으면 교환하는 과정을 요소 수 - 1번 반복하여 정렬을 수행한다. 이 반복은 교환이 일어나지 않게 된 시점에서 중단할 수 있다. 버블 정렬은 비교 교환 순서를 조정하여 효율성을 높인 여러 알고리즘의 기초가 되었다. 예를 들어, 버블 정렬은 병렬 처리와 친화성이 높으며, 하드웨어 구현에서는 시간 복잡도가 O(n)이 될 수 있다. 이러한 병렬 처리를 위해 비교 교환 순서를 조정한 알고리즘으로 짝수-홀수 정렬이 있다.

비교 횟수는 최대 n(n-1)/2회이다. 교환 횟수는 원래 데이터 열에 따라 다르지만, 한 번의 스캔에서 평균 n/2회이므로 전체적으로는 평균 n(n-1)/4회이다. (O(n^2))

버블 정렬에서 큰 수는 배열의 처음에 위치해도 문제가 없지만, 배열의 뒤쪽에 위치한 작은 수는 배열의 처음으로 이동하는 데 시간이 오래 걸린다. 이를 개선하기 위해 셰이커 정렬이나 콤 정렬이 제안되었다.

4. 1. 토끼와 거북이

정렬 과정에서 각 원소가 이동해야 하는 거리와 방향은 버블 정렬의 성능을 결정한다. 왜냐하면 요소들은 서로 다른 속도로 다른 방향으로 이동하기 때문이다. 리스트의 끝으로 이동해야 하는 요소는 빠르게 이동할 수 있다. 예를 들어, 리스트에서 가장 큰 요소는 모든 교환에서 이기므로, 처음에 시작 부분 근처에 있더라도 첫 번째 순회에서 정렬된 위치로 이동한다. 반면에 리스트의 시작 부분으로 이동해야 하는 요소는 순회당 한 단계 이상 이동할 수 없으므로 매우 느리게 시작 부분으로 이동한다. 가장 작은 요소가 리스트의 끝에 있으면 시작 부분으로 이동하는 데 n-1 순회가 걸린다. 이러한 요소들을 이솝 우화의 토끼와 거북이의 등장인물 이름을 따서 토끼와 거북이라고 부른다.

버블 정렬의 속도를 향상시키기 위해 거북이를 제거하려는 다양한 노력이 있었다. 칵테일 정렬은 양방향 버블 정렬로, 시작부터 끝까지, 그리고 다시 반대로 끝에서 시작으로 이동한다. 거북이를 꽤 잘 이동시킬 수 있지만, 최악의 경우 O(n^2) 복잡도를 유지한다. 빗질 정렬은 큰 간격으로 분리된 요소를 비교하며, 리스트를 부드럽게 만들기 위해 점점 더 작은 간격으로 진행하기 전에 거북이를 매우 빠르게 이동시킬 수 있다. 평균 속도는 퀵 정렬과 같은 더 빠른 알고리즘과 비슷하다.

4. 2. 단계별 예시

숫자 배열 "5 1 4 2 8"을 버블 정렬을 사용하여 오름차순으로 정렬하는 과정은 다음과 같다. 각 단계에서 비교되는 요소는 '''굵게''' 표시된다.

;첫 번째 패스

:( '''5''' '''1''' 4 2 8 ) → ( '''1''' '''5''' 4 2 8 ), 5 > 1이므로 교환

:( 1 '''5''' '''4''' 2 8 ) → ( 1 '''4''' '''5''' 2 8 ), 5 > 4이므로 교환

:( 1 4 '''5''' '''2''' 8 ) → ( 1 4 '''2''' '''5''' 8 ), 5 > 2이므로 교환

:( 1 4 2 '''5''' '''8''' ) → ( 1 4 2 '''5''' '''8''' ), 8 > 5이므로 교환하지 않음

;두 번째 패스

:( '''1''' '''4''' 2 5 8 ) → ( '''1''' '''4''' 2 5 8 )

:( 1 '''4''' '''2''' 5 8 ) → ( 1 '''2''' '''4''' 5 8 ), 4 > 2이므로 교환

:( 1 2 '''4''' '''5''' 8 ) → ( 1 2 '''4''' '''5''' 8 )

:( 1 2 4 '''5''' '''8''' ) → ( 1 2 4 '''5''' '''8''' )

;세 번째 패스

:( '''1''' '''2''' 4 5 8 ) → ( '''1''' '''2''' 4 5 8 )

:( 1 '''2''' '''4''' 5 8 ) → ( 1 '''2''' '''4''' 5 8 )

:( 1 2 '''4''' '''5''' 8 ) → ( 1 2 '''4''' '''5''' 8 )

:( 1 2 4 '''5''' '''8''' ) → ( 1 2 4 '''5''' '''8''' )

두 번째 패스 이후 배열이 이미 정렬되었지만, 알고리즘은 추가적인 패스를 통해 교환이 전혀 발생하지 않는지 확인해야 완료되었음을 알 수 있다.[1] 세 번째 패스에서 교환이 전혀 발생하지 않았으므로 정렬이 완료되었다.

5. 구현

버블 정렬은 배열의 인접한 두 원소를 비교하여 정렬되지 않은 순서(오름차순 또는 내림차순)로 되어 있으면 서로 교환하는 방식으로 작동한다. 이 과정을 배열 전체에 대해 반복하여 정렬을 완료한다.

다음은 다양한 프로그래밍 언어로 구현된 버블 정렬의 예시이다.


  • C



#include

# define MAX 10

int* bubble_sort(int arr[], int n) {

int i, j, temp;

for (i=n-1; i>0; i--) {

for (j=0; j
if (arr[j] > arr[j+1]) {

temp = arr[j];

arr[j] = arr[j+1];

arr[j+1] = temp;

}

}

}

return arr;

}

int main() {

int arr[MAX] = { 2, 6, 4, 8, 10, 12, 89, 68, 45, 37 };

int* arr_new = bubble_sort(arr, MAX);

for (int i = 0; i < MAX; i++) {

printf("%d\n", *(arr_new+i));

}

return 0;

}


  • C++



#include

using namespace std;

#include

using std::setw;

void printBubbles(const int bubbles[], const int n);

void lineup(int& large, int& small);

int main()

{

const int n = 10;

int bubbles[n] = { 2, 6, 4, 8, 10, 12, 89, 68, 45, 37 };

cout << "Data items in original order\n";

printBubbles(bubbles, n);

for (int level = 0; level < n - 1; level++) {

for (int i = 0; i < n - level - 1; i++) {

if (bubbles[i] > bubbles[i + 1])

lineup(bubbles[i], bubbles[i + 1]);

}

}

cout << "\nData items in ascending order\n";

printBubbles(bubbles, n);

return 0;

}

void printBubbles(const int bubbles[], const int n) {

for (int i = 0; i < n; i++)

cout << setw(4) << bubbles[i];

cout << endl;

}

void lineup(int& large, int& small) {

int save = large;

large = small;

small = save;

}

  • C#



int[] data = new int[] { 3, 6, 2, 4, 1, 7, 9, 8, 5 };

int hold = 0;

int[] BubbleSort = new int[] { };

for(int i = 0; i < data.Length - 1; i++)

{

for (int j = 0; j < data.Length - 1 - i; j++)

{

if (data[j] > data[j + 1])

{

hold = data[j];

data[j] = data[j + 1];

data[j + 1] = hold;

}

}

}

for (int i = 0; i < data.Length; i++)

{

Console.WriteLine(data[i]);

}

  • F#



let sort (arr:'a[]) =

let arr = Array.copy arr

let swap i j =

let tmp = arr.[i] in arr.[i] <- arr.[j]; arr.[j] <- tmp

for i = arr.Length - 1 downto 0 do

for j = 1 to i do

if (arr.[j - 1] > arr.[j]) then swap (j-1) j

arr

printfn "%A" (sort [|3;4;2;1|])

  • Java



void bubbleSort(int[] arr) {

int temp = 0;

for(int i = 0; i < arr.length - 1; i++) {

for(int j= 1 ; j < arr.length-i; j++) {

if(arr[j]
temp = arr[j-1];

arr[j-1] = arr[j];

arr[j] = temp;

}

}

}

System.out.println(Arrays.toString(arr));

}

  • Python



def bubbleSort(x):

length = len(x)-1

for i in range(length):

for j in range(length-i):

if x[j] > x[j+1]:

x[j], x[j+1] = x[j+1], x[j]

return x


  • Scala



def bubbleSort(arr: Array[Int]):Array[Int] = {

var tmp = 0

for(i <- 0 until arr.length; j <- 1 until arr.length-i) {

if (arr(j-1) > arr(j)) {

tmp = arr(j-1)

arr(j-1) = arr(j)

arr(j) = tmp

}

}

arr

}


5. 1. 의사 코드 구현

버블 정렬은 배열의 두 수(a, b)를 선택하여, 만약 정렬되지 않았다면 두 수를 바꾸는 방식으로 진행된다. 오름차순에서는 a, 내림차순에서는 a>b여야 정렬된 것으로 판단한다. 이를 배열의 처음부터 끝까지 반복하고, 이 과정을 배열에 변화가 없을 때까지 반복한다.

다음은 의사 코드로 표현한 알고리즘이다 (0부터 시작하는 배열):

```pascal

procedure bubbleSort(A : 정렬 가능한 항목들의 목록)

n := A의 길이

repeat

swapped := false

for i := 1 to n-1 까지 반복

if A[i-1] > A[i] then

swap(A[i-1], A[i])

swapped := true

end if

end for

until not swapped

end procedure

```

모든 요소에 대해 인접한 요소와 비교하여 순서가 역전되어 있으면 교환한다. 이를 요소 수 - 1번 반복하여 정렬을 수행한다. 이 반복은 교환이 일어나지 않게 된 시점에서 중단할 수 있다.

개선된 버블 정렬에 대한 의사 코드는 다음과 같다.

```pseudocode

procedure bubbleSort( A : 정렬 가능한 항목의 목록 )

for each i in 1 to length(A) - 1 do:

for each j in 2 to length(A) - i + 1 do:

if A[ j ] < A[ j - 1 ] then

swap( A[ j ], A[ j - 1 ] )

end if

end for

end for

end procedure

5. 2. 버블 정렬 최적화

버블 정렬 알고리즘은 ''n''번째 과정이 ''n''번째로 큰 요소를 찾아 마지막 위치에 배치한다는 점을 이용하여 최적화할 수 있다. 즉, 내부 루프는 ''n''번째 실행 시 마지막 ''n'' - 1개 항목을 확인할 필요가 없다.

한 번의 과정에서 둘 이상의 요소가 최종 위치에 배치될 수도 있다. 모든 과정이 끝난 후 마지막 교환 이후의 모든 요소는 정렬된 상태이므로 다시 확인할 필요가 없다. 이를 통해 많은 요소를 건너뛸 수 있으며, 최악의 경우 비교 횟수를 약 50% 개선할 수 있다. (단, 교환 횟수는 개선되지 않는다.)

이를 의사 코드로 나타내면 다음과 같다.

```pascal

procedure bubbleSort(A : 정렬 가능한 항목 목록)

n := A의 길이

repeat

newn := 0

for i := 1 to n - 1 inclusive do

if A[i - 1] > A[i] then

swap(A[i - 1], A[i])

newn := i

end if

end for

n := newn

until n ≤ 1

end procedure

```

칵테일 정렬과 같은 다른 방법도 인접한 항목을 반복적으로 비교하고 교환하는 같은 아이디어를 유지하면서 버블 정렬의 성능을 개선하려고 시도한다.

모든 요소에 대해 인접한 요소와 비교하여 순서가 맞지 않으면 교환하는 작업을 요소 수 - 1번 반복하여 정렬을 수행한다. 이 반복은 교환이 일어나지 않을 때 중단할 수 있다.[1]

이러한 특징으로 인해 버블 정렬은 병렬 처리와 잘 맞으며, 비교 교환 순서를 조정한 하드웨어 구현에서는 시간 복잡도가 O(n)이 된다. 이러한 병렬 처리를 위해 비교 교환 순서를 조정한 알고리즘으로 짝수-홀수 정렬이 있다.[1]

소프트웨어 구현의 경우, 처음부터 순차적으로 처리되는 특성을 이용하여 불필요한 비교 교환을 하지 않도록 효율성을 높이는 것이 일반적이며, 이러한 알고리즘을 버블 정렬이라고 부르기도 한다. 비교 교환 순서를 역순으로 하여 비교 교환을 쉽게 만든 알고리즘에는 삽입 정렬이 있다.[1]

6. 활용

버블 정렬은 이해하고 구현하기 쉬워 컴퓨터 과학 입문 과정에서 정렬 알고리즘의 개념을 소개하는 데 자주 사용된다.[8] 그러나 O(n^2)의 시간 복잡도로 인해 소수의 요소 목록을 제외하고는 효율성이 크게 감소하며, 실제 사용에는 적합하지 않다. 대신 삽입 정렬과 같은 더 효율적인 알고리즘이 선호된다.[8]

도널드 커누스는 "버블 정렬은 매력적인 이름과 몇 가지 흥미로운 이론적 문제를 야기한다는 점을 제외하면 추천할 만한 것이 없다"고 평가했다.[7] 자르곤 파일은 보고 정렬을 "전형적인 [sic] 지독한 알고리즘"이라고 부르며, 버블 정렬을 "일반적인 나쁜 알고리즘"이라고 부른다.[6]

컴퓨터 그래픽 분야에서는 거의 정렬된 배열에서 작은 오류(단 두 요소의 교환과 같은)를 감지하고 선형 복잡도(2''n'')로 수정할 수 있다. 예를 들어 다각형 채우기 알고리즘에서 특정 스캔 라인(x축과 평행한 선)에서 경계선을 해당 x 좌표로 정렬하고 y를 증가시키면 두 선의 교차점에서만 순서가 변경된다.

7. 변형


  • 홀짝 정렬은 메시지 전달 시스템을 위한 버블 정렬의 병렬 버전이다.
  • 칵테일 정렬은 왼쪽과 오른쪽으로 번갈아 가며 정렬을 수행하는 방식이다.[2]

8. 명칭에 대한 논쟁

버블 정렬은 "가라앉는 정렬(Sinking sort)"이라고도 불린다.[9]

도널드 커누스는 저서에서 원하는 위치에 값을 삽입하는 것을 "[값을] 적절한 수준으로 가라앉히는 것"이라고 묘사하며, "이 정렬 방법은 때때로 '체질' 또는 '가라앉는' 기술이라고 불린다."라고 언급했다.[10]

이러한 논쟁은 알고리즘을 두 가지 관점에서 볼 수 있기 때문에 지속된다.


  • '더 큰' 값은 '더 무거운' 것으로 간주되어 목록의 '바닥'으로 점진적으로 '가라앉는다'고 볼 수 있다.
  • '더 작은' 값은 '더 가벼운' 것으로 간주되어 목록의 '맨 위'로 점진적으로 '떠오른다'고 볼 수 있다.

9. 대중문화

2007년 인터뷰에서 구글(Google) CEO 에릭 슈미트(Eric Schmidt)는 당시 대통령 후보 버락 오바마(Barack Obama)에게 100만 개의 정수를 정렬하는 가장 좋은 방법에 대해 질문했고, 오바마는 잠시 멈칫하더니 "버블 정렬은 잘못된 방법이라고 생각합니다."라고 답했다.[11][12]

참조

[1] 웹사이트 Visualising Sorting Algorithms https://corte.si/pos[...] 2007-04-27
[2] 웹사이트 "[JDK-6804124] (coll) Replace \"modified mergesort\" in java.util.Arrays.sort with timsort - Java Bug System" https://bugs.openjdk[...] 2020-01-11
[3] 웹사이트 "[Python-Dev] Sorting" https://mail.python.[...] 2002-07-20
[4] 웹사이트 EDWARD FRIEND Obituary (2019) - Washington, DC - The Washington Post https://www.legacy.c[...]
[5] 논문 Sorting on Electronic Computer Systems
[6] 웹사이트 jargon, node: bogo-sort http://www.jargon.ne[...]
[7] 서적 The Art of Computer Programming
[8] 논문 Bubble sort: an archaeological algorithmic analysis http://www.cs.duke.e[...]
[9] 웹사이트 bubble sort https://xlinux.nist.[...] National Institute of Standards and Technology 2014-10-01
[10] 서적 The Art of Computer Programming: Volume 3: Searching and Sorting Addison-Wesley
[11] 간행물 Obama Passes His Google Interview https://www.wired.co[...] 2020-10-27
[12] AV media Barack Obama | Candidates at Google https://www.youtube.[...] Talks at Google 2019-09-18
[13] 문서 バブルソートの意味 https://dictionary.g[...]
[14] 간행물 Bubble Sort -- An Archaelogical Algorithmic Analysis 2003-01-11
[15] 웹인용 Visualising Sorting Algorithms https://corte.si/pos[...] 2007-04-27


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com