부다브로

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 발견
- 2.1. 초기 발견
- 2.2. 명칭의 유래
3. 렌더링 방법
- 3.1. 수학적 기초
- 3.2. 알고리즘
4. 뉘앙스
5. [[로지스틱 맵]]과의 관계
- 5.1. 이차 변환
- 5.2. 3차원적 관계 (안티-부다브로)
참조

1. 개요

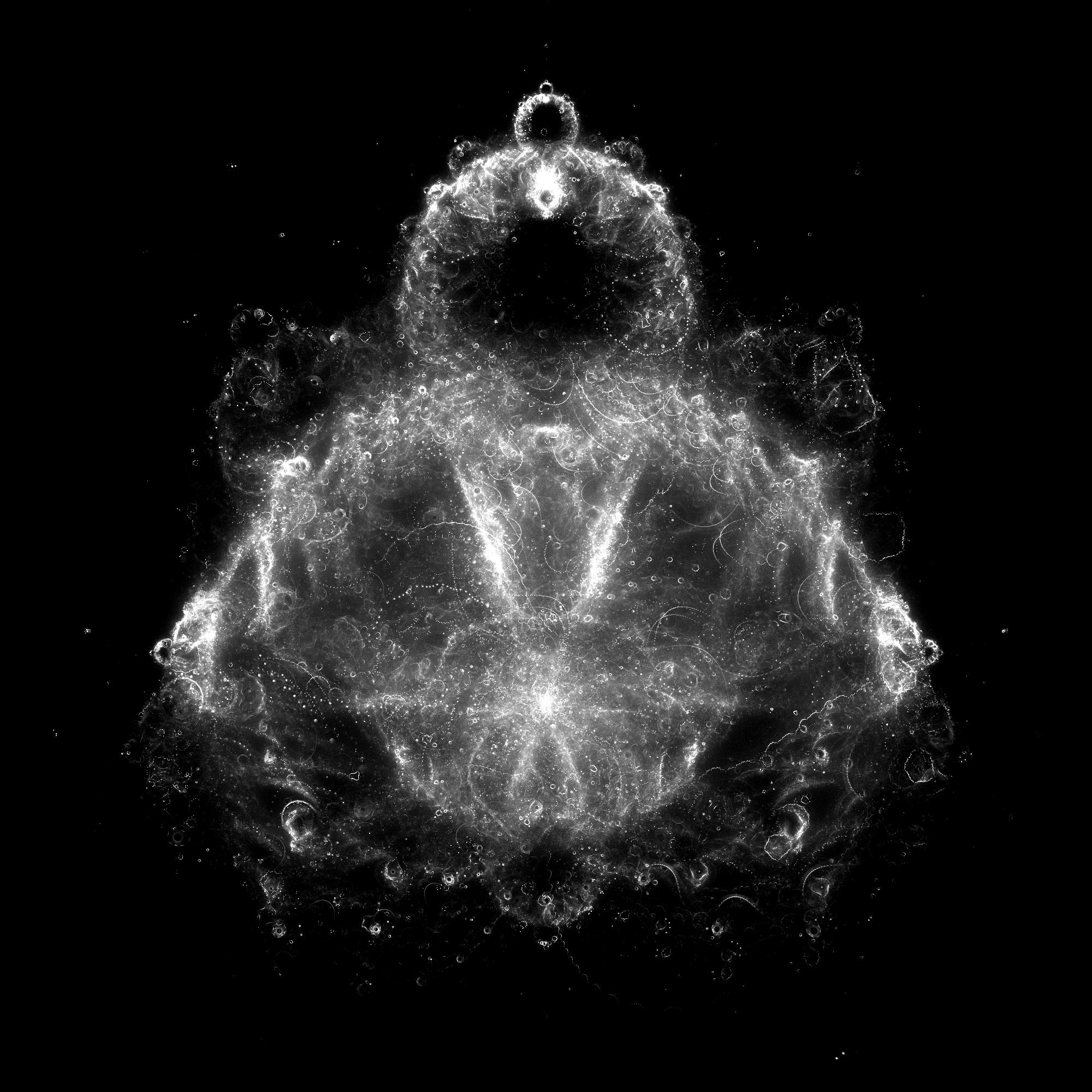
부다브로는 1993년 멜린다 그린이 발견한 렌더링 기법으로, 망델브로 집합에 속하지 않는 점들의 경로를 추적하여 이미지를 생성한다. 이 기법은 망델브로 집합과 로지스틱 맵과 연관성이 있으며, 렌더링 과정에서 반복 횟수와 색상 조합을 통해 다양한 시각적 효과를 나타낸다. 특히, 여러 그레이스케일 이미지를 합성하여 색상 이미지를 만드는 네뷸라브로(Nebulabrot) 기법은 천문학의 성운 이미지와 유사한 결과를 만들어낸다.

더 읽어볼만한 페이지

프랙탈 - 브라운 운동
브라운 운동은 액체나 기체 속 미세 입자가 매질 분자와 충돌하여 불규칙하게 움직이는 현상으로, 아인슈타인과 스몰루호프스키의 이론적 설명과 페랭의 실험적 검증을 통해 원자 존재 입증에 기여했으며, 확산/랑주뱅 방정식으로 모델링되어 다양한 분야에 응용된다.
프랙탈 - 프랙탈 우주론
프랙탈 우주론은 우주의 구조가 프랙탈 기하학적 특성을 갖는다는 이론이며, 관측 결과는 우주가 균질하다는 것을 보여주지만, 이론적 연구에서는 큰 규모나 미시적 규모에서 프랙탈 구조를 제안하기도 한다.

부다브로
개요
부다브로트 밀도 플롯
유형	프랙탈
발견자	멜빈 캘빈 (추정)
이름 유래	불교의 형상과 유사성에서 유래
수학적 정의
정의	점화 $z_{k+1} = z_k^2 + c$가 발산하는 복소 평면의 점 $c$의 궤적을 히스토그램으로 그린 것
관련 집합	만델브로 집합
계산 방법	만델브로 집합 외부의 $c$ 값을 선택 임의의 $z_0$ 값 (일반적으로 $z_0 = 0$)에서 시작하여 $z_{k+1} = z_k^2 + c$를 반복 궤적이 특정 임계값 (일반적으로 반지름 2의 원)을 벗어날 때까지 반복 궤적의 각 점 ($z_k$)을 히스토그램에 기록 다른 $c$ 값에 대해 반복
변형
반부다브로트	만델브로 집합 내부의 $c$ 값을 사용하여 궤적을 그림
줄리아브로트	만델브로 집합 외부의 $c$ 값을 고정하고 다양한 $z_0$ 값에 대해 궤적을 그림
다른 변형	다양한 색상 매핑, 필터링, 3D 표현 등
역사
발견	멜빈 캘빈이 1993년에 처음 발견한 것으로 추정되지만, 1980년대 후반에 이미 일부 사람들이 알고 있었을 가능성이 있음. 공식적으로는 1993년 뉴스그룹 comp.fractals에 게시되면서 알려짐
이름	로리 가디가 1993년에 불교의 형상과 유사하다는 점에 착안하여 '부다브로트'라는 이름을 붙임
대중화	위키피디아와 같은 온라인 플랫폼을 통해 널리 알려지게 됨
계산
소프트웨어	Fractint Mandelbulb 3D XaoS 기타 프랙탈 생성 소프트웨어
최적화	SIMD 명령어 활용 멀티스레딩 분산 컴퓨팅
기타
참고 자료	만델브로 집합 프랙탈

2. 발견

1993년 멜린다 그린이 유즈넷의 sci.fractal 뉴스그룹에 게시한 글을 통해 부다브로 렌더링 기법을 발견했다.^[1]^[3]

1988년 리나스 벱스타스는 클리프 피코버에게 유사한 이미지를 전달하여 피코버 줄기 발견의 계기가 되었다. 그러나 이들 연구자들은 빠져나오지 못하는 궤도를 걸러내지 않아 힌두교 예술과 유사한 형태를 얻지 못했다.

멜린다 그린은 인도인 동료의 제안으로 이 패턴을 처음에 '가네쉬'라고 명명했다. 가네샤는 코끼리 머리 형상을 한 인도의 신이다. 이후 로리 가우디가 "부다브로"라는 새로운 이름을 제안했다.

2. 1. 초기 발견

1993년 멜린다 그린이 유즈넷의 sci.fractal 뉴스그룹에 게시한 글을 통해 부다브로 기법이 발견되었다.^[1]^[3]

1988년 리나스 벱스타스는 유사한 이미지를 클리프 피코버에게 전달하여 피코버의 저서 ''컴퓨터, 패턴, 카오스와 뷰티''에 포함되었고, 이는 피코버 줄기의 발견으로 이어졌다. 1993년 노엘 그리핀 또한 Fractint 렌더러의 "만델클라우드" 옵션에서 이와 유사한 아이디어를 구현했다. 그러나 이들은 힌두 예술을 연상시키는 유령 같은 형태를 만드는 데 필요한, 빠져나가지 않는 궤적을 걸러내지 못했다.

그린은 처음에 이 패턴을 '가네쉬'라고 이름 붙였는데, 인도인 동료가 "코끼리 머리를 가진 신 가네샤"를 떠올렸기 때문이다.^[3] 이후 로리 가우디가 "부다브로"라는 이름을 새로 만들었다.^[4]

2. 2. 명칭의 유래

1993년 멜린다 그린이 유즈넷의 sci.fractal 뉴스그룹에 부다브로 렌더링 기법을 처음 소개했다.^[1]^[3] 그린은 이 기법을 처음에는 '가네쉬'라고 불렀는데, 이는 그녀의 인도인 동료가 이 도형에서 코끼리 머리 형상을 한 인도의 신 가네샤를 떠올렸기 때문이다.^[3]^[10] 이후 '부다브로'라는 이름은 로리 가우디(Lori Gardi)가 제안했다.^[4]^[11]

3. 렌더링 방법

부다브로는 망델브로 집합에서 파생된 개념으로, 망델브로 집합의 반복 과정에서 나타나는 점들의 궤적을 시각화한다. 일반적인 망델브로 집합이 수렴하는 점들의 집합을 나타내는 반면, 부다브로는 발산하는 점들이 지나가는 경로를 표시하여 독특한 이미지를 만들어낸다.

부다브로 이미지는 2차원 배열을 생성하여 만들 수 있다. 각 배열은 이미지의 픽셀에 해당하며 0으로 초기화된다. 그 후, 복소평면 상의 점 c를 무작위로 선택하여 망델브로 함수를 통해 반복 계산한다. 이 과정에서 선택된 최대 반복 횟수 내에 발산하는 점들의 궤적을 배열에 기록한다. 즉, 점이 궤적 상의 픽셀을 지나갈 때마다 해당 픽셀의 배열 값을 1씩 증가시킨다.

충분한 수의 점 c에 대해 반복 계산을 완료한 후, 배열에 기록된 값을 기반으로 각 픽셀에 색상을 할당한다. 이 때, 회색조를 사용하거나, 천문학에서 성운을 표현하는 방식과 유사하게 가짜 색상을 사용할 수 있다. 이러한 가짜 색상을 사용한 이미지는 '''네뷸라브로(Nebulabrot)'''라고 불린다.^[10] 배열 값이 클수록, 즉 해당 픽셀을 지나는 궤적이 많을수록 더 밝은 색으로 표현된다. 이를 통해 z값이 무한대로 발산하는 동안 가장 많은 시간을 보내는 영역이 강조된 밀도 플롯 형태의 이미지가 생성된다.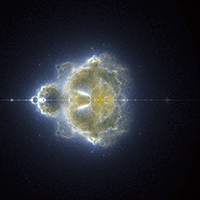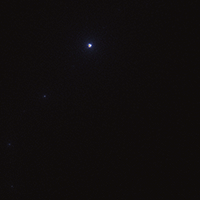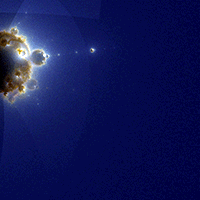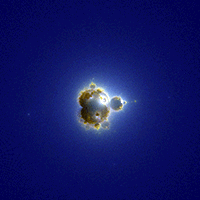

빨강, 초록, 파랑 채널의 최대 반복 횟수가 각각 5000, 500, 50인 가짜 색상 부다브로트 줌.

3. 1. 수학적 기초

망델브로 집합은 복소평면에서 다음 수열을 반복적으로 정의하여 구성된다.

:z_n+1 = z_n² + c

여기서 z₀=0 일 때, n이 무한대로 갈 때 발산하지 않는 c의 집합이다. 즉,

:

M=\{\gamma \vert z_{n+1} = {z_n}^2 + c, z_{0} = 0, \lim_{n \to \infty}\left| z_n \right\vert < \infty\}

를 만족하는 집합이다.^[12]

부다브로는 이 망델브로 수열을 이용하여, 발산하는 점들의 경로를 시각화한다. 먼저 가우스 평면 내의 실수부와 허수부 각각 -2~2 범위를 화면으로 간주하고, 점의 세밀함을 정한다. 화면에서 점 c를 무작위로 선택하고, z_n을 n=1부터 순서대로 계산하여 |z_n+1|>2 가 되는 시점(발산이 분명해지는 시점)에서 z₁부터 z_n의 위치에 점을 그린다. 이미 점이 그려져 있는 경우에는 더 밝게 표시한다. 단, n의 상한 N을 정해두고, 그 이상이 되면 수렴했다고 간주하여 점을 그리지 않는다.^[10] 이 과정을 반복하여 새로운 c를 무작위로 선택하고 계산을 반복한다.

반복 횟수는 이미지 형태에 큰 영향을 준다. 반복 횟수가 커지면, 이전에는 어두웠던 부분에도 그림이 그려지게 된다.

최대 반복 횟수	결과
20
100
1,000
20,000
1,000,000

3. 2. 알고리즘

부다브로 렌더링 알고리즘은 다음과 같이 요약할 수 있다.

1. 2차원 배열 초기화: 이미지의 각 픽셀에 해당하는 2차원 배열(계수기)을 생성하고, 모든 값을 0으로 초기화한다.

2. 무작위 샘플링 및 반복: 복소 평면에서 무작위 점 c를 선택하고, 다음의 망델브로 집합 함수를 반복 계산한다.

`z_(n+1) = z_n^2 + c` (단, `z_0 = 0`)

3. 경로 추적 및 카운팅:

만약 `z_n`이 특정 임계값을 넘어 발산하면 (즉, 망델브로 집합에 속하지 않으면), 해당 점이 지나가는 경로 상의 모든 픽셀에 해당하는 배열 값을 1씩 증가시킨다.
`z_n`이 발산하지 않고 특정 횟수(최대 반복 횟수) 안에 머무르면, 해당 점은 버려진다.

4. 색상 할당: 충분한 수의 점 c에 대해 위 과정을 반복한 후, 배열에 기록된 값(각 픽셀을 지나간 경로의 수)을 기반으로 회색조 또는 가짜 색상(false color)을 할당한다. 값이 클수록 더 밝게 표현하여, z값이 무한대로 발산하는 동안 가장 많은 시간을 보낸 영역을 강조한다.

반복 횟수는 이미지의 형태에 큰 영향을 준다. 반복 횟수가 커질수록, 낮은 반복 횟수에서는 어두웠던 부분에도 궤적이 그려지면서 더 세밀한 구조가 나타난다.

최대 반복 횟수	이미지
20
100
1,000
2만
백만

원색별로 반복 횟수를 다르게 설정하여 색상을 입힐 수 있는데, 이는 천문학에서 성운 이미지에 사용하는 가짜 색상 기법과 유사하다. 이러한 이미지를 '''네뷸라브로(Nebulabrot)'''라고 부르기도 한다.^[10]

빨강, 초록 및 파랑 채널의 최대 반복 값이 각각 5000, 500, 50인 가짜 색상 네뷸라브로

4. 뉘앙스

Buddhabrot^영어 렌더링은 각 샘플을 두 번 이상 반복할 가능성이 있어, 망델브로 렌더링보다 계산이 더 철저하게 요구된다.^[5] 고배율로 확대할 때도 더 많은 계산이 필요하다. 선택하는 반복 횟수는 이미지에 큰 영향을 주는데, 값이 높으면 밀도가 낮고 더 자세한 모습을 나타낸다. 낮은 반복 횟수를 사용하면 점들이 빠져나오지 못하고, 모두 빠져나오지 않은 것으로 간주된다.

반복 횟수와 색상을 다르게 하여 세 가지 이미지를 합성할 수도 있다. 예를 들어, 2,000번 반복한 적색 이미지와 200번 반복한 녹색 이미지를 조합하는 것은 천문학자들이 적외선 화상을 만드는 방법과 비슷하다. 어떤 이미지들은 성운과 매우 유사하여 ''네뷸라브로''(Nebulabrot^영어)라고 부르기도 한다.^[5]

4. 1. 계산 집약성

`부다브로` 렌더링은 표준 망델브로 렌더링보다 계산 집약적인데, 이는 선명한 이미지를 얻기 위해 이미지의 픽셀보다 더 많은 무작위 점을 반복해야 하기 때문이다.^[5] 각 샘플은 (테스트에서 점이 빠져나가면 그 점의 경로를 다시 그려야 하므로) 두 번 이상 반복될 수 있다. 또한, 빠져나온 점을 바깥에서 안쪽으로 들어가도록 경로를 설정하는 것처럼 고배율 확대 시에도 더 많은 계산이 필요하다.

표준 망델브로 이미지는 줌 레벨에 관계없이 주어진 픽셀을 직접 계산할 수 있지만, 부다브로 이미지의 확대된 영역의 픽셀은 렌더링되는 영역 외부의 초기 점에 영향을 받을 수 있다. 따라서 더 복잡한 확률적 기술을 사용하지 않으면,^[5] `부다브로`의 확대된 부분은 단순히 큰 전체 크기 렌더링을 잘라내는 방식으로 렌더링된다.

4. 2. 반복 횟수의 영향

부다브로 이미지에서 선택된 반복 횟수는 이미지의 형태에 큰 영향을 준다. 반복 횟수가 높으면 소수의 점들이 많은 픽셀을 거쳐 탈출하면서 경로가 더 뚜렷해진다. 이에 따라 밀도는 낮아지고, 더 세밀한 표현이 가능해진다. 반면, 반복 횟수가 낮으면 점들이 탈출하지 못하고, 탈출하지 않은 것으로 간주되어 세부 묘사가 줄어든다.^[5]

다음 표는 반복 횟수에 따른 이미지 변화를 보여준다.

반복 횟수에 따른 부다브로 이미지 변화
최대 반복 횟수	이미지	설명
20		낮음, 대부분 점 탈출 실패, 세부 묘사 부족
100		일부 점 탈출, 경로 나타남
1,000		더 많은 점 탈출, 밀도 낮고 세밀한 표현
20,000		높음, 더욱 세밀한 표현
1,000,000		매우 높음, 가장 세밀하고 복잡한 구조

서로 다른 반복 횟수와 색상을 조합하여 이미지를 합성할 수도 있다. 예를 들어, 2,000번 반복한 적색 이미지와 200번 반복한 녹색 이미지를 결합하는 것은 천문학자들이 적외선 이미지를 만드는 방식과 유사하다. 이러한 이미지는 성운과 흡사하여 ''네뷸라브로''라고도 불린다.^[5]

4. 3. 색상 합성 (네뷸라브로)

멜린다 그린은 최대 반복 횟수만 다른 세 개의 그레이스케일 이미지를 가져와, 천문학자들이 성운 및 기타 천체를 가짜 색상 이미지로 만드는 데 사용하는 것과 동일한 방식으로 단일 색상 이미지로 결합하여 컬러 부다브로 이미지를 만드는 방법을 고안했다. 예를 들어, 2,000회의 최대 반복 이미지 하나를 빨간색 채널에, 200회의 최대 반복 이미지 하나를 녹색 채널에, 20회의 최대 반복 이미지 하나를 RGB 색상 공간 이미지의 파란색 채널에 할당할 수 있다.^[5]

이러한 기법을 사용하는 부다브로 이미지는, 성운과 매우 유사한 이미지의 결과로 나타나기 때문에, 일부에서는 ''네뷸라브로''라고 명명했다.^[5]

이 방법은 천문학자들이 적외선 화상을 만드는 방법과 비슷하며, 반복 횟수를 3원색마다 각각 바꾸어 이미지에 색을 입히는 것은 천문학자들이 성운의 이미지를 의사 컬러화하는 수법과 유사하다. 이렇게 컬러화된 이미지는 '''네뷸라브로'''(Nebulabrot)라고 불리기도 한다.

5. [[로지스틱 맵]]과의 관계

망델브로 집합은

z^2+c

의 반복에 의해, 로지스틱 맵은

\lambda x(1-x)

에 의해 정의되는데, 이 둘은 이차 변환을 통해 서로 연관되어 있다.^[10] 이 관계는 멜린다 그린에 의해 발견되었다.

5. 1. 이차 변환

망델브로 집합과 로지스틱 맵은 다음 이차 변환을 통해 연관된다.^[10]

:

c_r = \lambda(2-\lambda)/4

:

c_i =0

:

z_r =-\lambda(2x-1)/2

:

z_i = 0

이 관계를 설명하기 위해,

c_r

과

\lambda

를 같은 x축에 놓고 y축은 다르게 하여 1차원적인 관계를 보였다.^[10]

멜린다 그린은 안티-부다브로가 로지스틱 맵과 통합된다는 것을 발견했다. 이들은 주어진 변환을 사용하여,

z^2 + c

의 안티-부다브로에서

c=(random,0)

과

z_0=(0,0)

로 경로를 그리면,

\{c_r,z_r\}

평면에서 로지스틱 맵을 볼 수 있다.^[10]

5. 2. 3차원적 관계 (안티-부다브로)

멜린다 그린은 '안티-부다브로' 패러다임이 로지스틱 맵과 완전히 통합된다는 것을 발견했다. 두 가지 모두 무작위 시작점에서 반복되는, 삐져나오지 못하는 점들에서 시작하는 투사 경로들을 기반으로 하고 있으며, 반복 함수들은 주어진 변환 공식들과 관련이 있다. z²+c^영어의 안티-부다브로에서 c=(random,0)과 z₀=(0,0)으로 경로들을 그릴 때, {c_r,z_r} 평면에 간단하게 생성되는 병참 본뜨기를 쉽게 볼 수 있다. 렌더링을 위해 z₀=(random,0) 공식을 사용하는데, 병참 본뜨기의 모든 z_r0 공식은 결국 같은 경로를 생성한다는 것을 알 수 있다.

만델브로 집합과 로지스틱 본뜨기는 3차원 축 {c_r,c_i,z_r}을 사용하는 애니메이션에서 3차원적으로 연관된다. 이 애니메이션은 고전적인 반-부다브로를 보여주고, 이것은 {c_r,c_i} 평면에서의 2차원 망델브로 집합이며, c=(random,0)과 z₀=(0,0)의 반-부다브롯이기도 하며, 이것은 2차원 병참 본뜨기이다. {c_i,z_r} 평면을 c_r-축을 중심으로 회전시켜서, 먼저 {c_r,c_i}을 보여주고, 그 다음에는 {c_r,z_r}를 보여주기 위해 90°회전하며, 그리고 나서 {c_r,-c_i}를 보여주기 위해 90°도를 더 회전한다.

로지스틱 본뜨기의 안티-부다브로는 3차원 {c_r,c_i,z_r}과 {c_r,c_i} 평면의 수직선상의 {c_r,z_r} (또는 c_i=0) 평면에 놓여있다. 그러므로 그것은 사실상 고전적인 안티-부다브로의 부분집합이다.

참조

_[1] 웹사이트 The Buddhabrot Technique http://www.superlimi[...]
_[2] 웹사이트 Interior Sketchbook Diary http://www.linas.org[...]
_[3] 웹사이트 The deity hiding in the m-set https://groups.googl[...]
_[4] 뉴스 Chaos (theory) rules for software developer https://news.western[...] Western News: The University of Western Ontario’s newspaper
_[5] 웹사이트 The Buddhabrot http://www.steckles.[...]
_[6] 문서 マンデルブロー集合 http://www.math.nago[...]
_[7] 서적 フラクタルと数の世界海文堂出版
_[8] 문서 'コンピュータ・カオス・フラクタル―見えない世界のグラフィックス'
_[9] 뉴스 Chaos (theory) rules for software developer http://communication[...] The University of Western Ontario’s newspaper
_[10] 웹사이트 The diety hiding in the m-set https://groups.googl[...]
_[11] 웹사이트 The Buddhabrot Technique http://www.superlimi[...]
_[12] 서적 フラクタル数学東京図書

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com