비용함수
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
비용 함수는 기업의 생산량과 관련된 비용을 나타내는 함수로, 총비용, 평균비용, 한계비용 등 다양한 종류가 있다. 총비용은 고정 비용과 가변 비용의 합이며, 평균비용은 총비용을 생산량으로 나눈 값, 한계비용은 생산량 한 단위를 추가 생산할 때 발생하는 비용의 증가분을 의미한다. 비용 함수는 단기와 장기로 구분되며, 단기에는 고정 생산 요소가 존재하지만 장기에는 모든 생산 요소가 가변적이다. 장기 평균 비용 곡선은 단기 평균 비용 곡선의 포락선 형태를 가지며, 규모의 경제와 불경제를 반영한다. 비용 곡선은 생산 함수와 밀접한 관련이 있으며, 생산 요소 가격이 일정할 경우 생산 함수가 비용 함수를 결정한다. U자형 곡선은 단기 및 장기 평균 비용 곡선의 일반적인 형태이나, 실제로는 일정한 비용이나 감소하는 비용을 보고하는 기업도 존재한다.
더 읽어볼만한 페이지
- 생산 - 프로토타입
프로토타입은 새로운 기술이나 기구의 검증, 기능 검증을 위해 제작되며, 대량 생산 전에 문제점을 파악하기 위해 사용되며, 다양한 유형의 프로토타입이 존재하며, 비용 증가와 같은 단점이 있다. - 생산 - OEM
OEM은 주문자 위탁 생산 또는 주문자 상표 부착 생산을 의미하며, 생산 비용 절감 등의 장점이 있지만 품질 관리 문제 등의 단점도 존재하는 제조 방식으로, 다양한 산업에서 활용된다. - 경제학 곡선 - 수요와 공급
수요와 공급은 시장에서 재화나 서비스의 가격과 거래량을 결정하는 경제학의 기본 원리이며, 가격 변화에 따라 수요량과 공급량이 변동하고, 수요와 공급이 일치하는 지점에서 시장 균형이 이루어진다. - 경제학 곡선 - 필립스 곡선
필립스 곡선은 실업률과 인플레이션 간의 관계를 설명하는 경제 이론으로, 단기적으로는 역의 상관관계를 보이나 장기적으로는 자연실업률 개념에 따라 상충관계가 성립하지 않을 수 있으며, 현대 경제학에서는 기대인플레이션을 고려한 수정된 형태로 사용된다. - 비용 - 기회비용
기회비용은 경제학적 개념으로, 어떤 선택을 함으로써 포기해야 하는 다른 선택들 중 가장 가치 있는 것을 의미하며, 경제 주체의 모든 선택에 내재된 비용을 찾아내는 데 중요한 역할을 한다. - 비용 - 거래 비용
거래 비용은 계획, 협상, 계약 이행, 분쟁 해결 등 경제 활동 전반에 걸쳐 발생하는 모든 비용을 의미하며, 거래 빈도, 자산 특수성, 불확실성 등이 주요 결정 요인으로 작용하고 블록체인 기술 등으로 감소될 잠재력이 있지만 사회적 불평등 심화에 대한 우려도 존재한다.
2. 비용함수의 종류
비용함수는 총비용, 평균비용, 한계비용 등 다양한 형태로 나타낼 수 있으며, 각각 다른 경제적 의미를 가진다.
- '''총비용함수''':
- '''평균 비용''':
- '''한계 비용''':
한계비용곡선은 반드시 평균비용이 최소가 되는 점을 통과하며, 평균비용이 최소화되는 산출량이 기업의 효율적 생산량(efficient scale)이 된다.[21]
다음은 각 비용 개념에 대한 표준 약어이다.
이 약어들을 조합하여 다양한 단기 및 장기 비용 곡선을 나타낼 수 있다.
단기 비용 곡선:
장기 비용 곡선:
2. 1. 총비용 (Total Cost, TC)
총비용은 특정 생산량 수준에서 기업이 지출하는 모든 비용의 합계를 의미한다. 총비용함수는 로 표현된다.[21]
'''단기 총비용(SRTC)'''과 '''장기 총비용(LRTC)''' 곡선은 생산량 증가에 따라 증가한다. 이는 더 많은 생산량을 생산하기 위해 단기에는 더 많은 노동 투입이 필요하고, 장기적으로는 더 많은 물리적 자본 투입을 사용해야 하기 때문이다. 그리고 이러한 투입을 더 많이 사용하면 투입 비용이 더 많이 발생한다.
단기에는 하나의 가변 투입 요소(노동 투입)만 있기 때문에 각 가능한 생산량은 특정 양의 노동 투입을 필요로 한다. 따라서 생산량 수준의 함수로서의 단기 총비용은 이 고유한 노동량에 노동의 단위 비용을 곱한 것이다. 그러나 장기적으로는 노동과 물리적 자본의 양을 모두 선택할 수 있으므로, 특정 생산량 수준을 생산하는 총 비용은 최적화 문제의 결과이다. 노동 지출(임금률에 선택된 노동 투입량을 곱한 값)과 자본 지출(자본의 단위 비용에 선택된 물리적 자본 투입량을 곱한 값)의 합은 생산 함수 등식에 따라 노동 투입량과 자본 투입량에 대해 최소화되며, 이는 생산량을 두 가지 투입량 사용과 관련시킨다. 그런 다음 (최소) 총 비용 수준은 주어진 생산량을 생산하는 총 비용이다.

총비용 곡선(TC)은 한계 생산력이 초기에 체증하고(=비용이 체감하고), 어느 지점부터는 체감하는(=비용이 체증하는) (수확 체감의 법칙) 것에 대응하여 위로 볼록, 아래로 볼록이라는 우상향 곡선으로, 역 S자 형태로 나타난다.
2. 2. 평균비용 (Average Cost, AC)
평균비용(Average Cost, AC)은 생산량 한 단위당 발생하는 비용으로, 총비용을 생산량으로 나눈 값이다.Average Cost|애버리지 코스트영어 수식으로 표현하면 다음과 같다.:
평균 비용 곡선(AC)은 원점과 총 비용 곡선 상의 각 점을 연결한 직선의 기울기로 구할 수 있으며, 일반적으로 U자형 곡선으로 나타난다. 원점을 지나는 직선과 비용 곡선이 접하는 지점에서 평균 비용이 최소화된다.
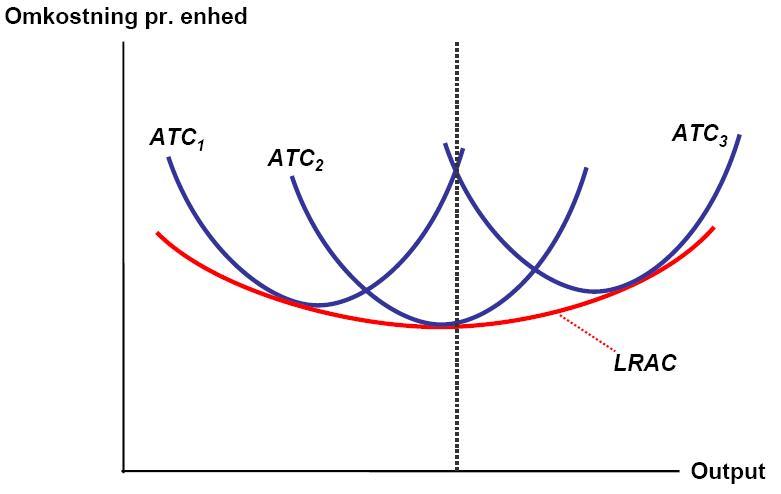
단기 평균 비용(SRATC 또는 SRAC)은 평균 고정 비용과 평균 가변 비용을 합한 값과 같다. 단기에는 고정된 생산 요소(일반적으로 자본)가 존재하기 때문에, 생산량이 증가함에 따라 평균 고정 비용은 지속적으로 감소한다. 평균 가변 비용 곡선의 형태는 가변 투입 요소(일반적으로 노동)에 대한 한계 수익의 증가 및 감소에 따라 결정된다.[4]
장기 평균 비용(LRATC 또는 LRAC) 곡선은 단기 평균 비용 곡선과 유사한 형태를 보이지만, 장기에는 물리적 자본의 사용량을 조절할 수 있다는 차이점이 있다.
한계 비용 곡선은 반드시 평균 비용이 최소가 되는 점을 통과하며, 평균 비용이 최소화되는 생산량이 기업의 효율적 생산 규모(efficient scale)가 된다.[21]
2. 3. 한계비용 (Marginal Cost, MC)
한계비용(Marginal Cost, MC)은 생산량을 한 단위 추가로 늘릴 때 드는 총비용의 증가분이다. 수식으로는 와 같이 표현할 수 있다.[21] 한계비용곡선은 일반적으로 U자형으로 나타나는데, 생산량이 적을 때는 한계비용이 높지만, 생산량이 늘면서 점차 감소하다가 일정 수준을 넘어서면 다시 증가한다. 이는 처음에는 생산 효율이 높아지다가, 일정 수준을 넘어서면 오히려 효율이 떨어지는 수확 체감의 법칙 때문이다.[3]한계비용곡선은 평균비용곡선의 최저점을 통과한다.[21] 이때 평균비용이 최소가 되는 생산량이 기업의 효율적인 생산 규모(efficient scale)가 된다. 한계비용이 평균비용보다 낮으면 평균비용은 감소하고, 한계비용이 평균비용보다 높으면 평균비용은 증가한다.[5]

장기적으로는 모든 생산 요소를 조절할 수 있기 때문에, 장기 한계비용(LRMC)은 규모의 수익에 따라 결정된다. 장기 한계비용 곡선은 장기 평균비용 곡선의 최저점을 지난다.[3] 장기 한계비용이 장기 평균비용보다 낮으면 장기 평균비용은 감소하고, 높으면 증가한다.[2]
기업은 이윤을 최대로 만들기 위해 한계비용과 한계 수입(MR)이 같아지는 지점에서 생산량을 결정한다.
2. 4. 기타 비용
다음은 다양한 비용 개념에 대한 표준 약어이다.
이 약어들을 조합하여 다양한 단기 및 장기 비용 곡선을 나타낼 수 있다.
단기 비용 곡선:
장기 비용 곡선:
3. 장기 생산비용과 단기 생산비용의 구분
생산비용은 고정 생산요소의 존재 여부에 따라 장기와 단기로 구분된다. 단기에는 투입량을 조절할 수 없는 고정 생산 요소가 하나 이상 존재하지만, 장기에는 모든 생산 요소가 가변적이다. 이러한 특성으로 인해 장기 비용함수(LTC)는 을 만족하는 반면, 단기 비용함수(STC)는 고정 생산 요소 때문에 이 된다. 단기 생산비용은 장기 생산비용과 접하는 지점을 제외하고는 항상 장기 생산비용보다 크다.[22]
총 비용 곡선(TC)은 한계 생산력이 초기에 체증(비용 체감)하다가 어느 시점부터 체감(비용 체증)하는 수확 체감의 법칙에 따라 위로 볼록, 아래로 볼록한 우상향 곡선, 즉 역 S자 형태로 나타난다.
단기 총 비용 (SRTC)과 장기 총 비용 (LRTC) 곡선은 모두 생산량 증가에 따라 증가한다. 이는 더 많은 생산을 위해 단기적으로는 더 많은 노동 투입이, 장기적으로는 더 많은 노동 투입과 물리적 자본 투입이 필요하며, 이로 인해 투입 비용이 증가하기 때문이다.
단기에는 가변 투입 요소가 노동뿐이므로, 각 생산량에 필요한 노동 투입량이 정해져 있다. 따라서 단기 총 비용은 이 노동량에 노동의 단위 비용을 곱한 값이다. 장기에는 노동과 자본량을 모두 선택할 수 있어, 특정 생산량의 총 비용은 최적화 문제의 결과가 된다. 즉, 노동 지출(임금률과 노동 투입량의 곱)과 자본 지출(자본 단위 비용과 자본 투입량의 곱)의 합은 생산 함수에 따라 최소화된다. 이 최소화된 총 비용이 주어진 생산량의 총 비용이 된다.
3. 1. 장기와 단기의 구분
장기와 단기의 구분은 고정 생산요소의 존재 여부에 따라 결정된다. 단기에는 투입량을 변화시킬 수 없는 하나 이상의 고정 생산 요소가 존재하며, 장기에는 모든 생산요소가 가변 요소이다. 따라서 장기 비용함수(LTC)의 경우 이 성립한다. 한편 단기 비용함수(STC)의 경우 고정 생산요소가 적어도 하나 이상 존재하기 때문에 이 된다. 단기 생산비용은 장기 생산비용과 접하는 점을 제외하고는 항상 장기 생산비용보다 크다.[22]
3. 2. 단기평균비용과 장기평균비용
장기평균비용곡선은 단기평균비용함수(SAC)에서 고정 요소를 변화시켰을 때 각 곡선의 포락선(envelope curve) 형태를 띤다.[22] 즉, 단기 비용을 계산할 때 자본 K를 고정하고 평균비용곡선을 그렸다면, 장기 평균비용곡선은 에서 각각의 단기평균비용곡선과 접하는 곡선이다. 장기에는 기업이 더 유연하게 대처할 수 있어 단기보다 장기에서 평균비용곡선이 완만하게 나타나며, 단기비용이 장기비용곡선에 접하거나 그 위에 그려진다.[21]
장기 평균 비용 (LRATC/LRAC) 곡선은 단기 곡선과 비슷하지만, 물리적 자본의 사용을 변경할 수 있다는 점이 다르다. 각 생산량에 대해 자본의 비용을 최소화하는 수준이 하나씩 있으며, 주어진 생산량을 생산하는 것과 관련된 고유한 단기 평균 비용 곡선이 존재한다.[12] 만약 기업이 생산량에 맞는 최적의 자본 수준을 사용하고 있지 않다면, SRAC 곡선은 LRAC 위에 놓이게 되며 어떤 점에서도 접하지 않는다.
다음은 장기평균비용곡선(LRAC)과 단기평균비용곡선(SRAC)의 관계를 나타낸 표이다.
3. 3. 단기 가변 비용과 고정 비용
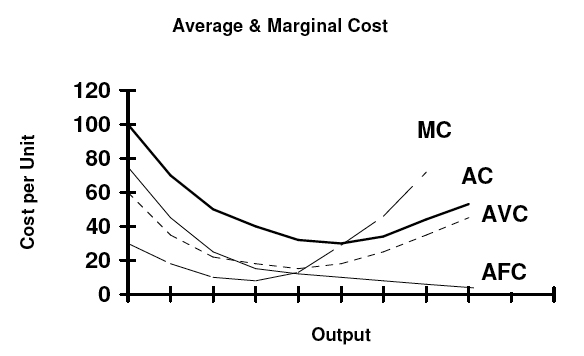
'''단기 고정 비용(FC/SRFC)'''은 생산량 수준에 따라 변동하지 않으므로, 그림과 같이 수평선으로 나타난다. '''단기 가변 비용(VC/SRVC)'''은 생산량이 많을수록 가변 투입물을 더 많이 사용하고 지불해야 하기 때문에 생산량 수준에 따라 증가한다.[1]
3. 4. 단기 평균 가변 비용 (AVC or SRAVC)
평균 가변 비용(AVC/SRAVC)(단기적 개념)은 산출량 단위당 가변 비용(일반적으로 노동 비용)을 의미한다. SRAVC = wL / Q이며, 여기서 w는 임금률, L은 사용된 노동량, Q는 생산된 산출량이다. SRAVC 곡선은 산출량 수준에 따른 단기 평균 가변 비용을 나타내며, 일반적으로 U자형으로 그려진다.[1][2] 그러나 이는 경제 이론에는 편리하지만, 실제 세계와는 거의 관련이 없다는 주장이 제기되어 왔다. 일부 추정에 따르면, 최소한 제조업의 경우 U자형 비용 곡선을 보고하는 기업의 비율은 5~11% 범위에 있다.평균 가변 비용 곡선(Average variable cost curve, AVC)은 절편과 총 비용 곡선상의 각 점을 연결한 직선의 기울기로부터 도출되며, U자형 곡선으로 표시되고, 절편을 통과하는 직선과 비용 곡선의 접점에서 평균 가변 비용이 최소화된다.
3. 5. 단기 평균 고정 비용 (SRAFC)
정의에 따라 고정비는 생산량에 따라 변동하지 않으므로, '''단기 평균 고정 비용(SRAFC)'''(즉, 생산량 단위당 단기 고정 비용)은 생산량이 높아질수록 낮아지며, 이에 따라 아래로 기울어진 곡선이 나타난다.3. 6. 단기 및 장기 평균 총 비용 (SRATC or SRAC and LRATC or LRAC)
평균 총비용 곡선은 산출량 단위당 비용과 산출량 수준 간의 관계를 나타낸다. 완전 경쟁적이고 생산 효율적인 기업은 생산할 주어진 산출량 수준에서 생산 요소의 사용을 가능한 한 낮게 유지하도록 조직한다. 단기에는 적어도 하나의 생산 요소가 고정되어 있는데, 이때 생산량 증가로 얻을 수 있는 모든 가능한 평균 비용 이점을 누린 산출량 수준에서 장기 평균 비용이 발생한다.단기 총비용은 다음과 같이 나타낼 수 있다.
:
여기서 PK는 단위 시간당 물리적 자본 사용의 단위 가격, PL은 단위 시간당 노동의 단위 가격(임금률), K는 사용된 물리적 자본의 양, L은 사용된 노동의 양이다. 이 식을 통해 단기 평균 비용(SRATC 또는 SRAC)을 구할 수 있다.
:
여기서 는 자본의 평균 생산량, 는 노동의 평균 생산량이다.[3]
'''단기 평균 비용 (SRATC/SRAC)'''은 평균 고정 비용과 평균 가변 비용을 더한 값과 같다. 단기에는 K가 고정되어 있으므로 생산량이 증가함에 따라 평균 고정 비용은 지속적으로 감소한다. 평균 가변 비용 곡선의 모양은 가변 투입(일반적으로 노동)에 대한 한계 수익의 증가와 감소에 의해 직접적으로 결정된다.[4]
'''장기 평균 비용 (LRATC/LRAC)''' 곡선은 단기 곡선과 유사하지만, 물리적 자본의 사용을 변경할 수 있다는 점이 다르다.
3. 7. 단기 한계 비용 (SRMC)
'''단기 한계 비용(SRMC)''' 곡선은 기업이 단기적으로 재화나 서비스 생산을 위해 투입하는 한계 (즉, 증분) 비용과 생산량 간의 관계를 도표로 나타낸 것이다. 이 곡선은 기술 및 자원 가격과 같은 다른 변수를 일정하게 유지하면서 한계 비용과 생산량 수준 간의 관계를 파악하도록 구성되었다. 한계 비용 곡선은 일반적으로 U자형이다. 한계 비용은 소량의 생산량에서는 비교적 높게 나타나며, 생산량이 증가함에 따라 한계 비용은 감소하고, 최소값에 도달한 후 다시 증가한다. 한계 비용은 한계 수입(MR), 즉 제품이나 서비스의 추가 단위가 기업에 가져다 줄 판매 수입의 증분과 관련하여 표시된다.[3] 이러한 한계 비용 곡선의 형태는 증가하는 한계 수확률과 감소하는 한계 수확률(그리고 수확 체감의 법칙)에 직접적으로 기인한다. 한계 비용은 w/MPL과 같다.[3] 대부분의 생산 과정에서 노동의 한계 생산성은 초기에 증가하고, 최대값에 도달한 후 생산이 증가함에 따라 지속적으로 감소한다. 따라서 한계 비용은 처음에 감소하고, 최소값에 도달한 후 증가한다.[4] 한계 비용 곡선은 평균 가변 비용 곡선과 (단기) 평균 총 비용 곡선의 최저점에서 교차한다. 한계 비용 곡선이 평균 비용 곡선보다 위에 있으면 평균 곡선은 상승한다. 한계 비용 곡선이 평균 곡선보다 아래에 있으면 평균 곡선은 하락한다. 이러한 관계는 한계 곡선이 상승하거나 하락하는지에 관계없이 유지된다.[5]3. 8. 장기 한계 비용 (LRMC)
장기 한계 비용(LRMC) 곡선은 모든 생산 요소가 가변적인 개념적 기간인 장기에 생산량의 각 단위에 대해 발생하는 추가 총 비용을 보여준다.[6] 즉, LRMC는 모든 투입 요소가 가변적일 때 생산량 1단위 증가와 관련된 총 비용의 최소 증가분이다.[6]장기 한계 비용 곡선은 규모의 수익에 의해 결정된다. 장기 한계 비용 곡선은 투입 요소의 유연성이 증가하여 단기 곡선보다 더 완만하다. 장기 한계 비용 곡선은 장기 평균 비용 곡선의 최저점에서 교차한다.[3] 장기 한계 비용이 장기 평균 비용보다 낮으면 장기 평균 비용은 감소한다(추가 생산량을 고려할 때).[2] 장기 한계 비용이 장기 평균 비용보다 높으면 평균 비용은 증가한다. 장기 한계 비용은 최소 장기 평균 비용 생산 수준에서 단기 한계 비용과 같다. LRMC는 장기 총 비용 함수의 기울기이다.
4. 규모의 경제
산출량을 늘릴수록 비용이 감소할 때, 즉, 평균비용이 감소하는 구간에서 기업은 규모의 경제를 누린다. 한편 평균비용이 증가하는 구간에서는 규모의 불경제가 일어난다.
장기 한계 비용 곡선은 규모의 수익에 의해 결정된다. 장기 한계 비용이 장기 평균 비용보다 낮으면 장기 평균 비용은 감소하고, 장기 한계 비용이 장기 평균 비용보다 높으면 평균 비용은 증가한다. 장기 한계 비용은 최소 장기 평균 비용 생산 수준에서 단기 한계 비용과 같다.[3] [2] [6]
5. 비용 곡선과 생산 함수의 관계
생산 요소 가격이 일정하면, 생산 함수는 모든 비용 함수를 결정한다.[4] 기업이 모든 투입 시장에서 완전 경쟁자라면, 특정 생산량 수준에서 규모의 경제(장기 평균 비용 곡선의 하향 기울기 영역)를 가질 경우 규모의 수익이 증가한다.[8][9][10]
가변 비용 곡선은 가변 투입 요소의 일정 가격에 단기 생산 함수 또는 총생산 곡선의 역수를 곱한 것이며, 그 동작과 속성은 생산 함수에 의해 결정된다.[3] [7] 생산 함수는 가변 비용 함수를 결정하므로, 필연적으로 한계 비용 곡선과 평균 비용 곡선의 모양과 속성을 결정한다.[4]
기업이 투입 시장에서 완전 경쟁자가 아닌 경우 위의 결론은 수정된다. 예를 들어, 특정 생산량 범위에서 규모의 수익이 증가하지만, 기업이 하나 이상의 투입 시장에서 너무 커서 투입물 구매를 늘리면 투입물의 단위당 비용이 증가하는 경우, 해당 생산량 범위에서 규모의 불경제를 가질 수 있다. 반면, 기업이 투입물에 대한 대량 할인을 받을 수 있다면, 해당 생산량 범위에서 생산에 대한 수익이 감소하더라도 일부 생산량 범위에서 규모의 경제를 가질 수 있다.
총비용 곡선(TC)은 수확(한계 생산력)이 초기에 체증하고(비용이 체감), 어느 지점부터는 체감하는(비용이 체증) (수확 체감의 법칙) 것에 대응하여 위로 볼록, 아래로 볼록인 우상향 곡선으로, 역 S자 형태로 나타난다.
6. 다양한 비용 곡선 간의 관계
- 한계 비용(MC) 곡선이 평균 총 비용 또는 평균 가변 비용 곡선 위에 있는 생산량(Q) 수준에서 후자의 곡선은 상승한다.[11]
- MC가 평균 총 비용 또는 평균 가변 비용보다 낮으면 후자의 곡선은 하락한다.
- MC가 평균 총 비용과 같으면 평균 총 비용은 최소값에 있다.
- MC가 평균 가변 비용과 같으면 평균 가변 비용은 최소값에 있다.
- 각 생산량에 대해 자본의 비용 최소화 수준이 하나씩 있으며, 주어진 생산량을 생산하는 것과 관련된 고유한 단기 평균 비용 곡선이 존재한다.[12] 기업이 생산량에 맞는 최적의 자본 수준을 사용하고 있다고 가정하면, 단기 평균 비용(SRAC) 곡선은 장기 평균 비용(LRAC) 곡선과 접하게 된다. 그렇지 않다면, SRAC 곡선은 LRAC "전체를 위"에 놓이게 되며 어떤 점에서도 접하지 않을 것이다.
다음은 위의 내용을 표로 정리한 것이다.
- 각 단기 총 비용(STC) 곡선은 장기 총 비용(LRTC) 곡선에 단 한 점에서만 접할 수 있다. STC 곡선은 LRTC 곡선을 가로지를 수 없다.[4][11] STC 곡선은 접점 없이 LRTC 곡선 "전체 위에" 놓일 수 있다.[13]
- 하나의 STC 곡선은 장기 비용 최소화 생산 수준에서 LRTC에 접한다. 접점에서 LRTC = STC이다. 다른 모든 생산 수준에서 STC는 LRTC를 초과할 것이다.[14]
- 평균 비용 함수는 총 비용 함수를 생산량 수준으로 나눈 것이다. 따라서 단기 평균 총 비용(SATC) 곡선도 비용 최소화 생산 수준에서 장기 평균 총 비용(LRATC) 곡선에 접한다. 접점에서 LRATC = SATC이다. 다른 모든 생산 수준에서 SATC > LRATC이다.[14] 접점의 왼쪽에 있는 기업은 과도한 자본을 사용하고 있으며 고정 비용이 너무 높다. 접점의 오른쪽에 있는 기업은 너무 적은 자본을 사용하고 있으며 노동력에 대한 수확 체감으로 인해 비용이 증가하고 있다.[15]
- 총 비용 곡선의 기울기는 한계 비용과 같다. 따라서 STC가 장기 총 비용(LTC)에 접할 때 단기 한계 비용(SMC) = 장기 한계 비용(LRMC)이다.
- 장기 비용 최소화 생산 수준에서 LRTC = STC, LRATC = SATC, LRMC = SMC이다.[14]
- 장기 비용 최소화 생산 수준은 최소 SATC와 다를 수 있다.[11][16]
- 고정된 투입 단위 비용으로, 생산 함수가 규모에 대한 불변 수확을 갖는 경우, SATC 곡선의 최소 수준에서 SATC = LRATC = SMC = LRMC이다.[14]
- 고정된 투입 단위 비용으로, 생산 함수가 규모에 대한 증가 수확을 갖는 경우, SATC 곡선의 최소값은 LRAC와 SATC 곡선 간의 접점 오른쪽에 있다.[14] 여기서 LRTC = STC, LRATC = SATC, LRMC = SMC이다.
- 고정된 투입 단위 비용과 수확 체감의 경우, SATC 곡선의 최소값은 LRAC와 SATC 간의 접점 왼쪽에 있다.[14] 여기서 LRTC = STC, LRATC = SATC, LRMC = SMC이다.
- 고정된 투입 비용이 있는 기업이 규모에 대한 증가(감소) 수확을 경험하고 최소 SAC에서 생산하고 있다면, 고정 투입의 사용을 확대(축소)하여 장기적으로 평균 비용을 항상 줄일 수 있다.[14] [16]
- LRATC는 항상 SATC와 같거나 SATC보다 작을 것이다.[3]
- 생산 과정이 규모에 대한 불변 수확을 나타내는 경우, 최소 SRAC는 최소 장기 평균 비용과 같다. LRAC와 SRAC는 공통 최소값에서 교차한다. 따라서 규모에 대한 불변 수확에서 SRMC = LRMC = LRAC = SRAC이다.
- 생산 과정이 감소 또는 증가를 경험하는 경우, 최소 단기 평균 비용은 최소 장기 평균 비용과 같지 않다. 규모에 대한 증가 수확이 존재하는 경우, 장기 최소값은 SRAC보다 낮은 수준의 생산에서 발생할 것이다. 이것은 활용되지 않은 규모의 경제가 있기 때문에 장기적으로 기업은 더 큰 설비를 사용하여 최소 단기 평균 비용보다 낮은 가격으로 항상 수량을 생산할 수 있기 때문이다.[17]
- 수확 체감의 경우, 최소 SRAC는 기업이 운영 규모를 단순히 줄임으로써 평균 비용을 줄일 수 있기 때문에 최소 LRAC보다 낮은 생산 수준에서 발생한다.
- SRAC의 최소값은 기울기가 0일 때 발생한다.[18] 따라서 U자형 LRAC 곡선과 SRAC 곡선의 최소값 사이의 접점은 규모의 경제가 일정한 LRAC 곡선의 해당 부분과 일치할 것이다. 규모에 대한 증가 수확의 경우, LRAC와 SRAC 간의 접점은 SRAC 곡선의 최소값과 관련된 수준보다 낮은 수준의 생산에서 발생해야 한다.
7. U자형 곡선
단기 총 평균 비용(SRAC) 곡선과 장기 총 평균 비용(LRAC) 곡선은 일반적으로 U자형으로 나타난다.[11] [16] 그러나 단기 곡선과 장기 곡선의 모양은 같은 요인 때문에 나타나는 것은 아니다.
단기 곡선의 초기 하향 경사는 주로 평균 고정 비용의 감소로 나타난다.[4] 낮은 생산 수준에서는 가변 투입 요소의 수확 체증[19]도 하향 경사에 영향을 준다. 반면 상향 경사는 가변 투입 요소의 수확 체감[4] 때문에 발생한다.
장기 곡선의 모양은 규모의 경제와 불경제에 의해 결정된다.[16] 낮은 생산 수준에서는 일반적으로 규모의 경제가 나타나 장기 평균 비용이 감소한다.[4] 이는 투입 시장에서 완전 경쟁하는 기업의 경우에 해당한다. 높은 생산량 수준에서는 규모의 수확 체감으로 장기 평균 비용 함수의 상향 경사가 나타난다.[4]
평균 비용 곡선(AC)은 원점과 총 비용 곡선 상의 각 점을 연결한 직선의 기울기로 나타낼 수 있으며, U자형 곡선으로 표현된다. 원점을 지나는 직선과 비용 곡선의 접점에서 평균 비용이 최소가 된다.
8. 평균 비용 곡선의 실제 형태
평균 비용 곡선이 일반적으로 U자형이 아니라는 증거가 일부 있다. 1952년 윌포드 J. 아이테만(Wilford J. Eiteman)과 글렌 E. 구트리(Glenn E. Guthrie)는 334개 회사의 관리자들에게 여러 가지 비용 곡선을 보여주고 회사의 비용 곡선을 가장 잘 나타내는 곡선을 지정하도록 설문 조사를 했다. 설문에 응답한 관리자의 95%가 일정한 비용 또는 감소하는 비용을 보고했다.[1]
앨런 블라인더(Alan Blinder) 전 미국 경제 협회(American Economics Association) 부회장은 1998년에 미국 경제를 대표하는 200개의 미국 회사를 표본으로 하여 동일한 유형의 설문 조사를 실시했다. 그는 약 40%의 회사가 감소하는 가변 비용 또는 한계 비용을 보고했으며, 48.4%가 일정한 한계/가변 비용을 보고했음을 발견했다.[20]
참조
[1]
학술지
The Shape of the Average Cost Curve
[2]
서적
Asking about prices: a new approach to understanding price stickiness
Russell Sage Foundation
[3]
서적
Microeconomics
Pearson
[4]
서적
Microeconomics: Theory & Applications with Calculus
Pearson
[5]
서적
An introduction to positive economics
Weidenfeld & Nicolson
[6]
학술지
The Short- and Long-Run Marginal Cost Curve: A Pedagogical Note
https://mpra.ub.uni-[...]
[7]
문서
[8]
학술지
Returns to Scale and Economies of Scale: Further Observations
[9]
서적
Theory of Production
D. Reidel
[10]
서적
The Neoclassical Theory of Production and Distribution
Cambridge Univ. Press
[11]
서적
Microeconomics
Prentice-Hall
[12]
서적
Microeconomic Theory
Thomson
[13]
서적
A Course in Microeconomic Theory
Princeton Univ. Press
[14]
서적
Microeconomics with Calculus
Addison-Wesley
[15]
서적
Microeconomics and Behavior
Mc-Graw-Hill
[16]
서적
Microeconomics
Houghton Mifflin
[17]
서적
Microeconomics Theory & Application with Calculus
Pearson
[18]
서적
Microeconomic Theory
Thomson
[19]
서적
The New Managerial Economics
Houghton Mifflin
[20]
서적
Asking about Prices: A New Approach to Understanding Price Stickiness
Russell Sage Foundation
[21]
서적
맨큐의 경제학
Cengage
2009
[22]
서적
Microeconomics
Wiley
2011
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com