원그래프
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
원그래프는 전체에 대한 각 항목의 비율을 부채꼴의 면적으로 나타내는 통계 도표이다. 1801년 윌리엄 플레이페어가 처음 사용했으며, 플로렌스 나이팅게일은 극좌표 다이어그램 형태로 개선하여 널리 사용되도록 기여했다. 샤를 조제프 미나르는 1858년 지도에 원그래프를 활용하기도 했다. 원그래프는 3차원, 도넛, 분리형, 극좌표 영역, 링, 스파이, 사각형 등 다양한 종류가 있으며, 전체 대비 각 부분의 비율을 직관적으로 보여주는 장점이 있다. 하지만, 여러 값의 비교나 데이터 집합 간의 비교에는 막대 그래프보다 효과적이지 않으며, 작은 비율을 나타내기 어렵다는 단점이 있다. 통계학자들은 원그래프를 정보 표시 방법으로 권장하지 않는 경우가 많다.
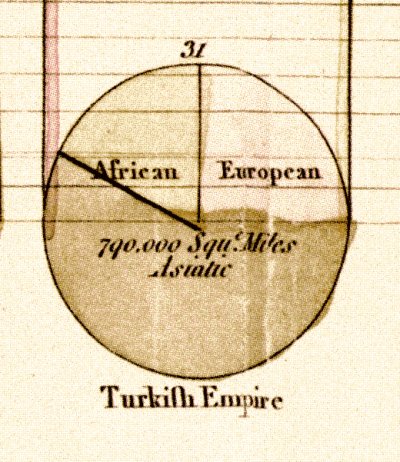
일반적으로 원그래프는 1801년 윌리엄 플레이페어의 ''통계 요약''에 처음 등장한 것으로 알려져 있다.[1][9] 플레이페어는 여러 개의 원그래프를 제시했는데, 그 중 하나는 1789년 이전 아시아, 유럽, 아프리카에 걸쳐 있던 터키 제국의 영토 비율을 나타낸 것이었다. 하지만 원그래프는 처음에는 널리 사용되지 않았다.[1] 플레이페어는 원그래프에 더 많은 정보를 담기 위해서는 3차원이 필요하다고 생각했다.[10]
원그래프는 전체에 대한 각 항목의 백분율을 계산하여, 해당 백분율만큼 원을 나누어 작성한다. 각 항목의 명칭과 백분율을 명시하고, 백분율의 합이 100%가 되는지 확인해야 한다.[30]
2. 역사
플로렌스 나이팅게일은 원그래프를 직접 발명하지는 않았지만, 사람들이 더 읽기 쉽도록 개선하여 널리 퍼뜨리는 데 큰 역할을 했다. 나이팅게일은 원그래프의 각 조각 폭 대신 길이를 다르게 하여 수탉 볏과 비슷한 모양으로 만들었다.[11] 이후 사람들은 윌리엄 플레이페어의 원그래프가 이해하기 어렵고 실용적이지 않다고 생각하여, 나이팅게일이 원그래프를 발명한 것으로 여기게 되었다.[12]
샤를 조제프 미나르는 1858년에 지도에 원그래프를 활용하여 프랑스 각 지역에서 파리로 보내는 소의 양을 나타냈다.
2. 1. 초기 역사
가장 초기의 원그래프는 일반적으로 1801년 윌리엄 플레이페어의 ''통계 요약''에 실린 것으로 여겨지며, 이 책에는 두 개의 원그래프가 사용되었다.[1][9] 플레이페어는 일련의 원그래프가 포함된 삽화를 제시했다. 그중 하나는 1789년 이전에 아시아, 유럽 및 아프리카에 위치한 터키 제국의 영토 비율을 묘사했다. 그러나 이 발명은 처음에는 널리 사용되지 않았다.[1]
플레이페어는 원그래프에 추가 정보를 나타내려면 세 번째 차원이 필요하다고 생각했다.[10]
플로렌스 나이팅게일이 원그래프를 발명한 것은 아니지만, 원그래프를 더 읽기 쉽도록 개조하여 널리 사용되는 데 기여했다. 나이팅게일은 원그래프에서 웨지의 폭 대신 길이를 변수로 하여 수탉 볏과 비슷한 모양으로 재구성했다.[11] 나중에 그녀는 플레이페어의 작품이 모호하고 실용성이 부족했기 때문에 이 차트를 발명한 것으로 추정되었다.[12] '''나이팅게일 로즈 다이어그램'''이라고도 불리는 나이팅게일의 극좌표 다이어그램은[13] 현대의 원형 히스토그램과 동일하며, 그녀가 관리했던 군 병원 환자들의 계절별 사망 원인을 설명하기 위해 사용되었다. 이 다이어그램은 1858년 빅토리아 여왕에게 보내진 영국군의 건강, 효율성 및 병원 행정에 영향을 미치는 문제에 대한 노트에 게재되었다. 역사가 휴 스몰은 "그녀는 변화의 필요성을 사람들에게 설득하기 위해 [원그래프]를 사용한 최초의 사람이었을 수도 있다."라고 평가했다.[11]
프랑스 엔지니어 샤를 조제프 미나르도 1858년에 원그래프를 사용했다. 그의 1858년 지도에는 프랑스 전역에서 파리로 보내진 소의 수를 나타내기 위해 원그래프가 사용되었다.
2. 2. 플로렌스 나이팅게일의 기여
플로렌스 나이팅게일은 파이 차트를 발명하지는 않았지만, 더 읽기 쉽도록 개선하여 널리 사용되도록 기여했다.[11] 나이팅게일은 파이 차트에서 각 조각(wedge)의 폭 대신 길이를 변수로 하는 방식으로 재구성했다. 이렇게 만들어진 그래프는 수탉 볏을 닮았다고 하여 콕스콤(coxcomb)이라고 불렸다.[11] 윌리엄 플레이페어의 원본 파이 차트가 모호하고 실용성이 부족했기 때문에, 나중에는 나이팅게일이 이 차트를 발명한 것으로 생각되기도 했다.[12]
극좌표 다이어그램(나이팅게일 로즈 다이어그램이라고도 함)은[13] 현대의 원형 히스토그램과 유사하며, 나이팅게일이 관리했던 군 병원 환자들의 사망 원인을 계절별로 나타내기 위해 사용되었다. 이 다이어그램은 1858년 빅토리아 여왕에게 보내진 《영국군의 건강, 효율성 및 병원 행정에 영향을 미치는 문제에 대한 노트》에 게재되었다. 역사학자 휴 스몰에 따르면, 나이팅게일은 "변화의 필요성을 사람들에게 설득하기 위해 [파이 차트]를 사용한 최초의 사람이었을 수도 있다."[11]
나이팅게일은 1858년, "계두도(polar area diagram)", "닭 볏"[39]이라고 불리는 일종의 원 그래프를 고안했다(Nightingale rose diagram이라고도 함). 일본어로 "계두"라고 명명된 것은, 그 그림이 게재된 저서를 나이팅게일이 "coxcomb"(cockscomb는 맨드라미의 뜻)라고 불렀기 때문에, 그림 그 자체를 "coxcomb"라고 오인하여 부르게 된 데에서 유래한다[40].
일반적인 원 그래프와 달리, 계두도의 각 영역의 중심각은 일정하다.
나이팅게일이 이 그림을 고안했다고 여겨지지만, 더 이른 시기에 이것을 사용한 예가 있다. 레옹 랄란느(Léon Lalanne)는 1843년, 32방위에서의 풍향의 빈도를 계두도로 나타냈다. 1829년, 앙드레-미셸 게리(André-Michel Guerry)는 주기적 현상의 빈도를 계두도로 나타낸 것을 논문에 게재했다.
2. 3. 샤를 조제프 미나르의 활용
프랑스 엔지니어 샤를 조제프 미나르는 1858년에 지도에 원그래프를 사용하여 프랑스 전역에서 파리로 보내지는 소의 양을 나타냈다.[1]
3. 작성 방법
2004년 유럽 의회 선거의 예비 결과를 바탕으로 원그래프를 작성하는 방법은 다음과 같다.그룹 의석 백분율(%) 중심각(°) EUL 39 5.3 19.2 PES 200 27.3 98.4 EFA 42 5.7 20.7 EDD 15 2.0 7.4 ELDR 67 9.2 33.0 EPP 276 37.7 135.7 UEN 27 3.7 13.3 기타 66 9.0 32.5 합계 732 99.9* 360.2*
각 정당 그룹에 할당된 의석 수를 백분율로 나타내고, 그 백분율에 360을 곱하여 각 부채꼴의 중심각을 구한다. 예를 들어 EPP의 경우, 37.7%에 360을 곱하여 135.7°의 중심각을 얻는다.
원그래프는 12시 방향에서 시작하여 구성비가 큰 순서대로 시계 방향으로 배열하며, 구성비가 작은 데이터는 마지막에 묶어 '기타'로 표시하는 것이 일반적이다.[30]
4. 종류
원그래프에는 여러 종류가 있다.
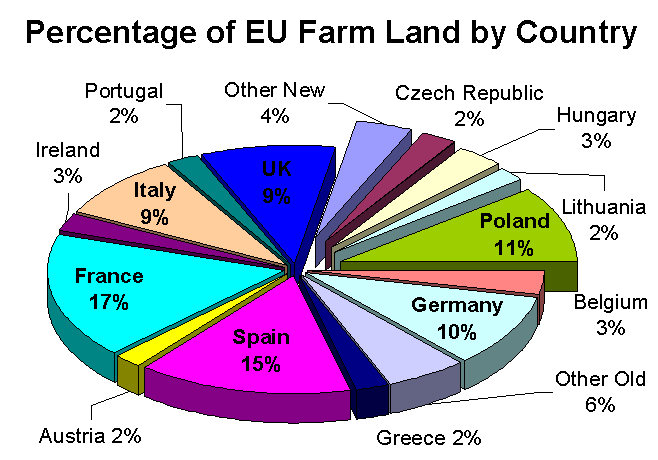
- '''도넛 차트''': 가운데가 비어 있고, 빈 공간에 전체 데이터 정보를 추가할 수 있다.[15][16]
- '''분리형 원그래프''': 하나 이상의 부채꼴이 분리되어 특정 부분을 강조한다.
- '''극좌표 영역 다이어그램 (콕스콤)''': 각도는 같지만, 부채꼴이 중심에서 얼마나 멀리 뻗어 있는지에 따라 값이 달라진다. polar area diagram영어이라고도 불리며, 순환 현상을 나타내는 데 유용하다. 플로렌스 나이팅게일이 활용한 것으로 유명하다.[17]
- '''링 차트 (선버스트 차트, 다단계 원그래프)''': 동심원으로 계층적 데이터를 나타내며, 중심에서 바깥쪽으로 이동하면서 계층 구조를 표현한다.[19][20]
- '''스파이 차트''': 일반 원그래프와 극좌표 영역 차트를 겹쳐서 두 세트의 관련 데이터를 비교한다.[21]
- '''사각형 차트 (와플 차트)''': 사각형으로 백분율을 나타내며, 작은 비율을 나타내는 데 유용하다.[28]
4. 1. 3차원 원그래프
3차원 원그래프 또는 원근 원그래프는 그래프에 3차원 모양을 부여하는 데 사용된다. 종종 미적인 이유로 사용되지만, 세 번째 차원은 데이터의 판독을 개선하지 않는다. 반대로, 이러한 플롯은 세 번째 차원과 관련된 원근법의 왜곡된 효과 때문에 해석하기 어렵다. 관심 있는 데이터를 표시하는 데 사용되지 않는 불필요한 차원의 사용은 일반적으로 원그래프뿐만 아니라 차트에서도 권장되지 않는다.[7][14][38]4. 2. 도넛 차트
도넛 차트는 파이 차트의 변형으로, 중앙이 비어 있어 전체 데이터에 대한 추가 정보를 포함할 수 있다.[15][16] 비율을 나타내는 것을 목표로 한다는 점에서 파이 차트와 유사하며, 한 번에 여러 통계를 지원할 수 있고 표준 파이 차트에 비해 더 나은 데이터 밀도 비율을 제공한다.[16] 중앙에 정보를 포함할 필요는 없다.
4. 3. 분리형 원그래프
하나 이상의 부채꼴이 디스크의 나머지 부분과 분리된 차트는 '''분리형 원형 차트'''라고 한다. 이 효과는 부채꼴을 강조하거나, 작은 비율의 차트 작은 세그먼트를 강조하는 데 사용된다. -- 해당 부분(분리된 부채꼴)을 눈에 띄게 하는 효과가 있으며, 특히 작은 부분을 강조할 때 자주 사용된다.[2]4. 4. 극좌표 영역 다이어그램 (콕스콤)
극좌표 영역 다이어그램은 일반적인 원그래프와 유사하지만, 부채꼴의 각도는 모두 같고 각 부채꼴이 원의 중심에서 얼마나 멀리 뻗어 있는지에 따라 값이 달라진다. polar area diagram영어이라고도 불린다.극좌표 영역 다이어그램은 순환 현상(예: 월별 사망자 수)을 표시하는 데 사용된다.[17] 예를 들어, 1년 동안 각 달의 사망자 수를 표시하려면 12개의 부채꼴(달별로 하나씩)이 있으며, 각 부채꼴은 30도의 동일한 각도를 갖는다. 각 부채꼴의 반경은 해당 달의 사망률의 제곱근에 비례하므로 부채꼴의 면적은 해당 달의 사망률을 나타낸다. 각 달의 사망률이 사망 원인별로 세분화되면 플로렌스 나이팅게일이 개발한 유명한 극좌표 영역 다이어그램에서 볼 수 있듯이 하나의 다이어그램에서 여러 비교를 수행할 수 있다.
극좌표 영역 다이어그램을 처음 사용한 사례는 앙드레-미셸 게리가 1829년 논문에서 풍향의 계절 및 일별 변화와 하루 중 시간별 출생 및 사망률을 보여주기 위해 courbes circulaires프랑스어(원형 곡선)라고 부른 것이었다.[17] 레옹 랄란느는 1843년에 극좌표 다이어그램을 사용하여 나침반 지점 주변의 풍향 빈도를 표시했다. 풍향도는 여전히 기상학자들이 사용한다. 플로렌스 나이팅게일은 1858년에 자신의 로즈 다이어그램을 발표했다. "콕스콤"이라는 이름이 이 유형의 다이어그램과 연관되어 있지만, 나이팅게일은 원래 이 다이어그램을 이 유형의 특정 다이어그램이 아닌 차트와 표로 구성된 시선을 사로잡는 책인 이 다이어그램이 처음 등장한 출판물을 지칭하는 데 사용했다.[18]
플로렌스 나이팅게일은 1858년, "계두도(polar area diagram)", "닭 볏[39]"이라고 불리는 일종의 원 그래프를 고안했다(Nightingale rose diagram영어이라고도 함). 일본어로 "계두"라고 명명된 것은, 그 그림이 게재된 저서를 나이팅게일이 "coxcomb"(cockscomb영어는 맨드라미의 뜻)라고 불렀기 때문에, 그림 그 자체를 "coxcomb"라고 오인하여 부르게 된 데에서 유래한다.[40]
수량이 반지름에 비례하도록 그려진다고도 하지만,[41] 적어도 나이팅게일의 예에서는 면적에 비례하도록 그려져 있다.[42][43] 일반적인 원 그래프와 달리, 계두도의 각 영역의 중심각은 일정하다.
나이팅게일이 이 그림을 고안했다고 여겨지지만, 더 이른 시기에 이것을 사용한 예가 있다. 레옹 랄란느는 1843년, 32방위에서의 풍향의 빈도를 계두도로 나타냈다. 1829년, 앙드레-미셸 게리는 주기적 현상의 빈도를 계두도로 나타낸 것을 논문에 게재했다.
4. 5. 링 차트 (선버스트 차트, 다단계 원그래프)
링 차트는 선버스트 차트 또는 다단계 원형 차트라고도 하며, 계층적 데이터를 시각화하는 데 사용되며 동심원을 사용하여 표현된다.[19] 중심의 원은 루트 노드를 나타내며, 계층 구조는 중심에서 바깥쪽으로 이동한다. 내부 원의 세그먼트는 부모 세그먼트의 각도 범위 내에 있는 외부 원의 해당 세그먼트와 계층적 관계를 가진다.[20]4. 6. 스파이 차트
스파이 차트는 극좌표 영역 차트의 변형으로, 드로어 페이텔슨(Dror Feitelson)이 디자인하였다.[21] 스파이 차트는 일반적인 원그래프와 극좌표 영역 차트를 중첩시켜 두 세트의 관련 데이터를 비교한다. 기본 원그래프는 첫 번째 데이터 세트를 일반적인 방식으로 나타내며, 각 슬라이스의 크기는 서로 다르다. 두 번째 세트는 기본 차트와 동일한 각도를 사용하고 데이터를 맞추기 위해 반경을 조정하는 중첩된 극좌표 영역 차트로 표현된다. 예를 들어, 기본 원그래프는 인구의 연령 및 성별 그룹 분포를 보여주고, 도로 사고 피해자 중 해당 그룹의 표현을 중첩할 수 있다. 사고에 특히 취약한 연령 및 성별 그룹은 원래 원그래프를 넘어 확장되는 슬라이스로 두드러지게 나타난다.
4. 7. 사각형 차트 (와플 차트)
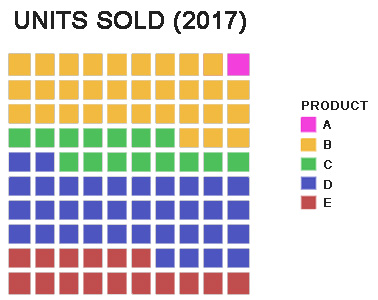
사각형 차트는 와플 차트라고도 하며, 원 대신 사각형을 사용하여 백분율을 나타내는 원그래프의 한 형태이다. 기본적인 원형 원그래프와 유사하게, 사각형 파이 차트는 총 100%에서 각 백분율을 추출한다. 이들은 종종 10x10 격자이며, 각 셀은 1%를 나타낸다. 이름과 달리 사각형 대신 원, 그림 문자(예: 사람) 및 기타 모양을 사용할 수 있다. 사각형 차트의 주요 장점 중 하나는 전통적인 파이 차트에서 보기 어려운 작은 백분율을 쉽게 묘사할 수 있다는 것이다.[28]
5. 평가
원그래프는 비즈니스나 매스 미디어에서 흔히 사용되지만, 과학이나 공학 분야에서는 자주 사용되지 않는다.[31] 원그래프에 대한 비판도 많으며,[32] 통계학자들은 원그래프 사용을 권장하지 않는 경우가 많다.[33][34]
원그래프의 주된 문제점은 원그래프 내에서 서로 다른 영역을 비교하거나, 여러 개의 원그래프를 서로 비교하기 어렵다는 것이다. 그러나 특정 영역(부채꼴)과 전체(원)를 비교하는 경우에는 원그래프가 효과적일 수 있다.[35]
5. 1. 장점
원 그래프는 전체에 대한 각 부분의 비율을 한눈에 보여주어 직관적으로 이해할 수 있다는 장점이 있다. 특히, 특정 부분이 전체에서 차지하는 비중을 강조할 때 효과적이다.[35] 부채꼴이 전체의 25%나 50%를 차지할 때 원 그래프는 가장 이해하기 쉽다.[36]2004년 유럽 의회 선거 결과를 예로 들어보자. 다음 표는 각 정당의 획득 의석수, 비율(%), 중심각(°)을 나타낸다. 중심각은 해당 비율에 360°를 곱해 계산한다.
| 정당 | 의석수 | 비율 (%) | 중심각 (°) |
|---|---|---|---|
| EUL | 39 | 5.3 | 19.2 |
| PES | 200 | 27.3 | 98.4 |
| CPC | 42 | 5.7 | 20.7 |
| CRAIG | 15 | 2.0 | 7.4 |
| ERIC | 67 | 9.2 | 33.0 |
| AKINS | 276 | 37.7 | 135.7 |
| GEI | 27 | 3.7 | 13.3 |
| 기타 | 66 | 9.0 | 32.5 |
| 합계 | 732 | 99.9* | 360.2* |
- 반올림 오차로 인해 합계가 정확히 100 또는 360이 되지 않을 수 있다.
이처럼 원 그래프를 사용하면 각 정당이 차지하는 비율을 시각적으로 쉽게 파악할 수 있다.
5. 2. 단점
원 그래프는 몇 가지 값을 표시할 때 시각적 인코딩("조각")과 데이터(일반적으로 백분율)를 분리하기 어렵다는 단점이 있다. 조각이 너무 작아지면 색상, 질감, 화살표 등에 의존해야 하므로 독자가 이해하기 어렵고, 많은 양의 데이터를 표시하기에 부적합하다. 또한, 원 그래프는 별도의 범례가 필요하고, 평균이나 목표와 같은 다른 값을 동시에 표시할 수 있는 막대 그래프보다 페이지에서 더 많은 공간을 차지한다.[7]통계학자들은 일반적으로 원 그래프를 정보를 표시하는 데 좋지 않은 방법으로 간주하며, 과학 문헌에서는 흔하지 않다. 길이 대신 면적을 사용할 때 차트 항목의 크기를 비교하기가 더 어렵고, 다른 항목이 다른 모양으로 표시될 때 더욱 어렵기 때문이다.[22]
AT&T 벨 연구소의 연구에 따르면 각도별 비교는 길이별 비교보다 정확성이 떨어진다. 대부분의 피실험자는 원 그래프의 조각을 크기별로 정렬하는 데 어려움을 겪었으며, 막대 그래프를 사용하면 비교가 훨씬 쉬웠다.[23] 데이터 집합 간의 비교 역시 막대 그래프를 사용하는 것이 더 쉽다. 그러나 단일 차트에서 주어진 범주(파이 조각)를 전체(전체 파이)와 비교하고, 배수가 25% 또는 50%에 가까운 경우에는 원 그래프가 막대 그래프보다 효과적일 수 있다.[24][25]
thumb
섹션이 많은 원 그래프에서는 여러 값이 동일하거나 유사한 색상으로 표시되어 해석하기 어려울 수 있다.
thumb
''유럽 시각화 컨퍼런스''에서 발표된 여러 연구에 따르면, 원 그래프와 도넛 그래프는 읽을 때 유사한 오류 수준을 생성하고, 정사각형 원 그래프가 가장 정확한 판독 값을 제공한다.[26][27][28][29]
5. 3. 효과적인 활용
AT&T 벨 연구소의 연구에 따르면, 각도 비교는 길이 비교보다 정확성이 떨어진다. 대부분의 피실험자는 원 그래프의 조각을 크기별로 정렬하는 데 어려움을 겪었으며, 막대 그래프를 사용했을 때 비교가 훨씬 더 쉬웠다.[23] 데이터 집합 간의 비교도 막대 그래프를 사용하는 것이 더 쉽다.[23] 그러나 단일 차트에서 주어진 범주(파이 조각)를 전체(전체 파이)와 비교하고, 그 비율이 25% 또는 50%에 가까울 때는 원 그래프가 막대 그래프보다 더 효과적일 수 있다.[24][25]벨 연구소의 연구에서는 인간이 각도를 비교하는 것이 길이를 비교하는 것만큼 정확하지 않다는 사실이 밝혀졌다. 오른쪽 그림은 3개의 원그래프와 각각 동일한 데이터를 나타내는 막대 그래프를 보여준다. 원그래프에서는 각 영역의 크기를 비교하기 어렵지만, 막대 그래프에서는 크기 비교가 쉽다.[37] 그러나 전체(원)와 각 영역(부채꼴)을 비교하고, 각 영역이 전체의 25%나 50%일 때는 원그래프가 더 이해하기 쉽다.
참조
[1]
문서
Spence (2005)
[2]
문서
Tufte, p. 44
[3]
문서
Cleveland, p. 262
[4]
문서
Wilkinson, p. 23
[5]
문서
Tufte, p. 178
[6]
문서
van Belle, p. 160–162
[7]
간행물
Save the Pies for Dessert
http://www.perceptua[...]
Stephen Few
2007-08
[8]
간행물
Pie Charts Are Bad
http://www.stevefent[...]
Steve Fenton
[9]
웹사이트
Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization
http://www.datavis.c[...]
[10]
문서
Palsky, p. 144–145
[11]
뉴스
Who Made That Pie Chart?
https://www.nytimes.[...]
2012-04-20
[12]
간행물
Dave article on this information on QI
http://uktv.co.uk/da[...]
[13]
논문
Florence Nightingale
http://www.unc.edu/~[...]
1984-03
[14]
문서
Good and Hardin, chapter 8
[15]
서적
Information graphics : a comprehensive illustrated reference
Oxford University Press
1999
[16]
웹사이트
Data Design by Juergen Kai-Uwe Brock on iBooks
https://itunes.apple[...]
2017-06-10
[17]
문서
Friendly, p. 509
[18]
웹사이트
Florence Nightingale's Statistical Diagrams
http://www.florence-[...]
2010-11-22
[19]
웹사이트
Multi-level Pie Charts
http://www.neoformix[...]
[20]
문서
Webber Richard, Herbert Ric, Jiangbc Wel. "Space-filling Techniques in Visualizing Output from Computer Based Economic Models"
[21]
웹사이트
Feitelson, Dror (2003) Comparing Partitions With Spie Charts
http://www.cs.huji.a[...]
2010-08-31
[22]
웹사이트
Perceptual Scaling of Map Symbols
http://makingmaps.ne[...]
2015-05-03
[23]
문서
Cleveland, p. 86–87
[24]
웹사이트
In Defense of Pie Charts
http://eagereyes.org[...]
2011-04-13
[25]
논문
Displaying proportions and percentages
1991-01-01
[26]
뉴스
An Illustrated Tour of the Pie Chart Study Results
https://eagereyes.or[...]
2016-11-28
[27]
논문
Arcs, Angles, or Areas: Individual Data Encodings in Pie and Donut Charts
http://kosara.net/pu[...]
[28]
논문
Judgment Error in Pie Chart Variations
http://kosara.net/pu[...]
[29]
뉴스
A Reanalysis of A Study About (Square) Pie Charts from 2009
https://eagereyes.or[...]
2016-11-28
[30]
웹사이트
円グラフ : 総務省統計局
https://www.stat.go.[...]
2021-08-17
[31]
문서
"{{Harvnb|Cleveland|1985|p=262}}"
[32]
문서
"{{Harvnb|Wilkinson|2005|p=23}}"
[33]
문서
"{{Harvnb|Tufte|2001|p=178}}"
[34]
문서
"{{Harvnb|van Belle|2002|pp=160–162}}"
[35]
문서
"{{Harvnb|Spence|2005}}"
[36]
서적
[37]
서적
[38]
서적
[39]
웹사이트
ナイチンゲールと統計
http://www.stat.go.j[...]
総務省 統計局
2015-08-29
[40]
웹사이트
Florence Nightingale's Statistical Diagrams
http://www.florence-[...]
Florence Nightingale Museum
2006-11-21
[41]
웹사이트
鸛頭図
https://kotobank.jp/[...]
[42]
웹사이트
https://blog.goo.ne.[...]
[43]
웹사이트
https://wild.maths.o[...]
[44]
서적
[45]
서적
[46]
서적
[47]
서적
[48]
서적
[49]
서적
[50]
서적
[51]
서적
[52]
간행물
Save the Pies for Dessert
http://www.perceptua[...]
2007-08
[53]
웹인용
Pie Charts Are Bad
http://www.stevefent[...]
2015-06-30
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com