Fold (고차 함수)
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
Fold는 리스트의 각 요소를 결합하여 단일 값을 생성하는 고차 함수이다. 리스트의 쉼표를 특정 연산자로 대체하는 것으로 이해할 수 있으며, 왼쪽 또는 오른쪽으로 결합하는 방식에 따라 두 가지 주요 유형이 있다. 왼쪽 폴드는 초기 값과 리스트의 첫 번째 요소를 함수에 적용하고, 그 결과를 다음 요소와 함께 반복하며, 오른쪽 폴드는 리스트의 마지막 요소와 초기값을 함수에 적용하고, 그 결과를 이전 요소와 함께 반복한다.
Fold는 다양한 프로그래밍 언어에서 지원되며, 함수형 언어에서는 핵심 기능으로 제공된다. 또한 C#, C++, Java, Python, Ruby, JavaScript 등 객체 지향 및 스크립트 언어에서도 폴드와 유사한 기능을 찾아볼 수 있다. 폴드는 데이터 구조의 구조적 구성 요소를 함수와 값으로 대체하는 구조적 변환으로 볼 수 있으며, 다양한 자료형에 적용될 수 있다. 엄격한 평가와 지연 평가 환경에서의 평가 순서에 따라 효율성이 달라질 수 있으며, 다형성을 가지므로 다른 함수를 표현하는 데 사용될 수 있다.
더 읽어볼만한 페이지
- 고차 함수 - 커링
커링은 다수의 인수를 취하는 함수를 단일 인수를 취하는 함수들의 연속으로 변환하는 기법으로, 함수형 프로그래밍에서 다인수 함수를 분해하여 적용하는 방식이며, 논리학과 컴퓨터 과학에서 널리 활용되는 중요한 개념이다. - 고차 함수 - Map (고차 함수)
Map 고차 함수는 함수형 프로그래밍에서 컬렉션의 각 요소에 함수를 적용해 새로운 컬렉션을 생성하는 기능으로, Lisp에서 처음 소개된 후 다양한 언어에서 구현되어 요소별 연산을 간결하게 표현하며, 구현 방식과 기능은 언어별로 차이가 있다. - 재귀 - 무한 루프
무한 루프는 컴퓨터 프로그램에서 루프가 종료되지 않고 무한히 반복되는 현상으로, 프로그램 오류나 의도적인 경우에 발생하며 시스템 응답 불능을 초래하거나 특정 상황에서 사용되기도 한다. - 재귀 - 점화식
점화식은 수열의 각 항을 이전 항들의 함수로 표현하는 방정식으로, 피보나치 수열, 로지스틱 맵, 이항 계수 등의 예시가 있으며, 선형대수학이나 Z변환 등을 이용하여 풀고 다양한 분야에 응용된다.
2. 역사적 배경
폴드의 개념은 함수형 프로그래밍 언어의 발전과 함께 나타났다.
리스트 `[1, 2, 3, 4, 5]`를 덧셈 연산자로 폴드하면 15가 되는데, 이는 리스트의 모든 원소의 합이다.[1] 이를 쉼표를 '+' 연산으로 대체하는 것으로 생각하면, `1 + 2 + 3 + 4 + 5`가 된다.[1]
3. 리스트에 관하여
'+' 연산은 결합 법칙이 성립하므로, 괄호의 배치에 관계없이 결과는 동일하다. 그러나 결합 법칙이 성립하지 않는 이진 함수에서는 원소들이 결합되는 순서가 최종 결과에 영향을 줄 수 있다. 리스트에 대해 폴드를 수행하는 방법에는 오른쪽 폴드와 왼쪽 폴드 두 가지가 있다.
이는 Haskell (프로그래밍 언어) 또는 프롤로그에서 이진 연산자가 오른쪽 결합 또는 왼쪽 결합을 하는 것에 해당한다. 오른쪽 폴드의 경우 합은 `1 + (2 + (3 + (4 + 5)))`와 같이, 왼쪽 폴드의 경우 `(((1 + 2) + 3) + 4) + 5`와 같이 괄호로 묶인다.
초기값을 사용하면 편리하다. 오른쪽 폴드는 리스트의 끝에, 왼쪽 폴드는 리스트의 첫 번째 원소와 처음에 결합되는 초기값을 갖는다. 덧셈의 경우 덧셈 항등원인 0을 초기값으로 선택하면, 오른쪽 폴드는 `1 + (2 + (3 + (4 + (5 + 0))))`, 왼쪽 폴드는 `((((0 + 1) + 2) + 3) + 4) + 5`가 된다. 곱셈의 항등원은 1이며, 이를 초기값으로 사용하면 `1 * 1 * 2 * 3 * 4 * 5 = 120 = 5!`가 된다.
3. 1. 선형 폴드
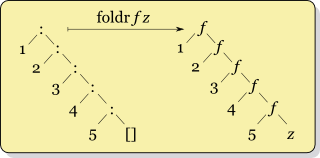
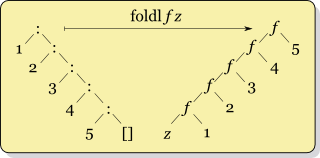
선형 폴드는 리스트의 각 요소를 순차적으로 처리하며, 연산을 왼쪽에서 오른쪽으로 (좌측 폴드, `foldl`) 또는 오른쪽에서 왼쪽으로 (우측 폴드, `foldr`) 수행한다.
예를 들어, 리스트 `[1, 2, 3, 4, 5]`를 덧셈 연산자로 폴드하면 15가 된다. 이는 리스트의 쉼표를 '+' 연산자로 대체하는 것과 유사하며, `1 + 2 + 3 + 4 + 5`가 된다.[1]
Haskell (프로그래밍 언어)에서 `foldl`과 `foldr` 함수는 다음과 같이 표현될 수 있다.
```haskell
foldl :: (b -> a -> b) -> b -> [a] -> b
foldl f z [] = z
foldl f z (x:xs) = foldl f (f z x) xs
```
```haskell
foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f z [] = z
foldr f z (x:xs) = f x (foldr f z xs)
```
좌측 폴드는 꼬리 재귀 최적화가 가능하여 메모리 효율성이 높을 수 있지만, 무한 리스트에는 적용할 수 없다. 반면 우측 폴드는 게으른 계산을 이용하면 무한 리스트에도 적용 가능하지만, 꼬리 재귀 최적화가 어려워 메모리 효율성이 떨어질 수 있다.
게으른 계산을 사용하는 왼쪽 폴드의 경우, 새로운 초기 매개변수가 재귀 호출 전에 평가되지 않아 스택 오버플로를 유발할 수 있다. 이를 방지하기 위해 Haskell에서는 `foldl'` (작은따옴표, 'prime'으로 발음) 함수를 제공하여 재귀 호출 전에 초기 매개변수의 평가를 강제한다.
3. 2. 트리형 폴드
트리형 폴드는 리스트를 이진 트리 형태로 구성하여 연산을 수행한다. 각 노드에서 함수를 적용하여 부분 결과를 계산하고, 이를 상위 노드에서 다시 결합하는 방식으로 진행된다. 이항 연산 ''f''가 결합 법칙을 만족하면, 연산 방식의 세부 사항은 달라도 괄호 배치에 관계없이 같은 값을 가진다.[1]
함수가 마그마인 경우, 즉 타입이 대칭적이고(a → a → a), 결과 타입이 리스트 요소의 타입과 동일한 경우, 괄호를 임의의 방식으로 배치하여 중첩된 하위 표현식의 이진 트리를 만들 수 있다. 이는 ''f''가 비엄격적일 경우 효율성에 큰 영향을 줄 수 있다.[1]
선형 폴드는 노드 지향적이며 리스트의 각 노드에 대해 일관된 방식으로 작동하는 반면, 트리형 폴드는 전체 리스트 지향적이며 노드 ''그룹'' 전체에 대해 일관된 방식으로 작동한다.[1]
리스트는 유한 및 무한히 정의된 리스트 모두에 대해 트리 형태 방식으로 폴드될 수 있다. foldi 함수의 경우, ''무한히'' 정의된 리스트에서 실행이 중단되지 않도록 하려면 함수 f가 적어도 전부 또는 즉시 두 번째 인수의 값을 ''항상'' 요구해서는 안 된다.[1]
유한 목록의 경우, 합병 정렬은 트리 형태의 폴딩을 사용하여 정의할 수 있다.
3. 3. 비어 있지 않은 리스트를 위한 특별한 폴드
초기값이 필요 없는 경우, 비어 있지 않은 리스트에 대해 `foldl1`과 `foldr1`과 같은 함수를 사용할 수 있다. `foldl1`은 리스트의 첫 번째 요소를 초기값으로 사용하고, `foldr1`은 리스트의 마지막 요소를 초기값으로 사용한다.[1] 이러한 함수들은 초기값을 명시적으로 지정할 필요가 없어 편리하지만, 비어 있는 리스트에는 적용할 수 없다.
이러한 fold는 형식 대칭 이진 연산을 사용한다. 즉, 두 인수와 결과의 형식이 같아야 한다. Richard Bird는 2010년 저서에서[2] "비어 있지 않은 목록에 대한 일반적인 fold 함수" `foldrn`을 제안했는데, 이 함수는 추가 인수 함수를 적용하여 마지막 요소를 변환하여, fold 자체를 시작하기 전에 결과 형식의 값으로 변환한다. 따라서 일반적인 `foldr`과 같이 형식 비대칭 이진 연산을 사용하여 목록 요소 형식과 다른 형식의 결과를 생성할 수 있다.
```haskell
foldl1 f [x] = x
foldl1 f (x:y:xs) = foldl1 f (f x y : xs)
foldr1 f [x] = x
foldr1 f (x:xs) = f x (foldr1 f xs)
foldt1 f [x] = x
foldt1 f (x:y:xs) = foldt1 f (f x y : pairs f xs)
foldi1 f [x] = x
foldi1 f (x:xs) = f x (foldi1 f (pairs f xs))
4. 다양한 언어에서의 폴드
. initval,array
verb/ array,initvalverb/ arrayfoldl(op, itr; [init])foldr(op, itr; [init])foldl(op, itr)foldr(op, itr)Iterable.fold(initval, func)Iterable.foldRight(initval, func)Iterable.reduce(func)Iterable.reduceRight(func)fold_left(Closure, Initial, List, Result)fold_right(Closure, Initial, List, Result)foldl(func, initval, sequence)foldr(func, initval, sequence)Fold[func, initval, list]Fold[func, initval, Reverse[list]]Fold[func, list]Fold[func, Reverse[list]]NestWhileList[func,, initval, predicate]fold(@func, list, defaultVal)fold(@func, flip(list), defaultVal)fold(@func, list)fold(@func, flip(list))lreduce(func, list, initval)rreduce(func, list, initval)lreduce(func, list)rreduce(func, list)fold_left func initval list vector::fold_left func initval vectorfold_right func initval list vector::fold_right func initval vector{FoldL List Func InitVal}{FoldR List Func InitVal}fold( f, A )reduce block initval, listreduce block listarray_reduce(array, func, initval)array_reduce(array_reverse(array), func, initval)array_reduce(array, func)array_reduce(array_reverse(array), func)Reduce(func, list, initval)Reduce(func, list, initval, right=TRUE)Reduce(func, list)Reduce(func, list, right=TRUE)iterator.fold(initval, func)iterator.rev().fold(initval, func)aCollection inject: aValue into: aBlockaCollection reduce: aBlockarray.reduce(initval, func) reduce(sequence, initval, func)array.reverse().reduce(initval, func)iterable.fold(initval,[func])iterable.reduce[func]