구각형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정구각형
3. 구각형과 관련된 도형
4. 기타 구각형 관련 내용
참조

1. 개요

구각형은 9개의 변과 9개의 꼭짓점을 가진 다각형을 의미한다. 정구각형은 각의 크기가 같고 변의 길이가 같은 구각형으로, 한 내각의 크기는 140°, 외각은 40°이며 슐래플리 기호 {9}로 나타낸다. 정구각형의 작도는 일반적인 자와 컴퍼스만으로는 불가능하지만, 뉴시스 작도나 토마호크를 이용한 각의 삼등분으로 작도할 수 있다. 구각형은 대칭성을 가지며, K9 완전 그래프나 유클리드 타일링과 관련되기도 한다. 또한, 에니어그램, 바하이 사원, 대중문화, 건축 등 다양한 분야에서 활용된다.

더 읽어볼만한 페이지

9 - 구진법
구진법은 9를 밑으로 하는 위치 기수법으로 0부터 8까지의 숫자를 사용하여 수를 나타내며, 3의 배수 표현이 간결하고 3의 역수는 유한소수로 표현되는 특징이 있다.
9 - 인마궁
인마궁 또는 사수자리는 점성술에서 황도 12궁 중 아홉 번째 별자리로, 궁수 또는 켄타우로스로 묘사되며 11월 22/23일부터 12월 21/22일에 해당하고 주 행성은 목성이다.
변의 수에 따른 다각형 - 오각형
다섯 변으로 이루어진 다각형인 오각형은 변의 길이와 각의 크기가 모두 같은 정오각형을 포함하며, 정오각형은 컴퍼스와 자로 작도할 수 있고 자연에서도 발견된다.
변의 수에 따른 다각형 - 육각형
육각형은 여섯 변과 꼭짓점으로 이루어진 다각형으로, 특히 모든 변과 각이 같은 정육각형은 평면 테셀레이션이 가능하고 벌집 구조, 건축, 자연 현상, 한국 전통 문양 등 다양한 분야에서 활용된다.

구각형
개요
종류	다각형
변의 수	9
꼭짓점의 수	9
슈플리 기호	{9}
속성	볼록
정구각형
내각	140°
슈플리 기호	{9}
콕서터 다이어그램
대칭군	Dih9, 차수 18
넓이 (변의 길이 t)	A = (9/4)cot(π/9)t2 ≈ 6.18182 t2

2. 정구각형

정구각형은 아홉 개의 변과 아홉 개의 각을 가진 도형이다. 정구각형의 내각의 합은 1260도이며, 한 내각의 크기는 140도이다. 따라서 외각의 크기는 40도이다.

한 변의 길이를 ''a''라고 할 때, 정구각형의 면적을 구하는 공식은 다음과 같다.

: $A = \frac{9}{4}a^2\cot\frac{\pi}{9}\simeq6.18182\,a^2.$

2. 1. 성질

정구각형의 한 내각의 크기는 140도이며, 외각은 40도이다. 슐래플리 기호로는 {9}로 표시한다.

한 변의 길이가 ''a''인 정구각형의 면적은 다음과 같다.

:

A = \frac{9}{4}a^2\cot\frac{\pi}{9}\simeq6.18182\,a^2.

정구각형의 내접원의 반지름 ''r''은 다음과 같다.

:

r=(a/2)\cot(\pi/9)

''R''은 외접원의 반지름이며, 다음과 같다.

:

R = \sqrt{(a/2)^2 + r^2 }=r\sec(\pi/9)=(a/2)\csc(\pi/9).

\cos (2\pi/9)

를 제곱근과 세제곱근으로 나타내면 다음과 같다.^[6]

:

\cos\frac{2\pi}{9} = \frac {\sqrt[3]{-4+4\sqrt{3}i}+\sqrt[3]{-4-4\sqrt{3}i}}{4} = \frac {\sqrt[3]{-1+\sqrt{3}i}+\sqrt[3]{-1-\sqrt{3}i}}{\sqrt[3]{2^4}} = \frac {\sqrt[3]{\frac {-1+\sqrt{3}i}{2}}+\sqrt[3]{\frac {-1-\sqrt{3}i}{2}}} {2} = \frac {\sqrt[3]{\omega}+\sqrt[3]{\omega^2}}{2} =  0.766044443...

정구각형은 자 와 컴퍼스 작도가 불가능한 도형이다. 60°의 삼등분이 불가능하므로 작도는 불가능하지만, 눈금 있는 자를 이용한 뉴시스 작도로는 작도가 가능하다.

정구각형의 꼭짓점을 두 개씩 건너뛰어 선으로 연결하면 정삼각형이 만들어진다.

2. 2. 작도

정구각형은 작도가 불가능하다. 60° 각의 삼등분이 불가능하기 때문이다. 그러나 눈금 있는 자를 이용한 뉴시스 작도로는 작도가 가능하다.^[2]

정구각형, 토마호크를 이용한 120° 각 삼등분법을 기반으로 한 뉴시스 작도 애니메이션 (마지막 10초 휴지)

정구각형, 아르키메데스에 따른 각 삼등분을 사용하여 육각형을 기반으로 한 뉴시스 작도법

^[3]

뉴시스 작도나 각 삼등분 도구를 사용하면 정구각형을 작도할 수 있다.

2. 3. 대칭

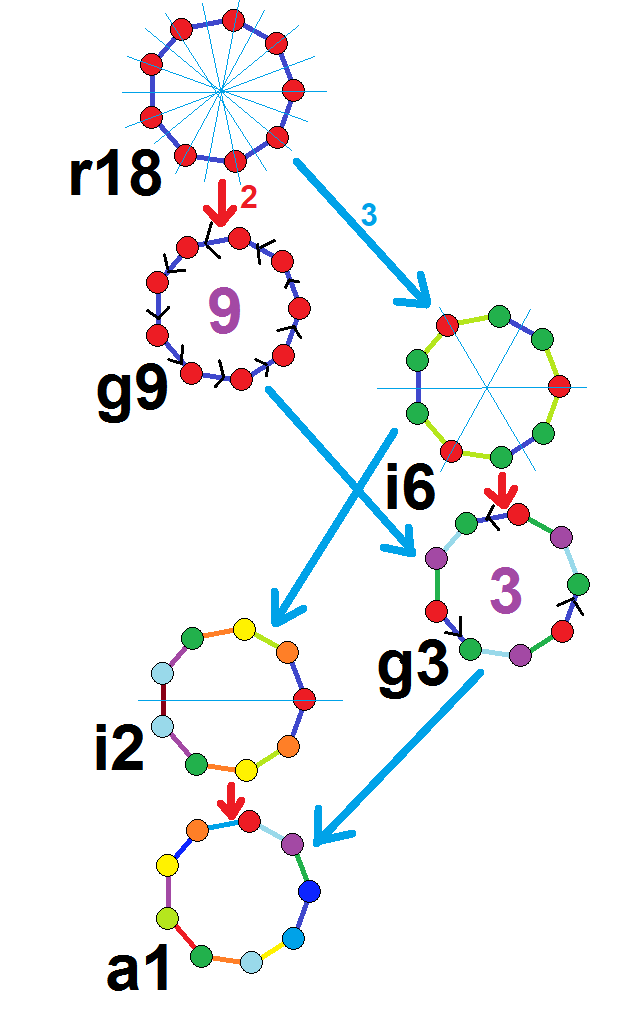
정구각형의 대칭. 꼭짓점은 대칭 위치에 따라 색상이 지정되어 있다. 파란색 거울은 꼭짓점을 통과하고, 보라색 거울은 변을 통과하여 그려진다. 회전 차수는 중앙에 표시되어 있다.

정구각형은 Dih₉ 대칭을 가지며, 차수는 18이다. Dih₃와 Dih₁의 2개의 부분군 이면각 대칭과 Z₉, Z₃, Z₁의 3개의 순환군 대칭이 있다.

이 6개의 대칭은 정구각형에서 6개의 뚜렷한 대칭으로 볼 수 있다. 존 콘웨이는 이를 문자와 군의 차수로 표시한다.^[4] 정규 형태의 전체 대칭은 '''r18'''이며, 대칭이 없는 경우는 '''a1'''로 표시된다. 이면각 대칭은 꼭짓점을 통과하는지('''d'''는 대각선), 변을 통과하는지('''p'''는 수직선)에 따라 나뉘며, '''i'''는 반사선이 변과 꼭짓점 모두를 통과할 때 사용된다. 중앙 열의 순환 대칭은 중심 회전 차수에 따라 '''g'''로 표시된다.

각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용한다. '''g9''' 부분군만이 자유도가 없지만, 방향 모서리로 볼 수 있다.

3. 구각형과 관련된 도형

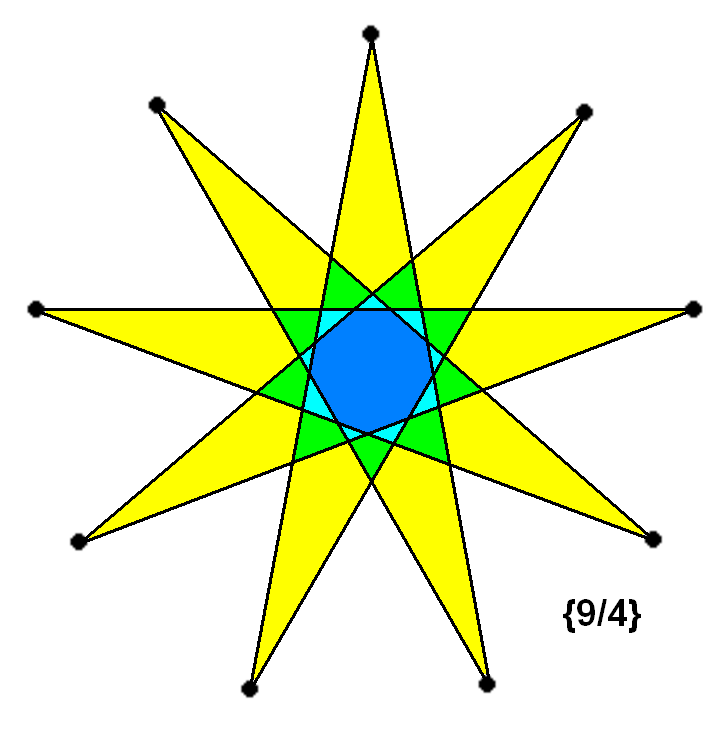
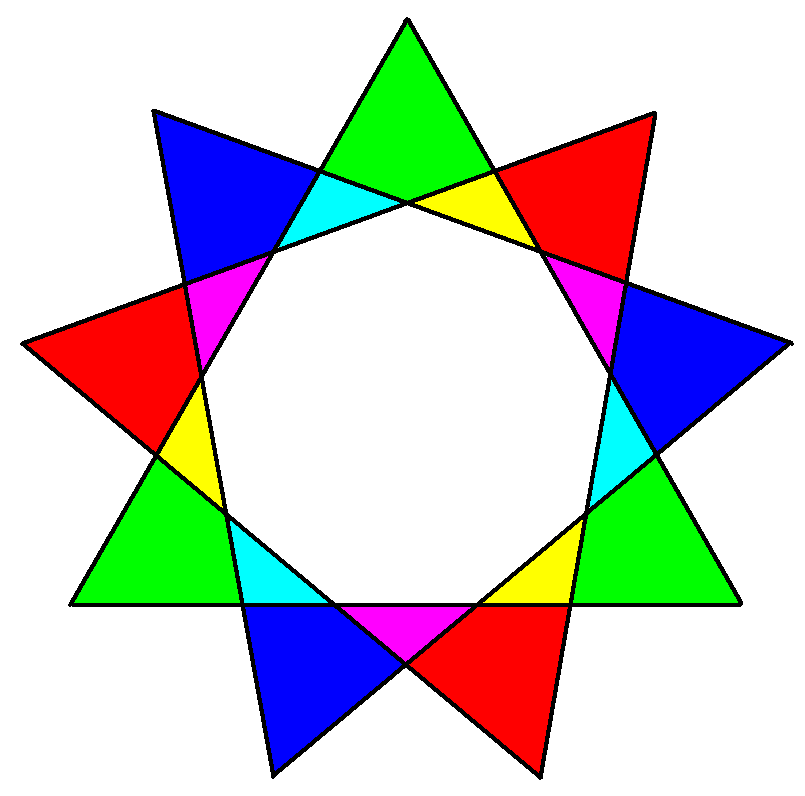
정구각형의 꼭짓점들을 모두 이으면 완전 그래프가 되며, 이 안에는 세 가지 종류의 별모양이 존재한다. 특히 셋째 별모양은 정삼각형 세 개를 겹쳐 놓은 모양이다.^[6]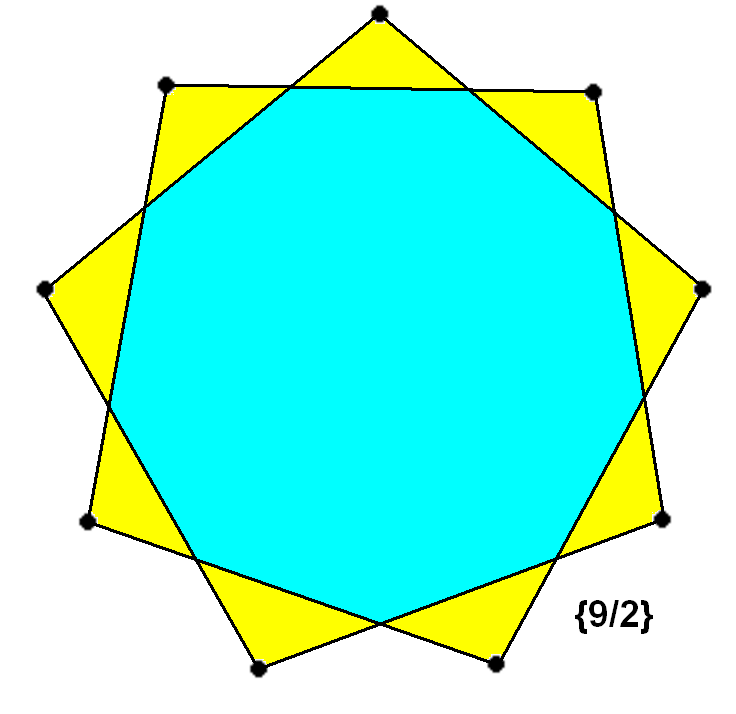

정구각형은 정육각형, 이등변삼각형과 함께 사용하여 빈틈없이 평면을 채울 수 있는 타일링을 만들 수 있다.

또한, 9개의 꼭짓점과 36개의 변을 가진 8-단순체의 정사영을 완전 그래프 K₉ (

)로 나타낼 수 있으며, 이는 정구각형으로 표현된다.

8-단순체 (8D)

3. 1. 별모양

정구각형의 꼭짓점들을 모두 이으면 위와 같이 된다. 이 그림에서 별모양을 세 개 찾을 수 있다.

셋째 별모양은 정삼각형을 세 개 붙인 것이다. 정구각형의 꼭짓점을 두 개씩 건너뛰어 선으로 연결하면 정삼각형이 만들어진다.^[6]

3. 2. 타일링

정구각형은 빈 공간이 있는 유클리드 타일을 채울 수 있다. 이러한 빈 공간은 정육각형과 이등변삼각형으로 채울 수 있다. 대칭다면체 표기법에서 이 타일링은 평면에서 *632 육각형 대칭을 나타내는 H(*;3;*;[2])라고 불린다.

3. 3. 그래프

K₉ 완전 그래프는 종종 36개의 모든 변이 연결된 정구각형으로 그려진다. 이 그래프는 또한 8-단순체의 9개 꼭짓점과 36개 변의 정사영을 나타낸다.

8-단순체 (8D)

4. 기타 구각형 관련 내용

성격을 9가지로 분류한 표를 에니어그램이라고 하는데, 구각형을 그리는 방법을 에니어그램이라고 부르기도 한다. 바하이교의 사원은 구각형이다.^[2]

4. 1. 대중문화

데이 마이트 비 자이언츠는 어린이 앨범 ''히어 컴 더 123s''에 "논아곤"이라는 제목의 노래를 수록했다. 이 노래는 "파티에 있는 모든 사람이 다각형"인 파티의 참석자와 그들이 이 파티에서 추는 춤을 언급한다.^[5]
슬립낫의 로고는 아홉 개의 꼭짓점을 가진 별 모양의 구각형으로, 세 개의 삼각형으로 만들어졌으며, 밴드의 아홉 멤버를 나타낸다.
킹 기저드 앤 더 리자드 위저드는 '논아곤 인피니티'라는 앨범을 발매했으며, 앨범 표지에는 구각형 완전 그래프가 그려져 있다. 이 앨범은 아홉 곡으로 구성되어 있으며 순환적으로 반복된다.

4. 2. 건축

바하이 신앙의 사원인 바하이 예배당은 구각형으로 지어져야 한다.^[1]

U.S. 스틸 타워는 불규칙한 구각형 건물이다.^[2]

이탈리아의 팔마노바는 구각형 모양의 도시이다.^[4]

리투아니아의 가르수 가우디클레도 구각형 모양이다.^[3]

4. 3. 기타

성격을 9가지로 분류한 표를 '''에니어그램'''이라고 하는데, 구각형을 그리는 방법을 '''에니어그램'''이라고 부르기도 한다. 바하이교의 사원은 구각형이다.^[2]

참조

_[1] Mathworld Nonagon
_[2] 서적 Episodes in the Mathematics of Medieval Islam https://books.google[...] Springer-Verlag New York, Inc. 2015-12-11
_[3] 웹사이트 KLASSISCHE PROBLEME DES GRIECHISCHENALTERTUMS IM MATHEMATIKUNTERRICHT DER OBERSTUFE https://www.erziehun[...] Bund der Freien Waldorfschulen Deutschlands 2019-07-14
_[4] 서적 The Symmetries of Things
_[5] TMBW Nonagon http://tmbw.net/wiki[...]
_[6] Socratic How do you evaluate Cos((2pi)/9)? | Socratic https://socratic.org[...]
_[7] 웹사이트 特殊なツールを使った角の三等分 http://www.takayaiwa[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com