범위 부호화
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
범위 부호화는 메시지의 각 기호를 하나의 숫자로 부호화하는 데이터 압축 방식이다. 허프만 부호화보다 더 높은 압축률을 달성할 수 있으며, 2의 거듭제곱이 아닌 확률도 효율적으로 처리한다. 초기 범위를 기호의 확률에 따라 분할하고, 각 기호를 현재 범위를 해당 기호의 하위 범위로 축소하는 방식으로 작동한다. 디코더는 인코더와 동일한 확률 추정값을 사용하여 인코딩된 숫자를 원래 메시지로 복원한다. 산술 부호화와 개념적으로 유사하며, 정수를 분수로 간주하는 방식의 차이만 존재한다.
더 읽어볼만한 페이지
- 무손실 압축 알고리즘 - VP9
VP9는 구글이 개발한 오픈 소스 비디오 코덱으로, VP8보다 압축 효율을 높이고 HEVC보다 나은 성능을 목표로 개발되었으며, WebM 형식으로 사용되고 주요 웹 브라우저와 넷플릭스, 유튜브 등에서 지원했으나 AV1의 등장으로 개발이 중단되었다. - 무손실 압축 알고리즘 - FLAC
FLAC은 조시 콜슨이 개발한 무손실 오디오 코덱으로, 원본 음질을 유지하면서 파일 크기를 줄이기 위해 오디오 데이터를 압축하며, 4~32비트 샘플 크기, 최대 8 채널을 지원하고, 미국 국립 문서 기록 관리청에서 디지털 오디오에 선호되는 형식으로 지정되었다.
2. 범위 부호화의 작동 원리
범위 부호화는 메시지에 포함된 모든 기호를 개념적으로 하나의 숫자로 표현하는 데이터 압축 방식이다. 이는 각 기호마다 고정된 비트 패턴을 할당하는 허프만 부호화와 대조되는 특징으로, 특정 조건에서 더 높은 압축률을 달성할 수 있게 한다. 특히, 기호의 출현 확률이 정확히 2의 거듭제곱 형태가 아닐 때 발생하는 허프만 부호화의 비효율성을 피할 수 있다.
핵심 원리는 충분히 큰 정수 범위를 설정하고, 메시지를 구성하는 각 기호의 출현 확률에 비례하여 이 범위를 하위 범위로 나누는 것이다. 메시지의 기호를 하나씩 처리하면서, 현재 범위를 해당 기호에 할당된 하위 범위로 계속해서 좁혀나간다. 모든 기호가 처리되면 최종적으로 좁혀진 하위 범위를 나타내는 정보(예: 해당 범위 내의 특정 정수 또는 그 정수의 일부 접두사)만 전송하여 원본 메시지를 표현한다.
이 과정을 통해 메시지를 복원하기 위해서는 디코더 역시 인코더가 사용한 것과 동일한 기호 확률 정보를 가지고 있어야 한다. 이 확률 정보는 미리 공유되거나, 데이터 자체에서 추론될 수 있다.
2. 1. 기본 개념
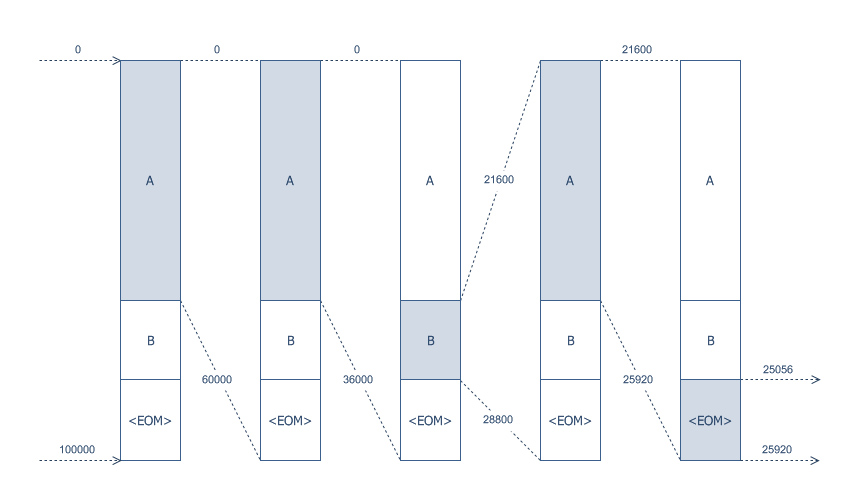
범위 부호화는 각 기호에 비트 패턴을 할당하고 이를 연결하는 허프만 부호화와 달리, 메시지의 모든 기호를 개념적으로 하나의 숫자로 부호화한다. 이 방식을 통해 범위 부호화는 허프만 부호화의 기호당 1비트 하한보다 더 높은 압축률을 달성할 수 있다. 또한, 각 기호의 출현 확률이 정확히 2의 거듭제곱이 아닐 때 허프만 부호화에서 발생하는 비효율성을 피할 수 있다는 장점이 있다.
범위 부호화의 핵심 원리는 다음과 같다. 먼저 충분히 큰 정수 범위와 각 기호의 확률 추정값이 주어진다. 이 정보를 바탕으로 초기 범위를 각 기호가 나타날 확률에 비례하는 크기의 하위 범위들로 나눈다. 메시지를 인코딩할 때는 각 기호를 순서대로 처리하며, 현재 범위를 해당 기호에 할당된 하위 범위로 계속해서 줄여나간다.
디코더는 인코딩된 메시지를 복원하기 위해 인코더가 사용한 것과 동일한 확률 추정 정보를 가지고 있어야 한다. 이 확률 정보는 미리 전송되거나, 이미 전송된 데이터로부터 추론되거나, 압축기와 압축 해제기 자체에 내장될 수 있다.
메시지의 모든 기호가 인코딩되고 나면, 최종적으로 얻어진 하위 범위를 식별하는 정보만으로 전체 메시지를 전달하는 것이 가능하다. 이때 디코더는 메시지의 끝을 인식할 수 있어야 한다. 전체 하위 범위를 명시할 필요 없이, 해당 범위 내에 속하는 단일 정수 하나만으로도 충분하다. 심지어는 그 정수의 전체값이 아니라, 해당 정수가 속한 하위 범위를 유일하게 결정할 수 있는 앞부분의 숫자들(접두사)만 전송해도 원래 메시지를 복원할 수 있다.
2. 2. 예시
예시로, 메시지 "AABA첫 번째 기호는 'A'이므로, 부호기는 초기 범위를 A에 해당하는
두 번째 기호 역시 'A'이므로, 범위는
세 번째 기호는 'B'이다. 따라서 범위는 두 번째 선택지인
- A: 7200 * 0.60 = 4320
- B: 7200 * 0.20 = 1440
: 7200 * 0.20 = 1440
이를 이용하여 하위 범위를 계산하면 다음과 같다.
네 번째 기호는 'A'이므로, 범위는
- A: 4320 * 0.60 = 2592
- B: 4320 * 0.20 = 864
: 4320 * 0.20 = 864
하위 범위는 다음과 같다.
마지막 기호가
핵심 아이디어는 부호화할 기호가 많아도 항상 0이 아닌 하위 범위로 나눌 수 있도록 충분히 큰 초기 범위를 선택하는 것이다. 하지만 실제 구현에서는 매우 큰 범위에서 시작하여 점차 좁히는 대신, 점진적(incremental) 방식을 사용한다. 즉, 부호화 과정에서 범위의 가장 왼쪽 숫자가 확정되면 해당 숫자를 바로 출력하고, 범위를 재조정하여(rescaling) 정밀도 손실 없이 계속 진행한다. 아래는 이러한 점진적 부호화 과정을 보여주는 C# 코드 예시이다.
int low = 0; // 현재 범위의 하한
int range = 100000; // 현재 범위의 크기 (초기값은 10^5)
// 메시지 "AABA
void RunEncoder()
{
// 각 기호의 확률 구간 정보 (start, size, total):
// A: [0, 6) / 10 => start=0, size=6, total=10
// B: [6, 8) / 10 => start=6, size=2, total=10
//
Encode(0, 6, 10); // A
Encode(0, 6, 10); // A
Encode(6, 2, 10); // B
Encode(0, 6, 10); // A
Encode(8, 2, 10); //
// 부호화 종료 후 남아있는 숫자를 출력 (아래 설명 참조)
FlushEncoder();
}
// 확정된 가장 왼쪽 숫자를 출력하고 범위를 재조정하는 함수
void EmitDigit()
{
Console.Write(low / 10000); // 가장 왼쪽 숫자 출력
low = (low % 10000) * 10; // 왼쪽 숫자 제거 및 왼쪽 시프트 효과
range *= 10; // 범위 크기 조정
}
// 한 기호를 부호화하는 함수
void Encode(int start, int size, int total)
{
// 기호의 확률 구간에 따라 현재 범위를 갱신
range /= total; // 전체 확률(total)로 나누어 단위 범위 크기 계산
low += start * range; // 현재 기호의 시작 확률(start)만큼 하한(low) 이동
range *= size; // 현재 기호의 확률 크기(size)만큼 범위(range) 조정
// 범위의 상한과 하한의 가장 왼쪽 숫자가 동일하면 해당 숫자를 출력 (확정)
// 상한은 low + range - 1 이므로 이에 맞춰 비교
while (low / 10000 == (low + range - 1) / 10000)
{
EmitDigit();
}
// 범위가 너무 작아져 정밀도 문제가 발생할 가능성이 있을 때 처리 (Underflow handling)
// low와 low+range-1의 첫 자리는 다르지만, 내부적으로 교착 상태(예: [49xxx, 50yyy])에 빠질 수 있음
// 이 경우, 범위를 인위적으로 넓혀서(renormalization) 진행
while (range < 1000) // 임계값 (여기서는 1000) 보다 작아지면
{
// 이 로직은 특정 underflow 상황(low와 low+range의 두 번째 숫자가 9와 0인 경우 등)을 처리하기 위함
// 정확한 구현은 복잡하며, 아래는 원본 소스의 단순화된 재조정 로직 예시
EmitDigit(); // 잠정적으로 숫자 하나 출력
EmitDigit(); // 추가 출력 (원본 코드 로직)
range = 100000 - low; // 범위를 강제로 넓힘 (원본 코드 로직)
// 주의: 이 재조정 방식은 특정 상황을 가정한 단순화된 처리일 수 있음.
}
}
// 부호화 종료 시 남아있는 숫자를 출력하는 함수
void FlushEncoder()
{
// 마지막 low 값 기준으로 최종 숫자 출력
// 최종 범위 [low, low+range) 내에서 가장 짧은 고유 표현을 출력해야 함
// 원본 소스의 마무리 로직 예시:
while (range < 10000) // range가 작으면 추가 숫자 출력 필요 가능성
EmitDigit();
// 최종 모호성을 없애기 위해 low 값 조정 후 마지막 숫자 출력 (원본 코드 로직)
low += 10000;
EmitDigit();
}
복호화 과정은 부호화 과정과 거의 동일한 원리를 따른다. 부호화된 숫자 스트림을 읽으면서, 현재 숫자가 어떤 기호의 확률 구간에 해당하는지를 판별하여 원래 메시지를 복원한다. 부호화 시 사용했던 것과 동일한 확률 분포와 점진적 범위 조정 및 재조정 로직을 사용한다.
int code = 0; // 압축 스트림에서 읽은 현재 부호 값
int low = 0; // 현재 범위의 하한
int range = 1; // 현재 범위의 크기 (초기값 1)
// 복호기 초기화: 부호 스트림에서 초기 숫자를 읽어 code와 range 설정
void InitializeDecoder(System.IO.TextReader inputStream)
{
// 초기 code 값을 만들기 위해 충분한 자릿수 읽기 (여기서는 5자리)
for (int i = 0; i < 5; i++)
AppendDigit(ReadNextDigit(inputStream)); // AppendDigit은 아래 정의
// 5자리 숫자를 읽어 code를 초기화했으므로, range는 100000이 됨
range = 100000;
low = 0; // low는 0에서 시작
}
// 스트림에서 다음 숫자(0-9)를 읽는 함수 (예시)
int ReadNextDigit(System.IO.TextReader inputStream)
{
int digitChar = inputStream.Read();
if (digitChar == -1) throw new System.IO.EndOfStreamException("End of stream reached unexpectedly.");
int digit = digitChar - '0'; // 문자 '0'~'9'를 정수 0~9로 변환
if (digit < 0 || digit > 9) throw new System.IO.InvalidDataException("Invalid digit in stream");
return digit;
}
// 부호 스트림에서 숫자를 읽어 code 갱신 및 범위 재조정 (EmitDigit 역할 대체)
void AppendDigit(int digit)
{
// code, low, range를 동기화하여 갱신 (EmitDigit과 유사하게 동작)
int oldLowTopDigit = low / 10000; // 제거될 low의 가장 왼쪽 숫자
// code에서 oldLowTopDigit에 해당하는 값을 빼고, 10을 곱한 후 새 digit을 더함
code = (code - oldLowTopDigit * 10000) * 10 + digit;
low = (low % 10000) * 10; // low도 동일하게 시프트
range *= 10; // range도 확장
}
// 현재 code 값으로 다음 기호를 결정하는 함수
int GetValue(int total)
{
// 현재 범위(range)를 전체 확률(total)로 나누어 단위 확률당 크기 계산
int unitRange = range / total;
// code 값이 현재 범위(low ~ low+range) 내에서 몇 번째 단위 확률 구간에 속하는지 계산
// (code - low)는 현재 범위 내에서의 상대적 위치
return (code - low) / unitRange;
}
// 한 기호를 복호화하는 함수
void Decode(int start, int size, int total, System.IO.TextReader inputStream)
{
// 부호화 시와 동일하게 범위를 갱신
range /= total;
low += start * range;
range *= size;
// 부호화 시와 동일하게 범위의 상한/하한 첫 자리가 같으면 숫자 읽어 갱신
while (low / 10000 == (low + range - 1) / 10000)
{
AppendDigit(ReadNextDigit(inputStream));
}
// 부호화 시와 동일하게 underflow 처리 (재조정)
while (range < 1000)
{
// AppendDigit 두 번 호출 및 range 재조정 (부호화 로직과 동기화)
AppendDigit(ReadNextDigit(inputStream));
AppendDigit(ReadNextDigit(inputStream));
range = 100000 - low; // 부호화 시와 동일한 재조정
}
}
// 메시지 복호화 실행 함수 예시
void RunDecoder(System.IO.TextReader inputStream, System.IO.TextWriter outputStream)
{
InitializeDecoder(inputStream);
int total = 10; // 전체 확률 분모
while (true)
{
int v = GetValue(total); // 현재 code가 속하는 확률 구간 값(0-9) 얻기
int start, size;
char symbol;
// 확률 구간 값(v)을 기호와 해당 확률 구간 정보(start, size)로 변환
if (v >= 0 && v < 6) { start = 0; size = 6; symbol = 'A'; } // A: 0-5 (6/10)
else if (v >= 6 && v < 8) { start = 6; size = 2; symbol = 'B'; } // B: 6-7 (2/10)
else if (v >= 8 && v < 10) { start = 8; size = 2; symbol = 'E'; } //
else throw new System.IO.InvalidDataException("Invalid value decoded: " + v);
if (symbol == 'E') //
{
// outputStream.WriteLine("
break;
}
outputStream.Write(symbol); // 복호화된 기호 출력
// 복호화된 기호 정보를 사용하여 Decode 함수 호출 (다음 숫자 읽기 및 범위 갱신)
Decode(start, size, total, inputStream);
}
}
위 예시에서는 10진법을 사용했지만, 실제 구현에서는 컴퓨터 내부 표현에 자연스러운 2진법을 사용하며, 정수형 변수의 전체 범위를 활용한다. 숫자 대신 바이트(byte) 단위로 입출력하고, 10을 곱하는 대신 비트 시프트(bit shift) 연산을 사용하여 효율성을 높인다.
2. 3. 구현
아래는 C# 코드를 사용하여 범위 부호화의 인코딩 및 디코딩 과정을 구현하는 예시이다. 실제 구현에서는 10진수 대신 2진수를 사용하고, 바이트 단위로 처리하여 효율성을 높인다.
=== 인코딩 ===
인코딩 과정은 현재 범위를 입력 기호의 확률에 따라 계속 좁혀나가는 방식으로 진행된다. `low` 변수는 현재 범위의 시작점을, `range` 변수는 현재 범위의 크기를 나타낸다.
다음은 "AABA
int low = 0;
int range = 100000; // 초기 범위 크기
// 인코딩 실행 함수 (예시)
void Run()
{
// 각 기호에 해당하는 시작(start)과 크기(size), 전체(total)를 Encode 함수에 전달
Encode(0, 6, 10); // A (start=0, size=6)
Encode(0, 6, 10); // A (start=0, size=6)
Encode(6, 2, 10); // B (start=6, size=2)
Encode(0, 6, 10); // A (start=0, size=6)
Encode(8, 2, 10); //
// 인코딩 종료 후 남은 숫자 출력 (아래 설명 참조)
while (range < 10000)
EmitDigit();
low += 10000; // 마지막 자리 올림 처리
EmitDigit();
}
// 숫자를 출력하고 범위를 조정하는 함수
void EmitDigit()
{
Console.Write(low / 10000); // 가장 왼쪽 숫자 출력
low = (low % 10000) * 10; // low 값 업데이트 (왼쪽으로 시프트 효과)
range *= 10; // range 값 업데이트
}
// 특정 기호를 인코딩하는 함수
void Encode(int start, int size, int total)
{
// 1. 기호의 확률 구간에 따라 현재 범위를 조정
range /= total; // 전체 확률 합으로 나누어 단위 크기 계산
low += start * range; // 현재 범위의 시작점(low) 업데이트
range *= size; // 현재 범위의 크기(range) 업데이트
// 2. 범위의 최상위 숫자가 확정되면 출력
// low와 low + range의 가장 왼쪽 숫자가 같으면 해당 숫자는 더 이상 변하지 않음
while (low / 10000 == (low + range) / 10000)
{
EmitDigit(); // 확정된 숫자 출력 및 범위 조정
}
// 3. 정밀도 문제 처리 (Renormalization)
// range가 너무 작아지면 정밀도 손실 발생 가능
if (range < 1000)
{
// 이 경우, 다음 두 숫자를 잠정적으로 출력하고 범위를 재조정
EmitDigit();
EmitDigit();
// 범위를 [low, 100000) 로 강제 확장
range = 100000 - low;
}
}
==== 정밀도 문제 처리 (Renormalization) ====
인코딩 과정에서 `range` 값이 계속 작아지다 보면, 정수 연산의 표현 범위 제약 등으로 인해 더 이상 다음 기호를 구분할 수 없는 상태가 될 수 있다. 예를 들어, `range`가 1000 미만으로 작아졌지만 `low`와 `low + range`의 첫 번째 숫자가 다른 경우가 발생할 수 있다 (`low = 59888`, `range = 300` 인 경우).
이 문제를 해결하기 위해 `range`가 특정 임계값(예제에서는 1000) 미만으로 떨어지면 재정규화(Renormalization) 과정을 수행한다. 위 코드의 `Encode` 함수 마지막 부분에 있는 `if (range < 1000)` 블록이 이 역할을 한다.
1. 현재 `low` 값의 첫 두 자리를 `EmitDigit()`를 통해 출력한다. 이 값은 약간의 오차를 포함할 수 있지만, 디코더도 동일한 로직을 따르므로 문제가 되지 않는다.
2. `range`를 `100000 - low`로 재설정하여 표현 가능한 최대 범위로 다시 넓혀준다. 이는 마치 `low` 값을 왼쪽으로 두 자리 시프트하고 새로운 두 자리를 채워 넣는 효과를 준다. 디코더 역시 동일한 조건에서 이 재정규화 과정을 수행하여 동기화를 유지한다.
==== 인코딩 종료 처리 ====
모든 기호를 인코딩한 후, `low`에 남아있는 값을 명확히 표현하기 위해 추가적인 숫자 출력이 필요할 수 있다. `while (range < 10000)` 루프는 `range`가 충분히 커질 때까지 `EmitDigit()`를 호출하여 `low`의 남은 숫자들을 출력한다. 마지막으로 `low += 10000`을 통해 올림 처리를 해주고 마지막 숫자를 출력하여 최종 인코딩된 숫자를 완성한다.
// 인코딩 종료 시 마지막 숫자들을 출력하는 부분
while (range < 10000)
EmitDigit();
low += 10000; // 마지막 자리 올림 처리
EmitDigit();
=== 디코딩 ===
디코딩 과정은 인코딩과 거의 동일한 로직을 따르지만, 입력 스트림에서 숫자를 읽어 `code` 변수에 유지하며 진행된다. 인코더가 숫자를 출력(`EmitDigit`)하는 대신, 디코더는 숫자를 입력받아(`AppendDigit`) `code` 변수를 업데이트한다.
int code = 0; // 입력 스트림에서 읽은 현재 값
int low = 0;
int range = 1; // 초기 range는 1로 시작 (AppendDigit에서 조정됨)
// 디코더 초기화 함수
void InitializeDecoder()
{
// 인코딩된 숫자 스트림의 첫 부분을 읽어 code, low, range 초기화
// 예제에서는 5자리 숫자를 사용하므로 5번 호출
AppendDigit();
AppendDigit();
AppendDigit();
AppendDigit();
AppendDigit();
}
// 입력 스트림에서 다음 숫자를 읽어 code, low, range 업데이트
void AppendDigit()
{
// 실제 구현에서는 ReadNextDigit() 함수가 입력 스트림에서 다음 숫자를 읽어옴
code = (code % 10000) * 10 + ReadNextDigit(); // code 업데이트 (왼쪽 시프트 및 새 숫자 추가 효과)
low = (low % 10000) * 10; // low 업데이트 (왼쪽 시프트 효과)
range *= 10; // range 업데이트
}
// 특정 기호를 디코딩하는 함수 (Encode와 거의 동일, EmitDigit 대신 AppendDigit 사용)
void Decode(int start, int size, int total)
{
// 1. 기호의 확률 구간에 따라 현재 범위를 조정 (인코딩과 동일)
range /= total;
low += start * range;
range *= size;
// 2. 범위의 최상위 숫자가 확정되면 입력 스트림에서 다음 숫자 읽기
while (low / 10000 == (low + range) / 10000)
{
AppendDigit(); // 다음 숫자 읽기 및 범위 조정
}
// 3. 정밀도 문제 처리 (인코딩과 동일한 로직 및 조건으로 수행)
if (range < 1000)
{
AppendDigit();
AppendDigit();
range = 100000 - low;
}
}
디코더는 현재 `code` 값이
// 현재 code 값에 해당하는 기호의 상대적 위치(값)를 반환하는 함수
int GetValue(int total)
{
// (code - low)는 현재 범위 내에서의 상대적 위치
// (range / total)은 단위 확률 구간의 크기
// 나누면 code가 몇 번째 확률 구간에 속하는지 알 수 있음
return (code - low) / (range / total);
}
// 디코딩 실행 함수 (예시)
void Run()
{
int start = 0; // 현재 디코딩된 기호의 시작 확률 값
int size; // 현재 디코딩된 기호의 확률 크기
int total = 10; // 전체 확률 합
InitializeDecoder(); // 디코더 초기화
// 메시지 종료 기호(
while (start < 8)
{
// 1. 현재 code 값으로 다음 기호 판별
int v = GetValue(total);
// 2. 판별된 값(v)에 따라 기호 결정 및 출력
switch (v)
{
case 0: case 1: case 2: case 3: case 4: case 5: // 값 0~5는 'A'
start = 0; size = 6; Console.Write("A"); break;
case 6: case 7: // 값 6~7은 'B'
start = 6; size = 2; Console.Write("B"); break;
default: // 값 8~9는 '
start = 8; size = 2; Console.WriteLine(""); break;
}
// 3. 디코딩된 기호 정보를 사용하여 Decode 함수 호출 (범위 업데이트)
Decode(start, size, total);
}
}
=== 실제 구현 시 고려사항 ===
위 예제는 이해를 돕기 위해 십진법을 사용했지만, 실제 구현에서는 다음과 같은 방식으로 효율성을 높인다.
- 2진수 사용: 컴퓨터는 2진수 연산에 최적화되어 있으므로, 10진수 대신 정수형 변수가 표현할 수 있는 전체 범위를 활용하는 2진수로 구현하는 것이 일반적이다. 예를 들어, 32비트 정수를 사용하면 `range`는 232까지 표현 가능하다.
- 바이트 단위 처리: 숫자를 한 자리씩 처리하는 대신, 바이트(8비트) 단위로 입출력하고 처리한다. 이렇게 하면 입출력 횟수를 줄이고 비트 시프트 연산을 활용하여 속도를 높일 수 있다.
- 16진수 상수 사용: 코드에서 범위 관련 상수를 표현할 때, 2의 거듭제곱 형태를 명확히 나타내기 위해 `0x1000000` (224)이나 `0x10000` (216) 같은 16진수 상수를 사용하는 경우가 많다. 곱셈/나눗셈 연산 대신 비트 시프트 연산(`<<`, `>>`)을 사용한다.
3. 산술 부호화와의 관계
산술 부호화는 범위 부호화와 거의 동일한 부호화 방법이지만, 정수를 분수의 분자로 간주한다는 점에서 개념적인 차이가 있다. 이 분수들은 암묵적인 공통 분모를 가지며, 모든 값은
산술 부호화와 범위 부호화는 본질적으로 동일한 부호화 과정을 다른 관점에서 설명하는 방식이며, 결과 코드도 같다. 따라서 모든 산술 부호기는 그에 대응하는 범위 부호기이며, 그 반대도 마찬가지이다.
하지만 실제 구현에서는 차이가 나타나는 경우가 많다. '범위 인코더'라고 불리는 구현체들은 마틴(Martin)의 논문[1]에 설명된 대로 구현되는 경향이 있다. 이러한 범위 인코더의 특징 중 하나는 재정규화(renormalization) 과정을 비트 단위가 아닌 바이트 단위로 한 번에 수행하는 경향이 있다는 점이다. 즉, 부호화된 숫자를 나타낼 때 비트 대신 바이트를 기본 단위로 사용한다. 이 방식은 비트 단위로 재정규화를 수행하는 것보다 처리 속도가 빠르지만, 압축 효율은 아주 약간 감소할 수 있다. 반면, '산술 부호기'라고 불리는 구현체들이 반드시 이러한 바이트 단위 재정규화 방식을 따르는 것은 아니다.
참조
[1]
간행물
"Range encoding: An algorithm for removing redundancy from a digitized message"
http://www.compressc[...]
Video & Data Recording Conference, Southampton, UK
1979-07-24
[2]
서적
Source coding algorithms for fast data compression
Stanford, CA
1976
[3]
문서
On the Overhead of Range Coders
http://people.xiph.o[...]
Technical Note
2008
[4]
특허
US patent 4122440
IBM
1978-10-24
[5]
간행물
"Range encoding: An algorithm for removing redundancy from a digitized message"
http://www.compressc[...]
Video & Data Recording Conference, Southampton, UK
1979-07-24
[6]
서적
Source coding algorithms for fast data compression
Stanford, CA
1976
[7]
문서
On the Overhead of Range Coders
http://people.xiph.o[...]
Technical Note
2008
[8]
특허
US patent 4122440
IBM
1978-10-24
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
