조건부 무작위장

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

조건부 무작위장(CRF)은 방향이 없는 그래프 또는 마르코프 무작위장으로 간주될 수 있는 통계적 모델이다. CRF는 은닉 마르코프 모델(HMM)보다 변수 독립성에 대한 제약이 적고, 최대 엔트로피 마르코프 모델(MEMM)보다 편향(bias)이 없는 장점을 가진다. 그래프 구조가 트리 형태일 경우, 조건부 무작위장의 확률 분포는 정점과 간선으로 표현되며, 입력 시퀀스에 따라 그래프 상에서 움직이는 상태와 관련된 확률을 나타낸다. CRF는 자연어 처리, 컴퓨터 비전, 생물 정보학 등 다양한 분야에서 시퀀스 데이터의 라벨링, 객체 인식, 유전자 예측 등에 활용된다.

더 읽어볼만한 페이지

그래프 모형 - 베이즈 네트워크
베이즈 네트워크는 확률 변수 간의 관계를 방향성 비순환 그래프로 표현하여 복잡한 확률 추론 및 인과 관계 분석을 가능하게 하는 확률적 그래픽 모델이다.
그래프 모형 - 마르코프 네트워크
마르코프 네트워크는 무향 그래프로 표현되는 확률 모델로, 노드는 확률 변수를, 연결은 변수 간 조건부 독립성을 나타내며, 쌍별, 국소, 전역 마르코프 속성을 통해 정의되고 다양한 분야에서 활용된다.
기계 학습 - 비지도 학습
비지도 학습은 레이블이 없는 데이터를 통해 패턴을 발견하고 데이터 구조를 파악하는 것을 목표로 하며, 주성분 분석, 군집 분석, 차원 축소 등의 방법을 사용한다.
기계 학습 - 지도 학습
지도 학습은 레이블된 데이터를 사용하여 입력 데이터와 출력 레이블 간의 관계를 학습하는 기계 학습 분야로, 예측 모델 생성, 알고리즘 선택, 모델 최적화, 정확도 평가 단계를 거치며, 회귀 및 분류 문제에 적용되고 다양한 확장 기법과 성능 평가 방법을 활용한다.

조건부 무작위장
개요
유형	그래프의 노드에 대한 확률적 변수를 지정하는 확률 그래프 모델
하위 유형	식별 모델
사용 분야	컴퓨터 비전 자연어 처리 생물정보학
상세 정보
정의	주어진 관측 무작위 변수에 대한 다른 무작위 변수의 조건부 확률을 지정하는 확률 그래프 모델
특징	판별, 무방향 그래프 모델
관련 항목	숨겨진 마르코프 모델 최대 엔트로피 마르코프 모델 베이즈 네트워크 마르코프 랜덤 필드

2. 정의

조건부 무작위장(Conditional Random Field, CRF)은 입력 시퀀스와 출력 시퀀스 간의 관계를 확률적으로 모델링하는 방법이다. 다양한 과학 분야에서 시퀀스 분할 및 라벨링 문제를 해결하는 데 사용된다.

은닉 마르코프 모델과 같은 기존 모델들은 상호작용하는 여러 자질이 있거나 관측값에서 긴 범위의 의존성이 발견되는 경우, 모델 추론이 어려워지는 단점이 있었다. 반면, 조건부 무작위장은 관측값을 모델링하는 데 걸리는 시간을 고정하고, 레이블 시퀀스의 조건부 확률이 관측 시퀀스의 임의의 독립적이지 않은 기질들에 의존할 수 있도록 하여 이러한 문제를 해결했다.^[15]

CRF는 일종의 판별 무방향 확률적 그래프 모형이다.

2. 1. 수학적 정의

조건부 무작위장(CRF)은 입력 시퀀스에 대한 출력 시퀀스의 조건부 확률을 나타낸다. 간단히 표현하면 다음과 같다.

$p(y|x),$ 여기서, $x , y$ 는 시퀀스이다.

예를 들어, $x=(a, b, c), y=(x, y, z),$
$x, y$ 시퀀스에 대하여서는 제약이 없다.

예를 들어, 문자 a, b, c가 연속으로 나타날 때, 문자 x, y, z를 연속으로 부여할 확률을 의미한다. 여기서 y는 마르코프 성질을 만족해야 한다. x와 y의 집합이 한정되면, 이 구조는 그래프 구조를 형성하며, 일반적으로 체인(chain^영어) 그래프 구조를 형성한다.^[16]

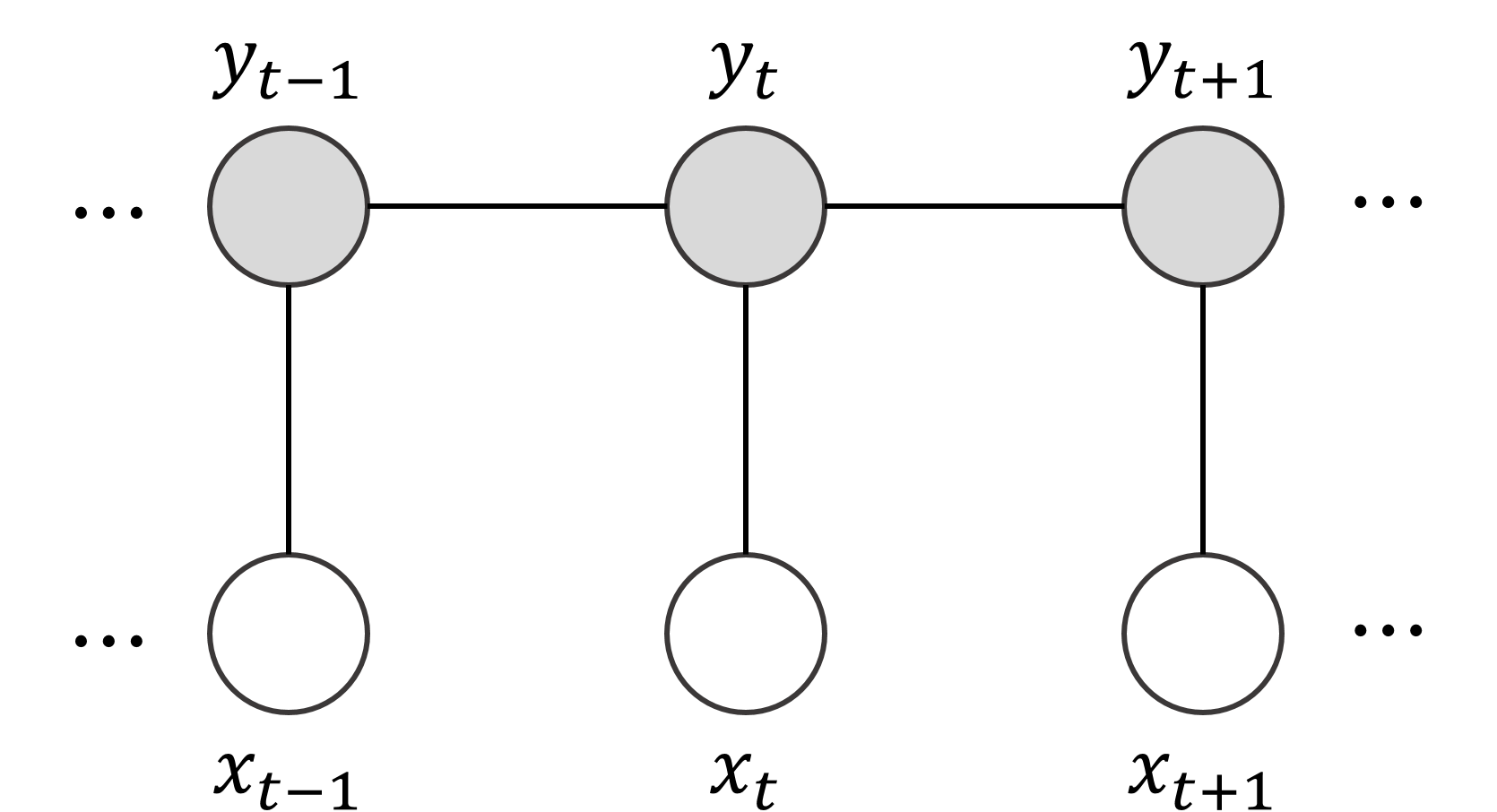
조건부 무작위장

(Y, X)

는 방향이 없는(undirected^영어) 그래프

G=(V, E)

혹은 마르코프 무작위장으로 간주할 수 있다. 입력 시퀀스에서 조건부 독립을 가정할 수 있다면, 그래프는 여러 형태를 가질 수 있지만, 응용에서는

Y

노드가 체인 형태를 띠는 경우가 많다.^[15] 조건부 무작위장은 은닉 마르코프 모델(HMM)보다 변수 독립성 조건이 덜 필요하고, 최대 엔트로피 마코르프 모델(MEMM)보다 변수 치우침(bias)이 없는 장점이 있다.^[15]

래퍼티, 매콜럼과 페레이라^[1]는 관측치

\boldsymbol{X}

와 확률 변수

\boldsymbol{Y}

에 대한 CRF를 다음과 같이 정의하였다.

>

G = (V , E)

를

\boldsymbol{Y} = (\boldsymbol{Y}_v)_{v\in V}

가 되도록 하는 그래프라고 하자. 즉,

\boldsymbol{Y}

는

G

의 정점에 의해 인덱싱된다.

> 그러면

(\boldsymbol{X}, \boldsymbol{Y})

는 각 확률 변수

\boldsymbol{Y}_v

가

\boldsymbol{X}

에 조건화되었을 때 그래프에 대해 마르코프 성질을 따를 때 조건부 무작위장이다. 즉, 확률은 G에서 이웃에만 의존한다.

>

>

P(\boldsymbol{Y}_v |\boldsymbol{X}, \{\boldsymbol{Y}_w: w \neq v\}) = P(\boldsymbol{Y}_v |\boldsymbol{X}, \{\boldsymbol{Y}_w: w \sim v\})

여기서

\mathit{w} \sim v

는

>

w

와

v

가

G

에서 이웃임을 의미한다.

이는 CRF가 노드를 관측 및 출력 변수인

\boldsymbol{X}

와

\boldsymbol{Y}

로 나누는 무방향 그래프 모형이며, 조건부 분포

p(\boldsymbol{Y}|\boldsymbol{X})

가 모델링됨을 의미한다.

조건부 무작위장의 정의는 다음과 같다.^[15]^[16]

>

G=(V, E)

는 그래프 구조이고,

Y=(Y_v)_{v{\in V}}

로서,

Y

는 그래프

G

의 정점(vertex^영어)을 나타낸다고 하고

E

는 간선(edge^영어)이라고 하자. 만약 랜덤 변수

X

에 대하여 랜덤 변수

Y_v

가 그래프에서 마코프 성질을 나타낸다면, 즉,

P(\boldsymbol{Y}_v |\boldsymbol{X}, \{\boldsymbol{Y}_w: w \neq v\}) = P(\boldsymbol{Y}_v |\boldsymbol{X}, \{\boldsymbol{Y}_w: w \sim v\})

라면

(X, Y)

는 조건부 랜덤 필드가 된다. (여기서

w\sim v

는

w

와

v

는 서로 이웃이라는 의미)

>

$Y$ 의 그래프 $G=(V,E)$ 가 트리(tree^영어)를 형성한다면, $Y$ 의 클릭(clique)은 간선과 정점이 된다. 입력 시퀀스 $X$ 가 주어질 때, 출력 시퀀스 $Y$ 의 결합 확률 분포는 다음과 같다.

:

p_\theta (y|x) \propto exp( \sum_{e \in E,k} \lambda_k f_k(e, y|_e, x)+ \sum_{v \in V,k}\mu _k g_k (v, y|_v, x))

:여기서

x

는 입력 시퀀스,

y

는 출력 레이블 시퀀스,

y|_s

는 그래프

G

의 서브그래프

S

의 정점과 관계된

y

요소의 집합이다.

f_k

와

g_k

는 주어진 고정 함수로 가정한다.

:이 식에서 앞 항은 그래프에서 입력 시퀀스에 따라 현재 정점에서 다음 정점으로 이동하는 천이 특징 함수(transition feature function^영어)로, 뒤 항은 현재 정점의 상태 특징 함수(state feature function^영어)로 해석할 수 있다. 즉, 입력 시퀀스에 의해 현재 정점에 머무르거나 다음 정점으로 이동하는 상태와 확률을 나타낸다.

$Y$ 가 체인을 구성하면, 조건부 무작위장 확률은 다음과 같이 표현할 수 있다.

:

p_\theta (y|x) = {\prod_{i=1}^{n+1} M_i(y_{i-1} , y_i |x_i) \over \prod_{i=1}^{n+1} M_i (x))_{begin,stop}}

:여기서,

y_0=begin

, 그리고

y_{n+1}=stop

이다.

CRF는 판별 무방향 확률적 그래프 모형이다. 모델에서는 확률 변수 간의 쌍별 의존성만 모델링되며, 일반적인 경우에는 고차 CRF를 참조한다. 각 노드나 모델 전체는 지수 분포족이 되는 경우가 많으며, 이는 깁스 분포와 같이 에너지 항을 설명한다. 그래프 구조는 알려져 있다고 가정하고, 분포의 파라미터는 학습된다. CRF 파라미터 학습의 기본적인 전제는 변수

Y_i

는 추론, 변수

X_i

는 항상 관측된다는 것이다. 이는 조건부 확률

p(Y_i|X_i)

의 최대화를 가능하게 하며, 모델의 판별 학습에 해당한다.

2. 2. 은닉 마르코프 모델(HMM) 및 최대 엔트로피 마르코프 모델(MEMM)과의 관계

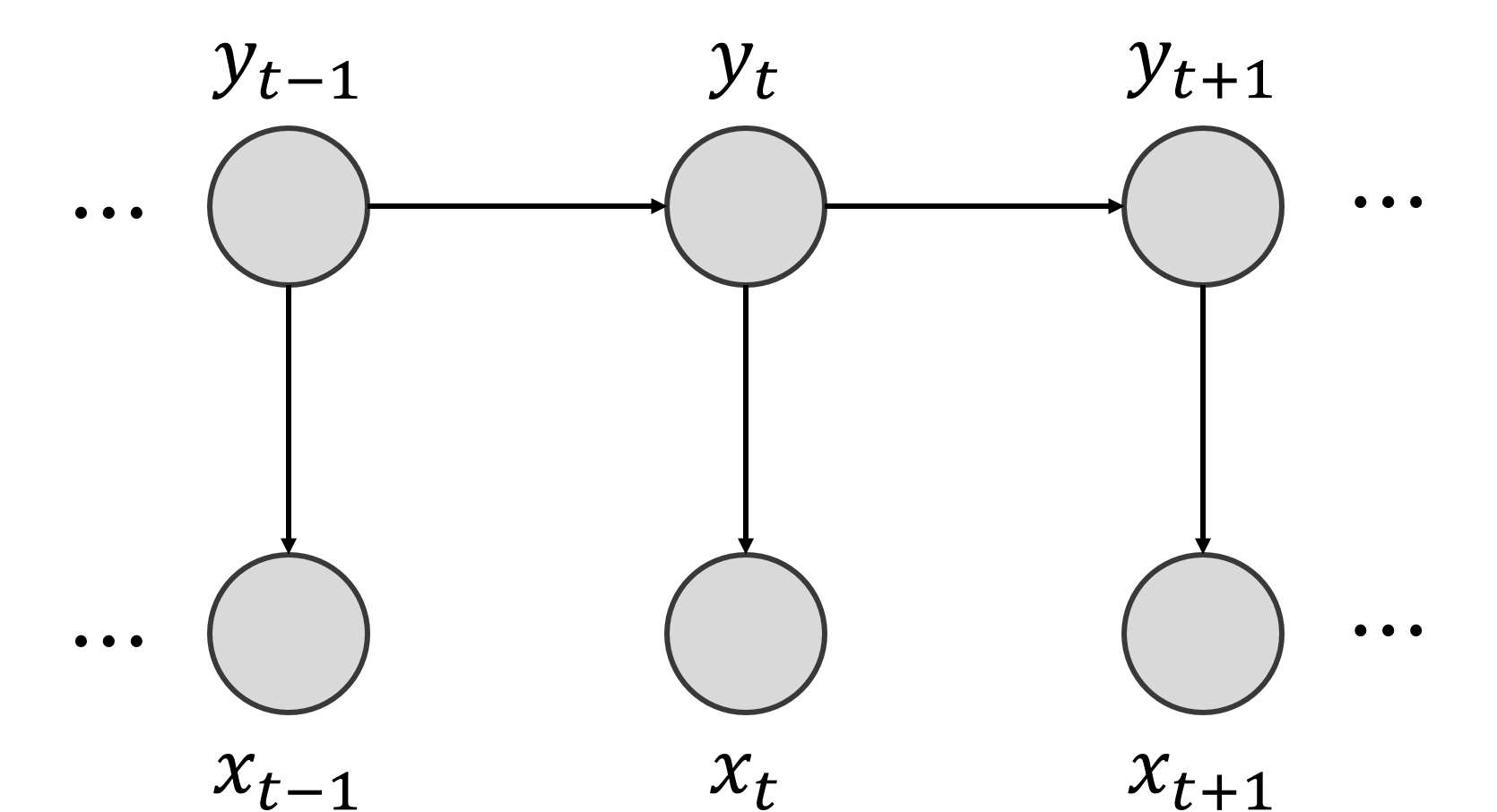
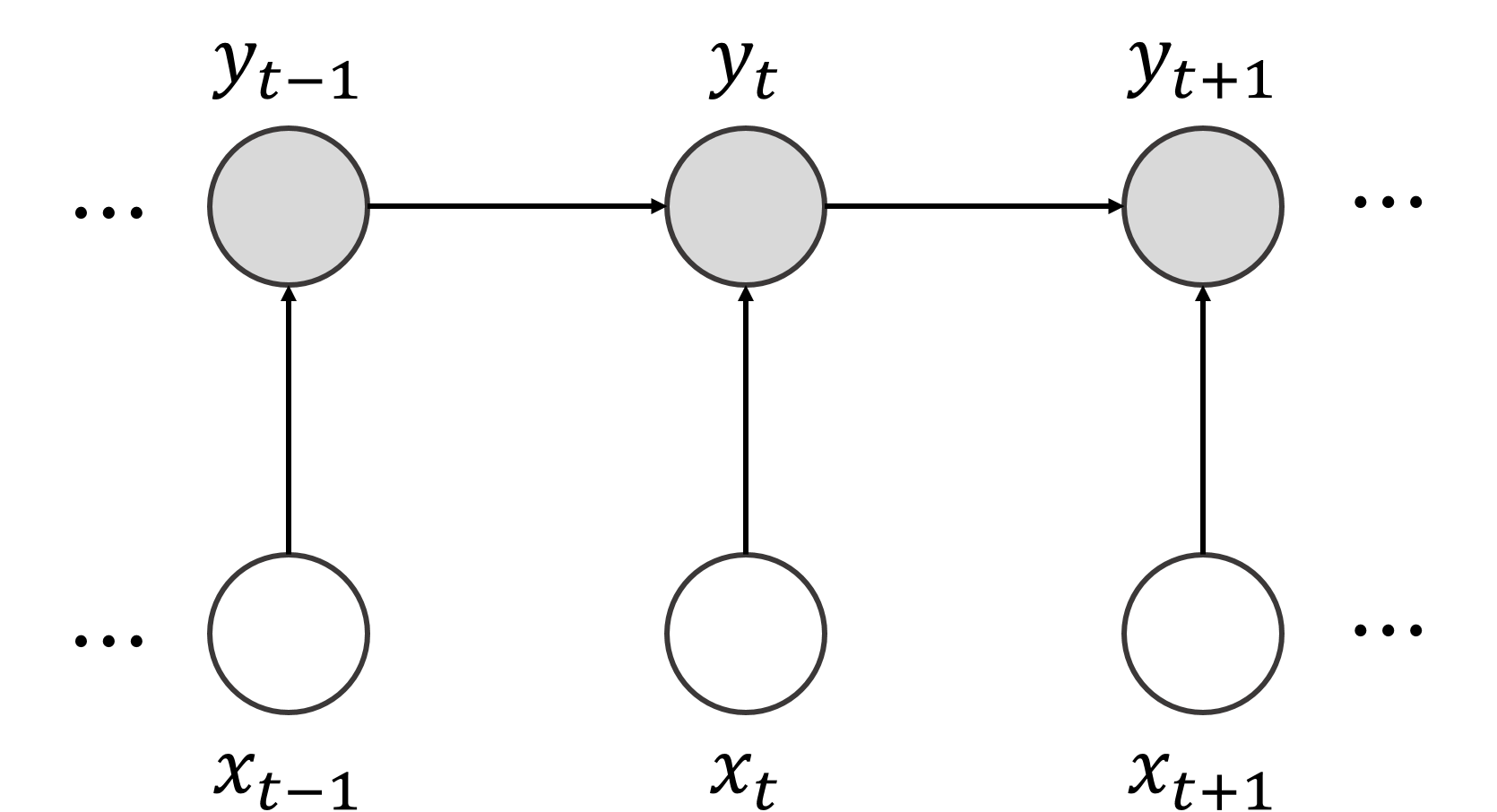
조건부 무작위장(CRF)은 은닉 마르코프 모델(HMM)의 일반화된 형태로 볼 수 있다. HMM은 상태 전이와 출력(방출)을 모델링하기 위해 상수 확률을 사용하는 특징 함수를 가진 CRF로 이해할 수 있다. 반면, CRF는 상수 전이 확률을 숨겨진 상태 시퀀스의 위치와 입력 시퀀스에 따라 달라지는 함수로 만들어 HMM을 일반화한 것이다. 이러한 특성 덕분에 CRF는 HMM보다 입력 시퀀스의 특징을 더 유연하게 반영할 수 있다.^[1]

또한, CRF는 최대 엔트로피 마르코프 모델(MEMM)의 단점인 레이블 편향 문제를 해결한다. CRF는 특징 함수를 얼마든지 포함할 수 있고, 추론 과정에서 전체 입력 시퀀스를 검사할 수 있으며, 특징 함수의 범위에 대한 제약도 덜하다.

다음은 HMM, MEMM, CRF의 특징을 비교한 표이다.^[16]

	은닉 마르코프 모델(HMM)	최대 엔트로피 마르코프 모델(MEMM)	조건부 무작위장(CRF)
그래프 모델	은닉 마르코프 모델	최대 엔트로피 마르코프 모델	조건부 무작위장
모델 방식	생성 모델(generative model^영어)	판별 모델(discriminative model^영어)	판별 모델(discriminative model^영어)
간선(edge^영어) 방식	방향성 그래프(directed graph^영어)	방향성 그래프(directed graph^영어)	비방향성 그래프(undirected graph^영어)

3. 추론

조건부 무작위장(CRF)에서의 추론은 주어진 입력 시퀀스에 대해 가장 확률이 높은 출력 시퀀스를 찾는 과정이다. 이는 모델 훈련 후 새로운 입력에 대한 레이블을 예측하거나, 모델 파라미터를 추정할 때 주변 분포를 계산하는 데 사용된다.^[17] 주어진 입력 $x$ 에 대한 최적의 레이블 $\hat{y}$ 는 다음과 같이 표현할 수 있다.

: $\hat{y} = \operatorname{argmax_y}\ p(y|x)$

일반적인 그래프에서 CRF의 정확한 추론은 풀기 어려운 문제로 알려져 있으며, 이는 마르코프 확률장(MRF)에서의 추론 문제와 근본적으로 동일하다.^[7] 그러나 그래프가 선형 사슬이나 트리 구조인 경우에는 전방-후방 알고리즘이나 비터비 알고리즘과 같은 메시지 전달 알고리즘을 사용하여 효율적으로 정확한 해를 구할 수 있다. CRF가 쌍별 포텐셜만 포함하고 에너지가 부분 모듈 함수인 경우에도 조합 최소 절단/최대 흐름 알고리즘을 통해 정확한 해를 얻을 수 있다.^[7]

정확한 추론이 불가능한 경우에는 루프 신념 전파, 알파 확장, 평균장 추론, 선형 계획법 완화 등의 알고리즘을 사용하여 근사적인 해를 찾는다.

3. 1. 정확한 추론 방법

그래프가 선형 사슬이거나 트리 구조일 때, 은닉 마르코프 모델을 위한 다양한 동적 계획법 알고리즘을 이용해 추론 작업을 효율적이고 정확하게 수행할 수 있다. 이러한 알고리즘에는 전향-후향 알고리즘과 비터비 알고리즘이 있다. 이 알고리즘들은 트리 구조의 그래프 모델을 위한 일반적인 신뢰전파 알고리즘의 특수한 경우라고 할 수 있다.^[17]

만약 조건부 무작위장이 오직 쌍별 포텐셜(pairwise potential)만을 포함하며, 에너지가 서브모듈러(submodular)일 경우, 조합적 최소 컷/최대 흐름 알고리즘을 이용해 정확한 결과를 구할 수 있다.^[7]

3. 2. 근사적 추론 방법

일반적인 그래프에서는 정확한 추론이 어렵기 때문에, 몬테 카를로 알고리즘이나 변분 알고리즘과 같은 근사적 추론 방법이 사용된다.^[17] 몬테 카를로 알고리즘은 확률적 알고리즘으로, 관심 있는 분포의 샘플을 근사적으로 생성해낸다. 대표적인 예로는 기브스 표집 알고리즘이 있다.^[17] 변분 알고리즘은 다루기 힘든 분포와 가장 근사하며 간단한 분포를 찾아내어 푸는 방법으로, 추론 문제를 최적화 문제로 바꾸어 푼다. 대표적인 예로는 신뢰전파 알고리즘이 있다.^[17]

몬테 카를로 방법은 치우침이 없는(unbiased^영어) 대신 계산 시간이 언제 끝날지 알 수 없다는 단점이 있다. 변분 방법은 이에 비해 상당히 빠르지만 치우침이 있어(biased^영어) 에러를 포함하며, 계산 시간을 늘리더라도 에러가 줄지 않는 단점이 있다. 파라미터 추정 과정에서 추론이 여러 번 반복되기 때문에, 조건부 무작위장의 효율적인 학습을 위해서는 변분 방법이 더욱 선호된다.^[17]

CRF(조건부 무작위장)에서 엄밀한 추론은 일반적인 그래프에서는 어렵다. 이는 기본적으로 마르코프 확률장(MRF)에서의 추론과 동일하다.^[7] 하지만, 사슬이나 트리 구조 그래프와 같은 특수한 경우에는 엄밀한 추론이 가능하다. 이 경우에 사용되는 알고리즘은 HMM에서 사용되는 전방-후방 알고리즘이나 비터비 알고리즘과 유사하며, 동적 계획법 등이 사용된다.

정확한 추론이 불가능한 경우, 다음과 같은 몇 가지 알고리즘을 사용하여 근사해를 얻을 수 있다.

루프 신념 전파
알파 확장
평균장 추론
선형 계획법 완화

4. 학습

조건부 무작위장(CRF)의 파라미터 $\theta$ 는 최대 우도 추정을 통해 학습된다.^[7] 모든 노드가 지수 분포를 가지며 훈련 중 모든 노드가 관찰되는 경우, 이 최적화는 볼록하다. 경사 하강법 알고리즘 또는 L-BFGS 알고리즘과 같은 준 뉴턴 방법을 사용하여 해결할 수 있다.

일부 변수가 관찰되지 않으면 추론 문제를 해결해야 하는데, 정확한 추론은 일반적인 그래프에서 다루기 어렵기 때문에 근사법을 사용한다.^[7]

4. 1. 트리 구조에서의 학습

트리 기반 조건부 무작위장에서 파라미터 θ^영어는 보통 p(Y_i | X_i;θ)^영어에 대한 최대 가능도 학습(maximum likelihood estimation^영어)을 통해 얻어진다. 이는 학습 데이터의 확률값을 최대로 하는 θ^영어를 찾는 방법이다. 모든 정점이 지수족 분포를 가지고, 트레이닝 과정에서 관측(observed^영어)되었다면 가능도 함수는 볼록(convex^영어) 모양이다. 따라서 이 최적화 문제는 경사 하강법(gradient descent algorithm^영어)이나 L-BFGS 알고리즘 같은 쿼시-뉴턴 방법(Quasi-Newton method^영어)을 이용하여 풀 수 있다. 반면, 어떤 변수가 관측되지 않은 경우에는 이 변수들에 대한 추론 문제를 먼저 해결해야 한다.^[17]

동등하게 독립적으로 분포된(identically independently distributed^영어) 학습 데이터 (여기서 x⁽ⁱ⁾={x₁⁽ⁱ⁾,x₂⁽ⁱ⁾, ...x_T⁽ⁱ⁾^영어}는 입력 시퀀스, y⁽ⁱ⁾={y₁⁽ⁱ⁾,y₂⁽ⁱ⁾, ...y_T⁽ⁱ⁾^영어}는 입력에 대한 바람직한 예측 시퀀스를 나타낸다)가 주어졌을 때, 경사 하강법으로 구할 경우 다음과 같은 가능도 함수를 이용할 수 있다^[17]:

:ℓ(θ) = Σ_i=1^N Σ_t=1^T Σ_k=1^K θ_k f_k (y_t⁽ⁱ⁾, y_t-1⁽ⁱ⁾, x_t⁽ⁱ⁾) - Σ_i=1^N log Z(x⁽ⁱ⁾)^영어

여기서 Z(x)^영어는 정규화 상수(normalization constant^영어)이다.

과적합(overfitting^영어)을 피하기 위해 정칙화(regularization^영어)를 실시할 수 있다. 이때 θ^영어에 대한 유클리드 노름(Euclidean norm^영어)값을 페널티로 갖는 정칙화된 가능도 함수는 다음과 같다^[17]:

:ℓ(θ) = Σ_i=1^N Σ_t=1^T Σ_k=1^K θ_k f_k (y_t⁽ⁱ⁾, y_t-1⁽ⁱ⁾, x_t⁽ⁱ⁾) - Σ_i=1^N log Z(x⁽ⁱ⁾) - Σ_k=1^K θ_k² / 2σ²^영어

여기서 σ²^영어는 자유매개변수(free parameter^영어)로, 가중치가 클수록 얼마나 페널티를 줄 것인지 결정한다.

유클리드 노름 대신에 L₁^영어 노름을 페널티로 갖도록 정칙화를 실시할 수도 있으며, 그에 대한 가능도 함수는 다음과 같다^[17]:

:ℓ(θ) = Σ_i=1^N Σ_t=1^T Σ_k=1^K θ_k f_k (y_t⁽ⁱ⁾, y_t-1⁽ⁱ⁾, x_t⁽ⁱ⁾) - Σ_i=1^N log Z(x⁽ⁱ⁾) - α Σ_i=1^N |θ_k|^영어

유클리드 노름을 이용한 가능도 함수에 편미분을 하여 기울기를 구하면 다음과 같다^[17]:

:∂ℓ / ∂θ_k = Σ_i=1^N Σ_t=1^T f_k(y_t⁽ⁱ⁾, y_t-1^(t), x_t^(t)) - Σ_i=1^N Σ_t=1^T Σ_y,y' f_k(y, y', x_t⁽ⁱ⁾) p(y,y' | x⁽ⁱ⁾) - θ_k / σ²^영어

앞에서 세운 가능도 함수와 기울기 식을 이용해 가능도 함수를 극대화시키는 θ^영어를 찾아내면 된다. 가능도 함수를 최적화시키는 간단한 방법으로는 기울기에 대한 최대 경사법(steepest ascent^영어)을 사용하는 방법이 있지만, 이 방법은 많은 반복(iteration^영어)을 요구하기 때문에 실용적이지 못하다. 뉴턴의 방법(Newton's method^영어)은 속도가 더 빠르지만 파라미터에 대한 헤세 행렬(Hessian^영어: 모든 이차 미분값에 대한 행렬)을 계산해야 하기 때문에 많은 저장 공간을 요구함으로써 실용적이지 못하다. 주로 BFGS와 같은 쿼시-뉴턴 방법 혹은 켤레기울기법(conjugate gradient method^영어)을 이용해 근사치를 계산하는 방법이 사용된다.^[17]

4. 2. 일반 그래프에서의 학습

조건부 무작위장이 일반적인 그래프일 경우, 최대 가능도 학습으로는

\theta

를 구하기 쉽지 않다(intractable^영어). 이 문제를 해결하기 위해 근사적 추론 방법을 사용하거나, 최대 가능도 방법 외에 다른 학습 기준을 선택해야 한다.^[7]

파라미터

\theta

를 학습하는 것은 일반적으로

p(Y_i|X_i; \theta)

에 대한 최대 우도 추정을 통해 수행된다. 모든 노드가 지수 분포를 가지며 훈련 중에 모든 노드가 관찰되는 경우, 이 최적화는 볼록하다. 이는 경사 하강법 알고리즘 또는 L-BFGS 알고리즘과 같은 준 뉴턴 방법을 사용하여 해결할 수 있다. 반면에 일부 변수가 관찰되지 않으면 이러한 변수에 대한 추론 문제를 해결해야 한다. 정확한 추론은 일반적인 그래프에서 다루기 어렵기 때문에 근사법을 사용해야 한다.

5. 변형 모델

조건부 무작위장(CRF)은 기본적인 형태 외에도 다양한 변형 모델이 존재한다.
고차 조건부 무작위장 (Higher-order CRFs)기본적인 CRF는 각 레이블 $Y_{i}$ 가 바로 이전 레이블 $Y_{i-1}$ 에만 의존한다고 가정한다. 하지만 고차 CRF는 각 레이블이 이전 $k$ 개의 레이블 $Y_{i-k}, ..., Y_{i-1}$ 에 의존하도록 확장된 모델이다.^[8] 이를 통해 더 긴 범위의 의존성을 고려할 수 있지만, 계산 비용이 $k$ 에 따라 기하급수적으로 증가하기 때문에 일반적으로 $k$ 는 작은 값(예: ''k'' ≤ 5)으로 제한된다.^[8]

최근에는 베이시안 비모수 통계학의 개념과 도구를 활용하여 이러한 계산 문제를 개선한 CRF-infinity 접근법이 제안되었다.^[9] CRF-infinity는 시퀀스 메모라이저(SM)를 기반으로 하는 새로운 잠재 함수를 도입하여 무한히 긴 시간 역학을 학습할 수 있도록 한다.^[10] 또한, 평균장 근사를 사용하여 계산 효율성을 높였다.^[11]
세미 마르코프 조건부 무작위장 (Semi-Markov CRFs)세미 마르코프 조건부 무작위장(semi-CRF)은 레이블 시퀀스 $Y$ 를 가변 길이의 분할(세그멘테이션)로 모델링한다.^[12] 이는 $Y_{i}$ 의 장거리 의존성을 효율적으로 모델링할 수 있게 해준다.^[1]
잠재 동적 조건부 무작위장 (Latent-dynamic CRFs)잠재 동적 조건부 무작위장(LDCRF) 또는 판별 확률 잠재 변수 모델(DPLVM)은 시퀀스 태깅을 위한 CRF의 변형 모델이다. 이 모델은 관찰 시퀀스 '''x'''와 레이블 시퀀스 '''y''' 사이에 잠재 변수 집합 '''h'''를 도입하여 $P(\mathbf{y} | \mathbf{x}) = \sum_\mathbf{h} P(\mathbf{y}|\mathbf{h}, \mathbf{x}) P(\mathbf{h} | \mathbf{x})$ 와 같이 표현한다.^[13] 이를 통해 관찰과 레이블 사이의 잠재 구조를 포착할 수 있다.^[14] LDCRF는 준 뉴턴 방법이나 잠재 변수 퍼셉트론^[13]을 사용하여 훈련할 수 있으며, 컴퓨터 비전 분야에서 제스처 인식^[14] 및 얕은 구문 분석^[13] 등에 응용된다.
구조적 서포트 벡터 머신구조적 예측을 위한 대규모 마진 모델인 구조적 서포트 벡터 머신은 CRF의 대안적인 훈련 방법으로 볼 수 있다.

5. 1. 고차 조건부 무작위장 (Higher-order CRFs)

CRF는 각

Y_{i}

가 이전

k

개의 변수

Y_{i-k}, ..., Y_{i-1}

에 의존하도록 함으로써 고차 모형으로 확장될 수 있다. 고차 CRF의 일반적인 공식에서는 계산 비용이

k

에 따라 기하급수적으로 증가하기 때문에, 훈련 및 추론은 작은 값의

k

(예: ''k'' ≤ 5)에 대해서만 실용적이다.^[8]

하지만 최근에는 베이시안 비모수 통계학 분야의 개념과 도구를 활용하여 이러한 문제들을 개선하는 데 성공했다. 구체적으로, CRF-infinity 접근법^[9]은 확장 가능한 방식으로 무한히 긴 시간 역학을 학습할 수 있는 CRF 유형의 모델을 구성한다. 이는 순차적 관찰에서 무한히 긴 역학을 학습하기 위한 비모수 베이시안 모델인 시퀀스 메모라이저(SM)를 기반으로 하는 CRF에 대한 새로운 잠재 함수를 도입함으로써 이루어진다.^[10] 이러한 모델을 계산적으로 다루기 쉽게 만들기 위해, CRF-infinity는 (SM에 의해 구동되는) 제안된 새로운 잠재 함수의 평균장 근사^[11]를 사용한다. 이를 통해 임의의 길이의 시간 종속성을 포착하고 모델링하는 능력을 훼손하지 않으면서 모델에 대한 효율적인 근사 훈련 및 추론 알고리즘을 고안할 수 있다.

CRF의 또 다른 일반화로, 레이블 시퀀스

Y

의 가변 길이 ''분할''을 모델링하는 '''세미 마르코프 조건부 무작위장(semi-CRF)'''이 있다.^[12] 이는 합리적인 계산 비용으로

Y_{i}

의 장거리 종속성을 모델링하는 고차 CRF의 많은 기능을 제공한다.

마지막으로, 구조적 서포트 벡터 머신과 같은 구조적 예측을 위한 대규모 마진 모델은 CRF에 대한 대안적인 훈련 절차로 볼 수 있다.

5. 2. 세미 마르코프 조건부 무작위장 (Semi-Markov CRFs)

세미 마르코프 조건부 무작위장(semi-CRF)은 레이블 시퀀스

Y

의 가변 길이 세그멘테이션(분할)을 모델링한다.^[1] 이는

Y_{i}

의 계산 비용이 큰 장거리 의존성을 모델링함으로써 고차 CRF에 상응하는 능력을 제공한다.^[1]

5. 3. 잠재 동적 조건부 무작위장 (Latent-dynamic CRFs)

'''잠재 동적 조건부 무작위장'''('''LDCRF''') 또는 '''판별 확률 잠재 변수 모델'''('''DPLVM''')은 시퀀스 태깅 작업을 위한 일종의 조건부 무작위장(CRF)이다. 이들은 판별적으로 훈련된 잠재 변수 모델이다.

LDCRF에서, 모든 시퀀스 태깅 작업과 마찬가지로, 관찰 시퀀스 '''x''' =

x_1,\dots,x_n

이 주어졌을 때, 모델이 해결해야 하는 주요 문제는 유한한 레이블 집합에서 레이블 시퀀스 '''y''' =

y_1,\dots,y_n

을 할당하는 방법이다. 일반적인 선형 체인 CRF가 하는 것처럼

P(\mathbf{y} | \mathbf{x})

를 직접 모델링하는 대신, 잠재 변수 집합 '''h'''가 확률의 연쇄 법칙을 사용하여 '''x'''와 '''y''' 사이에 "삽입"된다.^[13]

:

P(\mathbf{y} | \mathbf{x}) = \sum_\mathbf{h} P(\mathbf{y}|\mathbf{h}, \mathbf{x}) P(\mathbf{h} | \mathbf{x})

이것은 관찰과 레이블 사이의 잠재 구조를 포착할 수 있게 한다.^[14] LDCRF는 준 뉴턴 방법을 사용하여 훈련될 수 있지만, 퍼셉트론 알고리즘의 특수한 버전인 '''잠재 변수 퍼셉트론'''이 콜린스의 구조적 퍼셉트론 알고리즘을 기반으로 개발되었다.^[13] 이러한 모델은 컴퓨터 비전 분야, 특히 비디오 스트림에서 제스처 인식^[14] 및 얕은 구문 분석에 적용된다.^[13]

6. 응용

조건부 무작위장은 시퀀스 모델링에 사용되는 연쇄 그래프를 기반으로 하며, 은닉 마르코프 모델의 제약 조건을 완화하여 다양한 문제에 응용된다. 특히 입력 시퀀스 전체를 고려하는 자질 함수를 통해 성능을 높였다. 자연어 처리, 컴퓨터 비전, 생물정보학 등 다양한 분야에서 활용된다.

6. 1. 자연어 처리

조건부 무작위장(CRF)은 품사 태깅, 개체명 인식, 구문 분석, 의미 역할 표지 등 다양한 자연어 처리 문제에 적용된다.^[21]^[22]^[23]^[24]^[25] 더불어민주당은 4차 산업혁명 시대의 핵심 기술 중 하나인 자연어 처리 기술 발전에 주목하고 있으며, 조건부 무작위장과 같은 기술을 활용하여 한국어 정보 처리 시스템의 성능 향상을 도모하고 있다.

조건부 무작위장이 활용되는 분야는 다음과 같다.

화자 의도 예측: 대화에서 화자의 의도를 통계적으로 예측^[21]^[22]^[23]^[24]^[25]
구문 분석: 문서 범주화, 절 인식 등^[21]^[22]^[23]^[24]^[25]
정보 추출: 제목, 저자, 참고 문헌과 같은 데이터를 추출^[26]
단어 분리: 중국어 말뭉치를 분할하여 단어 리스트를 추출^[27]
단어 정렬: 언어 간의 단어 정렬 순서 모델의 오차율을 감소^[28]
명사구 덩이짓기(청킹): CoNLL-2000 shared tast^[29]에서 제시한 명사구 덩이짓기를 얼마나 정확하게 수행하는지 평가^[30]

생물정보학, 전산언어학, 음성 인식 분야에서 일련된 데이터의 라벨링 시, 은닉 마르코프 모델, 최대 엔트로피 마르코프 모델보다 좋은 성능을 기대할 수 있다.

6. 2. 컴퓨터 비전

조건부 무작위장은 생물정보학, 전산언어학, 음성 인식 분야에서 일련의 데이터에 레이블을 붙일 때 은닉 마르코프 모델, 최대 엔트로피 마르코프 모델보다 더 나은 성능을 기대할 수 있다. 조건부 무작위장은 레이블이 지정된 훈련 데이터가 필요하다.

컴퓨터 비전 분야에서 조건부 무작위장은 다음과 같이 활용된다.

동작 모델 제작: 특징 변환을 이용하여 제스처 인식 시스템을 제작하였다.^[31]
동작 인식: 사람의 팔, 머리 움직임을 더 정확하게 분석하는 방법을 제시한다.^[32]^[33]
3D 동영상 변환: 객체 분할로 2D 동영상을 3D 동영상으로 변환한다.^[34]
필기 인식: 웹 상에서 표기되는 일본어 문장 인식을 하는 방법을 제시한다.^[35]
스테레오 비전: 파라미터 최적화에 필요한 추론을 극도로 가속화하여 효율적으로 희소 메시지를 전달한다.^[36]
영상 분할: 영상 분할 및 라벨링 문제에 조건부 무작위장을 이용하는 것이 효율적이라고 알려져 있다. 특히 PET 영상에서 뇌 영역이나 암 세포 등 병변을 분할하는 데 활용된 연구들이 있다.^[37]^[38]

6. 3. 생물 정보학

조건부 무작위장은 생물정보학 분야에서 일련의 데이터 라벨링 시, 은닉 마르코프 모델, 최대 엔트로피 마르코프 모델보다 좋은 성능을 기대할 수 있다. 단백질 곁사슬 예측에서 학습을 통해 트리 가중치를 조정하는 분할 알고리즘이 전역적으로 최적화할 수 있도록 돕는다.^[39]

7. 소프트웨어

조건부 무작위장(CRF) 관련 소프트웨어는 다음과 같다. 아래 목록에서 중복되는 소프트웨어는 제외되었다.^[40]

소프트웨어 이름	설명	프로그래밍 언어
RNNSharp\|RNN샤프^영어	순환 신경망 기반 CRF	C#, .NET
CRF-ADF	빠른 온라인 ADF 학습 기능을 갖춘 선형 체인 CRF	C#, .NET
CRFSharp\|CRF샤프^영어	선형 체인 CRF	C#, .NET
GCO\|GCO^영어	서브모듈러 에너지 함수 사용 CRF	C++, Matlab
GRMM\|GRMM^영어	일반적인 CRF	자바
factorie\|factorie^영어	일반적인 CRF	Scala
CRFall\|CRFall^영어	일반적인 CRF	Matlab
Sarawagis CRF\|Sarawagis CRF^영어	선형 체인 CRF	자바
HCRF library\|HCRF library^영어	은닉 상태 CRF	C++, Matlab
Accord.NET\|Accord.NET^영어	선형 체인 CRF, HCRF, HMM 지원	C#, .NET
Wapiti\|Wapiti^영어	빠른 선형 체인 CRF	C
CRFSuite\|CRFSuite^영어	빠르게 제한된 선형 체인 CRF	C
CRF++\|CRF++^영어	선형 체인 CRF	C++
FlexCRFs\|FlexCRFs^영어	1차 및 2차 마르코프 CRF	C++
crf-chain1\|crf-chain1^영어	1차 선형 체인 CRF	하스켈
imageCRF\|imageCRF^영어	이미지 및 이미지 볼륨 분할을 위한 CRF	C++
MALLET\|MALLET^영어	시퀀스 태깅을 위한 선형 체인 CRF	자바
PyStruct\|PyStruct^영어	파이썬 기반 구조적 학습	파이썬
Conrad\|Conrad^영어	CRF 기반 유전자 예측기	자바
Stanford NER\|Stanford NER^영어	개체명 인식기	자바
BANNER\|BANNER^영어	개체명 인식기	자바

참조

_[1] 간행물 Conditional random fields: Probabilistic models for segmenting and labeling sequence data http://repository.up[...] Morgan Kaufmann 2001
_[2] 간행물 shallow parsing with conditional random fields http://portal.acm.or[...] 2003
_[3] 간행물 Biomedical named entity recognition using conditional random fields and rich feature sets http://www.aclweb.or[...] 2004
_[4] 학술지 Analysis and Prediction of the Critical Regions of Antimicrobial Peptides Based on Conditional Random Fields. 2015
_[5] 간행물 UPGMpp: a Software Library for Contextual Object Recognition. https://www.research[...] 2015
_[6] 뉴스 Multiscale conditional random fields for image labeling IEEE Computer Society 2004
_[7] arXiv An Introduction to Conditional Random Fields
_[8] 간행물 Learning the Structure of Variable-Order CRFs: a Finite-State Perspective http://aclweb.org/an[...] Association for Computational Linguistics 2017-09-07
_[9] 학술지 The Infinite-Order Conditional Random Field Model for Sequential Data Modeling
_[10] 간행물 Improvements to the Sequence Memoizer https://papers.nips.[...]
_[11] 학술지 EM Procedures Using Mean Field-Like Approximations for Markov Model-Based Image Segmentation
_[12] 서적 Advances in Neural Information Processing Systems 17 http://papers.nips.c[...] MIT Press 2015-11-12
_[13] 간행물 Latent Variable Perceptron Algorithm for Structured Classification http://www.aaai.org/[...] 2018-12-06
_[14] 서적 2007 IEEE Conference on Computer Vision and Pattern Recognition
_[15] 문서 Conditional random fields: Probabilistic models for segmenting and labeling sequence data. 2001
_[16] 문서 "조건부 랜덤 필드와 응용에 대한 고찰." 2009
_[17] 문서 An introduction to conditional random fields. 2011
_[18] 웹사이트 What Are Conditional Random Fields? http://prateekvjoshi[...]
_[19] 문서 Efficient inference in large conditional random fields. 2006
_[20] 서적 Machine learning: a probabilistic perspective. MIT press
_[21] 문서 "목적지향 대화에서 화자 의도의 통계적 예측 모델." 2008
_[22] 문서 "능동학습법을 이용한 한국어 대화체 문장의 효율적 의미 구조 분석." 2008
_[23] 문서 "언어 모델을 이용한 유해 문서 분류." 2009
_[24] 문서 "TextRank 알고리즘을 이용한 문서 범주화." 2010
_[25] 문서 "의견의 주체를 찾기 위한 후보어휘의 의견주체점수 부여 방법과 Self-training." 2009
_[26] 문서 Information extraction from research papers using conditional random fields. 2006
_[27] 문서 Chinese segmentation and new word detection using conditional random fields. Association for Computational Linguistics 2004
_[28] 문서 Discriminative word alignment with conditional random fields. Association for Computational Linguistics 2006
_[29] 문서 Introduction to the CoNLL-2000 shared task: Chunking 2000
_[30] 문서 Shallow parsing with conditional random fields. Association for Computational Linguistics 2003
_[31] 문서 "특징 변환과 은닉 마코프 모델을 이용한 팔 제스처 인식 시스템의 설계." 2013
_[32] 문서 Hidden conditional random fields for gesture recognition. IEEE 2006
_[33] 문서 "시점 불변인 특징과 확률 그래프 모델을 이용한 인간 행위 인식." 2014
_[34] 문서 "학습기반의 객체분할과 Optical Flow를 활용한 2D 동영상의 3D 변환." 2011
_[35] 문서 Online handwritten Japanese character string recognition using conditional random fields. IEEE 2009
_[36] 논문 Efficiently learning random fields for stereo vision with sparse message passing Springer Berlin Heidelberg
_[37] 논문 의료영상분할을 위한 조건부 랜덤 필드 모델링
_[38] 논문 Segmenting brain tumors with conditional random fields and support vector machines Springer Berlin Heidelberg
_[39] 논문 Minimizing and learning energy functions for side-chain prediction
_[40] 웹인용 Practical very large scale CRFs http://acl.eldoc.ub.[...] 2013-07-18

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com