맨위로가기

편차

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

편차는 관측값과 참값 또는 기대값 사이의 차이로, 오차를 나타낸다. 편차는 부호 있는 편차, 절대 편차로 구분되며, 절대 편차의 평균인 평균 편차 또는 평균 절대 편차, 최소 절대 편차(LAD) 등이 있다. 편차는 측정 척도의 단위를 가지며, 무차원화를 위해 척도로 나눌 수 있다. 표준 편차는 데이터 집합의 분산 척도로, 데이터의 퍼짐 정도를 나타낸다. 편차는 과학적, 사회과학적 예시에서 활용되며, 실험 결과의 정확도와 정밀도를 평가하는 데 도움을 준다.

더 읽어볼만한 페이지

  • 통계학 용어 - 퍼센트 포인트
    퍼센트포인트는 전체 비율을 나타내는 퍼센트와 달리 두 퍼센트 값의 차이를 나타내는 단위로, 경제 지표나 여론조사 등에서 명확한 정보 전달을 위해 중요하며 절대적 변화량을 나타낸다.
  • 통계학 용어 - 산포도
    산포도는 빈도분포에서 변량이 흩어진 정도를 나타내는 값으로, 데이터 간 차이가 클수록 커지며 표준 편차, 범위, 사분위 범위 등으로 측정하고, 물리학의 측정 오차나 생물학의 개체 차이 등 다양한 요인으로 발생한다.
  • 통계학 - 확률
    확률은 사건의 가능성을 수치화한 개념으로, 도박에서 시작되어 수학적으로 발전했으며, 다양한 해석과 요소, 응용 분야를 가지며 양자역학, 사회 현상 등에도 적용된다.
  • 통계학 - 사분위수
    사분위수는 정렬된 데이터를 4등분하는 세 개의 값으로 데이터 분포 요약 및 이상치 탐지에 활용되며, 제1사분위수(Q₁)는 하위 25%, 제2사분위수(Q₂ 또는 중앙값)는 하위 50%, 제3사분위수(Q₃)는 하위 75%를 나타낸다.
편차

2. 종류

편차에는 여러 종류가 있으며, 통계적 분산을 측정하는 데 사용된다.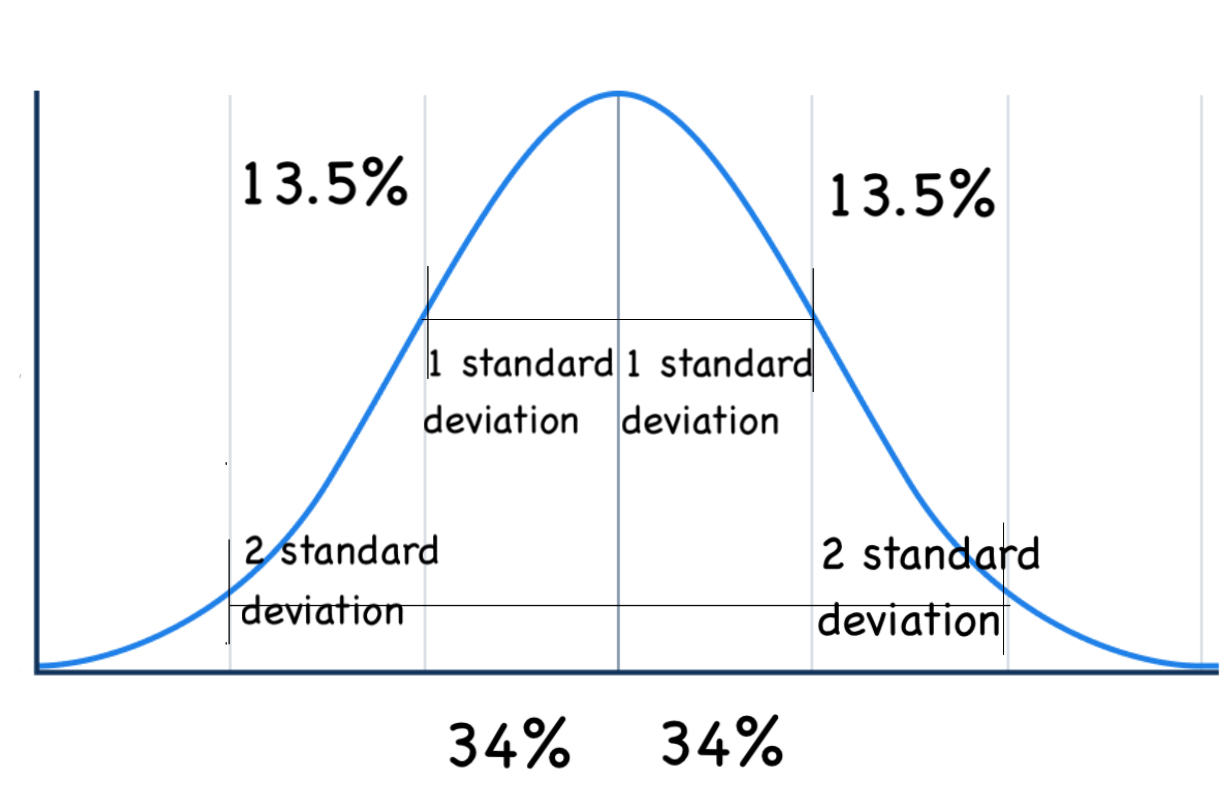

표준 편차에 따른 분포의 변화

  • '''표준 편차''': 데이터 집합의 퍼짐 정도를 나타내는 척도로, 개별 데이터가 평균에서 얼마나 떨어져 있는지 나타낸다. 제곱 편차를 사용하며, 극단적인 값에 민감하다.[7]
  • '''평균 절대 편차''': 각 데이터와 평균 간의 절대 차이를 평균하여 계산한다. 표준 편차보다 극단값의 영향을 덜 받는다.[8]
  • '''중간 절대 편차''': 중앙값을 사용하여 데이터의 퍼짐을 측정하는 통계이다. 각 데이터와 중앙값 간의 절대 차이의 중앙값을 계산한다. 이상값에 덜 민감하다.[9]
  • '''최대 절대 편차''': 개별 데이터와 평균 간의 최대 차이를 측정한다. 단일 극단값에 큰 영향을 받는다.[8]


편차는 측정 척도에 따라 단위를 가진다. (예: 길이는 미터, 피트) 편차를 무차원화하여 서로 다른 데이터 세트를 비교할 수 있다.

  • '''표준화''': 편차를 분산의 척도로 나눈다. (모집단 표준 편차 또는 표본 표준 편차 사용)
  • '''퍼센트 편차''': 관측값과 허용된 값의 차이를 허용된 값으로 나누고 100%를 곱한다.

예시

  • 특정 매질에서 소리 속도 측정: 이론값은 초당 343미터이다. 연구원 A는 340미터(-3미터 편차), 연구원 B는 345미터(+2미터 편차)를 측정했다.
  • 화학 반응: 예상 수율은 100g이다. 실험 1에서는 95g(-5g 편차), 실험 2에서는 102g(+2g 편차)을 얻었다.

2. 1. 부호 있는 편차 (Signed Deviation)

관심 대상의 관측값과 ''참값''(여기서 ''참값''은 모집단 평균과 같은 기대값을 나타냄) 사이의 차이는 오차이다.[2]

관측된 값과 실제 값의 추정치(예: 표본 평균)의 차이는 ''잔차''이다. 이러한 개념은 구간 척도 및 비율 척도 수준의 데이터에 적용할 수 있다.[3]

표준 점수는 평균으로부터의 편차 ÷ 표준 편차 × 10 + 50을 의미한다. 편차는 단순한 뺄셈의 결과이며 모집단에 따라 그 크기가 달라진다. 이러한 변동을 상쇄하여, 해당 요소가 모집단 내에서 얼마나 평균에서 벗어났는지를 나타내는 정도가 표준 점수이다.

2. 2. 절대 편차 (Unsigned or Absolute Deviation)

절대 편차(absolute deviation영어)는 편차의 절댓값을 의미한다. 기준값(평균이나 중앙값 등)과의 차이의 절댓값이다.[4] 통계학에서 절대 편차는 개별 데이터 포인트와 중심값(일반적으로 데이터 집합의 평균 또는 중앙값) 간의 전체 차이를 측정하는 지표이다. 각 데이터 포인트와 중심값 간의 차이의 절대값을 구한 다음 이러한 절대 차이를 평균하여 결정된다.[4]

절대 편차의 수식은 다음과 같이 표현된다.

:D_i = |x_i - m(X)|,

  • ''Di''는 절대 편차
  • ''xi''는 데이터 요소
  • ''m''(''X'')는 데이터 집합의 선택된 중심 경향성 측정값으로, 때로는 평균(\overline{x})이지만, 대부분 중앙값이다.

3. 요약 통계량

표준 점수는 평균으로부터의 편차를 표준 편차로 나눈 값에 10을 곱하고 50을 더한 것이다. 편차는 단순한 뺄셈의 결과이며 모집단에 따라 그 크기가 달라진다. 표준 점수는 이러한 변동을 상쇄하여, 해당 요소가 모집단 내에서 얼마나 평균에서 벗어났는지를 나타낸다.

절대 편차는 편차의 절댓값을 의미한다. 이는 기준값(평균이나 중앙값)과의 차이의 절대값이다.

평균 편차(mean deviation, average deviation) 또는 평균 절대 편차(mean absolute deviation, average absolute deviation)는 절대 편차의 평균이다. 이는 기준값과 측정값의 차이에 대한 절대값의 평균이며, 일반적으로 기준값으로 평균을 사용한다.[3]

표준 편차는 데이터의 산포도를 나타내는 지표이다. 원래 데이터 값들의 평균을 바꾸지 않고 절대 편차를 일정 값으로 재설정했을 때 (데이터 크기가 홀수일 때는 같은 데이터를 덧붙여 짝수로 만듦), 두 편차 벡터의 유클리드 노름이 같아지는 값을 의미한다. 표준 편차는 편차의 일부가 아니며, 값이 모두 유리수여도 표준 편차는 평균 편차와 달리 무리수가 되는 경우가 많다. 표준 편차는 항상 평균 편차 이상이다.

3. 1. 평균 부호 편차 (Mean Signed Deviation)

편향되지 않은 추정량의 경우, 관찰되지 않은 모집단 모수 값에서 모든 관측치 집합 전체에 걸친 부호 있는 편차의 평균은 임의로 큰 수의 표본에 걸쳐 0으로 평균화된다. 그러나 구성상 표본 평균 값에서 값의 부호 있는 편차의 평균은 항상 0이지만, 표본 중앙값과 같은 다른 중심 경향성 측정값의 평균 부호 있는 편차는 0일 필요는 없다.

부호 있는 평균 편차는 일반적으로 평균과 같은 중심점에서 일련의 값의 평균 편차를 평가하는 데 사용되는 통계적 척도이다. 각 데이터 지점과 데이터 집합의 평균 간의 부호 있는 차이의 산술 평균을 구하여 계산한다.

"부호 있는"이라는 용어는 편차가 해당 부호와 함께 고려됨을 나타내며, 이는 편차가 평균보다 높거나 낮은지 여부를 의미한다. 양의 편차(평균 이상)와 음의 편차(평균 이하)가 계산에 포함된다. 부호 있는 평균 편차는 평균에서 데이터 지점의 평균 거리와 방향을 측정하여 데이터의 전반적인 추세와 분포에 대한 통찰력을 제공한다.[3]

3. 2. 분산 (Dispersion)

통계학에서 절대 편차는 개별 데이터 포인트와 중심값(일반적으로 데이터 집합의 평균 또는 중앙값) 간의 차이를 측정하는 지표이다. 각 데이터 포인트와 중심값 간의 차이의 절대값을 구한 다음 이러한 절대 차이를 평균하여 결정된다.[4] 수식은 다음과 같이 표현된다.

: D_i = |x_i - m(X)|

  • `D_i`는 절대 편차
  • `x_i`는 데이터 요소
  • `m(X)`는 데이터 집합의 중심 경향성 측정값 (때로는 평균(\overline{x})이지만, 대부분 중앙값)

평균 절대 편차(AAD)는 중심값(일반적으로 평균 또는 중앙값)을 중심으로 한 데이터 포인트 집합의 분산 또는 퍼짐을 나타내는 척도이다. 각 데이터 포인트와 선택된 중심값 간의 절대 차이의 평균을 구하여 계산된다. AAD는 데이터 집합에서 중심값으로부터의 전형적인 편차의 크기를 측정하여 데이터의 전반적인 변동성에 대한 통찰력을 제공한다.[5]
최소 절대 편차(LAD)는 선형 모델의 계수를 추정하기 위해 회귀 분석에 사용되는 통계적 방법이다. 관찰된 값과 예측된 값 사이의 제곱 수직 거리(잔차)의 합을 최소화하는 보다 일반적인 최소 제곱 방법과 달리, LAD 방법은 절대 수직 거리의 합을 최소화한다.

선형 회귀의 맥락에서, (''x''1,''y''1), (''x''2,''y''2), ...이 데이터 포인트이고, ''a''와 ''b''가 선형 모델에 대해 추정할 계수라면

:y= b + (a * x)

최소 절대 편차 추정값(''a''와 ''b'')은 합을 최소화하여 얻는다.

LAD 방법은 왜곡되거나 헤비테일(heavy-tailed) 잔차 분포가 있는 경우 최소 제곱 방법에 비해 이상치에 덜 민감하여 강력한 회귀 기법이 된다.[6]

통계적 분산을 측정하는 데는 편차 분포에 대한 통계가 사용된다.

  • 표준 편차는 데이터 집합의 퍼짐 또는 분산에 대한 널리 사용되는 척도이다. 이는 데이터 집합의 평균으로부터 개별 데이터 포인트의 변동 또는 편차의 평균량을 정량화한다. 표준 편차는 제곱 편차를 사용하며 바람직한 속성을 가지고 있다. 표준 편차는 극단적인 값에 민감하므로 강건하지 않다.[7]
  • 평균 절대 편차는 극단적인 값의 영향을 덜 받는 데이터 집합의 분산에 대한 척도이다. 각 데이터 포인트와 평균 간의 절대 차이를 구하고, 이러한 절대 차이를 합한 다음 관측 횟수로 나누어 계산한다. 이 메트릭은 표준 편차에 비해 더욱 강건한 변동성 추정치를 제공한다.[8]
  • 중간 절대 편차는 평균 대신 중앙값을 사용하여 데이터 집합의 퍼짐을 측정하는 강건한 통계이다. 각 데이터 포인트와 중앙값 간의 절대 차이를 구한 다음, 이러한 절대 차이의 중앙값을 계산하여 계산한다. 따라서 중간 절대 편차는 이상값에 덜 민감하므로 표준 편차의 강력한 대안을 제공한다.[9]
  • 최대 절대 편차는 개별 데이터 포인트와 데이터 집합의 평균 간의 최대 차이를 측정하는 간단한 척도이다. 그러나 단일 극단값의 영향을 과도하게 받을 수 있으므로 매우 강건하지 않다. 이 메트릭은 이상값을 포함하는 데이터 집합을 처리할 때 분산에 대한 신뢰할 수 있는 척도를 제공하지 못할 수 있다.[8]

4. 정규화 (Normalization)

관측값과 기준점 간의 차이를 측정하는 편차는 기본적으로 사용된 측정 척도의 단위를 가진다. 예를 들어 길이를 측정하는 경우 편차는 미터 또는 피트와 같은 단위로 표현된다. 편차를 단위가 없게 만들고 서로 다른 데이터 세트 간의 비교를 쉽게 하기 위해 무차원화할 수 있다.

일반적인 한 가지 방법은 편차를 척도([통계적 분산])의 척도로 나누는 것이다. 표준화를 위해 모집단 표준 편차를 사용하거나 학생화를 위해 표본 표준 편차를 사용한다([학생화 잔차]] 등).[10]

무차원화에 대한 또 다른 접근 방식은 분산보다는 위치에 따라 척도를 조정하는 데 중점을 둔다. 퍼센트 편차는 관측값과 허용된 값의 차이를 허용된 값으로 나누고 100%를 곱하여 계산한다. 허용된 값을 기준으로 편차의 척도를 조정함으로써, 이 방법은 편차를 백분율로 표현하여 관측값과 허용된 값의 상대적 차이에 대한 명확한 관점을 제공한다. 두 가지 무차원화 방법 모두 편차를 비교 가능하고 특정 측정 단위 이상으로 해석 가능하게 하는 역할을 한다.[10]

5. 예시

특정 매질에서 소리의 속도를 측정한 경우, 이론적으로 예상되는 값은 초당 343미터이다. 여러 연구자가 측정을 수행했을 때, 연구원 A는 초당 340미터(-3미터 편차), 연구원 B는 초당 345미터(+2미터 편차)로 측정했다. 화학 반응에서 특정 화합물 100g이 생성될 것으로 예상되는 경우, 실제 실험에서 실험 1은 95g(-5g 편차), 실험 2는 102g(+2g 편차)의 수득량을 보였다.

5. 1. 과학적 예시

예시로, 특정 매질에서 소리의 속도를 측정한 경우가 있다. 이론적 계산에 따르면 이 매질에서 소리의 속도는 초당 343미터로 예상된다.

실험에서 여러 연구자가 측정을 수행했다. 연구원 A는 소리의 속도를 초당 340미터로 측정하여 예상 값에서 초당 -3미터의 편차를 보였다. 반면, 연구원 B는 속도를 초당 345미터로 측정하여 +2미터의 편차를 보였다.

이러한 과학적 맥락에서 편차는 개별 측정값이 이론적으로 예측되거나 허용되는 값과 얼마나 다른지 정량화하는 데 도움이 된다. 실험 결과의 정확도와 정밀도에 대한 통찰력을 제공하여, 연구자가 데이터의 신뢰성을 평가하고 불일치에 영향을 주는 요인을 식별할 수 있도록 한다.

또 다른 예로, 화학 반응에서 화학량론에 따라 특정 화합물 100g이 생성될 것으로 예상된다고 가정해 보자. 그러나 실제 실험실 실험에서는 서로 다른 조건에서 여러 번의 실험이 수행된다.

실험 1에서 실제 수득량은 95g으로 측정되어 예상 수득량에서 -5g의 편차가 발생했다. 실험 2에서 실제 수득량은 102g으로 측정되어 +2g의 편차가 발생했다. 예상 값에서 이러한 편차는 서로 다른 조건에서 화학 반응의 효율성과 재현성에 대한 귀중한 정보를 제공한다.

과학자들은 이러한 편차를 분석하여 반응 조건을 최적화하고, 잠재적인 오류 원인을 식별하며, 공정의 전반적인 수득량과 신뢰성을 향상시킬 수 있다. 편차의 개념은 실험 결과의 정확성을 평가하고 과학 실험의 결과를 개선하기 위한 정보에 입각한 결정을 내리는 데 매우 중요하다.

5. 2. 사회과학적 예시

표준 점수란, 평균으로부터의 편차 ÷ 표준 편차 × 10 + 50을 의미한다.[1] 편차는 단순한 뺄셈의 결과이며 모집단에 따라 그 크기가 달라진다.[1] 이러한 변동을 상쇄하여, 해당 요소가 모집단 내에서 얼마나 평균에서 벗어났는지를 나타내는 정도가 표준 점수이다.[1]

참조

[1] 논문 Standard deviation and standard error of the mean http://dx.doi.org/10[...] 2015
[2] 논문 The mean and standard deviation: what does it all mean? https://doi.org/10.1[...] 2004-06
[3] 서적 The Oxford Dictionary Of Statistical Terms http://dx.doi.org/10[...] Oxford University Press, Oxford 2003-08-07
[4] 논문 Mean-absolute deviation model http://www.tandfonli[...] 2005-10-01
[5] 논문 The mean and median absolute deviations https://www.scienced[...] 2001-10-01
[6] 논문 A counterexample to a conjecture concerning the Hall-Wellner band http://dx.doi.org/10[...] 1996-04-01
[7] 웹사이트 2. Mean and standard deviation https://www.bmj.com/[...] 2020-10-28
[8] 논문 The mean and median absolute deviations https://www.scienced[...] 2001-10-01
[9] 서적 Probability, Statistics and Other Frightening Stuff https://books.google[...] Routledge 2018-10-09
[10] 서적 Statistics Norton 2007


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com