절댓값
"오늘의AI위키" 는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다."오늘의AI위키" 의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차 보기/숨기기
2. 정의
임의의 실수 x 에 대해, '''절댓값''' 또는 '''모듈러스'''는 |x| 로 표기하며부호 를 제거한 값, 즉 0 또는 양수 값으로 정의된다. 해석기하학 적 관점에서 실수의 절댓값은 실수선 위에서 그 수가 나타내는 점과 원점(0) 사이의 거리 를 의미한다.복소수 의 경우, 실수의 절댓값 정의를 직접 적용하기 어렵기 때문에 기하학적 의미를 확장하여 정의한다. 복소수 z 의 절댓값 |z| 는 복소평면 에서 원점으로부터 복소수 z 가 나타내는 점까지의 유클리드 거리 로 정의된다.
2. 1. 실수의 절댓값
실수선 위에서, 실수 -3과 실수 0 사이의 거리는 3이다. 실수 x\in\mathbb R 의 '''절댓값''' |x|\in[0,\infty) 은 여러 방식으로 정의될 수 있다.|x| = -x 는 x 의 반수이다. 이 정의에 따르면, 실수의 절댓값은 그 실수의 숫자 부분만 남기고 부호를 제거하여 얻는, 영 또는 양수인 값이다. 즉, 절댓값은 절대로 음수가 될 수 없다. 만약 x 자체가 음수(x < 0 )라면, 그 절댓값 |x| 은 -x 로 정의되므로 반드시 양수가 된다(|x|=-x>0 ).제곱근 을 이용하는 것이다. 실수의 절댓값은 그 실수를 제곱 한 값의 주 제곱근과 같다.|x| = \sqrt{x^2} x^2 의 두 제곱근(x 와 -x ) 중 음수가 아닌 값을 택하는 것과 같으므로 위의 정의와 동일하다.해석기하학 적인 관점에서 보면, 실수의 절댓값은 실수선 위에서 그 실수가 나타내는 점과 원점(0) 사이의 거리 를 의미한다.a 와 b 의 차의 절댓값 |a-b| 는 실수선 위에서 두 실수 a 와 b 사이의 거리를 나타낸다. 수학에서 추상적인 거리 함수 개념은 이러한 절댓값 차이를 일반화한 것으로 볼 수 있다.a , b 는 임의의 실수).성질 설명 >a| \ge 0 비음성: 절댓값은 항상 0보다 크거나 같다. >a| = 0 \iff a = 0 양의 정부호성: 절댓값이 0인 경우는 실수가 0일 때뿐이다. >ab| = \left|a\right| \left|b\right| 곱셈성: 두 실수의 곱의 절댓값은 각각의 절댓값의 곱과 같다. >a+b| \le |a| + |b| 준가법성 (삼각 부등식 ): 두 실수의 합의 절댓값은 각각의 절댓값의 합보다 작거나 같다.
s \cdot x\leq |x| (단, s=\pm 1 )라는 사실을 이용하여 증명할 수 있다. 즉, |a+b|=s \cdot (a+b) = s \cdot a + s \cdot b \leq |a| + |b| 가 성립한다.\bigl| \left|a\right| \bigr| = |a| || 멱등성 : 절댓값의 절댓값은 원래의 절댓값과 같다.\left|-a\right| = |a| || 우함수: 절댓값 함수는 y축에 대해 대칭 이다.|a - b| = 0 \iff a = b || 항등식 : 두 실수의 차의 절댓값이 0이면 두 실수는 같다 (양의 정부호성과 동치).|a - b| \le |a - c| + |c - b| || 삼각 부등식 : 세 실수 a, b, c 에 대해 성립한다 (준가법성과 동치).\left|\frac{a}{b}\right| = \frac
\ (b \ne 0 일 때) || 나눗셈의 보존: 나눗셈의 절댓값은 절댓값의 나눗셈과 같다 (곱셈성과 동치).|a-b| \geq \bigl| \left|a\right| - \left|b\right| \bigr| || 역삼각 부등식: 두 실수의 차의 절댓값은 각각의 절댓값의 차보다 크거나 같다 (준가법성과 동치).부등식 동치 조건 >a| \le b -b \le a \le b >a| \ge b a \le -b\ 또는 a \ge b
|x-3| \le 9 라는 부등식은 -9 \le x-3 \le 9 와 같고, 이를 풀면 -6 \le x \le 12 를 얻는다.부호 를 제거한 값, 즉 |x|:=\max\{x,-x\} 로 정의되거나, 원점으로부터의 거리 인 |x|:=\sqrt{x^2} 로 정의될 수 있으며
2. 2. 복소수의 절댓값
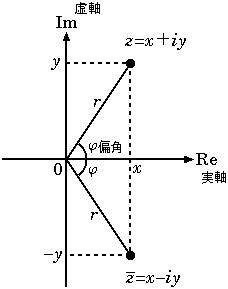
는 원점(0)으로부터 z 까지의 거리 r 과 같다. 복소수 z = a + bi (여기서 a, b 는 실수 )의 '''절댓값''' |z| 는 음이 아닌 실수값으로, 다음과 같이 정의된다.|z| = \sqrt{a^2 + b^2} a = \operatorname{Re}z 는 z 의 실수부, b = \operatorname{Im}z 는 z 의 허수부이다.복소평면 위에서 복소수 z 의 절댓값 |z| 는 원점으로부터 점 z 까지의 유클리드 거리 와 같다. 이는 피타고라스 정리 를 이용하여 \sqrt{a^2 + b^2} 로 계산할 수 있다.x 는 허수부가 0인 복소수 x + 0i 로 볼 수 있으므로, 복소수로서의 절댓값은 |x| = \sqrt{x^2 + 0^2} = \sqrt{x^2} 가 되어 실수 절댓값의 정의와 같다. 따라서 복소수의 절댓값은 실수의 절댓값을 일반화한 개념이라고 할 수 있다.복소평면 위에서, 복소수 z 와 그 켤레 복소수 \bar z 는 실수축에 대해 대칭이며, 원점으로부터의 거리가 같으므로 절댓값이 같다. z 와 그 켤레 복소수 \bar z = a - bi 는 같은 절댓값을 가진다. 즉, |z| = |\bar z| 이다. 또한, z 와 \bar z 의 곱은 다음과 같이 항상 음이 아닌 실수가 되며, 이는 절댓값의 제곱과 같다.z \bar z = (a+bi)(a-bi) = a^2 - (bi)^2 = a^2 + b^2 = |z|^2 |z| = \sqrt{z \bar z} 로도 표현할 수 있다.z 를 극형식 z = r(\cos\theta + i\sin\theta) = r e^{i\theta} (여기서 r = |z| \ge 0 이고 \theta 는 편각)으로 나타낼 때, 절댓값 |z| 는 r 과 같다.
3. 성질
실수 x 의 '''절댓값'''은 |x| 로 표기하며, 다음과 같이 정의된다.|x| = x 의 절댓값은 항상 양수 또는 0이며, 음수 가 될 수 없다. 해석기하학 적으로 실수의 절댓값은 수직선 위에서 0으로부터 그 수까지의 거리 를 나타낸다. 일반적으로 두 실수의 차의 절댓값(|a-b| )은 두 실수 사이의 거리를 의미한다.제곱근 을 이용하여 |x| = \sqrt{x^2} 와 같이 정의할 수도 있다.a, b 는 실수).
성질 설명 >a| \ge 0 비음성 >a| = 0 \iff a = 0 양의 정부호성 (비퇴화성) >ab| = |a 곱셈성 >a+b| \le |a| + |b| 삼각 부등식
\bigl| |a| \bigr| = |a| || 멱등성|-a| = |a| || 짝함수 성질|a - b| = 0 \iff a = b || 항등 관계|a - b| \le |a - c| + |c - b| || 삼각 부등식의 다른 형태\left|\frac{a}{b}\right| = \frac
(단, b \ne 0 ) || 나눗셈의 보존|a-b| \ge \bigl| |a| - |b| \bigr| || 역삼각 부등식|a| \le b \iff -b \le a \le b |a| \ge b \iff a \le -b \text{ 또는 } a \ge b 복소수 z = x + iy (여기서 x, y 는 실수)의 절댓값은 복소평면 에서 원점 (0, 0) 으로부터 점 (x, y) 까지의 유클리드 거리 로 정의된다. 피타고라스 정리 에 의해 다음과 같이 계산된다.|z| = \sqrt{x^2 + y^2} \operatorname{Re}(z)=x 는 z 의 실수부, \operatorname{Im}(z)=y 는 허수부를 나타낸다. 만약 z 가 실수이면 (y=0 ), 이 정의는 실수의 절댓값 정의와 일치한다.z 를 극형식 z = r e^{i \theta} 로 나타내면, 절댓값은 |z| = r 이다. 또한, 복소수와 그 켤레 복소수 \bar z = x - iy 의 곱을 이용하여 절댓값을 다음과 같이 표현할 수도 있다.|z| = \sqrt{z \bar z} z, w 에 대해 다음이 성립한다.|z| \ge 0 |z| = 0 \iff z = 0 |zw| = |z||w| |z+w| \le |z| + |w| 3. 1. 부등식
실수 의 절댓값을 포함하는 몇 가지 기본적인 부등식 과 그 해는 다음과 같다. (a 는 실수 )|x| \le a \iff -a \le x \le a |x| < a \iff -a < x < a |x| > a \iff x > a \text{ 또는 } x < -a |x| \ge a \iff x \ge a \text{ 또는 } x \le -a a \ge 0 인 경우에만 해가 존재하거나 의미를 가진다. 만약 a < 0 이면,|x| \le a 와 |x| < a 의 해는 존재하지 않는다 (공집합 \varnothing ). 왜냐하면 절댓값은 항상 0 이상이기 때문이다.|x| > a 와 |x| \ge a 는 모든 실수 x 에 대해 항상 성립한다.|x-3| \le 9 를 푸는 과정은 다음과 같다.|x-3| \le 9 는 -9 \le x-3 \le 9 와 동치이다.-9 + 3 \le x - 3 + 3 \le 9 + 3 -6 \le x \le 12 |x-3| \le 9 의 해는 -6 \le x \le 12 이다.3. 2. 항등식
실수 와 복소수 의 절댓값은 곱셈과 나눗셈 연산을 보존하는 다음과 같은 중요한 항등식 을 만족시킨다.실수 a, b 에 대하여: : |ab| = |a||b| (곱셈에 대한 동질성) : \left|\frac{a}{b}\right| = \frac\ (단, b \ne 0 ) (나눗셈의 보존)복소수 z, w 에 대하여: : |zw|=|z||w| : |z/w|=|z|/|w|\qquad (단, w\ne0 ) 멱등성: 절댓값을 여러 번 취해도 결과는 같다. : 실수 a 에 대해 \bigl| |a| \bigr| = |a| : 복소수 z 에 대해 ||z||=|z| 짝함수 성질 (반사 대칭): 부호가 반대인 수의 절댓값은 같다. : 실수 a 에 대해 |-a| = |a| : 복소수 z 에 대해 |-z|=|z| 켤레 복소수 와의 관계: 복소수와 그 켤레 복소수는 같은 절댓값을 가진다.: 복소수 z 에 대해 |\bar z|=|z| 3. 3. 미분
실수의 절댓값 함수 는 모든 점에서 연속 함수 이지만, 에서 미분 가능하지 않다. 이는 에서 그래프가 뾰족한 점을 가지기 때문이다. 인 모든 실수 에 대해서는 미분 가능하며, 그 도함수는 부호 함수 또는 계단 함수 로 주어진다.\frac{d}{dx}|x| = \frac{x} = \sgn x = \begin{cases} -1 & x < 0 \\ 1 & x > 0 \end{cases}연속 함수 의 예시이다.이계도함수 는 을 제외한 모든 곳에서 0이다. 에서는 이계도함수가 존재하지 않는다. 일반화 함수 이론에서는 절댓값 함수의 이계도함수를 디랙 델타 함수 의 2배로 정의하기도 한다.복소수 절댓값 함수 는 복소 평면 전체에서 연속 함수 이지만, 어떤 점에서도 복소 미분 가능하지 않다.코시-리만 방정식 을 만족하지 않기 때문이다.연쇄 법칙 을 이용하여 절댓값이 포함된 함수의 도함수를 구할 수 있다.절댓값 함수 내부에 다른 함수 가 있는 경우: {d \over dx} |f(x)| = \frac{f(x)} f'(x) \qquad (f(x) \ne 0){d \over dx} f(|x|) = \frac{x} f'(|x|) \qquad (x \ne 0)360px
4. 응용
실수의 절댓값 개념은 다양한 수학적 영역으로 확장되어 응용된다. 대표적으로 복소수 의 크기를 나타내는 데 사용된다. 실수는 전순서 를 이루지만 복소수는 그렇지 않으므로, 실수의 절댓값 정의를 복소수에 직접 적용하기는 어렵다. 그러나 절댓값을 원점으로부터의 거리로 해석하는 기하학적 관점은 일반화될 수 있다.복소수 의 절댓값은 복소평면 에서 해당 복소수가 나타내는 점과 원점 사이의 유클리드 거리 로 정의된다. 이는 복소수를 극형식으로 표현할 때 그 크기(거리)를 나타내는 핵심 요소가 된다.거리 를 정의하는 기본적인 도구로 사용된다. 두 실수 또는 두 복소수의 차의 절댓값은 각각 실수선 또는 복소평면 위에서 두 점 사이의 거리를 나타낸다. 이러한 절댓값을 이용한 거리 정의는 더 추상적인 거리 공간 의 개념으로 일반화되며, 해석학 등 여러 수학 분야의 기초를 이룬다. 나아가 절댓값은 벡터 공간에서 벡터의 '크기'나 '길이'를 측정하는 노름의 개념과도 밀접하게 연관되어 노름 공간 이론의 바탕이 되기도 한다.
4. 1. 복소수의 극형식
0이 아닌 복소수 에 대하여, 절댓값은 복소수가 원점으로부터 떨어진 거리, 편각 은 복소수가 가로축으로부터 회전한 각도를 뜻한다. 따라서 0이 아닌 복소수는 절댓값과 편각으로부터 유일하게 결정된다. 구체적으로, 복소수 z\ne0 는 절댓값 |z| 과 편각 \operatorname{arg}z 을 사용하여 다음과 같은 꼴로 나타낼 수 있으며, 이를 복소수의 극형식 이라고 한다.z=|z|(\cos\operatorname{arg}z+i\sin\operatorname{arg}z)=|z|e^{i\operatorname{arg}z} 실수 의 절댓값 정의는 실수가 전순서 를 이루지만 복소수는 그렇지 않으므로 복소수에 직접 적용될 수 없다. 그러나 실수 절댓값의 기하학적 의미인 원점으로부터의 거리는 복소수로 일반화될 수 있다. 복소수의 절댓값은 복소평면 에서 해당 점의 원점으로부터의 유클리드 거리 로 정의되며, 피타고라스 정리 를 사용하여 계산할 수 있다. 임의의 복소수 z = x + iy (여기서 x 와 y 는 실수)에 대해, z 의 절댓값 또는 모듈러스 는 |z| 로 표기하며 다음과 같이 정의된다.|z| = \sqrt{\operatorname{Re}(z)^2 + \operatorname{Im}(z)^2}=\sqrt{x^2 + y^2} \operatorname{Re}(z)=x 는 z 의 실수부, \operatorname{Im}(z)=y 는 허수부를 나타낸다. 허수부 y 가 0일 때, 즉 z 가 실수일 때 이 정의는 실수의 절댓값 정의와 일치한다. z 를 가우스 평면 위의 점으로 해석하면, |z| 는 원점으로부터 z 까지의 거리이다.z 가 극형식으로 z = r e^{i \theta} 로 표현될 때, 그 절댓값은 |z| = r 이다.z 와 그의 켤레 복소수 \bar z = x - iy 는 같은 절댓값을 가진다(|z| = |\bar{z}| ). 또한, z 와 \bar z 의 곱은 항상 음이 아닌 실수 z \cdot \overline{z} = x^2 + y^2 이므로, 복소수 z 의 절댓값은 z \cdot \overline{z} 의 제곱근으로도 표현할 수 있다.|z| = \sqrt{z \cdot \overline{z}} |x| = \sqrt{x^2} 를 일반화한 것이다. 이 관계식 |z|^2 = z\bar{z} 는 절댓값 제곱 또는 제곱 모듈러스 라고도 불린다. 복소수의 절댓값은 실수의 절댓값과 기본적인 성질들을 공유한다.4. 2. 거리 공간 구조
실수의 절댓값이 실수선 위에서 원점(0)과의 거리를 나타내듯이, 두 실수 x, y 사이의 거리 d(x, y) 는 절댓값을 사용하여 다음과 같이 정의할 수 있다.d(x, y) = |x - y| 복소수 의 절댓값이 복소평면 위에서 원점과의 거리를 나타내듯이, 두 복소수 z, w 사이의 거리 d(z, w) 는 절댓값을 사용하여 다음과 같이 정의할 수 있다.d(z, w) = |z - w| = \sqrt{(\operatorname{Re}z - \operatorname{Re}w)^2 + (\operatorname{Im}z - \operatorname{Im}w)^2} 피타고라스 정리 를 적용한 결과와 같다.거리 개념과 밀접하게 연관되어 있다. 실수 또는 복소수의 절댓값은 각각 실수선 또는 복소평면에서 원점으로부터의 거리를 의미하며, 두 실수 또는 복소수의 차의 절댓값은 두 수 사이의 거리를 나타낸다.유클리드 공간 에서의 표준적인 유클리드 거리 와 일치한다. 예를 들어, 1차원 유클리드 공간(실수선)에서 두 점 a_1, b_1 사이의 거리는 다음과 같다.|a_1 - b_1| = \sqrt{(a_1 - b_1)^2} 복소평면 )에서 두 점 a = a_1 + i a_2 와 b = b_1 + i b_2 사이의 거리는 다음과 같다.|a - b| = |(a_1 - b_1) + i(a_2 - b_2)| = \sqrt{(a_1 - b_1)^2 + (a_2 - b_2)^2} 거리 함수 의 개념으로 이어진다. 집합 X 위의 거리 함수 d 는 다음 네 가지 공리를 만족하는 실수값 함수이다.성질 공리 비음성 d(a, b) \ge 0 동일성 d(a, b) = 0 \iff a = b 대칭성 d(a, b) = d(b, a) 삼각 부등식 d(a, b) \le d(a, c) + d(c, b)
d(x, y) = |x - y| 는 이러한 거리 함수의 모든 공리를 만족하므로, 실수 집합 \mathbb R 또는 복소수 집합 \mathbb C 위에 거리 공간 구조를 부여한다. 즉, 절댓값은 실수를 1차원 거리 공간 으로, 복소수를 2차원 거리 공간으로 만드는 기본적인 도구이다. 더 나아가, 절댓값은 노름 공간 구조를 정의하며, 모든 노름 공간은 자연스럽게 거리 공간 구조를 갖는다.
5. 관련 개념
절댓값의 개념은 수학의 여러 분야에서 더 일반적인 형태로 확장될 수 있다. 대표적인 예로는 벡터 공간 에서 벡터의 '크기'나 '길이'를 일반화한 노름과, 정역 위에서 정의되는 정역 위의 절댓값이 있다. 이러한 일반화된 개념들은 함수해석학 , 대수학 , 수론 등 다양한 수학 분야에서 중요한 도구로 사용된다.
5. 1. 노름
노름은 벡터 공간 에서 벡터의 '크기'나 '길이'를 측정하는 개념으로, 실수 나 복소수 의 절댓값 개념을 일반화한 것이다. 실수체 \mathbb{R} 또는 복소수체 \mathbb{C} 를 스칼라 체 F 로 가지는 벡터 공간 V 위에 정의된 함수 \|\cdot\|: V \to \mathbb{R} 가 다음 네 가지 조건을 만족하면 노름 이라고 한다.노름의 공리 (모든 스칼라 a \in F 와 모든 벡터 \mathbf{v}, \mathbf{u} \in V 에 대해) 성질 설명 수식 비음성 (Non-negativity) 노름값은 항상 0보다 크거나 같다. \>\mathbf{v}\| \ge 0 정부호성 (Positive definiteness) 노름값이 0인 벡터는 영벡터뿐이며, 역도 성립한다. \>\mathbf{v}\| = 0 \iff \mathbf{v} = \mathbf{0} 절대 균질성 (Absolute homogeneity) 벡터에 스칼라를 곱한 것의 노름은, 벡터의 노름에 스칼라의 절댓값을 곱한 것과 같다. \>a \mathbf{v}\| = |a| \|\mathbf{v\| 삼각 부등식 (Triangle inequality) 또는 아첨가성 (Subadditivity) 두 벡터의 합의 노름은 각 벡터의 노름의 합보다 작거나 같다. \>\mathbf{v} + \mathbf{u}\| \le \|\mathbf{v}\| + \|\mathbf{u}\|
x 의 절댓값 |x| 와 복소수 z 의 절댓값(크기) |z| 는 모두 위의 노름 조건을 만족한다. 따라서 절댓값은 노름의 특수한 예라고 할 수 있다. 특히, 실수를 1차원 벡터 공간 \mathbb{R}^1 으로 생각하면, 절댓값은 \mathbb{R}^1 위의 노름이 된다. 더 나아가, 임의의 p \ge 1 에 대해 정의되는 L^p 노름의 특수한 경우이기도 하다. 사실상, \mathbb{R}^1 에서는 절댓값이 유일한 노름이라고 할 수 있는데, 이는 \mathbb{R}^1 의 모든 노름 \|\cdot\| 에 대해 \|x\| = \|1 \cdot x\| = |x| \|1\| 이 성립하여, 상수 \|1\| 배 차이밖에 나지 않기 때문이다.유클리드 공간 \mathbb{R}^n 에서 벡터 \mathbf{x} = (x_1, x_2, \dots, x_n) 의 유클리드 노름 은 다음과 같이 정의되며, 이는 가장 흔하게 사용되는 노름 중 하나이다.\|\mathbf{x}\|_2 = \sqrt{x_1^2 + x_2^2 + \dots + x_n^2} = \sqrt{\sum_{i=1}^{n} x_i^2} \mathbb{R}^2 와 동일시했을 때의 유클리드 노름과 같다. 이는 내적 공간 에서 유도되는 노름의 한 예이기도 하다.\|\cdot\| 는 그 공간 위에 거리 함수 d 를 자연스럽게 정의하는데, 두 벡터 \mathbf{x}, \mathbf{y} 사이의 거리는 두 벡터의 차의 노름으로 정의된다.d(\mathbf{x}, \mathbf{y}) = \|\mathbf{x} - \mathbf{y}\| d(x, y) = |x - y| 는 노름이 유도하는 거리의 특수한 경우이다.
5. 2. 정역 위의 절댓값
정역 위의 절댓값은 정역 에 정의되며, 음이 아닌 실수 값을 취하고, 양의 정부호성을 만족시키며, 곱셈을 보존하고, 삼각 부등식 을 만족시키는 함수이다. 모든 체 는 정역 이므로, 실수 또는 복소수 의 절댓값은 정역 위의 절댓값의 특수한 경우이다. 모든 정역 위의 절댓값 x \mapsto |x| 는 표준적인 거리 함수 (x,y) \mapsto |x-y| 를 유도한다.R 의 원소 a 가 있다면, a 의 '''절댓값'''은 |a| 로 표기되며 다음과 같이 정의된다.|a| = \begin{cases} a, & \text{if } a \ge 0 \\ -a, & \text{if } a < 0 \end{cases} -a 는 a 의 덧셈 역원 , 0 은 덧셈 항등원 이며, < 와 ≥는 환의 순서에 대한 일반적인 의미를 갖는다.F 에 대한 실숫값을 가지는 함수 v 는 다음 네 가지 공리를 만족하는 경우 '절댓값'(또는 '모듈러스', '크기', '값' 또는 '값매김')이라고 한다.수학적 표현 의미 v(a) \ge 0 비음성 v(a) = 0 \iff a = \mathbf{0} 양의 정부호성 v(ab) = v(a) v(b) 곱셈성 v(a+b) \le v(a) + v(b) 부가성 또는 삼각 부등식
\mathbf{0} 은 F 의 덧셈 항등원 을 나타낸다. 양의 정부호성과 곱셈성으로부터 v(\mathbf{1}) = 1 이 유도된다. 여기서 \mathbf{1} 은 F 의 곱셈 항등원을 나타낸다. 위에서 정의된 실수와 복소수의 절댓값은 임의의 체에 대한 절댓값의 예이다.v 가 F 에 대한 절댓값이라면, d(a, b) = v(a - b) 로 정의된 F \times F 에 대한 함수 d 는 거리 함수(metric)이며 다음은 동치이다.
d 는 모든 x, y, z \in F 에 대해 초메트릭 부등식 d(x, y) \leq \max(d(x,z),d(y,z)) 을 만족한다.\left\{ v\left( \sum_{k=1}^n \mathbf{1}\right) : n \in \mathbb{N} \right\} 은 \mathbb{R} 에서 유계 이다.모든 n \in \mathbb{N} 에 대해 v\left({\textstyle \sum_{k=1}^n } \mathbf{1}\right) \le 1\ 이다. 모든 a \in F 에 대해 v(a) \le 1 \Rightarrow v(1+a) \le 1\ 이다. 모든 a, b \in F 에 대해 v(a + b) \le \max \{v(a), v(b)\}\ 이다.
6. 역사
절댓값의 개념은 19세기 초 복소수 가 연구되면서 중요하게 다루어지기 시작했다. 1806년 장 로베르 아르강은 복소수의 크기를 나타내기 위해 프랑스어로 "측정 단위"를 의미하는 ''module''이라는 용어를 도입했다.수직선 을 그어 절댓값을 나타내는 기호 |''x''|는 1841년 카를 바이어슈트라스 가 도입했다.
6. 1. 용어 및 표기
1806년, 장 로베르 아르강(Jean-Robert Argand)은 프랑스어로 "측정 단위"를 의미하는 ''module''이라는 용어를 특히 복소수 의 절댓값을 나타내기 위해 처음 사용했다.수직선 을 사용하여 |''x''| 와 같이 표기하는 방식은 카를 바이어슈트라스 (Karl Weierstrass)가 1841년에 도입했다.행렬식 을 나타낸다. 따라서 수직선 기호가 절댓값을 의미하는지 판단하려면, 그 대상이 절댓값 개념이 정의된 대수적 구조(예: 실수 , 복소수 , 사원수 와 같은 노름 체)의 원소인지 확인해야 한다. 이와 밀접하게 관련되어 있지만 구별되는 표기법으로는 '''R'''''n'' 의 벡터에 대한 유클리드 놈2 및 ||•||∞ )을 사용하는 것이 더 일반적이다.
CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.help@durumis.com