관성 좌표계

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 관성 좌표계의 의미
4. 관성 좌표계의 특징 및 종류
- 4.1. 관성 좌표계의 특징
- 4.2. 관성 좌표계의 종류
5. 비관성 좌표계
- 5.1. 가상력 (관성력)
6. 관성 좌표계와 비관성 좌표계의 구분
7. 현대적 응용
8. 예시
참조

1. 개요

관성 좌표계는 물체의 자연 운동이 정지 또는 등속 직선 운동으로 나타나는 좌표계를 의미하며, 뉴턴의 운동 제1법칙을 만족한다. 아리스토텔레스는 자연스러운 위치로의 운동을 자연 운동으로 정의했지만, 데카르트와 뉴턴은 관성의 개념을 도입하여 자연 운동을 정지 또는 등속 직선 운동으로 정의했다. 뉴턴 역학에서는 절대 공간을 기준으로 관성 좌표계를 정의했으나, 아인슈타인의 특수 상대성 이론에서는 모든 관성 좌표계의 등가성을 가정하고 로렌츠 변환을 사용한다. 일반 상대성 이론은 시공간의 곡률을 고려하여 관성 원리를 수정한다. 관성 좌표계는 가상력이 존재하지 않는 좌표계로, 비관성 좌표계와 구분된다. 관성 항법 장치 및 자이로컴퍼스와 같은 기술에 활용되며, 일상생활에서 자동차의 움직임과 같은 다양한 예시를 통해 관성 좌표계의 개념을 이해할 수 있다.

2. 역사

관성 좌표계에 대한 논의는 아주 오래전부터 있어 왔다. 아리스토텔레스까지 거슬러 올라가 자연 운동에 대한 역사를 살펴본다.

아리스토텔레스는 사물의 자연스러운 위치를 결정함으로써 자연 운동을 정의하였다. 물과 흙은 무거우므로 지구 중심 방향으로 이동하려 하고 불과 공기는 가벼우므로 주변부로 이동하려 한다.^[58] 천상계를 이루는 물질은 제5원소인 에테르로서 완전성과 불변성의 상징인 원운동이 자연스러운 운동으로 간주되었다. 갈릴레오 갈릴레이는 자연 운동을 정지 또는 등속 직선 운동으로 이해한 부분들이 있으나, 이것은 원운동의 일부로서의 직선을 의미한 것으로 분석되므로 아리스토텔레스의 자연 운동 관점을 완전히 벗어났는지에 대해서는 논란의 여지가 많다.^[59]

--

데카르트는 자연을 거대한 기계장치처럼 보는 기계 철학의 선구자이다. 그의 철학에서 자연은 물질과 그 운동으로 설명할 수 있으며, 물질은 자체적으로 어떤 활성도 갖지 못한다. 데카르트는 자연 운동을 정지 또는 등속 직선 운동으로 정의하였고, 이는 현대의 관성 개념으로 이어진다. 그러나 행성 운동을 '소용돌이 이론'(Vortex Theory)으로 설명하려 했기에 그의 우주관에는 원운동을 당연하게 생각하는 경향이 남아 있었다.^[60]

데카르트는 원운동과 원심력에 관한 논의는 정성적인 차원에 머물렀다. 이를 정량적인 논의로 발전시킨 것은 호이겐스였다. 호이겐스는 원심적 경향을 '원심력'(centrifugal force)이라고 불렀다. 고대 이래 특수한 위치를 차지해 온 원운동의 중요성은 쉽게 소멸될 수 없었다.^[60]

항성에 대해 정지한 것으로 간주되는 절대 공간을 가정한 뉴턴은 관성 좌표계가 절대 공간에 대해 균일하게 이동하는 좌표계라고 보았다. 그러나 뉴턴 시대에도 일부 "상대론자"^[10]는 절대 공간 개념에 결함이 있으며 대체되어야 한다고 생각했다. 뉴턴은 자신의 운동 제1법칙(관성의 법칙)이 절대 공간에 대해 균일하게 운동하는 모든 좌표계에서 유효하다고 보았다. 뉴턴은 "절대 공간"을 고정된 별로 간주했다.^[18]^[19]

아인슈타인의 특수 상대성 이론은 모든 관성 좌표계가 동등하다는 가정을 바탕으로 한다. 진공에서의 광속이 불변하다고 가정하므로, 관성 좌표계 간의 변환은 갈릴레이 변환이 아닌 로렌츠 변환을 사용한다. 광속 불변성은 시간 지연, 길이 수축, 동시성의 상대성과 같은 직관에 어긋나는 현상을 초래하지만, 특수 상대성 이론의 예측은 실험적으로 널리 검증되었다.^[27]

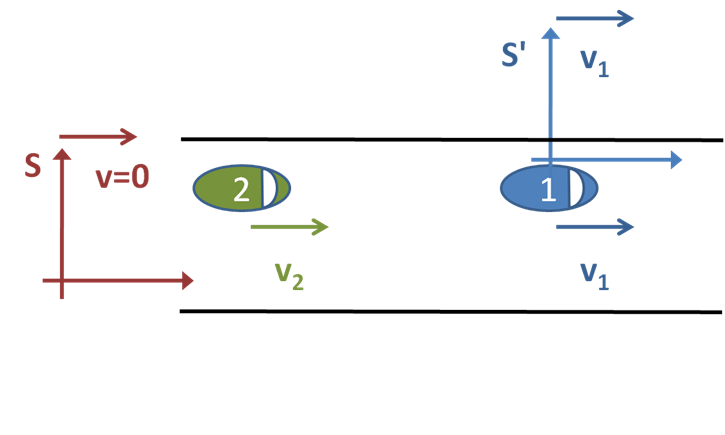
'''그림 1''': 도로에 고정된 관성 좌표계 ''S''와 첫 번째 자동차에 고정된 움직이는 관성 좌표계 ''S′''에서 관찰한 두 대의 자동차가 서로 다른 일정한 속도로 움직이는 모습.

일상생활에서 두 대의 자동차가 일정한 속도로 움직이는 상황을 통해 기준틀에 따라 문제를 쉽게 해결할 수 있음을 알 수 있다(그림 1 참조).

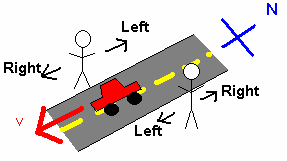
두 관찰자의 방향만 다른 간단한 예시(그림 2 참조)에서, 남북 방향 도로 양쪽에 서로 마주 보고 서 있는 두 사람에게 자동차가 남쪽으로 지나갈 때, 동쪽을 보는 사람에게는 자동차가 오른쪽으로, 서쪽을 보는 사람에게는 왼쪽으로 움직이는 것처럼 보인다. 이는 두 사람이 서로 다른 기준틀을 사용했기 때문이다.

일반 상대성 이론은 등가 원리에 기초한다.^[30]^[31] 등가 원리는 "관찰자가 중력 때문에 가속이 발생하는지, 아니면 자신의 기준틀이 가속되고 있기 때문에 가속이 발생하는지 구별할 수 있는 실험은 없다"는 것이다. 외트뵈시 실험은 모든 물체에 대해 관성 질량 대 중력 질량의 비율이 동일함을 보여주며, 이는 등가 원리를 뒷받침한다.^[33]

일반 상대성 이론에서 관성 원리는 측지선 운동의 원리로 대체된다. 즉, 물체는 시공간의 곡률에 따라 움직인다. 이 곡률 때문에, 서로 특정 속도로 움직이는 관성 물체가 계속 그렇게 움직인다고 단정할 수 없다. 측지선 이탈 현상은 관성 기준틀이 전역적으로 존재하지 않음을 의미한다.

그러나 일반 이론은 시공간의 충분히 작은 영역에서 특수 이론으로 축소되어, 곡률 효과가 덜 중요해지고 이전의 관성 기준틀 개념이 다시 적용될 수 있다.^[35]^[36] 현대 특수 상대성 이론은 "국소적 이론"으로 설명되기도 한다.^[37]

2. 1. 자연 운동(Natural Motion)

자연 운동이란 아무런 외부의 영향도 가해지지 않았을 때의 운동을 의미한다. 관성 좌표계는 자연 운동이 정지 또는 등속 직선 운동인 좌표계이다. 자연계의 기본 운동이 무엇이냐에 대한 논의는 아주 오래전부터 있어 왔다. 아리스토텔레스까지 거슬러 올라가 자연 운동에 대한 역사를 살펴본다.

2. 2. 아리스토텔레스(Aristotle, B.C 384~322)

아리스토텔레스는 자연스러운 위치를 결정함으로써 자연 운동을 정의하였다. 사물의 자연스러운 위치는 자연 운동을 일으키는 원인이 된다.^[57] 즉, 자연스러운 위치에서 벗어난 것은 원래 위치로 돌아가기 위해 스스로 움직인다. 아리스토텔레스는 지상계를 물, 불, 흙, 공기의 4가지 원소로 이루어져 있으며 이들은 촉촉함, 건조함, 차가움, 뜨거움의 4가지 성질과 관련있다고 보았다. 물과 흙은 무거우므로 지구 중심방향으로 이동하려 하고 불과 공기는 가벼우므로 주변부로 이동하려 한다.^[58]

천상계를 이루는 물질은 제5원소인 에테르로서 완전성과 불변성의 상징인 원운동이 자연스러운 운동으로 간주되었다. 즉, 아리스토텔레스의 자연 운동은 지구 중심 방향이나 그 반대 방향을 가진 직선운동, 그리고 원운동이었으며 그것은 물질 고유의 성질에 기인한 것이었다. 예를 들어 돌을 자유 낙하 시켰을 때 지구 중심방향으로 떨어지는 것은 4원소 중 흙으로 이루어진 돌이 자연스럽게 본연의 위치로 돌아가는 과정이므로 자연 운동에 해당한다. 후에 갈릴레오 갈릴레이(1564~1642)는 그의 논문 및 저서에서 자연 운동을 정지 또는 등속 직선 운동으로 이해한 부분들이 있으나 이것은 원운동의 일부로서의 직선을 의미한 것으로 분석되므로 아리스토텔레스의 자연 운동 관점을 완전히 벗어났느냐 하는 점에서는 논란의 여지가 많다.^[59]

2. 3. 데카르트 (Rene Descartes, 1596-1650)와 호이겐스(Christiaan Huygens, 1629-1695)

--

데카르트는 자연을 거대한 기계장치처럼 보는 기계철학의 선구자이다. 그의 철학에서 자연은 물질과 그 운동으로 설명할 수 있으며, 물질은 자체적으로 어떤 활성도 갖지 못한다. 이는 운동의 원인을 물질 내부에서 찾으려 했던 기존 관점에서 벗어났음을 의미한다. 물체를 운동하게 하는 것은 외부의 무엇이며, 운동을 지속시키는 외부적 요인이 없다면 운동은 물질이 처하는 하나의 상태이다. 따라서 외부 작용이 없는 한 물질은 자신의 운동 상태를 그대로 지속하려는 경향, 즉 관성을 지닌다고 보았다.^[60] 즉, 데카르트는 자연 운동을 정지 또는 등속 직선 운동으로 정의하였고, 이는 현대의 관성 개념으로 이어진다.

그러나 데카르트는 행성 운동을 '소용돌이 이론'(Vortex Theory)으로 설명하려 했다. 진공과 원거리 작용을 인정하지 않았던 데카르트는 우주를 채우고 있는 에테르의 소용돌이로 행성의 지속적인 원운동을 설명하려 했다. 이렇듯 그의 우주관에는 원운동을 당연하게 생각하는 경향이 남아 있었다.^[60]

데카르트는 원운동에도 관심이 많았지만, 원운동과 원심력에 관한 논의는 정성적인 차원에 머물렀다. 이를 정량적인 논의로 발전시킨 것은 호이겐스였다. 호이겐스는 원심적 경향을 '원심력'(centrifugal force)이라고 불렀다. 데카르트와 호이겐스는 원운동하는 물체가 지닌 원심적 경향에 주목하며, 그것이 원운동의 제약을 풀어 주었을 때 원운동으로부터 벗어나 접선 방향의 운동을 하게 하는 힘임을 주목했다. 이런 면에서 그들은 여전히 원운동을 당연한 운동으로 보고, 그로부터 벗어나려는 경향을 설명이 필요한 것으로 보았다. 고대 이래 특수한 위치를 차지해 온 원운동의 중요성은 쉽게 소멸될 수 없었다.^[60]

2. 4. 뉴턴(Isaac Newton, 1642-1727)

항성에 대해 정지한 것으로 간주되는 절대 공간을 가정한 뉴턴은 관성 좌표계가 절대 공간에 대해 균일하게 이동하는 좌표계라고 보았다. 그러나 뉴턴 시대에도 일부 "상대론자"^[10]는 절대 공간 개념에 결함이 있으며 대체되어야 한다고 생각했다.

뉴턴은 자신의 운동 제1법칙(관성의 법칙)이 절대 공간에 대해 균일하게 운동하는 모든 좌표계에서 유효하다고 보았다. 여기서 '균일하게 운동한다'는 것은 회전하거나 가속하지 않는 것을 의미한다. 뉴턴은 "절대 공간"을 고정된 별로 간주했다.^[18]^[19]

뉴턴은 운동 법칙의 따름 정리 중 하나에서 상대성 원리를 다음과 같이 직접 언급하기도 했다.^[24]^[25]

이 원리는 특수 상대성 원리와 두 가지 면에서 다른데, 첫째는 역학에만 국한된다는 점이고, 둘째는 단순성에 대한 언급이 없다는 점이다. 그러나 이 원리는 서로 변환되는 좌표계 간의 묘사 형태가 불변하다는 점을 공유한다.^[26]

2. 5. 아인슈타인(Albert Einstein, 1879~ 1955)

아인슈타인의 특수 상대성 이론은 모든 관성 좌표계가 동등하다는 가정을 바탕으로 한다. 특수 상대성 이론에서는 진공에서의 광속이 불변하다고 가정하므로, 관성 좌표계 간의 변환은 갈릴레이 변환이 아닌 로렌츠 변환을 사용한다.

광속 불변성은 시간 지연, 길이 수축, 동시성의 상대성과 같은 직관에 어긋나는 현상을 초래하지만, 특수 상대성 이론의 예측은 실험적으로 널리 검증되었다.^[27] 로렌츠 변환은 광속이 무한대에 접근하거나 좌표계 간의 상대 속도가 0에 접근하면 갈릴레이 변환으로 축소된다.^[28]

일상생활에서 두 대의 자동차가 일정한 속도로 움직이는 상황을 생각해 보자(그림 1 참조). 특정 시점에 두 자동차가 200m 떨어져 있고, 앞차는 초당 22m, 뒤차는 초당 30m로 이동한다면, 뒤차가 앞차를 따라잡는 데 걸리는 시간은 기준틀에 따라 달라진다.^[29]

도로 옆에서 관찰하는 경우 (기준틀 ''S''): 두 번째 자동차가 우리를 지나치는 순간 스톱워치를 시작한다. 두 자동차의 위치는 다음 공식으로 결정된다. : $x_1(t) = 200 + 22t,\quad x_2(t) = 30t.$ $x_1=x_2$ 가 되는 시간을 구하면, 25초가 걸린다.
첫 번째 자동차에서 관찰하는 경우 (기준틀 ''S′''): 첫 번째 자동차는 정지해 있고, 두 번째 자동차는 8m/s의 속도로 접근한다. 따라잡는 데 걸리는 시간은 25초로, 이전과 같다.

이처럼 적절한 기준틀을 선택하면 문제를 쉽게 해결할 수 있다.

두 관찰자의 방향만 다른 간단한 예시(그림 2 참조)에서, 남북 방향 도로 양쪽에 서로 마주 보고 서 있는 두 사람에게 자동차가 남쪽으로 지나갈 때, 동쪽을 보는 사람에게는 자동차가 오른쪽으로, 서쪽을 보는 사람에게는 왼쪽으로 움직이는 것처럼 보인다. 이는 두 사람이 서로 다른 기준틀을 사용했기 때문이다.

일반 상대성 이론은 등가 원리에 기초한다.^[30]^[31] 등가 원리는 "관찰자가 중력 때문에 가속이 발생하는지, 아니면 자신의 기준틀이 가속되고 있기 때문에 가속이 발생하는지 구별할 수 있는 실험은 없다"는 것이다.

이 아이디어는 아인슈타인의 1907년 논문 "상대성 원리와 중력"에서 소개되었고, 1911년에 발전되었다.^[32] 외트뵈시 실험은 모든 물체에 대해 관성 질량 대 중력 질량의 비율이 동일함을 보여주며, 이는 등가 원리를 뒷받침한다.^[33]

일반 상대성 이론에서 관성 원리는 측지선 운동의 원리로 대체된다. 즉, 물체는 시공간의 곡률에 따라 움직인다. 이 곡률 때문에, 서로 특정 속도로 움직이는 관성 물체가 계속 그렇게 움직인다고 단정할 수 없다. 측지선 이탈 현상은 관성 기준틀이 전역적으로 존재하지 않음을 의미한다.

그러나 일반 이론은 시공간의 충분히 작은 영역에서 특수 이론으로 축소되어, 곡률 효과가 덜 중요해지고 이전의 관성 기준틀 개념이 다시 적용될 수 있다.^[35]^[36] 현대 특수 상대성 이론은 "국소적 이론"으로 설명되기도 한다.^[37] 천문학자 카를 슈바르츠실트는 쌍성계의 운동을 관찰하여 은하수 내부의 관성 기준틀이 서로 회전하지 않으며, 은하수의 공간이 대략 갈릴레이 또는 민코프스키적이라는 결론을 내렸다.^[38]

3. 관성 좌표계의 의미

물체의 운동은 다른 물체, 관찰자, 또는 시공간 좌표 집합과 같은 다른 것을 기준으로 설명할 수 있다. 이를 관성 좌표계라고 한다. 특수 상대성 이론의 첫 번째 가정에 따르면, 모든 물리 법칙은 관성 좌표계에서 가장 단순한 형태를 가지며, 균일한 병진 운동으로 서로 연관된 여러 개의 관성 좌표계가 존재한다.^[3]

관성 좌표계는 외부 원인 없이 자급자족적인 물리학을 가지는 반면, '''비관성 좌표계'''는 외부 원인을 가진다.^[4] 이러한 단순성의 원리는 뉴턴 역학과 특수 상대성 이론 모두에서 사용될 수 있다.^[5]^[6]

실제로, 일정한 속도로 움직이는 상자 안의 과학자는 어떤 실험으로도 자신의 속도를 결정할 수 없다. 그렇지 않으면 절대적인 표준 기준 좌표계가 설정될 수 있다.^[7]^[8] 빛의 속도 불변성을 고려하면, 관성 좌표계는 푸앵카레 군의 대칭 변환에 따라 서로 변환되며, 로렌츠 변환은 그 부분군이다.^[9] 뉴턴 역학에서 관성 좌표계는 갈릴레이 군의 대칭성과 관련이 있다.

현재 태양계의 중심에 원점을 두고 항성계에 대해 회전하지 않는 좌표계는 관성계에 가깝다고 알려져 있다. 지구 지표는 관성계에 대해 가속 운동을 하지만, 그 운동과 자전이 완만하여 근사적으로 관성계로 간주할 수 있다. 그러나 태풍 등 거대한 규모의 운동이나, 대포 탄환과 같이 고속으로 운동하는 물체에 대해서는 이 근사가 성립하지 않는다.

3. 1. 자연 운동의 정의

자연 운동이란 아무런 외부의 영향도 가해지지 않았을 때의 운동을 의미한다. 관성 좌표계는 자연 운동이 정지 또는 등속 직선 운동인 좌표계이다. 자연계의 기본 운동이 무엇이냐에 대한 논의는 아주 오래전부터 있어 왔다. 아리스토텔레스까지 거슬러 올라가 자연 운동에 대한 역사를 살펴본다.

관성 좌표계는 뉴턴의 제1법칙을 만족하는 계로서 그 안에서 물체의 자연 운동은 정지 또는 등속 직선 운동이다. 따라서 자연운동에서 벗어나는 운동은 외부의 영향으로 설명되어야 하며 그 원인은 뉴턴 제2법칙에서 정의되고 있다. 현재 자연을 기술하는 가장 보편적인 도구는 뉴턴 역학이며 이 편리한 도구를 원활하게 사용하기 위해 관성 좌표계를 설정한 것이다. 자연 운동에 대한 정의는 앞에서 살펴보았듯이 시대에 따라 변해 왔으며 만일 다른 형태의 자연 운동을 받아들였다면 관성 좌표계의 정의와 역학 체계는 전혀 다른 형태로 발전했을 것이다. 예를 들어 ‘아무런 힘도 받지 않는 물체는 등속 원운동을 유지한다’고 정의하면 일정한 속력으로 회전하는 계를 관성 좌표계로 정의했을 것이며 등속 직선 운동은 외부의 영향으로 설명되어야 하는 운동이 된다. 즉, 현재 우리가 가상의 힘으로 정의하는 ‘원심력’이 실제적인 힘으로 바뀐다.

3. 2. 공간과 시간

뉴턴은 항성에 대해 정지한 것으로 간주되는 절대 공간을 가정했다. 관성 좌표계는 절대 공간에 대해 균일하게 이동하는 좌표계였다. 그러나 뉴턴 시대에도 일부 "상대론자"^[10]는 절대 공간이 이론의 결함이며 대체되어야 한다고 생각했다.

루트비히 란게는 1885년에 '관성 좌표계'(Inertialsystem^de)라는 표현을 만들었으며, 뉴턴의 "절대 공간과 시간"에 대한 정의를 좀 더 조작적 정의로 대체했다.^[11]^[12]

블라고예비치는 뉴턴 역학에서 "절대 공간" 개념의 부적절함을 다음과 같이 설명했다:^[14]

절대 공간의 존재는 고전 역학의 내부 논리에 모순된다. 갈릴레이 상대성 원리에 따르면 관성 좌표계 중 어느 것도 구별될 수 없기 때문이다.
절대 공간은 관성력을 설명하지 못한다. 관성력은 임의의 관성 좌표계에 대한 가속도와 관련이 있기 때문이다.
절대 공간은 물리적 대상에 가속에 대한 저항을 유도함으로써 작용하지만, 절대 공간은 작용받을 수 없다.

조작적 정의의 유용성은 특수 상대성 이론에서 훨씬 더 발전했다.^[15] 디살레는 운동 법칙이 좌표계를 결정하고 구성하는 절차를 결정한다고 요약했다.^[16]

3. 2. 1. 뉴턴의 절대 시공

Inertialsystem^de라는 표현은 1885년 루트비히 란게가 뉴턴의 "절대 공간과 시간" 정의를 대체하기 위해 사용한 것이다.^[11]^[12] 란게는 "질점이 서로 다른 세 방향(동일 평면이 아닌)으로 같은 지점에서 던져졌을 때 매번 직선 경로를 따르는 좌표계"를 관성 좌표계로 정의했다.^[13]

뉴턴은 자신의 저서 《프린키피아》에서 질량, 운동량, 힘에 대한 정의를 내리고 운동 법칙을 기술했다. 이후 'Schollium'에서 시간, 공간, 위치, 운동을 언급하며, 절대 공간은 외부와 관계없이 항상 유사하고 움직이지 않는다고 설명했다. 상대 공간은 절대 공간의 움직이는 척도이며, 우리가 감각으로 물체의 위치를 통해 결정한다고 했다. 뉴턴은 절대 시공이 불변의 존재라고 했지만, 뉴턴의 제1법칙에서 힘이 작용하지 않는 물체의 정지 또는 등속 직선 운동은 무엇에 대한 것인지 질문이 제기되었다. 뉴턴은 이를 절대 공간으로 보았고, 당시에는 항성을 기준으로 했다.^[62]

뉴턴은 절대 공간의 존재를 증명하기 위해 '뉴턴의 양동이 실험'을 수행했다. 물이 든 양동이가 회전하면 물이 바깥쪽으로 밀려나 수면이 높아진다. 상대론적 관점에서는 양동이가 정지하고 우주 전체가 회전하는 것과 같지만, 이 경우에는 수면 높이가 변하지 않는다. 뉴턴은 이 실험을 통해 절대 공간에 대한 가속만이 의미있는 가속도라고 주장했다.

뉴턴의 저서 《프린키피아》에는 공간 및 시간의 절대성에 대한 뉴턴의 신념이 신학적 관점과 함께 나타나 있다. 뉴턴에게 운동의 절대적 기준은 절대 공간에 대해 어떻게 움직이는가였다. 뉴턴 역학에서 관성 좌표계는 절대 공간에 대해 등속 직선 운동하는 무한개의 좌표계를 의미한다. 그러나 에테르 개념이 마이컬슨-몰리 실험으로 폐기되고 아인슈타인의 상대성이론이 등장하면서 뉴턴의 절대 시공 개념은 힘을 잃었다. 현대적 관성 좌표계는 '절대 공간'에 대해 일정한 속도로 움직이는 좌표계가 아니라 '가상힘'이 발생하지 않는 좌표계로 수정되었다.

뉴턴 시대에도 일부는 절대 공간이 이론의 결함이며 대체되어야 한다고 생각했다.^[10] 블라고예비치는 절대 공간의 존재가 고전 역학의 내부 논리에 모순되고, 관성력을 설명하지 못하며, 작용은 하지만 작용받을 수 없다고 지적했다.^[14] 조작적 정의의 유용성은 특수 상대성 이론에서 더 발전했다.^[15] 디살레는 운동 법칙이 좌표계를 결정하고 구성하는 절차를 결정한다고 요약했다.^[16]

3. 2. 2. 상대론(Relativism)

상대론에 따르면 절대 시공은 존재하지 않으며, 물질의 위치와 운동은 완전히 상대적으로만 파악할 수 있다. 뉴턴은 항성에 대해 정지한 것으로 간주되는 절대 공간을 가정했고, 관성 좌표계는 절대 공간에 대해 균일하게 이동하는 좌표계였다. 그러나 뉴턴 시대에도 일부 "상대론자"^[10]는 절대 공간이 이론의 결함이며 대체되어야 한다고 생각했다.

루트비히 란게는 1885년에 '관성 좌표계'(Inertialsystem^de)라는 표현을 만들었으며, 뉴턴의 "절대 공간과 시간"에 대한 정의를 좀 더 조작적 정의로 대체했다.^[11]^[12] 란게는 "질점이 서로 다른 세 방향(동일 평면이 아닌)으로 같은 지점에서 던져졌을 때 매번 직선 경로를 따르는 좌표계를 관성 좌표계라고 한다."^[13]라고 정의했다.

뉴턴 역학에서 "절대 공간" 개념의 부적절함은 다음과 같다:^[14]

절대 공간의 존재는 고전 역학의 내부 논리에 모순된다. 갈릴레이 상대성 원리에 따르면 관성 좌표계 중 어느 것도 구별될 수 없기 때문이다.
절대 공간은 관성력을 설명하지 못한다. 관성력은 임의의 관성 좌표계에 대한 가속도와 관련이 있기 때문이다.
절대 공간은 물리적 대상에 가속에 대한 저항을 유도함으로써 작용하지만, 절대 공간은 작용받을 수 없다.

조작적 정의의 유용성은 특수 상대성 이론에서 훨씬 더 발전했다.^[15] 란게의 정의를 포함한 몇 가지 역사적 배경을 살펴보면, "어떤 좌표계에 대해 운동 법칙이 성립하는가?"라는 원래의 질문은 잘못 제기된 것으로, 운동 법칙은 본질적으로 일련의 좌표계를 결정하고, (원칙적으로) 그 좌표계를 구성하는 절차를 결정한다.^[16]

3. 3. 공간과 시간의 균질성(space-time homogeneous)

뉴턴의 제1법칙에는 시간과 공간의 균일성이 내포되어 있다. 힘이 작용하지 않는 물체가 일정한 속력과 방향을 유지하려면, 단위 시간 동안의 운동 양상이 무한히 반복되어야 하기 때문이다. 이는 라그랑지안과 오일러 방정식을 통해 수학적으로 증명할 수 있다.^[67]

일반 좌표계를

(\mathbf{q}_1,\mathbf{q}_2,\mathbf{q}_3,...\mathbf{q}_s)

로 설정하면 라그랑지안은 다음과 같이 표현된다.

\mathbf{L}(\mathbf{q}_1,\mathbf{q}_2,\mathbf{q}_3,...\mathbf{q}_s,\dot{\mathbf{q}_1},\dot{\mathbf{q}_2},\dot{\mathbf{q}_3},...\dot{\mathbf{q}_s},t)

변분 원리에 따라 다음 적분식은 최솟값을 가져야 한다.

\textstyle \int_{t_1}^{t_2}\mathbf{L}(\mathbf{q},\dot{\mathbf{q}},t)\, dx

시간과 공간이 균일하다고 가정하면, 함수

\mathbf{L}

은 속도(

\mathit{v}

)만의 함수이며, 공간이 균일하므로 공간 변수는 스칼라 값을 갖는다. 따라서 함수

\mathbf{L}

은 다음과 같다.

\mathbf{L}=\mathbf{L}( \mathrm{v}^2)

공간의 균일성으로 인해 다음이 성립한다.

\partial\mathbf{L}/ \partial r =0

이를 오일러 방정식에 적용하면 다음과 같다.

{\operatorname{d}\over\operatorname{d}t}( \partial\mathbf{L}/ \partial\mathrm{v})=0

\partial\mathbf{L}/ \partial\mathrm{v}

는

\mathrm{v}

만의 함수이므로, 시간에 따라 일정한 속력을 가져야 한다. 즉, 시간과 공간이 균일한 관성 좌표계에서 물체의 속력은 크기와 방향이 일정하며, 이것이 관성의 법칙이다. 이처럼 공간과 시간의 균일성을 전제로 관성의 법칙이 도출되며, 뉴턴 역학은 무한개의 관성 좌표계에서 동일하게 성립한다.

3. 4. 아인슈타인의 상대성 이론과 관성 좌표계의 확장

알베르트 아인슈타인의 특수 상대성 이론은 뉴턴 역학과 마찬가지로 모든 관성 좌표계의 동등성을 가정한다. 그러나 특수 상대성 이론에서는 진공에서의 광속이 불변하다고 가정하기 때문에, 관성 좌표계 간의 변환은 뉴턴 역학에서 사용되는 갈릴레이 변환이 아닌 로렌츠 변환을 사용한다.

광속 불변성은 시간 지연, 길이 수축, 동시성의 상대성과 같은 직관에 어긋나는 현상을 초래한다. 특수 상대성 이론의 예측은 실험적으로 광범위하게 검증되었다.^[27] 로렌츠 변환은 광속이 무한대에 접근하거나 좌표계 간의 상대 속도가 0에 접근함에 따라 갈릴레이 변환으로 축소된다.^[28]

아인슈타인은 1916년 특수 상대성 이론을 일반 상대성 이론으로 발전시켰다. 특수 상대성 이론이 서로 등속 직선 운동하는 관성계라는 특수한 상황을 바탕으로 했다면, 일반 상대성 이론은 가속되는 좌표계까지 포함하는 이론이다. 일반 상대성 이론의 기본 원리는 ‘등가 원리(Equivalence Principle)’로서, 가속도의 효과와 힘은 구별할 수 없다는 것이다. 가속되는 계에서 나타나는 가속도 효과는 뉴턴 역학에서 말하는 가상의 힘인 ‘관성력’이다. 그러나 ‘관성력’과 ‘중력’은 구분할 수 없으며 동등하다. 예를 들어 구심 가속도가 g인 비관성계는 중력이 작용하는 관성계와 구분할 수 없다. 결국 어떤 계가 가속 운동을 하느냐, 등속 직선 운동을 하느냐와 관계없이 모든 좌표계는 동등하다. 가속되는 한 계의 관성력은 다른 계에서 다른 형태의 실제 힘으로 인식될 수 있기 때문이다.

뉴턴 역학의 적용을 위한 대전제였던 관성 좌표계는 특수 상대론에 의해 (뉴턴 역학과 전자기학을 포함하는) 모든 물리 법칙이 동일하게 적용되는 좌표계로 확장되었고, 절대 공간 개념은 폐기되었다. 또한 일반 상대론은 가속도 효과와 중력을 통합하고 그것을 모든 자연 현상에 적용함으로써 관성계와 비관성계의 경계를 허물었다.

일반 상대성 이론은 등가 원리에 기초한다.^[30]^[31] 이 아이디어는 아인슈타인의 1907년 논문 "상대성 원리와 중력"에서 소개되었고, 이후 1911년에 발전되었다.^[32] 이 원리에 대한 지지는 외트뵈시 실험에서 발견되었으며, 이 실험은 크기나 구성에 관계없이 모든 물체에 대해 관성 질량 대 중력 질량의 비율이 동일한지 여부를 결정한다. 지금까지 10¹¹의 몇 부분에서 차이가 발견되지 않았다.^[33]

아인슈타인의 일반 상대성 이론은 특수 상대성 이론의 "평평한" 민코프스키 공간을 비제로 곡률을 생성하는 메트릭으로 대체하여 명목상 "관성" 및 "비관성" 효과 간의 구분을 수정한다. 일반 상대성 이론에서 관성 원리는 측지선 운동의 원리로 대체되어, 물체가 시공간의 곡률에 의해 지시되는 방식으로 움직인다. 이 곡률의 결과로, 일반 상대성 이론에서는 서로 특정 속도로 움직이는 관성 물체가 계속 그렇게 할 것이라고 단정할 수 없다. 이 측지선 이탈 현상은 관성 기준틀이 뉴턴 역학과 특수 상대성 이론에서처럼 전역적으로 존재하지 않음을 의미한다.

그러나 일반 이론은 시공간의 충분히 작은 영역에서 특수 이론으로 축소되며, 여기서 곡률 효과가 덜 중요해지고 이전의 관성 기준틀 논쟁이 다시 작용할 수 있다.^[35]^[36] 결과적으로 현대 특수 상대성 이론은 이제 때때로 "국소적 이론"으로 설명된다.^[37]

4. 관성 좌표계의 특징 및 종류

관성 항법 장치는 자이로스코프와 가속도계를 이용하여 관성 공간에 대한 가속도를 결정한다. 자이로스코프는 각운동량 보존 법칙에 따라 외부 힘이 가해지지 않는 한 특정 방향을 유지한다.^[52] 관성 항법 장치는 세 개의 직교 자이로스코프를 통해 관성 기준 프레임을 설정하고, 가속도계로 해당 프레임에 대한 가속도를 측정한다. 이 가속도와 시간을 이용하여 위치 변화를 계산하므로, 관성 항법 장치는 외부 입력이 필요 없는 추측 항법의 일종이며 외부 신호에 의해 교란되지 않는다.^[53]

자이로컴퍼스는 해상 선박 항해에 사용되며, 지구 자기장이 아닌 관성 공간을 기준으로 기하학적 북쪽을 찾는다. 자이로컴퍼스 외부 케이스는 지역 연직선과 정렬된 상태로 고정되며, 내부 자이로스코프 휠이 회전하면 자이로스코프 휠은 점차 회전축을 지구 축에 정렬시킨다. 지구 축과의 정렬은 자이로스코프 회전축이 지구에 대해 정지하고 관성 공간에 대해 방향을 바꿀 필요가 없는 유일한 방향이기 때문이다. 자이로컴퍼스는 회전 후 약 15분 만에 지구 축과 정렬된 방향에 도달할 수 있다.^[54]

관성 좌표계는 다음과 같이 크게 두 가지로 분류할 수 있다.

태양계 중심에 원점을 두고 항성계에 대해 회전하지 않는 좌표계는 관성계에 가깝다.
지구 지표는 관성계에 대해 가속 운동을 하지만, 그 운동과 자전이 완만하여 근사적으로 관성계로 간주할 수 있다. 이는 관성의 법칙 조기 발견으로 이어졌다. 단, 태풍 등 거대한 규모의 운동이나 대포 탄환 등 고속 운동에는 이 근사가 성립하지 않는다.

4. 1. 관성 좌표계의 특징

관성 좌표계는 뉴턴의 제1법칙이 성립하는 좌표계이다.^[17] 하지만, 특수 상대성 이론은 뉴턴의 제1법칙뿐만 아니라 모든 물리 법칙을 포함하도록 관성 좌표계의 개념을 일반화한다.

뉴턴은 제1법칙을 절대 공간에 대해 균일하게 운동(회전하거나 가속하지 않음)하는 모든 좌표계에서 유효하다고 보았다. 여기서 "절대 공간"은 고정된 별로 간주되었다.^[18]^[19] 상대성 이론에서는 절대 공간 또는 특권 좌표계의 개념은 더 이상 사용되지 않으며, 고전 역학에서 관성 좌표계는 다음과 같이 정의된다.^[20]^[21]

즉, 관성 좌표계에서는 외부 힘이 없을 때, 정지 상태의 물체는 계속 정지해 있고, 운동하는 물체는 직선으로 일정하게 속도를 유지한다. 뉴턴의 관성 좌표계는 갈릴레이 대칭군에 따라 서로 변환된다.

만약 이 규칙이 직선 운동을 단순히 힘이 없는 상태로 해석한다면, 여러 좌표계에서 직선 운동을 관찰할 수 있기 때문에 관성 좌표계를 구별할 수 없다. 그러나 이 규칙을 관성 좌표계의 정의로 사용한다면, 힘이 없을 때를 결정해야 한다. 아인슈타인은 이 문제점을 다음과 같이 지적했다.^[22]

이 문제를 해결하기 위한 다양한 방법이 있다. 한 가지 방법은 모든 실제 힘이 소스에서 멀어질수록 감소한다고 가정하고, 물체가 모든 소스에서 충분히 멀리 떨어져 힘이 없도록 하는 것이다.^[23] 하지만 이 방법은 먼 우주가 영향을 줄 수 있다는 마흐의 원리와 같은 역사적인 견해와 충돌할 수 있다. 다른 방법은 실제 힘의 모든 소스를 확인하고 설명하는 것이지만, 이는 무언가를 놓치거나 우주에 대한 불완전한 이해로 인해 영향을 제대로 설명하지 못할 수 있다. 세 번째 방법은 좌표계를 이동할 때 힘의 변환 방식을 보는 것이다. 관성 좌표계에서는 좌표계 가속으로 발생하는 허구적인 힘이 사라지지만, 일반적인 경우에는 변환 규칙이 복잡하다. 물리 법칙의 보편성과 법칙이 가장 간단하게 표현되는 좌표계를 기준으로, 관성 좌표계는 이러한 허구적인 힘이 없다는 특징을 갖는다.

뉴턴은 운동 법칙의 따름 정리에서 상대성 원리를 언급했다.^[24]^[25]

이 원리는 특수 원리와 두 가지 차이점이 있다. 첫째, 역학에만 국한된다. 둘째, 단순성에 대한 언급이 없다. 그러나 서로 변환되는 좌표계 간의 묘사 형태의 불변성은 공유한다.^[26]

4. 2. 관성 좌표계의 종류

일상생활에서 흔히 볼 수 있는 상황으로 두 대의 자동차가 일정한 속도로 움직이는 상황을 생각해 보자. 그림 1에서처럼 특정 시점에 두 자동차가 200m 떨어져 있을 때, 앞차는 초당 22m, 뒤차는 초당 30m로 이동한다면, 뒤차가 앞차를 따라잡는 시간을 알고 싶을 때, 세 가지 "기준틀"을 선택할 수 있다.^[29]

첫째, 도로 옆에서 두 자동차를 관찰하여 ''S''를 정의하면, 두 번째 차가 옆을 지나는 순간 스톱워치를 시작하고, 이때 두 차는 200m 떨어져 있다. 두 자동차가 가속되지 않으므로, 다음 공식으로 위치를 결정할 수 있다. ( $x_1(t)$ 는 시간 ''t''초 후 첫 번째 자동차의 위치(미터), $x_2(t)$ 는 시간 ''t''초 후 두 번째 자동차의 위치(미터))

:

x_1(t) = d + v_1 t = 200 + 22t,\quad x_2(t) = v_2 t = 30t.

:

x_1=x_2

로 설정하고 풀면,

:

200 + 22t = 30t,

:

8t = 200,

:

t = 25\ \mathrm{초}.

둘째, 첫 번째 자동차에 위치한 기준틀 ''S′''을 선택하면, 첫 번째 차는 정지해 있고 두 번째 차는 초당 8m의 속도로 뒤에서 접근한다. 따라잡기 위해서는 200/8 = 25초가 걸린다.
셋째, 두 번째 자동차에 고정하면, 두 번째 차가 정지해 있고 첫 번째 차가 초당 8m로 뒤로 움직이는 경우와 유사하다.

회전하고 가속하는 움직이는 기준틀을 선택할 수도 있지만, 이는 문제를 불필요하게 복잡하게 만들 뿐이며, 한 좌표계에서 측정한 값을 다른 좌표계로 변환할 수도 있다.

두 관찰자의 방향만 관련된 간단한 예시를 위해, 남북 방향 도로 양쪽에 서로 마주 보고 서 있는 두 사람을 생각해 보자. 그림 2처럼 자동차가 옆을 남쪽으로 지나갈 때, 동쪽을 보는 사람에게는 오른쪽으로, 서쪽을 보는 사람에게는 왼쪽으로 움직인다. 이는 두 사람이 서로 다른 기준틀을 사용했기 때문이다.

상대적 운동 관찰자의 복잡한 예시로, 알프레드는 길가에 서서 자동차가 왼쪽에서 오른쪽으로 지나가는 것을 보고, 자신의 위치를 원점, 도로를 x축, 정면을 양의 y축으로 정의한다. 자동차는 양의 x 방향으로 속도 v를 가지고 x축을 따라 움직인다. 알프레드의 기준틀은 관성 기준틀로 간주된다.

자동차를 운전하는 베티는 자신의 위치를 원점, 오른쪽을 양의 x축, 정면을 양의 y축으로 정의하여, 베티는 정지해 있고 세상이 움직인다. 알프레드를 지나갈 때, 알프레드가 음의 y 방향으로 v 속도로 움직이는 것을 관찰한다. 북쪽으로 운전하면 북쪽이 양의 y 방향, 동쪽으로 방향을 틀면 동쪽이 양의 y 방향이 된다.

비관성 관찰자의 예시로, 캔디스가 차를 가속, 알프레드는 가속도를 측정하여 음의 x 방향으로 a임을 발견한다. 캔디스의 가속도가 일정할 때, 베티의 속도 v가 일정하다면, 자신의 기준틀에서 알프레드와 동일한 가속도(음의 y 방향으로 a)를 발견한다. 만약 음의 y 방향으로 A 비율로 가속(속도를 줄임)하면, 캔디스의 가속도가 음의 y 방향으로 a'= a - A임을 발견한다. 양의 y 방향으로 A 비율로 가속(속도를 높임)하면, 캔디스의 가속도를 음의 y 방향으로 a' = a + A로 관찰한다.

태양계의 중심에 원점을 두고, 항성계에 대해 회전하지 않는 좌표계는 관성계에 가깝다는 것이 현재 밝혀져 있다.
지구의 지표는 관성계에 대해 가속도 운동을 하고 있지만, 그 운동과 자전은 완만하므로, 근사적으로 관성계로 간주할 수 있다(이는 관성의 법칙의 조기 발견으로 이어졌다). 다만 태풍 등 거대한 규모를 가진 운동이나, 대포의 탄환 등 고속으로 운동하는 물체에 대해서는 이 근사는 성립하지 않는다.

5. 비관성 좌표계

비관성 좌표계는 가상의 힘(관성력)이 필요한 좌표계이다. 관성 좌표계와 비관성 좌표계의 주요 차이점은 가상력의 유무이며, 비관성 좌표계에서는 뉴턴의 운동 법칙을 적용하기 위해 가상력이 도입된다.^[39]

5. 1. 가상력 (관성력)

가상력(관성력)은 비관성 좌표계에서 뉴턴의 운동 법칙을 적용하기 위해 도입되는 힘이다. 관성 좌표계에서는 뉴턴의 제1법칙(관성의 법칙)이 성립하며, 뉴턴의 제2법칙은 다음과 같이 표현된다.^[39]

:

\mathbf{F} = m \mathbf{a} \ ,

여기서 '''F'''는 알짜힘, ''m''은 질량, '''a'''는 가속도이다.

반면, 각속도 ''Ω''로 회전하는 회전 좌표계 (비관성 좌표계)에서는 뉴턴의 제2법칙이 다음과 같이 변형된다.^[39]

:

\mathbf{F}' = m \mathbf{a} \ ,

이 식은 관성 좌표계와 같아 보이지만, 힘 '''F'''′는 실제 힘 '''F''' 외에 가상력 항들을 포함한다.^[39]

:

\mathbf{F}' = \mathbf{F} - 2m \mathbf{\Omega} \times \mathbf{v}_{B} - m \mathbf{\Omega} \times (\mathbf{\Omega} \times \mathbf{x}_B ) - m \frac{d \mathbf{\Omega}}{dt} \times \mathbf{x}_B \ ,

여기서 '''Ω'''는 각속도 벡터, ×는 벡터 외적, '''x'''_''B''는 물체의 위치, '''v'''_''B''는 회전하는 관찰자가 본 물체의 속도이다.

이 식에서 추가된 항들은 코리올리 힘, 원심력, 오일러 힘이며, 모두 가상력이다. 이 힘들은 ''Ω'' = 0 (즉, 관성 좌표계)일 때 사라지며, 회전 좌표계에서만 존재한다. 또한, 이 힘들은 식별 가능한 물리적 근원이 없고, 거리에 따라 감소하지 않는 특징을 가진다.^[39]

모든 관찰자는 실제 힘 '''F'''에 동의하지만, 비관성 관찰자만 가상력을 필요로 한다. 관성 좌표계에서는 이러한 불필요한 힘이 없으므로 물리 법칙이 더 간단하다.^[39]

뉴턴은 회전하는 구와 회전하는 양동이 실험을 통해 가상력의 존재를 설명했다. 회전하는 구를 연결하는 끈의 장력이나 회전하는 양동이 속 물 표면의 곡률은 가상력을 고려해야만 설명 가능하다.^[39]

관성 좌표계와 비관성 좌표계는 가상력의 유무로 구별할 수 있다.^[1]^[2] 가상력의 존재는 물리 법칙이 가장 간단한 형태가 아님을 나타내며, 특수 상대성 원리에 따르면 가상력이 존재하는 프레임은 관성 프레임이 아니다.^[49]

선형 가속도의 경우에도, 뉴턴은 직선 가속도의 감지 불가능성을 언급하며 관성 프레임의 개념을 확장했다.^[25] 예를 들어, 자유 낙하하는 엘리베이터 안의 사람은 자신이 중력에 의해 가속되고 있더라도 자신을 유효한 관성 프레임이라고 주장할 수 있다.

5. 1. 1. 코리올리 힘

회전하는 기준틀에서 관성의 발현은 힘을 가하는 것처럼 보인다. 이 힘은 원심력 방향이나 물체의 운동에 수직인 방향(코리올리 효과)으로 나타난다.^[1]

질량 ''m''을 곱하면 다음과 같은 식을 얻는다.^[1]

:

\mathbf {F'} = \mathbf {F}_{\mathrm {physical}} + \mathbf {F'} _{\mathrm {Euler}} + \mathbf {F'} _{\mathrm {Coriolis}} + \mathbf {F'} _{\mathrm {centripetal}} - m\mathbf {A} _{0},

여기서^[1]

:

\mathbf {F'} _{\mathrm {Coriolis}} = -2m{\boldsymbol {\omega }}\times \mathbf {v'}

(코리올리 힘)이다.^[1]

5. 1. 2. 원심력

회전 좌표계에서 뉴턴의 제2법칙을 적용할 때 나타나는 가상 힘 중 하나이다.^[39] 회전 좌표계에서의 뉴턴 제 2법칙은 다음과 같다.

:

\mathbf{F}' = m \mathbf{a} \ ,

이는 관성 좌표계와 동일해 보이지만, 힘 '''F'''′는 실제 힘 '''F'''뿐만 아니라 추가 항의 결과이다.

:

\mathbf{F}' = \mathbf{F} - 2m \mathbf{\Omega} \times \mathbf{v}_{B} - m \mathbf{\Omega} \times (\mathbf{\Omega} \times \mathbf{x}_B ) - m \frac{d \mathbf{\Omega}}{dt} \times \mathbf{x}_B \ ,

여기서 각 회전은 회전 축의 방향을 가리키는 벡터 '''Ω'''로 표현되며, 크기는 각속도 ''Ω''와 같다. ×는 벡터 외적을 나타내며, '''x'''_''B''는 물체의 위치, '''v'''_''B''는 회전하는 관찰자에 따른 물체의 속도이다.

힘 '''F'''′의 추가 항은 이 프레임에 대한 "가상" 힘이며, 그 원인은 프레임 내 시스템 외부에 있다. 두 번째 추가 항이 원심력이다.^[39]

원심력은 코리올리 힘, 오일러 힘과 함께 ''Ω'' = 0일 때 소멸된다. 즉, 관성 좌표계에서는 0이다. 모든 회전 프레임에서 특정 '''Ω''' 값에 따라 다른 크기와 방향을 가지며, 회전 프레임에서 어디에나 존재한다. 또한, 식별 가능한 물리적 근원을 갖지 않으며, 거리에 따라 감소하지 않는다. 예를 들어, 회전 프레임에서 회전축에서 발생하는 것처럼 보이는 원심력은 축으로부터의 거리가 증가함에 따라 증가한다.^[39]

뉴턴은 회전하는 구를 연결하는 끈의 장력과 회전하는 양동이 안의 물 표면의 곡률을 통해 원심력과 코리올리 힘을 적용하지 않고서는 뉴턴의 제2법칙을 적용할 수 없음을 보였다.^[39]

5. 1. 3. 오일러 힘

가속 좌표계는 "프라임" 프레임으로 묘사되며, 해당 프레임에 의존하는 모든 변수는 프라임(')을 사용하여 표기한다. 예를 들어, ''x′'', ''y′'', ''a′''와 같이 표현한다. 오일러 힘 (

\mathbf{F'}_\mathrm{Euler}

)은 다음과 같이 정의된다.^[1]

:

\mathbf{F'}_\mathrm{Euler} = -m\dot{\boldsymbol\omega} \times \mathbf{r'}

6. 관성 좌표계와 비관성 좌표계의 구분

관성 좌표계와 비관성 좌표계는 가상력의 유무로 구별할 수 있다.^[1]^[2] 가상력의 존재는 물리 법칙이 가장 간단한 형태가 아님을 나타내며, 특수 상대성 원리에 따르면 가상력이 존재하는 좌표계는 관성 좌표계가 아니다.^[49]

비관성 좌표계의 물체는 좌표계 자체의 가속으로 인해 발생하는 힘인 '가상' 힘(유사 힘)을 받는다. 회전 좌표계에서의 원심력과 코리올리 힘이 그 예시이다.

관성 좌표계에 대한 뉴턴의 정의를 적용하려면 "가상" 힘과 "실제" 힘을 구분해야 한다. 예를 들어, 관성 좌표계에서 정지한 물체는 순 힘이 작용하지 않는다. 그러나 고정된 축을 중심으로 회전하는 좌표계에서는 물체가 원을 그리며 움직이는 것처럼 보이고 구심력을 받는다.

이 문제를 해결하기 위한 두 가지 방법이 있다.

첫째, 가상력(코리올리 힘과 원심력)의 기원을 찾는다. 이러한 힘의 근원, 관련 힘 전달자, 기원 물체가 없음을 확인한다.^[50]
둘째, 다양한 좌표계를 살펴본다. 모든 관성 좌표계에서 코리올리 힘과 원심력이 사라지므로, 특수 상대성 원리에 따라 힘이 사라지는 좌표계를 동일하고 가장 간단한 물리 법칙을 공유하는 것으로 식별하여 회전 좌표계가 관성 좌표계가 아님을 판별한다.

뉴턴은 회전하는 구(그림 2, 3)를 통해 이 문제를 설명했다. 구가 회전하지 않으면 묶는 끈의 장력은 모든 좌표계에서 0이다.^[51] 구가 회전하는 것처럼 보일 때(회전 좌표계에서 정지한 구를 관찰)는 코리올리 힘과 원심력의 조합으로 구심력이 제공되어 장력이 필요하지 않다. 실제로 구가 회전하는 경우, 관찰된 장력은 원운동에 필요한 정확한 구심력이다. 따라서 끈의 장력을 측정하여 관성 좌표계를 식별할 수 있다. 관성 좌표계는 가상력이 사라지는 좌표계이다.

선형 가속도의 경우, 뉴턴은 직선 가속도의 감지 불가능성을 언급했다.^[25]

If bodies, any how moved among themselves, are urged in the direction of parallel lines by equal accelerative forces, they will continue to move among themselves, after the same manner as if they had been urged by no such forces.|물체가 서로 어떻게 움직이든, 같은 가속력에 의해 평행선 방향으로 가속된다면, 그런 힘에 의해 가속되지 않은 것처럼 서로 계속 움직일 것이다.^영어

이 원리는 관성 좌표계의 개념을 일반화한다. 예를 들어, 자유 낙하하는 엘리베이터 안의 관찰자는 자신이 유효한 관성 좌표계라고 주장할 수 있다. 엄밀히 말하면 관성 좌표계는 상대적인 개념이다. 따라서 관성 좌표계는 서로 정지해 있거나 일정한 속도로 움직이는 일련의 좌표계로 집합적으로 정의될 수 있으며, 단일 관성 좌표계는 이 집합의 요소로 정의된다.

이러한 아이디어가 적용되려면 좌표계에서 관찰된 모든 것이 좌표계 자체가 공유하는 기준선, 공통 가속도의 영향을 받아야 한다.

7. 현대적 응용

관성 항법 장치는 자이로스코프와 가속도계 클러스터를 사용하여 관성 공간에 대한 가속도를 결정한다. 자이로스코프가 관성 공간에서 특정 방향으로 회전한 후에는 각운동량 보존 법칙에 따라 외부 힘이 가해지지 않는 한 해당 방향을 유지해야 한다.^[52] 세 개의 직교 자이로스코프는 관성 기준 프레임을 설정하고 가속기는 해당 프레임에 대한 가속도를 측정한다. 시계와 함께 가속도를 사용하여 위치의 변화를 계산할 수 있다. 따라서 관성 항법은 외부 입력이 필요 없는 추측 항법의 한 형태이므로 외부 또는 내부 신호 소스에 의해 교란될 수 없다.^[53]

해상 선박의 항해에 사용되는 자이로컴퍼스는 기하학적 북쪽을 찾는다. 지구의 자기장을 감지하는 것이 아니라 관성 공간을 기준으로 사용한다. 자이로컴퍼스 장치의 외부 케이스는 지역 연직선과 정렬된 상태를 유지하도록 고정된다. 자이로컴퍼스 장치 내부의 자이로스코프 휠이 회전하면 자이로스코프 휠이 매달리는 방식에 따라 자이로스코프 휠은 점차적으로 회전축을 지구의 축에 정렬한다. 지구의 축과 정렬되는 것은 자이로스코프의 회전축이 지구에 대해 정지 상태일 수 있으며 관성 공간에 대해 방향을 변경할 필요가 없는 유일한 방향이다. 자이로컴퍼스는 회전 후 불과 15분 만에 지구의 축과 정렬되는 방향에 도달할 수 있다.^[54]

8. 예시

일상생활에서 흔히 볼 수 있는 상황으로, 두 대의 자동차가 일정한 속도로 움직이는 경우를 생각해보자. 그림 1에서처럼, 특정 시점에 두 자동차는 200미터 떨어져 있고, 앞차는 초당 22미터, 뒤차는 초당 30미터로 이동한다. 이때 뒤차가 앞차를 따라잡는 시간을 계산하기 위해 세 가지 기준틀을 고려할 수 있다.^[29]

첫 번째로, 도로 옆에서 두 자동차를 관찰하는 기준틀 ''S''를 정의할 수 있다. 두 번째 자동차가 관찰자를 지나치는 순간 스톱워치를 작동시키면, 두 자동차의 위치는 다음과 같이 표현된다.

: $x_1(t) = 200 + 22t,\quad x_2(t) = 30t.$

여기서 $x_1(t)$ 는 시간 ''t'' 초 후 첫 번째 자동차의 위치(미터), $x_2(t)$ 는 시간 ''t'' 초 후 두 번째 자동차의 위치이다. $x_1=x_2$ 인 시간을 찾으면, 200 + 22t = 30t, 즉 t = 25초가 된다.

두 번째로, 첫 번째 자동차에 위치한 기준틀 ''S′''을 선택할 수 있다. 이 경우 첫 번째 자동차는 정지해 있고, 두 번째 자동차는 8m/s (30m/s - 22m/s)의 속도로 접근한다. 따라서 따라잡는 데 걸리는 시간은 200m / 8m/s = 25초로, 이전과 동일하다.

세 번째 가능한 기준틀은 두 번째 자동차에 고정하는 것이다. 이 경우 두 번째 자동차는 정지해 있고, 첫 번째 자동차가 8m/s로 뒤로 움직이는 것과 유사하다.

이처럼 적절한 기준틀을 선택하면 문제를 쉽게 해결할 수 있다. 회전하거나 가속하는 복잡한 기준틀을 선택할 수도 있지만, 이는 문제를 불필요하게 복잡하게 만들 뿐이다.

그림 2와 같이, 두 사람이 남북 방향 도로 양쪽에 마주 보고 서 있고, 자동차가 남쪽으로 지나가는 경우를 생각해보자. 동쪽을 보는 사람에게 자동차는 오른쪽으로, 서쪽을 보는 사람에게는 왼쪽으로 움직인다. 이는 두 사람이 서로 다른 기준틀을 사용하기 때문이다.

알프레드가 길가에 서서 자동차가 왼쪽에서 오른쪽으로 지나가는 것을 보는 경우, 알프레드는 자신이 서 있는 지점을 원점, 도로를 x축, 정면 방향을 y축으로 정의한다. 자동차는 양의 x 방향으로 속도 v를 가지고 움직인다. 알프레드의 기준틀은 지구의 자전과 중력을 무시하고 가속하지 않으므로 관성 기준틀이다.

자동차를 운전하는 베티는 자신의 위치를 원점, 오른쪽을 양의 x축, 정면을 양의 y축으로 정의한다. 베티가 알프레드를 지나갈 때, 알프레드는 음의 y 방향으로 속도 v로 움직이는 것으로 관찰된다.

캔디스가 자신의 차를 가속하는 경우, 알프레드는 그녀의 가속도를 음의 x 방향으로 a로 측정한다. 베티의 속도가 일정하다면, 베티는 캔디스의 가속도를 음의 y 방향으로 a로 측정한다. 그러나 베티가 음의 y 방향으로 A의 비율로 가속(감속)한다면, 캔디스의 가속도는 a' = a - A가 된다. 베티가 양의 y 방향으로 A의 비율로 가속(증속)한다면, 캔디스의 가속도는 a' = a + A가 된다.

현재 태양계의 중심에 원점을 두고, 항성계에 대해 회전하지 않는 좌표계는 관성계에 가깝다고 알려져 있다.

지구의 지표는 관성계에 대해 가속도 운동을 하지만, 그 운동과 자전은 완만하여 근사적으로 관성계로 간주할 수 있다. 그러나 태풍 등 거대한 규모의 운동이나, 대포의 탄환 등 고속으로 운동하는 물체에 대해서는 이 근사가 성립하지 않는다.

참조

_[1] 서적 Discovering the Natural Laws: The Experimental Basis of Physics https://archive.org/[...] Courier Dover Publications 1989
_[2] 서적 A Contemporary View of Elementary Physics https://archive.org/[...] McGraw-Hill 1968
_[3] 서적 The Principle of Relativity: a collection of original memoirs on the special and general theory of relativity https://books.google[...] Courier Dover Publications 1952
_[4] 서적 Einstein's Space-Time: An Introduction to Special and General Relativity https://books.google[...] Springer Science & Business Media 2022-11-02
_[5] 서적 The Structure of Science https://books.google[...] Hackett Publishing 1979
_[6] 서적 Gravitation and Gauge Symmetries https://books.google[...] CRC Press 2002
_[7] 서적 Relativity: The Special and General Theory https://archive.org/[...] H. Holt and Company 1920
_[8] 서적 Six not-so-easy pieces: Einstein's relativity, symmetry, and space-time https://books.google[...] Basic Books 1998
_[9] 서적 Compendium of Theoretical Physics https://books.google[...] Birkhäuser 2006
_[10] 서적 The Science of Mechanics https://archive.org/[...] The Open Court Publishing Co. 1915
_[11] 간행물 Über die wissenschaftliche Fassung des Galileischen Beharrungsgesetzes 1885
_[12] 서적 The Discovery of Dynamics https://books.google[...] Oxford University Press 2001
_[13] 서적 A Modern Approach to Classical Mechanics https://books.google[...] World Scientific 2002
_[14] 서적 Gravitation and Gauge Symmetries https://books.google[...] CRC Press 2002
_[15] 서적 Special relativity https://books.google[...] Springer 2003
_[16] 서적 The Stanford Encyclopedia of Philosophy Metaphysics Research Lab, Stanford University 2008-09-09
_[17] 서적 The Theory of Relativity Oxford University Press 1976
_[18] 서적 Nothingness: The Science of Empty Space https://books.google[...] Da Capo Press 2001
_[19] 서적 Physics https://archive.org/[...] Wiley 2001
_[20] 서적 Introduction to classical mechanics https://books.google[...] Tata McGraw-Hill 1980
_[21] 서적 Special relativity https://books.google[...] Springer 2003
_[22] 서적 The Meaning of Relativity https://books.google[...] Princeton University Press 1950
_[23] 서적 Introductory Special Relativity https://books.google[...] CRC Press 1991
_[24] 서적 Six not-so-easy pieces: Einstein's relativity, symmetry, and space-time https://books.google[...] Basic Books 1998
_[25] 문서 See the ''Principia'' on line at [https://archive.org/stream/newtonspmathema00newtrich#page/n7/mode/2up Andrew Motte Translation] https://archive.org/[...]
_[26] 문서 However, in the Newtonian system the Galilean transformation connects these frames and in the special theory of relativity the [[Lorentz transformation]] connects them. The two transformations agree for speeds of translation much less than the [[speed of light]].
_[27] 서적 Relativity for Scientists and Engineers https://books.google[...] Courier Corporation 2014
_[28] 서적 The Classical Theory of Fields Pergamon Press 1975
_[29] 서적 Special relativity and classical field theory: the theoretical minimum Hachette UK 2017
_[30] 서적 Introduction to Classical Mechanics https://archive.org/[...] Cambridge University Press 2008
_[31] 서적 Physics for Scientists and Engineers with Modern Physics https://books.google[...] Pearson Prentice Hall 2007
_[32] 논문 On the influence of gravitation on the propagation of light http://www.relativit[...] 1911
_[33] 서적 Physics Through the Nineteen Nineties: Overview https://books.google[...] National Academies Press 1986
_[34] 서적 No Easy Answers: Science and the Pursuit of Knowledge https://books.google[...] University of Pittsburgh Press 2007
_[35] 서적 Information Theory and Quantum Physics: Physical Foundations for Understanding the Conscious Process https://books.google[...] Springer 2000
_[36] 서적 Theory of Special Relativity https://books.google[...] Academic Publishers 2000
_[37] 서적 Cosmological Inflation and Large-Scale Structure https://books.google[...] Cambridge University Press 2000
_[38] 웹사이트 In the Shadow of the Relativity Revolution http://www.mpiwg-ber[...] 2017-05-20
_[39] 서적 Mechanics https://archive.org/[...] Pergamon Press 1960
_[40] 서적 The Music of the Big Bang https://books.google[...] Springer 2008
_[41] 학술지 Constraints on the proper motion of the Andromeda Galaxy based on the survival of its satellite M33 http://www.mpifr-bon[...] 2005
_[42] 서적 Einstein from "B" to "Z" https://books.google[...] Springer 2002
_[43] 서적 In the Grip of the Distant Universe https://books.google[...] World Scientific 2006
_[44] 서적 Nothingness https://books.google[...] Da Capo Press 2001
_[45] 서적 Advances in Astronomy Imperial College Press 2005
_[46] 학술지 Dark energy and global rotation of the Universe 2003
_[47] 학술지 Is the Universe rotating? http://www.nature.co[...] 1982-07-29
_[48] 문서 Mach's Principle II 2004-09-01
_[49] 서적 Mathematical Methods of Classical Mechanics https://books.google[...] Springer 1989
_[50] 문서
_[51] 문서
_[52] 서적 Fundamentals of High Accuracy Inertial Navigation, Volume 174 AIAA 1997
_[53] 서적 Engineering Surveying Technology Taylor & Francis 1993
_[54] 간행물 The gyroscope pilots ships & planes https://books.google[...] 1943-03-15
_[55] 문서
_[56] 서적 時空図による特殊相対性理論森北出版
_[57] 문서 Concepts of space in Greek thought 1994
_[58] 문서 Aristotle’s Physics 1995
_[59] 문서 A. Koyre: 'Galilée et la loi d'inertie', Études Galiléennes
_[60] 문서 과학사개론 1999
_[61] 문서 "'Quantum in Se Est': Newton's Concept of Inertia in Relation to Descartes and Lucretius" Notes and Records of the Royal Society of London
_[62] 문서 Newton's absolute space, Mach's principle and the possible reality of fictitious forces Eur. J. Phys. 1994
_[63] 문서 Relativity and the Nature of Spacetime Springer 2009
_[64] 문서 Leibniz-Clarke Controversy: Absolute versus Relative Space and Time 1966
_[65] 문서 The Renaissance and 17th Century Rationalism 1999
_[66] 문서 Inertial forces, absolute space, and Mach’'s principle: The genesis of relativity 2006
_[67] 문서 Landau LD (1960) Mechanics (trans: Sykes JB, Bell JS)
_[68] 문서 뉴턴과 아인슈타인-우리가 몰랐던 천재들의 창조성
_[69] 문서 상대성 이론과 시간 공간의 철학 물리학과 첨단기술 2001

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com