로그 나선

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

로그 나선은 극좌표로 표현되는 평면 곡선으로, 자연 상수 e를 밑으로 하고 실수 상수 a와 k를 사용하여 r = ae^(kφ) 또는 φ = (1/k)ln(r/a)로 나타낼 수 있다. 이 나선은 등각 나선이라고도 불리며, 나선 위의 점에서 접선과 원점으로부터의 직선 사이의 각도가 일정하다는 특징을 갖는다. 로그 나선은 자기 유사성을 가지며, 확대 또는 축소해도 원래의 나선과 합동이다. 자연 현상, 건축, 공학 등 다양한 분야에서 관찰되며, 황금비를 따르는 황금 나선도 로그 나선의 일종이다.

더 읽어볼만한 페이지

와선 - 나선은하
나선은하는 별, 성간물질, 나선팔, 팽대부, 헤일로 등으로 구성된 은하의 한 유형으로, 나선팔은 밝은 별과 성간물질이 나선형으로 뻗어 있으며, 우리 은하 또한 막대나선은하이다.
와선 - 모기향
모기향은 모기를 쫓기 위해 사용되는 제품으로, 1886년 일본에서 처음 개발되었으며, 나선형, 매트형, 액상형 등 다양한 종류가 있고, 피레트린, 알레트린 등의 살충 성분을 포함하며, 연기, 유해 물질, 화재 위험에 주의하여 사용해야 한다.
로그 - 상용로그
상용로그는 10을 밑으로 하는 로그로, 십진법에 기반하여 log x 또는 lg x로 표기되며, 지표를 통해 진수의 자릿수 파악이 용이하여 과학적 측정에 활용되고 헨리 브리그스의 공로로 '브리그스의 로그'라고도 불린다.
로그 - 자연로그
자연로그는 밑이 e인 로그 함수로, ln(x) 등으로 표기되며 직교쌍곡선 아래 면적으로 정의되거나 지수 함수의 역함수로 정의될 수 있고, 다양한 수학적 성질과 함께 여러 분야에서 활용되며 복소 로그 함수로 확장되기도 한다.
평면 곡선 - 등시 곡선
등시 곡선은 중력의 영향으로 물체가 곡선을 따라 움직일 때 시작 지점과 관계없이 최하점에 도달하는 데 동일한 시간이 걸리는 곡선이며, 사이클로이드가 등시 곡선임을 크리스티안 호이겐스가 증명했다.
평면 곡선 - 렘니스케이트
렘니스케이트는 8자 모양 또는 무한대 기호와 유사한 대수 곡선으로, 베르누이, 제로노, 부스의 렘니스케이트 등이 있으며, 특히 베르누이의 렘니스케이트는 등시 곡선 문제와 관련되어 렘니스케이트 타원 함수 및 렘니스케이트 상수와 같은 개념을 낳았다.

로그 나선
정의
설명	자신과 닮은 꼴의 모양이 점점 확대되거나 축소되는 나선
특징	각도가 일정한 나선 크기는 변하지만 모양은 변하지 않음 극좌표에서 r = a * e^(bθ) (a, b는 상수)로 표현
명칭
다른 이름	등각나선(等角螺旋) 자기닮음나선
라틴어	Spira mirabilis (기묘한 나선)
제안자	야코프 베르누이
이유	모양은 같지만 끊임없이 변화하며, 자신을 파괴하지 않고도 재생할 수 있다는 의미
수학적 특징
극좌표 표현	r = a * e^(bθ) (a, b는 상수, e는 자연로그의 밑)
매개변수 방정식	x(t) = a * exp(bt) cos(t) y(t) = a * exp(bt) sin(t)
나선 감기기	\|θ\|가 증가함에 따라 기하급수적으로 증가
기울기 각	나선과 반지름 사이의 각도가 일정
각도	arctan(b) (b는 극좌표 표현식의 상수)
자기 유사성	크기를 조정해도 모양이 변하지 않음
중심에서의 길이	유한함
중심 도달	무한 번 감겨도 유한 시간 안에 도달
발생 예시
자연	앵무조개 껍데기 해바라기 씨앗 배열 은하 팔의 형태 매가 먹이를 향해 날아갈 때의 경로 (최소 저항 경로)
기타	로고 디자인 도로 디자인 시계 디자인 DNA 구조
관련 개념
황금 나선	황금비율과 관련된 특별한 로그 나선
페르마 나선	다른 종류의 나선으로, 로그 나선과 구별됨
참고 문헌
참고 도서	Albrecht Dürer의 "Underweysung der Messung, mit dem Zirckel und Richtscheyt, in Linien, Ebenen unnd gantzen corporen" (1525) Albrecht Dürer의 책 보기 Øyvind Hammer의 "The Perfect Shape: Spiral Stories" (2016) (Dürer's dirty secret)

2. 정의

로그 나선은 극좌표계에서 ( $r, \theta$ )로 나타낼 때, 다음과 같은 식으로 표현되는 평면 곡선이다.^[41]

나선형은 임의의 점에서 접선과 반지름 $(r, \theta)$ 간의 각도 $\phi$ 가 일정하며, 다음과 같이 미분 기하학 용어로 표현될 수 있다.

: $\arccos \frac{\langle \mathbf{r}(\theta), \mathbf{r}'(\theta) \rangle}{\|\mathbf{r}(\theta)\|\|\mathbf{r}'(\theta)\|} = \arctan \frac{1}{b} = \phi$

나선형 $r(\theta)$ 은 매개변수 $b$ 에 비례한다. 즉, $b$ 가 나선형의 종류와 방향을 결정한다.

$b= 0 \left(\phi = { {\pi}\over {2}} \right)$ 이고 $a=1 , \left(\phi = { {\pi}\over {2}} \to \pi \right)$ 인 극단적인 경우, 나선형은 반경 $1$ 의 원이 된다. $a=1$ 와 $b=0$ 에서, $\phi \to 0$ 으로 무한히 접근하는 나선형은 직선에 접근한다. 여기서 보완적인 개념의 $\phi$ 매개변수를 피치(축경사,pitch)라고 한다.

대수 나선은 (하나의 상수 ''B''만 사용하여)

: $r=B^\theta\,$

로 정의되기도 한다. (단, ''B''는 1이 아닌 양수)

2. 1. 극좌표 정의

극좌표에서 (

r, \theta

) 로그 나선형 곡선은 다음과 같이 표현할 수 있다.^[41]

:

r = ae^{b\theta}\,

또는,

:

\theta = \frac{1}{b} \ln{\left({r \over a}\right)}

여기서

e

는 자연로그의 밑이고,

a

와

b

는 임의의 양의 실수 상수이다.

극좌표 표시 (''r'', θ)에서

:

r=ae^{b\theta}\,

로 표시되는 평면 곡선을 대수 나선이라고 한다. 여기서 ''e''는 네이피어 수, ''a'', ''b''는 고정된 실수이다. ''r''이 원점으로부터의 거리를 나타내므로, ''a''는 양수여야 하지만, ''b''는 양수, 음수 모두 가능하다. 양수인 경우 중심에서 멀어질 때 왼쪽으로 굽는 나선이 되고, 음수인 경우에는 오른쪽으로 굽는 나선이 된다. 뒤집어서 왼쪽으로 굽는 것을 오른쪽으로 굽는 것으로 만들 수 있으므로, ''b'' > 0으로 한정하여 정의하기도 한다. 정의식에서 형식적으로 ''b'' = 0으로 하면 반지름 ''a''의 원이 된다.

정의식은

:

\theta=\frac{1}{b}\log \frac{r}{a}

로도 쓸 수 있다. 역사적으로 지수 함수보다 로그가 먼저 인지되었기 때문에 "대수 나선"이라고 불리게 되었다. ''b''가 양수인 경우, ''r''이 0에 가까워지면 θ는 얼마든지 작아진다. 마찬가지로, ''b''가 음수인 경우 ''r''이 0에 가까워지면 θ는 얼마든지 커진다. 따라서, 어느 경우든 원점 부근에서는 무한히 소용돌이친다.

2. 2. 직교 좌표 정의

극좌표 방정식

:

r = a e^{k\varphi}

으로 표현되는 로그 나선은 데카르트 좌표

(x=r\cos\varphi,\, y=r\sin\varphi)

에서 다음과 같이 나타낼 수 있다.

:

x = a e^{k\varphi}\cos \varphi, \qquad y = a e^{k\varphi}\sin \varphi.

복소 평면

(z=x+iy,\, e^{i\varphi}=\cos\varphi + i\sin\varphi)

에서는 다음과 같다.

:

z=ae^{(k+i)\varphi}.

^[41]

직교 좌표에서 매개 변수 표기는 다음과 같다.

:

x(\theta) = r \cos \theta = ae^{b\theta} \cos \theta\,

:

y(\theta) = r \sin \theta = ae^{b\theta} \sin \theta\,

2. 3. 복소 평면 정의

복소 평면에서 $`z=x+iy`$, $`e^{i\varphi}=\cos\varphi + i\sin\varphi`$일 때, 로그 나선은 다음과 같이 나타낼 수 있다.

`z=ae^{(k+i)\varphi}`

3. 성질

로그 나선은 스피라 미라빌리스(Spira mirabilis), 즉 "경이로운 나선"이라고도 불린다. 야코프 베르누이는 이 곡선의 크기가 증가해도 모양은 변하지 않는 자기 유사성이라는 독특한 수학적 특성에 매료되어 "경이로운 나선"이라는 이름을 붙였다. 그는 "Eadem mutata resurgo"(변했어도, 나는 똑같이 부활할 것이다)라는 문구와 함께 이 나선을 자신의 묘비에 새기기를 원했지만, 실수로 아르키메데스 나선이 새겨졌다.^[42]^[43]

로그 나선은 아르키메데스 나선과 비교했을 때, 나선이 회전하면서 중심으로부터 거리가 기하급수적으로 증가하는 반면, 아르키메데스 나선은 그 거리가 일정하다는 차이점이 있다.

로그 나선	아르키메데스의 나선
--
로그 나선	아르키메데스의 나선

로그 나선은 다양한 기하학적, 수학적 성질을 갖는다. 주요 성질은 다음과 같다.

'''피치 각도''': 피치 각도는 상수이며, 자세한 내용은 하위 섹션의 '''등각성'''을 참조한다.
'''자기 유사성''': 자세한 내용은 하위 섹션의 '''자기 유사성'''을 참조한다.
'''곡률''': 자세한 내용은 하위 섹션의 '''곡률'''을 참조한다.
'''호의 길이''': 자세한 내용은 하위 섹션의 '''호의 길이'''를 참조한다.
'''다른 곡선과의 관계''': 자세한 내용은 하위 섹션의 '''다른 곡선과의 관계'''를 참조한다.

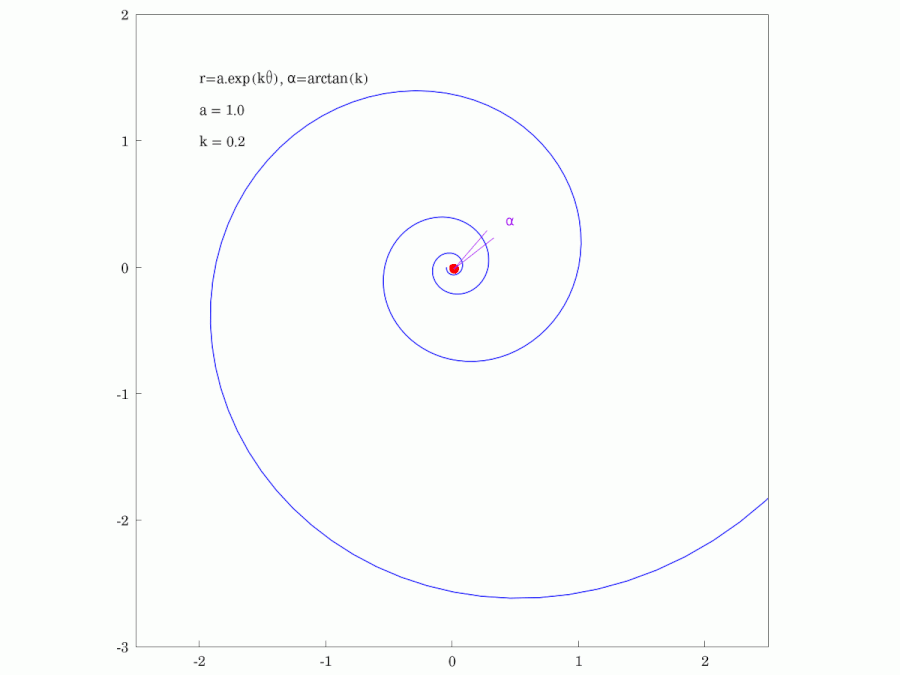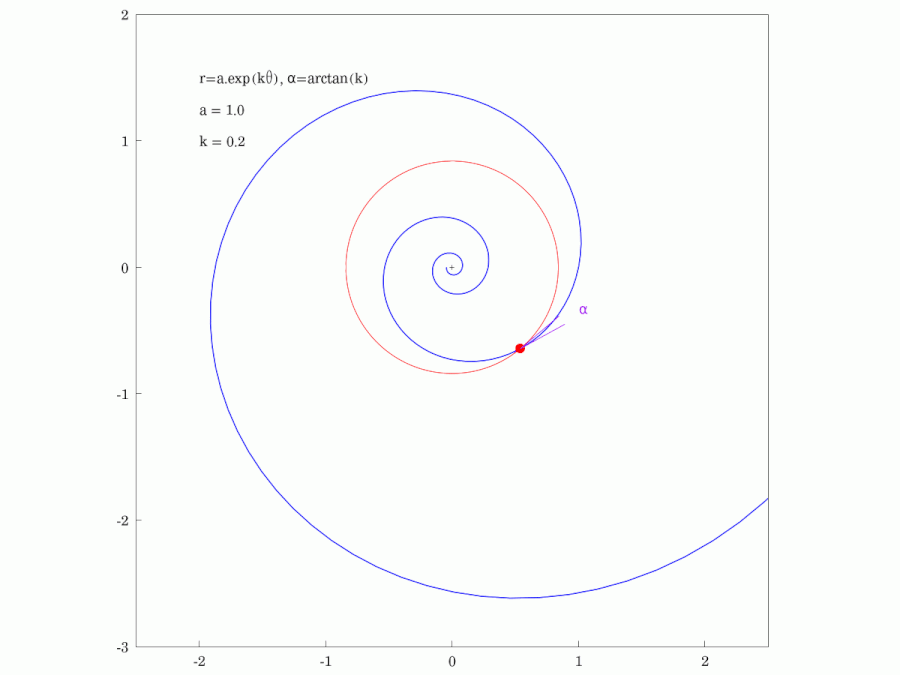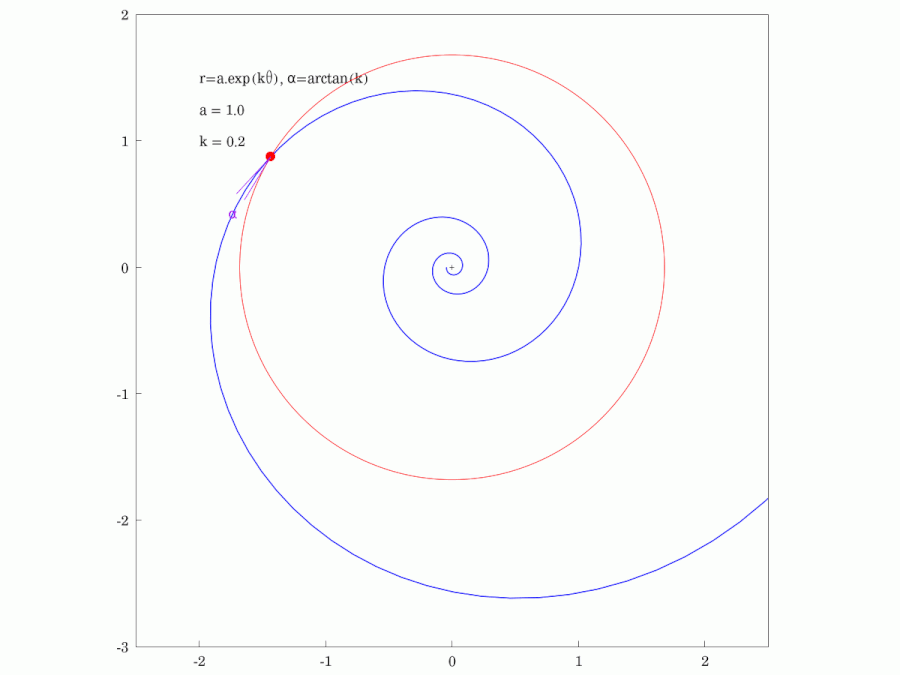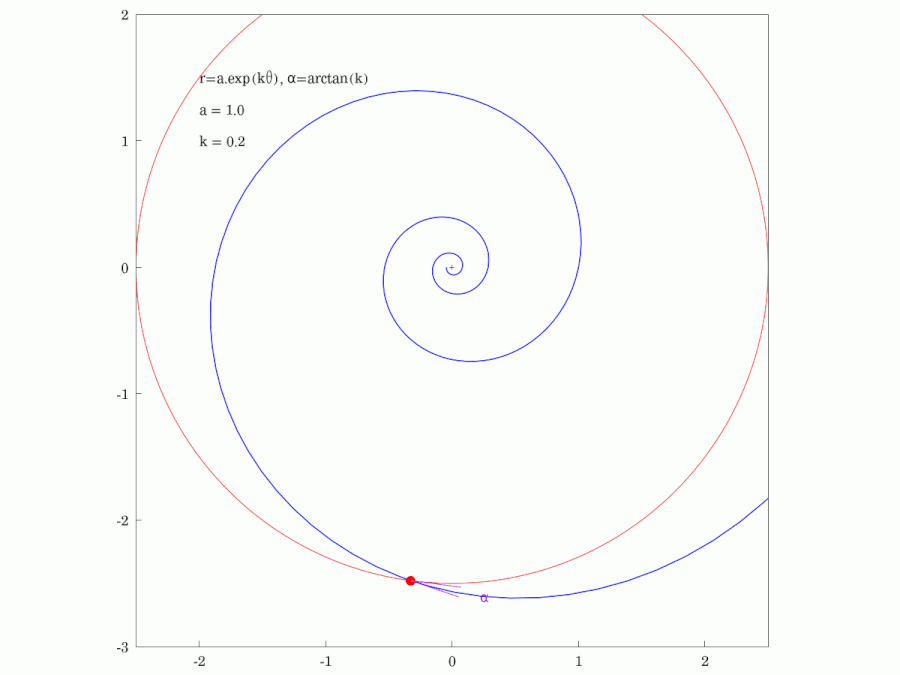
3. 1. 등각성 (피치 각)

로그 나선은 극좌표 (

r, \theta

)에서 다음과 같이 표현할 수 있다.^[41]

:

r = ae^{b\theta}\,

여기서

e

는 자연로그의 밑이고,

a

와

b

는 임의의 양의 실수 상수이다.

나선 위의 임의의 점에서 접선과 반지름

(r, \theta)

사이의 각도

\phi

는 일정하며, 다음과 같이 표현할 수 있다.

:

\arccos \frac{\langle \mathbf{r}(\theta), \mathbf{r}'(\theta) \rangle}{\|\mathbf{r}(\theta)\|\|\mathbf{r}'(\theta)\|} = \arctan \frac{1}{b} = \phi

\phi

의 여각을 피치(pitch) 또는 축경사라고 한다.

로그 나선

r=a e^{k\varphi} \;,\; k\ne 0,

은 다음과 같은 속성을 갖는다.

'''피치 각도''': $\tan\alpha=k$ (상수)이며, 피치 각도 $\alpha$ 는 그림 및 애니메이션을 참조한다. ( $k=0$ 인 경우 각도 $\alpha$ 는 0이 되고 곡선은 반지름이 $a$ 인 원이 된다.)

중심에서 뻗은 반직선과 대수 나선이 이루는 각은 일정하다. 등각 나선의 이름은 이 성질에서 유래한다. 실제로 그 각도 α는 다음과 같다.

:

\alpha = \arccot b

''b''가 양수일 때 α는 0도에서 90도 사이의 각이며, α의 여각 90°− α를 대수 나선의 '''피치'''라고 한다. ''b''가 음수일 때는 α는 90도에서 180도 사이의 각이며, α − 90°가 피치이다. 피치가 클수록, 나선을 따라 중심에서 멀어질 때, 중심으로부터의 직선 거리가 더 빠르게 커진다. 즉, 열린 형태가 된다. 피치가 0도에 가까워진 극한은 원이고, 피치가 90도에 가까워진 극한은 중심에서 뻗은 반직선으로 볼 수도 있다.

3. 2. 자기 유사성

로그 나선은 자기 유사성을 가지는데, 이는 임의의 배율로 확대하거나 축소해도 적당한 회전을 통해 원래의 나선과 일치하는 성질이다. 예를 들어 ''e''^2π''b'' 배로 확대한 것은 회전 없이 원래의 나선과 동일하다.^[21] 스피라 미라빌리스(Spira mirabilis)는 이러한 자기유사성으로 인해 그 모양은 변하지 않고 크기만 변하는 특징을 갖는다.

3. 3. 곡률

로그 나선

r=a e^{k\varphi} \;,\; k\ne 0,

은 다음과 같은 곡률을 갖는다. (나선 참조)

'''곡률''': $\kappa=\frac{1}{r\sqrt{1+k^2}}=\frac{\cos \alpha}{r}$

3. 4. 호의 길이

L(\varphi_1,\varphi_2) = \frac{\sqrt{k^2+1}}{k}(r(\varphi_2)-r(\varphi_1)) = \frac{r(\varphi_2)-r(\varphi_1)}{\sin \alpha}

^[6] 특히,

k > 0

인 경우

L(-\infty,\varphi_2) = \frac{r(\varphi_2)}{\sin \alpha}

(

\color{red}

유한!)이다. 이 속성은 미적분학이 발명되기도 전에 에반젤리스타 토리첼리에 의해 처음으로 인식되었다.^[6]

3. 5. 다른 곡선과의 관계

로그 나선

r=a e^{k\varphi} \;,\; k\ne 0,

은 다음과 같은 속성을 갖는다.

'''다른 곡선과의 관계''': 로그 나선은 자체 인볼루트, 에볼루트 및 중심을 기반으로 하는 페달 곡선과 합동이다.^[21]
'''복소 지수 함수''': 지수 함수는 복소 평면에서 실수축 또는 허수축과 평행하지 않은 모든 선을 복소 평면에서 중심이 $0$ 인 모든 로그 나선으로 정확하게 사상한다.^[21]

:

z(t)=\underbrace{(kt+b)\; +it}_{\text{line}}\quad  \to\quad  e^{z(t)}=e^{kt+b}\cdot e^{it}= \underbrace{e^b e^{kt}(\cos t+i\sin t)}_{\text{log. spiral}}

:로그 나선의 피치 각도

\alpha

는 선과 허수축 사이의 각도이다.

마찬가지로 복소 평면에서, 실수부와 허수부가 모두 0이 아닌 상수 ''k''에 대한 함수 ''x''^''k''는, 실수축을 대수 나선에 사상한다.

또한, 복소 평면에서 절대값이 1 이외이고, 음이 아닌 실수가 아닌 임의의 복소수의 실수승(의 주값)의 집합은 대수 나선을 이룬다.

4. 자연에서의 로그 나선

로그 나선은 자연 현상에서 폭넓게 관찰된다.

300px	300px
로그 나선, 축경사 10°	앵무조개 껍질의 단면 (파란색 점선은 성장률 매개 변수 $b = 0.1759$ 를 기반으로 한다)

각막 신경은 각막 상피층 근처에서 로그 나선 패턴으로 배열된다.^[12]
로그 나선 해변은 해안에 의한 파동 굴절과 회절의 결과로 형성될 수 있다. 캘리포니아주 하프 문 베이가 대표적인 예이다.^[15]

한편, 거미줄에서 보이는 가로실의 소용돌이는 아르키메데스 나선이다. 말똥고둥처럼 굵어지지 않은 채로 권수가 많은 달팽이도 아르키메데스 나선에 가깝다.

4. 1. 생물

몇몇 자연 현상에서 로그 나선에 가까운 곡선을 찾을 수 있다. 다음은 몇 가지 예시와 이유이다.

매가 먹이를 쫓아가는 방식은 먹이가 직선으로 이동한다고 가정할 때 고전적인 추격과 관련된다. 매의 가장 선명한 시야는 비행 방향에 대해 특정 각도를 이루며, 이 각도는 나선의 피치와 동일하다.^[7]
곤충이 광원에 접근하는 방식은 광원을 비행 경로에 대해 일정한 각도로 유지하는 데 익숙하기 때문이다. 일반적으로 태양(또는 야행성 종의 경우 달)이 유일한 광원이기 때문에 그렇게 비행하면 실질적으로 직선을 그리게 된다.^[8]
연체 동물의 껍질과 같은 생물학적 구조에서 나타난다.^[14] 이러한 경우, 다각형과 같이 확장되는 유사한 모양으로 구성되기 때문일 수 있다.

매가 먹이에 접근할 때, 벌이 꽃을 향해 날아갈 때 대수 나선을 그리며 비행하는 것을 볼 수 있다. 매는 먹이를 일정한 각도로 보기 위해,^[22] 벌은 꽃을 향해 일정한 각도로 날아가기 때문이다.^[23]

연체동물의 껍데기, 소나 양의 뿔, 코끼리의 엄니 등, 경화되는 부위에서 본체의 성장에 따라 차츰 큰 부분을 추가함으로써 성장하는 생물의 기관에서 대수 나선이 관찰된다.^[24] 그 이유는 그림과 같이 닮은 꼴로 조금씩 커지는 다각형이 차례로 형성되어 가면 나선에 가까운 형태가 그려지기 때문이라고 설명된다. 성장이 연속적이 되도록 각 단편을 작게 해나가면, 그 극한 도형의 경계선은 정확히 대수 나선을 그린다. 피치는 생물에 따라 다르며, 소라에서는 약 10도, 전복에서는 약 30도, 대합에서는 약 50도이다.^[25] 피치가 작은 경우에는 자신을 감을 수 있으므로 달팽이에서 보이며, 피치가 큰 것은 크게 입을 벌린 형태의 이매패나 전복, 삿갓조개와 같은 것에서 볼 수 있다.

4. 2. 천체

나선 은하의 팔은 피치가 약 10도에서 40도의 로그 나선 형태에 가깝다.^[9] 우리 은하는 여러 개의 나선 팔을 가지고 있으며, 각각은 약 12도의 피치를 가진 대략적인 로그 나선이다.^[10] 그러나 나선 은하는 종종 로그 나선, 아르키메데스 나선 또는 쌍곡 나선으로 모델링되었지만, 피치 각도는 로그 나선과 달리 은하 중심으로부터의 거리에 따라 달라지며, 또한 그들을 모델링하는 데 사용되는 다른 수학적 나선과도 다르다.^[11] 태양계를 포함하는 은하는 주요 나선 팔을 4개 가지고 있으며, 그 피치는 비교적 작고 12도 정도로 생각된다.^[26]

열대 저기압의 강우대, 예를 들어 허리케인에서도 로그나선이 발견된다.^[13]

4. 3. 기타

로그 나선은 자연 현상에서 다양한 형태로 나타난다.

동물의 행동:
매가 먹이에 접근할 때, 가장 선명한 시야를 확보하기 위해 비행 방향과 일정한 각도를 유지하며 로그 나선 궤적을 그린다.^[7]
곤충은 광원을 비행 경로에 일정한 각도로 유지하는 습성이 있다. 태양(또는 달)을 기준으로 비행하면 로그 나선 궤적이 나타난다.^[8] 등각 항로는 극지방 근처에서 로그 나선과 유사하다.
벌이 꽃을 향해 날아갈 때도 로그 나선 궤적을 보인다.^[23]

우주:
나선 은하의 팔은 로그 나선 형태를 띤다.^[9] 우리 은하는 약 12도의 피치를 가진 여러 개의 나선 팔을 가지고 있다.^[10] 다만, 은하의 피치 각도는 중심으로부터 거리에 따라 달라지기도 한다.^[11]
태양계를 포함하는 은하는 주요 나선 팔을 4개 가지고 있으며, 그 피치는 비교적 작고, 12도 정도로 생각된다.^[26]

생물학적 구조:
각막 신경은 각막 상피층 근처에서 로그 나선 패턴으로 배열된다.^[12]
열대 저기압의 강우대(예: 허리케인)도 로그 나선 형태를 보인다.^[13]
연체 동물의 껍질, 소나 양의 뿔, 코끼리의 엄니 등 생물 기관은 성장하면서 로그 나선 형태를 나타낸다.^[14]^[24] 이는 다각형처럼 유사한 모양이 확장되는 방식으로 구성되기 때문이다.
소라는 약 10도, 전복은 약 30도, 대합은 약 50도의 피치를 가진다.^[25]

해안 지형:
로그 나선 해변은 파동 굴절과 회절의 결과로 형성된다. 캘리포니아주 하프 문 베이가 대표적인 예이다.^[15]

5. 인공물에서의 로그 나선

아르키메데스의 나선만큼은 아니지만, 데카르트나 베르누이가 수학적으로 해석하기 전부터 자연계에 나타나는 로그 나선은 사람들에게 인식되었고, 미술 작품이나 건축물에 사용되었다.^[27]^[28]

자유 와류가 로그 나선을 그리는 것과 비점성 유체의 궤적이 로그 나선을 그리기 때문에,^[29] 수력 발전에 있어서 프란시스 수차 등의 수차 원동기나 와류 펌프의 디퓨저 및 케이싱 설계에는 오래전부터 로그 나선 곡선이 사용되고 있다.^[29]^[30] 비교적 저압의 시로코 팬의 날개 및 케이싱도 로그 나선이지만,^[31] 비용 상승 때문에 초소형 팬에서는 케이싱을 로그 나선이나 원통으로 대신하는 경우도 적지 않았다. 그러나 가정용 게임기의 열용량 향상에 따라 굳이 비용이 높아지는 로그 나선 케이싱의 채용을 결정하는 사례가 나왔다.^[32]

중심에서 뻗은 반직선과 로그 나선이 이루는 각이 일정하다는 것을 가위에 응용한 제품도 출시되었다. 문구 회사 플러스에서 칼날의 벌어진 각도를 항상 30°로 유지하도록 한쪽 칼날을 로그 나선 곡선 날^[33]로 만든 가위가 발매된 적이 있다.^[34]

5. 1. 건축

데카르트나 베르누이가 수학적으로 해석하기 전부터 자연계에 나타나는 로그 나선은 사람들에게 인식되었고, 미술 작품이나 건축물에 사용되었다. 예를 들어, 고대 그리스 건축 양식 중 하나인 이오니아식의 주두(기둥머리)의 특징은 쌍을 이루는 소용돌이 장식이며, 로그 나선에 가까운 것도 있다.^[27] 또한, 주세페 모모가 설계한 바티칸 미술관의 이중 나선 계단은 정면에서 보면 로그 나선이다.^[28]

5. 2. 공학

로그 나선은 다양한 공학 분야에서 응용된다.

수력 터빈 및 펌프: 프란시스 수차와 같은 수차 원동기나 와류 펌프의 디퓨저 및 케이싱 설계에는 비점성 유체의 궤적이 로그 나선을 그리는 특성을 활용하여 로그 나선 곡선이 사용된다.^[29]^[30]
시로코 팬: 비교적 저압의 시로코 팬의 날개 및 케이싱에도 로그 나선이 사용된다.^[31] 플레이스테이션 3 후기형이나 플레이스테이션 4와 같이, 내부 냉각 기구에 로그 나선 케이싱을 채택하여 열 처리 특성을 개선한 사례도 있다.^[32]
스프링 장착 캠밍 장치: 암벽 등반에서 사용되는 스프링 장착 캠밍 장치는 로그 나선 모양의 캠 표면을 가지고 있어, 바위 틈에 삽입 시 일정한 각도를 유지하며 결합된 너비를 틈의 너비에 맞게 확장한다.^[20]
로그 나선형 베벨 기어: 기어 이빨 중심선이 로그 나선인 나선형 베벨 기어는 맞물림 전송의 안정성을 높이는 데 사용된다.^[19]
로그 나선형 안테나: 나선형 안테나는 주파수 독립 안테나로, 광대역에서 복사 패턴, 임피던스 및 편파가 크게 변경되지 않는다.^[17]
레이저 커터 케프 제거 메커니즘: 레이저 커터와 같은 기계에서 발생하는 재료 제거량(커프) 차이로 인한 정밀도 손실을 보정하기 위해, 로그 나선의 자기 유사성 속성을 활용한 케프 제거 메커니즘이 설계되었다.^[18]
가위: 중심에서 뻗은 반직선과 로그 나선이 이루는 각도가 일정하다는 점을 응용하여, 칼날의 벌어진 각도를 항상 30°로 유지하는 로그 나선 곡선 날을 가진 가위도 있다.^[33]^[34]

5. 3. 기타

기원전 5세기에 완성된 이오니아식 건축 양식의 신전 에레크테이온의 주두에는 쌍을 이루는 소용돌이 장식이 있는데, 이는 로그 나선에 가까운 형태이다.^[27] 주세페 모모가 설계한 바티칸 미술관의 이중 나선 계단은 정면에서 보면 로그 나선 모양이다.^[28]

자유 와류와 비점성 유체의 궤적이 로그 나선을 그리기 때문에, 프란시스 수차와 같은 수차 원동기나 와류 펌프의 디퓨저 및 케이싱 설계에는 로그 나선 곡선이 오래전부터 사용되었다.^[29]^[30] 시로코 팬의 날개 및 케이싱도 로그 나선 형태이지만, 비용 문제로 인해 초소형 팬에서는 케이싱을 로그 나선이나 원통으로 대신하는 경우도 있었다. 그러나 플레이스테이션 3 후기형이나 플레이스테이션 4와 같이 가정용 게임기의 열용량 향상을 위해 로그 나선 케이싱을 채택하여 열 처리 특성을 개선한 사례도 있다.^[32]

중심에서 뻗은 반직선과 로그 나선이 이루는 각이 일정하다는 성질을 활용한 제품도 있다. 문구 회사 플러스는 칼날이 벌어진 각도를 항상 30°로 유지하도록 한쪽 칼날을 로그 나선 곡선으로 만든 가위를 출시했다.^[33]^[34]

6. 황금 나선

황금 나선은 황금비와 관련된 특별한 로그 나선으로, 피보나치 수에 비례하는 반원 시퀀스로 만들어진 "피보나치 나선"으로 근사할 수 있다. 앵무조개 껍데기 무늬가 황금 나선을 이룬다는 설이 있지만, 이에 대한 합리적인 이유는 알려져 있지 않다. 또한, 앵무조개 껍데기의 피치는 8도에서 10도로 황금 나선의 피치(약 17.03239도)와는 차이가 있어 황금 나선이 아니라는 지적도 있다.^[35]^[36]

6. 1. 정의

황금 나선은 90도 회전(피치 각도 약 17.03239도)마다 황금비만큼 바깥쪽으로 성장하는 로그 나선이다. 이는 피보나치 수에 비례하는 반원 시퀀스로 만들어진 "피보나치 나선"으로 근사할 수 있다.

황금 나선(golden spiral)은 황금비 φ와 관련된 대수 나선의 일종으로, 다음의 식으로 표현된다.

b|b^영어 = log φ|로그 φ^영어 / (π/2) ≈ 0.30634896253

위 식에서 상수 ''b''에 대하여 ''r'' = ''e''^''b''θ로 주어지는 것이다. 또한, ''B'' = ''e''^''b''라고 놓고, ''r'' = ''B''^θ로도 정의된다. 양의 ''b''에 대해서는 다음과 같다.

B|B^영어 = φ^2/π ≈ 1.358456274

음의 'b'에 대해서는 다음과 같다.

B|B^영어 = φ^-2/π ≈ 0.736129693

황금 나선의 피치는 약 17.03239도이다.

앵무조개의 껍데기 무늬는 황금 나선을 그리고 있다는 설이 유명하다. 그러나, 그 합리적인 이유는 알려져 있지 않으며, 실제로는 앵무조개 껍데기의 피치가 8도에서 10도로 17도와는 거리가 멀다는 등, 황금 나선이 아니라는 지적도 있다.^[35]^[36]

6. 2. 앵무조개 껍데기와의 관계 (논란)

앵무조개 껍데기 무늬가 황금 나선을 그린다는 설이 유명하지만, 그 합리적인 이유는 알려져 있지 않다. 실제 앵무조개 껍데기의 피치는 8도에서 10도로 17도와는 거리가 멀어, 황금 나선이 아니라는 지적도 있다.^[35]^[36]

7. 역사

대수 나선을 연구한 야코프 베르누이의 묘비. 하단에 ''Eadem mutata resurgo''라는 문구와 함께, 잘못 아르키메데스 나선이 새겨져 있다.

로그 나선(대수 나선)에 대한 수학적 연구는 17세기부터 시작되었다. 르네 데카르트는 처음으로 로그 나선을 수학적으로 고찰했고, 에반젤리스타 토리첼리는 대수 나선 상의 한 점에서 중심까지의 거리가 유한함을 보였다.^[38] 야코프 베르누이는 대수 나선의 신개선 및 축폐선이 자기 자신과 일치하며, "확대해도 변하지 않는다"는 성질에 매료되어 라틴어로 ''Spira mirabilis'' (경이로운 나선)라고 불렀다.^[39]

알브레히트 뒤러는 1525년 저서 『측량법 교칙』(Underweysung der Messung mit dem Zirckel und Richtscheyt)에서 아르키메데스 나선과 그 변형의 작도법에 대해 논하면서, 대수 나선으로 해석될 수 있는 곡선에 대한 개념을 언급했다.^[37]

7. 1. 알브레히트 뒤러 (1525)

알브레히트 뒤러는 1525년 저서 『측량법 교칙』(Underweysung der Messung mit dem Zirckel und Richtscheyt)에서 아르키메데스 나선과 그 변형의 작도법에 대해 논했다. 그는 "중심을 향하면서 동시에 상하로도 선회하는, 안으로도 밖으로도 무한히 나아가는 선이 생각될 수 있다. 이 선은 무한히 크고 작기 때문에 사람의 손으로 그릴 수 없다. 시작과 끝이 없고, 찾아낼 수 없으며, 단지 머릿속에서 이해될 뿐이다."라고 말했다.^[37]

아직 곡선을 식으로 나타내는 방법이 알려지지 않았던 시대였고, 모호한 표현이긴 하지만, 이는 대수 나선에 대해 말하고 있는 것으로 해석된다.^[37]

7. 2. 르네 데카르트 (17세기)

해석기하학의 시조인 르네 데카르트는 로그 나선을 처음으로 수학적으로 고찰하였다. 데카르트는 나선의 진행 방향이 중심에 대해 항상 일정한 각을 이룬다는 점에 주목하여 이 나선을 등각 나선이라고 불렀다.^[22]

7. 3. 에반젤리스타 토리첼리

에반젤리스타 토리첼리는 대수 나선 위의 한 점에서 중심까지의 거리가 유한함을 증명했다.^[38]

7. 4. 야코프 베르누이

야코프 베르누이는 대수 나선의 신개선 및 축폐선이 자기 자신과 일치함을 보였다. 그는 이 나선의 "확대해도 변하지 않는다"라는 등의 성질에 매료되어 ''Spira mirabilis'' (라틴어로 경이로운 나선)라고 불렀다. 베르누이는 ''Eadem mutata resurgo'' (변해도 똑같이 다시 태어난다)라는 문구와 함께 묘비에 이 나선을 새겨달라고 했지만, 잘못 아르키메데스 나선이 새겨졌다.^[39]

8. 한국에서의 로그 나선

한국에서는 로그 나선이 전통 건축, 예술, 그리고 현대 과학기술 분야에서 다양하게 나타난다.

참조

_[1] 서적 Underweysung der Messung, mit dem Zirckel und Richtscheyt, in Linien, Ebenen unnd gantzen corporen https://digital.slub[...]
_[2] 서적 The Perfect Shape: Spiral Stories Springer International Publishing
_[3] 서적 Divine Proportion: Φ Phi in Art, Nature, and Science Sterling Publishing Co
_[4] 서적 The Golden Ratio: The Story of Phi, The World's Most Astonishing Number https://archive.org/[...] Broadway Books
_[5] 문서 A Handbook on Curves and Their Properties J. W. Edwards
_[6] 서적 The history of the calculus and its conceptual development https://books.google[...] Courier Dover Publications
_[7] 간행물 Organismal Biology: Flying Along a Logarithmic Spiral 2000-12-08
_[8] 서적 Discovering Moths: Nighttime Jewels in Your Own Backyard https://books.google[...] Down East Enterprise Inc
_[9] 서적 Spiral structure in galaxies: a density wave theory https://books.google[...] MIT Press
_[10] 서적 The universal book of mathematics: from Abracadabra to Zeno's paradoxes https://books.google[...] John Wiley and Sons
_[11] 간행물 Pitch angle variations in spiral galaxies 2013-09
_[12] 문서 Transgenic corneal neurofluorescence in mice: a new model for in vivo investigation of nerve structure and regeneration 2007-04
_[13] 서적 Treatise on physics, Volume 1 https://archive.org/[...] Churchill
_[14] 서적 Spiral symmetry World Scientific
_[15] 서적 Beach management: principles and practice https://books.google[...] Earthscan
_[16] 웹사이트 kerf-canceling mechanisms https://hpi.de/baudi[...] 2020-12-26
_[17] 간행물 Frequency-independent antennas and broad-band derivatives thereof https://ieeexplore.i[...] 1992
_[18] 서적 Proceedings of the 33rd Annual ACM Symposium on User Interface Software and Technology ACM 2020-10-20
_[19] 간행물 Review on logarithmic spiral bevel gear 2020
_[20] 서적 Imagine Math 6: Between Culture and Mathematics Springer International Publishing
_[21] 문서 岩波数学辞典第4版 100.G
_[22] 문서 リヴィオ、p. 149
_[23] 문서 上村、p. 125
_[24] 문서 世界大百科事典平凡社
_[25] 문서 上村、p. 115
_[26] 문서 The spiral structure of our Galaxy determined from H II regions https://ui.adsabs.ha[...] 1976-05
_[27] 문서 アータレイ、p. 83
_[28] 문서 アータレイ、p. 110
_[29] 간행물 https://www.hitachih[...] 2023-11-15
_[30] 간행물 https://www.jstage.j[...] 日本機械学会 2023-11-15
_[31] 웹사이트 ファンケースの設計 https://sunriseyokoh[...] 有限会社サンライズ 2023-11-15
_[32] 웹사이트 国内発売まであと約1か月のPS4，筐体設計の秘密が明らかに https://www.4gamer.n[...] 4Gamer.net 2023-11-15
_[33] 웹사이트 ベルヌーイカーブ刃とは!? https://bungu.plus.c[...] PLUS 2023-11-15
_[34] 웹사이트 PLUS フィットカットカーブ https://bungu.plus.c[...] PLUS 2023-11-15
_[35] 문서 上村、p.129
_[36] 문서 Zell-Ravenheart
_[37] 문서 "『「測定法教則」注解』"
_[38] 문서 마올
_[39] 문서 마올
_[40] 웹사이트 Spira mirabilis http://jwilson.coe.u[...]
_[41] 서적 Divine Proportion: Φ Phi in Art, Nature, and Science https://archive.org/[...] Sterling Publishing Co
_[42] 서적 The Golden Ratio: The Story of Phi, The World's Most Astonishing Number https://archive.org/[...] Broadway Books
_[43] 서적 A Handbook on Curves and Their Properties J. W. Edwards

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com