문항 반응 이론
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
문항 반응 이론(IRT)은 응답자의 능력 수준과 문항의 특성을 수학적으로 모델링하여 시험 및 평가를 분석하는 심리 측정 이론이다. 고전 검사 이론(CTT)과 비교하여, IRT는 오차의 특성 규명에 있어 더 강력한 가정을 가지며, 문항 난이도와 능력의 척도를 동일하게 하여 유연성을 제공한다. IRT는 문항 반응 함수(IRF)를 통해 특정 능력 수준을 가진 사람이 정답을 맞힐 확률을 제시하며, 1PL, 2PL, 3PL과 같은 다양한 모델을 사용한다. 모델 적합도 분석을 통해 데이터의 적합성을 평가하고, 정보 함수를 통해 문항 및 검사의 신뢰도를 확장한다. 의학계 공통 시험, IT 관련 시험, 외국어 능력 시험 등 다양한 분야에서 활용되며, 대한민국에서도 의학계 시험과 IT 관련 시험에 적용되고 있다.
더 읽어볼만한 페이지
- 잠재 변수 모형 - 잠재 의미 분석
잠재 의미 분석은 텍스트 데이터의 의미 구조를 파악하기 위해 문서-단어 행렬에 특이값 분해를 적용하여 차원을 축소하고 잠재된 의미를 추출하는 정보 검색 기술이다. - 잠재 변수 모형 - 토픽 모델
토픽 모델은 텍스트 데이터에서 문서의 주제를 찾기 위해 사용되는 통계적 모델링 방법으로, 잠재 의미 분석(LSI)에서 잠재 디리클레 할당(LDA)까지 다양한 모델이 개발되어 텍스트 데이터 분석 외 여러 분야에 응용되며, Mallet, Gensim 등의 도구로 사용 가능하다. - 교육 평가 - 기능적 행동 평가
기능적 행동 평가는 응용 행동 분석에서 문제 행동을 유지하는 변인을 식별하는 방법으로, 문제 행동의 기능적인 선행 자극과 결과를 파악하여 문제 행동의 원인이 되는 교육 환경 내 요인을 분석하고 적절한 치료법과 긍정적인 지원 계획을 수립하는 데 기여한다. - 교육 평가 - 총괄평가
총괄 평가는 학습 활동 후 학습 성과를 측정하여 학생의 강점과 약점을 파악하고 교육 프로그램의 효과성을 검증하는 평가 방법이다. - 심리측정학 - 재현성
재현성은 과학적 연구의 신뢰성을 평가하는 요소로, 동일한 조건에서 유사한 결과를 얻을 수 있는 정도를 의미하며, 실험 방법과 데이터의 투명한 공개를 통해 확보해야 한다. - 심리측정학 - 조작주의
조작주의는 과학적 개념을 측정 과정을 통해 정의하는 과학적 실천 방법으로, 물리학에서 시작되어 다양한 분야에서 활용되지만, 경제학에서는 주관적인 개념을 정당화하는 데 사용된다는 비판과 함께 복잡한 사회 현상에 대한 신중한 검토가 필요하다.
| 문항 반응 이론 | |
|---|---|
| 개요 | |
| 분야 | 심리 측정학 |
| 다른 이름 | 잠재특성 이론 |
| 영어 | Item Response Theory (IRT) |
| 상세 정보 | |
| 목적 | 문항 분석, 시험 설계, 점수 산출 |
| 특징 | 문항 난이도와 변별도 추정 개인의 능력 추정 표본 의존성 극복 |
| 관련 개념 | 문항 특성 곡선 (ICC) 정보 함수 적합도 검정 |
| 모형 | 1-모수 로지스틱 모형 (1PL) 2-모수 로지스틱 모형 (2PL) 3-모수 로지스틱 모형 (3PL) 일반화된 부분 점수 모형 (GPCM) |
| 활용 분야 | 표준화 검사 적응적 검사 (CAT) 설문 조사 교육 평가 |
2. 역사적 배경
문항 반응 함수의 개념은 1950년 이전에 존재했다. 문항 반응 이론(IRT)을 이론으로 정립하는 선구적인 연구는 1950년대와 1960년대에 이루어졌다. 교육평가원(Educational Testing Service)의 심리측정학자 프레데릭 M. 로드(Frederic M. Lord), 덴마크 수학자 게오르그 라슈(Georg Rasch), 오스트리아 사회학자 폴 라자스펠트(Paul Lazarsfeld)는 독립적으로 유사한 연구를 수행한 세 명의 선구자이다.[4] 벤자민 드레이크 라이트(Benjamin Drake Wright)와 데이비드 안드리치(David Andrich)는 IRT의 발전을 이끈 주요 인물이다.
문항 반응 이론(IRT)은 평가 문항에 대한 응답을 바탕으로 피험자의 특성(인지 능력, 지식, 태도 등)이나 문항의 난이도, 변별도를 측정하는 검사 이론이다. 개인의 능력과 문항 난이도와 같은 모수를 구할 때, 정답/오답과 같은 이산적인 결과를 가지고 확률론적으로 접근한다.[4]
IRT는 1970년대 후반과 1980년대에 이르러서야 널리 사용되었는데, 이는 실무자들이 IRT의 유용성과 장점에 대해 알게 되었고, 개인용 컴퓨터가 많은 연구자들에게 IRT에 필요한 컴퓨팅 능력을 제공했기 때문이다. 1990년대에는 마가렛 우(Margaret Wu)가 PISA 및 TIMSS 데이터를 분석하는 두 개의 문항 반응 소프트웨어 프로그램인 ACER ConQuest(1998)와 R-패키지 TAM(2010)을 개발했다.
3. 주요 특징 및 장점
IRT의 주요 특징 및 장점은 다음과 같다:3. 1. 고전검사이론(CTT)과의 비교
문항 반응 이론(IRT)은 고전검사이론(CTT, Classical test theory)보다 일반적으로 더 큰 유연성과 정교한 정보를 제공하여 더 나은 평가를 가능하게 하는 이론이다.
IRT는 CTT와 비교하여 다음과 같은 차이점과 장점을 가진다.
CTT와 IRT 간의 개념적 상응 관계를 위한 몇 가지 구체적인 유사점은 다음과 같다.
IRT는 CTT 내에서 암묵적으로 나타나는 가설을 더 명시적으로 만들기 때문에, ''강력한 진실 점수 이론'' 또는 ''현대 심리 검사 이론''이라고 불리기도 한다.
4지 선다형 문제 100문항(1문항당 10점, 1000점 만점)으로 구성된 시험을 예시로, CTT와 IRT 관점을 비교하면 다음과 같다.
고전 검사 이론(CTT)의 문제점:
문항 반응 이론(IRT)의 이점:
4. 문항 반응 함수 (Item Response Function, IRF)
문항 반응 함수(Item Response Function, IRF)는 주어진 능력 수준을 가진 사람이 문항에 정답을 맞힐 확률을 나타내는 함수이다. 능력 수준이 낮은 사람은 정답 확률이 낮고, 높은 사람은 정답 확률이 높다. 예를 들어, 수학 능력이 높은 학생은 수학 문제에 정답을 맞힐 확률이 더 높다.
문항 반응 이론(IRT)의 목적은 평가와 평가의 개별 문항이 얼마나 잘 작동하는지를 평가하기 위한 틀을 제공하는 것이다. IRT는 주로 교육 분야에서 시험 개발 및 설계, 문항 뱅크 유지, 시험의 연속적인 버전 간 문항 난이도 동등화 등에 활용된다.[5]
IRT 모델은 '잠재 특성 모델'이라고도 불리는데, 이는 문항 반응이 직접 관찰되지 않고, 나타난 반응으로부터 추론해야 하는 가설적 특성(잠재 특성)의 징후로 간주되기 때문이다.
IRT는 세 가지 가정을 전제로 한다.
# 로 표시되는 단일 차원 특성
# 문항의 국소 독립성
# 한 사람이 문항에 응답하는 것은 수학적인 ''문항 반응 함수''(IRF)로 모델링할 수 있다.
여기서 단일 차원은 주어진 목적이나 사용과 관련하여 정의되거나 경험적으로 입증되어야 하는 동질성을 의미하며, 측정할 수 있는 양이 아니다. '국소 독립성'은 (a) 하나의 문항이 사용될 가능성이 다른 문항의 사용과 관련이 없고 (b) 문항에 대한 응답은 모든 시험 응시자의 독립적인 결정이며, 즉, 부정행위나 짝 또는 그룹 작업이 없음을 의미한다.
IRT 모델은 크게 단일 차원 모델과 다차원 모델로 나눌 수 있다. 단일 차원 모델은 하나의 능력 차원()을 필요로 하는 반면, 다차원 모델은 여러 특성에서 비롯될 것으로 가정한 응답 데이터를 모델링한다. 하지만 복잡성 때문에 대부분의 IRT 연구와 응용은 단일 차원 모델을 사용한다.
문항 반응 함수의 개념은 1950년 이전에 존재했으며, 1950년대와 1960년대에 교육평가원(Educational Testing Service)의 심리측정학자 프레데릭 M. 로드(Frederic M. Lord), 덴마크 수학자 게오르그 라슈(Georg Rasch), 오스트리아 사회학자 폴 라자스펠트(Paul Lazarsfeld) 등에 의해 이론으로 정립되었다.[4] 1970년대 후반과 1980년대에 개인용 컴퓨터의 발달로 IRT가 널리 사용되었으며, 1990년대에는 마가렛 우(Margaret Wu)가 PISA 및 TIMSS 데이터 분석을 위한 소프트웨어 프로그램을 개발했다.
IRT는 일반적으로 고전 검사 이론(CTT)보다 개선된 것으로 평가받는다. IRT는 더 큰 유연성과 정교한 정보를 제공하며, 컴퓨터 적응형 검사와 같은 일부 응용 프로그램은 IRT를 통해서만 가능하다. 또한 IRT는 연구자가 신뢰도(심리측정)을 향상시키는 데 도움을 준다.
IRT 모델은 채점되는 응답 수에 따라 이분형 모델과 다지선다형 모델로 분류할 수 있다. 이분형 모델은 전형적인 객관식 문제처럼 정답/오답으로만 채점되는 경우에 사용된다. 다지선다형 모델은 각 응답에 따라 다른 점수를 부여하는 경우에 사용되며, 리커트형 문항(예: "1에서 5까지의 척도로 평가")이 그 예시이다.
이분 문항 반응 모형은 사용되는 모수의 수에 따라 1PL, 2PL, 3PL, 4PL 등으로 구분된다. 3PL은 위치, 변별도, 추측도를 사용하며, 2PL은 추측도를 제외한 두 가지 모수를 사용한다. 1PL은 모든 문항의 변별도가 동일하다고 가정하고 위치만을 고려한다. 4PL은 이론적으로 존재하지만 거의 사용되지 않는다.
정규 확률 분포 기반의 문항 반응 함수를 사용하는 정규 오자이브 모델도 있다.
4. 1. 3 모수 로지스틱 모형 (3PL)
3 모수 로지스틱 모형(3PL)은 문항 반응 이론(IRT)에서 사용되는 모델 중 하나로, 객관식 문제와 같이 이분형(정답/오답) 문항에 대한 응답을 설명한다. 3PL은 문항의 특성을 나타내는 세 가지 매개변수를 사용하여 응시자의 능력()과 정답 확률 간의 관계를 설명한다.3PL에서 문항 ''i''에 대한 정답 확률은 다음과 같은 식으로 표현된다.
:
여기서 각 매개변수는 다음과 같은 의미를 갖는다.
- ''' (난이도)''': 문항의 난이도를 나타내는 값이다. 응시자의 능력이 일 때 정답 확률이 가 된다. 이는 (최소)와 1(최대) 사이의 중간 지점이자, 기울기가 최대인 지점이다.
- ''' (변별도)''': 문항이 응시자의 능력을 얼마나 잘 구별하는지를 나타내는 값으로, 문항 특성 곡선(ICC)의 기울기를 결정한다. 값이 클수록 능력이 높은 응시자와 낮은 응시자를 더 잘 구별한다. 최대 기울기는 이다.
- ''' (추측도)''': 응시자가 답을 몰라도 우연히 정답을 맞힐 확률을 나타내는 값으로, 문항 특성 곡선의 하한 점근선 역할을 한다. 예를 들어, 4지선다형 문제의 경우 는 약 0.25가 된다.
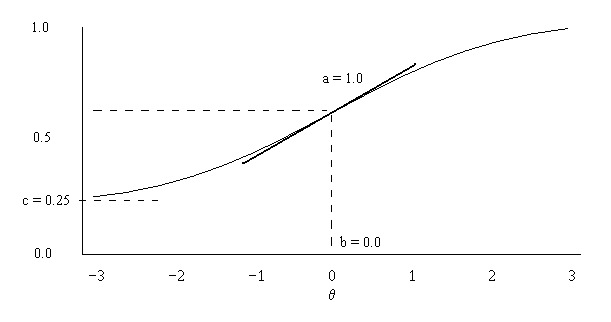
위 그림은 3PL 모델의 문항 특성 곡선(ICC) 예시를 보여준다. 곡선의 형태는 문항 매개변수에 의해 결정된다.
만약 이면, 및 로 단순화된다. 이는 ''b''가 50% 성공 수준(난이도)과 같고, ''a''(4로 나눈 값)가 최대 기울기(변별도)이며, 이는 50% 성공 수준에서 발생함을 의미한다. 또한, 정답에 대한 로짓(로그 오즈)은 이다( 가정). 특히 능력 ''θ''가 난이도 ''b''와 같으면 정답에 대한 오즈가 동일하며(1:1, 즉 로짓 0), 능력과 난이도 간의 차이가 클수록 정답일 가능성이 높아지며, 변별도 ''a''는 오즈가 능력에 따라 얼마나 빠르게 증가하거나 감소하는지를 결정한다.
객관식 항목과 같은 경우, 매개변수 는 정답 확률에 대한 추측의 영향을 설명하는 데 사용된다. 이는 매우 낮은 능력을 가진 개인이 우연히 이 항목을 맞힐 확률을 나타내며, 수학적으로 낮은 점근선으로 표현된다. 4개의 선택지가 있는 객관식 항목은 예시 항목과 같은 IRF를 가질 수 있다. 매우 낮은 능력의 지원자가 정답을 추측할 확률이 1/4이므로 는 약 0.25가 된다.[6]
3PL은 2 모수 로지스틱 모형(2PL) 및 1 모수 로지스틱 모형(1PL, 라쉬 모델)과 비교할 수 있다.
- 2PL: 3PL에서 인 경우와 동일하며, 추측 요인을 고려하지 않는다.
- 1PL (라쉬 모델): 모든 문항의 변별도가 동일하다고 가정하고, 난이도()만을 고려한다.
2PL은 정답을 맞힐 확률이 매우 낮은 문항(예: 빈칸 채우기 문항("121의 제곱근은 무엇입니까?")) 또는 무작위 추측의 개념이 적용되지 않는 문항(예: 성격, 태도 또는 흥미 문항("나는 브로드웨이 뮤지컬을 좋아한다. 동의/비동의"))에 적합하다.
1PL은 무작위 추측이 존재하지 않거나 관련이 없을 뿐만 아니라, 모든 문항이 변별도 측면에서 동일하다고 가정하며, 이는 모든 문항에 동일한 부하량이 있는 일반적인 요인 분석과 유사하다. 개별 문항 또는 개인은 이차 요인을 가질 수 있지만, 이는 상호 독립적이고 집합적으로 직교하는 것으로 가정된다.
4. 2. 다른 IRT 모형
IRT 모델은 채점되는 응답 수에 따라 분류할 수 있다. 전형적인 객관식 문제는 '이분형'으로, 정답과 오답으로만 채점된다. 반면, 각 응답에 따라 다른 점수를 부여하는 '다지선다형' 결과를 위한 모델도 있다.[7][8] 리커트형 문항(예: "1에서 5까지의 척도로 평가")이 그 예시이며, 부분 점수 채점에는 다지선다형 라쉬 모델 등이 적용될 수 있다.이분 문항 반응 모형은 사용되는 모수의 수에 따라 구분된다.[9] 3PL(3 모수 모형)은 위치(), 변별도(), 추측도()를 사용한다. 2PL(2 모수 모형)은 무작위 추측이 없다고 가정하고, 문항이 위치와 변별도에서 다양할 수 있다고 본다. 1PL(1 모수 모형)은 무작위 추측이 능력의 일부이며, 모든 문항이 동일한 변별도를 갖는다고 가정하여 문항을 위치()로만 설명한다. 1PL은 특정 객관성 속성을 가지는데, 이는 문항 난이도 순위가 능력과 관계없이 모든 응답자에게 동일하고, 개인 능력 순위가 난이도와 관계없이 문항에 대해 동일함을 의미한다. 즉, 1PL은 표본 독립적이다. 이론적으로 4PL(4 모수 모형)도 있지만 거의 사용되지 않는다.
2PL은 정답 확률이 매우 낮은 문항(예: 빈칸 채우기)이나 무작위 추측이 적용되지 않는 문항(예: 성격, 태도, 흥미 문항)에 적합하다. 1PL은 모든 문항이 변별도 측면에서 동일하다고 가정하며, 이는 모든 문항에 동일한 부하량이 있는 일반적인 요인 분석과 유사하다.
다른 공식으로는 정규 확률 분포 기반의 문항 반응 함수(IRF)를 구성하는 ''정규 오자이브 모델''이 있다. 2모수 정규-오자이브 IRF 공식은 다음과 같다.
여기서 '''Φ'''는 표준 정규 분포의 누적 분포 함수(CDF)이다. 변별력 모수는 항목 ''i''에 대한 측정 오차의 표준 편차인 이며, 1/''와 유사하다.
능력 모수를 재조정하면 2PL 로지스틱 모델이 누적 정규 분포 오자이브에 가깝게 근사할 수 있다.[11]
라쉬 모형은 1PL IRT 모형으로 간주되기도 하지만, 라쉬 모형 지지자들은 이를 데이터와 이론 간의 관계를 개념화하는 다른 접근 방식으로 본다.[14] IRT가 데이터에 대한 모형의 적합성을 강조하는 반면,[15] 라쉬 모형은 기본 측정을 위한 요구 사항을 우선시한다.[16] 즉, 데이터가 라쉬 모형에 적합하고 검사 항목 및 응시자가 모형에 부합하는 경우에만 잠재 특성의 존재를 주장할 수 있다. 부적합한 응답은 그 이유를 진단하여 데이터 세트에서 제외할 수 있다.[17]
IRT 접근 방식은 객관식 시험에서 추측을 설명하기 위해 왼쪽 점근선 매개변수를 포함하지만, 라쉬 모형은 추측이 데이터에 무작위로 분산된 노이즈를 추가한다고 가정하므로 포함하지 않는다. 3-매개변수 IRT는 특정 객관성을 희생하여 데이터에 맞는 모형을 선택한다.[18]
라쉬 모형은 IRT 접근 방식에 비해 두 가지 주요 장점을 갖는다. 첫째, 라쉬의 특정 요구 사항[19]은 ''기본적인'' 개인-무료 측정을 제공한다.[20] 둘째, 라쉬 모형에서는 매개변수 추정이 더 간단하다.[21]
일반적인 IRT 모델은 문항에 대한 이산적인 반응(정답/오답 등)의 확률이 하나의 능력치와 하나 이상의 문항 매개변수에 의한 함수라는 수학적 가설에 기초한다. 사용되는 변수는 다음과 같다.
- :능력치 (응시자 특성의 크기, 간격 척도)
- :변별도 (문항 i가 응시자 능력을 변별하는 힘)
- :난이도 (문항 i의 어려움, 일반적으로 각 문항에 50% 정답률을 가진 피험자의 능력치)
- :추측도 (응시자가 우연히 정답할 확률)
IRT에서 문항 특성 곡선(ICC)은 응시자의 능력치와 문항의 정답률 관계를 로지스틱 곡선으로 나타낸다.
1PL (Rasch 모델)에서는 와 만 사용하며, 문항 i에 정답할 확률은 다음과 같다.
2PL 모델에서는 를 추가로 사용하여 문항 i에 정답할 확률은 다음과 같다.
여기서 상수 ''D''는 1.701로, 로지스틱 함수를 누적 정규 분포 함수에 근사하기 위한 것이다.
3PL 모델에서는 객관식 형식의 경우 추측도 를 고려하여 문항 i에 정답할 확률은 다음과 같다.
시험 특성 곡선은 모든 문항 특성 곡선을 더하여 구할 수 있다.
시험 점수는 이 시험 특성 곡선으로 구해지며, 값이 응시자의 점수가 된다.
다치 라쉬 모델처럼 다치(예: 4점 척도) 응답을 위한 확장 모델이나 다차원 특성을 가정한 모델도 존재한다.
5. 모형 적합도 분석
어떤 수학적 모델을 사용하든, 데이터가 모델에 적합한지 평가하는 것은 중요하다. 객관식 시험에서 오해를 불러일으키는 오답 보기와 같이, 어떤 항목이 모델에 맞지 않는다면 해당 항목의 품질 저하로 진단될 수 있다. 이 경우 해당 항목은 시험 양식에서 제거하고 향후 시험 양식에서 다시 작성하거나 대체할 수 있다.[33] 그러나 상당수의 부적합 항목이 명확한 이유 없이 발생한다면, 시험의 구성 타당성을 재고하고 시험 명세서를 다시 작성해야 할 수 있다. 따라서 부적합은 시험 개발자에게 매우 귀중한 진단 도구를 제공하며, 시험 명세서의 기반이 되는 가설을 데이터에 대해 경험적으로 검증할 수 있게 한다.
카이 제곱 검정이나 그 표준화된 버전을 포함하여, 적합성을 평가하는 몇 가지 방법이 있다. 2-모수 및 3-모수 문항 반응 이론 모델은 문항 변별도를 조정하여 데이터-모델 적합도를 개선하므로, 적합도 통계는 이상적인 모델이 미리 지정된 1-모수 모델에서 발견되는 확인적 진단 가치를 갖지 못한다.
데이터가 모델에 부적합하다는 이유만으로 제거해서는 안 되며, 영어로 작성된 과학 시험을 치르는 영어가 모국어가 아닌 응시자와 같이, 부적합에 대한 구성 관련 이유가 진단되었을 때 제거해야 한다. 이러한 응시자는 시험의 차원에 따라 동일한 모집단에 속하지 않는다고 주장할 수 있다. 1-모수 문항 반응 이론 척도는 표본 독립적이라고 주장되지만, 모집단 독립적이지 않으므로 이와 같은 부적합은 구성 관련성이 있으며 시험이나 모델을 무효화하지 않는다. 이러한 접근 방식은 도구 타당성 검사의 필수적인 도구이다. 2-모수 및 3-모수 모델에서는 심리 측정 모델이 데이터에 맞게 조정되므로, 각 시행의 점수가 다른 시행으로 일반화된다는 가설을 확인하기 위해 시험의 향후 시행은 초기 타당성 검사에 사용된 동일한 모델에 대한 적합성을 확인해야 한다. 데이터-모델 적합성을 달성하기 위해 각 시행에 대해 다른 모델을 지정하는 경우, 다른 잠재 특성이 측정되고 있으며 시험 점수를 시행 간에 비교할 수 없다고 주장할 수 있다.
6. 정보 함수
IRT의 주요 기여 중 하나는 신뢰도 개념을 확장한 것이다. 전통적으로 신뢰도는 측정의 정밀도를 의미하며, 참값과 관측값 분산의 비율과 같이 단일 지표를 사용하여 측정한다. 그러나 IRT는 정밀도가 검사 점수의 전체 범위에 걸쳐 균일하지 않다는 것을 명확히 보여준다. 예를 들어, 검사 범위의 가장자리 점수는 일반적으로 범위 중간에 가까운 점수보다 더 많은 오류가 관련된다.
IRT는 신뢰도를 대체하기 위해 문항 및 검사 정보 개념을 발전시켰다. 정보는 모형 매개변수의 함수이다. 예를 들어, 피셔 정보 이론에 따르면 이분형 응답 데이터에 대한 1PL(라쉬 모델)의 경우 제공되는 문항 정보는 정답일 확률에 오답일 확률을 곱한 값이다. 즉,
추정 표준 오차(SE)는 주어진 특성 수준에서 검사 정보의 역수이며,
따라서 더 많은 정보는 측정 오차가 적다는 것을 의미한다.
2개 및 3개 매개변수 모형과 같은 다른 모형의 경우 변별 매개변수가 함수에서 중요한 역할을 한다. 2개 매개변수 모형의 문항 정보 함수는
3개 매개변수 모형의 문항 정보 함수는[22]
일반적으로 문항 정보 함수는 종 모양을 띈다. 변별력이 높은 문항은 높고 좁은 정보 함수를 가지며, 이는 좁은 범위에서 크게 기여한다. 변별력이 낮은 문항은 더 넓은 범위에서 더 적은 정보를 제공한다.
문항 정보의 플롯을 사용하여 문항이 얼마나 많은 정보를 제공하고 척도 점수 범위의 어떤 부분에 정보를 제공하는지 확인할 수 있다. 국부적 독립성으로 인해 문항 정보 함수는 가산된다. 따라서 검사 정보 함수는 시험에 있는 문항의 정보 함수의 합이다. 대규모 문항 은행과 함께 이 속성을 사용하면 검사 정보 함수를 형성하여 측정 오차를 매우 정확하게 제어할 수 있다.
검사 점수의 정확도를 특성화하는 것은 심리 측정 이론의 핵심 문제이며 IRT와 고전 검사 이론(CTT)의 주요 차이점이다. IRT 연구 결과는 CTT의 신뢰도 개념이 단순화된 것임을 보여준다. 신뢰도 대신 IRT는 서로 다른 세타(θ) 값에서 정밀도의 정도를 보여주는 검사 정보 함수를 제공한다.
이러한 결과는 심리 측정학자가 신중하게 선택된 문항을 포함시켜 서로 다른 범위의 능력에 대한 신뢰도 수준을 (잠재적으로) 신중하게 형성할 수 있게 한다. 예를 들어, 검사를 합격하거나 불합격할 수 있고, 단일 "컷 점수"만 있으며 실제 합격 점수가 중요하지 않은 자격증 상황에서 컷 점수 근처에 높은 정보를 가진 문항만 선택하여 매우 효율적인 검사를 개발할 수 있다. 이러한 문항은 일반적으로 컷 점수와 난이도가 거의 같은 문항에 해당한다.
7. 활용 분야
IRT는 평가가 얼마나 잘 작동하는지, 그리고 평가의 개별 문항이 얼마나 잘 작동하는지를 평가하기 위한 틀을 제공한다. IRT의 가장 일반적인 적용 분야는 교육 분야로, 심리측정학자들은 IRT를 사용하여 시험을 개발하고 설계하고, 시험을 위한 문항 뱅크를 유지하며, 시험의 연속적인 버전 간의 문항 난이도를 동등화한다(예: 시간에 따른 결과 비교를 허용하기 위해).[5]
IRT는 다음과 같은 시험들에 활용되고 있다.
| 시험 종류 | 시험 이름 |
|---|---|
| 의학계 공통 시험 | CBT |
| 일본 관련 시험 | 기본 정보 기술자 시험 |
| BJT 비즈니스 일본어 능력 테스트 | |
| J-CAT(일본어 적응형 테스트) | |
| 일본어 능력 시험 | |
| 닛케이 TEST | |
| 일본 유학 시험 | |
| IT 관련 시험 | IT 패스포트 시험, LPIC |
| 어학 시험 | 토플(TOEFL) |
| 기타 | 어휘·독해력 검정, TECC (중국어 커뮤니케이션 능력 검정), 리딩 스킬 테스트 |
8. 대한민국에서의 활용 사례
기본 정보 기술자 시험, 토플, BJT 비즈니스 일본어 능력 테스트, J-CAT, 일본어 능력 시험, JETRO 비즈니스 능력 일본어 시험, 닛케이 TEST, IT 패스포트 시험, 어휘·독해력 검정, Linux 인증 LPIC, 일본 유학 시험, TECC (중국어 커뮤니케이션 능력 검정), 리딩 스킬 테스트 등 다양한 시험에서 문항 반응 이론이 활용되고 있다. 특히 의학계에서는 공통 시험 CBT에 적용되고 있다.
참조
[1]
웹사이트
Glossary of Important Assessment and Measurement Terms
http://www.ncme.org/[...]
[2]
논문
Likert or Rasch? Nothing is more applicable than good theory
1994
[3]
서적
Item Response Theory for Psychologists
https://books.google[...]
Psychology Press
[4]
웹사이트
ETS Research Overview
http://www.ets.org/p[...]
[5]
서적
Fundamentals of Item Response Theory
Sage Press
1991
[6]
논문
Marginal maximum likelihood estimation of item parameters: application of an EM algorithm
[7]
서적
Polytomous Item Response Theory Models
https://books.google[...]
SAGE
[8]
서적
Handbook of polytomous item response theory models
https://books.google[...]
Taylor & Francis
[9]
문서
Item response theory for items scored in two categories
Lawrence Erlbaum Associates, Inc.
2001
[10]
문서
PRELIS 1 user's manual, version 1
Scientific Software, Inc.
1988
[11]
논문
Origin of the Scaling Constant d = 1.7 in Item Response Theory
[12]
서적
Handbook of Mathematical Functions
U. S. Government Printing Office
1972
[13]
논문
Probit latent class analysis with dichotomous or ordered category measures: conditional independence/dependence models
1999-12
[14]
문서
Distinctions between assumptions and requirements in measurement in the Social sciences
Elsevier Science Publishers, North Holland, Amsterdam
1989
[15]
뉴스
Frederic Lord, Who Devised Testing Yardstick, Dies at 87
New York Times
2000-02-10
[16]
논문
Controversy and the Rasch model: a characteristic of incompatible paradigms?
2004-01
[17]
논문
Theory and practice of fit
http://rasch.org/rmt[...]
[18]
논문
Effect of Rasch calibration on ability and DIF estimation in computer-adaptive tests
1995-12
[19]
서적
Probabilistic models for some intelligence and attainment tests
The University of Chicago Press
1960/1980
[20]
논문
IRT in the 1990s: Which Models Work Best?
[21]
서적
Rasch Models: Foundations, Recent Developments, and Applications
Springer
1995
[22]
서적
The Theory and Practice of Item Response Theory
The Guilford Press
2009
[23]
서적
Latent Structure Analysis
Houghton Mifflin
1968
[24]
웹사이트
Ability estimation with IRT
http://www.assess.co[...]
[25]
논문
Conditional Standard Errors of Measurement for Scale Scores Using IRT
1996-06
[26]
문서
Measuring Change in Teachers' Perceptions of the Impact that Staff Development Has on Teaching.
http://eric.ed.gov/E[...]
2000
[27]
서적
Applications of item response theory to practical testing problems
Lawrence Erlbaum Associates, Inc.
1980
[28]
논문
An index of person separation in latent trait theory, the traditional KR.20 index, and the Guttman scale response pattern
[29]
논문
mirt : A Multidimensional Item Response Theory Package for the R Environment
2012
[30]
논문
Bayesian Item Response Modeling in R with brms and Stan
2021
[31]
웹사이트
CRAN Task View: Psychometric Models and Methods
https://cran.r-proje[...]
2023-12-15
[32]
논문
py-irt : A Scalable Item Response Theory Library for Python
2023-01
[33]
문서
Psychometric theory
McGraw-Hill
1967
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com