마름모삼십면체

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 기하학적 성질
3. 다른 도형들과의 관계
4. 3차원 쌍곡 공간 채우기
5. 응용
참조

1. 개요

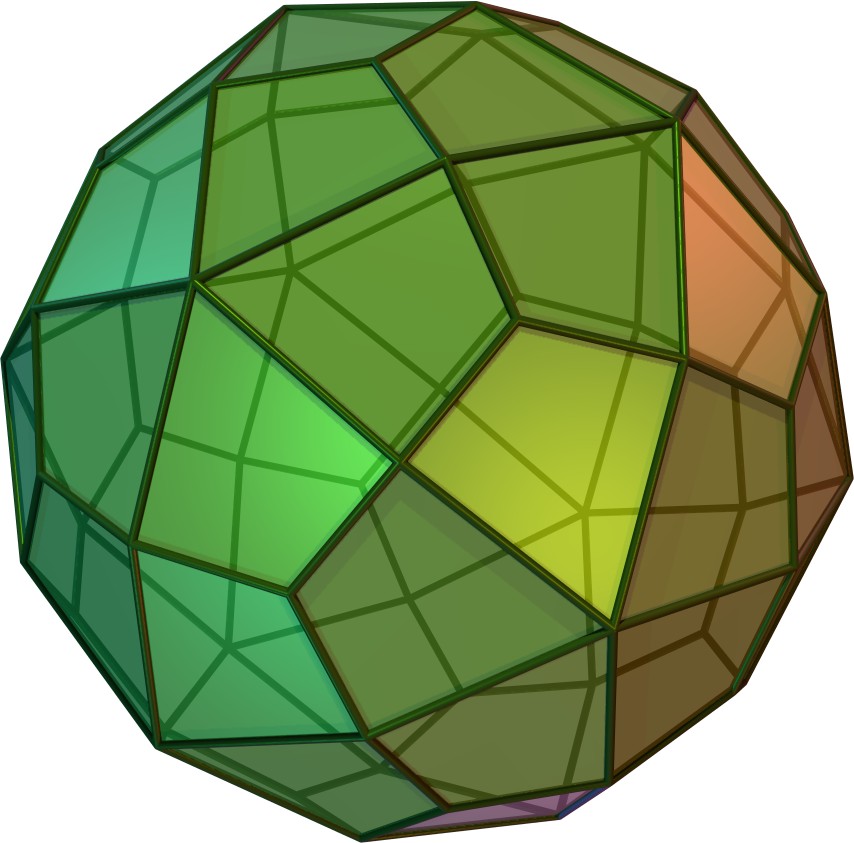
마름모삼십면체는 32개의 꼭짓점, 60개의 모서리, 30개의 면을 갖는 다면체로, 각 면이 마름모꼴이며, 면의 둔각은 약 116.57°, 예각은 약 63.43°이다. 겉넓이, 부피, 내접구의 반지름 등은 황금비와 관련된 식으로 표현된다. 이 도형은 20개의 황금 마름모로 분해될 수 있으며, 쌍대다면체는 십이이십면체이다. 정십이면체와 정이십면체를 마름모삼십면체 내부에 내접시킬 수 있으며, 3차원 쌍곡 공간을 채울 수 있다. 램프 디자인, 상자 제작, 주사위 등 다양한 분야에서 활용된다.

2. 기하학적 성질

마름모삼십면체는 30개의 마름모 면, 60개의 모서리, 32개의 꼭짓점을 가지며, 면, 모서리, 꼭짓점의 개수와 관련된 오일러 정리를 만족한다. 각 면은 마름모이며, 둔각은 약 116.57°, 예각은 약 63.43°이다. 마름모의 긴 대각선과 짧은 대각선의 길이 비는 황금비이다.

2. 1. 공식

한 모서리의 길이가

a

인 마름모삼십면체의 겉넓이

A

와 부피

V

는 다음과 같다.^[1]

:

A = 12\sqrt{5}~a^2 \approx 26.8328 a^2

:

V = 4\sqrt{5+2\sqrt{5}}~a^3 \approx 12.3107 a^3

마름모삼십면체의 모서리 길이가

a

일 때, 겉넓이, 부피, 내접구의 반지름(마름모삼십면체의 각 면에 접선으로 닿음)과 각 모서리의 중앙에 닿는 중반지름은 다음과 같으며, 여기서

\varphi

는 황금비이다.^[1]

내접구의 반지름: $r_\mathrm{i} = \frac{\varphi^2}{\sqrt{1 + \varphi^2}}\,a = \sqrt{1 + \frac{2}{\sqrt{5}}}\,a \approx 1.37638 a$
변의 중점을 지나는 구의 반지름: $r_\mathrm{m} = \left(1+\frac{1}{\sqrt{5}}\right)\,a \approx 1.44721 a$

2. 2. 면의 모양

마름모삼십면체의 각 면은 마름모 모양이다. 마름모의 둔각은 약 116.57°, 예각은 약 63.43°이다. 마름모의 긴 대각선, 짧은 대각선, 변의 길이 비는 황금비를 이룬다.

긴 대각선의 길이 : 짧은 대각선의 길이 : 변의 길이 = φ^영어 : 1 : $\frac{\sqrt{1+\varphi^2}}{2}$
: $\frac{1+\sqrt{5}}{2}(=1.618\cdots)$ : 1 : $\sqrt{\frac{5+\sqrt{5}}{2}}(=0.951\cdots)$ (대각선의 비가 황금비가 됨)

2. 3. 직교 좌표

황금비를 φ라고 하자. (0, ±1, ±φ)로 주어지는 12개의 점과 이 좌표들의 순환 순열은 정이십면체의 꼭짓점이다. 이십면체의 모서리와 직각으로 교차하는 이중 정십이면체는 (±1, ±1, ±1)의 8개의 점과 (0, ±φ, ±1/φ) 및 이 좌표들의 순환 순열로 주어지는 12개의 점을 꼭짓점으로 갖는다. 이 32개의 점은 원점에 중심을 둔 마름모삼십면체의 꼭짓점이다. 모서리의 길이는 √(3 – φ) ≈ 1.17557050458이다. 면은 길이가 2와 2/φ인 대각선을 갖는다.

2. 4. 분할

마름모삼십면체는 20개의 황금 마름모로 분해될 수 있는데, 10개는 예각이고 10개는 둔각이다.^[2]^[3]

10	10
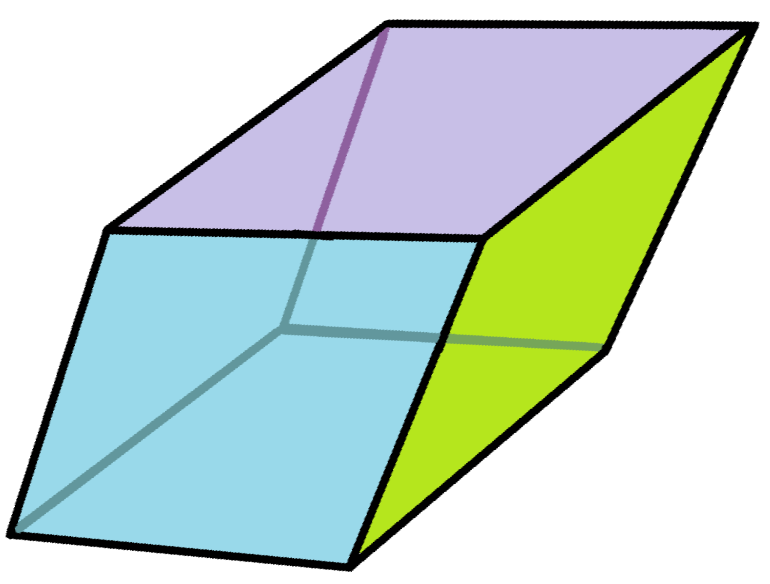예각 형태	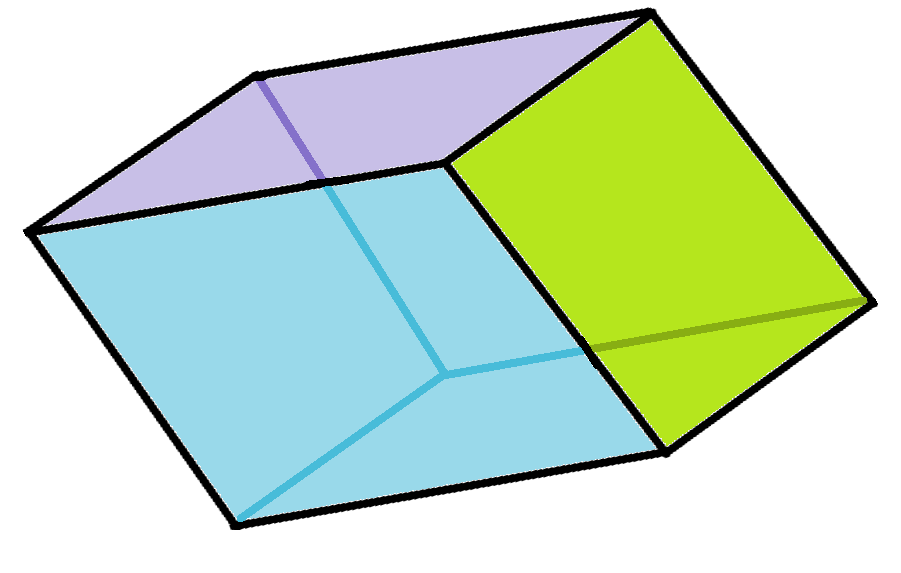둔각 형태

2. 5. 직교 투영

마름모삼십면체는 네 가지 대칭 위치를 가지는데, 두 개는 꼭짓점에, 하나는 면의 중앙에, 다른 하나는 모서리의 중앙에 위치한다. "10" 투영에 내장된 것은 "두꺼운" 마름모와 "얇은" 마름모로, 이 둘을 함께 사용하여 페로즈 타일링이라고 불리는 비주기적 테셀레이션을 생성할 수 있다.^[1]

직교 투영
투영 대칭	[2]	[2]	[6]	[10]
이미지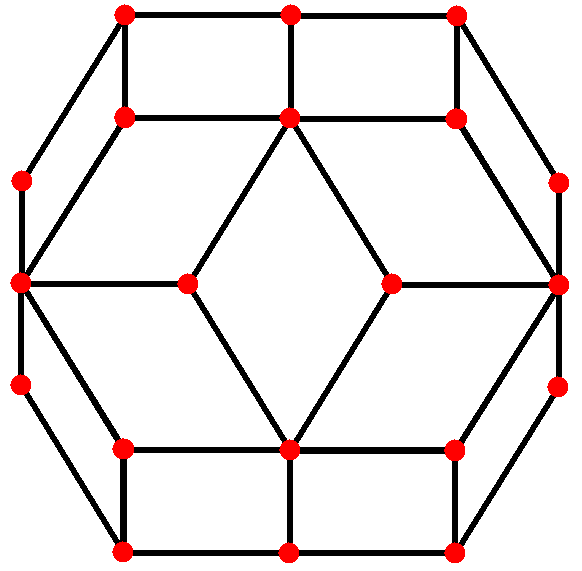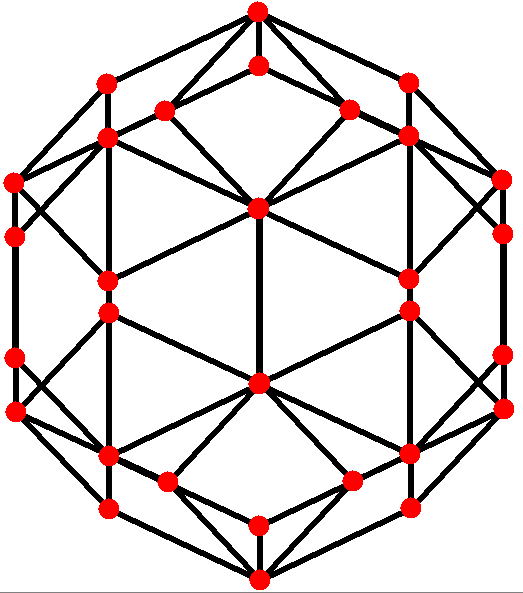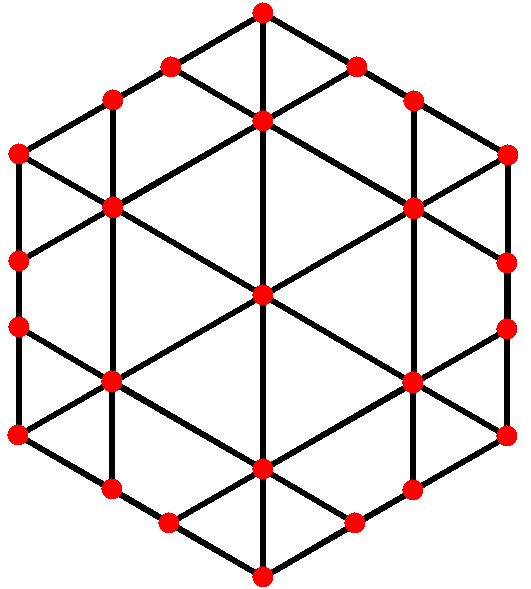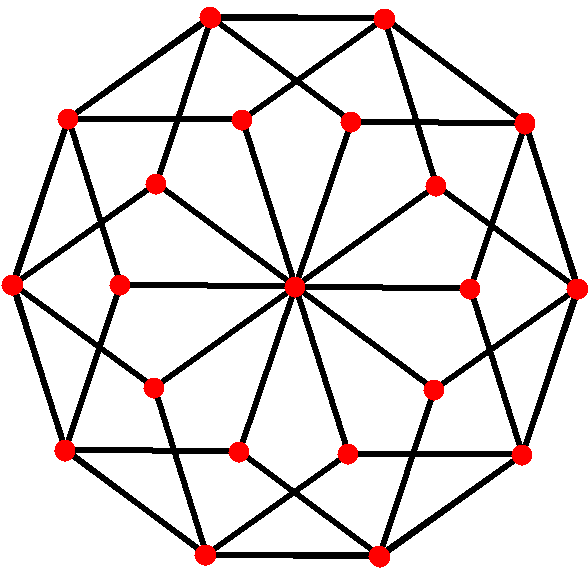
쌍대 이미지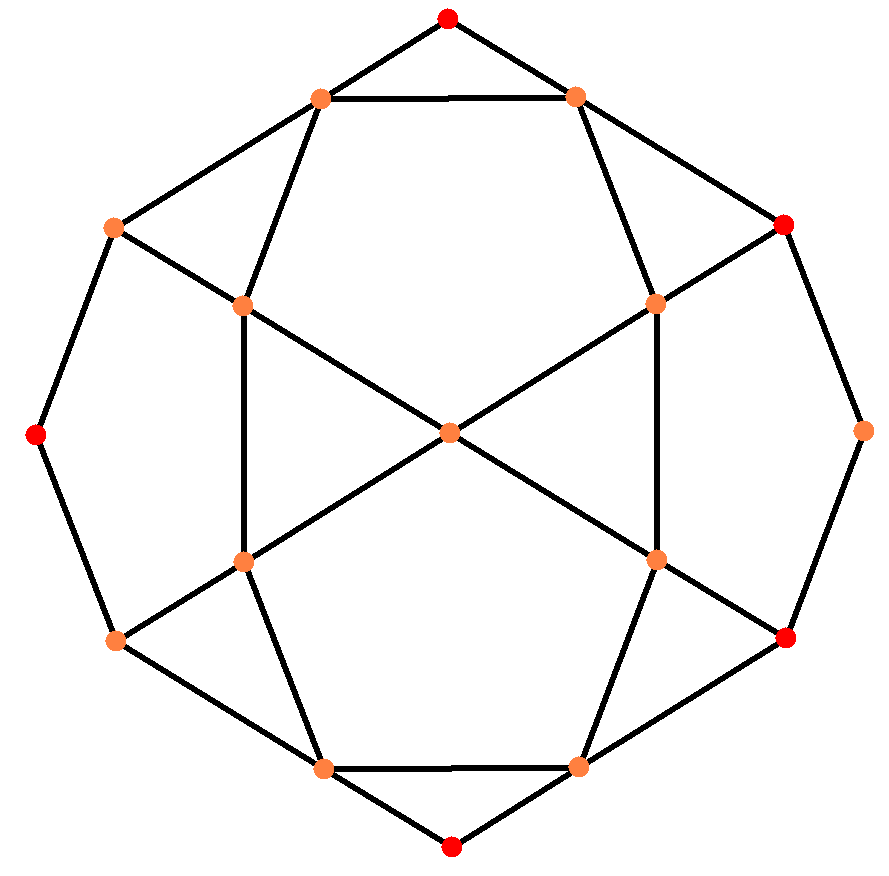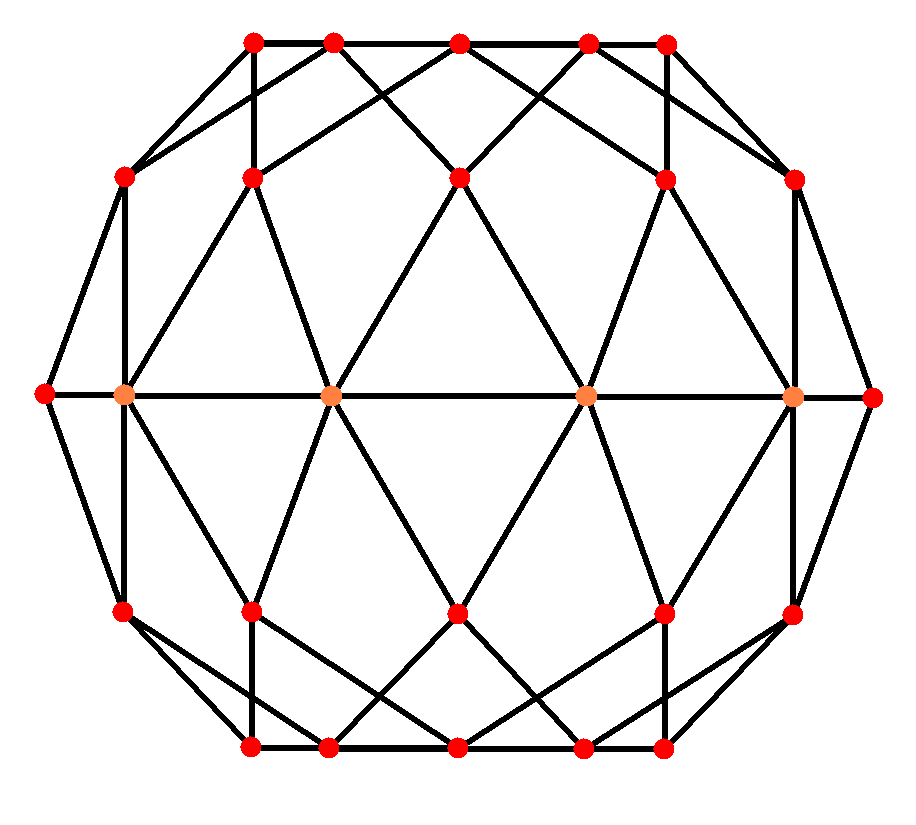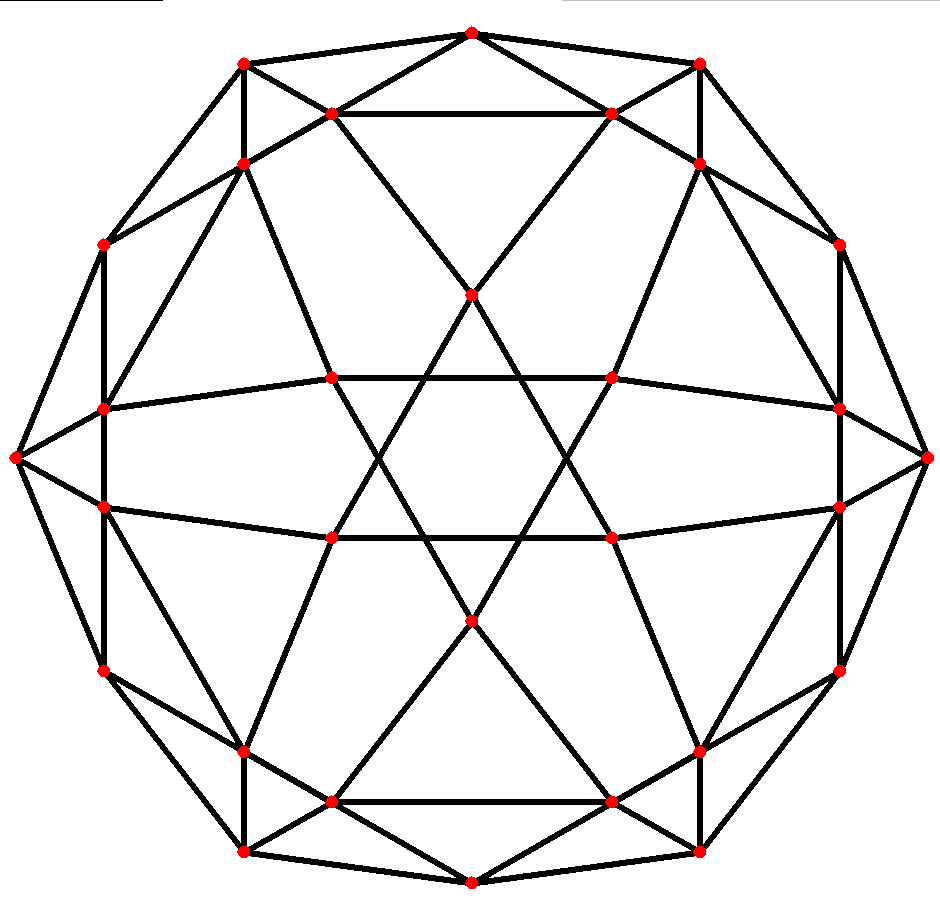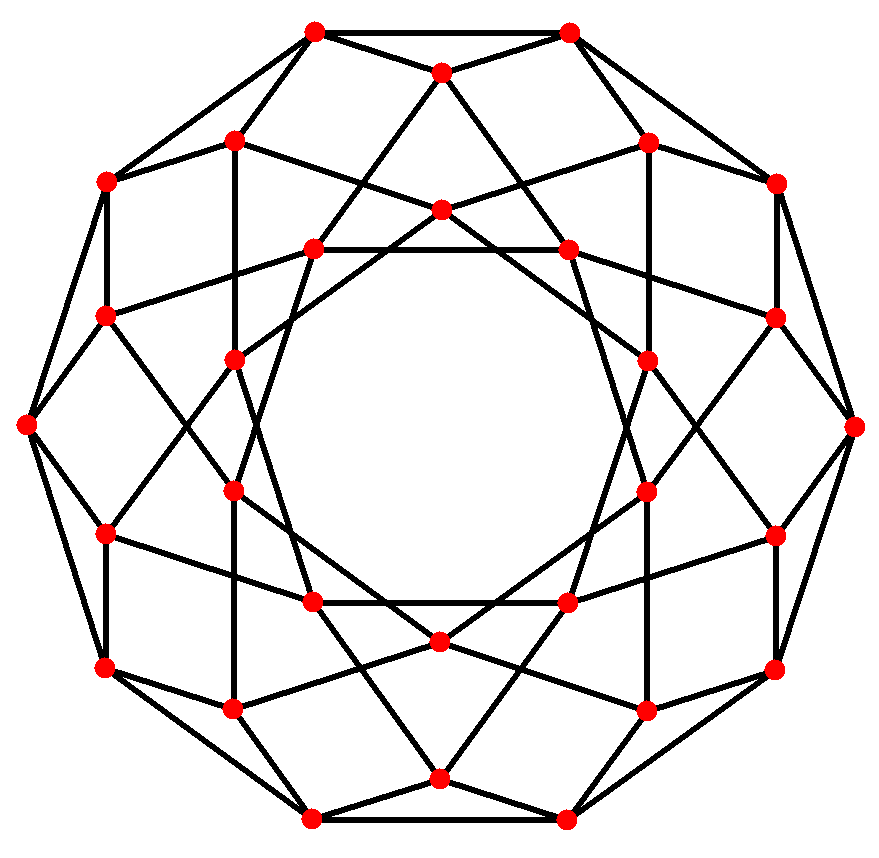

3. 다른 도형들과의 관계

십이이십면체는 마름모삼십면체의 쌍대다면체이다. 마름모삼십면체는 3차원 쌍곡 공간을 채울 수 있다.

3. 1. 정다면체와의 관계

마름모의 둔각 3개가 모인 꼭짓점 20개를 이으면 정십이면체가 되고, 마름모의 예각 5개가 모인 꼭짓점 12개를 이으면 정이십면체가 된다. 이 방법으로 만든 정십이면체와 정이십면체를 겹치면 서로의 모서리 중앙 부분이 완전히 겹치는 복합체가 된다.

3. 2. 별모양화

마름모삼십면체는 227개의 완전 지지 별모양화를 가진다.^[4]^[5] 이 중 하나는 다섯 개의 정육면체 화합물이다. 마름모삼십면체의 별모양화는 총 358,833,097개가 있다.

3. 3. 기타 관련 다면체

이 다면체는 콕서터 군 대칭을 갖는 능면체 다면체 및 타일링 수열의 일부이다. 정육면체는 능면체가 직사각형인 능육면체로 볼 수 있다.

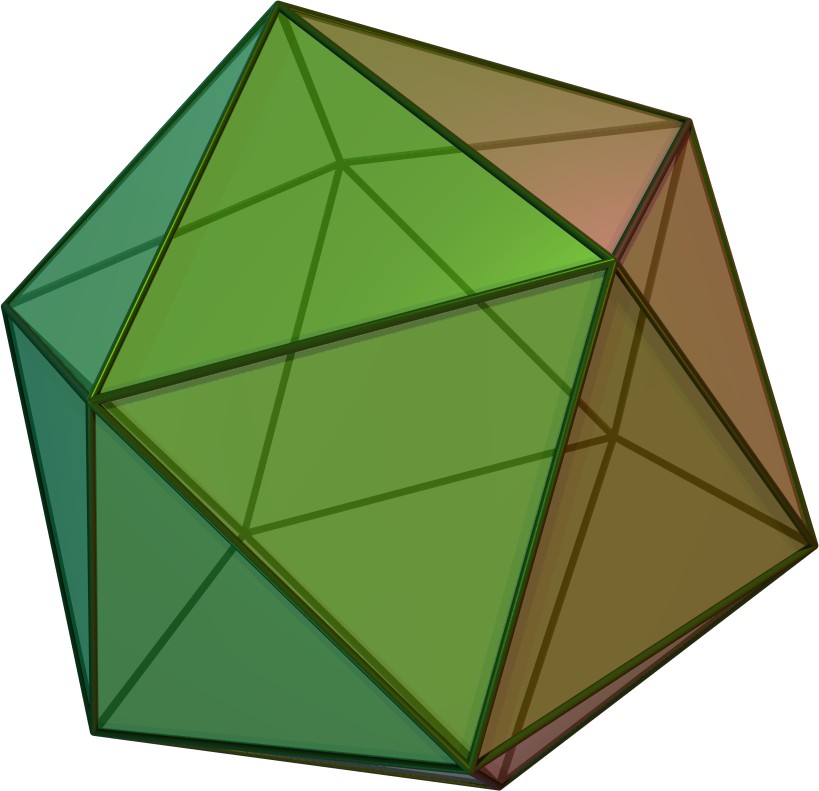
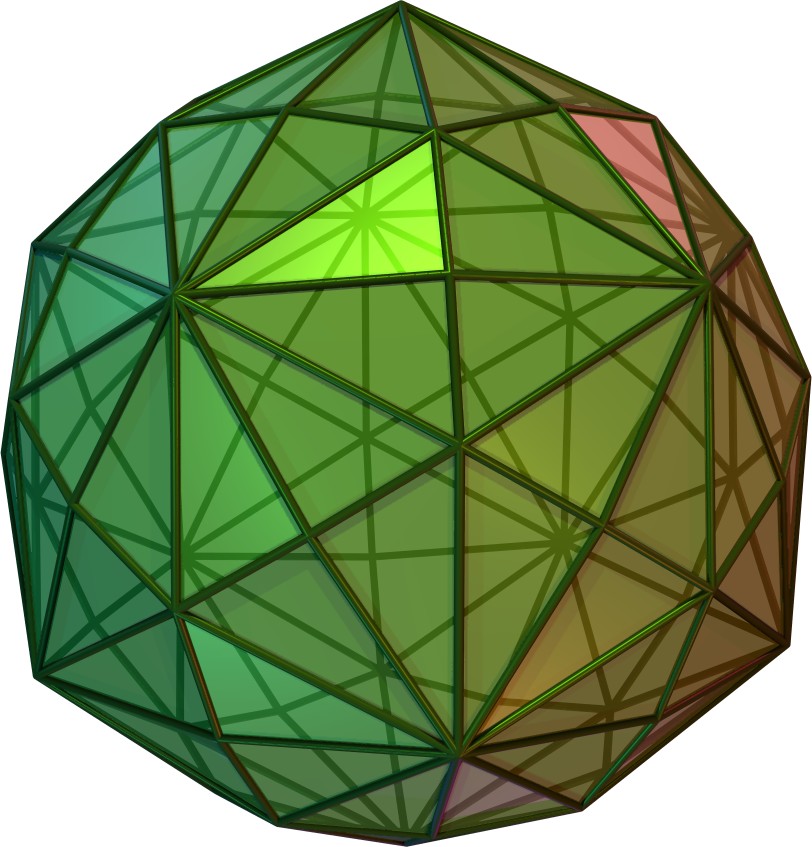
4. 3차원 쌍곡 공간 채우기

마름모삼십면체는 3차원 쌍곡 공간을 채울 수 있는 다면체 중 하나이다.

5. 응용

덴마크 디자이너 홀거 스트롬(Holger Strøm)은 조립식 램프 IQ-light (IQ는 "interlocking quadrilaterals"의 약자) 디자인에 마름모삼십면체를 활용했다.

STL 모델 마름모삼십면체 상자 (정육면체 구멍 주변에 6개의 패널로 구성) – 모델을 확대하여 내부 구멍 확인

목공예가 제인 코스틱(Jane Kostick)은 마름모삼십면체 모양의 상자를 제작한다.^[6] 이 구조는 마름모삼십면체와 정육면체 사이의 관계를 기반으로 한다.

로저 폰 외흐(Roger von Oech)의 "Ball of Whacks"는 마름모삼십면체 모양으로 제작된다.

마름모삼십면체는 일부 롤플레잉 게임에서 30면체 주사위 "d30"으로 사용되기도 한다.

참조

_[1] 웹사이트 rhombic triacontahedron http://www.wolframal[...] Stephen Wolfram 2013-01-07
_[2] 웹사이트 How to make golden rhombohedra out of paper http://www.cutoutfol[...]
_[3] 웹사이트 Dissection of the rhombic triacontahedron http://www.georgehar[...]
_[4] 논문 The 227 triacontahedra Kluwer Academic Publishers 1975
_[5] 논문 Stellations of the rhombic triacontahedron and Beyond 1995
_[6] 웹사이트 triacontahedron box - KO Sticks LLC http://kosticks.com/[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com