쌍곡기하학

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 성질
3. 표준 가우스 곡률
4. 좌표계
- 4.1. 거리
5. 역사
6. 쌍곡 평면의 물리적 실현
7. 쌍곡 평면의 모형
8. 쌍곡 평면의 등거리 변환
9. 예술에서의 쌍곡 기하학
10. 고차원
11. 동차 구조
12. 물리학에의 응용
13. 참고 도서
참조

1. 개요

쌍곡 기하학은 유클리드 기하학의 평행선 공준을 제외한 모든 공리를 공유하는 비유클리드 기하학의 한 종류이다. 유클리드 기하학과는 다르게, 쌍곡 기하학에서는 주어진 선 밖의 한 점을 지나면서 그 선과 만나지 않는 무한히 많은 선이 존재한다. 이러한 차이로 인해 유클리드 기하학의 개념이 다르게 나타나거나 새로운 개념이 도입되며, 삼각형의 각의 합은 180°보다 작다. 쌍곡 기하학은 클라인 모델, 푸앵카레 원반 모델 등 다양한 모델로 표현되며, 예술, 물리학, 특히 특수 상대성 이론에도 응용된다.

더 읽어볼만한 페이지

쌍곡기하학 - 무한원점
무한원점은 사영평면에서 z=0인 동차좌표로 표현되는 점들의 집합으로 무한원직선을 구성하며, 유클리드 기하학에는 없지만 사영기하학 등에서 평행선의 교점으로 정의되고 투영기하학에서 소실점과 관련되어 응용되지만 교육적 어려움을 야기한다는 비판도 있다.
쌍곡기하학 - 쌍곡선 함수
쌍곡선 함수는 삼각함수에서 파생된 함수로, 지수 함수를 사용하여 정의되며 삼각함수와 유사한 성질을 가지며 미분, 적분, 복소수까지 확장되어 사용된다.

쌍곡기하학

2. 성질

쌍곡 기하학은 유클리드 기하학과 평행선 공준에서만 차이가 있으며, 평행선 공준을 제외한 다른 공리들은 그대로 성립한다. 유클리드의 ''원론'' 1권의 처음 28개 명제를 포함한 절대 기하학의 모든 정리는 쌍곡 기하학에서도 유효하다.

쌍곡 기하학에서는 한 직선과 그 위에 있지 않은 한 점을 지나는 평행선이 무수히 많다. 이는 극한 평행선과 초평행선으로 나뉜다. 극한 평행선은 주어진 직선에 점근적으로 접근하지만 만나지 않는 선이고, 초평행선은 주어진 직선과 최소 거리를 갖는 점이 존재하며 양쪽으로 발산하는 선이다.

쌍곡 기하학에서는 각도와 거리 사이에 절대적인 관계인 절대 척도가 성립한다. 가우스 곡률을 K라고 할 때, R = 1/√-K라고 하면, 반지름 r인 원의 둘레는 2πR sinh(r/R)^영어이고, 원판의 면적은 2πR²(cosh(r/R) - 1)^영어이다. 따라서 원의 둘레와 면적은 유클리드 기하학보다 크다.

쌍곡 기하학에서는 다른 선으로부터 같은 거리에 있는 모든 점이 한 선 위에 있지 않고, 하이퍼사이클이라는 곡선 위에 놓인다. 또 다른 특수한 곡선은 호로사이클인데, 이 곡선의 법선 반경은 서로 극한 평행이다.

쌍곡 기하학에서 삼각형의 각의 합은 항상 180°보다 작으며, 이 차이를 결손이라고 한다. 쌍곡 삼각형의 면적은 결손에 R²을 곱한 값이다.

쌍곡 기하학에서는 변의 수가 무한대인 정규 아페이로곤과 Pseudogon^영어 균일 다각형이 존재한다. 또한, 유클리드 평면과 마찬가지로 쌍곡 평면도 정다각형을 면으로 사용하여 테셀레이션할 수 있다.

2. 1. 유클리드 기하학과의 관계

쌍곡 기하학은 유클리드 기하학과 평행선 공준을 제외한 모든 공리를 공유한다. 유클리드 기하학에서 평행선 공준을 제거하면 절대 기하학이 되며, 절대 기하학에는 유클리드 기하학과 쌍곡 기하학 두 종류가 있다. 유클리드의 ''원론'' 1권의 처음 28개 명제를 포함한 절대 기하학의 모든 정리는 유클리드 기하학과 쌍곡 기하학에서 모두 유효하다. 유클리드의 ''원론'' 1권의 명제 27과 28은 평행선 또는 교차하지 않는 선의 존재를 증명한다.

이러한 차이로 인해 유클리드 기하학에서 동일한 개념이 쌍곡 기하학에서는 다르게 나타나며, 새로운 개념이 도입되어야 한다. 또한, 평행각 때문에 쌍곡 기하학은 거리와 각도 측정 간의 관계인 절대 척도를 갖는다.

2. 2. 직선

쌍곡 기하학에서 직선은 유클리드 기하학의 직선과 같은 속성을 갖는다. 예를 들어, 두 점은 고유하게 선을 정의하며, 선분은 무한히 연장될 수 있다.

두 교차하는 선은 유클리드 기하학의 두 교차하는 선과 같은 속성을 갖는다. 예를 들어, 두 개의 서로 다른 선은 최대 한 점에서 교차할 수 있으며, 교차하는 선은 동일한 맞꼭지각을 형성하고, 교차하는 선의 인접각은 보충각이다.

세 번째 선이 도입되면 유클리드 기하학의 교차하는 선과 다른 교차하는 선의 속성이 있을 수 있다. 예를 들어, 주어진 두 교차하는 선에 대해, 그 두 선과 모두 교차하지 않는 무한히 많은 선이 존재한다.

이러한 속성은 사용된 모형과 관계없이 모두 독립적이다.

2. 2. 1. 평행선

쌍곡 기하학에서 비-교차선은 유클리드 기하학의 비-교차선과 다른 속성을 가진다.

선 ''R''과 ''R'' 위에 있지 않은 점 ''P''에 대해, 선 ''R''과 점 ''P''를 포함하는 평면에서 ''P''를 지나고 ''R''과 교차하지 않는 서로 다른 두 개 이상의 선이 존재한다. 이는 ''P''를 지나고 ''R''과 교차하지 않는 무한히 많은 공면선이 존재한다는 것을 의미한다.

이러한 비-교차선은 두 가지 부류로 나뉜다.

두 개의 선 (그림에서 ''x''와 ''y'')은 극한 평행선(때로는 임계 평행선, 호로평행 또는 그냥 평행선이라고도 함)이다. ''R''의 "끝"에 있는 각 이상점 방향으로 하나씩 존재하며, 점근적으로 ''R''에 접근하고 항상 ''R''에 더 가까워지지만 절대 만나지 않는다.
다른 모든 비-교차선은 최소 거리를 갖는 점을 가지며, 해당 점의 양쪽에서 발산하며, ''초평행'', ''발산 평행선'' 또는 때로는 ''비-교차''라고 불린다.

일부 기하학자들은 "''평행''선"이라는 구절을 "''극한 평행''선"을 의미하는 데 사용하며, ''초평행''선은 단순히 ''비-교차''를 의미한다.

이러한 극한 평행선은 ''PB''와 각도 ''θ''를 이루며, 이 각도는 평면의 가우스 곡률과 거리 ''PB''에만 의존하며, 평행각이라고 불린다.

초평행선에 대해 초평행선 정리는 쌍곡 평면에서 초평행선 쌍 각각에 수직인 유일한 선이 존재한다고 명시한다.

2. 3. 원과 원판

쌍곡 기하학에서 반지름 ''r''인 원의 둘레는 2πr^영어보다 크다.

R^영어 = 1/√-K라고 하자. 여기서 K^영어는 평면의 가우스 곡률이다. 쌍곡 기하학에서 K^영어는 음수이므로, 제곱근은 양수의 제곱근이다.

그러면 반지름 ''r''인 원의 둘레는 2πR sinh(r/R)이다.

그리고 둘러싸인 원판의 면적은 4πR²sinh²(r/2R) = 2πR²(cosh(r/R) - 1)이다.

따라서 쌍곡 기하학에서 원의 둘레와 반지름의 비율은 항상 2π^영어보다 엄격하게 크지만, 충분히 작은 원을 선택하여 임의로 가깝게 만들 수 있다.

평면의 가우스 곡률이 -1이면 반지름 ''r''인 원의 측지 곡률은 1/tanh(r)이다.^[1]

2. 4. 하이퍼사이클과 호로사이클

쌍곡 기하학에서는 다른 선으로부터 같은 거리에 있는 모든 점이 한 선 위에 있는 경우는 없다. 대신, 주어진 선에서 모두 같은 거리에 있는 점들은 하이퍼사이클이라는 곡선 위에 놓인다.^[1]

또 다른 특수한 곡선은 호로사이클인데, 이 곡선의 법선 반경 (수직선)은 서로 극한 평행이다(모두 한 방향으로 동일한 이상점으로 점근적으로 수렴하며, 호로사이클의 중심이 된다).^[1]

모든 두 점을 지나는 두 개의 호로사이클이 있다. 호로사이클의 중심은 그 점들 사이의 선분 수직 이등분선의 이상점이다.^[1]

임의의 세 개의 서로 다른 점이 주어지면, 그 점들은 모두 선, 하이퍼사이클, 호로사이클 또는 원 위에 놓인다.^[1]

선분의 '''길이'''는 두 점 사이의 최단 거리이다.^[1]

두 점을 연결하는 하이퍼사이클의 호 길이는 선분보다 길고, 동일한 두 점을 연결하는 호로사이클의 호 길이보다는 짧다.^[1]

두 점을 연결하는 두 호로사이클의 호 길이는 같다. 그리고 그 점들을 연결하는 하이퍼사이클의 호 길이보다 길고, 두 점을 연결하는 원의 호 길이보다 짧다.^[1]

평면의 가우스 곡률이 -1이면, 호로사이클의 측지 곡률은 1이고 하이퍼사이클의 측지 곡률은 0과 1 사이다.^[1]

2. 5. 삼각형

유클리드 기하학의 삼각형과 달리 쌍곡 공간에서 삼각형의 각의 합은 항상 π 라디안(180°, 평각)보다 작다. 이 차이를 결손이라고 한다.

쌍곡 삼각형의 면적은 라디안 단위의 결손에 ''R''²을 곱한 값이다.^[2] 따라서 모든 쌍곡 삼각형은 ''R''²π보다 작거나 같은 면적을 갖는다.

유클리드 기하학과 마찬가지로 각 쌍곡 삼각형은 내접원을 갖는다. 쌍곡 공간에서 세 꼭짓점이 모두 호로사이클 또는 초주기선 위에 놓여 있다면 삼각형은 외접원을 갖지 않는다.

구면 기하학과 타원 기하학과 마찬가지로 쌍곡 기하학에서도 두 삼각형이 닮음이면 합동이어야 한다.

2. 6. 정규 아페이로곤과 가짜 다각형

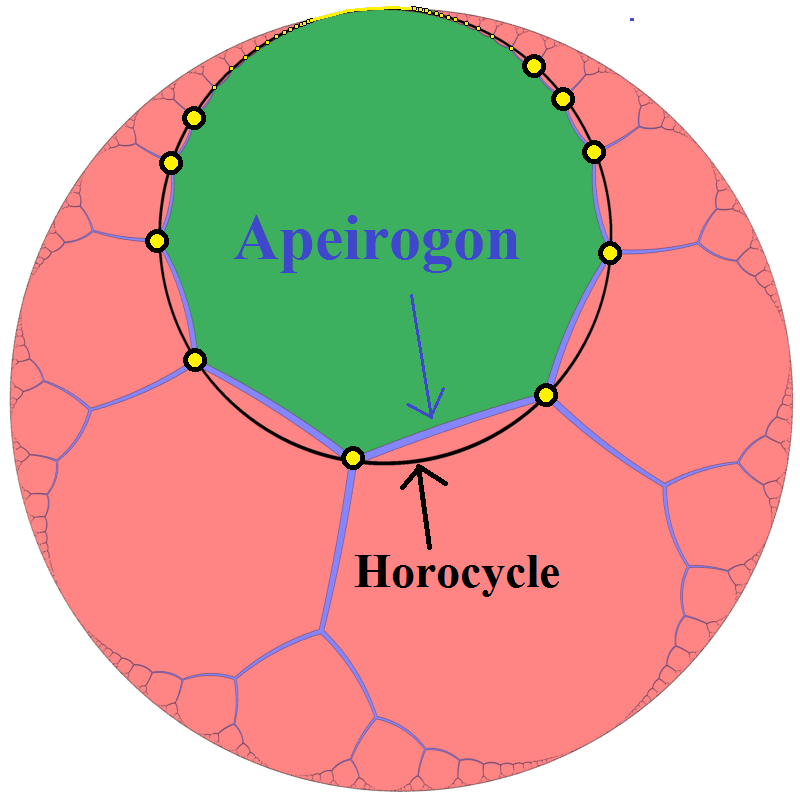
쌍곡 기하학에서 특별한 다각형은 변의 수가 무한대인 정규 아페이로곤과 Pseudogon^영어 균일 다각형이다.

유클리드 기하학에서는 변의 길이를 0으로 만들어서 아페이로곤이 원과 구별할 수 없게 하거나, 내각을 180°로 만들어서 아페이로곤이 직선에 접근하도록 해야 한다. 그러나 쌍곡 기하학에서 정규 아페이로곤 또는 가짜 다각형은 임의의 길이의 변을 갖는다.

변과 각 이등분선은 변의 길이와 변 사이의 각도에 따라 제한되거나 발산하는 평행선이 된다. 이등분선이 제한 평행선이면 아페이로곤이며 동심 호로사이클에 내접하고 외접할 수 있다. 이등분선이 발산 평행선이면 이는 가짜 다각형이며 하이퍼사이클에 내접하고 외접할 수 있다(모든 꼭짓점은 축인 선에서 같은 거리에 있으며, 변 세그먼트의 중간점도 모두 동일한 축에서 동일한 거리에 있다).

2. 7. 테셀레이션

유클리드 평면과 마찬가지로 쌍곡 평면도 정다각형을 면으로 사용하여 테셀레이션할 수 있다.

슈바르츠 삼각형 (''p'' ''q'' ''r'')을 기반으로 하는 무한히 많은 정규 테셀레이션이 있으며, 여기서 1/''p'' + 1/''q'' + 1/''r'' < 1이다. 여기서 ''p'', ''q'', ''r''은 각각 기본 영역 삼각형의 세 점에서의 반사 대칭의 차수이며, 대칭군은 쌍곡 삼각형군이다. 슈바르츠 삼각형에서 생성될 수 없는 무한히 많은 정규 테셀레이션도 있으며, 예를 들어 사각형을 기본 영역으로 요구하는 경우도 있다.^[3]

3. 표준 가우스 곡률

쌍곡 기하학은 상수 음의 가우스 곡률을 갖는 모든 표면에 적용되지만, 일반적으로 곡률 ''K'' = -1인 척도를 사용한다.^[1]

곡률 ''K'' = -1인 경우, 다음과 같은 특징을 갖는다.^[4]

삼각형의 면적은 라디안으로 나타낸 각 결손과 같다.
호로사이클의 호의 길이는 1이다.
두 개의 동심 호로사이클의 두 반지름 사이의 호 길이의 비율은 호로사이클이 1만큼 떨어져 있을 때 ''e''이다.

4. 좌표계

유클리드 기하학과 달리 쌍곡기하학은 좌표계 설정에 많은 어려움이 따른다. 사각형의 각의 합은 항상 360°보다 작고, 등거리선이 없으므로 적절한 직사각형은 두 개의 직선과 두 개의 쌍곡선으로 둘러싸여야 하며, 사각형 주위로 선분을 평행 이동하면 원래 위치로 돌아갈 때 회전한다.

하지만 쌍곡 평면 기하학에는 다양한 좌표계가 존재한다. 모든 좌표계는 선택된 점(원점)과 선택된 방향선(''x''축)을 기준으로 하며, 그 후 많은 선택이 가능하다.

로바체프스키 좌표 ''x''와 ''y''는 ''x''축에 수선을 내려 얻을 수 있다. ''x''는 수선의 발의 라벨이 된다. ''y''는 주어진 점에서 수선의 발까지의 수선 길이를 나타낸다(한쪽은 양수, 다른 쪽은 음수).

다른 좌표계는 원점을 통과하는 호로사이클까지의 거리와 이 호로사이클을 따른 길이를 측정한다.^[5]

다른 좌표계는 아래에 설명된 클라인 모델 또는 푸앵카레 원반 모델을 사용하고 유클리드 좌표를 쌍곡선으로 간주한다.

4. 1. 거리

이 좌표계에서 (''x''₁, ''y''₁)와 (''x''₂, ''y''₂)로 표시되는 두 점 사이의 거리는 다음과 같이 계산할 수 있다.^[5]

:

\operatorname{dist} (\langle x_1, y_1 \rangle, \langle x_2, y_2 \rangle) = \operatorname{arcosh} \left( \cosh y_1 \cosh (x_2 - x_1) \cosh y_2 - \sinh y_1 \sinh y_2 \right) \,.

이 공식은 쌍곡 삼각형에 대한 공식에서 파생될 수 있다.

해당 메트릭 텐서 필드는

(\mathrm{d} s)^2 = \cosh^2 y \, (\mathrm{d} x)^2 + (\mathrm{d} y)^2

이다.

5. 역사

유클리드의 ''원론''이 기원전 300년경 출판된 이후, 많은 기하학자들이 평행선 공준을 증명하려 했다. 일부는 귀류법을 사용하여 평행선 공준의 부정이 모순을 이끌어낸다고 시도했다. 이들 중 가장 두드러진 인물로는 프로클로스, 이븐 알하이삼 (알하젠), 오마르 하이얌^[6], 나시르 알딘 알투시, 비텔로, 게르소니데스, 알폰소, 조반니 제롤라모 사케리, 존 윌리스, 요한 하인리히 람베르트, 르장드르가 있다.^[7] 이들의 시도는 실패했지만, 쌍곡 기하학의 발견으로 이어졌다.

알하젠, 하이얌, 알투시의 사각형에 관한 정리(이븐 알하이삼-람베르트 사각형과 하이얌-사케리 사각형을 포함)는 쌍곡 기하학에 관한 최초의 정리였다. 이들의 연구는 비텔로, 게르소니데스, 알폰소, 존 윌리스, 사케리 등 후기 유럽 기하학자들에게 상당한 영향을 미쳤다.^[8]

18세기에는 요한 하인리히 람베르트가 쌍곡 함수를 도입하고^[9] 쌍곡 삼각형의 면적을 계산했다.^[10] 19세기에는 니콜라이 로바체프스키, 야노시 볼러이, 카를 프리드리히 가우스, 프란츠 타우리누스가 쌍곡 기하학을 광범위하게 탐구했다. 이전 연구자들과 달리 이들은 새로운 기하학을 발견했다는 것을 깨달았다.^[11]^[12]

가우스는 1824년 프란츠 타우리누스에게 보낸 편지에서 쌍곡 기하학을 구성했다고 썼지만, 자신의 연구 결과를 출판하지는 않았다. 가우스는 이를 "비유클리드 기하학"이라고 불렀으며^[13], 일부 현대 연구자들은 "비유클리드 기하학"과 "쌍곡 기하학"을 동의어로 간주하기도 한다. 타우리누스는 1826년에 쌍곡 삼각법에 대한 결과를 발표했고, 쌍곡 기하학이 자기 모순이 없다고 주장했지만, 여전히 유클리드 기하학의 특별한 역할을 믿었다. 쌍곡 기하학의 완전한 체계는 로바체프스키가 1829/1830년에 출판했으며, 볼러이는 이와 독립적으로 발견하여 1832년에 출판했다.

1868년, 에우제니오 벨트라미는 쌍곡 기하학의 모형을 제시하여 쌍곡 기하학과 유클리드 기하학이 동등하게 모순이 없음을 증명했다.

"쌍곡 기하학"이라는 용어는 1871년 펠릭스 클라인이 도입했다.^[14] 클라인은 사영 기하학의 변환을 사용하여 등거리 변환을 생성하려는 아서 케일리의 구상을 따랐다.

5. 1. 철학적 결과

쌍곡 기하학의 발견은 중요한 철학적 결과를 가져왔다. 쌍곡 기하학이 발견되기 전, 홉스와 스피노자를 비롯한 많은 철학자들은 철학적 엄밀성을 유클리드의 ''원론''에 사용된 추론 방식인 "기하학적 방법"의 관점에서 보았다.

칸트는 ''순수 이성 비판''에서 공간과 시간은 인간이 세상의 객관적인 특징으로 발견하는 것이 아니라, 우리의 경험을 조직하는 불가피한 체계적 틀의 일부라고 결론 내렸다.^[16]

가우스는 쌍곡 기하학에 대해 "보이오티아인"의 소란을 두려워하여 아무것도 출판하지 않았다고 한다. 여기서 "보이오티아인"은 고대 아테네인들이 멍청한 사람들의 전형으로 여겼던 사람들이다.^[17] 가우스는 ''princeps mathematicorum'' (princeps mathematicorum|수학자들의 제왕^la)으로서의 그의 지위가 이로 인해 손상될까 우려했다.^[18]

"보이오티아인들의 소란"은 일어났다가 사라졌고, 이는 수학적 엄밀성, 분석 철학 및 논리학의 획기적인 발전을 이끌었다. 쌍곡 기하학은 마침내 일관성이 증명되었고, 따라서 또 다른 유효한 기하학으로 인정받았다.

5. 2. 우주의 기하학 (공간적 차원)

유클리드 기하학, 쌍곡 기하학, 타원 기하학은 모두 모순이 없으므로, 어떤 기하학이 공간의 실제 기하학인지, 그리고 쌍곡 기하학 또는 타원 기하학이라면 곡률은 무엇인지에 대한 질문이 제기된다.

로바체프스키는 시리우스의 시차를 측정하고 시리우스를 평행각의 이상적인 점으로 취급하여 우주의 곡률을 측정하려 했다. 그는 자신의 측정이 확실한 답을 내릴 만큼 오차 범위가 정확하지 않다는 것을 깨달았지만, 우주의 기하학이 쌍곡 기하학이라면 절대 길이가 적어도 지구 궤도 지름의 백만 배 이상(2000000AU, 10 파섹)이라는 결론에 도달했다.^[19] 일부에서는 그의 측정이 방법론적으로 결함이 있다고 주장한다.^[20]

앙리 푸앵카레는 구면 세계 사고 실험을 통해, 일상적인 경험이 다른 기하학을 반드시 배제하는 것은 아니라는 결론에 도달했다.

5. 3. 우주의 기하학 (특수 상대성 이론)

특수 상대성 이론은 공간과 시간을 동등하게 취급하므로, 공간과 시간을 별도로 고려하는 대신 통일된 시공간의 기하학을 고려한다.^[22]^[23] 민코프스키 기하학은 갈릴레이 상대성 이론의 시간과 함께 3차원 유클리드 공간을 대체한다.^[24]

상대성 이론에서 유클리드 기하학, 타원 기하학, 쌍곡 기하학 대신 고려해야 할 적절한 기하학은 각각 0, 양수, 음의 곡률에 해당하는 민코프스키 공간, 드 지터 공간, 안티 드 시터 공간이다.^[25]^[26]

쌍곡 기하학은 속도를 대신하는 래피디티를 통해 특수 상대성 이론에 나타나며, 이는 쌍곡각으로 표현된다. 이러한 속도 기하학 연구는 운동학적 기하학이라고 불린다. 상대론적 속도의 공간은 3차원 쌍곡 기하학을 가지며, 여기서 거리 함수는 "인접"한 점(속도)의 상대 속도에서 결정된다.^[27]

6. 쌍곡 평면의 물리적 실현

유클리드 공간에는 유한한 면적의 상수 음의 가우스 곡률을 갖는 다양한 유사구가 존재한다.^[28]

힐베르트 정리에 따르면, 완전한 쌍곡면(상수 음 가우스 곡률의 완전한 정규 표면)을 3차원 유클리드 공간에 등거리적으로 매립할 수 없다.

쌍곡 기하학의 다른 유용한 모형들이 유클리드 공간에 존재하며, 이 모형에서는 거리가 보존되지 않는다. 특히 잘 알려진 종이 모형은 유사구를 기반으로 하며, 이는 윌리엄 서스턴의 작품이다.

크로셰 예술은 쌍곡면을 증명하는 데 사용되었으며, 최초의 시연은 다이나 타이미나에 의해 이루어졌다.^[28]

2000년, 키스 헨더슨은 "쌍곡선 축구공" (더 정확하게는, 절단된 7차 삼각 타일링)이라고 불리는 빠르게 만들 수 있는 종이 모형을 시연했다.^[29]^[30]

헬라만 퍼거슨이 디자인한 쌍곡선 퀼트를 만드는 방법에 대한 지침이 제프 위크스에 의해 제공되었다.^[31]^[32]

산호초를 모방한, Institute For Figuring의 손뜨개 쌍곡면 모음.

쌍곡면을 (일부) 근사하는 종이 모형인 "쌍곡선 축구공". 절단된 정이십면체가 구를 근사하는 것과 유사하다.

7. 쌍곡 평면의 모형

쌍곡 기하학에는 여러 가지 모델이 존재한다. 대표적으로 클라인 모델, 푸앵카레 원반 모델, 푸앵카레 반평면 모델, 쌍곡면 모델 등이 있다. 이 모델들은 모두 쌍곡 기하학의 공리를 만족하며, 서로 변환 가능하다.^[50]^[51]

의사구와 같이 음의 가우스 곡률이 일정한 표면은 3차원 공간에 표현될 수 있으며, 트랙토이드(또는 의사구)가 대표적이다. 트랙토이드는 원뿔이나 원기둥처럼 쌍곡 평면의 모델로 사용되지만, 전체 쌍곡 평면을 유클리드 공간에 담을 수는 없다. 따라서 쌍곡 기하학을 연구하기 위해 다양한 모델들이 사용된다.^[50]^[51]

타원 기하학에서는 구면 기하학이 모델로 사용되는 반면, 쌍곡 기하학에서는 벨트라미가 고안한 푸앵카레 상반평면 모델이나 푸앵카레 원반 모델이 널리 알려져 있다. 그 외에도 벨트라미의 의사구면이라고 불리는 깔때기 모양의 곡면 모델, 쌍곡면 모델, 클라인 모델 등도 존재한다.^[50]^[51]

이러한 모델들은 쌍곡 기하학이 성립하는 곡면으로, '''쌍곡 평면'''(2차원 쌍곡 다양체)이라고 불린다.^[50]^[51]

7. 1. 벨트라미-클라인 모델

클라인과 벨트라미의 이름을 따서 명명된 Beltrami–Klein 모델은 사영 원반 모델, 클라인 원반 모델이라고도 불린다.

2차원에서 이 모델은 완전한 쌍곡 평면을 위해 단위 원의 내부를 사용하며, 이 원의 현이 쌍곡선이다.^[50]^[51]

고차원에서는 이 모델이 단위 구의 내부를 사용하며, 이 ''n''-구의 현이 쌍곡선이다.

이 모델은 선이 직선이라는 장점이 있지만, 각도가 왜곡된다는 (이 매핑은 등각이 아님) 단점과, 원이 원으로 표현되지 않는다는 단점이 있다.
이 모델의 거리는 교차비의 로그의 절반이며, 이는 케일리에 의해 사영 기하학에서 도입되었다.

7. 2. 푸앵카레 원반 모델

푸앵카레 원반 모델은 등각 원반 모델이라고도 하며, 단위 원의 내부를 사용하지만, 선은 경계 원에 직교하는 원의 호와 경계 원의 지름으로 표시된다.^[50]^[51]

이 모델은 각도를 보존하며, 따라서 등각이다. 따라서 이 모델 내의 모든 등거리는 뫼비우스 변환이다.
원반 내부의 원은 원의 유클리드 중심이 원의 쌍곡선 중심보다 원반의 중심에 더 가깝더라도 원으로 유지된다.
호로사이클은 접점을 제외하고 경계 원에 접선인 원반 내의 원이다.
하이퍼사이클은 경계 원에서 직교하지 않는 각도로 끝나는 원반 내의 열린 현과 원호이다.

7. 3. 푸앵카레 반평면 모델

푸앵카레 상반평면 모형은 유클리드 평면의 절반을 사용하여 쌍곡 평면을 나타내는 모형으로, 이 절반은 평면의 선 ''B''에 의해 경계가 정해진다. 선 ''B''는 모형에 포함되지 않는다. 유클리드 평면은 데카르트 좌표계를 갖는 평면으로 간주될 수 있으며, x축은 선 ''B''로, 상반평면은 이 평면의 윗부분(''y'' > 0)으로 간주된다.

쌍곡선은 ''B''에 직교하는 반원 또는 ''B''에 수직인 반직선이다.
반직선 위의 간격의 길이는 로그 척도로 주어지므로, 호모세틱 변환 $(x, y) \mapsto (\lambda x, \lambda y),\quad \lambda > 0 .$ 에 대해 불변이다.
푸앵카레 원반 모델과 마찬가지로, 이 모형은 각도를 보존하며 따라서 등각 사상이다. 따라서 이 모형 내의 모든 등거리는 평면의 뫼비우스 변환이다.
상반평면 모형은 경계가 같은 점에서 ''B''에 접하고 원반 모형의 반지름이 무한대로 가는 푸앵카레 원반 모형의 극한이다.

타원 기하학에서는 구면 기하학이 그 모델이었지만, 쌍곡 기하학에서는 벨트라미가 고안한 푸앵카레 상반평면 모델이나 푸앵카레 원반 모델이 유명하다.^[50]^[51]

7. 4. 쌍곡면 모델

쌍곡면 모형은 3차원 민코프스키 공간에 내장된 2차원 회전 쌍곡면(두 겹 중 하나만 사용)을 사용한다.^[33] 이 모형은 특수 상대성 이론에 직접적으로 적용되는데, 민코프스키 3차원 공간은 하나의 공간적 차원을 억제한 시공간의 모형이기 때문이다. 쌍곡면은 공통 사건에서 시작하여 고정된 고유 시간에 도달하는 다양한 관성적으로 움직이는 관찰자의 사건(시공간의 위치)을 나타내는 것으로 간주할 수 있다.

쌍곡면 위의 두 점 사이의 쌍곡 거리는 두 해당 관찰자 간의 상대적 속도와 동일시될 수 있다. 이 모형은 추가 차원으로 직접 일반화된다. 쌍곡 3차원 공간, 즉 3차원 쌍곡 기하학은 민코프스키 4차원 공간과 관련이 있다.

7. 5. 반구 모델

반구 모델은 단위 구의 윗부분을 사용한다.^[50]

:

x^2 + y^2 + z^2 = 1 , z > 0.

쌍곡선은 반구의 경계에 직교하는 반원이다.^[50]

반구 모델은 그 자체로는 자주 사용되는 모델은 아니지만, 다른 모델 간의 변환을 시각화하는 데 유용한 도구 역할을 한다.^[50] 반구 모델은 리만 구의 일부이며, 다양한 투영을 통해 쌍곡 평면의 서로 다른 모델을 얻을 수 있다.^[50]

$(0,0, -1)$ 에서 평면 $z = 0$ 으로의 스테레오그래픽 투영은 푸앵카레 원반 모델의 해당 점을 투영한다.^[50]
$(0,0, -1)$ 에서 표면 $x^2 + y^2 - z^2 = -1 , z > 0$ 으로의 스테레오그래픽 투영은 쌍곡면 모델의 해당 점을 투영한다.^[50]
$(-1,0,0)$ 에서 평면 $x=1$ 으로의 스테레오그래픽 투영은 푸앵카레 상반평면 모델의 해당 점을 투영한다.^[50]
평면 $z = C$ 으로의 정사영은 벨트라미-클라인 모델의 해당 점을 투영한다.^[50]
구의 중심에서 평면 $z = 1$ 으로의 중심 투영은 간스 모델의 해당 점을 투영한다.^[50]

7. 6. 간스 모델

간스 모델은 1966년 데이비드 간스(David Gans)가 제안한 평면 쌍곡면 모형이다.^[34] 이는 쌍곡면 모델을 xy 평면에 직교 투영한 것이다. 다른 모델만큼 널리 사용되지는 않지만, 쌍곡 기하학을 이해하는 데 매우 유용하다.

클라인 모델이나 푸앵카레 원반 모델과는 달리, 전체 유클리드 평면을 사용한다.
이 모델에서 선은 쌍곡선의 가지로 표현된다.

7. 7. 등각 정사각형 모델

슈바르츠-크리스토펠 사상을 사용하여 푸앵카레 원반을 정사각형으로 변환하면 쌍곡 평면의 등각 정사각형 모델을 얻는다.^[36] 이 모델은 푸앵카레 원반처럼 유한한 범위를 가지지만, 모든 점이 정사각형 안에 있다. 이 모델은 등각이므로 예술적인 적용에 적합하다.

7. 8. 띠 모델

띠 모형은 두 개의 평행선 사이의 유클리드 평면의 일부를 사용한다.^[37] 거리는 띠의 중앙을 지나는 한 선을 따라 보존된다. 띠가

\{z \in \mathbb C:|\operatorname {Im} z| < \pi / 2\}

로 주어진다고 가정하면, 메트릭은

|dz| \sec (\operatorname{Im} z)

로 주어진다.

7. 9. 모델 간의 연결

모든 모델은 본질적으로 동일한 구조를 설명한다. 이들 간의 차이점은 동일한 거리 공간, 즉 쌍곡 평면에 놓인 서로 다른 좌표 차트를 나타낸다는 것이다. 쌍곡 평면 자체의 특징은 일정한 음의 가우스 곡률을 갖는다는 것이며, 이는 사용된 좌표 차트에 무관하다. 측지선도 유사하게 불변한다. 즉, 측지선은 좌표 변환 하에서 측지선으로 매핑된다.^[38]

네 개의 모델은 동일한 거리 공간을 설명하므로 서로 변환될 수 있다.

예를 들어 다음 관계를 참고할 수 있다.

벨트라미-클라인 모델과 쌍곡면 모델의 관계
벨트라미-클라인 모델과 푸앵카레 원반 모델의 관계
푸앵카레 원반 모델과 쌍곡면 모델의 관계

8. 쌍곡 평면의 등거리 변환

쌍곡 평면에서 자기 자신으로의 모든 등거리 변환(기하학적 변환 또는 운동)은 최대 세 개의 반사의 합성으로 나타낼 수 있다. ''n''차원 쌍곡 공간에서는 최대 ''n''+1개의 반사가 필요할 수 있다.

쌍곡 평면의 모든 등거리 변환은 다음과 같이 분류할 수 있다.

방향 보존
항등 등거리 변환 — 아무것도 움직이지 않음.
점을 통한 반전 (180도 회전) — 주어진 점을 지나는 서로 수직인 두 선에 대한 반사. 즉, 점을 중심으로 180도 회전.
정점을 중심으로 한 회전 — 주어진 점을 지나는 두 선에 대한 반사 (반전을 특수한 경우로 포함). 점들은 중심 주위의 원을 따라 움직임.
이상점을 중심으로 한 "회전" (호롤레이션) — 이상점으로 향하는 두 선에 대한 반사. 점들은 이상점을 중심으로 하는 호로사이클을 따라 움직임.
직선을 따라 평행 이동 — 주어진 선에 수직인 두 선에 대한 반사. 주어진 선에서 벗어난 점들은 하이퍼사이클을 따라 움직임.

방향 반전
선에 대한 반사 — 1번의 반사.
동일 선상에서의 선에 대한 반사와 평행 이동을 결합 — 반사와 평행 이동은 교환 가능. 3번의 반사 필요.

9. 예술에서의 쌍곡 기하학

M. C. 에셔의 판화 ''원의 극한 III''과 ''원의 극한 IV''는 푸앵카레 원반 모델을 잘 보여준다.^[36] ''III''의 흰색 선은 쌍곡선에 가깝다.^[36] 쌍곡 평면의 음의 곡률은 삼각형과 사각형의 각의 합에 미치는 영향을 통해 분명하게 확인할 수 있다.^[36]

''원의 극한 III''에서 각 꼭짓점은 세 개의 삼각형과 세 개의 사각형에 속한다. 유클리드 평면에서는 이 각도가 450°가 되지만, 쌍곡 평면에서 삼각형의 각의 합은 180°보다 작아야 한다.^[36] ''원의 극한 III''에서는 중심으로부터 거리 'n' 이내의 물고기 수가 지수적으로 증가하는 지수적 성장을 보인다. 물고기는 동일한 쌍곡 면적을 가지므로, 반지름 'n'인 구의 면적은 'n'에 따라 지수적으로 증가해야 한다.^[36]

코바늘뜨기는 다이나 타이미냐가 쌍곡 평면을 시연하는 데 처음으로 사용한 기술이다.^[28] 그녀의 저서 ''쌍곡 평면을 이용한 코바늘뜨기 모험''은 2009년 서점/다이어그램 상 가장 기묘한 제목을 수상했다.^[39]

하이퍼로그는 쌍곡 평면의 다양한 타일링을 배경으로 하는 로그라이크 게임이다.

10. 고차원

를 제거하고, '쌍곡 기하학'과 '쌍곡 공간'에 내부 링크를 추가한다.

쌍곡 기하학은 2차원에만 국한되지 않으며, 모든 더 높은 차원에서도 존재한다.

11. 동차 구조

''n''차원 쌍곡 공간은 다음과 같은 몫 공간과 동형이다.

: $\mathrm{O}(1,n)/(\mathrm{O}(1) \times \mathrm{O}(n)).$

직교군 O(1, ''n'')은 작용을 통해 민코프스키 공간 '''R'''^1,''n''의 노름을 보존하는 변환을 하며, 노름 1 벡터의 두 겹 쌍곡면에 추이적으로 작용한다. 원점을 지나는 시간적 선(즉, 양의 노름 접선을 갖는 선)은 쌍곡면의 대척점을 지나므로 이러한 선들의 공간은 쌍곡 ''n''-공간의 모델을 제공한다. 특정 선의 안정자는 직교군 O(''n'')과 O(1)의 곱과 동형이며, 여기서 O(''n'')은 쌍곡면의 한 점의 접선 공간에 작용하고 O(1)은 원점을 지나는 선을 반사한다.

낮은 차원에서는 리 군의 특별한 동형이 존재하여 쌍곡 공간의 대칭을 고려하는 추가적인 방법을 제공한다. 예를 들어, 2차원에서는 SO⁺(1, 2) ≅ PSL(2, '''R''') ≅ PSU(1, 1)을 통해 상반 평면 모델을 몫 SL(2, '''R''')/SO(2)로, 푸앵카레 원반 모델을 몫 SU(1, 1)/U(1)로 해석할 수 있다. 두 경우 모두 대칭군은 분수 선형 변환에 의해 작용하며, 두 군 모두 리만 구의 각 부분 공간에서 PGL(2, '''C''')의 방향을 보존하는 안정자이기 때문이다. 케일리 변환은 쌍곡 평면의 한 모델을 다른 모델로 가져갈 뿐만 아니라 더 큰 군에서 공액 관계를 통해 대칭 군의 동형을 실현한다. 3차원에서는 PGL(2, '''C''')의 리만 구에 대한 분수 선형 작용이 동형 O⁺(1, 3) ≅ PGL(2, '''C''')에 의해 유도된 쌍곡 3-공간의 등각 경계에 대한 작용과 동일시된다.

12. 물리학에의 응용

고속으로 회전하는 원반 위에서는 로렌츠 수축에 의해 물체의 길이가 줄어든다. 원반 중심에서 멀어질수록 회전 속도가 빨라지므로, 가장자리로 갈수록 로렌츠 수축 효과가 강하게 나타난다. 이 경우 두 점 사이의 최단 거리는 (원반의 지름을 제외하고) 회전이 느린 중심에 가까운 선이 되며, 정지 상태의 원반에서 보면 곡선이 된다. 즉, 고속으로 원반을 회전시켜 직선이 휘어져, '''3차원 공간이 음의 곡률'''을 가지게 된다.

13. 참고 도서

Norbert A'Campo^영어와 Athanase Papadopoulos^영어 (2012) "쌍곡 기하학에 대한 노트" in: 기하학에 관한 스트라스부르 석사 과정, 1–182쪽, IRMA 수학 및 이론 물리학 강의, Vol. 18, 취리히: 유럽 수학회(EMS), 461쪽, ISBN , DOI 10.4171–105.
콕세터, H. S. M. (1942) "비유클리드 기하학", 토론토 대학교 출판부, 토론토
로바체프스키, 니콜라이 I. (2010) "판기하학", Athanase Papadopoulos^영어 편집 및 번역, 유럽 수학 유산, Vol. 4. 취리히: 유럽 수학회(EMS). xii, 310쪽, ISBN
밀너, 존 W. (1982) "쌍곡 기하학: 처음 150년", Bull. Amer. Math. Soc. (N.S.) Volume 6, Number 1, 9–24쪽.
레이놀즈, 윌리엄 F. (1993) "쌍곡면에서의 쌍곡 기하학", 미국 수학 월간 100:442–455.
새뮤얼스, 데이비드, (2006년 3월) "니트 이론" 디스커버 매거진, 27권, 3호.
제임스 W. 앤더슨, "쌍곡 기하학", 스프링거 2005, ISBN
제임스 W. 캐넌, 윌리엄 J. 플로이드, 리처드 케년, 월터 R. 패리 (1997) "쌍곡 기하학", MSRI 출판물, 31권.

참조

_[1] 웹사이트 Curvature of curves on the hyperbolic plane https://math.stackex[...] 2017-09-24
_[2] 서적 Hyperbolic geometry: history, models, and axioms https://urn.kb.se/re[...] 2014
_[3] 간행물 Some novel three-dimensional Euclidean crystalline networks derived from two-dimensional hyperbolic tilings
_[4] 서적 The elements of non-Euclidean geometry Dover Publications 2005
_[5] 서적 Introduction to hyperbolic geometry https://archive.org/[...] Springer-Verlag 1995
_[6] 웹사이트 Omar Khayyam 1048–1131 http://www.resonance[...] 2008-01-05
_[7] 웹사이트 Non-Euclidean Geometry Seminar http://www.math.colu[...] 2018-01-21
_[8] 인용 Foundations and Fundamental Concepts of Mathematics https://books.google[...] Courier Dover Publications
_[9] 인용 Foundations of Hyperbolic Manifolds https://books.google[...] Springer
_[10] 서적 Non-Euclidean geometry: A critical and historical study of its development https://archive.org/[...] Open Court
_[11] 서적 Euclidean and non-Euclidean geometries: development and history https://archive.org/[...] Freeman 2003
_[12] 문서 Felix Klein, Elementary Mathematics from an Advanced Standpoint: Geometry Dover 1948
_[13] 문서 F. Klein. "Über die sogenannte Nicht-Euklidische Geometrie"
_[14] 문서 Rosenfeld, B.A. (1988) A History of Non-Euclidean Geometry Springer-Verlag
_[15] 서적 Space, Time and Causality Clarendon Press
_[16] 간행물 Some Greek stereotypes of other peoples 1959-04
_[17] 서적 Philosophy of Geometry from Riemann to Poincare Reidel 1978
_[18] 서적 Non-Euclidean geometry : a critical and historical study of its developments https://archive.org/[...] Dover 1955
_[19] 서적 Introduction to hyperbolic geometry https://archive.org/[...] Springer-Verlag 1995
_[20] 웹사이트 Mathematics Illuminated - Unit 8 - 8.8 Geometrization Conjecture http://www.learner.o[...] 2018-01-21
_[21] 서적 Classical Theory of Fields Butterworth Heinemann
_[22] 서적 Feynman Lectures on Physics Addison Wesley
_[23] 서적 Dynamics and Relativity https://archive.org/[...] Wiley
_[24] 서적 Gravitation https://archive.org/[...] 1973
_[25] 서적 Global Lorentzian Geometry 1996
_[26] 서적 Classical Theory of Fields Butterworth Heinemann
_[27] 웹사이트 Hyperbolic Space http://theiff.org/oe[...] 2007-01-15
_[28] 웹사이트 How to Build your own Hyperbolic Soccer Ball http://www.theiff.or[...] 2018-01-21
_[29] 웹사이트 Hyperbolic Football http://www.math.tamu[...] 2018-01-21
_[30] 웹사이트 Helaman Ferguson, Hyperbolic Quilt http://www.helasculp[...]
_[31] 웹사이트 How to sew a Hyperbolic Blanket http://www.geometryg[...] 2018-01-21
_[32] 문서 Reynolds, William F., (1993) Hyperbolic Geometry on a Hyperboloid
_[33] 간행물 A New Model of the Hyperbolic Plane 1966-03
_[34] 웹사이트 Computer Science Department http://www.d.umn.edu[...] 2015-05-08
_[36] 간행물 The Conformal Hyperbolic Square and Its Ilk http://archive.bridg[...] 2016
_[37] 서적 Teichmüller theory and applications to geometry, topology, and dynamics http://matrixedition[...] Matrix Editions
_[38] 서적 Introduction to Hyperbolic Geometry Springer 1995-12-16
_[39] 뉴스 Crocheting Adventures with Hyperbolic Planes wins oddest book title award https://www.telegrap[...] 2010-03-26
_[40] 서적 Hyperbolic geometry Springer Science & Business Media 2006
_[41] 서적 Hyperbolic geometry Cambridge University Press 1992
_[42] 서적 Lectures on hyperbolic geometry Springer Science & Business Media 2012
_[43] 서적 Foundations of geometry Courier Dover Publications 2018
_[44] 문서 双曲幾何学入門 2011
_[45] 서적 作図で身につく双曲幾何学共立出版 2016-05-25
_[46] 논문 Hyperbolic geometry: the first 150 years 1982
_[47] 서적 János Bolyai, non-euclidean geometry, and the nature of space Burndy Library MIT Press 2004
_[48] 논문 平行線を巡る平行な議論 2010
_[49] 논문 ユークリッド原論の平行線の定義 2011
_[50] 웹사이트 Hyperbolic Plane
_[51] 웹사이트 Hyperbolic plane

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com