미분학
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
미분학은 함수의 순간적인 변화율, 즉 접선의 기울기를 구하는 과정 또는 그 값을 의미한다. 미분은 선형 방정식의 기울기 계산에서 시작하여, 곡선의 기울기를 접선을 통해 계산하는 것으로 확장된다. 도함수는 접선의 기울기를 나타내며, 할선을 활용하여 기울기를 계산하고 극한을 통해 도함수를 정의한다. 미분의 기하학적 의미는 접선의 기울기이며, 편미분과 전미분 개념으로 확장된다. 미분은 최적화 문제, 물리학, 미분 방정식, 평균값 정리, 테일러 급수, 음함수 정리 등 다양한 분야에 응용된다. 특히 물리학에서는 속도와 가속도 계산에, 최적화 문제에서는 극대점과 극소점을 찾는 데 활용된다. 미분 방정식은 자연과학과 공학에서 널리 사용되며, 테일러 급수는 함수의 근사를 제공한다.
더 읽어볼만한 페이지
- 미분학 - 기울기 (벡터)
기울기(벡터)는 스칼라장의 특정 지점에서 값이 가장 빠르게 증가하는 방향과 변화율을 나타내는 벡터로, 함수의 등위면에 수직이며 크기는 해당 방향의 변화율을 나타내고, 스칼라 함수의 각 성분에 대한 편미분으로 구성되며 나블라 연산자로 표현된다. - 미분학 - 음함수와 양함수
음함수와 양함수는 함수의 표현 방식에 따른 분류로, 독립변수와 종속변수의 관계가 명시적으로 나타나는 경우를 양함수, 관계식이 한 식 안에 포함된 경우를 음함수라 하며, 음함수는 양함수로 표현하기 어렵거나 불가능한 경우가 있고, 음함수 미분법, 음함수 정리 등을 통해 여러 분야에서 활용된다.
| 미분학 | |
|---|---|
| 정의 | |
| 분야 | 수학 |
| 하위 분야 | 미적분학 |
| 개요 | |
| 주요 개념 | |
| 주요 연산 | |
| 미분 | "함수의 도함수를 구하는 연산이다. 다양한 미분법칙 (예: 곱의 미분법칙, 연쇄 법칙)을 사용하여 복잡한 함수의 도함수를 계산할 수 있다." |
| 응용 분야 | |
| 근사 | "복잡한 함수를 간단한 함수 (예: 선형 근사, 테일러 급수)로 근사하는 데 사용된다. 계산 복잡성을 줄이고 문제 해결을 용이하게 한다." |
2. 미분
미분은 함수의 특정 지점에서의 순간적인 변화율, 즉 접선의 기울기를 구하는 과정 또는 그 값을 의미한다.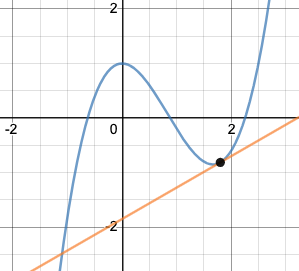
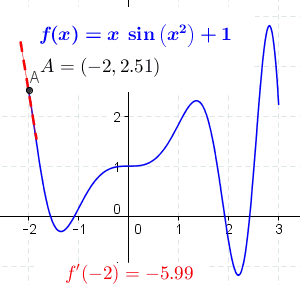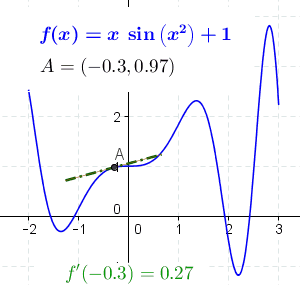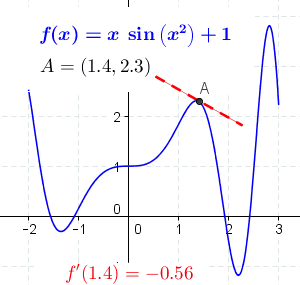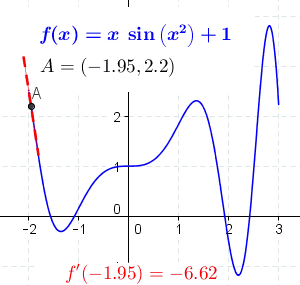
의 점 에서의 도함수는 에 접하는 접선의 기울기이다.[3]
일반적인 함수는 기울기를 갖지 않는 경우가 있다. 기하학적으로, 점 에서의 의 미분 계수는 함수 의 점 에서의 접선의 기울기를 의미하며, 차분 상의 극한('''미분 상''')과 같다.
의 정의역의 각 점 에서 미분 상이 존재한다면, 각 점 를 의 에서의 미분 상으로 보내는 함수('''도함수''')가 존재한다. 함수의 미분은 이와 관련된 개념이다. 와 가 실수 변수일 때, 의 에서의 미분 상은 그래프의 에서의 접선의 기울기이다. 의 시역과 종역은 1차원이므로, 의 미분 상은 실수이지만, 및 가 벡터 변수일 때는 의 그래프의 최적 선형 근사가 여러 방향으로 얼마나 변화하는지에 따라 달라진다.
2. 1. 도함수
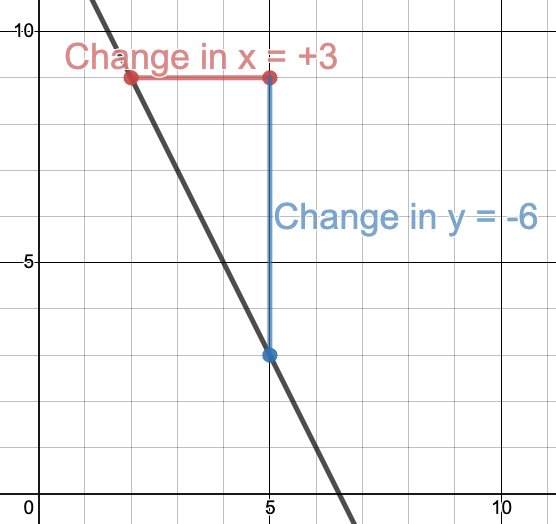
의 점 에서의 도함수는 에 접하는 접선의 기울기이다.[3] 이를 이해하려면 먼저 형식으로 쓰인 선형 방정식의 기울기를 구하는 방법을 알아야 한다. 방정식의 기울기는 가파름을 나타낸다. 임의의 두 점을 선택하여 의 변화량을 의 변화량으로 나누어 구할 수 있으며, 이는 임을 의미한다. 예를 들어, 의 그래프는 아래 그림과 같이 의 기울기를 가진다.
:
간결하게 은 종종 로 쓰이며, 여기서 는 그리스 문자 델타로 '변화량'을 의미한다. 선형 방정식의 기울기는 일정하며, 이는 가파름이 모든 곳에서 동일함을 의미한다. 그러나 와 같은 많은 그래프는 가파름이 다르다. 이는 더 이상 임의의 두 점을 선택하여 기울기를 계산할 수 없음을 의미한다. 대신, 그래프의 기울기는 접선을 고려하여 계산할 수 있는데, 접선은 특정 점을 '단지 터치'하는 선이다. 특정 점에서의 곡선의 기울기는 해당 점의 접선의 기울기와 같다. 예를 들어, 는 에서 의 기울기를 가지는데, 이는 해당 점에서의 접선의 기울기가 와 같기 때문이다.
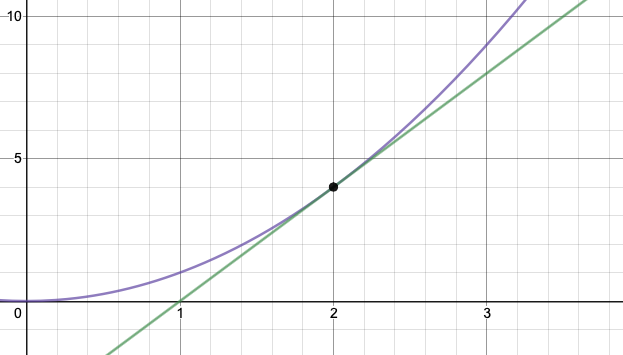
함수의 함수의 도함수는 이 접선의 기울기이다. 접선은 접점에서 단일 점만 터치하지만, 두 점을 통과하는 선으로 근사할 수 있다. 이를 할선이라고 한다. 할선이 통과하는 두 점이 서로 가까이 있으면, 할선은 접선과 매우 유사하며, 결과적으로 기울기도 매우 유사하다.
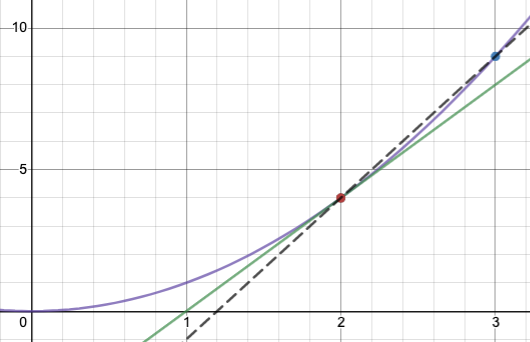
할선을 사용하면 기울기를 직접 계산할 수 있다는 장점이 있다. 그래프의 두 점 와 를 고려해 보자. 여기서 는 작은 숫자이다. 앞서 언급했듯이, 이 두 점을 통과하는 선의 기울기는 공식 를 사용하여 계산할 수 있다. 이는 다음을 제공한다.
:
가 에 점점 더 가까워짐에 따라, 할선의 기울기는 접선의 기울기에 점점 더 가까워진다. 이는 공식적으로 다음과 같이 쓰인다.
:
위 표현은 '가 0에 점점 더 가까워짐에 따라, 할선의 기울기는 특정 값에 점점 더 가까워진다'는 의미이다. 접근하는 값은 의 도함수이며, 이는 로 쓸 수 있다. 인 경우, 도함수는 로 쓸 수도 있으며, 여기서 는 무한소 변화를 나타낸다. 예를 들어, 는 x의 무한소 변화를 나타낸다. 요약하면, 인 경우, 의 도함수는 다음과 같다.
:
그러한 극한이 존재한다면 말이다.[4] 따라서 우리는 함수의 도함수를 적절하게 정의하는 데 성공했으며, '접선의 기울기'는 이제 정확한 수학적 의미를 갖는다. 위 정의를 사용하여 함수를 미분하는 것을 첫 번째 원리로부터의 미분이라고 한다. 다음은 첫 번째 원리로부터의 미분을 사용하여 의 도함수가 임을 증명하는 것이다.
:
가 에 접근함에 따라, 는 에 접근한다. 따라서, 이다.

및 는 실수이고, 는 의 함수, 즉 각 의 값에 대해 대응하는 의 값이 하나 존재한다고 가정한다. 이 관계를 로 쓸 수 있다. 가 직선에 대한 등식(선형 방정식)이라면 두 실수 및 가 존재하여 가 성립한다. 이 "기울기-절편 표준형"에서 은 기울기라고 불리며, 차분 상
:
에 의해 결정될 수 있다. 여기서 기호 (그리스 문자 대문자 델타)는 변화의 증분을 나타낸다. 따라서 이다.
직선이 아닌 일반 함수에서는 기울기를 갖지 않는 경우가 발생한다. 기하학적으로, '''점 에서의 의 미분 계수'''는 함수 의 점 에서의 접선의 기울기를 의미하며, 위의 차분 상의 극한('''미분 상''')과 같다. 이는 종종 미분 표기법에 따라 , 또는 라이프니츠 표기법에 따라 로 쓰인다.
의 정의역의 각 점 에서 미분 상이 존재한다면, 각 점 를 의 에서의 미분 상으로 보내는 함수('''도함수''')가 존재한다. 예를 들어, 라고 하면 도함수는 이다.
이와 가까운 관련 개념으로 함수의 미분이 있다. 접점 를 원점으로 하고, 각 축에 평행한 좌표축 , 를 갖는 국소 좌표계를 고려할 때, 이 좌표계에서 원점을 지나 기울기 의 직선(즉, 원래 좌표계에서 보면 의 에서의 접선)은 로 표시된다. 이는 에서의 증분 의 선형화, 선형 주요부이며, 는 의 에서의 '''미분'''이라고 불린다.
2. 1. 1. 미분 공식
거듭제곱 법칙에 따르면, ''a''와 ''n''이 상수이면 이다.[4] 예를 들어, 이다.그러나 다른 많은 함수들은 다항식 함수만큼 쉽게 미분될 수 없으며, 이는 함수의 도함수를 찾기 위해 때때로 추가적인 기술이 필요함을 의미한다. 이러한 기술에는 연쇄 법칙, 곱의 법칙, 몫의 법칙이 포함된다.
2. 1. 2. 편도함수
Partial derivative영어인 편도함수는 다변수 함수에서 특정 변수에 대해서만 미분하는 것을 의미하며, 이때 다른 변수들은 상수로 취급한다.x 및 y가 벡터 변수일 때, 함수 f의 그래프의 최적 선형 근사는 f가 동시에 여러 방향으로 얼마나 변화하는지에 달려 있다. 한 방향에 대한 최적 선형 근사를 취하면 편미분을 결정하며, 이는 일반적으로 로 표기한다.
2. 1. 3. 전도함수
및 가 벡터 변수일 때, 의 그래프의 최적 선형 근사는 가 동시에 여러 방향으로 얼마나 변화하는지에 달려 있다. 한 방향에 대한 최적 선형 근사를 취하면 편미분(일반적으로 로 쓰인다)을 결정한다. 동시에 모든 방향으로의 의 선형화는 함수의 전미분 이다.3. 미분의 역사
접선 개념은 고대 그리스의 유클리드(기원전 300년경), 아르키메데스(기원전 287–212년경), 페르가 아폴로니우스(기원전 262–190년경) 등이 알고 있었던 오래된 개념이다. 아르키메데스는 무한소를 사용했지만, 주로 면적과 부피 연구에 활용했다.
바스카라 2세(1114–1185)는 변화율 계산에 무한소를 사용하여 롤의 정리와 같은 미분학의 핵심 개념을 발전시켰다는 주장이 있다.
샤라프 알딘 알-투시(1135–1213)는 ''방정식 논문''에서 3차 방정식 해의 조건을 연구했다. 로쉬디 라셰드는 알-투시가 3차 함수 도함수를 사용했다고 주장했지만, 다른 학자들은 다른 방법을 사용했을 가능성을 제시한다.
아이작 뉴턴(1643–1727)과 고트프리트 빌헬름 라이프니츠(1646–1716)는 미분과 도함수에 대한 독립적이고 통일된 접근을 제공하며 현대 미분학을 발전시켰다.[16] 이들은 미적분학의 기본 정리를 통해 미분과 적분을 연결하여 이전의 면적, 부피 계산 방법을 대체했다. 뉴턴과 라이프니츠는 피에르 드 페르마(1607-1665), 아이작 배로(1630–1677) 등의 연구를 바탕으로 했다. 뉴턴은 미분을 이론 물리학에 처음 적용했고, 라이프니츠는 현대적 표기법을 체계화하여 미분학 발전에 핵심적 역할을 했다.
17세기 이후 오귀스탱 루이 코시(1789–1857), 베른하르트 리만(1826–1866), 카를 바이어슈트라스(1815–1897) 등 많은 수학자들이 미분 이론을 더욱 엄밀하게 정립했다. 19세기에는 미분이 유클리드 공간과 복소 평면으로 일반화되었다.
20세기에는 르베그 적분과 분포 이론을 통해 미분에 대한 이해가 더욱 확장되었다.
3. 1. 한국 수학사에서의 미분
조선 수학자 홍정하는 그의 저서 《구일집》에서 미분과 관련된 개념을 다루었지만, 현대적인 미분법과는 차이가 있었다. 한국에서는 서구 학문의 유입과 함께 미분 개념이 본격적으로 도입되었으며, 현대 수학 교육과정에서 핵심적인 내용으로 자리 잡았다.4. 미분의 응용
미분은 최적화 문제 해결, 뉴턴 역학에서 물체의 운동 분석, 미분 방정식을 통한 자연 현상 모델링, 평균값 정리를 이용한 함수 분석, 테일러 급수를 통한 함수 근사, 음함수 정리를 통한 도형 분석 등 다양한 분야에 응용된다.[1]
4. 1. 최적화 문제
미분가능 함수가 열린 구간에서 극대점 또는 극소점을 갖는다면, 그 점에서의 도함수는 0이다. 이 점을 임계점 또는 정지점이라고 하며, 함수값을 임계값이라고 한다. 만약 함수가 모든 곳에서 미분가능하지 않다면, 미분 불가능한 점 또한 임계점으로 지정된다.함수가 두 번 미분 가능하다면, 이계도함수를 통해 임계점에서 극대/극소 여부를 판별할 수 있다.
- 이계도함수가 양수이면, 그 점은 극소점이다.
- 이계도함수가 음수이면, 그 점은 극대점이다.
- 이계도함수가 0이면, 그 점은 극소점, 극대점, 또는 둘 다 아닐 수 있다.
이를 이계도함수 판정법이라고 한다.
도함수를 구하고 임계점을 푸는 것은 최적화 문제에서 극값(극소점 또는 극대점)을 찾는 간단한 방법이다. 최대 최소 정리에 따르면, 닫힌 구간에서 연속 함수는 최소값과 최대값을 적어도 한 번은 갖는다. 함수가 미분 가능하다면, 최소값과 최대값은 임계점 또는 구간의 경계점에서만 발생할 수 있다.
이는 그래프의 개형을 파악하는 데에도 활용된다. 미분 가능한 함수의 극소점과 극대점을 찾으면, 임계점 사이에서 함수가 증가 또는 감소하는지 관찰하여 그래프의 대략적인 형태를 알 수 있다.
고차원에서, 스칼라값 함수의 임계점은 기울기가 0인 점이다. 이계도함수 판정법은 임계점에서 함수의 이계 편도함수의 헤세 행렬의 고유값을 고려하여 극대/극소 여부를 판별하는 데 사용될 수 있다.
4. 1. 1. 변분법
변분법은 함수의 범함수를 최소화하는 문제를 다루는 분야이다. 예를 들어, 어떤 곡면 위의 두 점을 잇는 최단 곡선을 찾는 문제가 있다. 만약 곡면이 평면이라면 최단 곡선은 직선이 된다. 하지만 곡면이 달걀 모양처럼 복잡하다면, 최단 경로는 바로 명확해지지 않는다. 이러한 경로를 측지선이라고 하며, 변분법의 가장 기본적인 문제 중 하나는 측지선을 찾는 것이다. 또 다른 예로는 공간에서 닫힌 곡선이 둘러싸는 가장 작은 면적의 표면을 찾는 문제가 있다. 이러한 표면을 극소 곡면이라고 하며, 이 역시 변분법을 사용하여 찾을 수 있다.4. 2. 물리학
미분학은 물리학에서 매우 중요하다. 많은 물리적 과정은 미분 방정식으로 설명된다. 물리학은 특히 양이 시간에 따라 변화하고 발전하는 방식에 관심을 가지며, "'''시간 미분'''"(시간에 따른 변화율) 개념은 여러 중요한 개념을 정확하게 정의하는 데 필수적이다. 특히, 뉴턴 역학에서 물체의 위치에 대한 시간 미분은 중요하다.4. 2. 1. 뉴턴 역학
미분 방정식을 포함하는 방정식을 통해 많은 물리적 과정이 설명되는데, 이는 물리학에서 미분학이 매우 중요한 이유이다. 물리학은 특히 양이 시간에 따라 변화하고 발전하는 방식에 관심을 가지며, "'''시간 미분'''"(시간에 따른 변화율)의 개념은 여러 중요한 개념을 정확하게 정의하는 데 필수적이다. 특히, 뉴턴 역학에서 물체의 위치에 대한 시간 미분은 중요하다.예를 들어, 직선 상의 물체의 위치가 다음과 같이 주어지는 경우:
:
물체의 속도는 다음과 같다.
:
그리고 물체의 가속도는 다음과 같다.
:
이는 상수이다.
4. 2. 2. 열 방정식
주어진 소스에는 열 방정식에 대한 내용이 없으므로, 섹션 내용을 작성할 수 없다.4. 3. 미분 방정식
미분 방정식은 함수와 그 도함수 간의 관계를 나타내는 방정식으로, 자연 현상, 사회 현상 등 다양한 분야의 모델링에 사용된다. 미분 방정식은 크게 상미분 방정식과 편미분 방정식으로 나뉜다. 상미분 방정식은 하나의 독립 변수에 대한 함수와 그 도함수들의 관계를 나타내는 반면, 편미분 방정식은 여러 개의 독립 변수에 대한 함수와 그 편도함수들의 관계를 나타낸다.예를 들어, 뉴턴의 운동 제2법칙은 가속도와 힘의 관계를 설명하는 상미분 방정식으로 표현될 수 있다.
:
또한, 열 방정식은 곧은 막대기를 통해 열이 확산되는 현상을 설명하는 편미분 방정식의 한 예시이다.
:
여기서 u(x,t)|u(x,t)영어는 위치 x|x영어와 시간 t|t영어에서 막대의 온도이며, α|α영어는 막대를 통해 열이 얼마나 빨리 확산되는지에 따라 달라지는 상수이다.
4. 3. 1. 상미분 방정식
상미분 방정식은 하나의 독립 변수에 대한 함수와 그 도함수들의 관계를 나타내는 미분 방정식이다. 예를 들어, 가속도와 힘의 관계를 설명하는 뉴턴의 운동 제2법칙은 상미분 방정식으로 표현될 수 있다.4. 3. 2. 편미분 방정식
편미분 방정식은 여러 개의 독립 변수에 대한 함수와 그 편도함수들의 관계를 나타내는 방정식이다. 예를 들어, 곧은 막대기를 통해 열이 어떻게 확산되는지를 설명하는, 한 공간 변수의 열 방정식은 다음과 같은 편미분 방정식이다.:
여기서 u(x,t)|u(x,t)영어는 위치 x|x영어와 시간 t|t영어에서 막대의 온도이며, α|α영어는 막대를 통해 열이 얼마나 빨리 확산되는지에 따라 달라지는 상수이다.
4. 4. 평균값 정리

평균값 정리는 도함수의 값과 원래 함수의 값 사이의 관계를 설명한다. 만약 가 실수 값을 갖는 함수이고, 와 가 를 만족하는 수일 때, 평균값 정리는 두 점 와 사이의 기울기가 와 사이의 어떤 점 에서 의 접선의 기울기와 같다고 말한다. 즉, 다음이 성립한다.
:
실제로 평균값 정리는 도함수를 통해 함수를 제어한다. 예를 들어, 가 각 점에서 0과 같은 도함수를 갖는다고 가정하면, 이는 접선이 모든 점에서 수평임을 의미하므로 함수도 수평이어야 한다. 평균값 정리는 이것이 사실임을 증명한다. 그래프 위의 임의의 두 점 사이의 기울기는 의 접선 중 하나의 기울기와 같아야 하며, 그것은 모두 0이므로, 그래프 위의 한 점에서 다른 임의의 점으로 그은 임의의 직선도 기울기가 0이어야 한다. 그리고 그런 함수는 상승하거나 하강할 수 없으므로 수평선일 뿐이다. 도함수에 대해 더 복잡한 조건을 주면, 정확성은 떨어지지만 더 유효한 원래 함수에 대한 정보를 얻을 수 있다.
4. 5. 테일러 급수
테일러 다항식의 극한은 '''테일러 급수'''라고 하는 무한 급수이다. 테일러 급수는 원래 함수에 대한 매우 좋은 근사치가 되는 경우가 많다. 테일러 급수는 함수를 특정 점에서의 미분값들을 이용하여 나타낸다.[1]함수를 근사하는 방법으로, 주어진 점에서 함수의 최상의 선형 근사를 제공하는 도함수가 있다. 하지만, 이는 원래 함수와 매우 다를 수 있다. 근사를 향상시키는 한 가지 방법은 2차 근사를 사용하는 것이다. 점 $x_0$에서의 실수 값 함수 $f(x)$의 선형화는 선형 다항식 $a + b(x - x_0)$이며, 2차 다항식 $a + b(x - x_0) + c(x - x_0)^2$를 고려하여 더 나은 근사를 얻을 수 있다.
더 나아가 3차 다항식 $a + b(x - x_0) + c(x - x_0)^2 + d(x - x_0)^3$을 생각할 수 있으며, 이 아이디어는 임의로 높은 차수의 다항식으로 확장될 수 있다. 이러한 각 다항식에 대해 근사를 가능한 한 좋게 만드는 최상의 계수 $a$, $b$, $c$, $d$를 선택해야 한다. $x_0$의 근방에서, $a$에 대한 최상의 선택은 항상 $f(x_0)$이고, $b$에 대한 최상의 선택은 항상 $f'(x_0)$이다. $c$, $d$ 및 고차 계수의 경우, 이러한 계수는 $f$의 고차 도함수에 의해 결정된다. $c$는 항상 $\frac{f''(x_0)}{2}$이고, $d$는 항상 $\frac{f'''(x_0)}{3!}$이다. 이러한 계수를 사용하면 $f$의 '''테일러 다항식'''이 된다.
차수 $d$의 테일러 다항식은 $f$를 가장 잘 근사하는 차수 $d$의 다항식이며, 그 계수는 위의 공식의 일반화를 통해 찾을 수 있다. 테일러 정리는 근사가 얼마나 좋은지에 대한 정확한 경계를 제공한다. $f$가 $d$ 이하의 차수를 갖는 다항식인 경우, 차수 $d$의 테일러 다항식은 $f$와 같다.[1]
자신의 테일러 급수와 동일한 함수를 해석 함수라고 한다. 불연속점이나 날카로운 모서리가 있는 함수는 해석적일 수 없다. 또한, 해석적이지 않은 매끄러운 함수도 존재한다.[1]
4. 6. 음함수 정리
원과 같은 자연스러운 기하학적 도형은 함수의 그래프로 그릴 수 없다. 예를 들어, 인 경우, 원은 을 만족하는 모든 쌍 의 집합이다. 이 집합은 의 영점 집합이라고 하며, 포물면인 의 그래프와는 다르다. 음함수 정리는 과 같은 관계를 함수로 변환한다. 이 정리는 가 연속 미분 가능하면, 대부분의 점 주위에서 의 영점 집합은 함수 그래프를 붙여 놓은 것처럼 보인다고 말한다. 이 조건이 성립하지 않는 점은 의 도함수에 대한 조건에 의해 결정된다. 예를 들어, 원은 두 함수 의 그래프를 붙여서 만들 수 있다. 과 을 제외한 원의 모든 점의 근방에서 이 두 함수 중 하나는 원과 같은 그래프를 갖는다. (이 두 함수는 과 에서도 만나지만, 이는 음함수 정리에 의해 보장되는 것은 아니다.)
음함수 정리는 함수가 가역 함수의 그래프를 붙여 놓은 것처럼 보이는 경우를 나타내는 역함수 정리와 밀접한 관련이 있다.
참조
[1]
웹사이트
Definition of DIFFERENTIAL CALCULUS
https://www.merriam-[...]
2020-05-09
[2]
웹사이트
Definition of INTEGRAL CALCULUS
https://www.merriam-[...]
2020-05-09
[3]
서적
How to Think about Analysis
Oxford University Press
[4]
웹사이트
Derivative
https://mathworld.wo[...]
2020-07-26
[5]
문서
Euclid's Elements, The Archimedes Palimpsest and Apollonius of Perga
[6]
웹사이트
Bhaskaracharya II.
http://turnbull.mcs.[...]
2016-09-01
[7]
간행물
"Reviewed work(s): ''The History of Ancient Indian Mathematics'' by C. N. Srinivasiengar"
1968-10
[8]
서적
Theories of Light: From Descartes to Newton
Cambridge University Press
[9]
문서
[10]
문서
ユークリッド原論、アルキメデス・パリンプセストおよび Apollonius of Perga
[11]
MacTutor Biography
Aryabhata the Elder
[12]
간행물
"Reviewed work(s): ''The History of Ancient Indian Mathematics'' by C. N. Srinivasiengar"
1968-10
[13]
웹사이트
Bhaskaracharya II.
http://turnbull.mcs.[...]
[14]
간행물
Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat
[15]
MacTutor Biography
Sharaf al-Din al-Muzaffar al-Tusi
[16]
문서
ニュートンの研究は1666年に始まり、ライプニッツは1676年に始まる。が、ライプニッツが最初の論文を出すのが1684年で、1693年に出版のニュートンに先んじている。ライプニッツがニュートンの1673年か1676年の研究ドラフトを目にしたことや、あるいはニュートンがライプニッツの研究を自分の研究の洗練に用いたことなどは、可能性としてはあり得ることである。両者は互いに相手が自分の仕事を盗作したと主張した。この顛末は誰が微分積分学の創始者であるかを巡って両者の苦い論争となり、18世紀初頭の数学界に大きな衝撃を与えた。
[17]
간행물
Ideas of Calculus in Islam and India
[18]
문서
限定された特定の場合に関してはジェームス・グレゴリー (1638–1675) がすでに証明しており、いくつか重要な例に関してはピエール・ド・フェルマー (1601–1665) の仕事に見つけることができるとはいえ、これは記念碑的な到達点であった。
[19]
서적
An Introduction to the History of Mathematics
Saunders College Publishing
[20]
웹인용
Definition of DIFFERENTIAL CALCULUS
https://www.merriam-[...]
2020-05-09
[21]
웹인용
Definition of INTEGRAL CALCULUS
https://www.merriam-[...]
2020-05-09
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com