생존분석

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

생존분석은 특정 시점까지 사건이 발생하지 않을 확률을 추정하고 분석하는 통계적 방법론이다. 생존 함수, 사건분포함수, 위험함수 등 다양한 함수를 활용하며, 중도절단된 데이터를 처리하는 방법도 포함한다. 생존분석은 딥 러닝 기반 모델, 가능도 함수, 이산 시간 생존 모형 등 다양한 방법으로 수행되며, 카플란-마이어 추정량, 넬슨-앨런 추정량, 로그 순위 검정, 콕스 비례 위험 모형, 생존 트리 및 생존 랜덤 포레스트 등의 기법이 활용된다. 의학, 공학, 사회과학, 경제학 및 금융 등 광범위한 분야에서 환자 생존율 예측, 제품 수명 예측, 신용 위험 평가 등에 활용되며, 특히 한국에서는 암 생존율 분석 및 고령화 사회 문제 해결을 위한 연구에 중요하게 사용된다.

더 읽어볼만한 페이지

생존분석 - 감마 분포
감마 분포는 형상 모수와 척도 모수로 정의되는 연속 확률 분포로, 확률 밀도 함수가 감마 함수로 표현되며, 베이즈 통계학에서 켤레 사전 분포로 활용되고, 형상 모수가 양의 정수일 때는 얼랑 분포를 나타낸다.
생존분석 - 로그순위법
로그순위법은 생존 분석에서 두 그룹 간 생존 곡선을 비교하는 통계적 방법으로, 임상 시험과 역학 연구 등에서 치료법이나 요인이 생존 기간에 미치는 영향을 평가하는 데 활용된다.
통계학 - 확률
확률은 사건의 가능성을 수치화한 개념으로, 도박에서 시작되어 수학적으로 발전했으며, 다양한 해석과 요소, 응용 분야를 가지며 양자역학, 사회 현상 등에도 적용된다.
통계학 - 사분위수
사분위수는 정렬된 데이터를 4등분하는 세 개의 값으로 데이터 분포 요약 및 이상치 탐지에 활용되며, 제1사분위수(Q₁)는 하위 25%, 제2사분위수(Q₂ 또는 중앙값)는 하위 50%, 제3사분위수(Q₃)는 하위 75%를 나타낸다.

생존분석

2. 생존분석에 쓰이는 함수들

생존 분석의 핵심은 특정 시점까지 사건이 발생하지 않을 확률을 나타내는 생존 함수를 추정하고, 이를 바탕으로 다양한 분석을 수행하는 것이다.

== 생존함수 ==

생존 분석에서 생존함수(survival function) ''S(t)''는 특정 시점 ''t''보다 오래 생존할 확률을 나타내는 함수이다.

: $S(t) = \Pr(T > t)$

여기서 ''t''는 시간, ''T''는 사망에 이르는 시점을 나타내는 확률 변수이며, "Pr"은 확률을 나타낸다. 즉, 생존함수는 사망 시간이 특정 시간 ''t'' 이후일 확률이다. 생존함수는 생물학 분야에서는 생존자 함수(survivor function), 혹은 생존율 함수라고도 불리고, 공학 분야에서는 신뢰도 함수(reliability function)라고도 불린다. 신뢰도 함수의 경우 ''R(t)''로 표기한다.

일반적으로 $S(0)=1$ 이지만, 연구 시작 직후 표본이 사망하는 경우와 같이 즉시 사망하거나 실패할 가능성이 있는 경우 1 미만일 수도 있다.

생존함수는 단조감소함수이다: $S(u)\le S(t)$ if $u\ge t$ . 이는 더 늦은 나이까지 생존하는 것은 더 어린 나이를 모두 달성해야만 가능하다는 개념을 반영한다.

생존 함수는 일반적으로 나이가 무한정 증가함에 따라 0에 접근하는 것으로 가정되지만 (즉, ''t'' → ∞일 때 ''S''(''t'') → 0), 영원한 삶이 가능하다면 극한이 0보다 클 수 있다. 예를 들어, 안정적인 탄소 동위 원소와 불안정한 탄소 동위 원소의 혼합에 생존 분석을 적용할 수 있다. 불안정한 동위 원소는 조만간 붕괴되지만, 안정적인 동위 원소는 무기한으로 지속된다.

'''미래 생존 기간'''은 특정 시점 $t_0$ 에서의 사망까지 남은 시간으로, $t_0$ 까지 생존했을 때를 가정한다. 따라서 현재 표기법에서 $T - t_0$ 이다. '''기대 미래 생존 기간'''은 미래 생존 기간의 기대값이다.

신뢰성 문제에서, 기대 생존 기간은 ''평균 고장 시간''이라고 불리며, 기대 미래 생존 기간은 ''평균 잔여 수명''이라고 불린다.

개인이 ''t''세 또는 그 이후까지 생존할 확률이 정의에 따라 ''S''(''t'')이므로, 처음 인구 ''n''명의 신생아 중 ''t''세에 생존할 것으로 예상되는 생존자 수는 ''n'' × ''S''(''t'')이며, 모든 개인에 대해 동일한 생존 함수를 가정한다. 따라서 생존자의 예상 비율은 ''S''(''t'')이다. 다른 개인의 생존이 독립적인 경우, ''t''세의 생존자 수는 매개변수 ''n''과 ''S''(''t'')를 가진 이항 분포를 따르며, 생존자 비율의 분산은 ''S''(''t'') × (1-''S''(''t''))/''n''이다.

특정 비율의 생존자가 남아있는 나이는 ''S''(''t'') = ''q'' 방정식을 ''t''에 대해 풀어 찾을 수 있으며, 여기서 ''q''는 해당 분위수이다. 일반적으로 '''중앙값 생존 기간'''에 관심이 있으며, 이 경우 ''q'' = 1/2이고, 또는 ''q'' = 0.90 또는 ''q'' = 0.99와 같은 다른 분위수에도 관심이 있다.

== 생존분포함수와 사건밀도 ==

'''사건분포함수'''(lifetime distribution function) ''F(t)''는 특정 시점 ''t'' 이전에 사건이 발생할 확률을 나타내며, 생존 함수의 여집합으로 정의된다. 즉, ''F(t) = Pr(T ≤ t) = 1 - S(t)''이다.

만약 ''F(t)''가 미분 가능한 함수라면, 그 미분된 함수 ''f(t)''는 생존분포의 밀도라 하고, '''사건밀도'''(event density)라고도 부른다. 사건밀도는 단위 시간당 사망 또는 고장 사건의 비율을 의미한다. ''f(t) = F'(t) = (d/dt)F(t)''로 정의된다.

생존함수는 확률 분포 및 확률 밀도 함수를 사용하여 ''S(t) = Pr(T > t) = ∫_t^∞ f(u)du = 1 - F(t)'' 와 같이 표현할 수 있다.

마찬가지로, 생존 사건 밀도 함수는 ''s(t) = S'(t) = (d/dt)S(t) = (d/dt)∫_t^∞ f(u)du = (d/dt)[1 - F(t)] = -f(t)''로 정의할 수 있다. 통계 물리학 등 다른 분야에서는 생존 사건 밀도 함수를 최초 통과 시간 밀도(first passage time density)라고 한다.

== 위험함수와 누적위험함수 ==

위험함수(''h(t)'')는 특정 시점 ''t''까지 생존한 개체가 그 시점에서 사건을 경험할 순간적인 위험률을 나타낸다. 이는 다음과 같이 정의된다:

: $h(t) = \lim_{dt \rightarrow 0} \frac{\Pr(t \leq T < t+dt)}{dt\cdot S(t)} = \frac{f(t)}{S(t)} = -\frac{S'(t)}{S(t)}.$

위험 함수는 사망률(인구 통계학 및 보험 수학, $\mu$ 로 표시), 고장률(공학, $\lambda$ 로 표시) 등 다양한 이름으로 불린다. 예를 들어, 보험 수학에서 $\mu(x)$ 는 나이 $x$ 세의 사람들의 사망률을 나타내고, 신뢰성 공학에서 $\lambda(t)$ 는 시간 $t$ 동안 작동한 후 부품의 고장률을 나타낸다.

위험 함수는 다음의 속성을 만족해야 한다.

# $\forall x\geq0\left(h(x)\geq0\right)$

# $\int_{0}^{\infty} h(x)dx=\infty$

위험 함수는 음수가 아니어야 하고, $[0, \infty]$ 에 대한 적분은 무한대여야 한다. 그 외에는 증가, 감소, 비단조, 불연속 등 어떠한 형태도 가능하다. 욕조 곡선 위험 함수는 이러한 예시 중 하나이다.

누적위험함수(''H(t)'')는 위험함수의 적분으로, 특정 시점까지의 누적된 위험을 의미하며 다음과 같이 정의된다.

: $H(t) = \int_0^{t} h(u)\,du$

누적위험함수는 $\Lambda(t) = -\log S(t)$ 로도 표현 가능하다. 여기서 미분을 통해, $\frac{d}{dt} \Lambda(t) = -\frac{S'(t)}{S(t)} = \lambda(t)$ 임을 알 수 있다.

$\Lambda(t)$ 의 정의에서 ''t''가 무한대로 갈수록 무한대로 증가한다. 이는 정의상 누적 위험이 발산해야 하므로, $\lambda(t)$ 가 너무 빨리 감소해서는 안 된다는 것을 의미한다.

2. 1. 생존함수

생존분석에서 생존함수(survival function) ''S(t)''는 특정 시점 ''t''보다 오래 생존할 확률을 나타내는 함수로, 다음과 같이 정의한다.

:

S(t) = \Pr(T > t)

여기서 ''t''는 시간, ''T''는 사망에 이르는 시점을 나타내는 확률 변수이며, "Pr"은 확률을 나타낸다. 즉, 생존함수는 사망 시간이 특정 시간 ''t'' 이후일 확률이다. 생존함수는 생물학 분야에서는 생존자 함수(survivor function), 혹은 생존율 함수라고도 불리고, 공학 분야에서는 신뢰도 함수(reliability function)라고도 불린다. 신뢰도 함수의 경우 ''R(t)''로 표기한다.

일반적으로

S(0)=1

이지만, 연구 시작 직후 표본이 사망하는 경우와 같이 즉시 사망하거나 실패할 가능성이 있는 경우 1 미만일 수도 있다.

생존함수는 단조감소함수이다:

S(u)\le S(t)

if

u\ge t

. 이는 더 늦은 나이까지 생존하는 것은 더 어린 나이를 모두 달성해야만 가능하다는 개념을 반영한다.

생존 함수는 일반적으로 나이가 무한정 증가함에 따라 0에 접근하는 것으로 가정되지만 (즉, ''t'' → ∞일 때 ''S''(''t'') → 0), 영원한 삶이 가능하다면 극한이 0보다 클 수 있다. 예를 들어, 안정적인 탄소 동위 원소와 불안정한 탄소 동위 원소의 혼합에 생존 분석을 적용할 수 있다. 불안정한 동위 원소는 조만간 붕괴되지만, 안정적인 동위 원소는 무기한으로 지속된다.

'''미래 생존 기간'''은 특정 시점

t_0

에서의 사망까지 남은 시간으로,

t_0

까지 생존했을 때를 가정한다. 따라서 현재 표기법에서

T - t_0

이다. '''기대 미래 생존 기간'''은 미래 생존 기간의 기대값이다.

신뢰성 문제에서, 기대 생존 기간은 ''평균 고장 시간''이라고 불리며, 기대 미래 생존 기간은 ''평균 잔여 수명''이라고 불린다.

개인이 ''t''세 또는 그 이후까지 생존할 확률이 정의에 따라 ''S''(''t'')이므로, 처음 인구 ''n''명의 신생아 중 ''t''세에 생존할 것으로 예상되는 생존자 수는 ''n'' × ''S''(''t'')이며, 모든 개인에 대해 동일한 생존 함수를 가정한다. 따라서 생존자의 예상 비율은 ''S''(''t'')이다. 다른 개인의 생존이 독립적인 경우, ''t''세의 생존자 수는 매개변수 ''n''과 ''S''(''t'')를 가진 이항 분포를 따르며, 생존자 비율의 분산은 ''S''(''t'') × (1-''S''(''t''))/''n''이다.

특정 비율의 생존자가 남아있는 나이는 ''S''(''t'') = ''q'' 방정식을 ''t''에 대해 풀어 찾을 수 있으며, 여기서 ''q''는 해당 분위수이다. 일반적으로 '''중앙값 생존 기간'''에 관심이 있으며, 이 경우 ''q'' = 1/2이고, 또는 ''q'' = 0.90 또는 ''q'' = 0.99와 같은 다른 분위수에도 관심이 있다.

2. 2. 생존분포함수와 사건밀도

'''사건분포함수'''(lifetime distribution function) ''F(t)''는 특정 시점 ''t'' 이전에 사건이 발생할 확률을 나타내며, 생존함수의 여집합으로 정의된다. 즉, ''F(t) = Pr(T ≤ t) = 1 - S(t)''이다.

만약 ''F(t)''가 미분 가능한 함수라면, 그 미분된 함수 ''f(t)''는 생존분포의 밀도라 하고, '''사건밀도'''(event density)라고도 부른다. 사건밀도는 단위 시간당 사망 또는 고장 사건의 비율을 의미한다. ''f(t) = F'(t) = (d/dt)F(t)''로 정의된다.

생존함수는 확률 분포 및 확률 밀도 함수를 사용하여 ''S(t) = Pr(T > t) = ∫_t^∞ f(u)du = 1 - F(t)'' 와 같이 표현할 수 있다.

마찬가지로, 생존 사건 밀도 함수는 ''s(t) = S'(t) = (d/dt)S(t) = (d/dt)∫_t^∞ f(u)du = (d/dt)[1 - F(t)] = -f(t)''로 정의할 수 있다. 통계 물리학 등 다른 분야에서는 생존 사건 밀도 함수를 최초 통과 시간 밀도(first passage time density)라고 한다.

2. 3. 위험함수와 누적위험함수

위험함수(''h(t)'')는 특정 시점 ''t''까지 생존한 개체가 그 시점에서 사건을 경험할 순간적인 위험률을 나타낸다. 이는 다음과 같이 정의된다:

:

h(t) = \lim_{dt \rightarrow 0} \frac{\Pr(t \leq T < t+dt)}{dt\cdot S(t)} = \frac{f(t)}{S(t)} = -\frac{S'(t)}{S(t)}.

위험 함수는 사망률(인구 통계학 및 보험 수학,

\mu

로 표시), 고장률(공학,

\lambda

로 표시) 등 다양한 이름으로 불린다. 예를 들어, 보험 수학에서

\mu(x)

는 나이

x

세의 사람들의 사망률을 나타내고, 신뢰성 공학에서

\lambda(t)

는 시간

t

동안 작동한 후 부품의 고장률을 나타낸다.

위험 함수는 다음의 속성을 만족해야 한다.

#

\forall x\geq0\left(h(x)\geq0\right)

#

\int_{0}^{\infty} h(x)dx=\infty

위험 함수는 음수가 아니어야 하고,

[0, \infty]

에 대한 적분은 무한대여야 한다. 그 외에는 증가, 감소, 비단조, 불연속 등 어떠한 형태도 가능하다. 욕조 곡선 위험 함수는 이러한 예시 중 하나이다.

누적위험함수(''H(t)'')는 위험함수의 적분으로, 특정 시점까지의 누적된 위험을 의미하며 다음과 같이 정의된다.

:

H(t) = \int_0^{t} h(u)\,du

누적위험함수는

\Lambda(t) = -\log S(t)

로도 표현 가능하다. 여기서 미분을 통해,

\frac{d}{dt} \Lambda(t) = -\frac{S'(t)}{S(t)} = \lambda(t)

임을 알 수 있다.

\Lambda(t)

의 정의에서 ''t''가 무한대로 갈수록 무한대로 증가한다. 이는 정의상 누적 위험이 발산해야 하므로,

\lambda(t)

가 너무 빨리 감소해서는 안 된다는 것을 의미한다.

3. 중도절단

'''중도절단'''(censoring)은 생존 분석에서 손실된 데이터를 처리하는 방법이다.^[14]^[35] 이상적으로는 표본의 생일과 사망일을 통해 생존 기간을 파악하는 것이 좋지만, 그렇지 못한 경우에 중도절단을 사용한다.

우측 중도절단(right censoring): 참된 사건 발생 시간 ''T''에 대한 하한 ''l''만 알려져 있고 ''T'' > ''l''인 경우를 말한다.^[14] 예를 들어 출생 연도는 알려져 있지만 추적 관찰 중단되었거나 연구가 종료되었을 때 여전히 생존해 있는 대상에 대해 발생한다.^[14]^[35] 일반적으로 우측 절단된 데이터를 접하게 된다.
좌측 중도절단(left censoring): 관심 사건이 대상이 연구에 포함되기 전에 이미 발생했지만 언제 발생했는지 알 수 없는 경우를 말한다.^[14]^[35] 예를 들어, 생명 보험 및 연금 분야에서 흔히 사용된다.^[15]^[36]
구간 중도절단(interval censoring): 사건 발생 시점이 두 관측 시점 사이에 있는 경우를 말한다.^[14]^[35] HIV/AIDS 연구에서 자주 사용된다.^[35] HIV 혈청전환 시간은 일반적으로 의사 방문 후에 시작되는 실험실 평가를 통해서만 결정될 수 있기 때문에, 두 번의 검사 사이에 HIV 혈청전환이 발생했다는 것만 결론지을 수 있다.

절단은 사건 발생 시간(time to event)이 모든 모집 대상이 관심 사건을 보이기 전에 연구가 종료되거나, 대상이 사건을 경험하기 전에 연구를 떠나는 등의 이유로 관찰되지 않는, 누락된 데이터 문제의 한 형태이다. 절단은 생존 분석에서 흔히 발생한다.

좌측 절단된 데이터는 사람의 추적 관찰 기간의 왼쪽에 있는 생존 시간이 불완전해질 때 발생할 수 있다. 예를 들어, 역학적 예에서 감염 질환에 대해 검사 결과가 양성으로 나온 시점부터 환자를 모니터링할 수 있다. 관심 기간의 오른쪽은 알 수 있지만, 감염원에 노출된 정확한 시간은 알 수 없을 수 있다.^[16]

3. 1. 중도절단의 종류

중도절단(censoring)은 생존 분석에서 손실된 데이터를 처리하는 방법이다.^[14]^[35] 이상적으로는 표본의 생일과 사망일을 통해 생존 기간을 파악하는 것이 좋지만, 그렇지 못한 경우에 중도절단을 사용한다.

우측 중도절단(right censoring): 참된 사건 발생 시간 ''T''에 대한 하한 ''l''만 알려져 있고 ''T'' > ''l''인 경우를 말한다.^[14] 예를 들어 출생 연도는 알려져 있지만 추적 관찰 중단되었거나 연구가 종료되었을 때 여전히 생존해 있는 대상에 대해 발생한다.^[14]^[35] 일반적으로 우측 절단된 데이터를 접하게 된다.
좌측 중도절단(left censoring): 관심 사건이 대상이 연구에 포함되기 전에 이미 발생했지만 언제 발생했는지 알 수 없는 경우를 말한다.^[14]^[35] 예를 들어, 생명 보험 및 연금 분야에서 흔히 사용된다.^[15]^[36]
구간 중도절단(interval censoring): 사건 발생 시점이 두 관측 시점 사이에 있는 경우를 말한다.^[14]^[35] HIV/AIDS 연구에서 자주 사용된다.^[35] HIV 혈청전환 시간은 일반적으로 의사 방문 후에 시작되는 실험실 평가를 통해서만 결정될 수 있기 때문에, 두 번의 검사 사이에 HIV 혈청전환이 발생했다는 것만 결론지을 수 있다.

4. 생존분석의 방법

## 딥 러닝 기반 생존분석

최근 딥 표현 학습의 발전은 생존 추정 분야로 확장되었다. DeepSurv^[11] 모델은 CoxPH 모델의 로그-선형 매개변수화를 다층 퍼셉트론으로 대체할 것을 제안한다. Deep Survival Machines^[12] 및 Deep Cox Mixtures^[13]와 같은 추가적인 확장에는 잠재 변수 혼합 모델을 사용하여 사건 발생 시간 분포를 매개변수 또는 반매개변수 분포의 혼합으로 모델링하는 동시에 입력 공변량의 표현을 공동으로 학습하는 것이 포함된다. 딥 러닝 접근 방식은 특히 이미지 및 임상 시계열과 같은 복잡한 입력 데이터 양식에서 뛰어난 성능을 보여주었다.

## 가능도 함수 (Likelihood Function)

생존 모델은 반응 변수가 시간인 일반 회귀 모델로 유용하게 볼 수 있다. 그러나 모수를 맞추거나 다른 종류의 추론을 하기 위해 필요한 가능도 함수를 계산하는 것은 절단으로 인해 복잡해진다. 절단된 데이터가 있는 경우 생존 모델의 가능도 함수는 다음과 같이 공식화된다. 정의에 따르면 가능도 함수는 모델의 모수가 주어졌을 때 데이터의 조건부 확률이다.

데이터가 모수가 주어졌을 때 독립적이라고 가정하는 것이 일반적이다. 그러면 가능도 함수는 각 데이터의 가능도의 곱이다. 데이터를 비절단, 왼쪽 절단, 오른쪽 절단 및 구간 절단의 네 가지 범주로 나누는 것이 편리하다. 아래 방정식에서는 "unc.", "l.c.", "r.c.", "i.c."로 표시된다.

$L(\theta) = \prod_{T_i\in unc.} \Pr(T = T_i\mid\theta)\prod_{i\in l.c.} \Pr(T < T_i\mid\theta)\prod_{i\in r.c.} \Pr(T > T_i\mid\theta)\prod_{i\in i.c.} \Pr(T_{i,l} < T < T_{i,r}\mid\theta) .$

비절단 데이터의 경우 사망 시점의 나이가 $T_i$ 와 같으면 다음과 같다.

$\Pr(T = T_i\mid\theta) = f(T_i\mid\theta) .$

사망 시점의 나이가 $T_i$ 보다 작다는 것을 아는 왼쪽 절단 데이터의 경우 다음과 같다.

$\Pr(T < T_i\mid\theta) = F(T_i\mid\theta) = 1 - S(T_i\mid\theta) .$

사망 시점의 나이가 $T_i$ 보다 크다는 것을 아는 오른쪽 절단 데이터의 경우 다음과 같다.

$\Pr(T > T_i\mid\theta) = 1 - F(T_i\mid\theta) = S(T_i\mid\theta) .$

사망 시점의 나이가 $T_{i,r}$ 보다 작고 $T_{i,l}$ 보다 크다는 것을 아는 구간 절단 데이터의 경우 다음과 같다.

$\Pr(T_{i,l} < T < T_{i,r}\mid\theta)= S(T_{i,l}\mid\theta) - S(T_{i,r}\mid\theta) .$

구간 절단 데이터가 발생하는 중요한 응용 분야는 현재 상태 데이터입니다. 여기서 이벤트 $T_i$ 는 관찰 시간 전에 발생하지 않았고 다음 관찰 시간 전에 발생했다는 것을 알 수 있다.

## 이산 시간 생존 모형

많은 모수 모형이 연속 시간을 가정하는 반면, 이산 시간 생존 모형은 이진 분류 문제로 매핑될 수 있다. 이산 시간 생존 모형에서 생존 기간은 인위적으로 간격으로 재표본 추출되며, 각 간격에 대해 특정 시간 범위 내에서 사건이 발생하면 이진 대상 지표가 기록된다.^[17] 이진 분류기(문제의 더 많은 구조를 고려하기 위해 다른 가능성으로 잠재적으로 향상됨)가 보정되면, 분류기 점수는 위험 함수(즉, 실패의 조건부 확률)가 된다.^[17]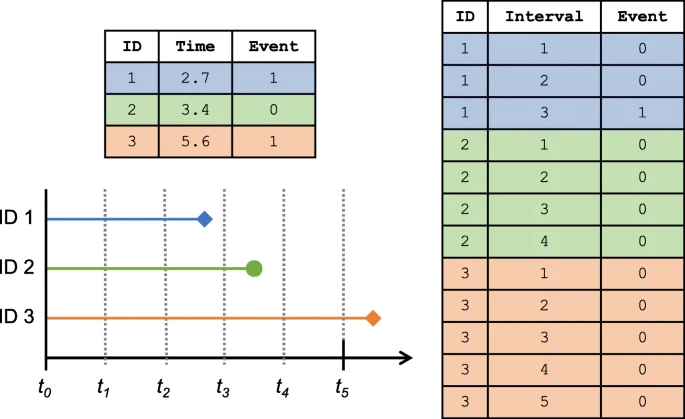

연속 시간 생존 데이터를 이산 시간 생존 데이터로 변환하는 설명. 개별 4는 검열 처리되고, 개별 5의 경우 사건이 관찰 창 5 외부에서 발생한다.

이산 시간 생존 모형은 경험적 우도와 관련이 있다.^[18]^[19]

## 생존 모델 적합성 평가

생존 모형의 적합성은 점수 규칙을 사용하여 평가할 수 있다.^[20]

## 생존 분석 예제 (R 활용)

클라인바움(Kleinbaum)의 교재에는 SAS, R 및 기타 패키지를 사용한 생존 분석 예제가 있다.^[21] 브로스트롬(Brostrom),^[22] 달가드(Dalgaard)^[2], 테이블만과 김(Tableman and Kim)^[23]의 교재에서는 R(또는 S를 사용하며, R에서 실행되는)을 사용한 생존 분석 예제를 제공한다.

## 예측 변수에 따른 분석 방법

카플란-마이어 곡선과 로그 순위 검정은 예측 변수가 범주형(예: 약물과 위약) 또는 범주적으로 취급할 수 있는 소수의 값(예: 약물 투여량 0, 20, 50, 100 mg/일)을 취하는 경우에 가장 유용하다. 반면, 로그 랭크 검정 및 카플란-마이어 곡선은 유전자 발현, 백혈구 수, 또는 연령 등과 같은 정량적 예측 변수에서는 쉽게 작동하지 않는다. 정량적 예측 변수의 경우, 대안으로 Cox 비례 위험 회귀 분석 (Cox proportional hazards regression analysis, Cox PH)이 있다. Cox PH 모형은 {0,1}의 지표 또는 더미 변수로 코딩된 범주형 예측 변수에서도 작동한다. 로그 순위 검정은 Cox PH 분석의 특수한 경우이며, Cox PH 소프트웨어를 사용하여 실행할 수 있다.

## 비모수적 방법

카플란-마이어 추정량은 생존 함수를 추정하는 데 사용될 수 있다. 넬슨-앨런 추정량은 누적 위험률 함수에 대한 비모수적 추정값을 제공하는 데 사용될 수 있다. 이러한 추정량은 생애 데이터를 필요로 한다. 주기적인 사례(코호트)와 사망(및 회복) 횟수는 생애 데이터 없이 생존 함수의 비모수적 최대 우도 및 최소 제곱 추정값을 만드는 데 통계적으로 충분하다.

### 카플란-마이어 추정량

카플란-마이어 추정량은 생존 함수를 추정하는 비모수적 방법 중 가장 널리 사용되는 방법이다. 관측된 생존 시간을 이용하여 계단 함수 형태의 생존 곡선을 그린다. 각 사건이 발생했을 때마다 생존 확률을 다시 계산한다.

생존 함수 ''S''(''t'')는 대상이 시간 ''t''보다 더 오래 생존할 확률이다. ''S''(''t'')는 이론적으로는 부드러운 곡선이지만, 일반적으로 Kaplan-Meier (KM) 곡선을 사용하여 추정된다. 그래프는 aml 데이터에 대한 KM 플롯을 보여주며 다음과 같이 해석할 수 있다.

''x'' 축은 시간이며, 0(관찰이 시작된 시점)부터 마지막 관찰 시점까지이다.
''y'' 축은 생존 대상의 비율이다. 시간 0에서 모든 대상의 100%가 사건 없이 살아있다.
실선(계단과 유사)은 사건 발생의 진행을 보여준다.
수직 하강은 사건을 나타낸다. 위에 표시된 aml 표에서 2명의 대상이 5주차에, 2명이 8주차에, 1명이 9주차에 사건을 겪는 등 이어진다. 5주, 8주 등 이러한 사건들은 해당 시점의 KM 플롯에서 수직 하강으로 표시된다.
KM 플롯의 맨 오른쪽 끝에는 161주차에 눈금 표시가 있다. 수직 눈금 표시는 환자가 이 시점에 중도 절단되었음을 나타낸다. aml 데이터 표에서 5명의 대상이 13주, 16주, 28주, 45주 및 161주에 중도 절단되었다. KM 플롯에는 이러한 중도 절단된 관측값에 해당하는 5개의 눈금 표시가 있다.

생명표는 각 사건 시간 지점에서 사건의 수와 생존 비율 측면에서 생존 데이터를 요약한다.

생명표는 각 사건 시간 지점에서 사건과 생존 비율을 요약한다. 생명표의 열은 다음과 같이 해석된다.

시간은 사건이 발생하는 시간 지점을 제공한다.
위험 인원은 시간 지점 t 직전의 위험에 처한 대상의 수이다. "위험에 처함"은 대상이 시간 t 이전에 사건을 겪지 않았고, 시간 t 이전 또는 t에 검열되지 않았음을 의미한다.
사건 인원은 시간 t에 사건이 발생한 대상의 수이다.
생존율은 Kaplan–Meier product-limit 추정치를 사용하여 결정된 생존 비율이다.
표준 오차는 추정된 생존율의 표준 오차이다. Kaplan–Meier product-limit 추정치의 표준 오차는 Greenwood의 공식을 사용하여 계산되며, 위험 인원(표의 n.risk), 사망자 수(표의 n.event) 및 생존 비율(표의 생존율)에 따라 달라진다.
하위 95% CI 및 상위 95% CI는 생존 비율에 대한 하한 및 상한 95% 신뢰 경계이다.

### 넬슨-알렌 추정량

넬슨-앨런 추정량은 누적 위험률 함수의 비모수적 추정에 사용될 수 있다. 카플란-마이어 추정량이 생존 함수를 추정하는 데 사용될 수 있는 것과 달리, 넬슨-알렌 추정량은 누적 위험률 함수를 추정한다. 이러한 추정량은 생애 데이터를 필요로 한다.

### 로그 순위 검정

로그 순위 검정은 둘 이상의 집단의 생존 시간을 비교하는 비모수적 검정 방법이다. 각 집단의 생존 곡선을 비교하여 통계적으로 유의미한 차이가 있는지 확인한다.

로그 순위 검정의 귀무 가설은 집단이 동일한 생존율을 가진다는 것이다. 각 시점에서의 생존 예상 인원수는 각 사건 시간에서 각 그룹의 위험에 처한 인원수를 기준으로 조정된다. 로그 순위 검정은 각 그룹에서 관찰된 사건의 수가 예상된 수와 유의하게 다른지 여부를 결정한다. 공식적인 검정은 카이 제곱 분포를 기반으로 한다. 로그 순위 통계량이 클 경우, 이는 그룹 간 생존 시간에 차이가 있음을 나타내는 증거이다. 로그 순위 통계량은 근사적으로 자유도가 1인 카이 제곱 분포를 가지며, p-값은 카이 제곱 검정을 사용하여 계산된다.

예제 데이터의 경우, 생존 차이에 대한 로그 순위 검정은 p=0.0653의 p-값을 제공하며, 이는 유의 수준을 0.05로 가정할 때 치료 그룹이 생존에서 유의한 차이를 보이지 않음을 나타낸다. 23명의 피험자라는 표본 크기 결정은 적기 때문에, 치료 그룹 간의 차이를 감지할 검정력이 거의 없다. 카이 제곱 검정은 점근적 근사에 기반하므로, 작은 표본 크기에 대해서는 p-값을 주의해서 고려해야 한다.

## 모수적 방법

지수 분포, 와이블 분포, 로그 로지스틱 분포, 감마 분포, 지수 로그 분포, 일반화 감마 분포 등 생존시간 분포에 대한 특정 모형을 가정하고, 모수를 추정하여 생존 함수를 추정한다.

## 콕스 비례 위험 모형

콕스 비례 위험 회귀 분석(Cox PH)은 생존분석에서 생존 시간에 영향을 미치는 요인(공변량)을 분석하는 데 사용되는 대표적인 준모수적 방법이다.^[2] 콕스 PH 모형은 예측 변수가 범주형이거나 정량적 예측 변수인 경우에도 적용 가능하다. 로그 순위 검정은 콕스 PH 분석의 특수한 경우이며, 콕스 PH 소프트웨어를 사용하여 수행할 수 있다.^[33]

흑색종 데이터 세트를 사용한 콕스 회귀 분석 결과는 다음과 같이 해석된다.^[2]

흑색종 데이터에 대한 콕스 비례 위험 회귀 분석 결과. 예측 변수는 성별 1: 여성, 2: 남성

성별(Sex): 숫자 벡터(1: 여성, 2: 남성)로 코딩된다. 콕스 모델은 남성에 대한 여성의 위험비(HR)를 제공한다.
coef: 0.662는 여성에 대한 남성의 위험비의 추정 로그이다.
exp(coef): 1.94 (= exp(0.662))는 위험비이다. 남성이 여성보다 사망 위험(생존율이 낮음)이 약 1.94배 높다는 것을 의미한다.
se(coef): 0.265는 로그 위험비의 표준 오차이다.
z: 2.5 (= 0.662 / 0.265)는 z 점수이다.
p-값: 0.013으로, 성별에 따른 생존율에 유의한 차이가 있음을 나타낸다. (p < 0.05)
위험비의 95% 신뢰 구간: 하한 1.15, 상한 3.26

모델 전체 유의성에 대한 세 가지 검정 (우도비 검정, 왈드 검정, 스코어(로그 순위) 검정) 결과는 다음과 같다.

우도비 검정 = 1 df에서 6.15, p=0.0131
Wald 검정 = 1 df에서 6.24, p=0.0125
스코어(로그 순위) 검정 = 1 df에서 6.47, p=0.0110

이 세 검정은 점근적으로 동일하며, 표본 크기가 충분히 크면 유사한 결과를 제공한다. 표본 크기가 작을 때는 우도비 검정이 더 나은 결과를 보이므로 일반적으로 선호된다. 스코어(로그 순위) 검정은 로그 순위 검정과 동일한 결과를 제공하는데, 이는 로그 순위 검정이 콕스 PH 회귀 분석의 특수한 경우이기 때문이다.^[3]

콕스 모델은 연속형 공변량을 포함하여 확장할 수 있다. 예를 들어 흑색종 데이터에서 종양 두께("thick")를 연속형 공변량으로 사용하여 분석할 수 있다.

|thumb|700px|흑색종 종양 두께의 히스토그램]]

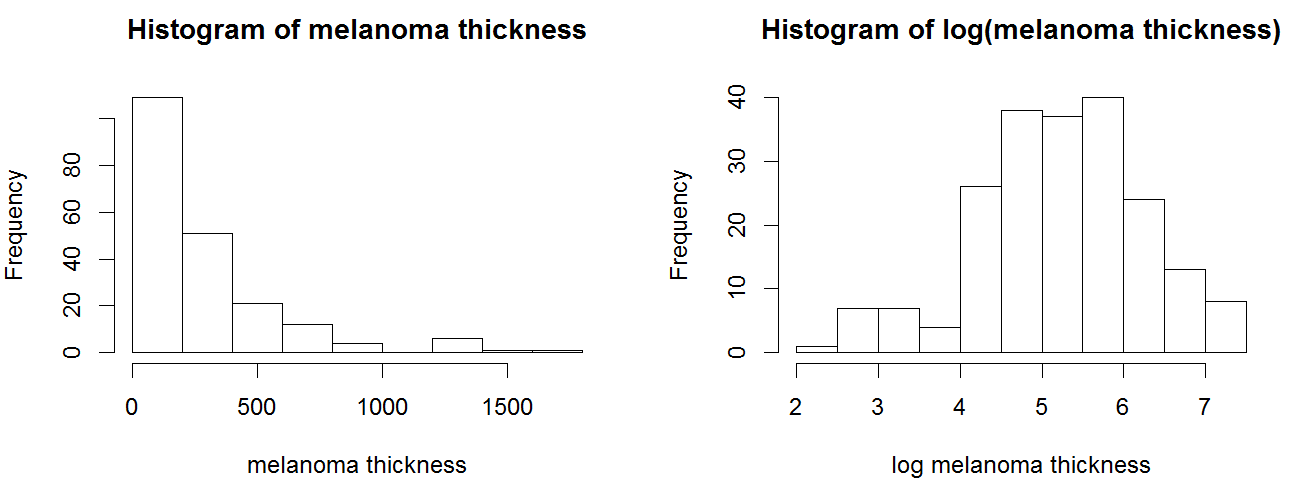
종양 두께 값은 양의 왜도를 가지므로, 로그 변환을 통해 정규 분포에 가깝게 만들어 분석에 사용한다.

|thumb|500px|공변량 로그 종양 두께를 사용한 흑색종 데이터 세트에 대한 콕스 PH 출력]]

세 가지 전체 검정(우도, 왈드, 스코어)의 p-값은 모두 유의미하여 모델이 유의함을 나타낸다.
log(thick)의 p-값은 6.9e-07, 위험비 HR = exp(coef) = 2.18로, 종양 두께와 사망 위험 증가 사이에 강한 관계가 있음을 나타낸다.
성별의 p-값은 0.088, 위험비 HR = 1.58, 95% 신뢰 구간은 0.934에서 2.68이다. HR의 신뢰 구간이 1을 포함하므로, 종양 두께를 통제하면 성별이 HR에 미치는 영향은 유의미하지 않다. 그러나, 처음 진료 시 남녀 간 종양 두께에 유의미한 차이가 존재한다.

콕스 모델은 위험이 비례한다는 가정을 기반으로 한다. 비례 위험 가정은 cox.zph() 함수를 사용하여 검증할 수 있으며, p-값이 0.05 미만이면 위험이 비례하지 않음을 나타낸다. 흑색종 데이터의 경우 p=0.222로, 위험이 비례한다는 귀무 가설을 기각할 수 없다.

콕스 모델은 다음과 같은 경우에 확장될 수 있다.

층화(Stratification): 연구 대상을 층으로 나누어 분석. 각 층에 대해 다른 기준 위험을 가정하지만, 회귀 모수는 층 전체에서 동일하다고 가정한다.
시간-변동 공변량(Time-varying covariates): 연구 과정에서 값이 변하는 공변량을 분석에 포함.

## 생존 트리 및 생존 랜덤 포레스트

콕스 비례 위험 회귀 모델은 선형 모델로, 선형 회귀 및 로지스틱 회귀와 유사하게 단일 선, 곡선, 평면 또는 표면만으로 그룹(생존, 사망)을 구분하거나 정량적 응답(생존 시간)을 추정한다. 그러나 경우에 따라 대체 분할이 더 정확한 분류 또는 정량적 추정치를 제공하기도 한다.

대체 방법 중 하나는 트리 구조 생존 모델이며,^[4]^[5]^[6] 여기에는 생존 랜덤 포레스트가 포함된다.^[7] 트리 구조 생존 모델은 콕스 모델보다 더 정확한 예측을 제공할 수 있어, 주어진 데이터 세트에 대해 두 가지 유형의 모델을 모두 검토하는 것이 합리적이다.

생존나무 분석의 예시는 R패키지 "rpart"를 사용한다.^[8] 이 예시는 rpart의 데이터 세트 stagec에 있는 146명의 stageC 전립선암 환자를 기반으로 한다. Rpart와 stagec 예시는 Atkinson과 Therneau (1997)에 설명되어 있으며,^[9] rpart 패키지의 비네트(vignette)로도 배포된다.^[8]

stages의 변수는 다음과 같다.

'''pgtime''': 진행까지의 시간 또는 진행이 없는 마지막 추적 관찰
'''pgstat''': 마지막 추적 관찰 시 상태 (1=진행, 0=중도절단)
'''age''': 진단 시 나이
'''eet''': 초기 내분비 요법 (1=아니오, 0=예)
'''ploidy''': 이배체/사배체/이수성 DNA 패턴
'''g2''': G2 단계 세포의 %
'''grade''': 종양 등급 (1-4)
'''gleason''': 글리슨 등급 분류 등급 (3-10)

분석에 의해 생성된 생존나무는 다음과 같다.

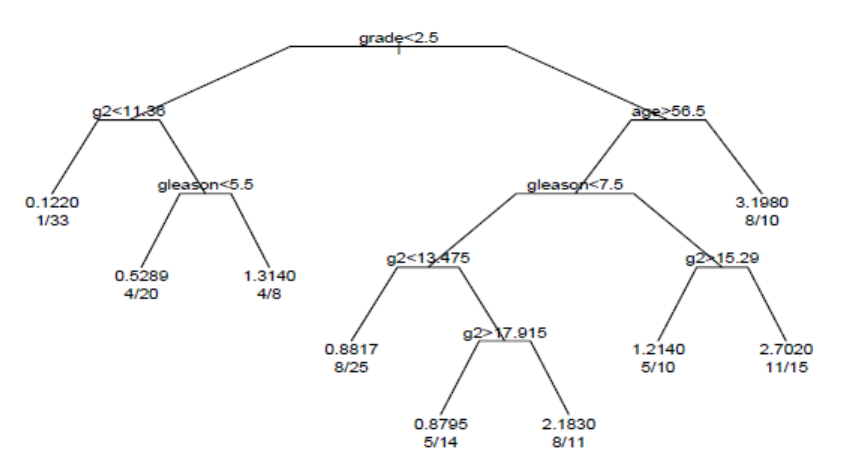
나무의 각 가지는 변수 값의 분할을 나타낸다. 예를 들어, 나무의 루트는 등급 < 2.5인 대상과 등급이 2.5 이상인 대상을 나눈다. 터미널 노드는 노드의 대상 수, 사건이 발생한 대상 수 및 루트와 비교한 상대적 사건 발생률을 나타낸다. 맨 왼쪽 노드에서 값 1/33은 노드에 있는 33명의 대상 중 한 명에게 사건이 발생했으며 상대적 사건 발생률이 0.122임을 나타낸다. 맨 오른쪽 하단 노드에서 값 11/15는 노드에 있는 15명의 대상 중 11명에게 사건이 발생했으며 상대적 사건 발생률이 2.7임을 나타낸다.

생존 트리 하나를 구축하는 대신, 여러 생존 트리를 구축하는 방법도 있다. 각 트리는 데이터의 샘플을 사용하여 구성되며, 이러한 트리를 평균하여 생존을 예측한다.^[7] 이는 생존 랜덤 포레스트 모델의 기반이 되는 방법이다. 생존 랜덤 포레스트 분석은 R패키지 "randomForestSRC"에서 사용할 수 있다.^[10]

randomForestSRC 패키지에는 pbc 데이터 세트를 사용한 생존 랜덤 포레스트 분석 예제가 포함되어 있다. 이 데이터는 1974년부터 1984년 사이에 진행된 메이요 클리닉 원발성 담즙성 간경변(PBC) 시험에서 얻은 것이다. 이 예제에서 랜덤 포레스트 생존 모델은 Cox PH 모델보다 더 정확한 생존 예측을 제공한다. 예측 오차는 부트스트래핑 재표본 추출을 통해 추정된다.

4. 1. 비모수적 방법

카플란-마이어 추정량은 생존 함수를 추정하는 데 사용될 수 있다. 넬슨-앨런 추정량은 누적 위험률 함수에 대한 비모수적 추정값을 제공하는 데 사용될 수 있다. 이러한 추정량은 생애 데이터를 필요로 한다. 주기적인 사례(코호트)와 사망(및 회복) 횟수는 생애 데이터 없이 생존 함수의 비모수적 최대 우도 및 최소 제곱 추정값을 만드는 데 통계적으로 충분하다.

==== 카플란-마이어 추정량 ====

카플란-마이어 추정량은 생존 함수를 추정하는 비모수적 방법 중 가장 널리 사용되는 방법이다. 관측된 생존 시간을 이용하여 계단 함수 형태의 생존 곡선을 그린다. 각 사건이 발생했을 때마다 생존 확률을 다시 계산한다.

생존 함수 ''S''(''t'')는 대상이 시간 ''t''보다 더 오래 생존할 확률이다. ''S''(''t'')는 이론적으로는 부드러운 곡선이지만, 일반적으로 Kaplan-Meier (KM) 곡선을 사용하여 추정된다. 그래프는 aml 데이터에 대한 KM 플롯을 보여주며 다음과 같이 해석할 수 있다.

''x'' 축은 시간이며, 0(관찰이 시작된 시점)부터 마지막 관찰 시점까지이다.
''y'' 축은 생존 대상의 비율이다. 시간 0에서 모든 대상의 100%가 사건 없이 살아있다.
실선(계단과 유사)은 사건 발생의 진행을 보여준다.
수직 하강은 사건을 나타낸다. 위에 표시된 aml 표에서 2명의 대상이 5주차에, 2명이 8주차에, 1명이 9주차에 사건을 겪는 등 이어진다. 5주, 8주 등 이러한 사건들은 해당 시점의 KM 플롯에서 수직 하강으로 표시된다.
KM 플롯의 맨 오른쪽 끝에는 161주차에 눈금 표시가 있다. 수직 눈금 표시는 환자가 이 시점에 중도 절단되었음을 나타낸다. aml 데이터 표에서 5명의 대상이 13주, 16주, 28주, 45주 및 161주에 중도 절단되었다. KM 플롯에는 이러한 중도 절단된 관측값에 해당하는 5개의 눈금 표시가 있다.

생명표는 각 사건 시간 지점에서 사건의 수와 생존 비율 측면에서 생존 데이터를 요약한다.

생명표는 각 사건 시간 지점에서 사건과 생존 비율을 요약한다. 생명표의 열은 다음과 같이 해석된다.

시간은 사건이 발생하는 시간 지점을 제공한다.
위험 인원은 시간 지점 t 직전의 위험에 처한 대상의 수이다. "위험에 처함"은 대상이 시간 t 이전에 사건을 겪지 않았고, 시간 t 이전 또는 t에 검열되지 않았음을 의미한다.
사건 인원은 시간 t에 사건이 발생한 대상의 수이다.
생존율은 Kaplan–Meier product-limit 추정치를 사용하여 결정된 생존 비율이다.
표준 오차는 추정된 생존율의 표준 오차이다. Kaplan–Meier product-limit 추정치의 표준 오차는 Greenwood의 공식을 사용하여 계산되며, 위험 인원(표의 n.risk), 사망자 수(표의 n.event) 및 생존 비율(표의 생존율)에 따라 달라진다.
하위 95% CI 및 상위 95% CI는 생존 비율에 대한 하한 및 상한 95% 신뢰 경계이다.

==== 넬슨-알렌 추정량 ====

넬슨-앨런 추정량은 누적 위험률 함수의 비모수적 추정에 사용될 수 있다. 카플란-마이어 추정량이 생존 함수를 추정하는 데 사용될 수 있는 것과 달리, 넬슨-알렌 추정량은 누적 위험률 함수를 추정한다. 이러한 추정량은 생애 데이터를 필요로 한다.

4. 1. 1. 카플란-마이어 추정량

카플란-마이어 추정량은 생존 함수를 추정하는 비모수적 방법 중 가장 널리 사용되는 방법이다. 관측된 생존 시간을 이용하여 계단 함수 형태의 생존 곡선을 그린다. 각 사건이 발생했을 때마다 생존 확률을 다시 계산한다.

생존 함수 ''S''(''t'')는 대상이 시간 ''t''보다 더 오래 생존할 확률이다. ''S''(''t'')는 이론적으로는 부드러운 곡선이지만, 일반적으로 Kaplan-Meier (KM) 곡선을 사용하여 추정된다. 그래프는 aml 데이터에 대한 KM 플롯을 보여주며 다음과 같이 해석할 수 있다.

''x'' 축은 시간이며, 0(관찰이 시작된 시점)부터 마지막 관찰 시점까지이다.
''y'' 축은 생존 대상의 비율이다. 시간 0에서 모든 대상의 100%가 사건 없이 살아있다.
실선(계단과 유사)은 사건 발생의 진행을 보여준다.
수직 하강은 사건을 나타낸다. 위에 표시된 aml 표에서 2명의 대상이 5주차에, 2명이 8주차에, 1명이 9주차에 사건을 겪는 등 이어진다. 5주, 8주 등 이러한 사건들은 해당 시점의 KM 플롯에서 수직 하강으로 표시된다.
KM 플롯의 맨 오른쪽 끝에는 161주차에 눈금 표시가 있다. 수직 눈금 표시는 환자가 이 시점에 중도 절단되었음을 나타낸다. aml 데이터 표에서 5명의 대상이 13주, 16주, 28주, 45주 및 161주에 중도 절단되었다. KM 플롯에는 이러한 중도 절단된 관측값에 해당하는 5개의 눈금 표시가 있다.

생명표는 각 사건 시간 지점에서 사건의 수와 생존 비율 측면에서 생존 데이터를 요약한다.

생명표는 각 사건 시간 지점에서 사건과 생존 비율을 요약한다. 생명표의 열은 다음과 같이 해석된다.

시간은 사건이 발생하는 시간 지점을 제공한다.
위험 인원은 시간 지점 t 직전의 위험에 처한 대상의 수이다. "위험에 처함"은 대상이 시간 t 이전에 사건을 겪지 않았고, 시간 t 이전 또는 t에 검열되지 않았음을 의미한다.
사건 인원은 시간 t에 사건이 발생한 대상의 수이다.
생존율은 Kaplan–Meier product-limit 추정치를 사용하여 결정된 생존 비율이다.
표준 오차는 추정된 생존율의 표준 오차이다. Kaplan–Meier product-limit 추정치의 표준 오차는 Greenwood의 공식을 사용하여 계산되며, 위험 인원(표의 n.risk), 사망자 수(표의 n.event) 및 생존 비율(표의 생존율)에 따라 달라진다.
하위 95% CI 및 상위 95% CI는 생존 비율에 대한 하한 및 상한 95% 신뢰 경계이다.

4. 1. 2. 넬슨-알렌 추정량

넬슨-앨런 추정량은 누적 위험률 함수의 비모수적 추정에 사용될 수 있다. 카플란-마이어 추정량이 생존 함수를 추정하는 데 사용될 수 있는 것과 달리, 넬슨-알렌 추정량은 누적 위험률 함수를 추정한다. 이러한 추정량은 생애 데이터를 필요로 한다.

4. 2. 로그 순위 검정

로그 순위 검정은 둘 이상의 집단의 생존 시간을 비교하는 비모수적 검정 방법이다. 각 집단의 생존 곡선을 비교하여 통계적으로 유의미한 차이가 있는지 확인한다.

로그 순위 검정의 귀무 가설은 집단이 동일한 생존율을 가진다는 것이다. 각 시점에서의 생존 예상 인원수는 각 사건 시간에서 각 그룹의 위험에 처한 인원수를 기준으로 조정된다. 로그 순위 검정은 각 그룹에서 관찰된 사건의 수가 예상된 수와 유의하게 다른지 여부를 결정한다. 공식적인 검정은 카이 제곱 분포를 기반으로 한다. 로그 순위 통계량이 클 경우, 이는 그룹 간 생존 시간에 차이가 있음을 나타내는 증거이다. 로그 순위 통계량은 근사적으로 자유도가 1인 카이 제곱 분포를 가지며, p-값은 카이 제곱 검정을 사용하여 계산된다.

예제 데이터의 경우, 생존 차이에 대한 로그 순위 검정은 p=0.0653의 p-값을 제공하며, 이는 유의 수준을 0.05로 가정할 때 치료 그룹이 생존에서 유의한 차이를 보이지 않음을 나타낸다. 23명의 피험자라는 표본 크기 결정은 적기 때문에, 치료 그룹 간의 차이를 감지할 검정력이 거의 없다. 카이 제곱 검정은 점근적 근사에 기반하므로, 작은 표본 크기에 대해서는 p-값을 주의해서 고려해야 한다.

4. 3. 모수적 방법

지수 분포, 와이블 분포, 로그 로지스틱 분포, 감마 분포, 지수 로그 분포, 일반화 감마 분포 등 생존시간 분포에 대한 특정 모형을 가정하고, 모수를 추정하여 생존 함수를 추정한다.

4. 3. 1. 콕스 비례 위험 모형

콕스 비례 위험 회귀 분석(Cox PH)은 생존분석에서 생존 시간에 영향을 미치는 요인(공변량)을 분석하는 데 사용되는 대표적인 준모수적 방법이다.^[2] 콕스 PH 모형은 예측 변수가 범주형이거나 정량적 예측 변수인 경우에도 적용 가능하다. 로그 순위 검정은 콕스 PH 분석의 특수한 경우이며, 콕스 PH 소프트웨어를 사용하여 수행할 수 있다.^[33]

흑색종 데이터 세트를 사용한 콕스 회귀 분석 결과는 다음과 같이 해석된다.^[2]

성별(Sex): 숫자 벡터(1: 여성, 2: 남성)로 코딩된다. 콕스 모델은 남성에 대한 여성의 위험비(HR)를 제공한다.
coef: 0.662는 여성에 대한 남성의 위험비의 추정 로그이다.
exp(coef): 1.94 (= exp(0.662))는 위험비이다. 남성이 여성보다 사망 위험(생존율이 낮음)이 약 1.94배 높다는 것을 의미한다.
se(coef): 0.265는 로그 위험비의 표준 오차이다.
z: 2.5 (= 0.662 / 0.265)는 z 점수이다.
p-값: 0.013으로, 성별에 따른 생존율에 유의한 차이가 있음을 나타낸다. (p < 0.05)
위험비의 95% 신뢰 구간: 하한 1.15, 상한 3.26

모델 전체 유의성에 대한 세 가지 검정 (우도비 검정, 왈드 검정, 스코어(로그 순위) 검정) 결과는 다음과 같다.

우도비 검정 = 1 df에서 6.15, p=0.0131
Wald 검정 = 1 df에서 6.24, p=0.0125
스코어(로그 순위) 검정 = 1 df에서 6.47, p=0.0110

이 세 검정은 점근적으로 동일하며, 표본 크기가 충분히 크면 유사한 결과를 제공한다. 표본 크기가 작을 때는 우도비 검정이 더 나은 결과를 보이므로 일반적으로 선호된다. 스코어(로그 순위) 검정은 로그 순위 검정과 동일한 결과를 제공하는데, 이는 로그 순위 검정이 콕스 PH 회귀 분석의 특수한 경우이기 때문이다.^[3]

콕스 모델은 연속형 공변량을 포함하여 확장할 수 있다. 예를 들어 흑색종 데이터에서 종양 두께("thick")를 연속형 공변량으로 사용하여 분석할 수 있다.

|thumb|700px|흑색종 종양 두께의 히스토그램]]

종양 두께 값은 양의 왜도를 가지므로, 로그 변환을 통해 정규 분포에 가깝게 만들어 분석에 사용한다.

|thumb|500px|공변량 로그 종양 두께를 사용한 흑색종 데이터 세트에 대한 콕스 PH 출력]]

세 가지 전체 검정(우도, 왈드, 스코어)의 p-값은 모두 유의미하여 모델이 유의함을 나타낸다.
log(thick)의 p-값은 6.9e-07, 위험비 HR = exp(coef) = 2.18로, 종양 두께와 사망 위험 증가 사이에 강한 관계가 있음을 나타낸다.
성별의 p-값은 0.088, 위험비 HR = 1.58, 95% 신뢰 구간은 0.934에서 2.68이다. HR의 신뢰 구간이 1을 포함하므로, 종양 두께를 통제하면 성별이 HR에 미치는 영향은 유의미하지 않다. 그러나, 처음 진료 시 남녀 간 종양 두께에 유의미한 차이가 존재한다.

콕스 모델은 위험이 비례한다는 가정을 기반으로 한다. 비례 위험 가정은 cox.zph() 함수를 사용하여 검증할 수 있으며, p-값이 0.05 미만이면 위험이 비례하지 않음을 나타낸다. 흑색종 데이터의 경우 p=0.222로, 위험이 비례한다는 귀무 가설을 기각할 수 없다.

콕스 모델은 다음과 같은 경우에 확장될 수 있다.

층화(Stratification): 연구 대상을 층으로 나누어 분석. 각 층에 대해 다른 기준 위험을 가정하지만, 회귀 모수는 층 전체에서 동일하다고 가정한다.
시간-변동 공변량(Time-varying covariates): 연구 과정에서 값이 변하는 공변량을 분석에 포함.

4. 3. 2. 생존 트리 및 생존 랜덤 포레스트

콕스 비례 위험 회귀 모델은 선형 모델로, 선형 회귀 및 로지스틱 회귀와 유사하게 단일 선, 곡선, 평면 또는 표면만으로 그룹(생존, 사망)을 구분하거나 정량적 응답(생존 시간)을 추정한다. 그러나 경우에 따라 대체 분할이 더 정확한 분류 또는 정량적 추정치를 제공하기도 한다.

대체 방법 중 하나는 트리 구조 생존 모델이며,^[4]^[5]^[6] 여기에는 생존 랜덤 포레스트가 포함된다.^[7] 트리 구조 생존 모델은 콕스 모델보다 더 정확한 예측을 제공할 수 있어, 주어진 데이터 세트에 대해 두 가지 유형의 모델을 모두 검토하는 것이 합리적이다.

생존나무 분석의 예시는 R패키지 "rpart"를 사용한다.^[8] 이 예시는 rpart의 데이터 세트 stagec에 있는 146명의 stageC 전립선암 환자를 기반으로 한다. Rpart와 stagec 예시는 Atkinson과 Therneau (1997)에 설명되어 있으며,^[9] rpart 패키지의 비네트(vignette)로도 배포된다.^[8]

stages의 변수는 다음과 같다.

'''pgtime''': 진행까지의 시간 또는 진행이 없는 마지막 추적 관찰
'''pgstat''': 마지막 추적 관찰 시 상태 (1=진행, 0=중도절단)
'''age''': 진단 시 나이
'''eet''': 초기 내분비 요법 (1=아니오, 0=예)
'''ploidy''': 이배체/사배체/이수성 DNA 패턴
'''g2''': G2 단계 세포의 %
'''grade''': 종양 등급 (1-4)
'''gleason''': 글리슨 등급 분류 등급 (3-10)

분석에 의해 생성된 생존나무는 다음과 같다.

나무의 각 가지는 변수 값의 분할을 나타낸다. 예를 들어, 나무의 루트는 등급 < 2.5인 대상과 등급이 2.5 이상인 대상을 나눈다. 터미널 노드는 노드의 대상 수, 사건이 발생한 대상 수 및 루트와 비교한 상대적 사건 발생률을 나타낸다. 맨 왼쪽 노드에서 값 1/33은 노드에 있는 33명의 대상 중 한 명에게 사건이 발생했으며 상대적 사건 발생률이 0.122임을 나타낸다. 맨 오른쪽 하단 노드에서 값 11/15는 노드에 있는 15명의 대상 중 11명에게 사건이 발생했으며 상대적 사건 발생률이 2.7임을 나타낸다.

생존 트리 하나를 구축하는 대신, 여러 생존 트리를 구축하는 방법도 있다. 각 트리는 데이터의 샘플을 사용하여 구성되며, 이러한 트리를 평균하여 생존을 예측한다.^[7] 이는 생존 랜덤 포레스트 모델의 기반이 되는 방법이다. 생존 랜덤 포레스트 분석은 R패키지 "randomForestSRC"에서 사용할 수 있다.^[10]

randomForestSRC 패키지에는 pbc 데이터 세트를 사용한 생존 랜덤 포레스트 분석 예제가 포함되어 있다. 이 데이터는 1974년부터 1984년 사이에 진행된 메이요 클리닉 원발성 담즙성 간경변(PBC) 시험에서 얻은 것이다. 이 예제에서 랜덤 포레스트 생존 모델은 Cox PH 모델보다 더 정확한 생존 예측을 제공한다. 예측 오차는 부트스트래핑 재표본 추출을 통해 추정된다.

5. 생존분석의 활용

생존분석은 다양한 분야에서 활용된다.

의학 및 보건학 분야에서 환자의 생존율 예측, 치료 효과 비교, 질병 발생 위험 요인 분석 등에 활용된다.^[32]^[33] 특히, 암 환자의 생존율 분석 및 새로운 치료법의 효과 평가에 널리 사용된다.^[32]

R 언어의 "survival" 패키지에 포함된 급성 골수성 백혈병(aml) 생존 데이터 세트는 표준 화학 요법 과정의 연장(유지) 여부에 따른 효과를 비교하는 데 사용된다.^[32] 유지 요법을 받은 환자가 그렇지 않은 환자에 비해 재발이 늦어지는지 여부를 분석한다.

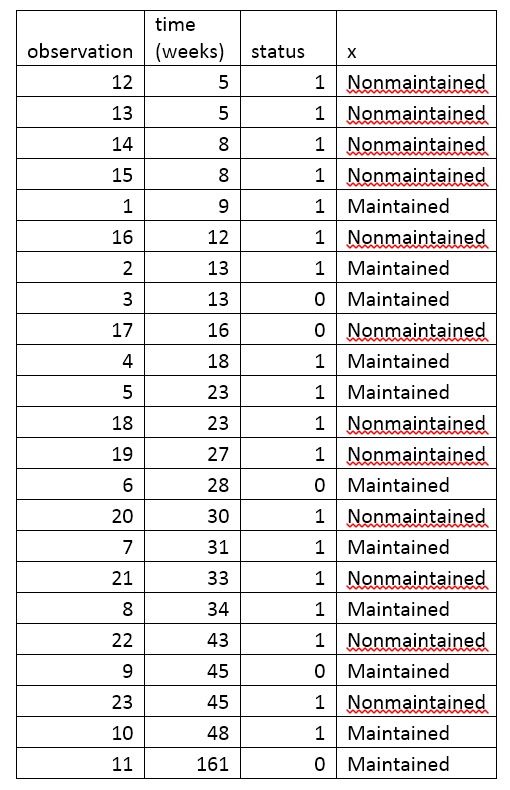
흑색종 데이터 세트를 이용한 Cox 비례 위험 회귀 분석 결과, 남성이 여성보다 생명의 위험이 더 높고(생존율이 낮음) (위험비 1.94, 95% 신뢰 구간 1.15-3.26), 성별에 따른 생존율에 유의미한 차이가 있음을 알 수 있다(p=0.013).^[33]

전립선암 환자 데이터를 이용한 생존 나무 분석에서는 종양의 악성도(grade)가 2.5 미만인 경우와 이상인 경우에 따라 생존율에 차이가 있음을 보여준다.

공학 분야에서 제품의 수명 예측, 신뢰성 평가, 고장 원인 분석 등에 활용된다.^[24]^[25]^[27]^[45] 예를 들어, 기계 부품의 고장 시간을 분석하여 제품의 수명을 예측하고, 보증 기간 설정 등에 활용할 수 있다. 항공우주 산업에서 금속 부품의 리드 타임을 예측하는 데에도 사용된다.^[27]^[45]

사회과학 분야에서 사회 현상의 지속 기간을 분석하고, 사건 발생 위험 요인을 파악하는 데 활용된다.^[24]^[25] 예를 들어, 실업 기간, 결혼 지속 기간, 기업의 생존 기간 등을 분석하는 데 사용될 수 있다. 신용 위험, 사법 오심에 따른 사형수의 오판율,^[26] 항공우주 산업에서 금속 부품의 리드 타임,^[27] 재범의 예측 변수,^[28] 동물 이동 추적에서 무선 꼬리표 부착 동물의 생존 분포,^[29] 로마 황제의 폭력적인 죽음에 이르는 시간,^[30] 주식의 거래소 내 대기 시간^[31]등 다양한 분야에서 활용된다.

경제학 및 금융 분야에서 신용 위험 평가, 기업 부도 예측, 보험 상품 개발 등에 활용된다.^[24]^[25]^[42]^[43] 예를 들어, 대출자의 상환 불이행 위험을 예측하거나, 보험 가입자의 사망 위험을 예측하는 데 사용될 수 있다. 전자 거래되는 주식의 거래소 내 대기 시간 분석에도 활용될 수 있다.^[31]

5. 1. 의학 및 보건학

생존분석은 의학 및 보건학 분야에서 환자의 생존율 예측, 치료 효과 비교, 질병 발생 위험 요인 분석 등에 활용된다.^[32]^[33] 특히, 암 환자의 생존율 분석 및 새로운 치료법의 효과 평가에 널리 사용된다.^[32]

R 언어의 "survival" 패키지에 포함된 급성 골수성 백혈병(aml) 생존 데이터 세트는 표준 화학 요법 과정의 연장(유지) 여부에 따른 효과를 비교하는 데 사용된다.^[32] 유지 요법을 받은 환자가 그렇지 않은 환자에 비해 재발이 늦어지는지 여부를 분석한다.

흑색종 데이터 세트를 이용한 Cox 비례 위험 회귀 분석 결과, 남성이 여성보다 생명의 위험이 더 높고(생존율이 낮음) (위험비 1.94, 95% 신뢰 구간 1.15-3.26), 성별에 따른 생존율에 유의미한 차이가 있음을 알 수 있다(p=0.013).^[33]

전립선암 환자 데이터를 이용한 생존 나무 분석에서는 종양의 악성도(grade)가 2.5 미만인 경우와 이상인 경우에 따라 생존율에 차이가 있음을 보여준다.

5. 2. 공학

생존분석은 제품의 수명 예측, 신뢰성 평가, 고장 원인 분석 등에 활용된다.^[24]^[25]^[27]^[45] 예를 들어, 기계 부품의 고장 시간을 분석하여 제품의 수명을 예측하고, 보증 기간 설정 등에 활용할 수 있다. 항공우주 산업에서 금속 부품의 리드 타임을 예측하는 데에도 사용된다.^[27]^[45]

5. 3. 사회과학

생존분석은 사회 현상의 지속 기간을 분석하고, 사건 발생 위험 요인을 파악하는 데 활용된다.^[24]^[25] 예를 들어, 실업 기간, 결혼 지속 기간, 기업의 생존 기간 등을 분석하는 데 사용될 수 있다. 신용 위험, 사법 오심에 따른 사형수의 오판율,^[26] 항공우주 산업에서 금속 부품의 리드 타임,^[27] 재범의 예측 변수,^[28] 무선 꼬리표 부착 동물의 생존 분포,^[29] 로마 황제의 폭력적인 죽음에 이르는 시간,^[30] 주식의 거래소 내 대기 시간^[31]등 다양한 분야에서 활용된다.

5. 4. 경제학 및 금융

생존분석은 신용 위험 평가, 기업 부도 예측, 보험 상품 개발 등에 활용된다.^[24]^[25]^[42]^[43] 예를 들어, 대출자의 상환 불이행 위험을 예측하거나, 보험 가입자의 사망 위험을 예측하는 데 사용될 수 있다. 전자 거래되는 주식의 거래소 내 대기 시간 분석에도 활용될 수 있다.^[31]

6. 한국에서의 생존분석

한국에서도 생존분석은 다양한 분야에서 활발하게 활용되고 있다. 특히, 한국의 높은 암 발병률과 고령화 사회 진입으로 인해 의학 및 보건학 분야에서의 활용이 두드러진다.

;한국의 암 생존율 분석

한국의 암 생존율은 지속적으로 향상되고 있지만, 여전히 암은 주요 사망 원인 중 하나이다. 생존분석은 암 환자의 생존율을 높이고, 암 치료 효과를 극대화하기 위한 연구에 필수적인 도구로 활용되고 있다.

;한국의 고령화 사회와 생존분석

한국은 세계적으로 고령화가 가장 빠르게 진행되는 국가 중 하나이다. 고령화 사회에서는 노인의 건강 관리 및 의료비 증가 문제가 중요한 사회적 과제로 대두되고 있으며, 생존분석은 이러한 문제를 해결하기 위한 정책 수립에 기여할 수 있다.

생존분석은 다양한 분야에서 활용되고 있는데, 그 예시는 다음과 같다.

신용 위험^[24]^[25]
사법 오심에 따른 사형수의 오판율^[26]
항공우주 산업에서 금속 부품의 리드 타임^[27]
재범의 예측 변수^[28]
동물 이동 추적에서 무선 꼬리표 부착 동물의 생존 분포^[29]
로마 황제의 폭력적인 죽음에 이르는 시간^[30]
전자 거래되는 주식의 거래소 내 대기 시간^[31]

6. 1. 한국의 암 생존율 분석

한국의 암 생존율은 지속적으로 향상되고 있지만, 여전히 암은 주요 사망 원인 중 하나이다. 생존분석은 암 환자의 생존율을 높이고, 암 치료 효과를 극대화하기 위한 연구에 필수적인 도구로 활용되고 있다.

6. 2. 한국의 고령화 사회와 생존분석

한국은 세계적으로 고령화가 가장 빠르게 진행되는 국가 중 하나이다. 고령화 사회에서는 노인의 건강 관리 및 의료비 증가 문제가 중요한 사회적 과제로 대두되고 있으며, 생존분석은 이러한 문제를 해결하기 위한 정책 수립에 기여할 수 있다.

생존분석은 다양한 분야에서 활용되고 있는데, 그 예시는 다음과 같다.

신용 위험^[24]^[25]
사법 오심에 따른 사형수의 오판율^[26]
항공우주 산업에서 금속 부품의 리드 타임^[27]
재범의 예측 변수^[28]
동물 이동 추적에서 무선 꼬리표 부착 동물의 생존 분포^[29]
로마 황제의 폭력적인 죽음에 이르는 시간^[30]
전자 거래되는 주식의 거래소 내 대기 시간^[31]

참조

_[1] 서적 Survival analysis John Wiley & Sons
_[2] 서적 Introductory Statistics with R Springer
_[3] 논문 Hypothesis testing for an extended cox model with time‐varying coefficients https://academic.oup[...] 2014-09
_[4] 논문 Regression Trees for Censored Data https://www.jstor.or[...] 1988
_[5] 논문 Survival Trees by Goodness of Split http://www.tandfonli[...] 1993
_[6] 논문 Mining event histories: a social science perspective http://www.inderscie[...] 2008
_[7] 논문 Random survival forests 2008-09-01
_[8] 웹사이트 rpart: Recursive Partitioning and Regression Trees https://CRAN.R-proje[...] 2021-11-12
_[9] 서적 An introduction to recursive partitioning using the RPART routines https://www.research[...] Mayo Foundation
_[10] 웹사이트 randomForestSRC: Fast Unified Random Forests for Survival, Regression, and Classification (RF-SRC) https://CRAN.R-proje[...] 2021-11-12
_[11] 논문 DeepSurv: personalized treatment recommender system using a Cox proportional hazards deep neural network
_[12] 논문 Deep survival machines: Fully parametric survival regression and representation learning for censored data with competing risks.
_[13] 논문 Deep Cox mixtures for survival regression.
_[14] 서적 International Encyclopedia of the Social Sciences Macmillan 2016-11-06
_[15] 논문 A handbook of parametric survival models for actuarial use
_[16] 논문 Survival analysis in clinical trials: Basics and must know areas
_[17] 문서 Suresh, K., Severn, C. & Ghosh, D. Survival prediction models: an introduction to discrete-time modeling. BMC Med Res Methodol 22, 207 (2022). https://doi.org/10.1186/s12874-022-01679-6 , https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/s12874-022-01679-6
_[18] 문서 Empirical Likelihood in Survival Analysis, Gang Li (U.S.A.), Runze Li (U.S.A.), and Mai Zhou (U.S.A.), Contemporary Multivariate Analysis and Design of Experiments. March 2005, 337-349, https://www.ms.uky.edu/~mai/research/llz.pdf
_[19] 문서 The Empirical Distribution Function with Arbitrarily Grouped, Censored and Truncated Data, Bruce W. Turnbull, Journal of the Royal Statistical Society. Series B (Methodological)\nVol. 38, No. 3 (1976), pp. 290-295 (6 pages), https://apps.dtic.mil/sti/tr/pdf/ADA030940.pdf
_[20] 문서 Proper Scoring Rules for Survival Analysis, Hiroki Yanagisawa, https://arxiv.org/abs/2305.00621v3
_[21] 서적 Survival analysis: A Self-learning text Springer
_[22] 서적 Event History Analysis with R Chapman & Hall/CRC
_[23] 서적 Survival Analysis Using S Chapman and Hall/CRC
_[24] 논문 Survival Analysis Methods for Personal Loan Data 2002-04-01
_[25] 논문 Measuring the Default Risk of Small Business Loans: A Survival Analysis Approach 2005
_[26] 논문 Rate of false conviction of criminal defendants who are sentenced to death 2014-05-20
_[27] 논문 Analysis of lead times of metallic components in the aerospace industry through a supported vector machine model 2010-10-01
_[28] 논문 Who Returns to Prison? A Survival Analysis of Recidivism among Adult Offenders Released in Oklahoma, 1985 – 2004 2006
_[29] 논문 Survival Analysis in Telemetry Studies: The Staggered Entry Design http://www.lib.ncsu.[...] 1989
_[30] 논문 Statistical reliability analysis for a most dangerous occupation: Roman emperor 2019-12-23
_[31] 논문 Censored expectation maximization algorithm for mixtures: Application to intertrade waiting times https://www.scienced[...] 2022
_[32] 서적 Survival analysis John Wiley & Sons
_[33] 서적 Introductory Statistics with R Springer
_[34] 웹사이트 An Introduction to Recursive Partitioning Using the RPART Routines https://www.mayo.edu[...] Mayo Foundation 2021-10-03
_[35] 서적 International Encyclopedia of the Social Sciences Macmillan 2016-11-06
_[36] 논문 A handbook of parametric survival models for actuarial use
_[37] 논문 Survival analysis in clinical trials: Basics and must know areas
_[38] 서적 Survival analysis: A Self-learning text Springer
_[39] 서적 エモリー大学クラインバウム教授の生存時間解析: 基礎から学べる教科書 https://www.worldcat[...] サイエンティスト社 2015-03
_[40] 서적 Event History Analysis with R Chapman & Hall/CRC
_[41] 서적 Survival Analysis Using S Chapman and Hall/CRC
_[42] 논문 Survival Analysis Methods for Personal Loan Data 2002-04-01
_[43] 논문 Measuring the Default Risk of Small Business Loans: A Survival Analysis Approach 2005
_[44] 논문 Rate of false conviction of criminal defendants who are sentenced to death 2014-05-20
_[45] 논문 Analysis of lead times of metallic components in the aerospace industry through a supported vector machine model 2010-10-01
_[46] 논문 Who Returns to Prison? A Survival Analysis of Recidivism among Adult Offenders Released in Oklahoma, 1985 – 2004 2006
_[47] 논문 Survival Analysis in Telemetry Studies: The Staggered Entry Design http://www.lib.ncsu.[...] 1989
_[48] 논문 Statistical reliability analysis for a most dangerous occupation: Roman emperor 2019-12-23

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com