선형 회귀

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 기본 모델
3. 선형 회귀에서의 가정
4. 선형 회귀의 해석
5. 손실 함수
- 5.1. 단순 선형 회귀의 손실 함수
- 5.2. 다변량 선형 회귀의 손실 함수
6. 선형 회귀 기법의 확장
7. 선형 회귀 모델 추정 기법
8. 선형 회귀의 응용
참조

1. 개요

선형 회귀는 종속 변수와 하나 이상의 독립 변수 간의 선형 관계를 모델링하는 통계적 방법이다. 주어진 데이터 집합에 대한 선형 함수를 모델링하며, 회귀 계수를 추정하여 변수 간의 관계를 정량화한다. 최소제곱법, 최대 가능도 추정, 릿지 회귀, 라쏘 회귀 등 다양한 추정 기법이 존재하며, 단순 선형 회귀, 다중 선형 회귀, 일반 선형 회귀 등으로 확장된다. 추세 분석, 역학 조사, 재무 관리, 경제학 등 다양한 분야에서 예측 및 변수 간의 관계 설명에 활용된다.

더 읽어볼만한 페이지

계량경제학 - 신경망
신경망은 생물학적 뉴런과 인공 뉴런을 아우르는 개념으로, 생물학적 신경망은 전기화학적 신호 전달을 통해 근육 운동을 제어하고, 인공 신경망은 예측 모델링과 인공 지능 문제 해결에 활용된다.
계량경제학 - 화폐유통속도
화폐유통속도는 경제 내 화폐가 재화와 서비스 구매에 사용되는 속도를 나타내는 지표로, 통화 수요를 이해하는 데 중요하며 거래 유통 속도와 소득 유통 속도로 나뉜다.
추정 이론 - 기댓값 최대화 알고리즘
추정 이론 - 델파이 기법
델파이 기법은 전문가들의 의견을 반복적인 피드백을 통해 수렴하여 문제를 해결하는 하향식 의견 도출 방법으로, 익명성, 정보 흐름의 구조화, 정기적인 피드백을 특징으로 하며 다양한 분야에서 활용된다.
회귀분석 - 회귀 분석
회귀 분석은 종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하고 분석하는 통계적 기법으로, 최소 제곱법 개발 이후 골턴의 연구로 '회귀' 용어가 도입되어 다양한 분야에서 예측 및 인과 관계 분석에 활용된다.
회귀분석 - 로지스틱 회귀
로지스틱 회귀는 범주형 종속 변수를 다루는 회귀 분석 기법으로, 특히 이항 종속 변수에 널리 사용되며, 오즈에 로짓 변환을 적용하여 결과값이 0과 1 사이의 값을 가지도록 하는 일반화 선형 모형의 특수한 경우이다.

선형 회귀
선형 회귀
유형	회귀 분석
모델	선형 모델
발명 연도	18세기
창시자	칼 프리드리히 가우스 아드리앵마리 르장드르
가정
선형성	독립 변수와 종속 변수 간의 선형 관계
독립성	오차항들의 독립성
등분산성	오차항들의 분산이 일정함
정규성	오차항들이 정규 분포를 따름
모수 추정
방법	최소자승법 최대우도법
관련 항목
관련 통계	결정 계수 분산 분석
일반화	일반화 선형 모형 비선형 회귀
관련 기법	로지스틱 회귀 다항 회귀

2. 기본 모델

선형 회귀는 ''n''개의 통계적 단위로 구성된 데이터 집합

\{y_i,\, x_{i1}, \ldots, x_{ip}\}_{i=1}^n

이 주어졌을 때, 종속 변수 ''y''와 설명 변수 '''x''' 벡터 사이의 관계를 선형 함수로 가정한다. 이러한 관계는 ''교란 항'' 또는 ''오차 변수'' ''ε''를 통해 모델링된다. ''ε''는 관측되지 않은 확률 변수로, 종속 변수와 회귀 변수 사이의 선형 관계에 "노이즈"를 추가한다.

선형 회귀 모델은 다음과 같은 형태를 취한다.

:

y_i = \beta_{0} + \beta_{1} x_{i1} + \cdots + \beta_{p} x_{ip} + \varepsilon_i= \mathbf{x}^\mathsf{T}_i\boldsymbol\beta + \varepsilon_i,\qquad i = 1, \ldots, n,

여기서 ^T는 전치 행렬을 나타내므로, '''x'''_''i''^T'''''β'''''는 좌표 벡터 '''x'''_''i''와 '''''β''''' 사이의 내적이다.

이러한 ''n''개의 방정식은 행렬 표기법으로 다음과 같이 표현된다.

:

\mathbf{y} = \mathbf{X} \boldsymbol\beta + \boldsymbol\varepsilon, \,

각 항은 다음과 같다.

:

\mathbf{y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}, \quad\mathbf{X} = \begin{bmatrix} \mathbf{x}^\mathsf{T}_1 \\ \mathbf{x}^\mathsf{T}_2 \\ \vdots \\ \mathbf{x}^\mathsf{T}_n \end{bmatrix}= \begin{bmatrix} 1 &  x_{11} & \cdots & x_{1p} \\1 & x_{21} & \cdots & x_{2p} \\\vdots & \vdots & \ddots & \vdots \\1 & x_{n1} & \cdots & x_{np}\end{bmatrix},

:

\boldsymbol\beta = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \\ \vdots \\ \beta_p \end{bmatrix}, \quad\boldsymbol\varepsilon = \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_n \end{bmatrix}.

선형 회귀는 설명 변수(또는 예측 변수)에 대한 목적 변수의 조건부 기대값이 아핀 사상으로 주어지는 관계를 모델링한다. 선형 회귀가 비선형 회귀에 비해 더 자주 사용되는 이유는, 미지의 파라미터에 선형적으로 의존하는 모델이 파라미터에 비선형적으로 의존하는 모델보다 피팅이 용이하고, 추정치의 통계적 성질을 결정하기 쉽기 때문이다.

선형 회귀 모델에서,

Y = \beta_0  + \beta_1 X_1 + \beta_2 X_2 +  \cdots +\beta_p X_p + \varepsilon\

이다.

여기서

\beta_0

는 절편,

\beta_i

는 각 설명 변수의 계수이며,

p

는 설명 변수의 개수이다. 교란항

\varepsilon

은 설명 변수

X

와 독립적이다.

벡터 공간·행렬 표기를 사용하면,

Y = X\beta + \varepsilon\

로 나타낼 수 있다.

2. 1. 선형 회귀 모델의 정의

선형 회귀는 주어진 데이터 집합

\{y_i,\, x_{i1}, \ldots, x_{ip}\}_{i=1}^n

에 대해, 종속 변수 ''y_i''와 p개의 설명 변수 ''x_i'' 사이의 선형 관계를 모델링한다. 모델은 다음과 같은 형태를 갖는다.

:

y_i = \beta_1 x_{i1} + \cdots + \beta_p x_{ip} + \varepsilon_i= \mathbf{x}^{\rm T}_i\boldsymbol\beta + \varepsilon_i,\qquad i = 1, \ldots, n,

주어진 식에서

\beta_i

는 각 독립변수의 계수이며,

p

는 선형 회귀로 추정되는 모수의 개수이다. ^T는 전치를 의미하고, '''''x'''_i''^T'''''β'''''는 '''''x'''_i''와 '''''β'''''의 내적을 의미한다.

\varepsilon_i

는 ''오차항'', ''오차 변수''로, 관찰되지 않은 확률 변수이며, 종속 변수와 독립 변수 사이에 오차를 의미한다.

이것이 선형 회귀라 불리는 것은, 종속변수가 독립변수에 대해 선형 함수(1차 함수)의 관계에 있을 것이라 가정하기 때문이다. 그러나

y_i = \mathbf{x}^{\rm T}_i\boldsymbol\beta + \varepsilon_i

의 그래프가 직선이고

y_i

가

x_i

의 선형 함수일 것이라고 생각하는 것은 잘못이다. 예를 들어

\mathbf{y} = \beta_1 + \beta_2 x + \beta_3 x^2 + \varepsilon

는

x

와

x^2

에 관해 선형이기 때문에, x축과 y축을 가진 그래프가 직선상에 있지 않더라도 선형회귀라고 할 수 있다.

이 식은 벡터 형식으로 표현하면 다음과 같이 표현할 수 있다.

:

\mathbf{y} = \mathbf{X}\boldsymbol\beta + \boldsymbol\varepsilon, \,

이 식에서 각 항의 의미는 다음과 같다.

:

\mathbf{y} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}, \quad\mathbf{X} = \begin{pmatrix} \mathbf{x}^{\rm T}_1 \\ \mathbf{x}^{\rm T}_2 \\ \vdots \\ \mathbf{x}^{\rm T}_n \end{pmatrix}= \begin{pmatrix} x_{11} & \cdots & x_{1p} \\x_{21} & \cdots & x_{2p} \\\vdots & \ddots & \vdots \\x_{n1} & \cdots & x_{np}\end{pmatrix}, \quad\boldsymbol\beta = \begin{pmatrix} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_p \end{pmatrix}, \quad\boldsymbol\varepsilon = \begin{pmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_n \end{pmatrix}.

몇 가지 중요한 용어를 확인하고 넘어가자.

$y_i\,$ 는 ''응답 변수'', ''종속 변수''라 불린다 (독립 변수와 종속 변수 참조.)
$x_{i1},\, x_{i2},\, \ldots,\, x_{ip}\,$ 는 ''입력 변수'', ''예측 변수'', ''독립 변수''라 불린다 (독립 변수와 종속 변수 참조. 독립 변수는 독립 확률 변수와는 다른 것이다.) 행렬 $\mathbf{X}$ 는 설계 행렬이라 불리기도 한다.
일반적으로 입력 변수에 상수가 포함된다. 예를 들어, ''x''_''i''1를 상수로 택한다 ( = 1 ''i'' = 1, ..., ''n'') ''x''_''i''1 앞에 붙는 상수 '''''β'''''를 절편이라 부른다.
때로 독립 변수는 다른 독립 변수 또는 데이터에 대해 비선형 함수이기도 하다. 이러한 경우에도 이 독립 변수가 파라미터 벡터 '''''β'''''에 대해서만 선형이기만 하면 여전히 선형 모델이라 부른다.
독립 변수 ''x''_''ij''는 확률 변수로 생각할 수도 있고, 또는 고정된 값으로 생각할 수도 있다.
$\boldsymbol\beta\,$ 는 ''p''차원 ''파라미터 벡터''이다. 이것의 각 원소는 ''회귀 계수''라고 불리기도 한다.
$\varepsilon_i$ 는 ''오차항'', ''노이즈''이다. 이 변수는 종속 변수 ''y''_''i''에 대한 모든 오차 요인을 포함한다.

'''예제'''. 작은 공을 던져 올리고, 그것의 높이 ''h_i''를 시간 ''t_i''에서 측정한다고 하자. 이를 수식으로 표현하면 다음과 같다.

:

h_i = \beta_1 t_i + \beta_2 t_i^2 + \varepsilon_i,

이 식에서 ''β''₁는 공의 초기 속도이며, ''β''₂는 중력에 비례하는 계수이다. ''ε''_''i''는 측정 오차를 의미한다. 선형 회귀는 측정한 데이터를 사용해 ''β''₁과 ''β''₂를 추정할 때 사용할 수 있다. 이렇게 세워진 모델은 시간 변수에 대해서는 비선형이지만, 파라미터 ''β''₁와 ''β''₂에 대해서는 선형이다. 만약 독립 변수를 다음과 같이 표현하면, '''''x'''''_''i'' = (''x''_''i''1, ''x''_''i''2) = (''t''_''i'', ''t''_''i''²), 식을 다음과 같이 쓸 수 있다.

:

h_i = \mathbf{x}^{\rm T}_i\boldsymbol\beta + \varepsilon_i.

''n''개의 통계적 단위로 구성된 데이터 집합

\{y_i,\, x_{i1}, \ldots, x_{ip}\}_{i=1}^n

이 주어지면, 선형 회귀 모델은 종속 변수 ''y''와 회귀 변수 '''x'''의 벡터 사이의 관계가 선형 함수라고 가정한다.

단순 선형 회귀(simple linear regression) 또는 단변량 선형 회귀의 경우, 설명 변수는 하나뿐이며 회귀 매개변수는 두 개이다.

최소제곱법을 사용한 경우,

\bar{x}

와

\bar{y}

를

x_i

와

y_i

의 평균이라고 할 때, 매개변수

a

와

b

의 추정량인

\hat{a}

와

\hat{b}

는 다음과 같이 구할 수 있다.

\begin{align}\hat{a} &= \bar{y} - \hat{b}\,\bar{x} \\\hat{b} &= \frac{ \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) }{ \sum_{i=1}^n (x_i - \bar{x})^2 }\end{align}

2. 2. 용어

$\mathbf{y}$ 는 $y_i\ (i=1,\ldots,n)$ 값들의 벡터이며, 종속 변수, 내생 변수, 반응 변수, 목표 변수, 측정 변수, 기준 변수 등으로 불린다. "예측 변수"라고도 불리지만, $\hat{y}$ 로 표시되는 "예측 값"과는 혼동하지 않아야 한다. 어떤 변수를 종속 변수로, 어떤 변수를 독립 변수로 모델링할지는 한 변수의 값이 다른 변수에 의해 발생하거나 직접 영향을 받는다는 추정에 기반할 수 있다. 또는 다른 변수로 한 변수를 모델링해야 할 작동상의 이유가 있을 수도 있으며, 이 경우 인과 관계 추정은 필요하지 않다.
$\mathbf{X}$ 는 행 벡터 $\mathbf{x}_{i\cdot}$ 또는 'n'차원 열 벡터 $\mathbf{x}_{\cdot j}$ 의 행렬로, 회귀 변수, 외생 변수, 설명 변수, 공변량, 입력 변수, 예측 변수, 독립 변수 등으로 불린다. (독립 확률 변수와 혼동 주의) $\mathbf{X}$ 는 "설계 행렬"이라고도 불린다.
* 일반적으로 상수는 회귀 변수에 포함된다. 특히 $i=1,\ldots,n$ 에 대해 $x_{i0}=1$ 이다. '''''β'''''의 해당 요소는 "절편"이다. 많은 선형 모델 통계적 추론 절차는 절편을 필요로 하므로, 이론적으로 0이어야 해도 포함되는 경우가 많다.
* 다항 회귀, 분할 회귀처럼 회귀 변수가 다른 변수나 데이터 값의 비선형 함수일 수 있다. 모델은 매개변수 벡터 '''''β'''''에 대해 선형이면 선형으로 유지된다.
* ''x''_''ij'' 값은 확률 변수 ''X''_''j''의 관측 값 또는 종속 변수 관찰 전 선택된 고정 값으로 볼 수 있다. 두 해석 모두 다른 경우에 적절하며, 보통 같은 추정 절차로 이어진다. 그러나 두 상황에서 다른 점근적 분석 방식이 사용된다.
$\boldsymbol\beta$ 는 $(p+1)$ 차원 "매개변수 벡터"이며, $\beta_0$ 는 절편 항이다(모델에 포함된 경우. 아니면 $\boldsymbol\beta$ 는 ''p''차원). 그 요소는 "효과" 또는 "회귀 계수"이다(후자는 "추정된" 효과에만 사용). 단순 선형 회귀에서 ''p''=1이고, 계수는 "회귀 기울기"이다. 선형 회귀의 통계적 추정 및 추론은 '''''β'''''에 초점을 맞춘다. 매개변수 벡터 요소는 독립 변수에 대한 종속 변수의 편미분으로 해석된다.
$\boldsymbol\varepsilon$ 는 $\varepsilon_i$ 값들의 벡터이다. "오차 항", "교란 항", 또는 "노이즈"(모델의 나머지 부분에서 제공하는 "신호"와 대조)라고 불린다. 이 변수는 회귀 변수 '''x''' 외에 종속 변수 ''y''에 영향을 주는 다른 모든 요소를 포함한다. 오차 항과 회귀 변수의 관계(예: 상관 관계)는 선형 회귀 모델 공식화의 중요한 고려 사항이며, 적절한 추정 방법을 결정한다.

2. 3. 선형성의 의미

선형 회귀에서 "선형성"은 종속 변수 ''Y''가 설명 변수 ''X''의 계수 '''β'''에 대해 선형이라는 것을 의미한다. 즉, 모델의 수식이 계수들에 대한 선형 결합으로 표현된다는 것이다.

예를 들어,

:

Y = \beta_0 + \beta_1 x + \beta_2 x^2 + \varepsilon

와 같은 회귀 모델은 변수 ''x'' 자체에 대해서는 비선형(2차 함수) 관계를 갖지만, 계수 ''β''₀, ''β''₁, ''β''₂에 대해서는 선형이다. 따라서 이 모델은 여전히 선형 회귀 모델로 간주된다.

이는 선형 회귀 모델이 반드시 직선 형태의 관계만을 나타내는 것이 아님을 의미한다. 설명 변수와 종속 변수 간의 관계가 곡선 형태를 띠더라도, 계수들에 대한 선형 결합으로 표현될 수 있다면 선형 회귀 모델을 적용할 수 있다.

단순 선형 회귀(simple linear regression) 또는 단변량 선형 회귀의 경우, 설명 변수는 하나뿐이며 회귀 매개변수는 두 개이다. 이때 식은 다음과 같다.

:

y = a+bx+\varepsilon

최소제곱법을 사용한 경우,

\bar{x}

와

\bar{y}

를

x_i

와

y_i

의 평균이라고 할 때, 매개변수

a

와

b

의 추정량인

\hat{a}

와

\hat{b}

는 다음과 같이 구할 수 있다.

\begin{align}\hat{a} &= \bar{y} - \hat{b}\,\bar{x} \\\hat{b} &= \frac{ \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) }{ \sum_{i=1}^n (x_i - \bar{x})^2 }\end{align}

동등한 공식화로, 선형 단일 회귀를 조건부 기대값 모델로 명시적으로 표현할 수 있다.

:

\mbox{E}(y | x) = \alpha + \beta x

여기서 주어진

x

에 대한

y

의 조건부 확률 분포는 교란항의 확률 분포와 일치한다.

3. 선형 회귀에서의 가정

표준 선형 회귀 모델은 예측 변수, 응답 변수, 그리고 그 사이의 관계에 대해 다양한 가정을 한다. 이러한 가정을 완화하거나 제거하는 확장된 선형 회귀 분석도 존재하지만, 이는 추정 과정을 더 복잡하게 만들거나 더 많은 데이터를 필요로 할 수 있다.

표준 선형 회귀의 주요 가정은 다음과 같다:

약한 외생성: 설명 변수 ''x''는 확률 변수가 아닌 고정된 값으로 취급되며, 측정 오차가 없다고 가정한다. 이는 현실적이지 않을 수 있으며, 이 가정을 제외하면 설명 변수에 오차를 포함하는 모델을 고려해야 한다.
선형성: 응답 변수가 예측 변수와 선형 회귀 계수의 선형 조합으로 표현될 수 있음을 의미한다. 예측 변수는 자유롭게 변형될 수 있으므로, 이는 파라미터에 대한 선형성만을 의미한다. 다항 회귀는 이러한 기법을 활용하는 예시이며, 응답 변수를 예측 변수에 대한 다항 함수로 모델링한다.
상수 분산 (등분산성): 서로 다른 응답 변수들의 오차가 설명 변수와 관계없이 항상 같은 분산을 가진다는 가정이다. 실제로는 응답 변수들의 오차 분산이 설명 변수에 영향을 받을 수 있다. 이분산성은 등분산성이 없는 것을 의미한다.

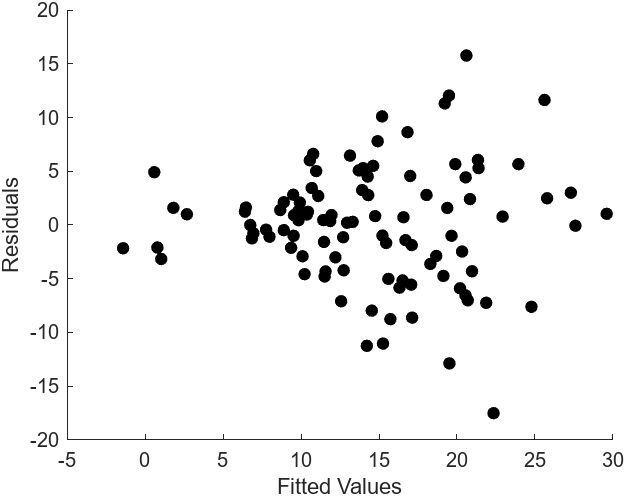
오차의 독립성: 독립 변수의 오차가 서로 상관 관계가 없음을 가정한다. 일반화된 최소제곱법과 같은 일부 선형 회귀 기법은 상관된 오차를 다룰 수 있지만, 더 많은 데이터를 필요로 하는 경우가 많다.

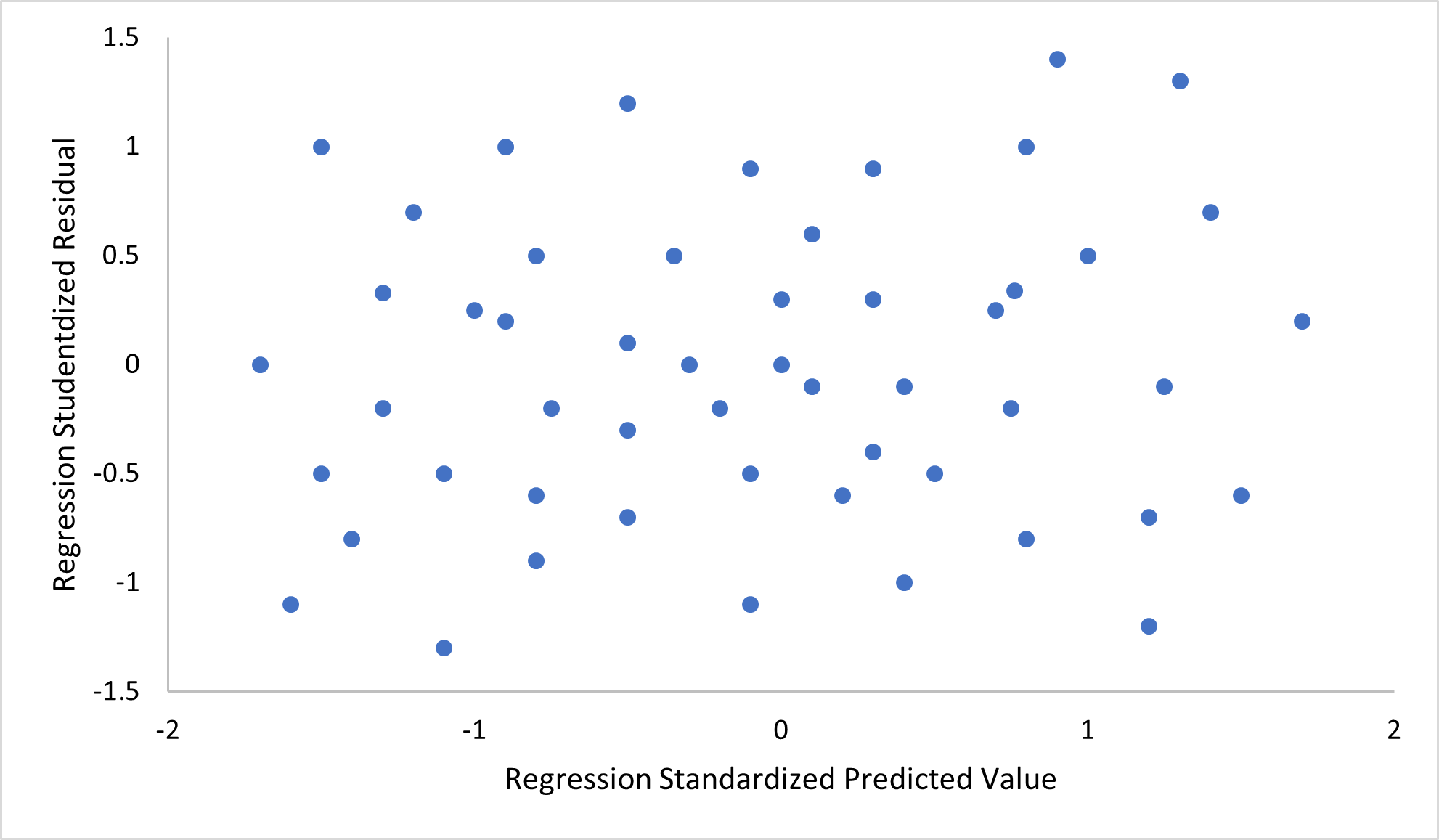
잔차를 예측 값에 대해 플롯하여 선형성, 등분산성 및 오차 독립성 가정을 확인

예측 변수에서의 다중공선성의 부재: 표준 최소제곱법 추정에서 설계 행렬 X는 전열계수 p를 가져야 한다. 그렇지 않으면 예측 변수 간에 다중공선성이 발생하여 파라미터 벡터 ''β''가 유일한 해를 갖지 않게 된다.

이러한 가정들이 위반되면, '''''β'''''의 편향된 추정, 신뢰 구간 및 유의성 검정 결과가 발생할 수 있다.

4. 선형 회귀의 해석

앤스컴의 4중주의 데이터 집합은 대략 동일한 선형 회귀선(거의 동일한 평균, 표준 편차 및 상관 관계 포함)을 갖도록 설계되었지만 그래프로 보면 매우 다르다. 이는 변수 간의 관계를 이해하기 위해 적합된 모델에만 의존하는 것의 위험성을 보여준다.

수립한 선형 회귀 모델을 사용해 예측 변수 ''x''_''j''가 응답 변수 ''y''에 미치는 영향을 확인할 수 있다. ''β''_''j''는 ''x''_''j''가 한 단위 변했을 때, ''y''의 기대 변화량을 의미한다. 이는 때로 ''y''에 대한 ''x''_''j''의 ''고유 영향''이라 불리기도 한다. 반면에, ''y''에 대한 ''x''_''j''의 한계 효과는 ''x''_''j''와 ''y'' 사이의 피어슨 상관 계수 또는 단순 선형 회귀 모델을 사용하여 평가할 수 있다.^[5]

회귀 결과를 해석할 때는 주의해야 한다. 일부 독립 변수가 응답 변수의 변화에 영향을 주지 않을 수 있기 때문이다 (무의미한 독립 변수일 수도 있고, Y절편에 해당할 수도 있기 때문이다). 한계 효과가 큰 상황에서도 고유 영향은 적을 수 있으며, 반대로 한계 효과는 적은데 고유 영향이 큰 상황이 있을 수도 있다.^[5]

"고정된 상태"라는 표현은 예측 변수의 값이 어떻게 발생하는지에 따라 의미가 달라진다. 실험자가 연구 설계에 따라 예측 변수의 값을 직접 설정하는 경우, 관심 있는 비교는 실험자가 예측 변수를 "고정"한 단위 간의 비교에 해당한다. 또는 데이터 분석의 맥락에서 "고정된 상태"는 주어진 예측 변수에 대해 공통 값을 갖는 데이터의 하위 집합에 주의를 집중하는 것을 의미한다. 이것은 관찰 연구에서 사용할 수 있는 유일한 해석이다.^[5]

"고유 효과"라는 개념은 여러 상호 관련된 구성 요소가 응답 변수에 영향을 미치는 복잡한 시스템을 연구할 때 매력적이다. 경우에 따라 예측 변수의 값과 관련된 개입의 인과적 효과로 해석될 수 있다. 그러나 많은 경우에 예측 변수가 서로 상관되어 있고 연구 설계를 따르지 않는 경우 다중 회귀 분석이 예측 변수와 응답 변수 간의 관계를 명확하게 하지 못한다는 주장이 제기되었다.^[5]

5. 손실 함수

선형 회귀에서 모델의 예측값과 실제값의 차이를 나타내는 손실 함수는 모델의 성능을 평가하는 중요한 지표이다. 손실 함수는 모델의 예측값과 실제값의 차이를 수치화하며, 이 값을 최소화하는 방향으로 모델을 학습시킨다.

손실 함수는 주어진 독립변수의 개수에 따라 다음과 같이 정의할 수 있다.

단순 선형 회귀의 손실 함수
다변량 선형 회귀의 손실 함수

5. 1. 단순 선형 회귀의 손실 함수

관측된 ''m''개의 데이터

(x, y)

에 대하여 단순 선형 회귀 모델을 다음과 같이 정의한다.

:

h_\beta=\beta_0+\beta_1x

손실 함수

J(\beta_0, \beta_1)

는 아래와 같이 정의할 수 있다.

:

J(\beta_0, \beta_1) = \frac{1}{2m}\sum_{i = 1}^{m}  (h_\beta(x^{i}) -y^{i})^{2}

단순 선형 회귀 또는 단변량 선형 회귀의 경우, 설명 변수는 하나뿐이며 회귀 매개변수는 두 개이다. 위의 식은 다음과 같다.

:

y = a+bx+\varepsilon\

최소제곱법을 사용한 경우,

\bar{x}

와

\bar{y}

를

x_i

와

y_i

의 평균이라고 할 때, 매개변수

a

와

b

의 추정량인

\hat{a}

와

\hat{b}

는 다음과 같이 구할 수 있다.

\begin{align}\hat{a} &= \bar{y} - \hat{b}\,\bar{x} \\\hat{b} &= \frac{ \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) }{ \sum_{i=1}^n (x_i - \bar{x})^2 }\end{align}

동등한 공식화로, 선형 단일 회귀를 조건부 기대값 모델로 명시적으로 표현할 수 있다.

:

\mbox{E}(y | x) = \alpha + \beta x \

여기서 주어진

x

에 대한

y

의 조건부 확률 분포는 교란항의 확률 분포와 일치한다.

5. 2. 다변량 선형 회귀의 손실 함수

n개의 독립 변수 ''X''와 관측된 ''m''개의 데이터

(x, y)

에 대하여 다변량 선형 회귀 모델을 다음과 같이 정의할 수 있다.

:

h_\beta=\beta_0+\beta_1x_1+...+\beta_n x_n

:이때 손실 함수

J(\mathbf{\beta})

는 아래와 같이 정의된다.

:

J(\mathbf{\beta}) = \frac{1}{2m}\sum_{i = 1}^{m}  (h_\beta(x_1^{i}, x_2^{i}, ..., x_n^{i}) -y^{i})^{2}

이후 교란항 가 서로 독립이며 평균

0

, 분산

\sigma^2

인 정규 분포를 따른다고 가정한다.

잔차는 관측값과 모델 예측값의 차이를 나타내며, 다음과 같이 결정된다.

:

\hat\vec\varepsilon = \vec{y} - \mathbf{X} \hat\beta\

이때, 통계량

S^2=\frac {\;}^\top \hat{\vec\varepsilon}} {n-p-1}

는 분산

\sigma^2

의 불편 추정량(

E[S^2]=\sigma^2

)이 된다^[38]。

6. 선형 회귀 기법의 확장

선형 회귀는 기본적인 가정들을 완화하거나 다른 가정을 추가하여 다양한 방식으로 확장될 수 있다. 이러한 확장된 기법들은 기본적인 선형 회귀 모델의 한계를 극복하고 더 넓은 범위의 데이터에 적용할 수 있도록 해준다.

교란항 $\varepsilon_i$ 가 서로 독립이며 평균 $0$ , 분산 $\sigma^2$ 인 정규 분포를 따른다고 가정하면, 잔차는 관측값과 모델 예측값의 차이로 다음과 같이 나타낼 수 있다.

: $\hat\vec\varepsilon = \vec{y} - \mathbf{X} \hat\beta$

여기서 $S^2=\frac {\;}^\top \hat{\vec\varepsilon}} {n-p-1}$ 는 분산 $\sigma^2$ 의 불편 추정량( $E[S^2]=\sigma^2$ )이 된다.^[38] 최소 제곱 추정량 $\widehat{\beta}$ 와 통계량 $S^2$ 에 대해 다음이 성립한다.^[39]^[40]

# $\widehat{\beta}$ 는 다차원 정규 분포 $\mathcal{N}\left(\beta, \sigma^2(\boldsymbol{X}^\top\boldsymbol{X})^{-1}\right)$ 를 따른다.

# $\frac{(N-P-1)S^2}{\sigma^2}$ 는 자유도 $n-p-1$ 의 $\chi^2_{n-p-1}$ 분포를 따른다.

# $\widehat{\beta}$ 와 $S^2$ 는 독립이다.

이러한 사실들을 바탕으로 회귀 계수의 유의성 검정, 신뢰 구간, 예측 구간 등을 구성할 수 있다.

6. 1. 단순 선형 회귀와 다중 선형 회귀

선형 회귀는 주어진 데이터 집합에 대해, 종속 변수와 하나 이상의 독립 변수 사이의 선형 관계를 모델링한다. 모델은 다음과 같은 형태를 갖는다.

:

y_i = \beta_1 x_{i1} + \cdots + \beta_p x_{ip} + \varepsilon_i = \mathbf{x}^{\rm T}_i\boldsymbol\beta + \varepsilon_i, \qquad i = 1, \ldots, n,

여기서

\beta_i

는 각 독립변수의 계수,

p

는 추정되는 모수의 개수,

\varepsilon_i

는 오차항이다.

이 식은 벡터 형식으로 다음과 같이 표현할 수 있다.

:

\mathbf{y} = \mathbf{X}\boldsymbol\beta + \boldsymbol\varepsilon, \,

여기서 각 항은 다음과 같다.

:

\mathbf{y} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}, \quad\mathbf{X} = \begin{pmatrix} \mathbf{x}^{\rm T}_1 \\ \mathbf{x}^{\rm T}_2 \\ \vdots \\ \mathbf{x}^{\rm T}_n \end{pmatrix}= \begin{pmatrix} x_{11} & \cdots & x_{1p} \\x_{21} & \cdots & x_{2p} \\\vdots & \ddots & \vdots \\x_{n1} & \cdots & x_{np}\end{pmatrix}, \quad\boldsymbol\beta = \begin{pmatrix} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_p \end{pmatrix}, \quad\boldsymbol\varepsilon = \begin{pmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_n \end{pmatrix}.

$y_i\,$ 는 ''응답 변수'', ''종속 변수''라고 불린다.
$x_{i1},\, x_{i2},\, \ldots,\, x_{ip}\,$ 는 ''입력 변수'', ''예측 변수'', ''독립 변수''라고 불린다.
$\boldsymbol\beta\,$ 는 ''파라미터 벡터''이며, 각 원소는 ''회귀 계수''라고 불린다.
$\varepsilon_i$ 는 ''오차항'', ''노이즈''이다.

'''예제'''. 작은 공을 던져 올리고, 그것의 높이 ''h_i''를 시간 ''t_i''에서 측정한다고 하면,

:

h_i = \beta_1 t_i + \beta_2 t_i^2 + \varepsilon_i,

이 식에서 ''β''₁는 공의 초기 속도, ''β''₂는 중력에 비례하는 계수, ''ε''_''i''는 측정 오차이다. '''''x'''''_''i'' = (''x''_''i''1, ''x''_''i''2) = (''t''_''i'', ''t''_''i''²)로 표현하면,

:

h_i = \mathbf{x}^{\rm T}_i\boldsymbol\beta + \varepsilon_i.

와 같다.

독립 변수가 하나인 경우를 '''단순 선형 회귀'''라고 한다.

:

y = a+bx+\varepsilon\

최소제곱법을 사용하면,

\bar{x}

와

\bar{y}

를

x_i

와

y_i

의 평균이라고 할 때, 매개변수

a

와

b

의 추정량인

\hat{a}

와

\hat{b}

는 다음과 같이 구할 수 있다.

:

\begin{align}\hat{a} &= \bar{y} - \hat{b}\,\bar{x} \\\hat{b} &= \frac{ \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) }{ \sum_{i=1}^n (x_i - \bar{x})^2 }\end{align}

독립 변수가 여러 개인 경우를 '''다중 선형 회귀'''라고 한다.

:

Y_i = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \ldots + \beta_p X_{ip} + \epsilon_i

응답 변수 ''y''가 벡터인 경우는 '''다변량 선형 회귀'''라고 하며, '''일반 선형 회귀'''라고도 한다.

6. 2. 일반 회귀 모델

선형 회귀는 주어진 데이터 집합

\{y_i,\, x_{i1}, \ldots, x_{ip}\}_{i=1}^n

에 대해, 종속 변수 ''y_i''와 p개의 설명 변수 ''x_i'' 사이의 선형 관계를 모델링한다. 모델은 다음과 같은 형태를 갖는다.

:

y_i = \beta_1 x_{i1} + \cdots + \beta_p x_{ip} + \varepsilon_i = \mathbf{x}^{\rm T}_i\boldsymbol\beta + \varepsilon_i, \qquad i = 1, \ldots, n,

주어진 식에서

\beta_i

는 각 독립변수의 계수이며,

p

는 선형 회귀로 추정되는 모수의 개수이다. ^T는 전치를 의미하고, '''''x'''_i''^T'''''β'''''는 '''''x'''_i''와 '''''β'''''의 내적을 의미한다.

\varepsilon_i

는 ''오차항'', ''오차 변수''로, 관찰되지 않은 확률 변수이며, 종속 변수와 독립 변수 사이에 오차를 의미한다.

이것이 선형 회귀라 불리는 것은, 종속변수가 독립변수에 대해 선형 함수(1차 함수)의 관계에 있을 것이라 가정하기 때문이다. 그러나

y_i = \mathbf{x}^{\rm T}_i\boldsymbol\beta + \varepsilon_i

의 그래프가 직선이고

y_i

가

x_i

의 선형 함수일 것이라고 생각하는 것은 잘못이다. 예를 들어

\mathbf{y} = \beta_1 + \beta_2 x + \beta_3 x^2 + \varepsilon

는

x

와

x^2

에 관해 선형이기 때문에, x축과 y축을 가진 그래프가 직선상에 있지 않더라도 선형회귀라고 할 수 있다.

이 식은 벡터 형식으로 표현하면 다음과 같이 표현할 수 있다.

:

\mathbf{y} = \mathbf{X}\boldsymbol\beta + \boldsymbol\varepsilon, \,

이 식에서 각 항의 의미는 다음과 같다.

:

\mathbf{y} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}, \quad\mathbf{X} = \begin{pmatrix} \mathbf{x}^{\rm T}_1 \\ \mathbf{x}^{\rm T}_2 \\ \vdots \\ \mathbf{x}^{\rm T}_n \end{pmatrix}= \begin{pmatrix} x_{11} & \cdots & x_{1p} \\x_{21} & \cdots & x_{2p} \\\vdots & \ddots & \vdots \\x_{n1} & \cdots & x_{np}\end{pmatrix}, \quad\boldsymbol\beta = \begin{pmatrix} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_p \end{pmatrix}, \quad\boldsymbol\varepsilon = \begin{pmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_n \end{pmatrix}.

몇 가지 중요한 용어를 확인하고 넘어가자.

$y_i\,$ 는 ''응답 변수'', ''종속 변수''라 불린다 (독립 변수와 종속 변수 참고.)
$x_{i1},\, x_{i2},\, \ldots,\, x_{ip}\,$ 는 ''입력 변수'', ''예측 변수'', ''독립 변수''라 불린다 (독립 변수와 종속 변수 참고. 독립 변수는 독립 확률 변수와는 다른 것이다.)
$\boldsymbol\beta\,$ 는 ''p''차원 ''파라미터 벡터''이다. 이것의 각 원소는 ''회귀 계수''라고 불리기도 한다.
$\varepsilon_i$ 는 ''오차항'', ''노이즈''이다.

일반 선형 모형은 반응 변수가 (각 관측치에 대해) 스칼라가 아닌 벡터 '''y'''_''i''인 상황을 고려한다. 고전적 선형 회귀 모형의 벡터 '''''β'''''를 대체하는 행렬 ''B''를 사용하여,

E(\mathbf{y}\mid\mathbf{x}_i)=\mathbf{x}_i^\mathsf{T}B

의 조건부 선형성은 여전히 가정한다. 최소제곱법 (OLS) 및 일반화된 최소제곱법 (GLS)의 다변량 유사체가 개발되었다. "일반 선형 모형"은 "다변량 선형 모형"이라고도 한다. 이것들은 다변수 선형 모형 (또는 "다중 선형 모형"이라고도 함)과는 다르다.

6. 3. 이분산 회귀 모델

다양한 모델들이 이분산성을 허용하기 위해 개발되었다. 즉, 서로 다른 반응 변수에 대한 오차는 서로 다른 분산을 가질 수 있다. 예를 들어, 가중 최소 제곱은 반응 변수가 서로 다른 오차 분산을 가질 수 있고, 잠재적으로 상관된 오차를 가질 수 있는 경우 선형 회귀 모델을 추정하는 방법이다. (가중 선형 최소 제곱 및 일반화 최소 제곱 참조). 이분산성 일치 표준 오차는 상관관계가 없지만 잠재적으로 이분산성을 갖는 오차에 사용할 수 있는 개선된 방법이다.

6. 4. 계층적 선형 모델

계층적 선형 모델은 데이터가 여러 겹으로 회귀되는 경우에 이용할 수 있다. 다시 말해 A가 B로 회귀되고, B가 C로 회귀되는 구조이다. 이러한 구조는 일상 생활에서 흔히 볼 수 있는데, 가령 학생은 학급에 속하고, 학급은 학년에 속하며 학년은 학교에 속하는 경우를 들 수 있다. 이런 경우 학생의 응답 변수로 시험 성적을 이용 한다면 학급, 학년, 학교에 대해 각각 다른 공변량을 얻을 수 있다.^[1]

계층 선형 모형(다층 회귀)은 데이터를 회귀의 계층 구조로 구성한다. 예를 들어, A가 B에 대해 회귀되고, B는 C에 대해 회귀되는 형태이다. 이는 변수들이 자연스러운 계층 구조를 가질 때 자주 사용된다. 예를 들어, 학생이 교실에 속하고, 교실이 학교에 속하며, 학교가 학교 구역과 같은 행정 구역에 속하는 교육 통계에서 사용될 수 있다. 반응 변수는 시험 점수와 같은 학생의 성취도 척도일 수 있으며, 교실, 학교 및 학교 구역 수준에서 다양한 공변량을 수집할 수 있다.^[1]

6. 5. 오차 변수 모델

오차 변수 모델(errors-in-variables) (또는 "오차 측정 모델")은 기존의 선형 회귀 모델에서 독립 변수 ''X''가 오차와 함께 관측될 수 있도록 확장한 것이다. 이 오차는 ''β''의 표준 추정량이 편향되는데 원인이 된다. 일반적으로 이 영향은 0에 가깝게 편향된다.

변수 오류 모형 (또는 "측정 오류 모형")은 전통적인 선형 회귀 모형을 확장하여 예측 변수 ''X''가 오류와 함께 관찰될 수 있도록 한다. 이러한 오류는 ''β''의 표준 추정량이 편향되도록 한다. 일반적으로 편향의 형태는 감쇠이며, 이는 효과가 0으로 편향된다는 것을 의미한다.

7. 선형 회귀 모델 추정 기법

선형 회귀에서는 파라미터를 추정하기 위해 다양한 기법들이 개발되었다. 각 기법은 알고리즘의 연산 복잡도, 닫힌 형태 해법의 존재 여부, 데이터 분포 및 변수의 관계에 대한 이론적 가정 등에서 차이를 보인다.

이상치를 포함한 데이터를 기반으로 한 테일 센 추정기(검은색)과 단순 선형 회귀 분석(파란색)의 비교

최소제곱법 (Least Squares Method): 가장 일반적인 방법으로, 오차의 제곱합을 최소화하는 파라미터를 찾는다. 카를 프리드리히 가우스가 1820년대에 발전시켰다.
최소제곱법(OLS)
일반화 최소제곱법(GLS)
가중 최소제곱법(Weighted least squares)
Percentage least squares
반복 재가중 최소제곱법(IRLS)
도구 변수(IV)
총 최소제곱(TLS)
최대가능도방법 (Maximum Likelihood Method): 주어진 데이터에서 모델의 가능도를 최대화하는 파라미터를 찾는다. 오차가 정규분포를 따른다고 가정하면 최소제곱법과 동일한 결과를 얻는다.
최대 가능도 추정(MLE)
잔차제곱합(RSS : Residual Sum of Squares)
능형 회귀 분석(Ridge regression)
기타 방법:
최소 절대 편차 (Least Absolute Deviations): 오차의 절대값 합을 최소화하는 방법으로, 이상치에 덜 민감하다.^[17]
적응 추정 (Adaptive estimation): 오차항의 분포를 비모수적으로 추정하여 최적의 추정량을 구한다.^[18]
베이시안 선형 회귀: 베이시안 통계의 틀을 선형 회귀에 적용한다.
분위수 회귀: ''X''가 주어졌을 때 ''y''의 조건부 평균이 아닌 조건부 분위수에 초점을 맞춘다.
혼합 모형: 종속 데이터가 포함된 선형 회귀 관계를 분석하는 데 널리 사용된다.
주성분 회귀(PCR):^[20]^[21] 예측 변수의 수가 많거나 예측 변수 간에 강한 상관 관계가 존재할 때 사용된다.
최소 각도 회귀:^[22] 관측치보다 더 많은 공변량을 가질 수 있는 고차원 공변량 벡터를 처리하기 위해 개발된 선형 회귀 모형에 대한 추정 절차이다.
바일-센 추정량: 적합선의 기울기를 표본 점 쌍을 통과하는 선의 기울기의 중앙값으로 선택하는 간단한 강건 추정 기술이다.^[23]

"최소제곱법"과 "선형 모델"은 밀접하게 관련되어 있지만, 동의어는 아니다. 최소제곱법은 선형 모델뿐만 아니라 비선형 모델에도 사용될 수 있다.

7. 1. 최소제곱법

선형 회귀 모델은 종종 최소제곱법을 사용하여 적합된다. 최소제곱법은 카를 프리드리히 가우스가 1820년대에 발전시킨 방법으로, 오차 항의 거동에 대해 다음과 같은 가정을 한다(가우스-마르코프 가정).

교란 $\varepsilon_i$의 기대값은 0이다.
:$E[\varepsilon] = 0 $
교란 $\varepsilon_i$는 서로 상관관계가 없다 (통계적 독립의 가정보다 약함).
:$\operatorname{cov}(\varepsilon_i, \varepsilon_j) = 0, \qquad i \ne j.$
교란 $\varepsilon_i$는 등분산이며, 모두 같은 분산을 갖는다 (가우스-마르코프 정리 참조).
:$V[\varepsilon_i] = \sigma^2, \qquad \forall i \isin [n].$

이러한 가정들은 최소제곱법이 최적의 파라미터 추정량을 제공함을 보장한다.

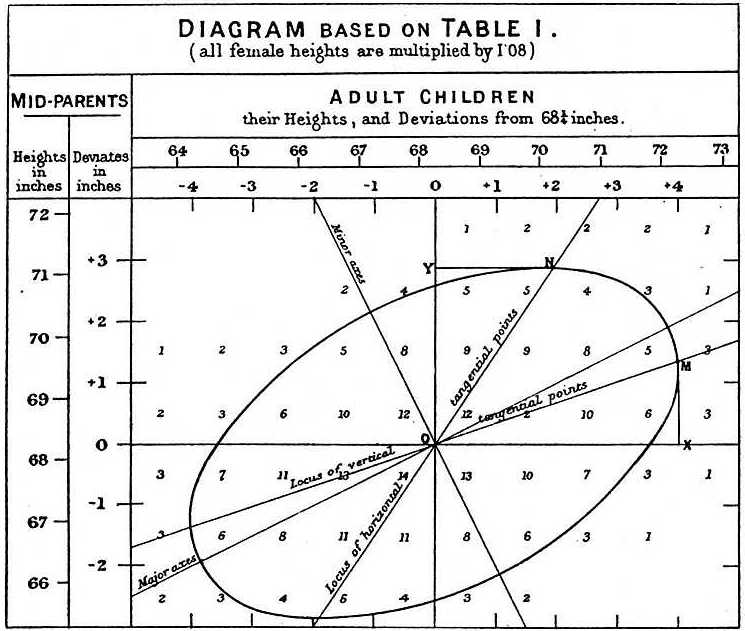
프랜시스 골턴은 1886년 성인과 그들의 부모 키 사이의 상관 관계를 그림으로 나타냈다.^[9] 성인 자녀의 키가 부모보다 평균 키에서 덜 벗어나는 경향(평균으로의 회귀) 현상을 관찰하여 회귀라는 이름을 붙였다.

독립 변수가 $\vec{x_i} = \left[x_1^i, x_2^i, \ldots, x_m^i\right]$이고 모델의 매개변수가 $\vec{\beta} = \left[\beta_0, \beta_1, \ldots, \beta_m\right]$이라고 가정하면, 모델의 예측은 다음과 같다.

:$y_i \approx \beta_0 + \sum_{j=1}^m \beta_j\times x_j^i$.

만약 $\vec{x_i}$가 $\vec{x_i} = \left[1, x_1^i, x_2^i, \ldots, x_m^i\right]$로 확장되면 $y_i$는 매개변수와 독립 벡터의 내적이 된다.

:$y_i \approx \sum_{j=0}^ m \beta_j \times x_j^i = \vec{\beta} \cdot \vec{x_i}$.

최소제곱법 설정에서 최적 매개변수 벡터는 평균 제곱 손실의 합을 최소화하도록 정의된다.

:$\vec{\hat{\beta}} = \underset{\vec{\beta}} \mbox{arg min}\,L\left(D, \vec{\beta}\right) = \underset{\vec{\beta}}\mbox{arg min} \sum_{i=1}^{n} \left(\vec{\beta} \cdot \vec{x_i} - y_i\right)^2$

최소 제곱합 외에도 최소 절대값법, 리지 회귀(L2 노름 페널티), 라쏘 회귀(L1 노름 페널티) 등 다양한 방법이 존재한다.

7. 1. 1. Ordinary least squares (OLS)

Ordinary least squares (OLS)는 가장 단순하고 많이 쓰이는 선형 회귀 추정 방법이다. 이 방법은 개념적으로 단순하며 계산이 간단하다는 장점을 가지고 있다. OLS 추정은 실험이나 관측치에 적용하고자 할 때 주로 사용된다.

OLS 기법은 오차의 제곱의 합을 최소화하는 방식으로, 추정하고자 하는 파라미터 $\vec{\beta}$는 다음과 같이 구할 수 있다.^[9]

:$\hat{\boldsymbol\beta} = (\mathbf{X}^{\rm T}\mathbf{X})^{-1} \mathbf{X}^{\rm T}\mathbf{y}

= \big(\,{\textstyle\sum} \mathbf{x}_i \mathbf{x}^{\rm T}_i \,\big)^{-1}

\big(\,{\textstyle\sum} \mathbf{x}_i y_i \,\big).$

오차가 유한한 분산을 가지고 독립 변수와 연관되어 있지 않다면, 추정은 편향되지 않고 일관성을 가진다.

:$\operatorname{E}[\,\mathbf{x}_i\varepsilon_i\,] = 0.$

프랜시스 골턴은 1886년 성인과 그들의 부모 키 사이의 상관 관계를 그림으로 나타냈다.^[9] 성인 자녀의 키가 부모보다 평균 키에서 덜 벗어나는 경향, 즉 "평균으로의 회귀" 현상을 관찰하여 회귀라는 이름을 붙였다.

독립 변수가 $\vec{x_i} = \left[x_1^i, x_2^i, \ldots, x_m^i\right]$이고 모델의 매개변수가 $\vec{\beta} = \left[\beta_0, \beta_1, \ldots, \beta_m\right]$이라고 가정하면, 모델의 예측은 다음과 같다.

:$y_i \approx \beta_0 + \sum_{j=1}^m \beta_j\times x_j^i$.

만약 $\vec{x_i}$가 $\vec{x_i} = \left[1, x_1^i, x_2^i, \ldots, x_m^i\right]$로 확장되면 $y_i$는 매개변수와 독립 벡터의 내적이 된다.

:$y_i \approx \sum_{j=0}^ m \beta_j \times x_j^i = \vec{\beta} \cdot \vec{x_i}$.

최소제곱법 설정에서 최적 매개변수 벡터는 평균 제곱 손실의 합을 최소화하도록 정의된다.

:$\vec{\hat{\beta}} = \underset{\vec{\beta}} \mbox{arg min}\,L\left(D, \vec{\beta}\right) = \underset{\vec{\beta}}\mbox{arg min} \sum_{i=1}^{n} \left(\vec{\beta} \cdot \vec{x_i} - y_i\right)^2$

독립 변수와 종속 변수를 각각 행렬 $X$와 $Y$에 넣으면 손실 함수는 다음과 같이 표현할 수 있다.

:$\begin{align}

L\left(D, \vec{\beta}\right)

&= \|X\vec{\beta} - Y\|^2 \\

&= \left(X\vec{\beta} - Y\right)^\textsf{T} \left(X\vec{\beta} - Y\right) \\

&= Y^\textsf{T}Y - Y^\textsf{T}X\vec{\beta} - \vec{\beta}^\textsf{T}X^\textsf{T} Y + \vec{\beta}^\textsf{T}X^\textsf{T} X\vec{\beta}

\end{align}$

손실 함수는 볼록 함수이므로 최적 해는 기울기가 0이 되는 지점에 존재한다. 손실 함수의 기울기는 다음과 같다 (분모 레이아웃 규칙 사용).

:$\begin{align}

\frac{\partial L\left(D, \vec{\beta}\right)}{\partial\vec{\beta}}

&= \frac{\partial \left(Y^\textsf{T}Y - Y^\textsf{T}X\vec{\beta} - \vec{\beta}^\textsf{T}X^\textsf{T}Y + \vec{\beta}^\textsf{T}X^\textsf{T}X\vec{\beta}\right)}{\partial \vec{\beta}} \\

&= -2X^\textsf{T}Y + 2X^\textsf{T}X\vec{\beta}

\end{align}$

기울기를 0으로 설정하면 최적 매개변수를 얻을 수 있다.

:\(\begin{align}

2X^\textsf{T}Y + 2X^\textsf{T}X\vec{\beta} &= 0 \\

\Rightarrow X^\textsf{T}X\vec{\beta} &= X^\textsf{T}Y \\

\Rightarrow \vec{\hat{\beta}} &= \left(X^\textsf{T}X\right)^{-1}X^\textsf{T}Y

\end{align}\)

카를 프리드리히 가우스는 1820년대에 최소제곱법을 발전시켰다. 이 방법은 교란항 $\varepsilon_i$의 거동에 대해 다음과 같은 가정을 한다 (가우스-마르코프 가정).

교란 $\varepsilon_i$의 기대값은 0이다.
:$E[\varepsilon] = 0 $
교란 $\varepsilon_i$는 서로 상관관계가 없다 (통계적 독립의 가정보다 약함).
:$\operatorname{cov}(\varepsilon_i, \varepsilon_j) = 0, \qquad i \ne j.$
교란 $\varepsilon_i$는 등분산이며, 모두 같은 분산을 갖는다 (가우스-마르코프 정리 참조).
:$V[\varepsilon_i] = \sigma^2, \qquad \forall i \isin [n].$

이러한 가정들은 최소제곱법이 최적의 파라미터 추정량을 제공함을 보장한다.

설명변수의 개수가 $p$개인 모델에서 선형 회귀로 결정해야 하는 파라미터는 계수 $\beta_1,..., \beta_p$와 절편 $\beta_0$를 포함하여 총 $p+1$개이다. 목적 변수와 설명 변수의 측정값 쌍 $(y_k; x_{k1},...,x_{kp})$을 하나의 데이터로 하고, $n$개의 데이터를 사용한 선형 회귀는 다음과 같이 나타낼 수 있다.

:$\begin{bmatrix}

y_{1} \\ y_{2} \\ \vdots \\ y_{n}

\end{bmatrix} =

\begin{bmatrix}

1 & x_{11} & x_{12} & \dots & x_{1p} \\

1 & x_{21} & x_{22} & \dots & x_{2p} \\

\vdots & \vdots & \vdots & & \vdots \\

1 & x_{n1} & x_{n2} & \dots & x_{np}

\end{bmatrix} \begin{bmatrix}

\beta_0 \\ \beta_1 \\ \vdots \\ \beta_p

\end{bmatrix} + \begin{bmatrix}

\varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_n

\end{bmatrix}$

위 연립 방정식은 행렬 표기를 사용하여 다음과 같이 나타낼 수 있다.

:$ Y = \mathbf{X}\beta + \varepsilon $

여기서 $Y$는 목적 변수의 관측값을 나타내는 $n$성분 열 벡터, $X$는 설명 변수의 관측값 및 절편 $\beta_0$의 계수(1)를 나타내는 $n \times (p+1)$ 행렬, $\beta$는 회귀 파라미터를 나타내는 $(p+1)$ 성분 열 벡터, $\varepsilon$는 관측마다의 교란을 나타내는 $n$ 성분 열 벡터이다.

$n=p$인 경우, 회귀 파라미터의 표준 오차는 산출할 수 없다. $n$이 $p$보다 작은 경우, 파라미터는 산출할 수 없다.

회귀 파라미터의 추정량은 다음과 같이 주어진다.

:$\widehat{\beta} =(\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top {\vec y}$

가우스-마르코프 정리에 의해 추정량$\widehat{\beta}$는 최량 선형 불편 추정량이 된다. 즉, 임의의 선형 불편 추정량 $\beta$에 대해 다음이 성립한다.

:$V[\beta] \geq V[\widehat{\beta}]$

회귀의 제곱합 $SSR$은 다음과 같이 주어진다.

:${\mathit{SSR} = \sum {\left( {\hat{y_i} - \bar y} \right)^2 } = {\hat\beta}^\top \mathbf{X}^\top \vec y - \frac{1}{n}\left( { {\vec y}^\top \vec u {\vec u}^\top \vec y} \right)}$

여기서 $\bar y = \frac{1}{n} \sum y_i$이며 $\vec u$는 $n$ × 1의 1 벡터(각 요소가 1)이다. 항 $\frac{1}{n} y^\top u u^\top y$는 $\frac{1}{n} (\sum y_i)^2$와 같다.

오차의 제곱합 $ESS$는 다음과 같이 주어진다.

:${\mathit{ESS} = \sum {\left( {y_i - \hat{y_i} } \right)^2 } = {\vec y}^\top \vec y - {\hat\beta}^\top \mathbf{X}^\top \vec y}$

제곱합의 전체 합 $TSS$는 다음과 같이 주어진다.

:${\mathit{TSS} = \sum {\left( {y_i - \bar y} \right)^2 } = \vec y^\top \vec y - \frac{1}{n}\left( { {\vec y}^\top \vec u {\vec u}^\top \vec y} \right) = \mathit{SSR}+ \mathit{ESS}}$

결정 계수, $R^2$는 다음과 같이 주어진다.

:${R^2 = \frac{\mathit{SSR}}{\mathit{TSS}}} = 1 - \frac{\mathit{ESS}}{\mathit{TSS}}}$

7. 1. 2. Generalized least squares (GLS)

일반화 최소제곱법(Generalized least squares, GLS)은 최소제곱법(OLS)을 확장한 방법으로, 모델의 오차들 간에 이분산성이나 상관성, 혹은 두 성질 모두 가질 때 ''β''를 더 효율적으로 예측할 수 있다. (이분산성이나 상관성의 형태는 데이터에 독립적이어야 한다.) 오차들이 서로 상관성이 없을 때 이분산성을 다루기 위해서 GLS는 OLS 회귀 결과로부터 잔차 제곱의 합으로 가중치를 최소화한다. 이때, ''i''번째 가중치는 var(''ε_i'')에 반비례한다. 이러한 GLS의 특별한 케이스를 "가중 최소제곱법(weighted least squares)"이라고 부른다. 추정 문제에 대한 GLS 솔루션은 다음과 같다.

:

\hat{\boldsymbol\beta} = (\mathbf{X}^{\rm T}\boldsymbol\Omega^{-1}\mathbf{X})^{-1}\mathbf{X}^{\rm T}\boldsymbol\Omega^{-1}\mathbf{y},

여기서 '''Ω'''는 오차에 대한 공분산 행렬이다. GLS는 데이터를 선형 변환하여 OLS에서의 가정들이 변형된 데이터에 만족하도록 한 것으로 볼 수 있다. GLS를 사용하려면 오차의 공분산 구조가 곱셈법 상수로 알려져야 한다.

7. 1. 3. Percentage least squares

Percentage least squares는 오차의 퍼센트를 줄이는 방법으로, 예측이나 시계열 데이터를 분석하는 분야에서 유용하게 쓰인다. OLS를 사용하면 상한선에서 큰 잔차가 우세한 값을 갖는 경우, 즉 종속 변수가 상수 분산을 가지지 않고 넓은 범위를 가질 때 유용하다. 오차의 퍼센티지나 상대 값이 표준 분포를 따를 때, percentage least squares 회귀 기법은 최대 가능도 추정을 제공한다. OLS는 가법 오차 모형과 관련있는 반면, 이 회귀 기법은 승법 오차 모형과 관련있다.^[47]

7. 1. 4. Iteratively reweighted least squares (IRLS)

IRLS는 모델의 오차 간에 이분산성이나 상관성이 존재하지만, 공분산 구조가 거의 알려지지 않을 때 사용된다.^[48] 첫 번째 반복에서 임시 공분산 구조를 가진 OLS(최소제곱법)나 GLS(일반화 최소제곱법)를 실행하여 잔차를 구한다. 이 잔차를 바탕으로 오차의 공분산 구조에 대한 향상된 추정치를 계산할 수 있다. 이 추정치를 사용하여 GLS를 실행, 가중치를 구한다. 이 과정은 수렴할 때까지 반복되지만, 대부분의 경우 한 번의 반복으로도 효율적인 추정치 ''β''를 얻을 수 있다.^[49]^[50]

7. 1. 5. Instrumental variables (IV)

IV 회귀 기법은 입력 변수가 오차와 상관성이 있을 때 사용된다. 이러한 경우, E['''z'''_''i''''ε''_''i''] = 0을 만족시키는 부가적인 ''instrumental variables'' '''z'''_''i''가 필요하다. 만약 Z가 행렬 형태의 instrument라면 추정량은 아래의 식과 같이 닫힌 형태로 주어진다.

:

\hat{\boldsymbol\beta} = (\mathbf{X}^{\rm T}\mathbf{Z}(\mathbf{Z}^{\rm T}\mathbf{Z})^{-1}\mathbf{Z}^{\rm T}\mathbf{X})^{-1}\mathbf{X}^{\rm T}\mathbf{Z}(\mathbf{Z}^{\rm T}\mathbf{Z})^{-1}\mathbf{Z}^{\rm T}\mathbf{y}.

이 회귀 기법은 전형적인 IV 회귀 기법을 확장한 것으로 E[''ε_i'''''z'''_''i''] = 0을 만족시키는 경우에 사용된다.

7. 1. 6. Total least squares (TLS)

총 최소제곱(Total Least Squares, TLS)^[51]은 최소제곱 추정 기법의 하나로, 독립 변수와 종속 변수를 보다 대칭적으로 다룬다. 이는 오차 변수 문제를 해결하는 한 방법으로, 독립 변수에 오차가 없다고 가정될 때 사용되기도 한다.

7. 2. 최대가능도방법

최대가능도방법(Maximum Likelihood Method, MLE)은 주어진 데이터에서 어떤 모델의 매개변수를 추정하는 방법 중 하나이다. 선형 회귀에서는 이 방법을 통해 최적의 회귀 계수를 찾을 수 있다.

선형 회귀에서 최대가능도추정법을 사용하기 위해서는, 종속 변수

y

가 정규 분포를 따르는 확률 변수라고 가정한다. 이때

y

의 평균은 독립 변수

\vec{x}

의 선형 조합으로 표현되며, 표준 편차는 고정된 값으로 가정한다.

데이터 집합

D

가 주어지고, 각 데이터 포인트가

(\vec{x_i}, y_i)

형태로 표현될 때, 선형 회귀의 목표는 다음 비용 함수를 최소화하는 매개변수

\vec{\beta}

를 찾는 것이다.

:

L(D, \vec{\beta}) = \sum_i(y_i - \vec{\beta} \, \cdot \, \vec{x_i})^2

이 식에서

y_i

는 종속 변수,

\vec{x_i}

는 독립 변수,

\vec{\beta}

는 회귀 계수 벡터를 나타낸다.

위의 비용 함수를 최소화 하는 대신, 가능도 함수

H(D, \vec{\beta})

를 최대화하는 문제로 변환할 수 있다.^[12]

:

H(D, \vec{\beta}) = \prod_{i=1}^{n}Pr(y_i|\vec{x_i}\,\,;\vec{\beta}, \sigma) = \prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{\left(y_i - \vec{\beta} \, \cdot \, \vec{x_i} \right)^2}{2\sigma^2}\right)

이 가능도 함수를 최대화하는 것은 계산 상 어려움이 있을 수 있으므로, 로그 함수를 사용하여 로그 가능도 함수

I(D, \vec{\beta})

를 최대화하는 문제로 변환한다. 로그 함수는 단조 증가 함수이므로, 로그 가능도를 최대화하는 것은 원래의 가능도를 최대화하는 것과 같다.^[12]

:

I(D, \vec{\beta}) = \log\prod_{i=1}^{n}Pr(y_i|\vec{x_i}\,\,;\vec{\beta}, \sigma) = n\log\frac{1}{\sqrt{2\pi}\sigma} - \frac{1}{2\sigma^2}\sum_{i=1}^n \left(y_i - \vec{\beta} \, \cdot \, \vec{x_i} \right)^2

결과적으로,

I(D, \vec{\beta})

를 최대화하는 매개변수

\vec{\hat{\beta}}

는

L(D, \vec{\beta})

를 최소화하는 매개변수와 동일하다. 즉, 선형 회귀에서 최소제곱법의 결과는 최대가능도추정법의 결과와 같다.^[12]

만약

p(y_i | \mathbf{x_i}, \theta)

가 가우시안 분포를 따른다고 가정하면, 다음과 같은 로그 가능도 함수를 구할 수 있다.

:

l(\theta) =  \sum_{i=1}^{N} \log[ (  \frac{1}{ 2\pi\sigma^{2} })^{2}  exp(-\frac{1}{2\sigma^{2}} (y_i - \boldsymbol\beta^{T} \mathbf{x_i})^{2}  )   ]

:

= - \frac{N}{2} \log(2\pi\sigma^{2})  - \frac{1}{2\sigma^{2}} \sum_{i = 1}^{N} {(y_i - \boldsymbol\beta^{T} \mathbf{x_i})^{2}}

최대 우도 추정은 오차항의 분포가 특정 모수적 가족 ''ƒ_θ''의 확률 분포에 속하는 것으로 알려진 경우 수행될 수 있다.^[11] ''f''_θ가 평균이 0이고 분산이 θ인 정규 분포일 때, 결과 추정치는 OLS 추정치와 동일하다.

7. 2. 1. 최대 가능도 추정 (MLE : Maximum likelihood estimation )

매개변수

\theta

(즉,

\theta =(\beta, \sigma^{2})

)의 argmax는 다음과 같다.

:

\underset{\theta}{\arg\max} \log(p(D|\theta)) = \sum_{i=1} \log(p(y_i | \mathbf{x_i}, \theta))

만약

p(y_i | \mathbf{x_i}, \theta)

가 가우시안 분포를 따른다고 가정하면,

:

p(y_i | \mathbf{x_i}, \theta) = \mathcal{N}(y| \boldsymbol\beta^{T} \mathbf{x},\sigma^{2})

다음과 같은 로그 가능도 함수를 구할 수 있다.

:

l(\theta) =  \sum_{i=1}^{N} \log[ (  \frac{1}{ 2\pi\sigma^{2} })^{2}  exp(-\frac{1}{2\sigma^{2}} (y_i - \boldsymbol\beta^{T} \mathbf{x_i})^{2}  )   ]

:

= - \frac{N}{2} \log(2\pi\sigma^{2})  - \frac{1}{2\sigma^{2}} \sum_{i = 1}^{N} {(y_i - \boldsymbol\beta^{T} \mathbf{x_i})^{2}}

위 식의 음수를 취한 음 로그 가능도 함수(NLL : negative log likelihood)는 아래와 같다.

:

NLL(\theta)= \frac{N}{2} \log(2\pi\sigma^{2})  + \frac{1}{2\sigma^{2}} \sum_{i = 1}^{N} {(y_i - \boldsymbol\beta^{T} \mathbf{x_i})^{2}}

NLL의 최솟값을 구하기 위해서는 위 식에서 아래의 부분을 최소화하면 된다.

:

RSS(\beta)= \sum_{i = 1}^{N} {(y_i - \boldsymbol\beta^{T} \mathbf{x_i})^{2}}

위 식은 잔차제곱합(RSS : Residual Sum of Squares)이며, 이를 통해 최적의

\boldsymbol\hat{\beta}

을 구할 수 있다.

최대 우도 추정은 오차항의 분포가 특정 모수적 가족 ''ƒ_θ''의 확률 분포에 속하는 것으로 알려진 경우 수행될 수 있다.^[11] ''f''_θ가 평균이 0이고 분산이 θ인 정규 분포일 때, 결과 추정치는 OLS 추정치와 동일하다. GLS 추정치는 ε가 알려진 공분산 행렬을 가진 다변량 정규 분포를 따를 때 최대 우도 추정치이다.

각 데이터 포인트를

(\vec{x_i}, y_i)

로, 회귀 매개변수를

\vec{\beta}

로, 모든 데이터 집합을

D

로, 비용 함수를

L(D, \vec{\beta}) = \sum_i(y_i - \vec{\beta} \, \cdot \, \vec{x_i})^2

로 나타내자.

L(D, \vec{\beta})

를 최소화하는 동일한 최적 매개변수는 최대 우도 또한 달성한다.^[12] 여기서의 가정은 종속 변수

y

가 정규 분포를 따르는 확률 변수이며, 표준 편차는 고정되어 있고 평균은

\vec{x}

의 선형 조합이라는 것이다.

:

\begin{align}H(D, \vec{\beta}) &= \prod_{i=1}^{n}Pr(y_i|\vec{x_i}\,\,;\vec{\beta}, \sigma) \\ &= \prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{\left(y_i - \vec{\beta} \, \cdot \, \vec{x_i} \right)^2}{2\sigma^2}\right)\end{align}

이제 이 우도 함수를 최대화하는 매개변수를 찾아야 한다. 로그 함수는 엄격하게 증가하므로, 이 함수를 최대화하는 대신, 그 로그를 최대화하여 최적 매개변수를 찾을 수도 있다.^[12]

\begin{align}I(D, \vec{\beta}) &= \log\prod_{i=1}^{n}Pr(y_i|\vec{x_i}\,\,;\vec{\beta}, \sigma) \\ &= \log\prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{\left(y_i - \vec{\beta} \, \cdot \, \vec{x_i} \right)^2}{2\sigma^2}\right) \\ &= n\log\frac{1}{\sqrt{2\pi}\sigma} - \frac{1}{2\sigma^2}\sum_{i=1}^n \left(y_i - \vec{\beta} \, \cdot \, \vec{x_i} \right)^2\end{align}

따라서 최적 매개변수는 다음과 같다.^[12]

\begin{align}\underset{\vec{\beta}}\mbox{arg max}\, I(D, \vec{\beta}) &= \underset{\vec{\beta}}\mbox{arg max} \left(n\log\frac{1}{\sqrt{2\pi}\sigma} - \frac{1}{2\sigma^2}\sum_{i=1}^n \left(y_i - \vec{\beta} \, \cdot \, \vec{x_i} \right)^2\right) \\ &= \underset{\vec{\beta}}\mbox{arg min} \sum_{i=1}^n \left(y_i - \vec{\beta} \, \cdot \, \vec{x_i} \right)^2 \\ &= \underset{\vec{\beta}}\mbox{arg min} \,L(D, \vec{\beta}) \\ &= \vec{\hat{\beta}}\end{align}

이러한 방식으로, '''

H(D, \vec{\beta})

'''를 최대화하는 매개변수는 '''

L(D, \vec{\beta})

'''를 최소화하는 매개변수와 동일하다. 즉, 선형 회귀에서 최소 제곱법의 결과는 최대 우도 추정법의 결과와 동일하다.^[12]

7. 2. 2. 능형 회귀 분석(Ridge regression)

가중치에 대한 사전 확률로 평균이 0인 가우시안 분포를 가정하면, 최대 사후 확률(MAP) 추정치는 다음 식을 최소화하는 해를 갖는다.

:

J(w) = \frac{1}{N} \sum_{i=1} ^ {N}(y_i - (\beta_{0} + \boldsymbol\beta^{T}\mathbf{x_i}))^{2}+\lambda||\boldsymbol\beta||_{2}^{2}, \lambda = \frac{\sigma^{2}}{\tau^{2}},||\boldsymbol\beta||_{2}^{2} = \sum_{j}\beta_{j}^{2} = \boldsymbol\beta^{T} \boldsymbol\beta

이 식에서 첫 번째 항은 최대가능도추정의 음로그가능도함수(NLL)와 같고, 두 번째 항은 가중치의 크기에 대한 제약 조건, 즉 복잡도 제약 조건에 해당한다. 이 해는 다음과 같이 표현된다.

:

\boldsymbol \hat{\beta} = (\lambda \boldsymbol{I_D + X^{T}X})^{-1} \boldsymbol{X^{T}y}

릿지 회귀^[13]^[14]^[15]는 편향을 도입하여 추정치의 분산을 줄이는 방법이다. Lasso 회귀^[16]와 같이 벌점(penalty)을 부과하는 다른 방법들도 비슷한 효과를 낼 수 있다. 릿지 회귀는 특히 다중공선성이 있거나 과적합이 우려되는 경우에 유용하며, 아직 관측되지 않은 예측 변수에 대한 반응 변수의 값을 예측하는 데 주로 사용된다. 하지만 편향 때문에 추론이 목표일 때는 잘 사용되지 않는다.

선형 회귀 모델은 보통 최소제곱법으로 적합하지만, 릿지 회귀나 라쏘 회귀처럼 비용 함수에 벌점을 추가하는 방법도 사용될 수 있다.

7. 2. 3. 최소 절대 편차

최소 절대 편차(LAD)는 이상치가 있을 때 OLS보다 덜 민감하게 반응하는 방법이다(단, 이상치가 없으면 OLS보다 비효율적이다). 이는 ''ε'' 라플라스 분포 모델의 최대가능도추정(Maximun Likelihood Estimation)과 같다.^[52] 최소 절대 편차(LAD) 회귀는 강건 회귀의 한 기법으로, 이상치가 있을 때 덜 민감하다는 점에서 OLS보다 뛰어나다. (하지만 이상치가 없을 때는 OLS보다 효율이 떨어진다.)^[17]

7. 2. 4. 적응 추정(Adaptive estimation)

오차항이 회귀값

\varepsilon_i \perp \mathbf{x}_i

으로부터 독립이라고 가정할 때, 최적 검출기는 2단계 MLE로 얻을 수 있으며, 첫 번째 단계는 오차항의 분포에 대한 비모수 추정이다.^[53] 오차항이 독립 변수

\varepsilon_i \perp \mathbf{x}_i

와 독립이라고 가정하면 최적의 추정기는 2단계 MLE이며, 첫 번째 단계는 오차항의 분포를 비모수적으로 추정하는 데 사용된다.^[18]

7. 3. 기타 선형 회귀 추정 기법

'''베이시안 선형 회귀'''는 베이시안 통계의 틀을 선형 회귀에 적용한다. 회귀 계수 β는 지정된 사전 분포를 갖는 확률 변수로 간주된다. 사전 분포는 릿지 회귀 또는 라쏘 회귀와 유사한 방식으로 회귀 계수에 대한 해를 편향시킬 수 있다. 베이시안 추정 과정은 회귀 계수의 "최적" 값에 대한 단일 점 추정치가 아닌 전체 사후 분포를 생성하여 불확실성을 설명한다.
'''분위수 회귀'''는 ''X''가 주어졌을 때 ''y''의 조건부 평균이 아닌 조건부 분위수에 초점을 맞춘다. 선형 분위수 회귀는 특정 조건부 분위수(예: 조건부 중앙값)를 예측 변수의 선형 함수 β^T''x''로 모델링한다.
'''혼합 모형'''은 종속 데이터가 포함된 선형 회귀 관계를 분석하는 데 널리 사용된다. 일반적인 응용 분야에는 종단 데이터와 같이 반복 측정이 포함된 데이터 또는 클러스터 표본 추출을 통해 얻은 데이터의 분석이 포함된다. 일반적으로 최대 가능도 또는 베이시안 추정을 사용하여 모수적 모형으로 적합된다. 오차가 정규 분포 확률 변수로 모델링되는 경우, 혼합 모형과 일반화된 최소 제곱 사이에는 밀접한 관련이 있다.^[19]
'''주성분 회귀'''(PCR)^[20]^[21]는 예측 변수의 수가 많거나 예측 변수 간에 강한 상관 관계가 존재할 때 사용된다. 이 2단계 절차는 먼저 주성분 분석을 사용하여 예측 변수를 줄인 다음 OLS 회귀 적합에 축소된 변수를 사용한다.
'''최소 각도 회귀'''^[22]는 관측치보다 더 많은 공변량을 가질 수 있는 고차원 공변량 벡터를 처리하기 위해 개발된 선형 회귀 모형에 대한 추정 절차이다.
'''바일-센 추정량'''은 적합선의 기울기를 표본 점 쌍을 통과하는 선의 기울기의 중앙값으로 선택하는 간단한 강건 추정 기술이다. 단순 선형 회귀와 유사한 통계적 효율성 속성을 갖지만 이상치에 훨씬 덜 민감하다.^[23]

8. 선형 회귀의 응용

선형 회귀는 생물학, 행동 과학, 사회과학 분야에서 변수 간의 관계를 설명하는 데 널리 사용되며, 이 분야에서 가장 중요한 도구 중 하나로 여겨진다. 선형 회귀는 크게 두 가지 목적으로 활용된다.

예측 및 예상: 반응 변수와 설명 변수 값의 관측된 데이터 집합에 예측 모델을 적합시켜, 설명 변수의 추가 값을 수집했을 때 반응 변수를 예측할 수 있다.
변동 설명: 반응과 설명 변수의 관계 강도를 정량화하여, 각 설명 변수가 반응과 선형 관계를 갖는지, 또는 어떤 설명 변수 하위 집합에 반응에 관한 중복된 정보가 포함되어 있는지 판단할 수 있다.

선형 최소제곱법 응용 분야도 참고.

8. 1. 추세 분석

생물학, 행동학, 경제학 및 기타 사회과학에서 변수들 사이의 관계를 설명하고자 할 때, 선형 회귀를 사용한다. 예를 들어, 추세 분석, 역학 조사, 재무 관리, 경제학에 응용된다.

추세선은 데이터를 시간 축으로 놓고 봤을 때, 데이터의 값이 장기적으로 어떻게 변하는지 직선으로 표현한 것이다. 추세선은 특정 데이터 집합(GDP, 원유 가격 또는 주식 가격 등)에서 값이 증가세에 있는지 감소세에 있는지 보여준다. 이러한 데이터의 추세는 데이터를 눈으로 확인하는 것만으로도 추정 가능하지만, 더 정확하게는 선형 회귀를 사용해 추세선을 그릴 수 있다. 추세선은 일반적으로 직선이며, 경우에 따라 더 높은 차수의 곡선을 사용하기도 한다.

경영 분석에서 시간에 따른 데이터 변화를 보고자 추세선을 사용하기도 한다. 추세선을 사용하면 특정 사건이 값에 미치는 영향을 매우 간단하게 확인할 수 있다. 추세선을 그리는 것은 대조군이 필요하지도 않고, 실험 설계가 필요하지도 않으며 간단하다는 장점이 있다. 하지만 과학적인 검증이 부족해, 예상한 것 이외의 요인이 잠재적으로 데이터에 미치는 영향은 놓칠 수 있다.

8. 2. 역학 조사

생물학, 행동학, 경제학 및 기타 사회과학에서 변수들 사이의 관계를 설명하고자 할 때, 선형 회귀를 사용한다. 예를 들어, 추세 분석·역학 조사·재무 관리·경제학에 응용된다.

흡연률과 사망률, 유병률 간의 연관성에 대한 증거는 회귀 분석을 적용한 관찰 연구에서 확인되었다. 관찰한 데이터에서 확신할 수 없는 상관 관계를 제거하기 위해, 연구자들은 일반적으로 실제로 관심있는 변수 외에도 여러 개의 변수를 삽입해 회귀 분석 모델을 수립한다. 예를 들어, 흡연률과 수명의 상관관계를 보고싶을때, 연구자들은 실제로 관심있는 독립 변수인 흡연률 외에도 사회경제적 조건 등을 독립 변수에 추가적으로 삽입해, 사회경제적 조건이 수명과 연관이 있는지 확인한다. 하지만 모든 가능한 변수를 추가할 수는 없으므로, 랜덤 통제 실험을 통해 상관관계를 조사하기도 한다.^[1]

초기 흡연과 사망률 및 이환율 간의 연관성에 대한 증거는 회귀 분석을 활용한 관찰 연구에서 나왔다. 관찰 데이터를 분석할 때 허위 상관 관계를 줄이기 위해, 연구자들은 일반적으로 주요 관심 변수 외에도 여러 변수를 회귀 모델에 포함한다. 예를 들어, 흡연을 주요 독립 변수로 하고, 기대 수명을 연 단위로 측정한 것을 종속 변수로 하는 회귀 모델에서 연구자들은 교육 수준과 소득을 추가적인 독립 변수로 포함하여, 흡연이 기대 수명에 미치는 관찰된 효과가 다른 사회 경제적 지위 요인에 기인하지 않도록 할 수 있다. 그러나 모든 가능한 교란 변수를 실증 분석에 포함하는 것은 불가능하다. 예를 들어, 가상의 유전자가 사망률을 높이고, 사람들의 흡연량을 증가시킬 수도 있다. 이러한 이유로, 무작위 대조 실험은 관찰 데이터의 회귀 분석을 사용하여 얻을 수 있는 것보다 더 설득력 있는 인과 관계의 증거를 생성할 수 있는 경우가 많다. 통제된 실험이 불가능할 경우, 도구 변수 회귀와 같은 회귀 분석의 변형을 사용하여 관찰 데이터로부터 인과 관계를 추정하려고 시도할 수 있다.^[1]

8. 3. 재무 관리

자본자산 가격결정 모형에서 체계적 위험은 베타에 대한 선형 회귀로 표현한다.^[1] 자본 자산 가격 모델은 투자의 체계적 위험을 분석하고 정량화하기 위해 선형 회귀와 베타 개념을 사용하는데, 이는 투자 수익률과 모든 위험 자산의 수익률을 관련시키는 선형 회귀 모델의 베타 계수에서 직접적으로 도출된다.^[1]

8. 4. 경제학

선형 회귀는 경제학에서 경험적인 데이터를 통해 미래를 예측하고자 할 때 주로 사용된다. 비용 예측^[54], 고정 투자 예측, 재고 관리 예측, 필요 유동 자산 예측^[55], 노동 수요 예측^[56], 노동 공급 예측^[56] 등에 선형 회귀를 사용할 수 있다.

선형 회귀는 경제학에서 지배적인 경험적 도구이다. 예를 들어, 소비 지출^[24], 고정 투자 지출, 재고 투자, 국가의 수출 구매^[25], 수입 지출^[25], 유동 자산 보유 수요^[26], 노동 수요^[27], 노동 공급을 예측하는 데 사용된다.^[27]

선형 회귀는 많은 실용적인 용도가 있으며, 크게 다음 두 가지 용도로 분류된다.

예측, 예상 또는 오류 감소를 목적으로 한다.
설명 변수의 변동에 기인하는 반응 변수의 변동을 설명하는 것을 목적으로 한다.

참조

_[1] 서적 Statistical Models: Theory and Practice Cambridge University Press
_[2] 간행물 Methods of Multivariate Analysis https://books.google[...] John Wiley & Sons 2015-02-07
_[3] 웹사이트 Linear Regression in Machine learning https://www.geeksfor[...] 2018-09-13
_[4] 간행물 Linear Regression Analysis: Theory and Computing https://books.google[...] World Scientific 2015-02-07
_[5] 논문 Regression Analysis: A Constructive Critique
_[6] 논문 Multivariate or Multivariable Regression? 2012-11-15
_[7] 논문 The Identification of a Particular Nonlinear Time Series System
_[8] 논문 Group least squares regression for linear models with strongly correlated predictor variables
_[9] 논문 Regression Towards Mediocrity in Hereditary Stature. https://www.jstor.or[...] 1886
_[10] 논문 The Linear Template Fit
_[11] 논문 Robust Statistical Modeling Using the t Distribution https://cloudfront.e[...] 2019-09-02
_[12] Webarchive Machine learning: a probabilistic perspective https://doc.lagout.o[...]
_[13] 논문 Geometry of Ridge Regression Illustrated
_[14] 논문 Ridge Regression and James-Stein Estimation: Review and Comments
_[15] 논문 Practical Use of Ridge Regression: A Challenge Met
_[16] 논문 Regression Shrinkage and Selection via the Lasso
_[17] 논문 The Minimum Sum of Absolute Errors Regression: A State of the Art Survey
_[18] 논문 Adaptive maximum likelihood estimators of a location parameter
_[19] 논문 Multilevel Mixed Linear Model Analysis Using Iterative Generalized Least Squares
_[20] 논문 On the Investigation of Alternative Regressions by Principal Component Analysis
_[21] 논문 A Note on the Use of Principal Components in Regression
_[22] 논문 Least Angle Regression
_[23] 논문 A rank-invariant method of linear and polynomial regression analysis. I, II, III
_[24] 서적 Understanding Consumption Oxford University Press
_[25] 서적 International Economics: Theory and Policy Pearson
_[26] 서적 The Demand for Money: Theories, Evidence, and Problems Harper Collins
_[27] 서적 Modern Labor Economics Addison-Wesley
_[28] 논문 A review of land-use regression models to assess spatial variation of outdoor air pollution https://www.scienced[...] 2008-10-01
_[29] 논문 A Systematic Review of Methodology: Time Series Regression Analysis for Environmental Factors and Infectious Diseases https://www.jstage.j[...] 2024-02-03
_[30] 논문 Regression and stochastic models for air pollution—I. Review, comments and suggestions https://dx.doi.org/1[...] 2024-05-07
_[31] 논문 Air Quality Modeling with the Use of Regression Neural Networks 2024-12-08
_[32] 웹사이트 Behind the Model: CDC's Tools to Assess Epidemic Trends https://www.cdc.gov/[...] 2024-11-14
_[33] 논문 Causal Thinking: Uncovering Hidden Assumptions and Interpretations of Statistical Analysis in Building Science 2024
_[34] 웹사이트 Linear Regression (Machine Learning) https://people.cs.pi[...] 2018-06-21
_[35] 서적 The History of Statistics: The Measurement of Uncertainty before 1900 https://archive.org/[...] Harvard
_[36] 문서
_[37] 문서
_[38] 웹사이트 有意に無意味な話: 重回帰モデルの最尤推定量と誤差分散の不偏推定量 https://starpentagon[...] 2020-08-14
_[39] 서적 現代数理統計学の基礎共立出版 2017-04-05
_[40] 웹사이트 有意に無意味な話: 重回帰モデルでの「回帰係数／誤差分散の確率分布」の導出 https://starpentagon[...] 2020-08-14
_[41] 웹사이트 有意に無意味な話: 重回帰モデルでの回帰係数の有意性検定 https://starpentagon[...] 2020-08-14
_[42] 웹사이트 有意に無意味な話: 重回帰モデルの信頼区間 https://starpentagon[...] 2020-08-14
_[43] 웹사이트 有意に無意味な話: 重回帰モデルの予測区間 https://starpentagon[...] 2020-08-14
_[44] 서적 Statistical Models: Theory and Practice Cambridge University Press
_[45] 인용 Methods of Multivariate Analysis https://books.google[...] John Wiley & Sons
_[46] 인용 Linear Regression Analysis: Theory and Computing https://books.google[...] World Scientific
_[47] 저널 Least Squares Percentage Regression http://papers.ssrn.c[...]
_[48] 저널 The Unifying Role of Iterative Generalized Least Squares in Statistical Algorithms https://archive.org/[...]
_[49] 저널 Adapting for Heteroscedasticity in Linear Models
_[50] 저널 Robust, Smoothly Heterogeneous Variance Regression https://archive.org/[...]
_[51] 저널 Total Least Squares: State-of-the-Art Regression in Numerical Analysis
_[52] 저널 The Minimum Sum of Absolute Errors Regression: A State of the Art Survey
_[53] 저널 Adaptive maximum likelihood estimators of a location parameter https://archive.org/[...]
_[54] 서적 Understanding Consumption https://archive.org/[...] Oxford University Press
_[55] 저널 The Demand for Money: Theories, Evidence, and Problems Harper Collins
_[56] 서적 Modern Labor Economics Addison-Wesley
_[57] 웹인용 EEMP webpage https://web.archive.[...] 2010-03-03

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com